第4章 非平稳序列的随机分析
非平稳时间序列建模步骤

非平稳时间序列建模步骤介绍非平稳时间序列是指其统计特性在时间上发生变化的序列。
在实际应用中,我们经常面临非平稳时间序列的建模问题,如股票价格、气温变化等。
本文将探讨非平稳时间序列建模的步骤和方法。
为什么要建立模型非平稳时间序列在其统计特性的变化中存在一定的规律性,因此建立模型可以帮助我们理解和预测序列的行为。
模型可以从数据中提取有用的信息,揭示序列的规律和动态特征。
步骤一:观察时间序列的特性在建立模型之前,我们首先需要观察时间序列的特性,包括趋势、周期性、季节性和随机性等。
这些特性是决定时间序列模型选择的重要因素。
步骤二:平稳化处理由于非平稳时间序列的统计特性随时间变化,不利于建模和分析。
因此,我们需要对时间序列进行平稳化处理。
常用的平稳化方法包括差分法和变换法。
2.1 差分法差分法是通过计算相邻两个观测值的差异来实现序列的平稳化。
一阶差分是指相邻观测值之间的差异,二阶差分是指一阶差分的差异,以此类推。
差分法可以有效地去除序列的趋势和季节性,使序列平稳。
2.2 变换法变换法是通过对时间序列进行数学变换,将非平稳序列转化为平稳序列。
常用的变换方法包括对数变换、平方根变换和 Box-Cox 变换等。
变换法可以改变序列的分布特性,使序列满足平稳性的要求。
步骤三:选择模型平稳化处理后,我们需要选择合适的模型进行建模。
常用的时间序列模型包括自回归移动平均模型(ARMA)、自回归积分移动平均模型(ARIMA)、季节性自回归移动平均模型(SARIMA)和指数平滑模型等。
3.1 自回归移动平均模型(ARMA)ARMA 模型是描述时间序列随机变动的经典模型,其包括自回归和移动平均两个部分。
自回归部分考虑了序列的历史值对当前值的影响,移动平均部分考虑了序列的误差对当前值的影响。
ARMA 模型适用于没有趋势和季节性的平稳序列。
3.2 自回归积分移动平均模型(ARIMA)ARIMA 模型是在 ARMA 模型基础上引入了积分项,用于处理非平稳序列。
现代信号处理思考题(含答案)

第一章 绪论1、 试举例说明信号与信息这两个概念的区别与联系。
信息反映了一个物理系统的状态或特性,是自然界、人类社会和人类思维活动中普遍存在的物质和事物的属性。
信号是传载信息的物理量是信息的表现形式,如文字、语言、图像等。
如人们常用qq 聊天,即是用文字形式的信号将所要表达的信息传递给别人。
2、 什么是信号的正交分解?如何理解正交分解在机械故障诊断中的重要价值?P9正交函数的定义信号的正交分解如傅里叶变换、小波分解等,即将信号分解成多个独立的相互正交的信号的叠加。
从而将信号独立的分解到不同空间中去,通常指滤波器频域内正交以便于故障分析和故障特征的提取。
傅里叶变换将信号分解成各个正交的傅里叶级数,将信号从时域转换到频域从而得到信号中的各个信号的频率。
正交小波变换能够将任意信号(平稳或非平稳)分解到各自独立的频带中;正交性保证了这些独立频带中状态信息无冗余、无疏漏,排除了干扰,浓缩了了动态分析与监测诊断的信息。
3、 为什么要从内积变换的角度来认识常见的几种信号处理方法?如何选择合适的信号处理方法?在信号处理各种运算中内积变换发挥了重要作用。
内积变换可视为信号与基函数关系紧密程度或相似性的一种度量。
对于平稳信号,是利用傅里叶变换将信号从时域变为频域函数实现的方式是信号函数x (t )与基函数i t e ω 通过内积运算。
匹配出信号x (t )中圆频率为w 的正弦波.而非平稳信号一般会用快速傅里叶变换、离散小波变换、连续小波变换等这些小波变换的内积变换内积运算旨在探求信号x (t )中包含与小波基函数最相关或最相似的分量。
“特征波形基函数信号分解”旨在灵活运用小波基函数 去更好地处理信号、提取故障特征。
用特定的基函数分解信号是为了获得具有不同物理意义的分类信息。
不同类型的机械故障会在动态信号中反应出不同的特征波形,如旋转机械失衡振动的波形与正弦波形有关,内燃机爆燃振动波形是具有钟形包络的高频波;齿轮轴承等机械零部件出现剥落。
时序—序列平稳、纯随机性检验

上机练习一上机时间: 2012年09月28日学号 200930980106 姓名何斌年级专业 10统计1班数据:问题1:以下数据是1975-1980年某火山每月释放的CO2330.45 330.97 331.64 332.87 333.61 333.55331.90 330.05 328.58 328.31 329.41 330.63331.63 332.46 333.36 334.45 334.82 334.32333.05 330.87 329.24 328.87 330.18 331.50332.81 333.23 334.55 335.82 336.44 335.99334.65 332.41 331.32 330.73 332.05 333.53334.66 335.07 336.33 337.39 337.65 337.57336.25 334.39 332.44 332.25 333.59 334.76335.89 336.44 337.63 338.54 339.06 338.95337.41 335.71 333.68 333.69 335.05 336.53337.81 338.16 339.88 340.57 341.19 340.87339.25 337.19 335.49 336.63 337.74 338.36(1)绘制该序列时序图,并判断该序列是否平稳。
(2)绘制该样本自相关图,并解释该图形。
SAS程序代码如下:data co2;input num @@;time=intnx('month','01jan1975'd,_n_-1);format time monyy.;cards;330.45 330.97 331.64 332.87 333.61 333.55 331.90 330.05 328.58 328.31 329.41 330.63 331.63 332.46 333.36 334.45 334.82 334.32 333.05 330.87 329.24 328.87 330.18 331.50 332.81 333.23 334.55 335.82 336.44 335.99 334.65 332.41 331.32 330.73 332.05 333.53 334.66 335.07 336.33 337.39 337.65 337.57 336.25 334.39 332.44 332.25 333.59 334.76 335.89 336.44 337.63 338.54 339.06 338.95 337.41 335.71 333.68 333.69 335.05 336.53 337.81 338.16 339.88 340.57 341.19 340.87 339.25 337.19 335.49 336.63 337.74 338.36 ;proc gplot data=co2;plot num*time;symbol i=join v=star cv=red ci=green;proc arima data=co2;identify var=num nlag=24;run;得到该序列的时序图如下:结果分析:该序列有周期波动且有单调上升趋势,故初步判断该序列为非平稳序列。
平稳信号与非平稳信号的概念与区别

平稳信号与⾮平稳信号的概念与区别在统计学⾥,平稳序列因其具有良好的统计特性和处理的⽅便性⽽成为时间序列分析的基础,然⽽我们所能观测到的序列经常受某些因素的影响⽽表现出⾮平稳性。
经典时间序列的分析中处理这类⾮平稳序列的主要思路是通过某些预处理的⽅法将其转化为平稳序列后再做分析。
根据统计学对平稳时间序列的定义可以知道平稳时间序列也有严平稳时间序列和宽平稳时间序列之分。
严平稳时间序列的任何有限维联合分布对于时间的平移是不变的。
宽平稳时间序列中的均值、⽅差与时间⽆关,任何时刻的序列和平移若⼲步后的序列有相同的协⽅差。
但是在⼯程应⽤领域的研究对于时间序列的平稳性定义较统计学弱,即平稳时间序列中其均值和⽅差都与时间⽆关,且⾃协⽅差函数只与时间间隔有关。
常见的平稳性检验⽅法有时序图判断法、⾃相关系数检验法、分段检验法、游程检验法以及ADF单位根检验法。
通过观察信号的可视化结果,因此根据时序图判断法可以得知电压⽐信号(序列)是⼀个⾮平稳序列。
在统计学领域处理⾮平稳的⽅法有确定性性因素分解法和随机性序列差分法。
在实际的⼯程应⽤⾥,主要是分析时间序列的⼀种,即信号。
从信号的统计性能描述的⾓度,信号可以被分为确定信号和随机信号。
确定信号可以使⽤数学表达式来描述,其数学统计特性能够确定。
随机信号⼜称不确定信号,⽆法⽤确定的时间函数来表达信号。
随机信号不能⽤确定的数学关系式描述,任何⼀次观测只代表其在变动范围内可能产⽣的结果之⼀,其值的变动服从统计规律。
从严格的意义上来讲,对信号平稳性的讨论前提是该信号必须为随机信号。
随机信号的平稳与⾮平稳的区别是集合总体意义统计的不同,⽽不是时间意义统计的不同。
在信号处理中,处理⾮平稳的主要⽅法有⾃适应滤波、短时傅⾥叶变换、短时⾃回归滑动平均参数谱、参数谱和时频分析等。
上述⼏种处理⾮平稳的⽅法的⽬的是去掉或抑制确定性因素的影响,⽽各态历经过程的参数则借助处理⽅法所隐含的时域平均来估计。
第一章 随机序列

第一章 随机序列前言:这一章是本书的预备知识. 我们借助于实例,用较通俗的语言引入平稳随机序列的概念. 然后介绍平稳随机序列的描述方法,并且对平稳序列中的“频谱分析方法”、“相关分析方法”及“参数化方法”之间的关系给予简要说明. 另外,还将介绍两种常用的估计方法,以备后用.讨论描述随机过程的方法必须注意①随机过程表面上杂乱无章(如Brownian Motion )但是,它既然是客观事物和数量表征,必然有其内在的规律;②为了掌握和利用这些随机过程所表现出来的规律,需要一定的数学工具,这就是随机过程理论.这章主要讨论随机序列的概率分布、参数表征、平稳随机序列(定义、谱分解、白噪声序列、线性运算、有理谱密度的平稳序列、随机差分方程、遍历性)、多维随机序列、两种估计和参数估计的优效性概念。
1.随机序列的概率分布:随机序列由无穷多个随机变量构成的,我们说给定了一个随机序列(1,2,)t x t =L 的概率分布,是指对于任意有穷多个时刻12,,,m t t t L ,相应的随机变量12,,,mt t t x x x L 的联合分布函数1212(,,,)mt t t m F x x x L L 都是被给定的,而且它们之间不能矛盾,即是说由高维联合分布推出的低维联合分布与原给定的低维分布相同. 有时我们也说给定了序列t x 的任意有穷维分布. t x 为独立的随机序列:若对于∀有穷个不相同时刻12,,,m t t t L 相应12,,,mt t t x x x L 是相互独立的random variable 即12121212(,,,)()()()mmt t t m t t t m F x x x F x F x F x =L L LExp :电话中的热噪声常常近似于这种独立序列.由于分布函数完整地描述了随机变量的统计特性,故严平稳随机过程的所有统计特性均不随时间的平移而变化. 故这一要求相当严格. 称之为严平稳(狭义平稳).而宽平稳过程对时间推移的不变性表现在统计平均的一、二阶矩上. 显然,严平稳过程比宽平稳过程之条件要求更“严”. t x 为狭义平稳序列(严平稳序列):若一个随机序列t x 的任意有穷维分布满足:Z τ∀∈(整数集),,(1,)i m t i m τ+=121212,,,12(,,,)(,,,)m m t t t m t t t m F x x x F x x x τττ+++=L L L L即1,,mt t x x L 和12,,,m t t t x x x τττ+++L 有相同的分布,无论对怎样的m 和时刻12,,,m t t t L 以及τ都如此.2.随机序列的参数表征:①均值函数:对每个t 而言,若把随机变量t x 的均值记为t t Ex μ=. 则随机序列t x 的均值函数就是(1,2,3,)t t μ=L ;若t x 的分布为()t F x ,若t x 具有密度()t f x ,则()()t t t t Ex xdF x xf x dx μ≡≡=⎰⎰. Remark :t μ可取常数(§1例4且电负荷量);可取周期函数(§1例2某点平均水温);或取其它形式,为方便计,称t t Ex μ=为t x 的均值.②自协方差函数:易知随机序列的均值只和随机序列的一维分布有关,为了分析随机序列t x 在不同时刻取值的统计关系,须要考虑t x 与s x 的协方差值,令()()()()(,)ts t t s s t s ts r E x Ex x Ex x y f x y dxdy μμ≡--≡--⎰⎰ts r 作为(,)t s 的二元函数,称为随机序列t x 的自协方差函数,特别称2()tt t t r E x Ex =-为t x 的方差函数,简称方差. 若一个随机序列t x 的任意有穷维分布都是正态分布,则称t x 为正态随机序列.若以f 表示相应于F 的分布密度,此时1212121(,,,)(2||)exp ()()(,)2m m t t t m m m m m m m m m f x x x x x N τπμμμ--⎧⎫=Γ⋅--Γ-≡Γ⎨⎬⎩⎭L L其中),,(1mt t m x x x Λ=τ;12(,,,)mm t t t τμμμμ≡L1112112m m m m m t t t t t t m t t t t t t r r r r r r ⎛⎫ ⎪Γ= ⎪ ⎪⎝⎭LL L很多实际应用的随机序列可近似当做正态序列,正态序列在数学处理上有很多方便之处.③自相关函数:序列的自相关函数ts ρ定义为ts r ρ≡它刻划了序列t x 在不同时刻取值的线性相关程度.Remark :随机序列的参数表征还有很多,与本书关系密切的就是以上三种量. 从上述表述易见,,t ts r μ和ts ρ被t x 的分布唯一确定. 但是,反之由,t ts r μ和ts ρ一般并不能唯一确定t x 的分布,即具有不同分布的随机序列可以有相同的均值、自协方差和自相关函数.3.平稳随机序列:为便于读者掌握,我们把本书的讨论几乎完全限于正态序列范围之内,这不会影响时序分析方法的介绍,且会使很多数学概念和性质有较为简单的形式,只是在某些个别情形下,我们指出对于非正态序列的类似结果. 特别,本书所介绍的各种方法的基础是广义平稳序列(宽平稳序列).(1)广义平稳序列的定义:若随机序列t x 的二阶矩有穷2()t Ex <∞且对任意时刻t 和s 满足: t Ex μ=2t s ts t s Ex x r r μ--== 为方便计,通常不妨设0μ=. 则称它为广义平稳序列(宽平稳序列),即μ与t 无关,ts r 只与t s -有关. “广义”是相对于“狭义”而言的,简称平稳过程.Remark :①若狭义平稳过程(序列)t x 的一、二阶都有穷2(,)t t Ex Ex <∞则它一定也是广义平稳的.112212,1212,012()()(,)(,)()t t t R R t t t t Ex xdF x xdF x a t Ex x x x dF x x x x dF x x f τττττ+++⎫⎛==≡⎪ ⎪ === ⎪⎝⎭⎰⎰⎰⎰⎰⎰ 与无关 ②若t x 是正态随机序列,t x 的狭义平稳性t x ⇔的广义平稳性. (()()t s E x x μμ--Q ,复旦大学《随机过程》第三册P 183特征函数) Proof :“⇒”若{},t x t T ∈是狭义平稳的(严平稳的),又正态过程有二阶矩,∴由①知{},t x t T ∈为宽平稳的. “⇐”若正态过程是宽平稳的,则,t Ex a t T ≡∈()()()()()ijt t i j i j E x a x a r t t r t t ττ--=-=+-+()(),,1,2,,i jt t i E x a x a t T i n ττ++=--∈=L表明12(,,,)nt t t x x x L 和12(,,,)nt t t x x x τττ+++L 具有相同的协方差矩阵和均值向量,而正态(多维)分布仅由它们确定(特征函数知识)因而11,,1,,1(,,)(,,)nnt t n t t n F x x F x x ττ++=L L L L{},t x t T ∈是严平稳(狭义平稳)过程.③Theorem. 设{},0,1,t x t =±L 为平稳列,则t x 要表为()i t t x x e dz πλπλ-=⎰其中{}(),[,]x z λλππ∈-是标准化的具有正交增量的,左2()L 连续的随机过程,且121212(()())(),,([,])x x x E z z F ππ∆∆=∆∆∆∆∈-I B 这样的正交增量过程唯一地由t x 所确定.(证明略)④实际应用中,平稳序列仅仅是对于真实随机序列的一种近似描述手段. 例:电路中的热噪声,陀螺仪的漂移速率及其它精密仪表的漂移误差,金融中的收益率序列等,第三章将给出一种粗略判别平稳序列手法.(2)自协方差函数与谱分布(t x 为实列)对于正态平稳序列t x ,其均值和自协方差函数s t r -唯一决定了它的分布((1.2.6)式知),从而也就决定了它的全部统计性质,故讨论自协方差函数s t r -的性质十分重要,也是首要任务. s t r -满足:①对称性:()t t t t r r r Ex x Ex x r ττττττ----====Q ②非负定性:对{}1,2,m z +∀∈=L ,方阵11102120m m m m m r r r r r r rr r ----⎛⎫⎪⎪Γ= ⎪⎪⎪⎝⎭LL L L L L L 是非负定的.(Q 对m ∀维实值非零向量011(,,,)m τξξξξ-=L 都有:11,0,0()()m m m i j ij i jiji j i j rE x xτξξξξξξμμ---==Γ==--∑∑120[()]0m i i i E x ξμ-==-≥∑)有时称满足上述性质1和性质2的实数列01,,,,m r r r L L 称为非负定列. 易知000,||r r r τ≥≤,反之,任意一个非负定列必为某平稳序列的自协方差函数([3],E.lukacs, Characteristic Functions, London, 1960). Theorem1. 设k r 为一平稳序列的自协方差函数,则存在一有界非降函数()G λ,使得1/221/2()i k k r e dG πλλ=⎰(相关函数的谱表示Th )()G λ称为平稳序列t x 的谱分布,若()G λ可微,并记()()dG g d λλλ≡则 1/221/2()i k k r e g d πλλλ-=⎰()g λ称为平稳序列t x 的谱密度.当||kk r∞=-∞<∞∑时,()g λ一定存在且2()i k kk g r eπλλ∞-=-∞=∑. 有的工程书上,称()g λ为序列的功率谱密度.(3)白噪声序列若平稳序列t a 的均值为0,自协方差函数20k a k r σδ=,我们称这样的t a 为白噪声序列,或简称白噪声,它的谱密度:2220()i k a a k a k g e πλλσδσ∞-=-∞=≡∑可见()a g λ为一常数,即序列t a 的谱密度在各个频率上具有相同的分量(正象白光一样,等量地包含了各种有色光的光频分量).Remark :很多随机序列可以近似地符合白噪声的性质. 虽纯粹的白噪声很难遇到(自然界).(4)平稳序列的线性运算随机变量可以进行加减等运算,随机序列也是如此.①设t x 是一平稳序列,,αβ是两个实数,τ是某一固定时刻,则t t t y x x ταβ-=+,还是平稳序列(令2t Ey μ=验证22()t t Ey y f τμτ--=). ①′假定k α是实数列,且2||k k α∞=-∞<∞∑,那么易验证t k t kk y xα∞-=-∞=∑也是平稳序列,其中k t k k x α∞-=-∞∑,作为当,M N →∞时Nk t kk Mxα-=-∑的均方极限. (Remark :设{}k x 为平稳序列,若2||0k k E x x →∞-→,称{}k x 均方收敛于x ,又称x 为{}k x 的均方极限).Remark :(A )取t t x a =为白噪声,当0k <时0k α=,这时平稳序列0t k t k k y a α∞-==∑称为t a 的滑动和;特别若再有0k α=,当k q >时(0k <时0k α=),则0qt k t k k y a α-==∑称为t a 的q 阶滑动平均.上两式所给出的平稳序列,其自协方差函数和谱密度可利用t a 的性质很方便求出,约定0k <时0k α=,0t k t k k y a α∞-==∑则0,0()ys tk t k j s j kjt ks j k j k j rE a a Eaa αααα∞∞∞-----=====∑∑∑22(),0,0,0,0akjs j t k akjs t k j k j k j σααδσααδ∞∞----+-====∑∑022,0s t k j ak k s tak k s tj s k t k j k σαασαα-+-=∞∞+-+-⇔=+-====∑∑2||||akk t s k t s σαα∞--=-=∑讨论:①当s t ≥时2()k s t my s tamm s t m s trσαα∞+-=---=-====∑.②当s t ≤时,由于0k <时0k α=,222()y s ta k k s takk s takk t s k t sk t sk t srσαασαασαα∞∞-+-+---=-=-=-===∑∑∑从而总有2||||y s takk t s k t s r σαα∞---=-=∑W .2220()y i i y akk k g r e e πτλπτλττττλσαα∞∞∞--+=-∞=-∞===∑∑∑22222()00i i k i k akk akk k kk keee πτλπλπτλττττσαασαα∞∞∞∞--+++==-==-==∑∑∑∑222()0i k i k akk k k ee πλπτλττσαα∞∞-++==-=∑∑22200m ki k i m a k mk m ee τπλπλσαα∞∞=+-====∑∑222222000||i k i k i k akkak k k k eee πλπλπλσαασα∞∞∞--=====∑∑∑若令 0()k k k A ωαω∞==∑则上式可表为: 222()|()|i y a g A e πλλσ-=.例下面介绍有理谱密度. 它比白噪声t a 的常值谱密度更具一般性,t y 具有较复杂连续谱密度.(5)具有有理谱的平稳序列:对于正态平稳序列,只要知道了它的自协方差函数k r ,或知道了它的谱分布()G λ,就等于掌握了它的统计性质. 主要利用k r 去分析时间序列时,称为“相关分析法”或“时域分析法”;利用后者时,称为“频谱分析法”. 怎样求得一个正态平稳序列t x 的k r 或()G λ呢?主要利用t x 的样本值12,,,N x x x L 对k r 或()G λ进行估计,这是时序分析要解决的主要问题之一,这有两个难点:①(0,1,2,)k r k =L 是由无穷多个值构成的,谱密度()G λ为在11[,]22-内取值的函数,用有穷个t x 的样本值对所有k r 或()G λ的所有取值进行估计,难点之一.②即使能对k r 或()G λ的所有取值做出估计,由于01,,r r L 或()G λ的形状复杂,也不利于在预报、控制或模拟等应用中使用. 于是为克服这两个困难,我们采取绪论中提到的“参数化”方法,即将()G λ局限在一个较窄的函数范围内讨论,我们只讨论这样一类正态平稳序列,它们的谱分布()G λ不仅可微,而且它的导函数(谱密度)()()dG g x d λλ≡为2i e πλ-的有理函数: 2222()()||()i a i e g e πλπλθλσϕ--= (I )其中()θω和()ϕω为ω的实系数多项式:212212()1()1q q pp θωθωθωθωϕωϕωϕωϕω=----=----L L (II )两者无公共因子,且限定()θω和()ϕω的根全在复平面的单位圆外. 这样一来,为了估计()G λ,只要估计2,,a p q σ和(II )中诸系数1,,q θθL 和1,,p ϕϕL 即可,这些只是有限个系数而已. 有了这些参数的估计值,利用(I )式即可得到()g λ在)21,21[-上的各处取值的估计. 在用于预报、控制和模拟等目的时,由于()g λ拥有(I )之形式,解决问题就方便多了. Remark :①谱密度有(I )这种形式的t x ,称为具有有理谱的平稳序列; ②对于()g λ为连续的情形,它可用有理谱来逼近真实的谱,这是较有效的一种方法.(6)随机差分方程:据前所述,具有有理谱的平稳序列的自协方差函数k r 也是被以上诸参数所决定.Q 由Th1知 21/222221/2()|| 0,1,2,()i i k k ai e r e d k e πλπλπλθσλϕ--==⎰L(III )反之,若k r 能表成(III )之形式,则随机序列也一定具有(I )形式的有理谱密度.例1 取 222()|,||1i k a g e πλλσϕϕ-=-< 则 1/222221/21|1|i k k a i r e d e πλπλσλϕ-=-⎰21/22221/2cos 2,0,1,2,12cos 21k a ak d k σπλσλϕϕπλϕϕ===-+-⎰L(Q21/2221/2cos 21cos 12cos 2212cos t k ktd dt t πλπππλλϕπλϕπϕϕ=--==-+-+⎰⎰当2||1ϕ<时221112cos 12cos m m mt t ϕϕϕϕ∞=-=+-+∑, 此级数对一切t 一致收敛,它的各项都乘以同一有界函数cos kt后仍然一致收敛,从而22cos (1)12cos ktdt t ππϕϕϕ---+⎰21cos 2cos cos 2cos m k m ktdt mt ktdt ktdt ππππππϕϕ∞---==+=∑⎰⎰⎰1cos 222kkkt dt ππϕπϕ-+==⎰从而 1/2221/21cos cos 2212cos 12cos 2kt k d dt t πππλλπϕϕϕπλϕ--=-+-+⎰⎰ 2(0,1,2,)1kk ϕϕ==-L若 21/222221/2()||()i i k k a i e r ed e πλπλπλθσλϕ---=⎰, 则随机序列{}t ω也一定有2222()()||()i a i e g e πλπλθλσϕ--=形式的有理谱密度. ( Theorem1 ()()()()n n a s P ξωξωξωξω⋅⇒u r u u u r令()(1,2,)n n ξω=L ,()ξω是r v ⋅,则{}111:lim ()():(|()()|)n n n m k n km ωξωξωωξωξω∞∞∞→∞===⎧⎫==-<⎨⎬⎩⎭I UI {}lim ()()n n ωξωξω→∞∈=⇔对∀一个m (正整数),∃一个正整数N ,使当n N >时均有()1|()|n mωξξω-<⇔对∀一正整数,m ω属于1(|()()|)n m ξωξω-<之下限事件. 111(|()()|)1n m k n kP m ξωξω∞∞∞===⎧⎫⇔-<=⎨⎬⎩⎭I UI or111(|()()|)0n m k n kP m ξωξω∞∞∞===⎧⎫-≥=⎨⎬⎩⎭UI U0ε⇔∀>成立1(|()()|)0n k n k P ξωξωε∞∞==⎧⎫-≥=⎨⎬⎩⎭I U{}lim (|()()|)n n n n P A A ξωξωε→∞==-≥)Theorem2 若()B ϕ没有模为1的因子(即2()0i e πλϕ-≠),若{}t ω为差分方程1111 ,1,0,1,t t p t p t t q t q x x x a a a t ϕϕθθ-------=---=-L L L L (IV )的平稳解(即它是平稳序列且满足(IV )),则{}t ω有有理谱密度2222()()||()i ai e g e πλπλθλσϕ--=. 反之,若平稳序列{}t ω有此谱密度,则{}t ω可表成(IV )形式.Theorem3 (Wiener-X HHYH )设{},0,1,t x t =±L 是平稳列,其相关函数(,0,1,)k r k =±L 满足||k k r ∞=-∞<+∞∑,则t x 必有非负谱密度函数()f λ,且()x r τ和()f λ是Fourier 变换的关系:()(),0,1,ik x r k e f d k πλπλλ-==±⎰L1()(), 2ik xk f r k eλλπλππ∞-=-∞=-≤≤∑W推论,若{},0,1,n x n =±L 是实平稳列,()x r τ绝对可和,则谱密度()f λ必存在,并且(a )()(),f f λλπλπ=--≤≤(b )101()(0)2()cos 2()2()cos x k xf R r k k r n f n d πλλπλλλ∞=⎧⎧⎫=+⎨⎬⎪⎪⎩⎭⎨⎪=⎪⎩∑⎰ 这表明自协方差函数为一指数型数列,反之,若221k ak r σϕϕ=-形式,则相应的随机序列一定具有谱密度222()|1|i a g e πλλσϕ-=-,||1ϕ<. 虽然(III )式反映了有理谱与其相应的自协方差函数之间的关系,但是,为了以后的时域分析,还要引进随机差分方程的概念. 上例中||k r <∞∑Q2222222()()1|1|i k i ka aki k k g r eee πλπλπσσλϕϕϕ∞∞---=-∞=-∞∴===--∑∑222() |1|ai g e πλσλϕ-∴=-W .]111[-1][-122222a 0122a πλπλπλϕϕϕϕσϕσi i i k k e e e ---∞=∞=-+-=+=∑∑ 设12,,,p ϕϕϕL 和12,,,q θθθL 分别是p 个和q 个实数,并设以它们为系数的两个多项式()ϕω和()θω无公共因子,且它们的根全在单位圆外(为了保证收敛性),若平稳序列t x 满足关系式:1111 ,1,0,1,t t p t p t t q t q x x x a a a t ϕϕθθ-------=---=-L L L L (IV ) 其中t a 是一白噪声,22t a Ea σ=,且当s t >时,0t s Ex a =,那么我们就说t x 是随机差分方程(IV )的一个平稳解. Q 根据平稳序列的理论([1]附录,§1Th1)知,具有有理谱密度()g λ(I )的平稳序列,一定是随机差分方程(IV )式的一个平稳解;反之,(IV )式的平稳解一定具有(I )()g λ的有理谱密度. 于是建立关系:具有有理谱的平稳序列11-←−→随机差分方程的平稳解.例1 (同前)具有谱密度222()|1|,||1i a g e πλλσϕϕ-=-<平稳序列t x ,它应满足差分方程:1t t t x x a ϕ--= (V )于是有: 10 ()0t k t k t t k t k E x x x Ex a ϕ---->-== 1,0k k r r k ϕ-=>又由(V )知:2222220100()(1)t t t a a r Ex E a x r r ϕσϕσϕ-==+=+⇒=-2212021kk ak k k r r r r σϕϕϕϕϕ--∴====⋅=-L W 这与前面解答完全一致,但计算方便. 另一方面,(V )又可写为1t t t x x a ϕ-=+,表明了t x 的前后依赖关系(这很类似t t t x y a ϕ=+的回归方程,1t t y x -=自身滞后一步),1t t t x x a ϕ-∴-=又称()t x 的平稳解t x 为一阶自回归序列,而参数ϕ表明t x 前后的相关程度. 由(V )推知:212121()t t t t t t t t x x a x a a x a alt ϕϕϕϕϕ-----=+=++=++1212n n n t n t n t n t x a a a ϕϕϕ----+-+==++++L L由于()1ϕωϕω=-的根在单位圆外(||1ϕ<Q )∴对上式两边取极限得到:122220(lim)||||||0n j n n t t j t n t n j E x a E x E x ϕϕϕ----=-==→∑1lim()n nj j t t n t j t j n j j x x a a ϕϕϕ-∞+---→∞===+=∑∑ (均方意义下)(t Ex μ=Q 1/221/2())i t x e Z d πλλ-=⎰)这恰如平稳列的滑动和(t x 只是1,,t t a a -L 的滑动和,而t a 是白噪声,∴当t s <时,t x 与s a 独立,0t s t s Ex a Ex Ea ∴==)下面再从滑动和回到谱密度,||1ϕ<Q ,由222()|()|i y a g A e πλλσ-=知01(),||11j j j A ωϕωωϕω∞===≤-∑ 222222()|()||i i a a g A e e πλπλλσσϕ--==-22(12cos 2)a σϕϕπλ=+-从此后,我们所讨论的平稳随机序列,不仅限于正态序列,而且都有有理谱密度. 即它们必是(IV )型的随机差分方程的平稳解,利用(IV ),下一章再详细分析相应k r 的各种性质.(7)遍历性:为了估计p ,q ,2a σ和()ϕω与()θω的系数等值,常用的统计方法显得不够用,应用新手段的一个重要前提:随机过程要具有遍历性.遍历性定义:设t x 为一随机序列,()t v x 是t x 的函数(如2||,,,etc t t t t x x x x τ+),若对任何使()t Ev x 存在的函数v ,概率为一地有(or 依概率1)11()lim()Nt t jN j Ev x v xN+→∞==∑则称t x 为具有遍历性的随机序列. Remark :①([5](U.Grenander and M. Rosenblatt )平稳时间序列的统计分析,郑绍谦译(1962))知:正态有理谱平稳序列一定具有遍历性. ②遍历性物理意义:随机序列t x 的函数(连续)()t v x 也是一个随机变量,其均值为()t Ev x ,可称之为()t v x 的总体平均(即依()t v x 的分布所求出的均值,或称相平均. )又当t 固定,而将(),1,2,3,t j v x j +=L视为一个随机序列时,11lim ()Nt jNj v xN+→∞=∑称为()t v x 的时域平均. 所谓t x 的遍历性,简而言之,就是对任何函数v ,()t v x 的总体平均等于它的时域平均. 粗略说:意味着t j x +的任何一个样本随j 的变化所能取的值,依随机变量t x 的概率分布,历经它所能取的各种值,11()lim()Nt t jN j Ev x v xN+→∞==∑.③若t x 具有遍历性,它的线性运算也具有此性质. 例1 遍历性用途取1()t t t v x x x +=,则由遍历性11111limNt t t j t jN j r Ex x xxN++++→∞===∑这说明当N 很大时上式右边平均值可作为1r 的近似估计值.4.多维随机序列:t y 为r -维随机序列:对每个固定的整数值时刻t 而言,t y 是-r 维随机向量,常记做2(1)(2)()(,,,)r t t t t y y y =L Y ,时刻(,)t ∈-∞+∞. 这r 个随机序列(1)(),,r t t y y L 相互之间有一定的统计联系.(1)t y 的均值函数(均值):(1)(2)()(,,,)r t t t t E Ey Ey Ey τ≡L Y对t Y 而言,固定t 时t E Y 为一个r 维向量(非随机的).(2)方差阵、自协方差阵与互协方差函数: 方差阵函数:(1)()(,,)r t t t y y τ=L Y()()t t t t E E E τ--Y Y Y Y这是一个r 阶非负定矩阵,其主对角线上的元恰是()(1,)k t y k r =的方差,而i 行j 列的元,则为()i t y 与()j t y 的互协方差. 为掌握t Y 在不同时刻取值的统计关系,定义()()ts t t s s E E E τ≡--¡Y Y Y Y为t Y 的自协方差阵函数;其主对角元素是()(1,)k t y k r =的自协方差函数,而i 行j 列的元()()()()()()i i j j t t s s E y Ey y Ey --称为()i t y 与()j s y 的互协方差函数. 当t s =时,tt ¡为t Y 的方差阵函数.ts ∴¡更进一步揭示了t Y 的各分量间及前后之间的相互联系.(3)多维平稳序列:设t Y 为r 维随机序列,若它还满足;()()t ts t t s s t s E u E E E R τ-==--=¡Y Y Y Y Y则称t Y 为r 维平稳随机序列. (略)5.两种估计及参数估计的优效性概念:(1)最小二乘法(Least Square简称LS 法)线性参数的最小二乘法是常用的估计方法之一,这里主要介绍非线性参数的最小二乘法(第四章将用之).考虑模型121(;,,,),1,2,k k k k y f y y y e k β-=+=L L ; (I ) 其中k e 仍表示残差,12(,,,)r τββββ=L 为未知参数矢量,k f 是11(,,,)k y y β-L 的函数,对β非线性,若获得了测量值12,,,n y y y L ,那么,使得残差平方和21211()[(;,,,)]nk k k k S y f y y y ββ-=≡-∑L达到极小的解µβ,即称为β的最小二乘估计,以后简称LS 估计(LeastSquare Estimation ). Remark :①一般说来,对非线参数而言,µβ的求解比线性情形要麻烦得多,且只能给出数值解法,无法得到线性参数明显解. 此外,k f 还可能是用迭代方式给出,而不必有明显的函数形式;②为了分析估计µβ的误差情况,应当引入k e 和k y 的统计特征. 假定k e 为白噪声,而且k e 与11,,k y y -L 独立;作为1,,n y y L 的函数的最小二乘估计µβ和真值β之间的接近程度可用下面介绍的几种估计量优效性来衡量. 可见附录§5关于最小二乘估计量各种优效性质.(2)最小方差估计(Least Mean Square or 简记LMS 估计)(第IV 、VII 、IX 等章常用之)设(11,,k M k N N M ω-<<+为整数 or 正、负无穷)是一组正态随机变量,且它们的均值都是0. 又设正态随机变量z 的均值亦为0,且z 与k ω的联合分布也是正态分布. 所谓根据(11)k M k N ω-<<+对z做的(或z 关于k ω的)LMS 估计z$是指存在如下的量:Nkkk Mz wβ==∑$其中系数k β使误差方差2()E z z-$达到极小,即 22()inf ()kNk k k ME z z E z ααω=-=-∑$我们把这种估计记为(|,11)kz E z M k N ω≡-<<+$最有用的情况是:每一k ω可以表成白噪声k)j 1-M (a j ≤<的和kk kjj j Ma ωξ==∑(I ),同时每一j a 也能表成(1)l M l j ω-<≤之和,即jj jl l l Ma ηω==∑(II ).且其中系数满足如下条件:22()()11||,||g k j g j l kj jl g e g e ξη----≤≤ (III )此处12,g g 表示与,,k j l 无关的正实数.(上述条件①当,M N 为有穷整数时易满足(E.P.Box 时序分析:预测与控制P 138-149)②当M =-∞时,由P 49~52和附录中将会有,若k ω是()()t t B x B a ϕθ=的平稳解,则上述条件满足(LMS 估计))对于这样的k ω,随机变量Z 的最小方差估计形式简便,易于讨论它们的性质.令≡A {|,Nj j j j My y a ββ==∑为实数,2Nj j Mβ=<∞∑}≡W {|,N l l l l My y w αα==∑为实数,2Nl l Mα=<∞∑}从A 与W 出发讨论LMS 估计的性质. 1.=A W当,M N 都为有穷时,显然. 我们只对,M N =-∞=+∞情形给予证明. 若y ∈A ,则∃-串j β使得2jl β∞=-∞<∞∑且jjj y aβ∞=-∞=∑,由上述讨论知:()jj jll jjll llj l l j ll y w w w βηβηα∞∞∞∞=-∞=-∞=-∞==-∞===∑∑∑∑∑其中l j jl j lαβη∞==∑,由(III )及Schwarz 不等式知:2()21,,||g j l k l z ljkjlklj kl l j k l l j k lg e αββηηββ∞∞∞∞∞--+-=-∞=-∞==-∞==≤∑∑∑∑∑ 22()22211,0(||)()()1m j l g m n m l n l l g n k lm n l l g g e eβββ∞∞∞=--+++-=-==-∞=-∞=≤<∞-∑∑∑ 21/221/2(||||()()m l n l m ln l l l l ββββ∞∞∞++++=-∞=-∞=-∞≤∑∑∑222211,)11g mg n g g m n ee ee∞∞----====--∑∑ 因此y ∈W ,y Q 是A 的任意元. ∴⊃W A ,同理⊂W A ,∴=A W . 利用泛函分析知识:=A W 是Hilbert 空间(估计量ˆ(|,11)k zE z w M k N =-<<+是z 在W 上的投影,∴也是在A 上投影,ˆ(|)(|)zE z E z ∴≡=W A ) 2.ˆzW ∈为z 的最小方差估计(LMS 估计)⇔对y ∀∈W ,必有ˆ()0E z zy -=. 首先注意,由性质1,y ∀∈W 可表为Njjj My aβ==∑,且2Njj Mβ=<∞∑,222Najj MEy σβ=∴=<∞∑“⇒”(反证法)设ˆz是Z 的LMS 估计,而且y ∃∈W 使ˆ()0E z zy -≠. 那么显然成立20(0)Ey y <<∞≠. 由最小方差性质,对R β∀∈有22222()()()2()E z zE z z y E z z Ey E z z y βββ-≤--=-+--$$$$ 由此有:222()Ey E z z y ββ≥-$. 取2()0E z z y Ey β-≠$@. 便导致21≥. 这与实数理论相矛盾,y ∴∀∈W 必有()0E z zy -=$这与z W ∈$为z 之最小方差估计矛盾.另证:令2(,)(),0z zy E z z y Ey α=-=-<<+∞$$则 222222222222(())()2()()()()E z z y E z z Ey E z z y E z z E z z Ey Ey Ey Eyαααα-+=-+--=--<-$$$$$ “⇐”设zW ∈$满足条件:()0E z z y -=$,对y ∀∈W 成立. 则对**,z zz ∀∈-∈$Q W W (H 氏空间)∴有0))(ˆ(=--*z z z z E ,于是 *2*22*2*2()()()()2()()()E z z E z zz z E z z E z z E z z z z E z z -=-+-=-+-+--≥-$$$$$$$ 这就证明了z$是LMS 估计. 又可注意,上式不等号当且仅当*z z =$时才取等号,z∴$中唯一的. 3.z 的的最小方差估计(LMS 估计)z$存在且唯一. 唯一性已在性质2的充分性证明过程得到. 现证存在性:令21()Njjj Maz Eza aσ==∑$,j a 为白噪声. 易算出:2220()2E z zEz Ezz Ez ≤-=-+$$$ 222()/Nj a j MEz Eza σ==-∑2222(/)/Nj a a j MEza Ez σσ=∴≤<∞∑“(利用上述不等式且z Q 为正态随机变量)从而$2()NN j j j j j M j MaEza za a ασ=====∑∑$中2Njj Mα=<∞∑. 由性质1,z ∈=$A W ,又对任意N j j j My a β==∈∑W221()()()N Nj j j j j j Mj M aE z zy Eza Eza Ea ββσ==-=-∑∑$()()0N Nj j j j j Mj MEza Eza ββ===-=∑∑因此由性质2,z$即为z 的最小方差估计. 4.若1112z z z ββ=+,其中12,ββ是实数,则1212z z z ββ=+$$$;若z ∈W ,则z z =$;若z 与W 的元都独立,则0z =$;若(11)kw M k N -<<+是相互独立的随机序列,则任意z 的最小方差估计为2(/)Njj j j MzEzwEw w ==∑$它们由性质2得到验证:0, ()0 (0)zy E z z y Ezy EzEy Ez =∀∈-====$$W ,Nj j j M y y w β=∀∈=∑W ,利用独立性易知()0N Njjjjj Mj ME z zy Ezw Ezwββ==-=-=∑∑$.5.若¢是r 维随机向量,且,M N 有穷,则¢的最小方差估计µ¢(µ¢的各分量为¢的对应分量的最小方差估计)可表为µ1()()E E ττ-=ⅱW WW W其中1(,,,)M M N w w w τ+=L W ,这也易由性质2得到.(3)参数估计的优效性概念:LS 估计与LMS 估计在概念上有本质的差别:LMS 估计是用随机变量或序列的样本的对另一随机变量做出估计,它们之间的概率分布是已知的(常为正态分布)(用于解决随机序列预报VII 章).LS 估计则是用随机变量或序列的样本去估计某些未知参数(参数化非线性估计问题IV 章).其它方未能:极大似然法或近似极大似然法来解决参数估计问题.从数理统计的角度怎样衡量参数估计的优劣程度,是另一个很重要的问题,我们在这里引进几个有关的定义. 参数估计:根据某种原则,将随机序列的样本(即测量值)12,,,N y y y L 进行各种运算,从而对于未知参数向量β作出估计与判断. 因此,一般可以把β的估计量µβ表成样本的函数形式,即µµ12(,,,)Ny y y =L ββ,为了衡量µβ与真值β的近似程度,需一些概念:1.无偏性与渐近无偏性:若估计量µβ满足µE =ββ,则称µβ为β无偏性. 若µlim NE →∞=ββ,则称µβ为β的渐近无偏估计量. 无偏估计比渐近无偏估计量难于寻找.2.相容性:若样本长度N →∞时,估计量µβ依概率收敛于β,即对任意小的0ε>,µ{}lim 0N P ε→∞->=ββ,其中{}12max ||,||,,||r βββ≡L β是β的范数(或称模量),这时我们称µβ为β的相容估计.3.优效性与渐近优效性:在相当一般的条件限制下,特别当限于讨论正态随机序列时,经典统计中的Cram ér-Rao 不等式仍成立,即有µµ11log log ()(()()()Np p E J E ττ--∂∂--≥≡⋅∂∂βββββββ 其中p 12,,,N y y y L 的联合概率密度,1()NJ -β称为Cram ér-Rao 下界,这一公式我们将在附录§4中证明(P 308-327).若估计量µβ能使上式等号成立,即 µµ1()()()NE J τ---=βββββ 则称µβ为优效估计,若估计量µβ只能成立极限关系式 µµ1122lim ()()()()N NN J E J I τ→∞--=ββββββ 其中I 表示单位矩阵,则称µβ为渐近优效估计. 4.渐近正态性:若存在一个矩阵列N B ,当N →∞时,N N B B τ的主对角线都无限地增大,而且使得µ()N B -ββ的联合分布NF 收敛于正态分布(0,)N I ,则称µβ具有渐近正态性,简单地用µ()~(0,)N B N I -ββ表示.5.优效渐近正态性,若µβ具有渐近正态性,而且其中的NB 满足 1lim ()N N N N B J B I τ-→∞=β 则称µβ具有优效渐近正态性,即µ12()()~(0,)NJ N I -βββ. 例 正态(,0)AR p 序列参数140()02pNa M J σ-⎛⎫= ⎪⎝⎭β 01110221120 p p p a p p p p r r r r r r M r r r σ-----⎛⎫ ⎪ ⎪=ΓΓ= ⎪ ⎪ ⎪⎝⎭L L L L L L L 2log log log ()N p p pJ E E βττ∂∂∂≡⋅=-∂∂∂∂ββββP 是t y 的似然函数.Remark :①随机序列的参数估计与经典统计有一点本质性的差别,经典统计中,样本12,,,N y y y L 常是相互独立同分布的随机变量,而参数β只是这一相同的分布中所含的未知参数(如正态分布的均值方差). 在这里,12,,,N y y y L 是随机序列的一段样本,它们一般不是相互独立的,而参数β是这些随机变量的联合分布中的未知参数(如自回归序列的系数).②估计量的渐近优效性和优效渐近正态性的渐近法则是不相同的,前者要求µµ()()E τ--ββββ与1()NJ -β渐近相同,由于1()N J -β是估计误差µ()-ββ的方差阵的下界,因此,渐近优效性又可以叫做渐近最小方差性. 而后者只要要求µ12()NJ -ββ的分布NF 与正态分布(0,)N I 渐近相等或说µ()-ββ的分布与1(0,())NN J -β渐近相等,这里并不要求µ()-ββ的方差阵的收敛性. (H.Cramer 曾弄错二者之间关系)③具体使用参数估计方法时,我们总希望估计量能具有上述的各种优效性质,即这些性质是检验估计优劣的重要标准.。
《时间序列分析及应用:R语言》读书笔记
《时间序列分析及应用:R语言》读书笔记姓名:石晓雨学号:1613152019(一)、时间序列研究目的主要有两个:认识产生观测序列的随机机制,即建立数据生成模型;基于序列的历史数据,也许还要考虑其他相关序列或者因素,对序列未来的可能取值给出预测或者预报。
通常我们不能假定观测值独立取自同一总体,时间序列分析的要点是研究具有相关性质的模型。
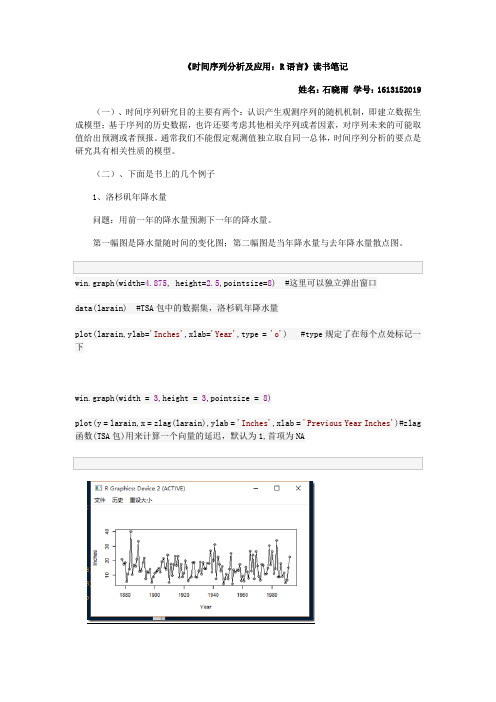
(二)、下面是书上的几个例子1、洛杉矶年降水量问题:用前一年的降水量预测下一年的降水量。
第一幅图是降水量随时间的变化图;第二幅图是当年降水量与去年降水量散点图。
win.graph(width=4.875, height=2.5,pointsize=8) #这里可以独立弹出窗口data(larain) #TSA包中的数据集,洛杉矶年降水量plot(larain,ylab='Inches',xlab='Year',type = 'o') #type规定了在每个点处标记一下win.graph(width = 3,height = 3,pointsize = 8)plot(y = larain,x = zlag(larain),ylab = 'Inches',xlab = 'Previous Year Inches')#zlag 函数(TSA包)用来计算一个向量的延迟,默认为1,首项为NA从第二幅图看出,前一年的降水量与下一年并没有什么特殊关系。
2、化工过程win.graph(width = 4.875,height = 2.5,pointsize = 8)data(color)plot(color,ylab = 'Color Property',xlab = 'Batch',type = 'o')win.graph(width = 3,height = 3,pointsize = 8)plot(y = color,x = zlag(color),ylab = 'Color Property',xlab = 'Previous Batch Color Property')len <- length(color)cor(color[2:len],zlag(color)[2:len])#相关系数>0.5549第一幅图是颜色属性随着批次的变化情况。
第五章非平稳时间序列的随机分析实验报告共10页文档

第五章非平稳时间序列随机性分析实验报告下表为1948-1981年美国女性(大于20岁)月度失业率数据。
表5-1 1948-1981年美国女性月度失业率数据来源:Andrews&Herzberg(1985)。
根据以上数据,下面用Eviewis6.0对1948-1981年美国女性(大于20岁)月度失业率数据进行随机性分析。
1.绘制时序图图5-1 1948-1981年美国女性月度失业率序列时序图从时序图可以看出序列中既有长期趋势又有周期性,因此进行1阶-12步差分。
2.1阶-12步差分在数据窗口中选择“Quick/Graph”,出现以下对话框,在空白窗口中输入D(S,1,12),如图5-2所示。
图5-2 1阶-12步差分图5-3 D(S,1,12) 时序图从时序图看,D(S,1,12)均值稳定,没有明显测周期性,方差有界;生成序列D1=D(S,1,12),通过相关分析,具体分析序列的平稳性。
如下图所示。
图5-4 D(S,1,12)的相关分析图5-4中,自相关2阶显著,但是12阶也是显著的,因此在趋势平稳中又包含了周期性因素。
以下对其进行ARMA模型分析。
3.ARMA模型拟合对平稳非白噪声序列D(S,1,12)尝试用ARMA模型拟合。
(1)对序列进行AR模型拟合。
在主窗口命令框中输入LS D(S,1,12) AR(1) AR(12),得到以下回归结果,如图5-5所示,并对其残差相关性进行检验,如图5-6。
图5-5 AR(1,12)模型拟合序列D (S ,1,12)残差相关性检验结果如下图:图5-6 AR(1,12)模型拟合序列D (S ,1,12)的残差相关图从上图看出模型残差非白噪声,模型提取信息不充分。
(2)对序列进行MA 模型拟合。
在主窗口命令框中输入LS D(S,1,12) MA(1) MA(12),得到以下回归结果,如图5-7所示,并对其残差相关性进行检验,如图5-8。
图5-7 MA(1,12)模型拟合序列D (S ,1,12) 图5-8 AR(1,12)模型拟合序列D (S ,1,12)的残差相关图从图5-8可以看出模型残差也非白噪声,模型提取信息仍然不充分。
《时间序列分析》课程教学大纲
《时间序列分析》课程教学大纲课程编号:33330775课程名称:时间序列分析课程基本情况:1.学分:3 学时:51学时(课内学时:45 课内实验:6)2.课程性质:专业必修课3.适用专业:统计学适用对象:本科4.先修课程:概率论、数理统计、随机过程5.首选教材:王燕:《应用时间序列分析》,中国人民大学出版社,2008出版。
备选教材:王振龙等编著:《时间序列分析》,中国统计出版社,2000年。
6.考核形式:闭卷考试7.教学环境:多媒体教室及实验室一、教学目的与要求本课程是数理统计学的一个重要分支,先期需完成的课程有概率论、随机过程。
通过本课程的学习,使学生掌握时间序列数据的分析方法,包括时间序列简介、平稳时间序列分析、时间序列分解、非平稳序列的随机分析、多元时间序列分析。
利用Eviews软件进行本课程的实验教学。
二、教学内容及学时分配课程内容及学时分配表三、教学内容安排第一章时间序列分析简介【教学目的】1、了解时间序列的定义及常用分析方法;2、掌握时间序列的几个基本概念:随机过程、平稳随机过程、非平稳随机过程、自相关、记忆性。
【教学重点】时间序列的相关概念。
【教学难点】随机过程、系统自相关性。
【教学方法】课堂讲授【教学内容】第一节时间序列的定义第二节时间序列分析方法第三节时间序列分析软件EVIEWS简介第二章时间序列的预处理【教学目的】1、掌握平稳性检验的原理和方法;2、掌握纯随机性检验的原理和方法。
【教学重点】平稳时间序列的定义及统计性质。
【教学难点】时间序列的相关统计量。
【教学方法】课堂讲授【教学内容】第一节平稳性检验一、特征统计量二、平稳时间序列的定义三、平稳时间序列的统计性质四、平稳时间序列的意义五、平稳时间序列的检验第二节纯随机性检验一、纯随机序列的定义二、白噪声序列的定义三、纯随机性检验第三章平稳时间序列序列分析【教学目的】1、理解ARMA模型的定义及性质。
2、掌握平稳序列建模方法。
3、掌握平稳时间序列的预测【教学重点】平稳时间序列建模【教学难点】模型识别,参数估计,序列预测【教学方法】课堂讲授与上机实验【教学内容】第一节方法性工具一、差分运算二、延迟算子三、线性差分方程第二节 ARMA模型的性质一、AR模型二、MA模型三、ARMA模型第三节平稳序列建模一、建模步骤二、样本自相关系数与偏相关系数三、模型识别四、参数估计五、模型检验六、模型优化第四节序列预测一、线性预测函数二、预测方差最小原则三、线性最小方差预测的性质四、修正预测第四章非平稳序列的确定性分析【教学目的】1、理解时间序列的分解原理。
