等比数列的前n项和_PPT课件
合集下载
等比数列的前n项和PPT课件

等比数列的前n项和ppt课件
xx年xx月xx日
contents
目录
• 引言 • 等比数列的前n项和公式推导 • 等比数列的前n项和的应用 • 特殊等比数列的前n项和 • 等比数列的前n项和求解方法 • 习题解答与练习
01
引言
课程背景
教学内容的重要性
等比数列是数学中的一个重要概念,其前n项和在数学、物理 、工程等领域有着广泛的应用。
特殊情况
当公比q不等于1时,等比数列的前n项和公式为 Sn=a1(1-q^n)/(1-q)。
05
等比数列的前n项和求解方法
利用公式求解等比数列的前n项和
公式法
利用等比数列的前n项和公式求解,当已知等比数列的首项a1和公比q时,可以直 接套用公式求出前n项和。
记忆口诀
为了方便记忆,可以总结一个简单的记忆口诀:“首项乘1减公比除以1减公比的 n次方”,这个口诀可以快速帮助我们记忆公式。
02
等比数列的前n项和公式推导
公比为r的等比数列求和公式推导
公式推导
$S_n = \frac{a_1}{1-r} * (1 - r^n)$
VS
推导步骤
将等比数列的每一项分别代入求和公式中 ,得到$S_n = a_1 + a_2 + \cdots + a_n$,再将$a_1 = ar, a_2 = ar^2, \cdots, a_n = ar^n$代入$S_n$中,经过 化简得到最终的求和公式。
04
特殊等比数列的前n项和
等差数列的前n项和公式
公式总结
等差数列的前n项和公式为Sn=n/2(a1+an),其中n为项数, a1为首项,an为末项。
公式证明
通过采用倒序相加法,将前n项和与后n项和相加,得到 2Sn=n(a1+an),从而得到前n项和公式。
xx年xx月xx日
contents
目录
• 引言 • 等比数列的前n项和公式推导 • 等比数列的前n项和的应用 • 特殊等比数列的前n项和 • 等比数列的前n项和求解方法 • 习题解答与练习
01
引言
课程背景
教学内容的重要性
等比数列是数学中的一个重要概念,其前n项和在数学、物理 、工程等领域有着广泛的应用。
特殊情况
当公比q不等于1时,等比数列的前n项和公式为 Sn=a1(1-q^n)/(1-q)。
05
等比数列的前n项和求解方法
利用公式求解等比数列的前n项和
公式法
利用等比数列的前n项和公式求解,当已知等比数列的首项a1和公比q时,可以直 接套用公式求出前n项和。
记忆口诀
为了方便记忆,可以总结一个简单的记忆口诀:“首项乘1减公比除以1减公比的 n次方”,这个口诀可以快速帮助我们记忆公式。
02
等比数列的前n项和公式推导
公比为r的等比数列求和公式推导
公式推导
$S_n = \frac{a_1}{1-r} * (1 - r^n)$
VS
推导步骤
将等比数列的每一项分别代入求和公式中 ,得到$S_n = a_1 + a_2 + \cdots + a_n$,再将$a_1 = ar, a_2 = ar^2, \cdots, a_n = ar^n$代入$S_n$中,经过 化简得到最终的求和公式。
04
特殊等比数列的前n项和
等差数列的前n项和公式
公式总结
等差数列的前n项和公式为Sn=n/2(a1+an),其中n为项数, a1为首项,an为末项。
公式证明
通过采用倒序相加法,将前n项和与后n项和相加,得到 2Sn=n(a1+an),从而得到前n项和公式。
第七章第三节 等比数列及其前n项和课件

3.能在具体的问题情境中,发现数 种题型都有可能出现.
列的等比关系,并解决相应的问题. 学科素养: 数学运算、逻辑推理、
4.体会等比数列与指数函数的关系.数学抽象.
知识·分步落实
⊲学生用书 P106
1.等比数列的有关概念 (1)定义 如果一个数列从_第__2_项__起,每一项与它的前一项的比等于_同__一__常__数_(不为 零),那么这个数列就叫做等比数列.这个常数叫做等比数列的_公__比_,通常用 字母_q_表示,定义的表达式为__a_an_+n_1 _=__q_.
D.83
(1)A (2)ABD [(1)根据等比数列性质知 a3a7a15=a29 a7=a28 a9=6,故
a9=a628 =23 . (2)依题意,数列是{an}是正项等比数列,∴a3>0,a7>0,a5>0,
∴ 6 =a23 +a37 ≥2 因为 a5>0,
a23·a37
=
2
6 a25
,
所以上式可化为 a5≥2,当且仅当 a3=236 ,a7= 6 时等号成立.
2.在数列{bn}中,点(bn,Tn)在直线 y=-12 x+1 上,其中 Tn 是数列{bn} 的前 n 项和.
求证:数列{bn}是等比数列. 证明: ∵点(bn,Tn)在直线 y=-12 x+1 上, ∴Tn=-12 bn+1.① ∴Tn-1=-12 bn-1+1(n≥2).②
①②两式相减,得 bn=-12 bn+12 bn-1(n≥2). ∴32 bn=12 bn-1,∴bn=13 bn-1. 由①,令 n=1,得 b1=-12 b1+1,∴b1=23 . ∴数列{bn}是以23 为首项,13 为公比的等比数列.
2.(必修 5P53 练习 T3 改编)对任意等比数列{an},下列说法一定正确
4.3.2.1等比数列的前n项和公式课件(人教版)
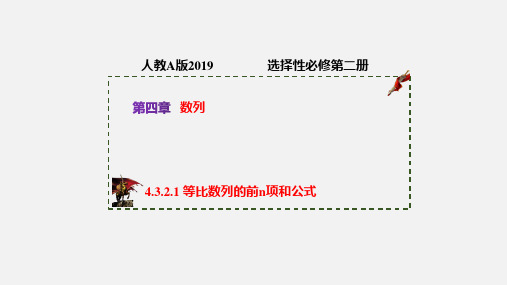
1-3n 解:(1)由题设知{an}是首项为 1,公比为 3 的等比数列,所以 an=3n-1,Sn= 1-3 =
12(3n-1). (2)因为 b1=a2=3,b3=1+3+9=13,b3-b1=10=2d,
所以公差 d=5, 故 T20=20×3+20×219×5=1 010.
6.将数列{an}中的所有项按“第一行三项,以下每一行比上一行多一项”的规则 排成如下数表. 记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知: ①在数列{bn}中,b1=1,对于任何n∈N*,都有(n+1)·bn+1-nbn=0; ②表中每一行的数从左到右均构成公比为q(q>0)的等比数列; ③a66=25.
当已知a1,q与an时,用Sn=a11--aqnq 比较方便.
在公差不为零的等差数列{an}中,a1=1,且a1,a2,a5成等比数列. (1)求{an}的通项公式. (2)设bn=2an,求数列{bn}的前n项和Sn.
【解析】(1)设等差数列{an}的公差为d,由已知得a22 =a1a5, 则(a1+d)2=a1(a1+4d),将a1=1代入并化简得d2-2d=0,解得d=2或d=0(舍去). 所以an=1+(n-1)×2=2n-1. (2)由(1)知bn=22n-1,所以bn+1=22n+1,所以bbn+n 1 =22n+1-(2n-1)=4,所以数列{bn} 是首项为2,公比为4的等比数列.
∴an=3an-1(n≥2),
∴数列{an}是首项 a1=-2,公比 q=3 的等比数列,
∴S5=a1
1-q5 1-q
-2× 1-35 =
1-3
=-242.故选 B.
5.设数列{an}满足:a1=1,an+1=3an,n∈N*. (1)求{an}的通项公式及前n项和Sn; (2)已知{bn}是等差数列,Tn为其前n项和,且b1=a2,b3=a1+a2+a3,求T20.
12(3n-1). (2)因为 b1=a2=3,b3=1+3+9=13,b3-b1=10=2d,
所以公差 d=5, 故 T20=20×3+20×219×5=1 010.
6.将数列{an}中的所有项按“第一行三项,以下每一行比上一行多一项”的规则 排成如下数表. 记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知: ①在数列{bn}中,b1=1,对于任何n∈N*,都有(n+1)·bn+1-nbn=0; ②表中每一行的数从左到右均构成公比为q(q>0)的等比数列; ③a66=25.
当已知a1,q与an时,用Sn=a11--aqnq 比较方便.
在公差不为零的等差数列{an}中,a1=1,且a1,a2,a5成等比数列. (1)求{an}的通项公式. (2)设bn=2an,求数列{bn}的前n项和Sn.
【解析】(1)设等差数列{an}的公差为d,由已知得a22 =a1a5, 则(a1+d)2=a1(a1+4d),将a1=1代入并化简得d2-2d=0,解得d=2或d=0(舍去). 所以an=1+(n-1)×2=2n-1. (2)由(1)知bn=22n-1,所以bn+1=22n+1,所以bbn+n 1 =22n+1-(2n-1)=4,所以数列{bn} 是首项为2,公比为4的等比数列.
∴an=3an-1(n≥2),
∴数列{an}是首项 a1=-2,公比 q=3 的等比数列,
∴S5=a1
1-q5 1-q
-2× 1-35 =
1-3
=-242.故选 B.
5.设数列{an}满足:a1=1,an+1=3an,n∈N*. (1)求{an}的通项公式及前n项和Sn; (2)已知{bn}是等差数列,Tn为其前n项和,且b1=a2,b3=a1+a2+a3,求T20.
等比数列的前n项和PPT课件

讲授新课
1 2 22 23 24 263
这一格放 的麦粒可 以堆成一 座山!!!
263
湖南省长沙市一中卫星远程学校
讲授新课
分析: 由于每格的麦粒数都是前一格的2倍,
共有64格每格所放的麦粒数依次为:
湖南省长沙市一中卫星远程学校
讲授新课
分析: 由于每格的麦粒数都是前一格的2倍,
共有64格每格所放的麦粒数依次为:
1, 2, 22 , 23 , , 263.
湖南省长沙市一中卫星远程学校
讲授新课
分析: 由于每格的麦粒数都是前一格的2倍,
共有64格每格所放的麦粒数依次为:
1, 2, 22 , 23 , , 263.
它是以1为首项,公比是2的等比数列,
湖南省长沙市一中卫星远程学校
讲授新课
分析: 由于每格的麦粒数都是前一格的2倍,
湖南省长沙市一中卫星远程学校
等比数列的前n项和公式的推导1
一般地,设等比数列a1, 它的前n项和是
a2,
a3,
…,
an这…种求和
的方法,就
是错位相
减法!
湖南省长沙市一中卫星远程学校
等比数列的前n项和公式的推导1
一般地,设等比数列a1, a2, a3, …, an… 它的前n项和是
∴当q≠1时,
①
湖南省长沙市一中卫星远程学校
讲授新课
请同学们考虑如何求出这个和?
S64 1 2 22 23 263 ① 2S64 2(1 2 22 23 263 )
即 2S64 2 22 23 263 264 ②
由②-①可得:
2S64 S64 (2 22 23 263 264) (1 2 22 23 263 )
等比数列前n项和公式课件PPT

等比数列的特殊前n项和
对于等比数列,当公比q=1时,前n项和公式为Sn=na1;当q=-1时,Sn=a1a1*q^n/1+q。
等比数列前n项和公式的变种
倒序相加法
错位相减法
将等比数列的前n项和公式倒序相加, 可以得到新的求和公式。
通过错位相减法,可以求出等比数列 的通项公式。
分组求和法
将等比数列分组求和,可以简化计算 过程。
公式与其他数学知识的结合
总结词:综合运用
详细描述:等比数列前n项和公式可以与其他数学知识结合使用,以解决更复杂的数学问题。例如,可以与等差数列、函数、 极限等知识结合,用于解决一些综合性数学问题。
03
等比数列前n项和公式的扩展
特殊等比数列的前n项和
等差数列的前n项和
等差数列是一种特殊的等比数列,其前n项和公式为Sn=n/2 * (a1+an),其中 a1为首项,an为第n项。
等比数列前n项和公式的证明方法
数学归纳法
通过数学归纳法证明等比数列的前n 项和公式。
累乘法
通过累乘法证明等比数列的前n项和公 式。
04
等比数列前n项和公式的练习 与巩固
基础练习题
详细描述:通过简单的等比数列求和问题,让 学生熟悉并掌握等比数列前n项和的公式。
解题思路:利用等比数列前n项和公式,将数列中的 每一项表示为2的幂,然后求和。
05
等比数列前n项和公式的总结 与回顾
本节课的重点回顾
等比数列前n项和公 式的推导过程
等比数列前n项和公 式的适用范围和限制 条件
如何应用等比数列前 n项和公式解决实际 问题
本节课的难点解析
如何理解和掌握等比数列前n项和公 式的推导过程
对于等比数列,当公比q=1时,前n项和公式为Sn=na1;当q=-1时,Sn=a1a1*q^n/1+q。
等比数列前n项和公式的变种
倒序相加法
错位相减法
将等比数列的前n项和公式倒序相加, 可以得到新的求和公式。
通过错位相减法,可以求出等比数列 的通项公式。
分组求和法
将等比数列分组求和,可以简化计算 过程。
公式与其他数学知识的结合
总结词:综合运用
详细描述:等比数列前n项和公式可以与其他数学知识结合使用,以解决更复杂的数学问题。例如,可以与等差数列、函数、 极限等知识结合,用于解决一些综合性数学问题。
03
等比数列前n项和公式的扩展
特殊等比数列的前n项和
等差数列的前n项和
等差数列是一种特殊的等比数列,其前n项和公式为Sn=n/2 * (a1+an),其中 a1为首项,an为第n项。
等比数列前n项和公式的证明方法
数学归纳法
通过数学归纳法证明等比数列的前n 项和公式。
累乘法
通过累乘法证明等比数列的前n项和公 式。
04
等比数列前n项和公式的练习 与巩固
基础练习题
详细描述:通过简单的等比数列求和问题,让 学生熟悉并掌握等比数列前n项和的公式。
解题思路:利用等比数列前n项和公式,将数列中的 每一项表示为2的幂,然后求和。
05
等比数列前n项和公式的总结 与回顾
本节课的重点回顾
等比数列前n项和公 式的推导过程
等比数列前n项和公 式的适用范围和限制 条件
如何应用等比数列前 n项和公式解决实际 问题
本节课的难点解析
如何理解和掌握等比数列前n项和公 式的推导过程
高中数学选择性必修二(人教版)《4.3.2等比数列的前n项和》课件

则数列{an}为等比数列,即 Sn=Aqn-A(A≠0,q≠0,q≠1,n∈N *) ⇔数列{an}为_等__比__数__列__.
(二)基本知能小试
1.已知等比数列的公比为 2,且前 5 项和为 1,那么前 10 项和等于 ( )
A.31
B.33
C.35
D.37
解析:根据等比数列性质得S10S-5 S5=q5,
8
C.3
D.3
()
解析:法一:因为数列{an}是等比数列,所以 S6=S3+q3S3,S9=S6 +q6S3=S3+q3S3+q6S3,于是SS63=1+Sq33S3=3,即 1+q3=3,所以 q3=2.于是SS96=1+1+q3+q3q6=1+1+2+2 4=73.
法二:由SS63=3,得 S6=3S3. 因为数列{an}是等比数列,且由题意知 q≠-1,所以 S3,S6-S3,S9 -S6 也成等比数列,所以(S6-S3)2=S3(S9-S6),解得 S9=7S3,所以 SS96=73. 答案:B
题型三 等比数列前 n 项和的实际应用 [学透用活]
[典例 3] 一个热气球在第 1 min 上升了 25 m 的高度,在以后的每 1 min 里,它上升的高度都是它在前 1 min 上升高度的 80%.这个热气球 上升的高度能达到 125 m 吗?
[解] 用 an 表示热气球在第 n min 上升的高度. 由题意,得 an+1=80%an=45an. 因此,数列{an}是首项 a1=25,公比 q=45的等比数列. 热气球在 n min 里上升的总高度为
[答案] 70
[方法技巧] 解决有关等比数列前 n 项和的问题时,若能恰当地使用等比数列前 n 项和的相关性质,则可以避繁就简.不仅可以减少解题步骤,而且可 以使运算简便,同时还可以避免对公比 q 的讨论.
(二)基本知能小试
1.已知等比数列的公比为 2,且前 5 项和为 1,那么前 10 项和等于 ( )
A.31
B.33
C.35
D.37
解析:根据等比数列性质得S10S-5 S5=q5,
8
C.3
D.3
()
解析:法一:因为数列{an}是等比数列,所以 S6=S3+q3S3,S9=S6 +q6S3=S3+q3S3+q6S3,于是SS63=1+Sq33S3=3,即 1+q3=3,所以 q3=2.于是SS96=1+1+q3+q3q6=1+1+2+2 4=73.
法二:由SS63=3,得 S6=3S3. 因为数列{an}是等比数列,且由题意知 q≠-1,所以 S3,S6-S3,S9 -S6 也成等比数列,所以(S6-S3)2=S3(S9-S6),解得 S9=7S3,所以 SS96=73. 答案:B
题型三 等比数列前 n 项和的实际应用 [学透用活]
[典例 3] 一个热气球在第 1 min 上升了 25 m 的高度,在以后的每 1 min 里,它上升的高度都是它在前 1 min 上升高度的 80%.这个热气球 上升的高度能达到 125 m 吗?
[解] 用 an 表示热气球在第 n min 上升的高度. 由题意,得 an+1=80%an=45an. 因此,数列{an}是首项 a1=25,公比 q=45的等比数列. 热气球在 n min 里上升的总高度为
[答案] 70
[方法技巧] 解决有关等比数列前 n 项和的问题时,若能恰当地使用等比数列前 n 项和的相关性质,则可以避繁就简.不仅可以减少解题步骤,而且可 以使运算简便,同时还可以避免对公比 q 的讨论.
高中数学等比数列的前n项和性质及应用课件
思路探究:(1 )由 S 2,S 4-S 2,S 6-S 4 成等比数列求解.
S偶
(2 )利用
S奇
=q ,及 S 2n=S
奇+S
偶求解.
合作探究
思
而
学
(1 )A (2)24 [(1)∵{a n}为等比数列, ∴S 2,S 4-S 2,S 6-S 4 也为等比数列, 即 7 ,S 4-7 ,9 1 -S 4 成等比数列, ∴(S 4-7 )2=7 (9 1 -S 4),解得 S 4=2 8 或 S 4=-2 1 . ∵S 4=a 1+a 2+a 3+a 4=a 1+a 2+a 1q 2+a 2q 2 =(a 1+a 2)(1 +q 2)=S 2(1 +q 2)> S 2,∴S 4=2 8 .
2
2
128
S偶
1
[解]
设等比数列为{a n },项数为
2n ,一个项数为
2n
的等比数列中, =q .则 S奇
q= , 2
3
3
又
an
和
a n +1
为中间两项,则
a
n
+a
n
+1
= 1
2
8
,即
a1q
n -1+a 1q
n= , 128
1
1
又
a
1
= 2
,q
= 2
,
1 ∴
2
·21
n
-1
1 +
2
·21
n
= 1
高中数学
数列
等比数列
等比数列的前n项 和性质及应用
学习目标
学
而
思
1.等比数列前 n 项和的变式
a 1 1 -q n
4.3.1等比数列的前n项和公式课件(人教版)
4.3.1等比数列的 前n项和公式
知识回顾
等差数列
定义
an1 an d
等比数列
an1 q an
公差/公比 公差可以是正数、 公比不可以是0. 负数和0.
知识回顾
等差(比) 中项
等差数列
2A=a b
递推公式 an1 an d
通项公式 an a1 (n 1)d
等比数列
G2 =ab
an1 q an an a1qn1
a1(1 qn ) 1-q
,
S2n
Sn
a1(1 q2n ) 1-q
a1(1 qn ) 1-q
a1qn (1 1-q
qn)
qnSn ,
S3n
S2n
a1(1 q3n ) 1-q
a1(1 q2n ) 1-q
a1q2n (1 1-q
qn)
qn
S2n
Sn
,
例题
例3.已知等比数列{an}的公比q -1,前n项和为Sn ,证明Sn,S2n -Sn,S3n -S2n 成等比数列, 求这个数列的公比q.
Sn
=
a1
(1 qn 1 q
)
(q
1)
需要a1和q
an a1qn1
Sn
=
a1 an 1 q
q
(q
1)
需要a1,an和q
探究
当q 1时,
a1 a2 an; Sn a1 a2 an ,
na1
新知讲解 首项为a1,公比为q的等比数列{an} 的前n 项和Sn 公式为:
Sn
=
na1,
若 S10 S5
31 32
,
求公比q.
解:①若q 1,则
S10 10a1 2 31 ,
知识回顾
等差数列
定义
an1 an d
等比数列
an1 q an
公差/公比 公差可以是正数、 公比不可以是0. 负数和0.
知识回顾
等差(比) 中项
等差数列
2A=a b
递推公式 an1 an d
通项公式 an a1 (n 1)d
等比数列
G2 =ab
an1 q an an a1qn1
a1(1 qn ) 1-q
,
S2n
Sn
a1(1 q2n ) 1-q
a1(1 qn ) 1-q
a1qn (1 1-q
qn)
qnSn ,
S3n
S2n
a1(1 q3n ) 1-q
a1(1 q2n ) 1-q
a1q2n (1 1-q
qn)
qn
S2n
Sn
,
例题
例3.已知等比数列{an}的公比q -1,前n项和为Sn ,证明Sn,S2n -Sn,S3n -S2n 成等比数列, 求这个数列的公比q.
Sn
=
a1
(1 qn 1 q
)
(q
1)
需要a1和q
an a1qn1
Sn
=
a1 an 1 q
q
(q
1)
需要a1,an和q
探究
当q 1时,
a1 a2 an; Sn a1 a2 an ,
na1
新知讲解 首项为a1,公比为q的等比数列{an} 的前n 项和Sn 公式为:
Sn
=
na1,
若 S10 S5
31 32
,
求公比q.
解:①若q 1,则
S10 10a1 2 31 ,
2.5等比数列前n项和公式的推导 PPT课件
• C.6
D.7
解析:an=a1·qn-1=96=3·qn-1,∴qn-1=32,Sn=
a1-anq 1-q
=31--9q6q=189,1-1-32qq=63.解得q=2.∴n=6.
答案:C
• 3.已知等比数列{an}中,an>0,n=1,2,3, …,a2=2,a4=8,则前5项和S5的值为 ________.
5, a1
1 2
.求an和s
n
(3)a1 1,an 512 ,sn 341 .求q和n
当q 1时,S 1 (1) 说明: 解 (3: ) (当将 代 12as因 解 )qq55入 a3为 2得 14aq11aa时a1: 2n1112n11q,即 1.n,21.并作 在 在4a1a,数an1a且 qn五 为 利2q311(列12q1要2个0n第 用n5为 n551根 变一 公 1q,,212常 25a1s据量 ,要 式14an所 1)1数12q具(a2素 , 111以 .列 ,解 体,q81来 q2一Saqn2,1题2)n得 考 定n15,1,52意a虑 要 , : 12n22q,1,q,。 注 [11qS3nn选((中 , 4意1得 311择12,))所 q1n代 2: 的 适(]只以 当 取 入 2知S)的值nn三S公, 1n可n式应 求a1。把二a1n1它,2aqnnq 可得
• 1.数列{2n-1}的前99项和为( )
• A.2100-1
B.1-2100
• C.299-1
D.1-299
解析:a1=1,q=2,∴S99=1×11--2299=299-1. 答案:C
• 2.在等比数列{an}中,已知a1=3,an=96 ,Sn=189,则n的值为( )
4321等比数列的前n项和公式课件共60张PPT
课堂篇·互动学习
类型一 等比数列基本量的计算
[例 1] 在等比数列{an}中, (1)若 a1=1,a5=16,且 q>0,求 S7; (2)若 Sn=189,q=2,an=96,求 a1 和 n; (3)若 a3=3,S3=9,求 a1 和公比 q. [思路分析] 根据题设条件,将已知量代入等比数列的通项公式与前 n 项和公 式进行求解.
(3)①当 q≠1 时,S3=a111--qq3=9,
又 a3=a1·q2=3,
∴a1(1+q+q2)=9,即q32(1+q+q2)=9,
解得 q=-12(q=1 舍去),∴a1=12.
②当 q=1 时,S3=3a1,∴a1=a3=3.
a1=12, 综上得q=-12
或aq1==13. ,
1.在等比数列中,对于 a1,q,n,an,Sn 五个量,若已知其中三个量就可求 出其余两个量,常常列方程组来解答问题,有时会涉及高次方程或指数方程,求解 可能遇到困难,这时要注意表达式有什么特点,再采取必要的数学处理方法,如换 元.
2.在解决与等比数列前 n 项和有关的问题时,首先要对公比 q=1 或 q≠1 进 行判断,若两种情况都有可能,则要分类讨论.
[变式训练 1] (1)在等比数列{an}中,若 a1+a3=10,a4+a6=54,求 a4 和 S5.
(2)在等比数列{an}中,若 q=2,S4=1,求 S8. (3)设等比数列{an}的前 n 项和为 Sn,已知 a2=6,6a1+a3=30.求 an 和 Sn.
3将实际问题抽象为数学问题,将已知与所求联系起来,列出满足题意的数 学关系式.
[变式训练 2] 小华准备购买一台售价为 5 000 元的电脑,采用分期付款方式, 并在一年内将款全部付清.商场提出的付款方式为:购买 2 个月后第 1 次付款,再 过 2 个月后第 2 次付款,……,购买 12 个月后第 6 次付款,每次付款金额相同, 约定月利率为 0.8%,每月利息按复利计算,求小华每期付款金额是多少? (1.00812≈1.10)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.在等比数列{an}中, (1)已知a1=3,an=96,Sn=189,求n; (2)已知S3=72,S6=623,求an; (3)a3=-12,前3项和S3=-9,求公比q. (4)a1+an=66,a2an-1=128,Sn=126,求n和q.
解析: (1)由Sn=a11--aqnq=3- 1-96qq=189,解得q=2. 又an=a1qn-1, ∴96=3·2n-1,即2n-1=32, ∴n-1=5,即n=6. (2)已知S6≠2S3,则q≠1, 又∵S3=72,S6=623,
[策略点睛]
[规范作答] 由题意知q≠1,且a111--qqn=4a1q[11--q2q2n2] 即14+qq=1,∴q=13. ∵a2·a4=9(a3+a4), ∴a1q·a1q3=9(a1q2+a1q3), ∴a1·q2=9(1+q), 即a1·132=91+13.
∴a1=108,∴an=108·13n-1=3n4-4, ∴lgan=2lg2-(n-4)lg3. ∴当n≥2时, lgan-lgan-1=2lg2-(n-4)lg3-[2lg2-(n-5)lg3] =-lg3<0. ∴数列{lgan}是 递减的等差数列,且lga1=lg(22×33)> 0. 设数列{lgan}的前n项和最大,则llggaann≥ +1<0,0,
(1)若Sn=189,q=2,an=96,求a1和n;
(2)若a1+a3=10,a4+a6=54,求a4和S5;
(3)若q=2,S4=1,求S8.
(1) Sn=a111--qqn,an=a1.qn-1 ―代―入――已―知―量→
列方程组 ―→ 求解
(2) 据an=a1qn-1 ―代――换→ 列方程组 ―→ 求a1,q ―→ 求a4和S5
列是Sn=aqn-a(a≠0,q≠0,n∈N+)的充分必要条件.
(3)在公比为字母参数的等比数列求和时,应分q=1与 q≠1两种情况进行讨论.
2.等比数列前n项和的性质
(1)数列{an}为公比不为-1的等比数列,Sn为其前n项 和,则Sn,S2n-Sn,S3n-S2n,…,仍构成等比数列.
(2)在等比数列的前n项和公式中,如果令A=
① 由②,得q4=2.
∴a17+a18+a19+a20=S20-S16=a111--qq20-a111--qq16 =a1q116-1-q q4=1·q16=24=16.
方法二:设S4=a,S8-S4=b,S12-S8=c,S16-S12= d,
S20-S16=e, 则a,b,c,d,e又成等比数列.
a1 q-1
―→
S30
[解题过程] 方法一:设公比为q,
则aa111111--- -qqqq1200==1300
① ②
② ①得1+q10=3,∴q10=2,
∴S30=a111--qq30 =a111--qq10(1+q10+q20)
=10×(1+2+4)=70.
方法二:∵S10,S20-S10,S30-S20仍成等比数列,
(2)设公比为q,由通项公式及已知条件得
a1+a1q2=10, a1q3+a1q5=54,
a11+q2=10, ① 即a1q31+q2=54. ②
∵a1≠0,1+q2≠0,∴②÷①得,q3=
1 8
,即q=
1 2
,∴a1
=8.
∴a4=a1q3=8×123=1,
S5=a111--qq5=8×11--12125=321.
若{an}是等差数列,则数列{aan}(a>0且a≠1) 是等比数列
(2)数列中与最值相关的问题,往往从单调性 考虑;求单调数列前n项和的最值的常用方法:
若{an}递增,且a1<0,则Sn有最小值,且满足aann≤+10≥,0
时Sn最小;
若{an}递减,且a1>0,则Sn有最大值,且满足aann≥-10≤,0 时, Sn最大.
所以q=12.
故an=a1qn-1=q-6·qn-1=6412n-1.
(2)证明:Sn=a111--qqn =6411--1212n =1281-12n<128.
1.在运用等比数列前n面和公式进行运算时应 注意以下几点:
(1)在等比数列的通项公式及前n项和公式中共 有a1,an,n,q,Sn五个量,知道其中任意三 个量,都可求出其余两个量.
(3)方法一:设首项为a1, ∵q=2,S4=1,∴a111--224=1,即a1=115, ∴S8=a111--qq8=11511--228=17. 方法二:∵S4=a111--qq4=1,且q=2, ∴S8=a111--qq8=a111--qq4(1+q4)=S4·(1+q4) =1×(1+24)=17.
等比数列的前n项和
等比数列的前n项和
1.理解并掌握等比数列前n项和公式及其推导过 程.
2.能够应用前n项和公式解决等比数列有关问题.
3.进一步提高解方程(组)的能力,以及整体代换思 想的应用能力.
1.对等比数列前n项和公式的考查是本课时的热点.
2.本课时常与函数、不等式、方程结合命题.
即22llgg22--nn--43llgg33≥<00,, ∴nn≤ >43+ +lloogg3344. ⇔3+log34<n≤4+log34. 又∵1<log34<2,n∈N+,∴n=5, ∴数列{lg an}的前5项和最大.
[题后感悟] (1)若{an}是等比数列,且an>0, 则数列{logaan}(a>0且a≠1)是等差数列;
(3) 据Sn=a111--qqn ―代―入―数―据→ 求出a1 ―再―用―公―式→ 求S8
[解题过程]
(1)由Sn=
a11-qn 1-q
,an=a1qn-1以及已知条
件得189=a111--22n, 96=a1·2n-1,
∴a1·2n=192,∴2n=1a912. ∴189=a1(2n-1)=a11a912-1,∴a1=3. 又∵2n-1=936=32,∴n=6.
a111--qq3=72
①
即a111--qq6=623
②
②÷①得1+q3=9,∴q=2.
将q=2代入①,可求得a1=12, 因此an=a1qn-1=2n-2. (3)方法一:由已知可得方程组
a3=a1·q2=-12
①
S3=a11+q+q2=-9 ②
②÷①得1+qq+ 2 q2=34,即q2+4q+4=0.
3.多以选择题、填空题的形式考查,有时也在解答题中 考查.
1.如何用数学语言表述等比数列的定义?
若
an+1 an
=q,其中n∈N+,q是非零常数,则称数列{an}
为等比数列.
2.等比数列的通项公式是:an=a1·qn-1(n∈N+). 3.还记得等差数列的前n项和公式吗?
若{an}是等差数列,则Sn=na12+an=na1+nn- 2 1d.
等比数列的前n项和公式
已知量 首项、公比与项数 首项、末项与公比
na1q=1
na1q=1
求和公式 Sn= a111--qqnq≠1 Sn= a11--aqnqq≠1
1.在等比数列{an}中,若a1=1,a4=
1 8
,则该数列的
前10项和为( )
A.2-218
B.2-219
C.2-2110
D.2-2111
∴qn= =26
或q=12 n=6
.
已知等比数列{an}中,前10项和S10=10, 前20项和S20=30,求S30.
方法一:
根据条件 设公比为q ―→ 列方程组 ―→ 解出q ―→ 代入求S30
方法二:
根据题意S10;S20-S10, S30-S20成等比数列
―→
S10=10, S20=30
3.已知实数列{an}是 等比数列,其中a7=1, 且a4,a5+1,a6成等差数列.
(1)求数列{an}的通项公式; (2) 数 列 {an} 的 前 n 项 和 记 为 Sn , 证 明 : Sn <
128(n=1,2,3,…).
解析: (1)设等比数列{an}的公比为q(q∈R), 由a7=a1q6=1,得a1=q-6, 从而a4=a1q3=q-3,a5=a1q4=q-2, a6=a1q5=q-1. 因为a4,a5+1,a6成等差数列, 所以a4+a6=2(a5+1), 即q-3+q-1=2(q-2+1), q-1(q-2+1)=2(q-2+1).
[题后感悟] (1)与等差数列类似.在等比数列 中,利用通项公式和前n项和公式同样可以在 五 个 基 本 量 a1 、 q 、 an 、 Sn 、 和 n 中 “ 知 三 求 二”.
(2)运用等比数列的前n项和公式时,必须注意 公比q是否为1,并且常用到等式两边约分或两 式相除的办法进行化简或消元.
答案: A
3.设{an}是公比为正数的等比数列,若a1=1, a5=16,则数列{an}前7项的和为________.
解析: ∵公比q4=aa15=16, 且q>0,∴q=2, ∴S7=11--227=127.
答案: 127
4.在等比数列{an}中,已知a1+a2+…+an= 2n-1,则a12+a22+…+an2等于________.
Hale Waihona Puke (2)在应用公式求和时,应注意到公式的使用条件为
q≠1,而当q=1时应按常数列求和,即Sn=na1,由于非常
数列的等比数列的前n项和Sn=
a11-qn 1-q
=-
a1 1-q
qn+
a1 1-q
,可以看出,式子的组成是由一个指数式与一个常数
的和构成的,而指数 式的系数与常数项互为相反数,由此
可以根据前n项和公式判断等比数列,即非常数列为等比数
又S10=10,S20=30, ∴S30-S20=S30-30=30-10102,
即S30=70.
[题后感悟] 通过两种解法比较可看出,利用 等比数列的性质解题,思路清晰,过程较为简 捷.
