质心力学 (2)
物理-质心与质心运动定理

x
——动量中心系
在质质心心参位考矢系中r:C x 质心速度 υC
0drC
dt
0
质点系m的i总i 动m量C 0
质心系是零动量系
质心的运动轨迹?
——抛物线.
0 O x1
m xC x2 C
mx
二、 质心运动定理
锥体为什么会上滚?
锥体上滚是由其质(重)心下降所引起的。
令人称奇的“水往高处流”。
上坡省力,下坡费劲的“怪坡 ”
三、 质心参考系
【质心参考系】:以质心为坐标原点的参考系。
y
r2
O
y
mi
m2 ri
ri
C
rC m1 r1
m1
l
C
m2
x
O
xC
m2 m1 m2
l
m1
l
C
m2
m1l1 m2l2
l1
l2
(与坐标系无关)
质心坐标与所选坐标系有关,
但质心相对物体各部分位置是确定的.
一、 质心
例2 求半径为R的匀质半圆环的质心.
y
Rdθ
dθ
R
θ
O R cos θ
y R sin θ
x
一、 质心
例2 求半径为R的匀质半圆环的质心.
C 恒矢量
当质点系所受合外力为零时,其质心保持原来的 静止或匀速直线运动状态不变。 ——质心的“惯性运动”
质心的“惯性运动”与质点系动量守恒等价!
随堂练习
例:设有一枚炮弹发射的初速率为 0,发射角为 ,它飞 行在最高点处爆炸成质量相等的两个碎片,其中一个竖直 下落,另一个水平抛出,求这两部分的着地点(忽略空气 阻力)。
(1) 直角坐标系中的质心坐标
06-6质心力学定理

V M
C O
的速度) 对 的速度 又 ∵ v ≈ v ′ ( v ′是m对M的速度 1 ∴ m υ ′ 2 + ∆E引 = 0 2 地球参考系不是惯性系⇒ • 地球参考系不是惯性系⇒ 动量守恒不成立 地球参考系仍可正确表示系统的功能 功能关系 • 地球参考系仍可正确表示系统的功能关系
03/2006 S.H.Deng
12
质点组总动能等于质心动能与相对质心动能之和. 质点组总动能等于质心动能与相对质心动能之和. S.H.Deng
理学院 邓胜华
第6章 质心力学定理
二.重力势能与质心势能
定义: 定义:E C = Mgh C
E =
i i i
——质心重力势能 质心重力势能
质点组重力势能 ∑ m gh ——质点组重力势能 M =∑m ∑m h E = ∑ m gh = g ∑ m h = g ∑m ∑m
× m i v iC ) + ∑ (riC × m i v C )
i
S.H.Deng
i
OiBiblioteka C03/200614
理学院 邓胜华
第6章 质心力学定理
L = rC × ∑ m i v C + ∑ (riC × m i v iC ) + rC × ∑ (m i v iC ) i i i + ∑ (m i riC ) × v C
质心动量的改变量等于和外力的冲量. 质心动量的改变量等于和外力的冲量.
dv C = 又:M dt
∑F
i
i
即 M aC =
∑F
i
i
——质心运动定理 质心运动定理
质点组总质量与质心加速度的乘 积等于质点组所受到的合外力. 积等于质点组所受到的合外力. S.H.Deng 03/2006
《理论力学》第10章 质心运动定理

第10章 质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力,受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章 质心运动定理
18
例题 图示机构,均质杆OA长l,质量为m1,滑块A的质量为m2, 滑道CD的质量为m3。OA杆在一力偶(图中未画出)作用下作 匀角度ω转动。试求O处的水平约束反力(机构位于铅直平面
内,各处摩擦不计)。 C
A
O
E
D
★理论力学电子教案
第10章 质心运动定理
第10章 质心运动定理
27
ma A
第10章 质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章 质心运动定理
§2 质点系动量、冲量
质点动量: 质点系动量:
p mv
P mivi mvC
问:刚体系动量?
元冲量:
dI F dt
冲量:
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章 质心运动定理
1
第十章 质心运动定理&动量定理
★理论力学电子教案
第10章 质心运动定理
例谈质心和质心系在解题中的应用

例谈质心和质心系在解题中的应用陈新学(杭州学军中学教育集团文渊中学ꎬ浙江杭州311200)摘㊀要:文章从质心的概念出发ꎬ推导质心运动定理ꎬ阐述质心参考系ꎬ探讨应用质心相关知识解题注意的问题.关键词:质心ꎻ质心运动定理ꎻ质心系ꎻ物理竞赛中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)19-0123-03收稿日期:2023-04-05作者简介:陈新学(1978.11-)ꎬ男ꎬ安徽省休宁人ꎬ硕士ꎬ中学一级教师ꎬ从事高中物理教学研究.㊀㊀质心是力学的一个重要概念ꎬ一些看似复杂的力学问题ꎬ如果应用质心的相关知识分析ꎬ解题思路会变得清晰ꎬ解题过程会变得简单.本文借助于几个典型问题探讨质心的概念㊁质心运动定理以及质心参考系在解题中的应用.1质心的相关概念1.1质心和质心运动定理设N个质点组成的系统(简称质点系或系统)中ꎬ各质点的位置矢量(简称位矢)分别为r1ꎬr2ꎬ ꎬrNꎬ定义此质点系的质心的位矢r⇀C=m1r⇀1+m2r⇀2+ +mNr⇀Nm1+m2+ +mN=ðNi=1mir⇀iðNi=1mi=ðNi=1mir⇀imꎬ(1)其中m=ðNi=1miꎬ为质点系的总质量.可知ꎬ质心的位矢是以质量为权重的质点系的加权位矢平均值.式(1)两边对时间求导得质心的速度vC=ðNi=1miv⇀imꎬ(2)或mv⇀C=ðNi=1miv⇀i可知质点系的总动量等于质心的动量.式(2)两边对时间求导得质心的加速度aC=ðNi=1mia⇀imꎬ(3)在惯性系中ꎬ对于质点系ꎬ由牛顿第二定律可得F外=ðNi=1mia⇀iꎬ(4)其中F外为质点系所受到的外力的矢量和ꎬ由式(3)和式(4)得F外=ma⇀Cꎬ(5)由式(5)知ꎬ质心的加速度由质点系受到的外力的矢量和确定ꎬ与质点系的内力无关ꎬ这个结论称为质心运动定理.1.2质心参考系质心参考系是指相对质心不动的参考系ꎬ简称质心系.如果质心相对惯性系做匀速直线运动ꎬ则质心系也是惯性系ꎻ如果质心相对惯性系做加速运动ꎬ321则质心系是非惯性系.2例题例1㊀在光滑的水平面上放一半径为a㊁质量为M的圆环ꎬ在某一瞬间有一质量为m的甲虫由静止开始沿此圆环爬行.求甲虫及圆环中心的运动轨迹.解析㊀甲虫和圆环组成的系统受到的外力的矢量和为0ꎬ且甲虫和圆环的初状态都是静止的ꎬ根据质心运动定理知ꎬ甲虫和圆环组成的系统的质心静止不动.甲虫沿圆环爬行ꎬ甲虫到圆环中心的距离不变ꎬ始终为圆环的半径ꎬ故甲虫㊁圆环中心到质心的距离都不变ꎬ分别为r1=MaM+mꎬr2=maM+mꎬ即甲虫㊁圆环的中心的轨迹都是圆.以系统质心为坐标原点ꎬ甲虫的轨迹方程为x2+y2=(MaM+m)2ꎬ圆环中心的轨迹方程为x2+y2=(maM+m)2.例2㊀一块长为L的大平板静放在光滑水平面上ꎬ一小孩骑着儿童自行车(小孩和车的大小可忽略不计)以v0的速度从板的一端驶上平板ꎬ在板上他的速度忽快忽慢ꎬ在将近板的另一端时ꎬ他突然刹车ꎬ停在板端.已知人在板上骑车的时间为tꎬ板的质量为Mꎬ小孩与车的总质量为m.求从车驶上平板到车相对板刚静止时板的位移[1].图1㊀例2示意图例3㊀如图2所示ꎬ用劲度系数为k的轻弹簧连接放在光滑水平面上质量分别为m1㊁m2的木块.让第一个木块紧靠竖直墙ꎬ在第二个木块的侧面上施加水平压力ꎬ将弹簧压缩L长度ꎬ撤去这一压力后ꎬ求系统质心可获得的最大加速度值和最大速度值.图2㊀例3示意图解析㊀由质心运动定理知ꎬ外力的矢量和最大时ꎬ质心的加速度最大.分析可知刚撤去压力时ꎬ弹簧弹力最大ꎬ竖直墙施加的外力最大ꎬ大小为kLꎬ所以系统质心可获得的最大加速度为aCm=kLm1+m2ꎬ此后弹簧弹力减小ꎬ系统质心做加速度减小的加速运动ꎬ直至木块m1离开墙ꎬ系统质心开始做匀速直线运动ꎬ所以木块m1刚离开墙时系统质心的速度最大ꎬ设此速度为vCmꎬ从撤去压力到木块m1刚离开墙ꎬ系统的机械能守恒:12kL2=12m2v22ꎬ其中v2为木块m1刚离开墙时木块m2的速度ꎬ得v2=Lkm2ꎬ由式(2)得系统质心的最大速度vCm=m1 0+m2v2m1+m2=Lkm2m1+m2.例4㊀三个等质量物块静止地放在光滑平面上ꎬ排成一直线ꎬm1=m2=m3=mꎬ其中m2和m3用弹性系数为k的弹簧相连ꎬ并保持自然长度ꎬ如图3所示.现在m1以速度v冲向m2ꎬ二者发生完全非弹性碰撞ꎬ求此后的运动中:(1)物块m3的最大动能ꎻ(2)物块m2的最小动能[1].图3㊀例4示意图答案:(1)29mv2㊀(2)172mv2421例5㊀如图4所示ꎬ长为L㊁质量线密度为λ的匀质软绳ꎬ开始时绳两端A和B一起悬挂在天花板上相距较近的两点.A端的天花板能够提供的最大拉力为1.5λLgꎬ其中g为当地重力加速度.求:(1)B端下落多长时间后ꎬA端与天花板脱离?(2)A端与天花板脱离后ꎬ经过多长时间绳子完全伸直?图4㊀例5示意图解析㊀(1)以天花板上的A点为原点ꎬ竖直向下为正方向建立x轴ꎬB端自由下落x时ꎬ右侧绳子质心的速度为u=2gxꎬ右侧绳长为L-x2ꎬ左侧绳子质心的速度始终为0ꎬ整条绳子质心的速度为vC=0+λ(L-x)2uλL=(L-x)2gx2Lꎬ整条绳子质心的加速度aC=dvCdt=g(L-3x)2Lꎬ计算时应用了u=dxdtꎬ对整条绳子应用质心运动定理得λLg-F=λLaCꎬ其中F为天花板对绳子A端的拉力ꎬ即F=(L+3x)λg2ꎬ当F=1.5λLg时ꎬx=23LꎬA端与天花板脱离ꎬ又x=12gt21ꎬ得t1=233Lgꎬ为所求的时间.(2)由第(1)问知ꎬA端与天花板脱离时ꎬx=23Lꎬ此时B端的速度uB=2gx=23gL3ꎬ左侧绳子速度为0ꎬ应用式(2)得整条绳子质心的速度vC=0+Lλ6uBLλ=3gL9ꎬ此后整条绳子质心和绳子B端都以加度度g向下做直线运动ꎬ在质心参考系中ꎬ绳子B端做匀速直线运动ꎬB端相对质心的速度vr=uB-uC=53gL9ꎬ刚脱离时整条绳子质心的坐标为xC=1736Lꎬ绳子B端坐标为xB=23LꎬB端到质心的距离为xB-xC=736Lꎬ绳子完全伸直时B端到整条绳子质心的距离为L2ꎬ从A端脱离到绳子完全伸直ꎬB端在质心系中的位移Δx=12L-736L=1136Lꎬ所求时间t2=Δxvr=11603Lg.综上所述ꎬ应用质心的相关知识解题时ꎬ一般先分析系统所受的外力ꎬ根据质心运动定理ꎬ结合质心的初速度ꎬ判断质心的运动情况ꎬ再分析各质点或系统的各部分相对质心的运动.在质心系中分析问题时ꎬ应注意质心系是惯性系还是非惯性系ꎬ如果质心系是非惯性系ꎬ受力分析时还要考虑到惯性力.解题时还应注意各物理量的值在质心系和其他惯性系(例如地面参考系)中的区别和联系ꎬ计算时不能混淆.参考文献:[1]程稼夫.中学奥林匹克竞赛物理教程力学篇:第2版[M].合肥:中国科学技术大学出版社ꎬ2013(06):436-437.[责任编辑:李㊀璟]521。
123质心运动定理理论力学
y A
A, Co
, C
, B
B mg
x
FN
解:以均质杆AB为研究对象,并以杆AB铅直时的 轴线为 y轴,建立图示坐标系。AB杆倒下过程中所受外力 有:重力mg,光滑水平面的法向反力FN, 杆在倒下的过程中有:
? FRex ? Fixe ? 0
即质点系动量在 x方向上守恒,
又:t=0时杆处于静止 故质心运动在x方向上守 恒,有:
§12.3 质心运动定理
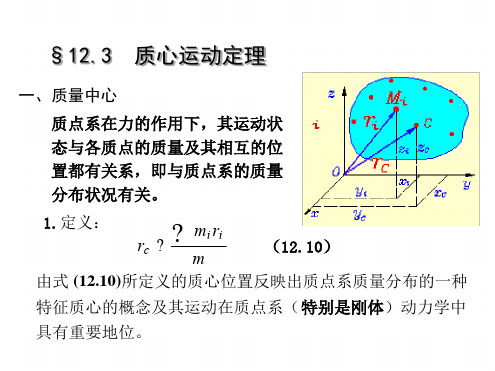
一、质量中心
质点系在力的作用下,其运动状 态与各质点的质量及其相互的位 置都有关系,即与质点系的质量 分布状况有关。
1.定义:
? rc ?
mi ri m
(12.10)
由式 (12.10)所定义的质心位置反映出质点系质量分布的一种
特征质心的概念及其运动在质点系( 特别是刚体)动力学中
具有重要地位。
? mi ri
rc ? 2.质心的力学意义
m
① 若质点系中各质点的质量相等,则:
rc
?
m r1 ? m r2 ? ......? m m? m? ......? m
rn
? ? r1 ? r2 ? ......? rn ? n
1 n ri
1/n 与 i 无关,为公因子。
(12.11)
式中: ri系数 1/n 表示第 i个质点的质量在质点系质量中 所占的比例,质心的矢径rc即为各质点的平均矢径。
(1)
x2 ? ecos? t y2 ? esin? t (2)
(3) 代入质心坐标公式得 质心 c 的运动方程:
? ??
xc
?
m2 m1 ? m2
e cos?
t
?
? ??
质心运动定理

(1)机构质心的运动方程。 (2)作用在 O 点的最大水平力。
解
(1)取曲柄、滑块和滑杆组成的系 统为研究对象。
图9-7
(2)受力分析。系统受力如图9-7所示。
(3)运动分析。取 O点为坐标原点,
x 轴水平向右为正,y轴铅垂向上为正,
则质点系的质心坐标为
xC
P1x1 P2 x2 P3x3 P1 P2 P3
n
MaC
F (e) i
(9-20)
i 1
式(9-20)就是质心运动定理,即质点系的质量与质心加 速度的乘积等于质点系所受外力的矢量和。
将(9-20)写成投影形式为
MaCx
n
F (e) ix
i 1
MaCy
n
F (e iy
)
i 1
n
MaCz
F (e) iz
i 1
(9-21)
例9-4
2P3
l 2
cost
所以
Fx,max
P1
2P2 2P3 2g
l 2
从质心运动定理可以看出:如果作用在质点系上的所有外力的
矢量和恒等于零,则质心做匀速直线运动或静止,即式(9-20)
n
中
F (e) i
0
,则有
i 1
vC 常矢量
如果作用在质点系上的所有外力在某轴上的投影的代数和恒等于
n
零,则质心速度在该轴上的投影保持不变。例如,
电机如不用螺杆固定,则其跳起地面的条件 Fy,min 0 ,即 (m1 m2 )g m2e2 0
解得
m1 m2 g m2e
当电机的转子的转速超过 m1 m2 g 时,电机会跳离地面。
质心运动课件
一.质心动能定理 (科尼希定理)
一个质点组的质心在C,如图.
z S
ric C
mi
rc
对某参照系S, 定义:
O
ri
EC
1 2
MvC2
——质心动能
x
y
是否相等?
Ek
i
1 2
mi
vi2——质点组总动能
可以证明:
对 质某点参组照 总系 动, 能:Ek EC ErC
——质心动能定理 (科尼希定理)
质点组总动能 = 质心动能 + 质点组相对质心的动能
ErC
vrriiCC
i
1 2
mi
vi2C
是质点组相对质心的总动能
是第i个质点相对于质心C的位 速率矢
18
科尼希定理: Ek EC ErC 证明如下: z
r riC
是第i
个质点相对于质心C的位矢
如图:对某参照系S,
ri
v
2 i
rC
i
1 2
mi vi2C
i
1 2
mi
2vC
viC
19
Ek
i
1 2
mi vC2
i
1 2
mi vi2C
i
rr mivC viC
r r r mivC viC vC
r mi viC
vC
0
0
i
i
质心系中质点组总动量
=质心系中的质心动量
Ek
i
1 2
dLrC dt
M rC
质点组对质心的 角动量变化定理
质点组的角动
质点组相对于质心的角动量的时间 量变化定理在
变化率 = 各外力对质心的总力矩
质点动力学-动量及动量定理 (2)
柔绳对桌面的冲力F=-F’ 即:
M 2 2 Fv v 而 v 2 g x FM 2 g x / L L
2
而已落到桌面上的柔绳的重量为mg=Mgx/L 所以F总=F+mg=2Mgx/L+Mgx/L=3mg
fi 0
i
'
f
质点系
结论:质点系的内力之和为零
F
外力: 系统外部对质点系内部质点的作用力 约定:系统内任一质点受力之和写成 外力之和
F i fi
内力之和
二、质点系的动量定理
•两个质点的系统
m
1
f
F1
F2
d P1 F1 f dt
m
2
f
d P P 1 d 2 F f F f 1 2 d t d t
解:以链条为系统,向上为X正向,地面为原点建立 坐标系。 t时刻,系统总动量 P X v xv a d x d v dP d(xv) v x x d t d t dt dt
v ax
2
O
变质量问题
系统动量对时间的变化率为:
d P 2 3 ax v ax 2 ax ax d t t时刻,系统受合外 Iy Iz
t2 t1 t2 t1 t2 t1
F x dt F y dt F z dt
+
0 t1 t2 t
(注意可取 + -号)
冲量的几何意义:冲量
I x 在数值上等于
Fx ~ t 图线与坐标轴所围的面积。
3、质点的动量定理
d v d P F m a m d t d t
6质心力学定理(2)
第6章 质心力学定理
二.重力势能与质心势能
定义:E C Mgh C
E
i i i
——质心重力势能
m gh ——质点组重力势能 M m m h E m gh g m h g m m
i i
是否相等?
i
i
i
i
i
i
i
i
i
i
i
i
Mgh C E C
即
E EC
d (r R) 1 1 相 f f 2 M dt m 减
2
31
第6章 质心力学定理
d (r R) 1 1 ( )f 2 dt m M
2
d r 1 1 ( )f 2 dt m M
2
1 1 m M
1
——约化质量(折合质量)
i
mi
i
MvC
rc
O
C
ric ri
m ivi
mi
ri m i v i rC riC m i v C v iC i i rC m i v C riC m i v iC i i rC m i v iC riC m i v C
28
第6章 质心力学定理
尽管质心系可能不是惯性系,但对质心来说, 角动量定理仍然成立。 这再次显示了质心的特殊之处 和选择质心系来讨论问题的优点。 若质心系是非惯性系,则外力矩中应包括 惯性力对质心的力矩:
i i 惯性力对质心的力矩之和为零。 这正是即使质心系为非惯性系,但质点系对质心的角 动量仍能满足角动量定理的原因。 29
i
大物力学第六章 质心力学
rc
l
两体运动体系: 两体运动体系:
质心位置: 质心位置
l2 l1 C
m2
m2 l l1 = m1 + m2
m1l l2 = m1 + m2
m1
m1l1 = m2l2
y m1 l
m1=m2=m3=m
l m3 l
m2
y m1 l
m1 * 0 + m2 * ( −l / 2) + m3 * (l / 2) =0 3m m1 * 3l / 2 + m2 * 0 + m3 * 0 x yc = = 3l / 6 3m xc =
例题: 例题: 计算质心位置
1)杆长为l,线密度为λ=cx,x为 杆长为l,线密度为λ=cx,x为 l,线密度为 离杆一端的距离,c为常量,求杆质心。 ,c为常量 离杆一端的距离,c为常量,求杆质心。
O
X
的质心,线密度为λ 的质心,线密度为λ
2)
的质心
)
4)
的质心
5)
的质心, 密度为ρ 的质心, 密度为ρ
i= 1
i
质心的动量
rc =
∑m r
i =1
n
c
i i
M
rc
i i
vc= i=1 M
∑mv
n
Mv c = ∑ m i v i = ∑ pi
结论: 结论:系统内各质点的动量的矢量和等于系统质心的速
度与系统质量的乘积
质心运动定理
F 力= 外
d(∑mvi ) i dt
=M
∑mv ) d(
i i
M dt
dvc = M = Mac dt
质心运动定律: 质心运动定律:作用在系统上的合外力等于系统的总
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22
第6章质心力学定理
§6-2.质心动能定理
如图:一.质心动能定理定义:2
C C M 21E v =——质心动能
∑=i 2
i i k m 2
1E v ——质点组总动能
iC C i r r r r r r +=是否相等?iC C i v v v r r r +=⇒i i 2
i v v r r ⋅=v ()()iC C iC C v v v v r r r r +⋅+=iC
C 2
iC 2C v v 2r r ⋅++=v v ∑
=i
2i i k m 2
1E v (
)
∑
⋅++=i
iC
C 2
iC 2C i v v 2m 2
1r r v v (科尼希定理)
x
y
z
m i
r c r i
C
r ic O
23
第6章质心力学定理
∑∑∑⎟
⎠⎞⎜⎝⎛⋅+⎟⎠⎞
⎜⎝⎛+⎟⎠⎞⎜⎝⎛=i iC C i i 2iC i i 2C i k v v 2m 21m 21m 21E r r v v ∑∑⋅⋅=⎟⎠⎞⎜⎝⎛⋅i
iC i C i iC C i v m v v v 2m 21
r r r r 质心系中质点组总动量
0v C ⋅=r 0=∑∑⎟⎠⎞
⎜⎝⎛+⎟⎠⎞⎜⎝⎛=i 2iC i i 2C i k m 21m 2
1E v v ∑⎟
⎠⎞⎜⎝⎛+=i 2iC i 2C m 21M 21v v rC
E C E rC
C k E E E +=——质心动能定理(科尼希定理)
质点组总动能等于质心动能与相对质心动能之和.
24
第6章质心力学定理
二.重力势能与质心势能
定义:C
C Mgh E =——质心重力势能
∑=
i
i
i
gh m E ——质点组重力势能是否相等?
∑=i i i gh m E ∑=i
i
i h m g ∑
∑∑=i
i
i
i
i
i
i m m
h
m g ∑=i
i
m
M C Mgh =C
E =C
E E =即
质心重力势能等于质点组总重力势能.
25
第6章质心力学定理
§6-3. 质心角动量定理定义:C C C v M r L r
r r ×=——质心角动量
——质点组总角动量∑=
i
i
m M 一.质心角动量
()∑×=i
i i i v m r L r
r r iC C i r r r r r r +=iC
C i v v v r
r r +=因为:是否相等?()∑×=
i i i i v m r L r r r ()()∑+×+=i iC C i iC C v v m r r r r r r ()∑×=i C i C v m r r r ()∑×+i iC i iC v m r r r ()∑×+i
iC i C v m r r r ()
∑×+i
C i iC v m r r
r m i
r c
r i
C
r ic C
v M r
i
i v m r i
F r O
26
第6章质心力学定理
L r C i i C v m r r
r ⎟⎟⎠⎞⎜⎜⎝⎛×=∑()∑×+i iC i iC v m r r r ()∑×+i iC i C v m r r r ()C
i
iC i v r m r
r ×+∑C C v M r r r ×=()∑×+i
iC i iC v m r r r 0r C ×+r C
v 0r
×+rC
L r rC
C L L r r +=rC
C L L L r r
r +=质点组总角动量等于质心角动量与相对质心角动量之和.
27
第6章质心力学定理
二.质心角动量变化定理
C
C
M dt
L d r r
=C C L M r r 和( 都对同一点O )
与单质点完全相同
∑
×
=i
i C C
F r M
r r r 三.相对质心角动量变化定理
质点组的角动量变化定理(
)
∑
×=i
i
i F r M dt L
d r r
r =外
iC
C i r r r r r
r +=rC
C L L L r r r +=dt
L d dt L d dt L d rC
C r r r
+=因为:左边:
28
第6章质心力学定理
C
C
M dt
L d r r
Q
=rC
rC
M dt
L d r r
=∴
(
)∑×i
i
i F r r r
(
)∑×=i
i C F r r r
(
)
∑×+
i
i
iC F r r r
C M r =rC
M r rC
M r +右边:
——相对质心角动量变化定理
相对质心角动量的时间变化率等于外力相对于质心的总力矩.
29
第6章质心力学定理
这再次显示了质心的特殊之处尽管质心系可能不是惯性系,但对质心来说,
角动量定理仍然成立。
和选择质心系来讨论问题的优点。
若质心系是非惯性系,则外力矩中应包括t
L M M C d d ′=
+′r r r 惯惯性力对质心的力矩:
∑−×′=i
i i C C a m r M )
(惯r
r r 设质心加速度为, C a r 则有
这正是即使质心系为非惯性系,但质点系对质心的角动量仍能满足角动量定理的原因。
∑=×′−=i i C i a r m 0r r )( 惯性力对质心的力矩之和为零。
第6章质心力学定理
§6-4. 有心运动方程与约化质量
行星
运动
30
31
第6章质心力学定理
一.有心运动方程
C
R r r
r r ′
r f ′
r f
r
M
m
R r r r r r −=′f
f r r −=′不考虑第三者的影响质心系可以是惯性系
f dt r d m 22r r =f dt R
d M 22′=r r f m 1dt r d 2
2r r =f M
1
dt R d 22′
=r r 相减
f M 1f m 1dt R r d 2
2
′−=−r r r
r )(
32
第6章质心力学定理
f M 1m 1dt R r d 22r r r )()(+=−f M 1m 1dt r d 22r r )(+=′
M 1
m 11
+=μμ——约化质量(折合质量)
f 1dt r d 22r r μ=′f dt r d 22
r r =′μ——行星运动方程
(有心运动方程)
虽然日心系是个非惯性系,但把行星的真实质量用约化质量替代,行星运动方程具有牛顿运动方程的表达形式。
33
第6章质心力学定理
二.日心系可作为准惯性系
f dt r d 22r r =′μ行星运动方程C R r
r r
r ′r f ′r f r M m
M>>m μ≈m f dt r d m 22r
r =′日心系可作为准惯性系
准惯性系的精度(相对偏差)
M
m
M m 111m m ≈+−=−=μ
Δ
第6章质心力学定理
•本章作业
•6.1, 6.3, 6.4,6.6,6.7
34。
