交集并集补集.ppt
3交集、并集

集合C ={| 是整数}
并集
• 定义:一般地,由所有属于A集合或者属
于B集合的元素组成的集合,称为集合A与集
合B的并集.记作:
• A∪B,读作“A并B”
• 符号语言表示为:
A∪B={| ∈A,或∈B}
• 图形语言为:
• 并集有哪些性质?
• 例1.(1)已知集合A={x|x>-1},B={x|x<2},
则A∩B=(
)
A.{x|x>-1}
B.{x|x<2}
C.{x|-1<x<2}
D.∅
• (2)若A={x∈N|1≤x≤10},B={x∈R|x2+x-6
=0},则图中阴影部分表示的集合为(
)
• A.{2} B.{3} C.{-3,2} D.{-2,3}
变式训练1
• 1.若集合A={x|-2<x<1},B={x|x<-1或
合的元素组成的集合,称为集合A与集合B的交
集.记作:
• A∩B,读作“A交B”
• 符号语言表示为:
A∩B={| ∈A且∈B}
• 图形语言为:
性质
观察下面的例子,你能发现集合之间有什么关
系吗?
(1)A={1,2,3},B={4,5,6},
C={1,2,3,4,5,6}
(2)集合A={| 是奇数},
交集、并集
集合的运算(补集):得到新的
集合
• 除了补集,还有哪些集合的运
算呢?
观察下面的例子,你能发现集合A,B
和C之间有什么关系吗?
(1)A={1,2,3},B={1,3,5},C={1,3}
(2)集合A={| 是菱形},
补集及综合应用 课件

对于一个集合 A,由全集 U 中不不属属于于集集合合AA的所有元素组成 的集合称为集合 A 相对于全集 U 的补集,记作_∁_U_A_____ ∁UA={x|x{∈x|xU∈,U且,—且—x —A}—A}
补集的运算 (1)已知全集为 U,集合 A={1,3,5,7},∁UA={2,4,6},∁UB={1,4,6}, 则集合 B=________; (2)已知全集 U={x|x≤5},集合 A={x|-3≤x<5},则∁UA=________.
[解] 法一(直接法):由 A={x|x+m≥0}={x|x≥-m},得∁UA={x|x<-m}. 因为 B={x|-2<x<4},(∁UA)∩B=∅,
所以-m≤-2,即 m≥2, 所以 m 的取值范围是 m≥2.
法二(集合间的关系):由(∁UA)∩B=∅可知 B⊆A, 又 B={x|-2<x<4},A={x|x+m≥0}={x|x≥-m}, 结合数轴:
与补集有关的参数值的求解 [探究问题] 1.若 A,B 是全集 U 的子集,且(∁UA)∩B=∅,则集合 A,B 存在怎样的关系? 提示:B⊆A 2.若 A,B 是全集 U 的子集,且(∁UA)∪B=U,则集合 A,B 存在怎样的关系? 提示:A⊆B
设集合 A={x|x+m≥0},B={x|-2<x<4},全集 U=R,且(∁UA)∩B =∅,求实数 m 的取值范围. 思路探究:法一: 由A求∁UA ∁结U―A合∩―数B→=轴∅ 建立m的不等关系 法二: ∁UA∩B=∅ 等―价―转→化 B⊆A
补集及综合应用
1.全集 (1)定义:如果一个集合含有我们所研究问题中涉及的所所有元素,那么就称这个 集合为全集. (2)记法:全集通常记作 UU. 思考:全集一定是实数集 R 吗? [提示] 全集是一个相对概念,因研究问题的不同而变化,如在实数范围内解 不等式,全集为实数集 R,而在整数范围内解不等式,则全集为整数集 Z.
集合的概念、子集、交集、并集、补集.

集合的概念、子集、交集、并集、补集课 题集合的概念、子集、交集、并集、补集教学目标1、了解集合的概念2、理解子集、补集以及全集的概念3、结合图形使学生理解交集并集的概念性质重点、难点重点:集合、子集、补集和全集的概念 难点:交集并集的概念,符号之间的区别与联系考点及考试要求理解集合及其表示;掌握子集、交集、并集、补集的概念。
教学内容一、知识回顾1、集合的概念。
2、集合的分类。
3、集合的性质。
4、常用的数集。
5、集合的表示。
6、元素与元素和集合与元素的关系以及集合与集合之间的关系。
二、全集与补集1 补集:一般地,设S 是一个集合,A 是S 的一个子集(即S A ⊆),由S 中所有不属于A 的元素组成的集合,叫做S 中子集A的补集(或余集),记作A C S ,即C S A=},|{A x S x x ∉∈且2、性质:C S (C S A )=A ,C S S=φ,C S φ=S3、全集:如果集合S 含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集,全集通常用U 表示S A三、典例分析例1、(1)若S={1,2,3,4,5,6},A={1,3,5},求C S A(2)若A={0},求证:C N A=N*A例2、已知全集U=R,集合A={x|1≤2x+1<9},求CUB的关系例3、已知S={x|-1≤x+2<8},A={x|-2<1-x≤1},B={x|5<2x-1<11},讨论A与CS四、课堂练习1、已知全集U={x|-1<x<9},A={x|1<x<a},若A≠φ,则a的取值范围是()(A)a<9(B)a≤9(C)a≥9(D)1<a≤92、已知全集U={2,4,1-a},A={2,a2-a+2}如果C U A={-1},那么a的值是?3、已知全集U,A是U的子集,φ是空集,B=C U A,求C U B,C Uφ,C U U4、设U={梯形},A={等腰梯形},求C U A.5、已知U=R ,A={x |x 2+3x+2<0}, 求C U A .6、集合U={(x ,y )|x ∈{1,2},y ∈{1,2}} ,A={(x ,y )|x ∈N*,y ∈N*,x+y=3},求C U A .7、设全集U (U ≠Φ),已知集合M ,N ,P ,且M=C U N ,N=C U P ,则M 与P 的关系是( )(A )M=C U P ; (B )M=P ; (C )M ⊇P ; (D )M ⊆P .五、交集和并集1.交集的定义一般地,由所有属于A 且属于B 的元素所组成的集合,叫做A,B 的交集.记作A B (读作‘A 交B ’), 即A B={x|x ∈A ,且x ∈B }.如:{1,2,3,6} {1,2,5,10}={1,2}.又如:A={a,b,c,d,e },B={c,d,e,f}.则A B={c,d,e}.2.并集的定义一般地,由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A,B 的并集.记作:A B (读作‘A 并B ’), 即A B ={x|x ∈A ,或x ∈B}).如:{1,2,3,6} {1,2,5,10}={1,2,3,5,6,10}.(1)交集与并集的定义仅一字之差,但结果却完全不同,交集中的且有时可以省略,而并集中的或不能省略,补集是相对于全集而言的,全集不同,响应的补集也不同;(2)交集的性质:A B B A =,A A A = ,∅=∅ A ,A B A ⊆ ,B B A ⊆ ;(3)并集的性质:A B B A =,A A A = ,A A =∅ ,B A A ⊆,B A B ⊆;(4)B A A B A ⊆⇔= ,A B A B A ⊆⇔= ;(5)集合的运算满足分配律:)()()(C A B A C B A =,)()()(C A B A C B A =;(6)补集的性质:∅=A C A u ,U A C A u = ,A A C C u u =)(;(7)摩根定律:B C A C B A C u u u =)(,B C A C B A C u u u =)(;六、典例分析例1 、设A={x|x>-2},B={x|x<3},求A B.例2 、设A={x|x 是等腰三角形},B={x|x 是直角三角形},求A B.例3 、A={4,5,6,8},B={3,5,7,8},求A B.例5、设A={x|-1<x<2},B={x|1<x<3},求A ∪B.说明:求两个集合的交集、并集时,往往先将集合化简,两个数集的交集、并集,可通过数轴直观显示;利用韦恩图表示两个集合的交集,有助于解题例6(课本第12页)已知集合A={(x,y)|y=x+3},{(x,y)|y=3x-1},求A B.注:本题中,(x,y)可以看作是直线上的的坐标,也可以看作二元一次方程的一个解.高考真题选录:一、选择题1.设集合{|32}M m m =∈-<<Z ,{|13}N n n MN =∈-=Z 则,≤≤( )A .{}01,B .{}101-,,C .{}012,,D .{}1012-,,, 2.已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合)(B C A U 等于( )A .{}|24x x -<≤B .{}|34x x x 或≤≥C .{}|21x x -<-≤D .{}|13x x -≤≤3.设集合{}{}{}1,2,3,4,5,1,2,3,2,3,4U A B ===,则=)(B A C U ( )(A){}2,3 (B){}1,4,5 (C){}4,5 (D){}1,54.设集合|0{8}x x N U =∈<≤,{1,2,4,5}S =,{3,5,7}T =,则=)(T C S U ( )(A ){1,2,4} (B ){1,2,3,4,5,7} (C ){1,2} (D ){1,2,4,5,6,8}5.集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1AB =-- B . ()(,0)RC A B =-∞C .(0,)A B =+∞D . }{()2,1R C A B =--6.满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1·a 2}的集合M 的个数是( )(A )1 (B)2 (C)3 (D)47.定义集合运算:{},,.A B z z xy x A y B *==∈∈设{}1,2A =,{}0,2B =,则集合A B *的所有元素之和为( )A .0B .2C .3D .68.已知全集{12345}U =,,,,,集合2{|320}A x x x =-+=,{|2}B x x a a A ==∈,,则集合)(B A C U 中元素的个数为( )A .1B .2C .3D .4二.填空题:1.若集合{}|2A x x =≤,{}|B x x a =≥满足{2}A B =,则实数a = .2.已知集合M={}R y x x y x ∈=+-,,01 ,N={}R y x y x y ∈=+,,122 则M ⋂N=______3.已知集合P={}{}R x x y y Q R x x y y ∈+-==∈+-=,2,,22,那么P ⋂Q=____________。
集合的交集、并集与补集

集合的交集、并集与补集集合是数学中的一个重要概念,它是由一些确定的对象组成的整体。
在集合论中,我们通常会涉及到集合的交集、并集与补集等操作。
这些操作不仅在数学中有广泛的应用,也在计算机科学、逻辑学等领域中起着重要的作用。
本文将详细介绍集合的交集、并集与补集的定义和性质,并给出一些具体的例子。
一、交集(Intersection)集合的交集是指包含同时属于两个集合的所有元素的新集合。
记为A ∩ B,读作“集合A与集合B的交集”。
如果一个元素同时属于A和B,那么它就属于A ∩ B。
交集的定义可以扩展到多个集合之间。
对于n个集合A1, A2, …, An,它们的交集是同时属于所有这些集合的元素的集合,记为A1 ∩ A2 ∩ … ∩ An。
交集的运算特性如下: 1. 交换律:A ∩ B = B ∩ A 2. 结合律:(A ∩ B) ∩ C = A ∩ (B ∩ C) 3. 吸收律:A ∩ (A ∪ B) = A 4. 分配律:A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)以下是一个具体的例子来说明交集的概念。
假设有两个集合A = {1, 2, 3}和B = {2, 3, 4},它们的交集是A ∩ B = {2, 3}。
因为数字2和3同时属于集合A和B,所以它们也属于它们的交集。
二、并集(Union)集合的并集是指包含至少属于两个集合中的所有元素的新集合。
记为A ∪ B,读作“集合A与集合B的并集”。
如果一个元素属于A或B中的一个,那么它就属于A ∪ B。
并集的定义同样可以扩展到多个集合之间。
对于n个集合A1, A2, …, An,它们的并集是至少属于其中一个集合的元素的集合,记为A1 ∪ A2 ∪ … ∪ An。
并集的运算特性如下: 1. 交换律:A ∪ B =B ∪ A 2. 结合律:(A ∪ B) ∪ C = A ∪ (B ∪ C) 3. 吸收律:A ∪ (A ∩ B) = A 4. 分配律:A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)继续以上面的集合A和B为例,它们的并集是A ∪ B = {1, 2, 3, 4}。
1.3交集、并集课件

例1 设A={-1,0,1},B={0,1,2,3}, 求A∩B和A∪B.
例2.学校举办了排球赛,某班45名同学中 有12名同学参赛,后来又举办了田径赛, 这个班有20名同学参赛.已知两项比赛都 参加的有6名同学.两项比赛中,这个班共 有多少名同学没有参加比赛?
6 A
6
14 B
19
学生练习: P13练习2,3,4
1.3交集、并集
复习巩固
1、对于A与B两个集合:如果集合A中的任何
一集个合元A叫素做都集是合集B合的B_中_子_的_集_元_,素记,作我_A_们_ _就_说_B__
如果A B且_B_中__至__少__有_一__个__元__素__不__属_于__A
我如们 果_就A_说_ _集_B_合_且_A_是B_ 集__合A__B_的,那真么子A集=B,. 记作__A__≠__B
2、φ是_任__何__集__合_的子集,是__任__何_非__空__集__合_的真子集。 3、如果A是全集U的一个子集,由U中_不_属__于__A_的所有
元素构成的集合,叫做A在U中的补集,记作_C__U_A__
CUA={x︱x∈U且__x___A__}
思考:1.两个实数可以进行加、减、乘、 除四则运算,那么两个集合是否也可以进 行某种运算呢?若可以,请举个我们已学 过的例子 .
问题4.A∪(CUA)=?A∩(CUA)=?
填表 ∩ Ø A B
ØAB ØØ Ø Ø A A∩B Ø B∩A B
∪Ø A B ØØAB A A A A∪B B B B∪A B
∩Ø ØØ AØ CUA Ø
A CUA ØØ AØ Ø CUA
∪ØA CUA源自Ø Ø A CUAA A AU
CUA CUA U CUA
交集定义ppt课件

(3) A∩B ____A
A∩B ____B
练习(三)
1.若A={0, a},B={1, 2},A∩B={1},
则a=___1_____。
2.若A={0, 1, 2x-1},B={y+1, 2, 3},
3
A∩B={0, 2},则x=___2__,y=__-_1__。
2x-1=2 y+1=0
小结
• 本节课要求我们掌握三个方 面的问题
• 1.什么叫交集. • 2.交集的三条重要性质. • 3.根据交集的定义及性质
能进行简单的计算.
A∩B={x|x∈A且x∈B}
例1. 已知A={玫瑰,兰花,牡丹,菊花,杜鹃}, B={兰花,月季,梅花,杜鹃},求A∩B
解 A∩B= {玫瑰,兰花,牡丹,菊花,杜鹃} ∩ {兰花,月季,梅花,杜鹃}= {兰花,杜鹃}
设A={2,3,5},B={-1,0.1,2},求A∩B.
解 A∩B= {2,3,5} ∩ {-1,0.1,2}={2}
在下列各小题中,求A∩B
• 1.A= {x|x≥-2}.B={x|x≤5} • A∩B={x|-2≤x≤5} • 2.A={x|x≤-3},B={x|x≥1} • A∩B=Φ • 3.A={(x,y)|2x+y=1},B={(x,y)|x-y=2} • A∩B={(1,-1)}
交集的性质 (1) A∩B __=_ B∩A
(5)设A= {a,b,c,d },B={a,b },则
A ∩B=__{ _a__, _b__}_=_B
即当 B A 时,A∩B=B 即当 A B 时,A∩B=A
黑色部分表示集合A与集合B的交集
并集交集补集
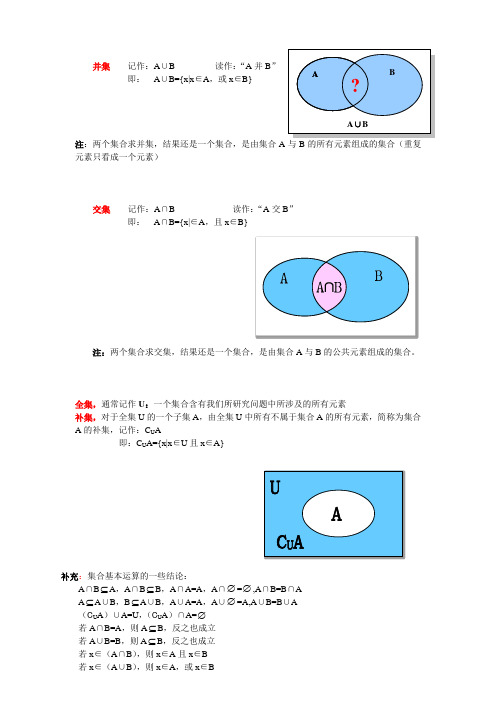
并集 记作:A ∪B 读作:“A 并B ”
即: A ∪B={x|x ∈A ,或x ∈B}
注:两个集合求并集,结果还是一个集合,是由集合A
与B 的所有元素组成的集合(重复元素只看成一个元素)
交集 记作:A ∩B 读作:“A 交B ”
即: A ∩B={x|∈A ,且x ∈B} 注:两个集合求交集,结果还是一个集合,是由集合A 与B 的公共元素组成的集合。
全集,通常记作U :一个集合含有我们所研究问题中所涉及的所有元素
补集,对于全集U 的一个子集A ,由全集U 中所有不属于集合A 的所有元素,简称为集合A 的补集,记作:C U A
即:C U A={x|x ∈U 且x ∈A}
A
U
C U A
A ∪
B B
A ? 补充:集合基本运算的一些结论:
A ∩
B ⊆A ,A ∩B ⊆B ,A ∩A=A ,A ∩∅=∅,A ∩B=B ∩A
A ⊆A ∪
B ,B ⊆A ∪B ,A ∪A=A ,A ∪∅=A,A ∪B=B ∪A
(C U A )∪A=U ,(C U A )∩A=∅
若A ∩B=A ,则A ⊆B ,反之也成立
若A ∪B=B ,则A ⊆B ,反之也成立
若x ∈(A ∩B ),则x ∈A 且x ∈B
若x ∈(A ∪B ),则x ∈A ,或x ∈B。
集合的基本运算-补集 课件

题型一 补集的简单运算 【例 1】 已知全集为 U,集合 A={1,3,5,7},∁UA={2,4,6},∁UB ={1,4,6},求集合 B. [思路探索] 先结合条件,利用补集性质求出全集 U,再由补集 定义求集合 B.
解 法一 ∵A={1,3,5,7},∁UA={2,4,6}, ∴U={1,2,3,4,5,6,7}, 又∁UB={1,4,6},∴B={2,3,5,7}. 法二 借助 Venn 图,如图所示,
2.补集的性质 利用补集的定义可知,补集仍是一个集合,具有如下性质: (1)∁UU=∅,∁U∅=U; (2)A∪∁UA=U,A∩∁UA=∅; (3)∁U(∁UA)=A. 拓展 补集除具有以上较为明显的性质外,还有如下两个性质: ∁U(A∩B)=(∁UA)∪(∁UB); ∁U(A∪B)=(∁UA)∩(∁UB).
题型三 补集的综合应用 【例 3】 (12 分)已知集合 A={x|2a-2<x<a},B={x|1<x<2}, 且 A ∁RB,求 a 的取值范围. 审题指导 先求∁RB → 分情况讨论 → 由A ∁RB,求a
[规范解答] ∁RB={x|x≤1 或 x≥2}≠∅,(2 分) ∵A ∁RB, ∴分 A=∅和 A≠∅两种情况讨论.(4 分) (1)若 A=∅,此时有 2a-2≥a, ∴a≥2.(7 分) (2)若 A≠∅, 则有2aa≤-12<a, 或22aa--22<≥a2,. ∴a≤1.(11 分) 综上所述,a≤1 或 a≥2.(12 分)
【题后反思】 解答本题的关键是利用 A ∁RB,对 A=∅与 A≠∅ 进行分类讨论,转化为等价不等式(组)求解,同时要注意区域 端点的问题.
误区警示 考虑问题不全面,等价变换时易出错 【示例】 已知全集 U={1,2,3,4,5},A={x|x2+px+4=0},求 ∁UA. [错解] 由已知得 A⊆U,设方程 x2+px+4=0 的两根为 x1,x2, 所以 x1x2=4. 当 A={1,4}时,p=-5,∁UA={2,3,5}. 当 A={2}时,p=-4,∁UA={1,3,4,5}.
