04-05_材料力学-课程总结与复习-公式小结
(完整版)材料力学重点总结

(完整版)材料力学重点总结材料力学阶段总结一. 材料力学的一些基本概念 1. 材料力学的任务:解决安全可靠与经济适用的矛盾. 研究对象:杆件强度:抵抗破坏的能力 刚度:抵抗变形的能力稳定性:细长压杆不失稳。
2. 材料力学中的物性假设连续性:物体内部的各物理量可用连续函数表示。
均匀性:构件内各处的力学性能相同。
各向同性:物体内各方向力学性能相同。
3。
材力与理力的关系, 内力、应力、位移、变形、应变的概念材力与理力:平衡问题,两者相同; 理力:刚体,材力:变形体。
内力:附加内力。
应指明作用位置、作用截面、作用方向、和符号规定。
应力:正应力、剪应力、一点处的应力。
应了解作用截面、作用位置(点)、作用方向、和符号规定。
正应力⎩⎨⎧拉应力压应力应变:反映杆件的变形程度⎩⎨⎧角应变线应变变形基本形式:拉伸或压缩、剪切、扭转、弯曲。
4. 物理关系、本构关系 虎克定律;剪切虎克定律:⎪⎩⎪⎨⎧==∆=Gr EA Pl l E τεσ夹角的变化。
剪切虎克定律:两线段——拉伸或压缩。
拉压虎克定律:线段的适用条件:应力~应变是线性关系:材料比例极限以内。
5。
材料的力学性能(拉压):一张σ-ε图,两个塑性指标δ、ψ,三个应力特征点:b s pσσσ、、,四个变化阶段:弹性阶段、屈服阶段、强化阶段、颈缩阶段。
拉压弹性模量E ,剪切弹性模量G ,泊松比v ,)(V EG +=126. 安全系数、 许用应力、工作应力、应力集中系数安全系数:大于1的系数,使用材料时确定安全性与经济性矛盾的关键。
过小,使构件安全性下降;过大,浪费材料。
许用应力:极限应力除以安全系数.塑性材料[]ssn σσ=s σσ=0脆性材料[]bbn σσ=b σσ=07. 材料力学的研究方法1) 所用材料的力学性能:通过实验获得。
2) 对构件的力学要求:以实验为基础,运用力学及数学分析方法建立理论,预测理论应用的未来状态。
3) 截面法:将内力转化成“外力”。
材料力学复习总结

1、 材料力学的任务:强度、刚度和稳定性;应力 单位面积上的内力。
平均应力(1.1) 全应力(1.2)正应力 垂直于截面的应力分量,用符号表示。
切应力 相切于截面的应力分量,用符号表示。
应力的量纲:G Pa MPa )m /N (Pa 2、、国际单位制:22cm /kgf m /kgf 、工程单位制:线应变 单位xx 上的变形量,无量纲,其物理意义是构件上一点沿某一方向变形量的大小。
外力偶矩传动轴所受的外力偶矩通常不是直接给出,而是根据轴的转速n 与传递的功率P 来计算。
当功率P 单位为千瓦(kW ),转速为n (r/min )时,外力偶矩为m).(N 9549e nPM = 当功率P 单位为马力(PS ),转速为n (r/min )时,外力偶矩为m).(N 7024e nPM =拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力,且为平均分布,其计算公式为(3-1)式中为该横截面的轴力,A为横截面面积。
正负号规定拉应力为正,压应力为负。
公式(3-1)的适用条件:(1)杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件;(2)适用于离杆件受力区域稍远处的横截面;(3)杆件上有xx或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角时拉压杆件任意斜截面(a图)上的应力为平均分布,其计算公式为全应力 (3-2)正应力(3-3)切应力(3-4)式中为横截面上的应力。
正负号规定:由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
拉应力为正,压应力为负。
对脱离体内一点产生顺时针力矩的为正,反之为负。
两点结论:(1)当时,即横截面上,达到最大值,即。
当=时,即纵截面上,==0。
(2)当时,即与杆轴成的斜截面上,达到最大值,即1.2 拉(压)杆的应变和胡克定律(1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
材料力学重点及公式(期末复习)

1、材料力学的任务:刚度和稳定性;正应力垂直于截面的应力分量,用符号 b 表示。
应力的量纲:園际单位制:PMP 总GPa 工程单位制三kgf /沁kgf / cn?线应变 单位长度上的变形量,无量纲,其物理意义是构件上一点沿某一方向变 形量的大小。
外力偶矩 传动轴所受的外力偶矩通常不是直接给出,而是根据轴的转速n 与传递的功率P 来计算。
当功率P 单位为千瓦(kW),转速为n (r/min )时,外力偶矩为Me 二巧4勺一禺应力 单位面积上的内力。
P 尺 ---平均应力(1.1 )全应力厂戸「縮竺二竺 (1.2 )切应力相切于截面的应力分量,用符号百 表示。
3mb]当功率P 单位为马力(PS ),转速为n (r/min )时,外力偶矩为Mg =7024 —(TXT. m)拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力 b ,且为平均分布,其计算公式为-1)式中巧为该横截面的轴力, A 为横截面面积。
正负号规定 拉应力为正,压应力为负 。
公式(3-1 )的适用条件:(1 )杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件; (2)适用于离杆件受力区域稍远处的横截面;(3 )杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不 均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角E 笙2讯时 拉压杆件任意斜截面(a 图)上的应力为平均分布,其计算公式为皿(3-2)式中b 为横截面上的应力。
正负号规定: 配由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
全应力 正应力耳a ( 3-3)切应力 q =-sin 2兌2( 3-4 )% 拉应力为正,压应力为负。
J 对脱离体内一点产生顺时针力矩的J为正, 反之为负。
两点结论:(1)当圧=0°时,即横截面上,门《达到最大值, 即Gkx = D。
当凸=90°时,即纵截面上,兀=9卯=0。
(2 )当心二無时,即与杆轴成仍U的斜截面上,(%()皿轨一~ 达到最大值,即21 . 2拉(压)杆的应变和胡克定律(1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
(完整)材料力学知识点总结,推荐文档
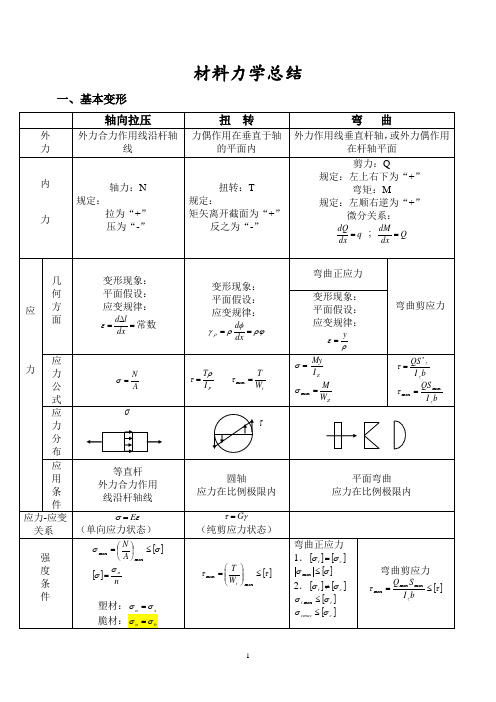
材料力学总结一、基本变形二、还有:(1)外力偶矩:)(9549m N nNm •= N —千瓦;n —转/分 (2)薄壁圆管扭转剪应力:tr T22πτ=(3)矩形截面杆扭转剪应力:hb G Th b T 32max ;βϕατ==三、截面几何性质(1)平行移轴公式:;2A a I I ZC Z += abA I I c c Y Z YZ += (2)组合截面: 1.形 心:∑∑===ni ini cii c AyA y 11; ∑∑===ni ini cii c AzA z 112.静 矩:∑=ci i Z y A S ; ∑=ci i y z A S 3. 惯性矩:∑=i Z Z I I )( ;∑=i y y I I )(四、应力分析:(1)二向应力状态(解析法、图解法)a . 解析法: b.应力圆:σ:拉为“+”,压为“-” τ:使单元体顺时针转动为“+”α:从x 轴逆时针转到截面的 法线为“+”ατασσσσσα2sin 2cos 22x yx yx --++=ατασστα2cos 2sin 2x yx +-=yx xtg σστα--=220 22minmax 22x y x yx τσσσσσ+⎪⎪⎭⎫⎝⎛-±+=c :适用条件:平衡状态(2)三向应力圆:1max σσ=; 3min σσ=;231max σστ-=x(3)广义虎克定律:[])(13211σσνσε+-=E [])(1z y x x E σσνσε+-=[])(11322σσνσε+-=E [])(1x z y y E σσνσε+-=[])(12133σσνσε+-=E [])(1y x z z E σσνσε+-=*适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态 1.纯剪切应力状态:τσ=1 ,02=σ,τσ-=32.一种常见的二向应力状态:223122τσσσ+⎪⎭⎫⎝⎛±=2234τσσ+=r2243τσσ+=r五、强度理论*相当应力:r σ11σσ=r ,313σσσ-=r ,()()()][212132322214σσσσσσσ-+-+-=r σxσ六、材料的力学性质脆性材料 δ<5% 塑性材料 δ≥5%低碳钢四阶段: (1)弹性阶段(2)屈服阶段 (3)强化阶段 (4)局部收缩阶段 强度指标 σσb s ,塑性指标 δψ,E tg ==σα七.组合变形ε八、压杆稳定欧拉公式:2min2)(l EI P cr μπ=,22λπσE cr =,应用范围:线弹性范围,σcr <σp ,λ>λp柔度:iul =λ;ρρσπλE=;ba s σλ-=0,柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:22λπσE cr =λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σs稳定校核:安全系数法:w I cr n P P n ≥=,折减系数法:][σϕσ≤=AP提高杆件稳定性的措施有:1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
材料力学重点及公式(期末复习)

1、材料力学的任务:强度、刚度和稳定性;应力单位面积上的内力。
平均应力(1.1)全应力(1.2)正应力垂直于截面的应力分量,用符号表示。
切应力相切于截面的应力分量,用符号表示。
应力的量纲:线应变单位长度上的变形量,无量纲,其物理意义是构件上一点沿某一方向变形量的大小。
外力偶矩传动轴所受的外力偶矩通常不是直接给出,而是根据轴的转速n与传递的功率P 来计算。
当功率P单位为千瓦(kW),转速为n(r/min)时,外力偶矩为当功率P单位为马力(PS),转速为n(r/min)时,外力偶矩为拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力,且为平均分布,其计算公式为 (3 -1)式中为该横截面的轴力,A为横截面面积。
正负号规定拉应力为正,压应力为负。
公式(3-1)的适用条件:(1)杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件;(2)适用于离杆件受力区域稍远处的横截面;(3)杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角时拉压杆件任意斜截面(a图)上的应力为平均分布,其计算公式为全应力 (3-2)正应力(3-3)切应力(3-4)式中为横截面上的应力。
正负号规定:由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
拉应力为正,压应力为负。
对脱离体内一点产生顺时针力矩的为正,反之为负。
两点结论:(1)当时,即横截面上,达到最大值,即。
当=时,即纵截面上,==0。
(2)当时,即与杆轴成的斜截面上,达到最大值,即1.2 拉(压)杆的应变和胡克定律(1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
如图3-2。
图3-2轴向变形轴向线应变横向变形横向线应变正负号规定伸长为正,缩短为负。
(2)胡克定律当应力不超过材料的比例极限时,应力与应变成正比。
即(3-5)或用轴力及杆件的变形量表示为 (3-6)式中EA称为杆件的抗拉(压)刚度,是表征杆件抵抗拉压弹性变形能力的量。
(完整版)材料力学知识点总结
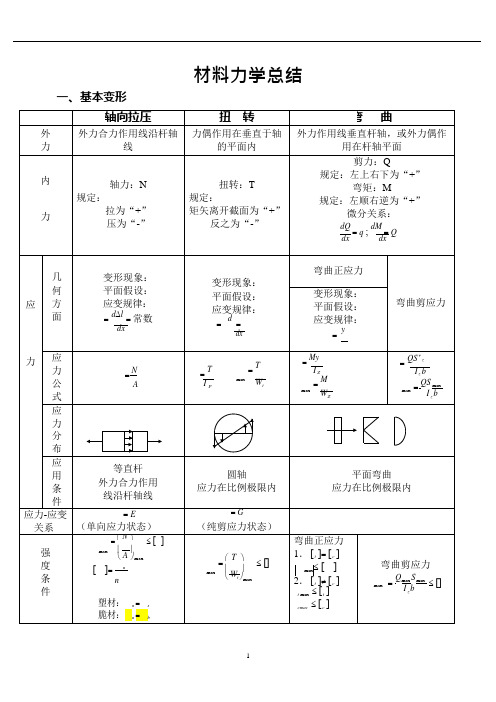
一、基本变形材料力学总结变形现象: 平面假设: 应变规律: = d ∆l = 常数dx变形现象:平面假设: 应变规律:=d = dx变形现象:平面假设: 应变规律:= y= N =T= T = MyI Z = M max WZ= QS * z I z b = QS max max I bz max W= E (单向应力状态) = G(纯剪应力状态)=⎛ N ⎫≤ []maxA ⎪ ⎝ ⎭max[]=un塑材:u=s 脆材:u =bmax= ⎛ T ⎫ ≤ [] ⎪ ⎝ W t ⎭max弯曲正应力 1. [t ]= [c ]max≤ []2. [t ]≠ [c ] t max ≤ [t ] cmac ≤ [c ]弯曲剪应力=Q max S max ≤ [] max I bz轴向拉压扭转弯曲刚度条=T ⋅180 ≤[]max GIP注意:单位统一ymax≤[y]max≤[]件变形d∆l=N ; ∆L =NLdx EA EAEA—抗拉压刚度=d=Tdx GIZ=TLGIPGI p—抗扭刚度1=M (x)(x) EIy '' =M (x)EIEI—抗弯刚度应用条件应力在比例极限圆截面杆,应力在比例极限小变形,应力在比例极限矩形A=bhbh 3bh 2IZ=12;WZ=6实心圆A= d 24d4d3IP=32;Wt=16d4d3IZ=64;WZ=32空心圆D 2A =(1-2)4d44IP=32(1 -)d 3W =(1 -4)t16d 4I =(1-4)Z64d34WZ=32(1-)其(1)'剪切(1)强度条件:=Q≤[]A—剪切面积A(2)挤压条件:=P bs ≤[]bs A bsJA j—挤压面积矩形:=3Qmax 2 A圆形:=4Qmax 3A环形:= 2Qmax Amax均发生在中性轴上它公(2)GE式2(1 )二、还有:(1)外力偶矩:m = 9549 N (N •m)n(2)薄壁圆管扭转剪应力:=TN—千瓦;n—转/分2r 2t(3)矩形截面杆扭转剪应力:max =Tb2h;=TG b3hDB c AD 'Z ZC c cn n三、截面几何性质(1)平行移轴公式:I =I +a 2A;(2)组合截面:IYZ=IZ Y+abA1.形心:y c∑A i y ci=i =1 ;∑A ii =1∑A i z ciz =i =1∑A ii =12.静矩:S Z =∑A i y ci ;S y =∑A i z ci3.惯性矩:I Z =∑(I Z ) i ;I y =∑(I y ) i四、应力分析:(1)二向应力状态(解析法、图解法)a.解析法: b.应力圆:n σ:拉为“+”,压为“-”xτ:使单元体顺时针转动为“+”x yx y cos 2sin 2α:从x 轴逆时针转到截面的法线为“+”2 2 xx y sin 2cos 22 xtg22xmaxminxx yy2c:适用条件:平衡状态(2)三向应力圆:;; 1 3max 1 min 3 max 2nn2x y22xyxc121223311(3) 广义虎克定律:1(1 (1E 123xE xyz1 ( 1(2E 231yE yzx1(1(3E3 1 2zExy*适用条件:各向同性材料;材料服从虎克定律(4) 常用的二向应力状态 31. 纯剪切应力状态:1,20 ,3x2. 一种常见的二向应力状态:132r 3r 4五、强度理论破坏形式脆性断裂塑性断裂强度理论 第一强度理论(最大拉应力理论)莫尔强度理论 第三强度理论 (最大剪应力理论) 第四强度理论(形状改变比能理论) 破坏主要因素 单元体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件 1 = bmax =su f = u fs强度条件 1 ≤ [] 1-3≤ []适用条件 脆性材料 脆性材料 塑性材料 塑性材料*相当应力:r,,]r 11r 313r 4222242232r=2+42≤[]=2+32≤[]4r22(M +N ) + 4≤ []r3 =r=(M+N)2+32≤[]WM 2 +T 2r3 =圆截面WM 2 + 0.75T 2r4=(M+N)2 + 4(T)2W Z A W t(M+N)2 + 4(T)2W Z A W t α 中性轴ZMpr3 =≤ []r 4 =≤ []i 2I Z*y =-=-ZAe y e ytg=y=-I ZtgZ I y中性轴Z≤ []Z≤ []A W≤ []P Mmax =±max ±max≤ []sincos( +)W Z W y=max maxM强度条件43=±P ±MA W)I yI Z=M (y c os+z s in公式简图弯扭拉(压)弯扭拉(压)弯斜弯曲类型六、材料的力学性质脆性材料<5%塑性材料≥5%低碳钢四阶段:(1)弹性阶段(2)屈服阶段(3)强化阶段(4)局部收缩阶段b强度指标s ,b e sα塑性指标,tg E七.组合变形只有σs,无σbb剪断断口垂直轴线拉断断口与轴夹角45ºb45º拉断铸铁断口垂直轴线剪断s b 滑移线与轴线45︒,剪45低碳钢扭压拉八、压杆稳定欧拉公式: P=2EI min,=2E,应用范围:线弹性范围,σ<σ ,λ>λcr(l ) 2cr2crpp柔度:=ul;=E;0 =a -s, σib柔度是一个与杆件长度、约束、截面尺寸、形状有关的数据,λ↑P cr ↓σcr ↓λ>λp ——大柔度杆:cr =2E2临界应力λo <λ<λp ——中柔度杆:σcr=a-b λλ<λ0——小柔度杆:σcr =σsλoλPλ稳定校核:安全系数法: n P c rP I n w ,折减系数法:P []A提高杆件稳定性的措施有: 1、减少长度2、选择合理截面3、加强约束4、合理选择材料九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
材料力学知识点总结
、基本变形材料力学总结轴向拉压外力合力作用线沿杆轴线力偶作用在垂直于轴的平面内规定:轴力:N拉为“ +” 压为“-”扭转:T规定:矩矢离开截面为“ +”反之为“-”外力作用线垂直杆轴,或外力偶作用在杆轴平面剪力: Q规定:左上右下为“ +”弯矩:M规定:左顺右逆为“ +”微分关系:dQ dM 小一q ; 一Qdx dx几何方面变形现象平面假设应变规律dx常数变形现象平面假设应变规律ddx弯曲正应力变形现象平面假设应变规律y弯曲剪应力应力公式maxTW tmaxMyI ZMW ZQS*zI z bI z bmax应力分布应用条件应力-应变关系强度条件等直杆外力合力作用线沿杆轴线E(单向应力状态)maxmax塑材:脆材:圆轴应力在比例极限内平面弯曲应力在比例极限内G(纯剪应力状态)弯曲正应力1.maxTW tmaxmax2.t maxcmac c弯曲剪应力maxmaxSmaxI z b、还有:(1)外力偶矩:m 9549N(N?m) N —千瓦;n—转/分n(2)薄壁圆管扭转剪应力: T2 r2t(3)矩形截面杆扭转剪应力: Tb2hT G b3h三、截面几何性质(1 )平行移轴公式:I Z (2)组合截面:nA i y ci1 .形 心: y cAi 12 .静矩:S Z A i y c3•惯性矩:I z (l z )i ;四、应力分析:(1)二向应力状态(解析法、图解法)b.应力圆::拉为“ + ”,压为“-” :使单元体顺时针转动为“ +” :从x 轴逆时针转到截面的 法线为“ +”maxminc :适用条件:平衡状态⑵三向应力圆:..13max1;min3; maxtg2 0 x ysin 22ycos2 cos 2x sin 22I ZC a A ; I YZ I Z c Y cabAZ cnA i zcii 1nAi 1S yA i Z ciy (I y )ia .解析法:nx2适用条件:各向同性材料;材料服从虎克定律(4)常用的二向应力状态2.—种常见的二向应力状态:五、强度理论破坏形式脆性断裂塑性断裂强度理论第一强度理论(取大拉应力理论)莫尔强度理论第三强度理论(最大剪应力理论)第四强度理论(形状改变比能理论)破坏主要因素单兀体内的最大拉应力单元体内的最大剪应力单元体内的改变比能破坏条件1 b max su f u fs强度条件1 1 3适用条件脆性材料脆性材料塑性材料塑性材料相当应力:1 3r4(3)广义虎克定律:1E13)1)2)xyzz)x)y)1 •纯剪切应力状态:r1xr423六、材料的力学性质七.组合变形八、压杆稳定提高杆件稳定性的措施有:1减少长度 2、选择合理截面 3、加强约束九、交变应力金属疲劳破坏特点:应力特征:破坏应力小于静荷强度; 断裂特征:断裂前无显著塑性变形; 断口特征:断口成光滑区和粗糙区。
材料力学复习总结
小。
外力偶矩传动轴所受的外力偶矩通常不是直接给出,而是根据轴的转速n 与传递的功率P 来计算。
当功率P 单位为千瓦(kW ),转速为n (r/min )时,外力偶矩为当功率P 单位为马力(PS ),转速为n (r/min )时,外力偶矩为拉(压)杆横截面上的正应力拉压杆件横截面上只有正应力σ,且为平均分布,其计算公式为 NF Aσ= (3-1)式中N F 为该横截面的轴力,A 为横截面面积。
正负号规定 拉应力为正,压应力为负。
公式(3-1)的适用条件:(1)杆端外力的合力作用线与杆轴线重合,即只适于轴向拉(压)杆件;(2)适用于离杆件受力区域稍远处的横截面;(3)杆件上有孔洞或凹槽时,该处将产生局部应力集中现象,横截面上应力分布很不均匀;(4)截面连续变化的直杆,杆件两侧棱边的夹角020α≤时拉压杆件任意斜截面(a 图)上的应力为平均分布,其计算公式为全应力 cos p ασα= (3-2) 正应力 2cos ασσα=(3-3)切应力1sin 22ατα= (3-4)式中σ为横截面上的应力。
正负号规定:α 由横截面外法线转至斜截面的外法线,逆时针转向为正,反之为负。
ασ 拉应力为正,压应力为负。
ατ 对脱离体内一点产生顺时针力矩的ατ为正,反之为负。
两点结论:(1)当00α=时,即横截面上,ασ达到最大值,即()max ασσ=。
当α=090时,即纵截面上,ασ=090=0。
(2)当045α=时,即与杆轴成045的斜截面上,ατ达到最大值,即max ()2αατ=1.2 拉(压)杆的应变和胡克定律(1)变形及应变杆件受到轴向拉力时,轴向伸长,横向缩短;受到轴向压力时,轴向缩短,横向伸长。
如图3-2。
图3-2轴向变形 1l l l ∆=- 轴向线应变 llε∆= 横向变形 1b b b ∆=- 横向线应变 bbε∆'=正负号规定 伸长为正,缩短为负。
(2)胡克定律当应力不超过材料的比例极限时,应力与应变成正比。
可打印总结材料力学公式总结
轴力弯矩的作用线的方向用右手螺旋弯矩材料的失效形式强度计算准则位移刚度计算准则应力状态和强度理论斜截面上的正应力和切应力:主应力:然后根据代数值进行排列(其中有一个主应力=0)强度理论:弯扭组合变形圆形运用强度理论(第三、第四):资料什么叫解决方案?一、什么是解决方案?我们一直在尝试解决问题,但是很少有人真正去想一下:什么是解决方案?没错!大部分人从来就没有想过什么叫做“解决方案”。
我去某驾校学习科目二的时候,同车的学员(包括我)并没有向教练期望地那样以迅雷之势学会倒车入库—对我们来说,驾驶的动作的确太陌生了,需要一定的训练才能慢慢掌握。
教练一定想加速这个学习过程,“你们真是太笨了!教了2遍了还不会!”“向左打!向左打!跟你说了多少次了!你怎么这么笨!”“你们啊,就是不开窍!”我觉得教练的沟通方式太无效了,忍不住提醒教练:“吴教练啊,我觉得你这样频繁地骂反而降低了教学效果。
这样的语言提高了我们的紧张程度,从而让我们达到‘唤起’状态,这种状态的确对熟练或者简单工作是有利的—比如搬砖(这就是为什么体力劳动需要鞭策和口号)。
但是对于陌生及复杂的工作—比如我们学习驾驶的过程,‘唤起’反而会降低学习效果,提高失误率。
相反,相对放松和鼓励的环境更加容易帮助你达到目的—提高训练效果。
”教练:“……你说我唤起了什么?”……我不知道教练是否最终接受了这个心理学的理论,反正过后教练对我们尊重了很多。
那么问题来了,这个教练的对我们学习太慢的解决方案存在什么问题呢?二、目标不是解决方案!问题就是他把“目标”当成了“解决方案”。
他的目标是“减少学习失误”,而他对应的解决方案只不过是把这个目标以辱骂的方式说了一遍“这么笨!失误这么多!”从而导致该解决方案(把目标说一遍)不但没有帮助达成目标,反而损害了目标—让我们学习地更慢。
这也是无数人难以解决问题,反而让问题越来越糟的原因:错把目标当方案。
很多人天真地认为,自己一旦发现某个目标,所需要的解决方案只不过是把这个目标说一遍。
材料力学知识点总结
A=bh
扭转
max
T
GI P
1800
注意:单位统一
d T dx GI Z
TL GI P
GIp—抗扭刚度
圆截面杆, 应力在比例极限
A= d 2
4
d 4
d 3
I P 32 ;Wt 16
A D2 (1 2 ) 4
(1) ' (2) G E
2(1 )
IP
d 4 32
(1 4 )
r4 2 3 2
3
x 1
五、强度理论
破坏形式
脆性断裂
塑性断裂
强度理论
破坏主要 因素
破坏条件 强度条件 适用条件
第一强度理论 (最大拉应力理
论) 单元体内的最大拉
应力
1 b
1
脆性材料
莫尔强度理 论
脆性材料
第三强度理论 (最大剪应力理
论) 单元体内的最大
剪应力
max s
1 3
WZ A
Wt
[ ]
5
八、压杆稳定
欧拉公式: Pcr
2 EI min (l ) 2
, cr
2E 2
,应用范围:线弹性范围,cr<p,>p
柔度:
ul i
;
E
;
0
a
b
s
,
柔度是一个与杆件长度、约束、截面尺寸、 形状有关的数据,λ↑Pcr↓σcr↓
临界应力
>p——大柔度杆:
cr
2E 2
o<<p——中柔度杆:cr=a-b
3
1 E
3
( 1
2 )
x
1 E
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学-四种基本变形计算的主要公式
变形
项目
轴向拉压 扭转 弯曲 剪切
应力
][
A
F
N
PIT ][maxPWT z
I
My
][max
z
W
M
][
S
S
A
F
][bsbsbsdF
][
A
F
N
截面性质
4
2DA 324DIP 163DWP )1(3244DIP )1(1643DWP 644DIz 323DWz 123bhIz 62bhWz 42
D
AAs
胡克定律
E G
E
应变
EAFll ][PGITl ][180maxPGIT EIxMw)( ][maxlwl
w
][max
刚度
EA GIP EIz
外力偶矩
n
P
T31055.9
泊松比
惯性矩平行
移轴定理
AaIIcxx2
AbIIcyy2
强度理论
22
4
rs
22
43r
