第七章_静电场
大学物理-电子教案第7章 静电场

N⋅
⨯≈
m
9880c
10
/
通过曲面S 的总电通量 ⎰⎰⋅=Φ=ΦS S e e S d E d
S 为闭合曲面时 ⎰⋅=ΦS e S d E
无关,只与被球面所包围的电量q 有关
虚线表示等势面,实线表示电力线 二、场强与电势梯度的关系 电势与场强的积分关系:⎰⋅=零点
l d E U
,
求出场强分布后可由该式求得电势分布.
空腔内有带电体q时,空腔内表面感应电荷为-q,导体外表面感应电荷为静电屏蔽
)在导体内部有空腔时,空腔内的物体不受外电场的影响。
)接地的导体空腔,空腔内的带电物体的电场不影响外界。
三、有导体存在的静电场场强与电势的计算
有极分子电介质的极化:在外电场作用下分子偶极矩转向与外电场接近平行的方向,叫取向极化。
五、极化强度和极化电荷
极化强度P
)。
第七章 静电场

er
r
q e ( r R ) 2 r E 4 0 r 0( r R )
q 4 0 R 2
O
R
r
7(14)
例7-7:【书P267例题7-8(1)】求均匀带电球体的电场分布。已 知R,q 。 (设q>0) 解:电荷分布的球对称性 电场分布的球对称性 选取同心球面为“高斯面”
§7-3 静电场的高斯定理 (重点、难点)
一、静电场的高斯定理
e
S
E dS
q内
0
二、高斯定理的应用 (重点、难点)
解题步骤:
e
S
E dS
q内
0
E
重点:选择一个合适的闭合曲面作为高斯面
要求:高斯面首先应是通过待求场强点的闭合面,其次高斯 面上各点的场强应大小处处相等,方向与高斯面正交;若有的地 方场强大小不等,或不能肯定相等,则应使这部分高斯面上的场 强与高斯面相切。
7(2)
§7-2
静电场 电场强度
(SI)V/m ;1V/m = 1N/c
F 定义场强: E = q0
一、点电荷的场强
F 1 qq0 er 2 4πε0 r
F E q0
E
1 q e 2 r 4πε0 r
7(3)
二、电场强度的计算
1. 点电荷系的场强计算
上 下 侧
r
h
h 0 ( r R ) 0 0 E dS E 2 rh 2 2 侧 hr 0 R r R )
2 r er ( r R ) 0 E r e r R ) 2 0 R 2 r
大学物理第7章静电场中的导体和电介质课后习题及答案

大学物理第7章静电场中的导体和电介质课后习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1σ和2σ。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr=21σσ 。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为R R V 0211π4επσ=14εσR= 半径为r 的导体球的电势为r r V 0222π4επσ=24εσr= 用细导线连接两球,有21V V =,所以R r =21σσ 2. 证明:对于两个无限大的平行平面带电导体板来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ(1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得S S d E S ∆+==⋅⎰)(10320σσε 故 +2σ03=σ上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又 +2σ03=σ 故 1σ4σ=3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
解:如图所示,设金属球表面感应电荷为q ',金属球接地时电势0=V由电势叠加原理,球心电势为=O V R qdq R 3π4π4100εε+⎰03π4π400=+'=Rq R q εε故 -='q 3q 4.半径为1R 的导体球,带有电量q ,球外有内外半径分别为2R 、3R 的同心导体球壳,球壳带有电量Q 。
大学物理 第7章 真空中的静电场 答案
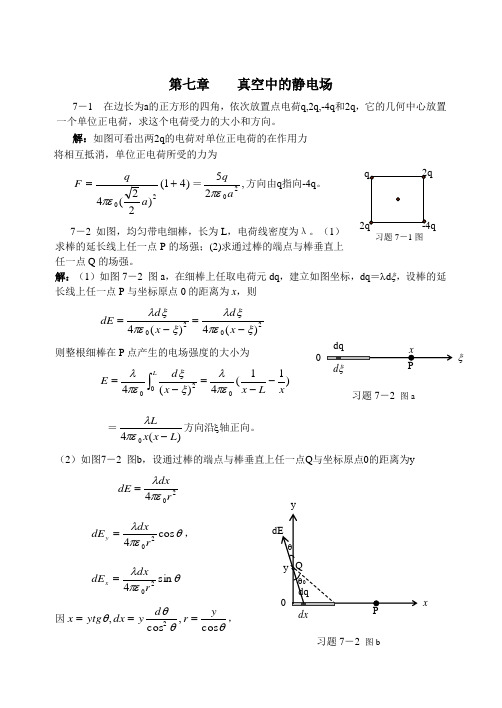
第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y204rdxdE πελ=θπελcos 420r dxdE y =,θπελsin 420rdxdE x = 因θθθθcos ,cos ,2yr d y dx ytg x ===,习题7-1图dq ξd ξ习题7-2 图axxdx习题7-2 图by代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y +--πελ,方向沿x 轴负向。
θθπελθd y dE E y y ⎰⎰==00cos 400sin 4θπελy ==2204Ly y L+πελ 7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420R Rd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ=2022Rq επ=,如图,方向沿x 轴正向。
大学物理第7章 静电场

设北京事件时空坐标为 x1 , t1 ,天津事件时空坐标为
x2 , t 2
x2 x1 120km
u x 2 c t 1 u2 c2 t
t 2 t1 0.0003s
5 t 2 t1 3.3 10 s
电场强度的叠加原理
1 qi q0 ri 3 4 π 0 ri
q2 q3
r2 q r3 0
r1
F3 F2
F1
E Ei
i
第七章 静电场
例1 电偶极子的电场强度 电偶极子的轴
r0
q讨论源自 r0 p q
(1)电偶极子轴线延长线上一点的电场强度
(微观领域中,万有引力比库仑力小得多,可忽略不计.)
第七章 静电场
三
电力的叠加原理——多个点电荷或连续带电体
1. 多个点电荷之间的库仑力计算
两个点电荷之间的作用力并不因第三个点电荷的存
在而有所改变。
N 离散状态 F Fi i 1
q1
q2 q3
r2 q r3 0
r1
F3 F2
琥珀
经过摩擦才具有吸引力 吸引任何小物体
为了表明与磁性的不同,他采用琥珀的希腊字 母拼音把这种性质称为“电的” “琥珀体” electric
第一台摩擦起电机
大约在1660年 马德堡的盖利克
发现电的传导
1729年 英国的格雷
格雷还做过一个有趣的实验:把 一个小孩用几根粗丝绳水平吊起来, 用摩擦过的带电玻璃管接触小孩的胳 臂,孩子的手和身体便能吸引羽毛和 铜屑。这表明,人体也是导电体。
y
第七章静电场

E、n
+q
+ + ++
+ +
+
+ +
的球面( 2)作半径为r的球面(球体外) (r ≥ R) 作半径为 的球面 球体外) S
v E
v dS
由高斯定理: 由高斯定理:
+ + + + + + + +
+q
+ + ++
第七章 静电场
第一节 电场 电场强度
一 电荷 1. 电荷 单位:库仑(C) 单位:库仑 2. 电荷具有量子性 电荷是电子电量e 电荷是电子电量 (e=1.602×10-19 C)的整数倍 × 3. 点电荷 形状和大小可以忽略的带电体称为点电荷 形状和大小可以忽略的带电体称为点电荷 二 库仑定律 在真空中两个静止点电荷间的相互作用力为 其中 k=1/4πε0 ε0=8.85×10-12 C2 N-1m-2 称为真空介电常数 称为真空介电常数 ×
静电学基本实 验定律之一
返 回 *
三 电场
1. 电场 是存在于带电体周围空间的特殊物质. 电场是存在于带电体周围空间的特殊物质 电场是存在于带电体周围空间的特殊物质. 场源电荷 静电场
2. 静电场的两个重要特性 ① 力的性质 放入电场中的任何电荷都受到电场力的作用. 放入电场中的任何电荷都受到电场力的作用. ② 能的性质 电荷在电场中移动时,电场力对电荷作功. 电荷在电场中移动时,电场力对电荷作功.
++ ++ + + + + + + +
r
00 R
②取高斯面S 取高斯面 以球心为圆心, 为半径作一球形高 以球心为圆心,r为半径作一球形高 斯面S。 斯面 。
+ + + + + + ++ + + + + +++
S
③高斯公式左边: 高斯公式左边:
第七章-静电场PPT课件
有一半径为 R ,电荷均匀分布的薄圆盘,其电荷面
密度为 . 求通过盘心且垂直盘面的轴线上任意一点
处的电场强度. 解 由例3
y dq2πrdr
qx
E4π0(x2R2)32
dEx
dqx
4π0(x2r2)32
r (x2 R2)1/2
o
R
x
P
dEx
z dr qπR02
2021/7/24 28
7-1 静电场的描述
q1q2 r2
er
2021/7/24 9
7-1 静电场的描述
库仑力的叠加
q1
r1
q
q2
r2 rn
Fn
F2
F1
qn 由力的叠加原理得 q 所受合力:
2021/7/24 F F 1F 2F 3F n4π 10i n1q rii2 qe ri 10
7-1 静电场的描述
羊之间的战争:
开篇问题
电荷与电荷之间的作用力怎么实现?
Q
dE
P
dq
E dEdE
2021/7/24 16
7-1 静电场的描述
3、 解题思路及应 体 、面 和 线;
求电荷元电量:体dq= dV, 面dq= dS, 线dq= dl;
(3)确定电荷元的场
dE
1
40
dq r2 er
(4)求场强分量Ex、Ey
q
O
q
x
l0
电偶极子轴线中垂线上,电场强度与电偶极矩成
正20比21/7,/24 大小与场点到O点距离三次方成反比。 20
7-1 静电场的描述
例题2 均匀带电直线,长为 2l ,带电量 q ,求中垂线
上一点的电场强度。
第7章+静电场+习题和思考题
Q
Q
Q
2 0a 2 j ( 2 0a 2 j ) 16 0a 2 i
Q
16 0a 2
i
从 O 点指向 x 轴正向
y
a 2Q Q O a 2a x a 2Q
(4)
Uo
3 i 1
1
4 0
qi ri
2Q 2Q
Q
4 0a 4 0a 4 0 (2a)
答:错误 。
根据静电感应,当导体达到静电平 衡时,导体内部电场强度处处为 0, 根据高斯定理,导体内表面所带电 荷与空腔导体包围的电荷代数和为 0,所以内表面带-Q 的电量 。
A Q
B
习题图7-3
第第七七章 章习题习解答题解答
三、综合题
1.如习题图 7-4,三个点电荷分别分布 在 x , y轴上。 (1) 分析各点电荷在 O 点产生电场强度的方向; (2) 写出各点 电荷在 O 点产生的电场强度的大小; (3) 计算 O 点的电场 强度大小; (4)计算 O 点电势的大小 。
(3)计算
利用高斯定理
e
1
EdS
S
0
qi
S内
1
E
dS
S
0
qi
S内
Q
+ +
+R + +
O
dq
·
+ +r +
++ +
+·
S
d E
· P
dE
E
d q
E4
r2 1
0
qi
大学物理第七章静电场思维导图
绝缘体在静电场中表现特性
电荷保持
绝缘体不易导电,因此在静电场中,绝缘体上的电荷 难以移动或消失,能够长时间保持电荷。
极化现象
在静电场作用下,绝缘体中的正负电荷中心会发生相 对位移,形成电偶极子,从而产生极化现象。
介电常数
绝缘体的介电常数反映了其在静电场中的极化程度。 介电常数越大,绝缘体的极化能力越强。
导体和绝缘体之间相互作用
静电感应现象
当导体靠近绝缘体时,由于静电感应作用,导体会在靠近绝缘体的一侧感应出异号电荷,而绝缘体也会因为 极化作用在靠近导体的一侧出现束缚电荷。
电荷转移
在特定条件下,如导体与绝缘体接触或存在电位差时,可能会发生电荷转移现象。例如,在雷电天气中,云 层中的电荷可能会通过空气中的绝缘体(如水滴)转移到地面上的导体上。
电荷与电场关系
电荷
带正负电的粒子,是电场的源。
电场
电荷周围存在的一种特殊物质, 对放入其中的电荷有力的作用。
电荷与电场关系
电荷产生电场,电场对电荷有 力的作用。
电场强度与电势差
电场强度
描述电场的力的性质的物理量,表示电场的强弱和方向。
电势差
描述电场的能的性质的物理量,表示两点间电势的差值。
关系
电场强度与电势差密切相关,电场强度的方向是电势降低最快的 方向。
静电场中的导体和绝缘体
导体
内部存在自由电荷,能够导电的 物体。在静电场中,导体内部电 场为零,电荷分布在导体表面。
绝缘体
内部几乎没有自由电荷,不能导 电的物体。在静电场中,绝缘体 内部和表面都可能存在电荷。
静电感应
当导体靠近带电体时,由于静电 感应作用,导体内部电荷重新分 布,使得导体两端出现等量异号 电荷的现象。
第7章 静电场习题
q 4πε 0 r 2
。由此可知,球外空间的场强与气球吹大过程无关。
(3)因为球表面的场强 E 表=
q 4πε 0 R 2
,在球吹大的过程中,R 变大,所以,
球表面的场强随气球的吹大而变小。 通过该立方体各面的 7-7 一个点电荷 q 位于一个边长为 a 的立方体的中心, 电通量是多少? 答:点电荷位于立方体中心时,通过该立方体各面的电通量都相等,并且等 于总通量的 1/6。由高斯定理可知总通量为
ε0
∑q
i
i
E2 4πr 2 =
由此可解得区域 II 的电场强度为
Q1
ε0
E2 =
4πε 0 r 2
Q1
在区域 III,做半径 r﹥R2 的球形高斯面。由于该高斯面内的电荷为 Q1+Q2, 由高斯定理可得
∫∫
S
r 1 r E 3 ⋅ dS =
ε0
∑q
i
i
E3 4πr 2 =
Q1 + Q2
ε0
E3 =
( 方向向上 )
7-5 如图 7-46 所示,长为 l 的细直线 OA 带电线密度为 λ ,求下面两种情 况下在线的延长线上距线的端点 O 点为 b 的 P 点的电场强度: (1) λ 为常量,且 λ >0;(2) λ =kx,k 为大于零的常量,(0≤x≤1)。
P O A x
b
54
第七章 静电场
合力的大小为
F = Fx = 2 F1cosθ = 2 ⋅
1 4πε 0
⋅
2e 2 d x2 + 2
2
⋅
2
x d x + 2
2
=
1
4πε 0 4 x 2 + d 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-1 静电场的描述
例题2 均匀带电直线,长为 2l ,带电量 q ,求中垂线
上一点的电场强度。
y
解: 线电荷密度
q 2l
dqdy
dE
1
40
dq r2 er
dq o
dyyr
dE y
dE
x
x
dE
. 21
7-1 静电场的描述
由场对称性, Ey=0
y
E Ex
l
E
cos
dEx
l dEcos
l
q
4 0 x 2
相当于点电荷的电场。 .
y
x px
24
7-1 静电场的描述
例题3 均匀带电圆环的电场
一均匀带电圆环,所带电量为q,试求圆环轴线
积分得
l
E
20
xx2
l2
1/2
讨论 1. l >>x ,无限长均匀带电直线
x2 l2 l2,
E 2 0 x
.
y
x px
23
7-1 静电场的描述
2.推论:
半无限长带电直导线垂直断面上一点的电场
E
(i j)
40x
3. x>>l ,无穷远点场强
x2l2 x2
E
l 2 0x2
2l 4 0 x 2
F2
F1
F F 1F 2F 3 . F n4π 10i n1q rii2 qe ri 10
7-1 静电场的描述
羊之间的战争:
开篇问题
电荷与电荷之间的作用力怎么实现? . 11
2、电场
7-1 静电场的描述
电荷
电场
电荷
电场是在带电体周围的一种特殊物质,其基本 特性是对处于电场中的其它电荷或带电体将要施加 电场力的作用。
. 4
7-1 静电场的描述
电场在食品工程中的应用:
新鲜的什锦牛奶
变质后的牛奶
电场使细胞膜正负电荷分离,而破坏细菌的细胞, 从而达到杀菌的作用 .
5
7-1 静电场的描述
电场在医学上的应用:
一种电场靶向治疗脑部 癌症患者迅速增生的癌 细胞的新方法。
通过肿瘤治疗电场装置产生 电场,干扰癌症细胞分裂从而 达到破坏肿瘤生长的目的。
被闪电击中起火
电场的应用
闪电
通过富兰克林对闪电的观察研究,
得出电荷的基本性质
.
避雷针
避雷针在不同领域的应用, 比如航天、民用等。 3
7-1 静电场的描述
电场在航天上的应用:
离子推进器,又称离子 发动机。
原理:先将气体电离,然 后用电场力将带电的离 子加速后喷出,以其反 作用力推动火箭。
这是目前已实用化的火箭技术中,最为经济的一种。
和试验电荷无关
位置的函数
E(r)
. 14
7-1 静电场的描述
2、 电场强度的计算 (1)点电荷的电场强度
r E
P
F
1
4πε0
qq0 r2
er
rr q
E F 1 q0 4πε0
rq2e r 正
点
电
荷
负点电荷
+
. 15
7-1 静电场的描述
(2)点电荷系的电场强度
E E 1E 2E 3E n4π 10i n1rqi2 ie ri
第七章 静电场
目录
7-1 静电场的描述 7-2 静电场的高斯定理 7-3 静电场的环路定理 7-4 电势 7-5 电场与物质的相互作用 7-6 静电场的能量 7-7 静电场的应用
. 2
7-1 静电场的描述
对电的最早认识
电荷的基本性质
2009年7月1日,美 国马萨诸塞州麦德威 市190岁的教堂尖塔
(4)求场强分量Ex、Ey
Ex dEx ,
Ey dEy
(5)求总场
E Ex2 Ey2
. 17
7-1 静电场的描述
例题1 电偶极子的电场强度
偶极电子量。相若等设的lv 0 两为个从异q号指点向电荷q 组的成矢的量点,电定荷义系Pr称为q电lv0 为电偶极子的电偶极矩(电矩)。试求在电偶极子轴线的
7-1 静电场的描述
Байду номын сангаас
点电荷
q1
Fd
r q2
er
(d r)
F
库仑定律
F
k
q1q2 r2
er
. 8
7-1 静电场的描述
SI制
k 1
4π 0
08.85 412 0 1F 2/m
F
1
4π0
q1q2 r2
er
. 9
7-1 静电场的描述
库仑力的叠加
q1
r1
q
r2
q2
r n Fn
qn
由力的叠加原理得 q 所受合力:
(3)任意带电体的电场强度
dE
1
4π0
drq2 er
E dEdE
Q
dE
P
dq
. 16
7-1 静电场的描述
3、 解题思路及应用举例
(1)建立坐标系;
(2)确定电荷密度: 体 、面 和 线; 求电荷元电量:体dq= dV, 面dq= dS, 线dq= dl;
(3)确定电荷元的场
dE
1
40
dq r2 er
x r
dq o
dy dE
yr
x
y'
dE' dE x 'x dE x
r(x2y2)1/2
dq '
dE y dE
l
E2
l 0
1
40
dqx r2 r
l xdy
2
04. 0(x2y2)3/2
22
7-1 静电场的描述
l
E2
1
dqx
0 40 r2 r
20l 40(x2xyd2)y3/2
0l(x2dy2y)3/2x2(x2 yy2)1/2
中垂线上电场强度的分布。
解:建立如图坐标系
E
1
4π0
q r2
er
y
E
E
P
E
E 4π10
q r2
er
er
q
.
O l0
er
q
x
18
7-1 静电场的描述
y
E
E
P
E
er
q
O
l0
由图知:
r r r
(l0)2 y2 2
E 4 π q0r r 34 πq 0r3(l2 0i y j)
er E 4 π q0r r 3 4 π q 0 r3(l2 0i y j)
q x
. 19
7-1 静电场的描述
E
E
E
y 则:E E E 4 π q0 0 r3 li 4 π q l0 0 r3
讨论: 当: y l0 时
P
r
r
E v4πql00y3 4πP0y3
er
er
q
O
l0
q x
电偶极子轴线中垂线上,电场强度与电偶极矩成
正比,大小与场点到O点距离. 三次方成反比。 20
该电场治疗只靶向针对增殖活跃的细胞,因此对增殖不活跃 的正常细胞可免受伤害
. 6
7-1 静电场的描述
一、电荷与电场
1.库仑定律
库仑于 1785~1789年用扭称 测量静电力和磁力,导出著名 的库仑定律。
库仑定律使电磁学的研究从定 性进入定量阶段,是电磁学上 一个重要的里程碑。
法国物理学家库仑
.
7
(C.A.Coulomb1736 --1806 )
静电场: 静止电荷周围存在的电场。
. 12
7-1 静电场的描述
二、电场强度
1、电场强度的引入
E
F
q0
C FC
v
A
r q0
FA
r Q
q0
rB v q0 F B
Q :场源电荷 q 0 :试验电荷
. 13
7-1 静电场的描述
电场强度的性质
大小: 单位试验电荷所受的电场力
方向: 正电荷受力方向
单位: NC1,Vm1
