6-05 麦克斯韦气体分子速率分布定律
麦克斯韦气体分子速率分布律知识
第十二章 气体动理论
16
物理学
第五版
本章目录
选择进入下一节:
12-4 理想气体分子的平均平动动能
与温度的关系
12-5 能量均分定理 理想气体内能
12-6 麦克斯韦气体分子速率分布律
*12-7 玻耳兹曼能量分布律 等温气压公式
12-8 气体分子平均碰撞次数和 平均自由程
第十二章 气体动理论
17
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
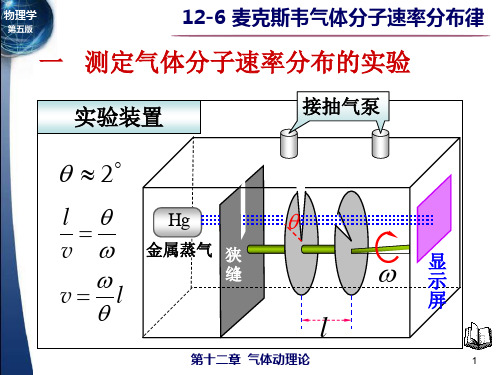
一 测定气体分子速率分布的实验
实验装置
接抽气泵
2
l v vl
Hg
金属蒸气 狭 缝
l
第十二章 气体动理论
显 示
屏
1
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
分子速率分布图 N : 分子总数
N /(Nv)
N: v v v间的分子数.
S
o
v v v
第十二章 气体动理论
3
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
第十二章 气体动理论
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
f (v) 物理意义
表示在温度为 T 的平衡状态下,速
率在 v 附近单位速率区间 的分子数占总
数的百分比 .
f (v)dv 的物理意义:
表示速率在v v dv区间的分 子数占总分子数的百分比.
v
S N 表示速率在 v v v 区间
N 的分子数占总数的百分比 .
第十二章 气体动理论
2
物理学
12-6 麦克斯韦气体分子速率分布律
第五版
分布函数 f (v) lim N 1 lim N 1 dN v0 Nv N v0 v N dv
第十一章 第三讲 麦克斯韦速率分布律

的那些分子的平均速率
v N
v0
vdN f (v)dv
v0
vf (v ) dv vf v (v)dv f (v)dv
v0 0 v0
10
v 2
v v dv
dN
v
速率在 v~v+dv: 内的分子数占总分子数的百分比 . 曲线下的总面积 归一化条件 S f (v)dv 1 0 v~v+dv内的几率. 也表示单个分子速率在区间
f ( v ) dv N
6
说明: 速率分布曲线 2).曲线峰值对应的速率:
最概然速率 vp vp vp 的物理意义:
2kT
f (v) 2 1 T1 , 2 T1 , 1 T2 T1T Nhomakorabea , 1
在一定温度下, 对相同的速率间隔 vp 所在的间隔内的分子数最多.
vp
曲线下总面积不变!
v
或者说,对一个分子来说,出现在 vp 所在的间隔内的概率最大. 3). 曲线形状与 T 和
的关系
① 同种气体,T , vp . 曲线顶点右移. 曲线变 平坦. ② 温度相同, , v p .
二、了解自由度概念,理解能量均分定理(重点) ,会计 算理想气体(刚性分子模型) 的内能 (重点). 三、了解麦克斯韦速率分布律、 分布函数和分布曲线
的物理意义 . 了解气体分子平均碰撞次数和平均自由程.
1
第十一章 气体动理论
( 第三讲 )
本讲主要内容: 麦克斯韦速率分布律
§11-5 麦克斯韦气体分子速率分布律 装置置于高真空之中 一、气体分子速率分布的测定 兰媚尔实验(了解)
vp v
1气体分子的速率分布率

mv 2 2kT
2
2πkT
说明:1、 f (v)dv dN / N
f (v) dN / N dv
dS
表示某一温度下,气体分子速率 o v v dv
v
在v~v+dv区间内分子数占总分子数的百分比。或分子
的速率落在v~ v+dv 区间内的几率。
2、求具有某一速率的分子数无意义。
3、曲线下的总面积为1。归一化条件 f (v)dv 1 0
(1)f (v)dv dN N
表示在平衡态时,某一温度下,气体分 子速率在v~ v +dv区间内分子数占总分子 数的百分比。或:
一个分子速率落在v~ v +dv区间内的几率. (2)Nf (v)dv dN 表示在平衡态时,某一温度下,气体
分子速率在v~ v +dv区间内分子数。
(3
)v2 v1
f (v)dv
速率区间内的分子对平均速率的贡献。
(6) v2 Nv f (v)dv v1
表示在平衡态时,某一温度下,在 v1~v2 速率区间内分子速率的总和。
(7) vP f (v)dv 0
表示在平衡态时,某一温度下,在 0~vP速率间隔内的分子数占总分子数
的百分比。
(8) v2 f (v)dv vP
表示在平衡态时,某一温度下,在速率
利用此公式可计算分子的平均速率、方均根速率。
平均速率
8kT
8RT
v
m
M mol
3.方均根速率
v2 3kT 3RT
m
M mol
与前面温度公式中所讲的方均根速率相同。
三种速率的比较
f (v )
vp v v2
说明:
o
气体分子速率分布

教案适用对象批准人<附讲稿:页)教研室教员年月日课目:第十八讲气体分子速率分布目的:理解速率分布函数及麦克斯韦速率分布律的意义。
了解三种速率,了解自由程的概念。
重点:一、麦克斯韦气体分子速率分布率1、测定气体分子速率分布的实验2、麦克斯韦气体分子速率分布定律3、三种统计定律二、分子平均碰撞次数和平均自由程三、气体迁移现象1、粘滞现象2、热传导现象3、扩散现象难点:理解速率分布函数及麦克斯韦速率分布律的意义,了解三种速率,了解自由程的概念。
主要方法:讲授讨论练习基本要求:理解速率分布函数及麦克斯韦速率分布律的意义。
了解3中速率,了解验证速率分布律的实验依据。
了解玻耳兹曼能量分布律的意义及在重力场中粒子数密度公式。
了解分子平均碰撞频率及平均自由程的概念。
b5E2RGbCAP教案内容:6.6 麦克斯韦速率分布律6.6.1实验小孔充分小,改变w,测D上的沉积厚度,图6-7 测定分子速率的实验装置示意图就可测气体速率分布。
给定w。
粒子速率分布实验曲线如图6-8所示。
6.6.2气体分子速率分布律<函数)由于分子数目巨大且碰撞频繁,故单个分子速率取值任意偶然。
但又由分子平均平动动能公式知:温度T一定时,大量分子的方均根速率却又是确定的。
p1EanqFDPw 说明:平衡态时,虽然单个分子的速率取值偶然,但大量分子的速率满足一定的统计规律。
麦克斯韦从理论上得出如下规律:DXDiTa9E3d图6-8 分子速率分布实验曲线满足归一化条件:1. 速率分布的概念分子可能的速率值:速率区间:使得:内的分子数为,表示第i个速图6-9 不同温度下的速率分布曲线率间隔中的分子数占总分子数的百分比或表示单个分子速率值落在区间内的概率。
实验证明:平衡态时,分布在不同区间的不同,但却是确定的。
2. 气体分子速率分布律由实验知:与速率区间有关。
当时,与无关,仅是的连续函数,即速率分布函数物理意义:速率在v附近单位速率间隔内的分子数占总分子数的百分比,或某分子速率出现在v 附近的单位速率间隔内的概率。
2022-2023学年高二物理竞赛课件:麦克斯韦速率分布律

麦克斯韦速率分布律
图6-5
6.4 麦克斯韦速率分布律
用速率分布函数求分子速率的统计平均值
麦克斯韦速率分布律
1. 平均速率
分子速率的统计平均值称为分子平均速率,用v表示.由于此 时V=v,故
(6-34)
麦克斯韦速率分布律
2. 方均根速率
由前述内容可知,理想气体模型主要在忽略气体分子的体积和相 互作用这两个方面对实际气体分子进行了简化.前面已指出,在高温、 低压条件下实际气体的特性接近理想气体,从简化的两方面来推断, 可知在高温、低压条件下,实际气体分子的体积和分子力作用是可以 忽略的.由此我们得出这样的结论:当温度越低、压强越大时,实际 气体的行为特性与理想气体偏差越大,也就是说,此时研究气体时, 不可以将实际气体作为理想气体来研究.下面我们就从分子的体积和 分子力的作用这两个方面对理想气体状态方程进行修正,从而得出更 能描述实际气体行为的范德瓦耳斯方程.
称为速率分布曲线,它形象地给出了气体分子按速率的分布情况.速
率分布曲线从原点出发经过一极大值后,随速率的增加而渐近于横
轴,这说明气体分子的速率可以取0~∞的一切数值,但速率很大
和很小的分子所占的概率实际都很小,而具有中等速率的分子所占
的比率则很大.图6-4中在任一(v,v+Δv)区间内曲线下的窄条面
麦克斯韦速率分布律
图6-4
麦克斯韦速率分布律
式(6-32)表明,对某种气体(μ一定),温度越高, vp越大;在相同温度下,分子质量越大,vp越小.对于给定的 某种气体,当温度升高时,由于vp要变大,分子的平均平动 动能也要增大,即分子中速率较小的分子数的比率减小,速 率较大的分子数的比率增加;又要维持分布曲线下的总面积 恒等于1.由此速率分布曲线的高峰将向速率大的一方移动, 而整个曲线将变得宽度增大,高度较低,显得较为平坦.图65画出了同一气体在不同温度下的速率分布曲线.
麦克斯韦速率分布律的推导和验证

完美WORD 格式 编辑麦克斯韦速度分布律的推导与实验验证摘要:本文对麦克斯韦速度分布律的内容及其历史来历做了简略概述,重点是用初等方法推导了麦克斯韦速度分布律,同时简单地描述了一下它的实验验证。
关键词:速度分布函数,实验验证。
一. 内容1、麦克斯韦速度分布律的内容当气体处于平衡态时,气体分子的速度在v ~v dv +间隔内,及分子速度分量在x x x v ~v dv +,y y y v ~v dv +,z z z v ~v dv +间隔内的分子数dN(v)占总分子数N的比率为:2223()/22x y z d v m ()v v v N 2kTx y z m v v v kTN e d d d π-++=(), 其中m 为分子的质量,T 为气体温度,k 为波尔兹曼常数,222211()v 22x y z m v v v m ++=为气体分子平动能。
d v NN ()表示速度矢量的端点在速度体元d τ内的分子数占总分子数的比率,换言之,一个分子取得v ~v dv +间隔内速度的几率。
2、分子速度分布函数2223()/22m f ()2kTx y zm v v v kTe π-++=x y z dN(v)(v )=Ndv dv dvf (v )的物理意义是:分子速度在v 附近,单位时间间隔内的分子数占总分子数的比率。
3、速度分量分布函数2221/221/221/22m f ()2kTm f ()2kTm f ()2kTx y z mv kTmv kTmv kTee eπππ---===x x x y y y z z z dN(v )(v )=Ndv dN(v )(v )=Ndv dN(v )(v )=Ndv3、麦克斯韦速率分布律将以,,x y z v v v 为轴的笛氏坐标进行坐标变换,变为球坐标2,,,,sin {x y z v v v v v d d dv θϕθθϕ→→xyzdvdv dv 分子速度在v ~v dv +,~,~d d θθθϕϕϕ++内的分子数占总分子数的比率为23/222m ()sin 2kTmv kT e v d d dv θθϕπ-=dN(v)N 对θ,ϕ积分,得分子的速度在v ~v dv +内分子数占总分子数的比率为23/222m 4()2kTmv kT e v dv ππ-=dN(v)N 4、分子速率分布函数23/222m f v 4()2kTmv kT e v ππ-=dN(v)()=Ndv物理意义:分子速率在v 附近,单位速率间隔内的几率。
麦克斯韦速率分布律
粒子速率分布实验曲线如下所示
结论:气体分子速率分布符合麦克斯韦分布率
理想气体状态方程
或
三个速率
麦克斯韦速率分布率
上节基本概念回顾
速率分布函数
温度越高,速率大的分子数越多
讨论:1、同一气体不同温度下速率分布比较
比较 的高低
讨论:2、同一温度下不同种气体速率分布比较
分子质量越小,速率大的分子数越多。
比较 的大小
--- 用于讨论分子碰撞
三种速率的使用场合
地球形成之初,大气中应有大量的氢、氦, 但很多H2分子和He原子的方均根速率超过了地球表面的逃逸速率(11.2km/s),故现今地球大气中已没有氢和氦了。 N2和O2分子的方均根速率只有逃逸速率的1/25,故地球大气中有大量的氮气 (占大气质量的76%)和氧气(占大气质量的23%)。
气体分子速率的算术平均值。
(2)平均速率:
气体分子速率平方的平均值的平方根。
(3)方均根速率:
三种速率均与 成正比,与 成反比,但三者有一个确定的比例关系;三种速率使用于不同的场合。
三个速率的比较
vp --- 用于讨论速率分布
---用于计算分子的平均平动动能
把速率分成很多相等的间隔
+
o
统计出每个间隔内的分子数N
间隔内分子数与分子总数N之比
某 处单位速率间隔内分子数与总数之比
速率分布函数表达式 的意义
(1)速率分布函数 意义是v处单位速率间隔内的分子数占总 数的比值。
(2)如果分布函数 确定,则处于速率 内的分子数占总 数的比值为
例 伽尔顿板实验中, 设粒子总数为N,i为小槽的序号,Ni为落入第i个小槽的粒子数
大学物理第十二章气体动理论第6节 麦克斯韦气体分子速率分布律综述
第十二章 气体动理论
9
p的物理意义:
物理学
第五版
f ( ) f ( p1 )
f ( p2 )
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
T1
最概然速率与温度关系
A. 某种气体,分子质量 一定,温度不同时 T3
T2
f ( p3 )
T1 T2 T3 p1 p 2 p 3
m1 相同温度下,不同种气体
f ( ) f ( p1 )
f ( p2 ) f ( p3 )
m1 m2 m3
m2
m3
p1 p 2 p 3
0
p p2
1
p
3
11
质量越小,速率大的分子数越多。
第十二章 气体动理论
物理学
第五版
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
(1)最概然速率 p df ( ) 0 d 根据分布函数求得
p
三 三种统计速率
f max
f ( )
2kT kT RT p 1.41 1.41 m m M
o
p
一定温度下,对相同的速率区间, p所在区间内 的分子数占总分子数的百分比最大,气体分子出现 在 p所在区间内的几率最大。 8m 1 ) 2 e 1 最概然速率对应的速率分布 f( p) (
3
2
速率分布曲线图
o
第十二章 气体动理论
6
物理学
第五版
ቤተ መጻሕፍቲ ባይዱ
12-6 麦克斯韦气体分子速率分布律 麦克斯韦气体分子速率分布律 12-6
麦克斯韦速率分布律课件-高中物理竞赛
一个分子在单位时间内所受到的平均碰撞次数叫平均碰撞频率,用 表示。 气体运动的复杂性可见一斑。 即在标准状态下,一秒钟内,一个氢分子的碰撞次数约为80 亿次。
分子数为 nu t 。这些分子在时间t内均会与A分 气体分子速率与最概然速率之差不超过1% 的分子占全部分子的百分之几?
例题
求标准状态下氢的平均自由程和平均碰撞频 率。已知氢分子的有效直径为2×10-10m 。
解:根据气体分子平均速率公式
v 8RT
M mol
v
8RT
M mol
88.31 273 3.14 2103
m
s1
1.70
103
m
s1
第七章 气体动理论
§7-6 气体分子的平均自由程
按 p=nkT
n
p kT
求标准状态下氢的平均自由程和平均碰撞频率。 二、 平均自由程的计算
子碰撞。
第七章 气体动理论
§7-6 气体分子的平均自由程
z n ut n u
t
再由 u 2v
z 2 vn 2d 2nv
v 1 1 z 2n 2d 2n
kT 2d 2 p
平均自由程.ppt
第七章 气体动理论
§7-6 气体分子的平均自由程
1.013105 1.381023 273
m3
2.691025 m3
因此 1 2.14107 m (约为分子直径1000倍) 2d 2n
z v 7.95109 s1
即在标准状态下,一秒钟内,一个氢分子的碰 撞次数约为80 亿次。气体运动的复杂性可见一斑。
麦克斯韦分子速率分布定律(-28)
例(P247)计算在0℃时,氧气、氢气和氮气分子的 方均根速率。
说明气体 vrms v2 ~100m/s
历史上,曾因气体分子的方均根速率(或平均速率) 具有数百米每秒这一计算结果,引起一些人对早期 的气体动理论的怀疑和责难。
克劳修斯为说明这类分子碰撞问题,还提出了分子 碰撞次数和自由程的概念,它不仅解决了上述质疑, 而且使气体动理论建立在更加坚实的基础上,并向 前推进了一步。
x
v v
vf S
A
Bx
f x
粘度(又称粘性系数)
•国际单位制中,η的单位:kg m1 s1
~气体粘度与气体的性质和状态有关,可由实验测定
•微观机制(气体动理论的观点)
•气体流动时,气体分子除具有热运动的速度外, 还具有定向运动速度(即气体的流动速度).
•由于,假定气体的温度T=C(即气体分子的热运动平 均速率为一常量),气体分子数密度 n=C 。
用dN代表气体分子速率在 v v dv 区间内的分子
数,则
v
vdN
0
vNf (v)dv
0
f (v)vdv 4 (
m
3
)2
e
mv2 2kT
v3dv
N
N
0
2 kT 0
令 m
2kT
利用积分式:
e x2
0
x3dx
1
2 2
v 4 (
m
3
)2
ev2 v3dv 4 (
m
3
)2
1
2 kT 0
f(v)
1)最概然速率 vp
在 f (v) v的关系曲线中
,f (v)与的极大值相对应的
速率叫做最概然速率,也称 O 为最可几速率。
