第十三讲§5.3 静电场的环路定理 电势习题课
静电场的环路定理静电场力的功电势能

静电场力的功
02
电场力的定义
电场力是电荷在电场中受到的 力,其大小和方向由电场强度
和电荷的乘积决定。
电场力的大小为 F=qE,其 中 F 是电场力,q 是电荷量,
E 是电场强度。
电场力的方向与电场强度的方 向相同,即由正电荷指向负电
荷。
电场力做功的计算
电场力做功可以通过积分计算,即 W=∫F·dr,其中 W 是电场力做的功, F 是电场力,dr 是位移矢量。
在匀强电场中,电场力做功可以通过 W=qEd计算,其中 W 是电场力做 的功,q 是电荷量,E 是电场强度,d 是位移。
在非匀强电场中,需要计算电场力在路径上的积分来计算电场力做的功。
电场力做功的特点
01
电场力做功与路径无关,只与初末位置的电势差有关。
02
电场力做功是标量,没有方向。
03
电场力做功的过程是能量转化的过程,可以转化为其他形式 的能量。
电势能
03
电势能的定义
电势能是指电荷在电场中由于位置差 异而具有的能量。
电势能是电荷与电场共同具有的能量, 其大小由电场强度和电荷量共同决定。
电势能是相对的,与零电势点的选择 有关。
电势能的变化规律
1
电场力做功与路径无关,只与初末位置有关。
2
电场力做正功,电势能减少;电场力做负功,电 势能增加。
3
静电力做功与电荷的运动路径无关,只与初末位 置有关。
电势能与电场力的关系
01
电场力做功等于电势能的减少量。
02
电势能的变化量等于电场力做的功。
03 电势能与电场力做功的关系是能量守恒定律在静 电场中的具体表现。
THANKS.
静电场的环路定理、静 电场力的功、电势能
3静电场的环路定理电势(精)
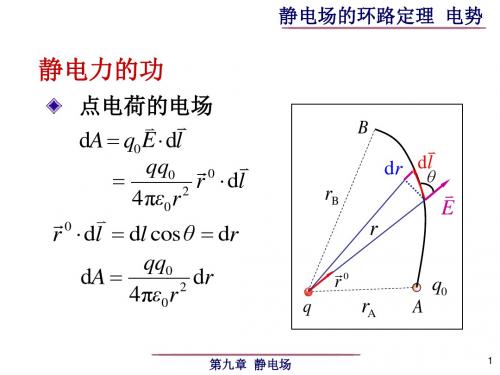
R
oA
B
A dr B
rA dr
r
r
rB
19
第九章 静电场
静电场的环路定理 电势
( 3) r R
令
rB U 0
Q U (r ) 4πε0 r
Q 1 1 U A UB ( ) 4πε0 rA rB
(4)r R
U
Q R U (r ) E dr E dr r R 4 πε0 R
第九章 静电场势
AAB q0 E dl (WB WA )
AB
令 U A WA / q0 A点电势, U B WB / q0 B点电势
AB
E dl (U B U A )
AB
UA
E dl U B
U pA A A E
1 U dq 4πε0 r q 4πε0 r q 2 2 4πε0 x R
dq
R
r
x
o
x
P
x
第九章 静电场
15
静电场的环路定理 电势
讨论
U
q 4πε0 x 2 R 2
q x R,U 4πε0 x
dl
q x 0,U 0 4πε0 R
U
q 4 πε0 R
q 4πε0 x 2 R 2
静电场的环路定理 电势
静电力的功
点电荷的电场
dA q0 E dl qq0 0 r dl 2 4πε0 r
r 0 dl dl cos θ dr qq0 dA dr 2 4πε0 r
第九章 静电场
B
rB
l dr d
r
r0
高二物理竞赛课件:静电场的环路定理、电势

q E 4πε0r 2
(r R)
r1 R
球体内的电场:
r2
ΦE
E 4πr2
1 ε0
4
q πR3
4 3
πr 3
1 ε0
qr 3 R3
3
E
qr 4πε0 R3
ρ 3ε0
r
(r R)
E
q
E连续
q
ρ 4 πR3
为电荷体密度。
oR
r
3
(3) 无限长均匀带电圆柱体的电场
(λ、R):
电场具有轴对称分布。
➢ 静电场为保守场,静电场力质3
电势能、电势:
静电场为保守场,因而可引入电势能的概念:
静电场力对试探电荷q0所作的功等于q0电势能增量
的负值。
Q
APQ q0 E dl (WQ WP ) ΔW
P
APQ>0时,q0电势能减少; APQ<0时,q0电势能增加。
E
2 0
σ S
E
讨论:两块无限大带等量异号电荷的平行平面间的 电场分布。
+σ −σ
+σ −σ
AB
AB
两板外: E0
两板间:
E
0
习题习9-2题9 :一电荷体密度为ρ的均匀带电球体,r为球心
指向球内一点的位矢,球内挖一球形空腔,求空腔 内的场强。
均匀带电球E体内ρ的r 电场分布:(P.159式9.4-7) 3ε0
荷由P移到Q时,电场力所作的功。
将电荷由P点移到Q点时电场力所作的功为: Q
APQ q E dl q( U P UQ )
P
➢ 电场中某点的电势能(电势)的值是相对的,而 两点间的电势能差(电势差)是绝对的,与零点的 选择无关。电势的零点也可选在其它地方。
【大学物理】静电场的环路定理 电势 等势面 电势梯度
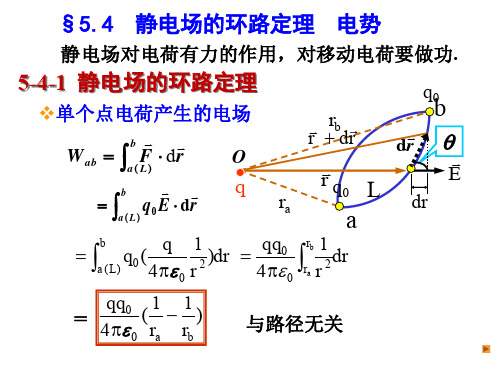
r r r r- r l cos
r
r
r+
q l
q+
3. 连续分布电荷电场中的电势 利用电势叠加原理:
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远 处为电势零点;积分是对整个带电体的积分。 E 利用电势定义式: dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R
q R
R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…,移动q0, 静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r = qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意:
• 电势能的零点可以任意选取,但是在习惯上, 当场源电荷为有限带电体时,通常把电势能的零 点选取在无穷远处。 这时,空间a点的电势能:
E pa
a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所 共有。
2023-2024学年高二下学期物理竞赛课件:静电场的环路定理和电势

四、电势差
Q Aab qo
bv v a E dl Wa Wb
电势差:
b
E dl
Wa
Wb
a
qo b qvo v
Uab Va Vb
E dl
a
结论:静电场中a,b两点的电势差,在数值上等于 将单位正电荷从a点移至b点电场力所作的功。
Aab W Wa Wb qo (Va Vb )
二、电势能(W)
Wa q0
Wb
保守力作功等于势能的减少 a
b
b
Aab qo a E dl Wa Wb W
Wa,Wb的量值是相对的量;与零势能参考点的选取 有关,而势能的增量 W与零势能点选取无关是绝对
的量.
1、对有限的带电体选无限远处作为电势能零点,
Aa
qo
a
E dl
Wa W
1) rib
电场力是保守力
qi ria
qn a
qo
3、若q0在电场中沿L运动一周
A lqo E dl 0
q0
静电场的环路定理:
l
静电场中电场强度 E的环流为零。
l E dl 0
结论:一定量的电荷在静电场中移动时,电场力所作 的功只与电荷的起点和终点的位置有关,而与路径无 关。即电场力是保守力。静电场是保守场。
致冷系数:
Q2 Q2
A Q1 Q2
K‘系观察者测得相对他静止的棒的长度为:
l0 x2 ' x1 ' l0 称为固有长度
问:在K系中观察者(相对棒运动的观察者)测得
的棒的长度为多少?
他测得棒两端的坐标为x1和x2, t1=t2=t(同时测)
则棒长 l= x2-x1
2023-2024学年高二物理竞赛课件:静电场的环路定理习题

势,球外的电势等效于将电荷集中于球心的点电荷
的电势。
qE
4 0R2
r 2
场强分布曲线
O
R
r
电势分布曲线
V
q
4 0R
O
r 1
r
例: 设两球面同心放置,半径分别为R1和R2 ,电荷分
别为q1、q2,求其电势分布。 解:解法一: 按高斯定理可得电场强度分布
E
0
q1
4 0r 2
er
(r R1)
(R1 r R2 )
a o
r≥R2时:
V3
r E3dr
q1 q2 dr q1 q2
r 4π0r 2
4π 0 r
q2 q1
r
解法二:运用多个带电体的电势叠加法计算
V V1 V2
q1
V1
4π 0 R1
q1
4π0r
(r R1)
V2 (r R1)
q2
4π 0 R2
q2
4π0r
(r R2 ) (r R2 )
解: E
0
Q
4π 0r 2
r
(r R) (r R)
取“”为电势零点
rP r
球外:U
E dl
p
球内:U
Q
r
4π
0
r2
dr
R
Q
4πቤተ መጻሕፍቲ ባይዱ0r
E dl
p
r
E内 dr
积分路径: 沿矢径方向
R E外 dr
R
0 dr
r
Q
R 4π 0r 2
dr
Q
4π 0 R
结论:均匀带电球面,球内的电势等于球表面的电
静电场环路定理电势能和电势.pptx
V
dV
1dq
Q440r0
r
Q
dq
Q
4 0 R2 x 2
(解毕 )
第23页/共43页
x a
x V (x) dr R o Qr
4 0R
o
x
课堂练习 求均匀带电园盘( R, σ )轴线上电势分布。
提示: 建立坐标系,取元,如图所示。
选∞处为电势零点,则:
dV 2dqrdr 4 0 r 2 x 2
q
r
r
r
4
q
0 r 2
dr
aq r
r 10V
E
8V 6V
V (r )
q
4 0r
( 球对称分布 )
等势面分布
第14页/共43页
课堂练习 求半径为R均匀带电 Q 的球面电势分布。
解 选∞处为电势零点,则:
V (r) r E dr
0
E(r) Q
4 0r 2
(r R) (r R)
r
4
即:电势 V 的叠加为标量叠加,而 叠加,后者运算较繁。
的叠加却为矢量
E
第13页/共43页
E
☻由于静电场的保守特性,
b
V与a积分路a 径E无 dr
关,可选取一合理的路径进行积分。
例 求点电荷 q 的电势分布。
解 选∞处为电势零点,则:
V (r)
E dr
E dr cos 0
(r (r)
R)
E
dr
R
E
dr
E dr
r
r
R
V (r) 0
Q
R 4 0r2
dr
cos
0
Q
静电场的环路定理 电势
E2
B
AAB q0
A i 1
n n qq 1 B 1 Ei dl qo Ei dl 0 i ( ) A rAi rBi i 1 4πε0 i 1
试探电荷在任何静电场中移动时, 电场力所做的功只与试探 3 电荷的电量及路径的起点和终点的位置有关, 而与路径无关 .
0
13
[ 例1] 均匀带电球面场中电势分布(
q , R)
q
由高斯定理
o R
E
P r
E
E
0 qr 3 4 0 r
(r R) (r R)
r
o
R
令 V 0 沿径向积分 1 面外 2
r
qr dr V外 E 外 dr 3 4 0 r P r 1 4 0 r r q
AAB W (WB WA ) WA WB
若取 B点 : WB 0
AAB
B
A
B F dl q0 E dl
A
A WA
"0"
q0 在 A 点处的电势能:W A
AA"0" q0
A
E dl
1)电势能零点的选取是任意的, 一般视问题方便而定, 通常参 考点不同 ,电势能不同。对于有限带电体,一般选无限远为势 能零点 , 实际应用中或研究电路问题时常取大地、仪器外壳等 为势能零点;对于无限大带电体,常取有限远为势能零点; 2)电势能是属于系统的 (电场 + 试验电荷) 5
21
a
E dr
6
2、电势
WA q0
WA A q0
" 0"
大学物理练习题 静电场的环路定理 电势
3. 真空中一半径为 R 的球面均匀带电 Q, 在球心 O 处有一带电量为 q 的点电荷, 如图所示, 设无穷远处为电势零点,则在球内离球心 O 距离为 r 的 P 点处的电势为: Q q 。 q Q⎞ (A) ( B) 1 ⎛ ⎜ + ⎟。 4 πε 0 r 4 πε 0 ⎝ r R ⎠ O r • q P 1 ⎛q Q−q⎞。 R ( C) q + Q 。 (D) ⎜ + ⎟
(A)
( B)
( C)
(D)
二、填空题
v - 1. 一均匀静电场,电场强度 E = 400iˆ + 600 ˆ j V⋅m 1,则点a(3,2)和点b(1,0)之间的电势 差Uab =__________________。(点的坐标x,y以米计)
(
)
2. 两平行无限大均匀带电平面,相距为 d,其面电荷密度分别为+σ 和-σ,则两平面间的电 势差为 。 3. 在电量为 q 的点电荷的电场中,若取与点电荷距离为 r0 的一点为电势零点,则与点电荷 距离为 r 处的电势为_____ 。 v 4. 在场强分布为 E 的静电场中,任意两点a和b间的电势差的表示式为Ua - Ub = 。
5. 巳知空气的击穿场强为 30kV/cm, 空气中一带电球壳半径为 1m, 以无限远处为电势零点, 则这球壳能达到的最高电势是 。 6. 把一个均匀带电量+Q的球形肥皂泡由半径r1,吹胀到r2,则半径为R(r1<R<r2)的高斯球 面上任一点的场强大小E由 变为 ;电势U由 变为 (选无穷远处为电势零点)。 7. 半径为r的均匀带电球面 1,带电量q;其外有一同心的半径为R的均匀带电球面 2,带电 量Q。则此两球面之间的电势差ϕ 1 - ϕ2为 。 8. “无限大”均匀带电平板附近,有一点电荷 q,沿电场线方向移动距离 d 时,电场力做的功 为 A,则平板上的电荷面密度σ = 。 9. 如图所示,一半径为 R 的球壳上均匀带有电量 Q,将一个点电荷 q(q << Q)从球内 A 点经球壳上 一个小孔移到球外 B 点, 则此过程中电场力作功 A = 。 R A O r B
5-3静电场的环路定理 电势能 电势1
5–3 静电场的环路定理 电势一 静电场的环路定理1 静电场力所做的功(1) 点电荷的电场l E q Wd d0⋅=l e r qq rd π4200⋅=εdr dl l e r ==⋅θcos d⎰=BA r r r r qq W 200d π4ε)11( π400BA r r qq -=ε(与路径无关)(2) 任意电荷的电场∑=i i E E,⎰⋅=l l E q W d 0⎰∑⋅=l i i l E q d 0(与路径无关)2 静电场的环路定理⎰⎰⋅=⋅BA B A l E q l E q 2010d d0)d d (210=⋅+⋅⎰⎰AB B A l E l E q0d =⋅⎰l l E二 电势和电势差1 电势能保守力的功=相应势能的减少p p p 0d E E E l E q W B A AB B A ∆-=-=⋅=⎰→令0p =B E⎰⋅=AB A l E q E d 0p令0p =∞E ,点电荷的电势能:rqq E P 00 π4ε= 2 电势 电势差(1) 电势B A AB E E l E q p p 0d -=⋅⎰p 0p d q E q E l E B A AB -=⋅⎰ 0p q E V BB =,0p q E V A A = B AB A V l E V +⋅=⎰ d令0=B V⎰⋅=ABA l E V d 单位:v(伏特)有限带电体令0=∞V⎰∞⋅=A A l E V d 把单位正试验电荷从点A 移到无穷远时,静电场力所作的功(2) 电势差⎰⋅=-=ABB A AB l E V V U d 将单位正电荷从A 移到B 电场力作的功注意电势差是绝对的,与电势零点的选择无关;电势大小是相对的,与电势零点的选择有关。
点电荷电势能:V q E p 0=静电场力的功AB B A AB U q V q V q W 000=-=原子物理中能量单位J 10602.1eV 119-⨯=3 电势的计算(1) 点电荷的电势r e r qE20 π4ε=0=∞V⎰∞⋅=r r l e rqV d π420ε⎰∞=r rrq 20 π4d εrqV 0 π4ε=(2) 电势的叠加原理点电荷系∑=ii E E⎰∞⋅=A A l E V d l E i Aid ⋅=∑⎰∞∑∑==i iii Ai A r q V V 0π4ε电荷连续分布⎰=rqV P 0 π4d ε(3) 求电势的方法 (a) ⎰=rqV P 0 π4d ε(无限远处为电势零点)(b) l E V V A A d 0⋅=⎰=点(E 好求或已知)例1 求正电荷q 均匀分布在半径为 R 的细圆环上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十三讲:§5.3 静电场的环路定理 电势习题课 一、静电场的环路定理
o d =⋅⎰
静电场是保守场,是有源场
二、电势和电势差
d E q a
a a ⋅===⎰∞
∞0
a 0q W
W U
d E d E d E U b
a
b
a
b a ⋅=⋅-⋅=-⇒⎰⎰⎰∞∞U
☆电势的计算(两种方法)
①已知电场,求电势。
d E U U U P
P b b
a ⋅=+⋅=⎰⎰∞
;或d E a
②已知电荷,求电势。
⎰=r
dq U 0P 41
πε
例题1:均匀带电圆盘其轴线上P 的电势(R ,σ) 由均匀带电圆环其轴线上P 的电势(R,q )
⇒+=
2
2
0P 4q U R
x πε 2
2
0P r
4dq dU +=
x πε
l R 0220
R 02220220
R 0P P r x 24r x dr 4r 4rdr
2dU U +=+=+==⎰⎰⎰εσεσπεπσx ()
x -R x
222
+=
εσ
例题2:无限长均匀带电直线的电势(λ)
b b
a a U d -⋅=⎰ U ;已知:r r
02πελ
=
令:0=b U r e dr d =
r
r dr r dU b r r
b ln 2200πελ
πελ==⎰
例题3:均匀带电球面的电势(R ,q ) 已知:0:r 1=R
r r
q 2
024πε=
d E U P
P ⋅=⎰∞
R
q dr r q d d d U R r R
R
R r
P
P 02
02
1
44:πεπε==⋅+⋅=⋅=⎰
⎰⎰⎰∞
∞∞
r
q
dr r
q d d U R r r
r
P
P 02
02
44:πεπε==⋅=⋅=⎰
⎰⎰∞
∞∞
三、电势面 电势梯度 1、电势面由电
①在任何静电场中,等势面与电场线处处正交。
②电场线总是指向电势降低的方向。
2、电势梯度
①电场强度:单位长度上的电势变化率的负值。
d dU
U -lim U -=∆∆=∆∆= 总是指向电势降低的方向。
②电势梯度:
⎪⎪⎭
⎫
⎝⎛∂∂+∂∂+∂∂=∇==z U y U x U -U --gradU z
y x ∂∂+∂∂+∂∂=∇汉密尔顿算子 ()z y x ,,U U = dx d U -=
四、应用举例:
例题4:均匀带电圆环其轴线上P 的场强(R ,q ) 已知:2
2
0P 4q U R
x +=πε ()()
11
`
d
--=⇒==n n
n n n
nx dx
dx dx nx x x
求: P
解:
()
(
)
x
R xq x x R q dx d 2
322012
12
2042214U +=
+⎪⎭
⎫ ⎝⎛--=-=--πεπε
例题5:均匀带电圆盘其轴线上P 的场强(R ,2
R q
πσ=
) 已知:()
x
R x
-+=
22
0P 2U εσ
求:P
解:
()
x R x
x x R dx d ⎪⎪⎭
⎫
⎝⎛+-=⎥⎦⎤⎢⎣
⎡-+-=-=-22012
12
201212212U εσεσ
小结:环路定律,电势,电势差 作业:P201 5-22;5-23 预习:§5.4 静电场中的导体
第十三讲:§5.3 静电场的环路定理 电势习题课
5-22 由高斯定理可求得两无限长同轴圆柱面间的场强为
r
02πελ
,所以两圆柱面间的电势差 1
200ln 2d 22
1
R R r r u R R πελ
πελ==
∆⎰
5-23 静电平衡时,导体球壳内、外表面均有感应电荷,由于带电系统具有球对称性,所以
内表面均匀分布有-q 电荷,外表面均匀分布+q 电荷,可判断电场分布具有球对称性,以任意半径r 作一与球壳同心的高斯球面S ,由高斯定理可得
⎰
∑==⋅0
2
4d επi q E r S E 2
04r
q E i
πε∑=
当q q R r i =∑<1 ∴ 2
014r
q E πε=
021=-+=∑<<q q q R r R i ∴ 02=E q q R r i =∑≥2
∴ 2
034r q E πε=
由电势定义式可求得电势分布
1R r <
⎰⎰⎰∞
++=12
1
2
d d d 3211R r
R R R r E r E r E u
2
0102
02
041114d 4d 41
2
R q R r q r
r
q r r
q R r
R πεπεπεπε+⎪⎪⎭⎫ ⎝⎛-=+=⎰
⎰
∞
21R r R <<
⎰⎰∞
+=2
2
d d 322R r
R r E r E u
202041d 42
R q
r r
q R ⋅
==
⎰
∞
πεπε 2R r > ⎰⎰
∞
∞
==r
r
r r r E u d 41
d 2
033πεr
q 041
πε=。
