四边形典型例题
平行四边形知识点及典型例题
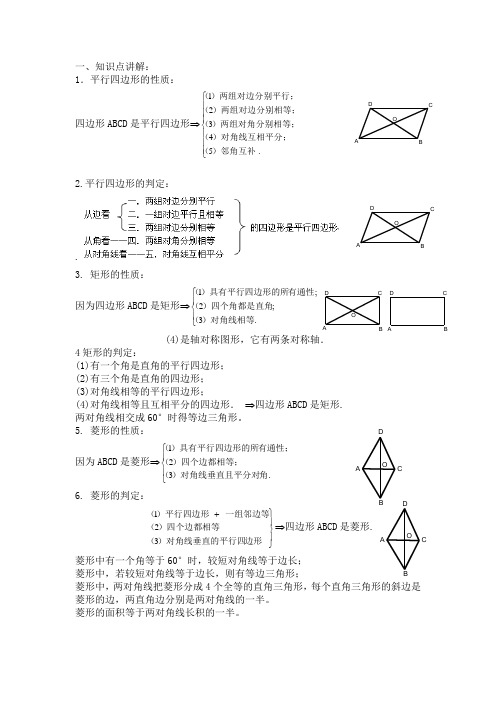
一、知识点讲解:1.平行四边形的性质:四边形ABCD 是平行四边形⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧.54321)邻角互补()对角线互相平分;()两组对角分别相等;()两组对边分别相等;()两组对边分别平行;(2.平行四边形的判定:.3. 矩形的性质:因为四边形ABCD 是矩形⇒⎪⎩⎪⎨⎧.3;2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所( (4)是轴对称图形,它有两条对称轴.4矩形的判定:(1)有一个角是直角的平行四边形; (2)有三个角是直角的四边形; (3)对角线相等的平行四边形;(4)对角线相等且互相平分的四边形. ⇒四边形ABCD 是矩形. 两对角线相交成60°时得等边三角形。
5. 菱形的性质:因为ABCD 是菱形⇒⎪⎩⎪⎨⎧.321角)对角线垂直且平分对()四个边都相等;(有通性;)具有平行四边形的所( 6. 菱形的判定:⎪⎭⎪⎬⎫+边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321⇒四边形ABCD 是菱形.菱形中有一个角等于60°时,较短对角线等于边长;菱形中,若较短对角线等于边长,则有等边三角形;菱形中,两对角线把菱形分成4个全等的直角三角形,每个直角三角形的斜边是菱形的边,两直角边分别是两对角线的一半。
菱形的面积等于两对角线长积的一半。
ABDOCABDOCAD BCAD B C OCDB AOCDB A OC DABA BCDO7.正方形的性质:四边形ABCD 是正方形⇒⎪⎩⎪⎨⎧.321分对角)对角线相等垂直且平(角都是直角;)四个边都相等,四个(有通性;)具有平行四边形的所(8. 正方形的判定:⎪⎪⎪⎭⎪⎪⎪⎬⎫++++++对角线互相垂直矩形)(一组邻边等矩形)(对角线相等)菱形(一个直角)菱形(一个直角一组邻边等)平行四边形(54321⇒四边形ABCD 是正方形.9. 1.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。
《平行四边形的判定》典型例题知识讲解

《平行四边形的判定》典型例题《平行四边形的判定》典型例题例1如图,△DAB、△EBC、△FAC都是等边三角形,试说明四边形AFED是平行四边形.例2如图,E、F分别是ABCD边AD和BC上的点,并且AE=CF,AF 和BE相交于G,CE和DF相交于H、EF与GH是否互相平分,请说明理由.例3如图,在平行四边形ABCD中,A1、A2、A3、A4和B1、B2、B3、B4分别是AB和DC的五等分点,C1、C2和D1、D2分别是AD和BC的三等分点,若四边形C1A4D2B1的面积为1,求S平行四边形ABCD.例4已知:如图,E,F分别为ABCD的边CD,AB上一点,AE∥CF,BE,CF分别交CF,AE于H,G.求证:EG=FH.例5如图,已知:四边形ABCD中,AE⊥BD,CF⊥BD,E,F为垂足,且AE=CF,∠BAC=DCA.求证:四边形ABCD是平行四边形.参考答案例1分析要证四边形AFED是平行四边形,应观察:两组对边是否相等、两组对角是否相等,或一组对边是否平行且相等、对角线是否相互平分.但在本题中没有对角线,也没有明显的对角之间的关系,因此可以先考虑去证明四边形AFED的对边是否相等.事实上,AD=AB=BD,EF是否能等于这三条边中的一条呢?可以看到,∴EF=AB=BD.同理DE=AC=AF,因此,所要证的四边形AFED是平行四边形.证明,∴,且,∴,∴又,同理.∴AFED是平行四边形.例2分析若EF、GH互相平分,那么四边形EGFH应是平行四边形.观察已知条件,可以证明四边形EGFH是平行四边形.证明是平行四边形,∴又,∴,且∴四边形AECF是平行四边形,∴,∴又四边形EDFB是平行四边形,∴,∴在四边形GEHF中,,∴四边形GEHF是平行四边形,∴EF和GH互相平分.说明:本题中多次使用了平行四边形的性质:对边平行且相等以及平行四边形的判断方法:对边平行且相等的四边形是平行四边形.通过解题应熟悉平行四边形的性质及判别.例3 分析平行四边形ABCD被和分别成15个相等的小平行四边形。
第1章特殊平行四边形《特殊四边形》典型题型1 特殊四边形中的多结论题型-北师大版九年级数学上册

《特殊四边形》典型题型1 特殊四边形中的多结论题型【知识梳理】 总体解题思路和方法:①直接证明:不一定按顺序,哪个结论最好证就先证哪个; ②已证明的结论可以作为题目的已知条件;③假设法:遇到不好证的,可以假设它成立,倒过去反推,若推出的结论与题目已知条件相符,说明假设成立,即结论也成立,反之,结论错误;④涉及几何计算时,常用解题技巧是:特殊值法或字母参数法【典型例题】例1.如图,在平行四边形ABCD 中,CD=2AD ,BE ⊥AD 于点E ,F 为DC 的中点,连接EF 、BF ,下列结论:①∠ABC=2∠ABF ;②EF=BF ;③;④∠CFE=3∠DEF ;其中正确结论的个数有( D )个 A. 1 B. 2 C. 3 D. 4解析:多结论题型,几何综合题型,压轴题(1)数学典型模型:“等腰△+平行线=角平分线”,∵FC=BC ,FC//AB , ∴∠CFB=∠ABF=∠CBF ,∴∠ABC=2∠ABF ,①正确;(2)数学典型模型:“中线倍长”;延长BC 交EF 的延长线于点G ,由AAS 易证△DEF ≌△CGF ,则EF=FG ,∵AD//BC ,∴∠AEB=∠EBC=90°,则BF 是Rt △EBG 斜边上的中线,∴BF=EF=FG ,②正确; (3)由△DEF ≌△CGF 可得,由BF 是中线,可得, ∴,③正确;CBADEFGFEDABC(4)依几何图形的审题技巧:想办法拉近∠CFE与∠DEF的位置距离,由AD//BG,可得∠DEF=∠G,由BF=FG可得∠G=∠FBG,由CF=CB可得∠FBG=∠CFB,∴∠DEF=∠CFB,由外角定理可得∠EFB=∠G+∠FBC=2∠FBC=2∠CFB,∴∠CFE=3∠CFB=3∠DEF,④正确,故选D.例2.已知如图,四边形ABCD为矩形,点O是AC的中点,过点O的一直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO,若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD 是菱形;④MB:OE=3:2,其中正确结论是___________解析:多结论题型,压轴题。
期末典例专练07:平行四边形、梯形基本题型和周长应用问题-四年级数学上册典型例题系列(原卷版)人教版

四年级数学上册典型例题系列期末典例专练07:平行四边形梯形基本题型和周长应用问题一、填空题。
1.两个完全一样的梯形能拼成( )、( )和( )。
2.把长方形拉成平行四边形它的周长( )(填“变”或“不变”),依据是( )。
3.图中a∥b,两条平行线之间有( )个梯形,( )个平行四边形。
4.平行四边形和梯形都有( )条高,如图的梯形中,高为( )厘米。
5.用一根铁丝围成了平行四边形(如图),这个平行四边形的周长是( )cm,如果用这根铁丝围成一个半圆形,半圆形的周长是( )cm。
6.两个完全相同的梯形,上底长3cm,下底长5cm,高4cm,把它们拼成一个平行四边形,则这个平行四边形的底是( )cm,高是( )cm。
7.下图是用两个完全一样的梯形拼成的平行四边形,已知梯形的上底是3厘米,下底是5厘米,高4厘米,那么平行四边形的底是( )厘米,对应的高是( )厘米。
8.一个等腰梯形的上底是8厘米,下底是12厘米,一条腰长14厘米,它的周长是( )厘米。
9.一个等腰梯形的周长是28厘米,上底与下底的和是14厘米,这个等腰梯形的腰是( )厘米。
10.一个直角梯形的高是20厘米,其中一条腰长25厘米,如果上底增加5厘米,就变成正方形,那么原来梯形的周长是( )厘米。
二、解答题。
11.一根48厘米长的铁丝刚好围成一个平行四边形,其中一条边长15厘米,其他三条边的长度各是多少厘米?12.一面平行四边形镜子的一条边是15厘米,它的一条邻边比它长5厘米。
如果用木条给这面镜子的边缘镶上镜框,至少需要多长的木条?13.劳动教育是五育并举中的重要一环,衡阳市一所小学特地在后山开辟一块等腰梯形的菜地,上底长12米,下底长15米,腰长13米。
这块菜地的周长是多少米?14.一个等腰梯形,它的下底比上底长9厘米,上底和一条腰的长都是6厘米,这个梯形的周长是多少厘米?15.一块菜地是一个等腰梯形,它的腰长7米,上底长12米,下底比上底长4米,如果在菜地四周围上篱笆,至少需要篱笆多少米?16.将一个平行四边形分割成两个完全相同的等腰梯形,如图所示。
四年级数学上册典型例题系列之第5单元:平行与垂直、平行四边形与梯形综合作图专项练习(解析版)人教版

四年级数学上册典型例题系列之第五单元:平行与垂直、平行四边形与梯形综合作图专项练习(解析版)1.过A点分别画已知直线的平行线和垂线。
【答案】见详解【分析】(1)把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线即可。
(2)把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和A点重合,过A点沿三角板的直角边画直线即可。
【详解】【点睛】本题考查了平行线和垂线的作法,培养学生的作图能力。
2.过点A分别画出直线的垂线和平行线。
【答案】见详解【分析】把三角板的一条直角边与已知直线重合,沿直线移动三角板,使三角板的另一条直角边和A点重合,过A点沿三角板的直角边,向已知直线画直线,并画上垂直符号。
这条直线就是已知直线的垂线;过直线外一点作已知直线的平行线的方法:先把三角尺的一条直角边与已知直线重合;再用直尺紧靠着三角尺的另一条直角边。
固定直尺,然后沿着直尺平移三角尺,使直线外的A点在三角尺上。
沿直角边画出另一条直线即可。
【详解】【点睛】熟练掌握用三角板画平行线和垂线的方法,是解答此题的关键。
3.小东要去河边画画,请你画出从A点处到河边的最短路线。
【答案】见详解【分析】从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
据此可知,要求从A点处到河边的最短路线,则从A向河边作垂线,这条垂线即为所求。
【详解】【点睛】解决本题的关键是明确从直线外一点到这条直线的线段中,垂直线段最短。
这个性质常用于解决求最短路线的问题。
4.阳光小区的居民准备安装天然气管道,为了节省安装费用,请帮助工人叔叔设计出安装管道的最短路线。
【答案】见详解【分析】从直线外一点到这条直线的线段中,垂直线段最短,这条垂直线段的长度叫做点到直线的距离。
据此可知,要使装管道的路线最短,则从阳光小区向天然气管道作垂线,这条垂线即为所求。
平行四边形的判定例题和练习题
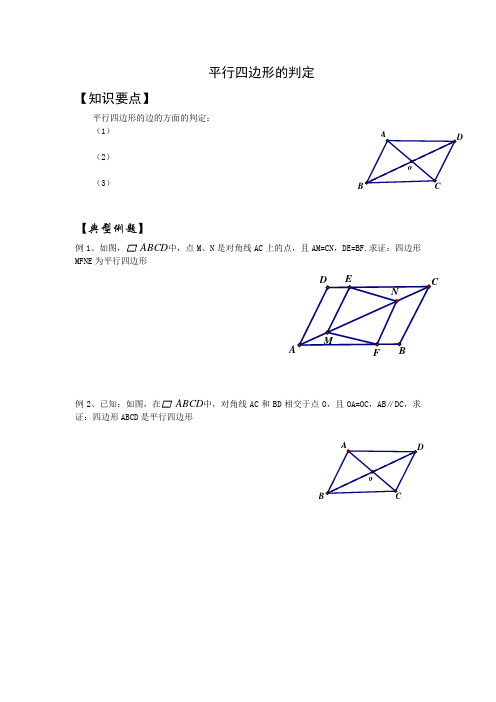
平行四边形的判定【知识要点】平行四边形的边的方面的判定:(1)(3)【典型例题】例1、如图,ABCD中,点M、N是对角线AC上的点,且AM=CN,DE=BF.求证:四边形MFNE为平行四边形例2、已知:如图,在ABCD中,对角线AC和BD相交于点O,且OA=OC,AB∥DC,求证:四边形ABCD是平行四边形CD【知识要点】平行四边形角的方面和对角线的方面的判定(1)由角方面的判定(2)由对角线方面的判定【经典例题】例1、如图所示,在平行四边形ABCD中,点E、F是对角线AC上两点,且AE=CF.求证四边形BEDF是平行四边形。
例2、已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.连接AF、BE,求证:AF//BE.练习1、如图,在 ABCD 中,AE=CG ,求证:GF=HE 。
2、如图,AB//CD ,∠ABC=∠ADC ,AE=CF ,BE=DF ,求证:EF 与AC 互相平分。
3、已知:如图,在平行四边形ABCD 中,BE ⊥AC 于点E ,DF ⊥AC 于点F ,又M 、N 分别是DC 、AB 的中点。
求证:四边形EMFN 是平行四边形。
·A BCDEFHACNM4、已知:如图,分别以△ABC 的三边为边长在BC 边的同侧面作等边△ABD 、△BCE 、△ACF ,连结DE 、EF 。
求证:四边形ADEF 是平行四边形。
5、如图,△ABC 为等边三角形,D 、F 分别为CB 、BA 上的点,且CD=BF ,以AD为一边作等边△ADE 。
求证:(1)△ACD ≌△CBF ;(2)四边形CDEF 为平行四边形。
6、如图,以ABCD 的边AD 、BC 为一边向外作等边△ADE 和等边△BCF ,连结AC 、EF 求证:AC 和EF 互相平分EFCB。
等底等高的三角形和平行四边形问题-2024-2025学年五年级数学上册典型例题系列(教师版)苏教版
第二单元专练篇·06:等底等高的三角形和平行四边形问题一、填空题。
1.一个长方形的面积是50平方厘米,从中剪出一个最大的三角形,这个三角形的面积是( )平方厘米。
【答案】25【分析】在这个长方形中剪下的最大三角形的底等于长方形的长(或宽),高等于长形的宽(或长),根据等底等高的三角形的面积是平行四边形面积的一半,用长方形的面积除以2解答。
【详解】50÷2=25(平方厘米)所以这个三角形的面积是25平方厘米。
2.一个平行四边形的面积是72cm2,与它等底等高的三角形的底是18cm,这个三角形中与这条底对应的高是( )cm。
【答案】4【分析】等底等高的三角形面积是平行四边形面积的一半,用平行四边形面积÷2,求出三角形面积;再根据三角形面积公式:面积=底×高÷2,高=面积×2÷底,代入数据,即可解答。
【详解】72÷2×2÷18=36×2÷18=72÷18=4(cm)一个平行四边形的面积是72cm2,与它等底等高的三角形的底是18cm,这个三角形中与这条底对应的高是4cm。
3.一个三角形和一个平行四边形的面积和底都相等,如果平行四边形的高是3厘米,那么三角形的高是( )厘米。
【答案】6【分析】根据三角形的面积=底×高÷2,平行四边形的面积=底×高;一个三角形和一个平行四边形的面积和底相等,设三角形和平行四边形的面积均为12平方厘米,计算出平行四边形的底;用12乘2,再除以平行四边形的底,所得结果即为三角形的高。
【详解】设三角形和平行四边形的面积均为12平方厘米。
12÷3=4(厘米)这个三角形的底为4厘米。
12×2÷4=24÷4=6(厘米)因此这个三角形的高是6厘米。
4.一个三角形的底是8分米,高是6分米,和它等底等高的平行四边形的面积是( )平方分米。
数学 四边形之长方形知识点总结 附典型例题
数学四边形之长方形知识点总结附典型例题
长方形是四边形的一种,它的对边相等,并且每个角都是直角。
以下是一些关于长方形的基本知识点,以及一些例题。
知识点总结:
1. 定义:长方形是一个四边形,其中对边相等且每个角都是直角。
2. 性质:
对边相等:长方形的对边长度相等。
四个直角:长方形的每个角都是直角。
对角线相等:长方形的对角线长度相等。
3. 周长和面积公式:
周长公式:P = 2(l + w),其中l是长度,w是宽度。
面积公式:A = l × w,其中l是长度,w是宽度。
典型例题:
1. 题目:一个长方形的周长是20厘米,长是a厘米,则宽是 ( )
A. (20 - a)厘米
B. (20 - 2a)厘米
C. (10 - a)厘米
D. 10 - a厘米
答案:C
2. 题目:已知一个长方形的周长是20厘米,则这个长方形的面积最大是多少平方厘米.
答案:解:假设这个长方形的长为a厘米,宽为b厘米.
由题意得:2(a+b)=20,
a+b=10;
长方形的面积=长×宽,所以要求长方形的面积最大就是要用长和宽的积最大,所以当a=5时,b=5时,面积最大.
即:5×5=25(平方厘米).
答:这个长方形的面积最大是25平方厘米.。
北京市2013届中考数学二轮专题突破《四边形中档解答题》(知识概括+典型例题点拨)
在 Rt△AFB 中, BF 1 ∵cosB=AB= , 2 ∴∠B=60°. ∵BF=1, ∴AF= 3. ∵FC=3,由勾股定理,得 AC=2 3. ∴∠B=60°,AC=2 3.
方法二:过 A 点作 AE∥DC 交 BC 于点 E. ∵AD∥BC, ∴四边形 AECD 是平行四边形. ∴AD=EC,AE=DC. ∵AB=DC=AD=2,BC=4, ∴AE=BE=EC=AB. 可证△BAC 是直角三角形,△ABE 是等边三角形. ∴∠BAC=90°,∠B=60°. 在 Rt△ABC 中,AC=AB· tan60°=2 3. ∴∠B=60°,AC=2 3.
►
热考一
四边形中有关计算
例 1 四边形 ABCD 中,∠ABC =90°,∠CAB=30°,DE⊥AC 于 E, 且 AE=CE, 若 DE=5, EB=12, 求四边形 ABCD 的周长.
解:∵∠ABC=90°,AE=CE,EB=12, ∴EB=AE=CE=12. ∴AC=AE+CE=24. ∵在 Rt△ABC 中,∠CAB=30°, ∴BC=12,AB=AC· cos30°=12 3. ∵DE⊥AC,AE=CE,∴AD=DC. 在 Rt△ADE 中, 由勾股定理得 AD= AE2+DE2= 122+52=13. ∴DC=13. ∴四边形 ABCD 的周长=AB+BC+CD+DA=38+12 3.
例 3 如图 Z3-3,在梯形 ABCD 中, AD∥BC, ∠B=90°, ∠C=45°, AD=1,BC=4,E 为 AB 的中点, EF∥Dຫໍສະໝຸດ 交 BC 于点 F,求 EF 的长.
解: 方法一:如图,过点 D 作 DG⊥BC 于点 G. ∵AD∥BC,∠B=90°,∴∠A=90°.∴四边形 ABGD 为矩形. ∴BG=AD=1,AB=DG. ∵BC=4,∴GC=3. ∵∠DGC=90°,∠C=45°, ∴∠CDG=45°.∴DG=GC=3. ∴AB=3. 又∵E 为 AB 的中点,∴BE= ∵EF∥DC,∴∠EFB=45°. 在△BEF 中,∠B=90°. ∴EF= BE 3 2 = . 2 sin45° 1 3 AB= . 2 2
特殊平行四边形典型例题
特殊的平行四边形复习几种特殊的平行四边形的特征及识别方;去一览表边4角4对角线Q对称性2识别方迭Q口P P P矩形|护菱形0.正方形P1.Mffl; BUftAABC 中zTABC 的平弁堀DE//BC交AB 于E, DF AB交BC于斷四边形BFDE的形状并说明理由屮例2.已知如虱平行四边形ABCD的对角线AC的垂直平分W垢边AEk BC分别交于臥F。
试判断四边形AFCE的形状并说明理由.屮T例3.如亂点\【是矩形ABCD的边AD中点,点P是B6 边上一动点,PE丄\IC, PF丄BM,垂足分别为E、F。
*(1〉当四边形PEXff为矩形时,矩形ABCD的长与宾应满足什么条件?"<2>在(1>中,当点卩运动至卅么位羞时,四边形PEX1F 变为正方形?为什么? 2例4.已知妇图'奏形ABCD中,E是BC上一点'AE、BD交干M,若AB=AE,"iZEAI>2ZBAEo 求证:卩(-)迭择1•对为线相竽的四边形星(HA.矩形B.正方形C.等脖梯形D.矩形、正方形、等腰佛形作为结论都不对a2.下面几种说法:①正方形是有一组对边平行的四丈形;②矩形是菱形;③矩形是正方形④正方邢是矩形•那么(戸A.①②©④都不正确;B.只有②是错误的;C只有④是正确的;D.只有②③是错的。
3.有三个角相等的四边形是(〉aA•矩形 D.菱形C.正方形D-矩形、菱形、正方形作沟结论都不只扣4.下面几种说法:①对角线互相垂直的四边形是菱形;②一组对边平行一组邻边相等的四边是菱形;③两条对角线相等的平行四边形定矩形;④对角线互相平分耳垂直的四边形是菱形,那么正确的i兑法是(〉和A.①②③B.②③C.③④D.②④a5 .下列團形既是中心对称又是轴对称團形的是(*A•平行四边形不或巨形; B.矩形和菱形屮C.正三角形和正方形;D.平行四边形和正方形a<5.矩形两杂对角絃文点到V、边距离比到大边距离多4厘米,若矩形周长为50厘米,贝U矩形两邻边长九(”A.18相10厘米B. 1(5相12厘米C.8相10厘米D.5和9厘抹>*(二)解翻"1.菱形ABCD中,ZA=60° ,对角线BD=2,求菱形的周长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图:在梯形ABCD中,
21.已知:在△ABC中,∠ABC=-90°,点B在直线AB上,ED与直线AC垂直,垂足为D,
且点M为EC中点,连接BM,DM.
(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关
系,并直接写出你得到的结论;
(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想
并加以证明:
20.如图,四边形ABCD为矩形,AB=4,AD=3,动点M从D点出发,以1个单位/秒的速度
沿DA向终点A运动,同时动点N从A点出发,以2个单位/秒的速度沿AB向终点B
运动.当其中一点到达终点时,运动结束.过点N作NP⊥AB,交AC于点P1连结MP.已
知动点运动了x秒.
(1)试求△MPA的面积S与时间x秒的函数关系式,写出自变量x的取值范围,并求出S
的最大值;
(2)在这个运动过程中,△MPA能否为一个等腰三角形.若能,求出所有x的对应值;
若不能,请说明理由.
