2012-2013第二学期概率论与数理统计试卷 参考答案
2016年中南财经政法大学《概率论与数理统计》2012-2013学年第二学期期末试卷B(金融、会计等专业)

2. 设 X ~ N (0,1), 求Y 2 X 2 1 的概率密度.
1000 3. 某种型号的电子的寿命 X(以小时计)具有以下的概率密度: f ( x) x 2 0
x 1000 其它
现有一大批此种管子 (设各电子管损坏与否相互独立) 。任取 5 只,问其中至少有 2 只寿 命大于 1500 小时的概率是多少?
第 2 页(共 3
页)
4. 设二维随机变量 ( X , Y ) 的概率密度函数为
------------------------------------------------- 密 ---------------------------------- 封 ----------------------------- 线 ---------------------------------------------------------
得分
评阅人
学生姓名:
一、填空题: (共 8 题,每题 2 分,总分 16 分)
1. 在房间里有 10 人,分别佩代着从 1 号到 10 号的纪念章,任意选 3 人记录其纪念章的号码。则最小的号 码为 5 的概率是 。
2. 在(0, 1)内随机取两个数,则两数之积小于
年级:
1 的概率为 3
。
。
3. 已知 A B, P( A) 0.2, P( B) 0.3 ,则 P( AB) = 4. 设 X~B(10,p) ,E(X)=5,则 p = 5. 已知 E(X)=3,D(X) =5,则 E ( X 2)2 = 。
评阅人
三、判断说明题: (共 4 题,每题 5 分,总分 20 分) )
1. 若事件 A , B 和 C 相互独立,则 AB 与 C 相互独立。 (
概率论与数理统计 B+参考答案

《概率论与数理统计》试题(B )+参考答案一、填空题:(每题4分,共20分)1、 设,A B 为两事件,()()12,(|)15P A P B P A B ===,求()P AB =2、 已知2(2,),(24)0.3XN P X σ<<=,则(0)P X <=3、 设K 在(2,4)-服从均匀分布,x 的方程22220x Kx K +++=有实根的概率= 4、 若随机变量X 的数学期望2EX =,方差4DX =,则(28)P X -≥≤ 5、若随机变量(1,3),(1,4)XU Y N -,且它们相互独立,则(32)E X Y ++=二、单选题:(在上表对应题号下填入正确选项。
每题3分,共21分)1、在随机事件C B A ,,中,A 和B 两事件至少有一个发生而C 事件不发生的随机事件可表示为( ) A 、C B C AB 、C AB C 、BC A C B A C ABD 、C B A2、设连续型随机变量X 的分布函数为2,0()00x B Ae x F x x -⎧+>=⎨≤⎩,则,A B 的值为( )A 、1,1AB ==- B 、1,1A B ==C 、1,1A B =-=-D 、1,1A B =-= 3、若(0,1)XN ,其密度函数为()f x ,则下列说法错误的是( )A 、()f x 关于y 轴对称B 、()f x 的最大值是C 、()()()P a X b b a <<=Φ-ΦD 、()0f x >4、已知随机变量X 的密度函数为()X f x ,令2Y X =,则Y 的密度函数()Y f y =( )A 、2()y X f x dx ∞⎰ B 、1()22X y f C 、()y X f x dx ∞⎰ D 、1()2X f y5、对任意随机变量X ,若DX 存在,则()E DX 等于( )A 、0B 、XC 、()E XD 、()D X 6、已知随机变量(,)XB n p ,且()E X =3.6,() 1.44D X =,则其参数,n p 的值为( )A 、6,0.6n p == ;B 、6,0.4n p == ;C 、8,0.3n p == ;D 、24,0.1n p == 7、(,)0Cov X Y =是随机变量,X Y 相互独立的( ) A 、充分非必要条件 B 、必要非充分条件C 、充要条件D 、既不充分也不必要三、计算题:(第1小题10分,第2-4每小题13分,第5小题10分,共59分)1、设某人按如下原则决定某日的活动:如该天下雨则以0.2的概率外出购物,以0.8的概率外出探访朋友;如该天不下雨则以0.9的概率外出购物,以0.1的概率外出探访朋友。
122概率论与数理统计试卷B答案(最新整理)

江西财经大学12—13第二学期期末考试答案与评分标准课程代码:03054(B ) 授课课时:64 考试用时:110分钟课程名称:概率论与数理统计(主干课程) 适用对象:11级经管类本科生 试卷命题人: 王平平 试卷审核人: 徐慧植一、填空题1. 0.9;2. 1/9;3. 4/3;4. 1/6;5. ),1(n F 二、单项选择题DBCDB三、计算题解:(1)记 :国道上行驶的高速客车;:国道上行驶的一般客车;:国道上有客车因1A 2A B 发生故障需要停驶检修; …… 2分由全概率公式…… 9分0084.001.08.0002.02.0)()()()()(2211=⨯+⨯=+=A B P A P A B P A P B P (2) …… 12分2110084.0002.02.0)()()()(111=⨯==B P A B P A P B A P 四、计算题解:(1)⎩⎨⎧>=⎪⎩⎪⎨⎧≤>=--⎰00,000,)(0x xe x x dy e x f x x x X ,……… 8分 ⎩⎨⎧≤>=⎪⎩⎪⎨⎧≤>=-∞-⎰0,00,0,00,)(y y e y y dx e y f y yx Y(2)由于,故X 与Y 不相互独立。
……… 10分)()(),(y f x f y x f Y X ⋅≠(3) 212101121022)()1(------=-==≤+⎰⎰⎰e dye e dxe dy Y X P y y y y x……… 12分五、计算题解:2511051)10(51(~--∞==>⎰e dx e X P E X x, ……… 8分(1)的分布律为: (10)分Y 5,4,3,2,1,0,)1()(5225=-==---k e e C k Y P k kk (2) ………… 12分52)1(1)0(1)1(---==-=≥e Y P Y P 六、计算题解:似然函数为………… 3分对数似然函数为:………… 6分令 ………… 10分解之得: ………… 12分x x np n i iL 1ˆ1==∑=七、应用题解: (1) ……… 2分10:,10:10>μ≤μH H 统计量 ,当为真时 …… 4分)8(~8/10t S X T -=0H 原假设的拒绝域为0H ……… 6分}8595.1)8({95.0=>=t T W 由样本观测值得11)1()(-=-=∏i x ni p p p L ())],1ln(1[ln )(ln 1p x p p L i n i --+∑==,01)1()(ln 1=-∑--==p xp n p L p ni i d d……… 8分8595.140.28/4.141022.13>=-=T 故拒绝原假设,接受备择假设,即认为服用某种药物一定份量使病人每分钟脉搏增1H 加的次数大于10. ………10分(2)σ的置信度为0.95的置信区间为(2.720,7.710)……… 12分八、证明题由P (A |B )>P (A |)得B )()()()())()(())(1)(()()()()()()()()(B P A P AB P B P AB P A P B P AB P B P B A P B P AB P B P B A P B P AB P >⇒->-⇒>⇒> ………6分于是)()()())()()(()())(1()()()()(>-=---=-B P A P AB P AB P B P A P AB P A P B A P A P AB P A P 即………… 10分()()()()()(A B P A B P A P B A P A P AB P >⇒>。
集美大学试卷参考答案及评分标准
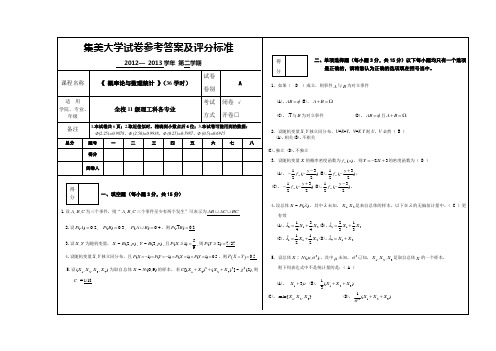
(C). (D). .
4.设总体 ,其中 未知, 是来自总体的样本,以下在 的无偏估计量中,(C)更有效.
(A). (B).
(C). (D).
5.设总体 ,其中 未知, 已知, 是取自总体 的一个样本,
则下列表达式中不是统计量的是:(A)
(A). (B).
(C). (D).
三、(本题12分)某人准备驾校报名学车,他选甲、乙、丙三所驾校的概率分别为0.5,0.3,0.2.已知甲、乙、丙三所驾校的学生能顺利通过考试的概率分别为0.7,0.9,0.75.(1)求此人顺利通过考试的概率;(2)如果顺利通过考试,求此人报名甲这所驾校的概率.
总分
题号
一
二
三
四
五
六
七
八
得分
阅卷人
一、填空题(每小题3分,共15分)
1.设 为三个事件,则“ 三个事件至少有两个发生”可表示为
2.设 ,则 0.2
3.设 为随机变量, , ,且 ,则 7/27
4.设随机变量X,Y独立同分布,且 ,则 0.5
5.设 为取自总体 的样本,若 则 =1/18
二、单项选择题(每小题3分,共15分)以下每小题均只有一个选项
(3) ………13分
七、(共10分)某袋茶叶用机器装袋,每袋的净重为随机变量,其期望值为100克,标准差为10克.若一大盒内装该茶叶400袋,求一大盒茶叶净重大于40.5千克的概率.
解:设 表示第 袋重量,则
相互独立,…………………2分
设 表示400袋的重量,则
, …………………5分
由中心极限定理 …………………6分
当x≥1时,F(x)=1…………………10分
五、(本题12分)设随机变量 ,相关系数 ,设 ,求(1) 和 ;(2) 与 的相关系数
安徽建筑大学 2012-2013第二学期概率论与数理统计试卷

(1)任意抽查一个产品,它被判为合格品的概率;
… …
1、设 A, B 为两个相互独立随机事件, P(A) = 0.4 , P(B) = 0.3 ,则 P(A ∪ B) =
. (2)一个经检查被判为合格的产品确实是合格品的概率.
… … 装
2、设随机变量 X 服从参数为 λ 的泊松分布,即 P{X = k} = λke−λ , k = 0,1, 2, . 且
.
… …
5、设总体 X ∼ N (μ,σ 2 ) ,其中 μ,σ 2 已知,( X1, X 2
Xn ) 为来自 X 的一个样本,X 为
四、解答题(本大题 18 分,每小题 9 分) 1、袋中有 2 个白球,3 个红球,今从袋中随机抽取 2 个球,以 X 表示取到的红
草
订 …
样本均值,则 D(X ) =
(B)1;
(C) −0.8 ;
(D) 0.7 .
不 … 4、设二维随机变量 (X ,Y ) 的分布律为:并且已知
得
… …
事件{X = 0}与{X + Y = 1} 相互独立,则
.
Y0
X
1
⎧0
2、设连续型随机变量
X
的分布函数为:
F ( x)
=
⎪ ⎨
Ax2
⎪⎩ 1
x<0 0 ≤ x <1,
x ≥1
求:(1)常数 A ;(2) X 概率密度 f (x) ;(3) X 落在区间 (0.3, 0.7) 的概率.
… …
本容量 n 一定时,下列说法中正确的是
… …
(A) α 减小时 β 也减小;
(B) α 增大时 β 也增大;
(C) α , β 其中一个减小,另一个会增大; (D) (A)和(B)同时成立.
重庆理工大学概率论与数理统计期末试卷

重庆理工大学考试试卷学年第 学期班级 学号 姓名 考试科目 概率与数理统计 A 卷 闭卷 共 3 页 ···································· 密························封························线································)0.7AB =, B 、0.4 服从参数为(λλ,,n X 是来自正态总体2(,)N μσ2)μ- 2)X - C2、已知随机变量X的分布律为101~0.40.30.3X-⎡⎤⎢⎥⎣⎦,则X的分布函数()F x=。
概率试卷A12-13-2本科 评分标准

2012-2013学年 第2学期 概率论与数理统计A 卷评分标准一、单项选择题(本大题共5小题,每小题3分,共15分). 1. 事件,A B 独立,且0()1P A <<,则下列选项不正确的是(A )(|)()P B A P B =;(B )(|)()P B A P A =;(C )(|)()P B A P B =;(D )(|)()P B A P B =.答:(B )2. 已知离散型随机变量X 的分布律为4567125522a a a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭,则概率(6)P X ≥等于 (A )516; (B )58; (C )78; (D )1.答:(B ) 3. 设随机变量X 的概率密度函数为(),f x x R ∈,若2Y X =-,则Y 的概率密度函数为 (A )1,22y f y R ⎛⎫-∈ ⎪⎝⎭; (B ),2y f y R ⎛⎫-∈ ⎪⎝⎭; (C )2(2),f y y R -∈; (D )(2),f y y R -∈.答:(A )4. 已知随机变量X 服从正态分布2(,6)N μ,Y 服从正态分布2(,8)N μ,记1(6)p P X μ=≤-,2(8)p P Y μ=≥+,则 (A )12p p <; (B )12p p >; (C )12p p =; (D )无法判断12,p p 的大小.答:(C )5. 设12,,,n X X X L 为来自总体2(0,)N σ的简单样本,X 为样本均值,则下列选项不正确的是 (A )22211()nii Xn χσ=∑:; (B )22211()(1)nii XX n χσ=--∑:;(C)(0,1)N σ:; (D )2122(1,1)nii X F n X=-∑:.答:(D )二、填空题(本大题共5小题,每小题3分,共15分).6. 某人有10把外形相同的钥匙, 其中只有一把能打开门. 他随意地试用这些钥匙开门(用后不放回), 则此人试了3次就把门打开的概率为110.7. 已知随机变量X 的概率密度函数为22,0()0,0x ae x f x x -⎧>=⎨≤⎩,则常系数a =1.8. 某餐厅每天接待300名顾客,据以往经验每位顾客的消费额(单位:元)服从区间[20,80]上的均匀分布, 若顾客的消费额是相互独立的,则该餐厅每天营业额的期望值为15000元.9. 设,X Y 为两个独立随机变量,若25,4DX DY ==,则(21)D X Y ++=41.10. 用机器包装牛肉罐头, 已知罐头重量(单位:kg )服从正态分布2(,0.05)N μ,随机抽取25个罐头测其重量, 算得样本均值 1.01x =, 则μ的置信度为95%的置信区间为(0.9904,1.0296) (备用数据:0.025 1.96z =,0.05 1.65z =). 三、解答题(本大题共6小题,每小题10分,共60分).11.某仪器上装有大、小2个不同功率的灯泡.已知当2个灯泡都完好时,仪器发生故障的概率为1%;当只有1个灯泡烧坏时,仪器发生故障的概率为20%;当2个灯泡都烧坏时,仪器发生故障的概率为85%.设这两个灯泡被烧坏与否互不影响,并且它们被烧坏的概率分别为0.1,0.2,若仪器发生了故障,求此时两个灯泡都烧坏的概率. 解:设A 表示仪器发生故障;i B 表示烧坏了i 个灯泡,0,1,2i =,则所求概率为222220()(|)()(|).........................................(6')()(|)()85%(0.10.2)....(9')1%(0.90.8)20%(0.10.80.20.9)85%(0.10.2)85. (381)i i i P AB P A B P B P B A P A P A B P B ===⨯⨯=⨯⨯+⨯⨯+⨯+⨯⨯=∑.................................................................(10')12.已知随机变量X 的概率密度函数为 0,0()2(1),012,1x x x f x e x x e x --≤⎧⎪=+-<<⎨⎪≥⎩,求:(1){02}P X <<;(2)()X E e -. 解:(1)由密度函数的性质21212{02}().............................................(2')2(1)2.....................................(4')12...........................................................x x P X f x dx e x dx e dx e ---<<==+-+=-⎰⎰⎰............(5')(2)由题意111()()....................................................(7')2(1)2.................(9')12.. (X)x x xx x E ee f x dx e e x dx e e dx e +∞---∞+∞-----==+-+=-⎰⎰⎰.(10')13.设二维随机变量(,)X Y 的联合概率密度函数为6(1),01,0(,)0,x x y xf x y -<<<<⎧=⎨⎩其它, (1)求概率{12}P X Y +≤;(2)求出(,)X Y 关于X 的边缘概率密度函数()X f x ,进一步求出在14X =的条件 下,Y 关于X 的条件概率密度函数|1(|)4Y X f y .解:(1)由题意{(,):12}14120{12}(,)..................(2')6(1)..............................................(4')9 (32)x y x y y yP X Y f x y dxdy dy x dx +≤-+≤==-=⎰⎰⎰⎰.......(5')(2)由边缘密度函数的定义0()(,)................................................................(6')6(1),016(1),01.........(8')0,0,X x f x f x y dy x x x x dy x +∞-∞=⎧-<<-<<⎧⎪==⎨⎨⎩⎪⎩⎰⎰其它其它 故|4,0141(14,)(|)..............................(10')0,4(14)Y X X y f y f y f <<⎧==⎨⎩其它14.已知连续型随机变量X 的分布函数为(1),0(),011,1x x Ae x F x B x Ae x --⎧<⎪=≤<⎨⎪-≥⎩, (1)确定常系数,A B ;(2)求{122}P X <<;(3)求X 的概率密度函数()f x . 解:(1)由分布函数的性质(0)(0).......................................................(1')F F A B -+=⇒= (1)(1)1...................................................(2')F F B A -+=⇒=-因此可得12,12............................................................(3')A B == (2)由分布函数的性质(21)1{122}(2)(12).................................................(5')1111(1)......................................................(7')222P X F F e e ---<<=-=--=- (3)由密度函数定义可得(1)1,021(), 1......................................(10')20,xx e x f x e x --⎧<⎪⎪⎪=>⎨⎪⎪⎪⎩其它15. 设二维离散型随机变量(,)X Y 的联合分布律为已知0.2EX =-,且,X Y 的协方差(,)0.18Cov X Y =, 求,,a b c 的值.解:由题意,可得(,)X Y 关于X 的边缘分布律为1010.10.2a b c -⎛⎫ ⎪++⎝⎭,故0.10.2EX c a =-+=-,即0.3....................................................(2')a c -=又(,)X Y 关于Y 的边缘分布律为100.3a c b -⎛⎫ ⎪++⎝⎭,XY 的分布律为1010.3c b a -⎛⎫ ⎪+⎝⎭,故有(,)()()0.2()0.18Cov X Y E XY EXEY a c a c =-=--+=即0.6..................................................................................................(6')a c += 又111{,}1i j P X i Y j =-=-===∑∑,可得0.7.......................................(8')a b c ++=故0.45,0.1,0.15..........................................................................(10')a b c ===16.设总体X的概率密度函数为21(ln )2,0()0,0x x f x x μ--⎧>=≤⎩,其中μ是未知参数. 若12,,,n X X X L 是来自该总体的一个容量为n 的简单样本,求μ的最大似然估计量µμ.解:21(ln )21()......................................(3')i nx i L μμ--==似然函数为对数似然函数2111ln[()])(ln ).......................(5')2nni i i i L x μμ===---∑∑1ln[()]0(ln )0.......................................................(8')ni i d L x d μμμ==⇒-=∑令故^1ln ..................................................(10')ni i X n μμ==∑的最大似然估计量四、证明题(本大题共1个小题,5分).17.设,X Y 为两个随机变量,若22(),()E X E Y 存在且至少有一个不为0,证明:222[()]()()E XY E X E Y ≤.证明:不防假定2()0E X ≠,对于任意实数t ,有2222[()]()2()()0.............(2')E tX Y t E X tE XY E Y +=++≥因此判别式222222[2()]4()()4[()]4()()0...............................(4')E XY E X E Y E XY E X E Y ∆=-=-≤此即 222[()]()()........................................(5')E XY E X E Y ≤ 五、应用题(本大题共1个小题,5分).18. 某幼儿园准备举行一次六一文艺汇演,为了做好准备工作,学校现要统计来参加此次汇演的家长人数. 设各学生来参加汇演的家长数相互独立,且每个学生无家长,有1名家长或2名家长来参加此次汇演的概率约为0.05,0.8,0.15.已知此幼儿园共有400名学生,用中心极限定理估计来参加此次汇演的家长数超过450的概率(备用数据:4.36=,(1.15)0.8749Φ=).解:设i X 表示第i 个学生来参加文艺汇演的家长数,1,2,,400i =L .由题意,{,1,2,,400}i X i =L 独立同分布,且分布律为0120.050.80.15⎛⎫ ⎪⎝⎭. 由中心极限定理,4001ii X=∑近似服从正态分布(440,76).......................................................(3')N因此所求概率为4004001440450...........................(4')i i i X P X P =⎧⎫-⎪⎪⎧⎫>=>⎨⎬⎩⎭⎪⎪⎩⎭∑∑(()11 1.1510.87490.1251...........................(5')≈-Φ≈-Φ≈-=。
第二学期概率论与数理统计试卷 参考答案
重庆大学概率论与数理统计课程试卷A卷B卷2012 ~2013 学年 第 二 学期开课学院: 数统学院 课程号:10029830 考试日期:考试方式:开卷闭卷 其他 考试时间: 120分钟分位数:220.0050.975(39)20,(39)58.12χχ==,0.975 1.96u =,(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =一、填空题(每空3分,共42分)1.已知()0.3P A =,()0.4P B =,()0.5P AB =,则()P B A B ⋃= 0.25 。
2.从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
3.从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为p 。
如果他最后选对了,则他确实知道答案的概率为541pp +。
5.重复抛一颗骰子5次得到点数为6 的次数记为X ,则(3)P X >= 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y 的密度函数为1//4()0 ,Y y f y elseπ⎧<<⎪=⎨⎪⎩。
8.已知(,)(1,9;0,16;0.5) ,32X YX Y N Z -=+且,则Z 的密度函数21()36z Z f --(z )。
9.设总体2(,)X N μσ,其中2σ已知,从该总体中抽取容量为40n =的样本1,240,,X X X ,则()222110.5 1.453nii P X X n σσ=⎧⎫≤-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)XN σ的样本,则Y =服从 t(8) 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆大学概率论与数理统计课程试卷
2012 ~2013 学年 第 二 学期
开课学院: 数统学院 课程号:10029830 考试日期:
考试方式:
考试时间: 120分钟
分位数:220.005
0.975
(39)20,(39)58.12
χχ==,
0.975 1.96
u =,
(2.68)0.9963,(1.79)0.9633Φ=Φ=,0.025(35) 2.0301t =
一、填空题(每空3分,共42分)
1.
已知()0.3P A =,()0.4P B =,
()0.5P AB =,则()P B A B ⋃= 0.25 。
2.从一副扑克牌(52张)中任取3张(不重复),则取出的3张牌中至少有2张花色相同的概率为 0.602 。
3.从1到9的9个整数中有放回地随机取3次,每次取一个数,则取出的3个数之积能被10整除的概率为 0.214 。
4.一个有5个选项的考题,其中只有一个选择是正确的。
假定应 考人知道正确答案的概率为
p 。
如果他最后选对了,则他确实知
道答案的概率为5
41
p
p +。
5.重复抛一颗骰子5次得到点数为6 的次数记为X ,则(3)P X >
= 13/3888 。
6.设X 服从泊松分布,且(1)(2)P X P X ===,则(4)P X ==0.0902 。
7.设圆的直径X 服从区间(0,1)上的均匀分布,则圆的面积Y 的密度函数为1//4()0 ,Y y f y else
π⎧<<⎪=⎨
⎪⎩。
8.已知(,)(1,9;0,16;
0.5) ,3
2
X Y X Y N Z -=+ 且,则Z 的密度函数
2
1()36
z Z f --(z )。
9.设总体2(,)X N μσ ,其中2σ已知,从该总体中抽取容量为40n = 的样本1,240,,X X X ,则()222110.5 1.453n
i
i P X X n σσ=⎧
⎫≤
-≤⎨⎬⎩⎭∑= 0.97。
10.设1,210,,X X X 是来自总体2(0,)X N σ 的样本,则Y =
服从 t(8) 。
11.设由来自总体(,0.81)X N μ 容量为9的样本,得样本均值为
5x =,则参数μ的置信度为0.95的置信区间为(4.412,5.588)。
12.设12,,,n x x x 是来自(,1)N μ的样本,考虑如下假设检验问题
01=2 vs :3H H μμ=:,若检验由拒绝域为{}2.6W x =≥确定,则当
20n =时检验犯第一、二类错误的概率分别为 0.0037、0.0367。
命
题人:
组题人:
审
题人:
命
题时间:
教务处制
学院 专业、班 年级 学号 姓名
公平竞争、诚实守信、严肃考纪、拒绝作弊
封
线
密
二、 (18分)设随机变量(),X Y 的联合密度函数为 , 0(,)0 ,y cxe x y f x y else -⎧<<<+∞=⎨⎩
(1)求常数c ;
(2)X Y 与是否独立?为什么? (3)求Z X Y =+的密度函数 (4)求(min(,)1)P X Y <
解:(1)1=(,)1f x y dxdy c +∞+∞
-∞-∞⇒=⎰⎰ (2),0
()(,)0 ,0x
X xe x f x f x y dy x -+∞
-∞
⎧>==⎨≤⎩
⎰
21e ,0
()(,)2
0 ,0
y
Y y y f y f x y dx y -+∞
-∞
⎧>⎪==⎨⎪≤⎩⎰
由于0,(,)()()X Y x y f x y f x f y <<<+∞≠⋅,故X 与Y 不独立。
(3)
2
1,0
()(,)20 ,0z
z Z z e e z f z f x z x dx z --+∞
-∞
⎧⎛⎫+-≥⎪ ⎪=-=⎨⎝⎭⎪<⎩
⎰
(4)
1
1
0(min(,)1)1(1,1)
5112
v v P X Y P X Y dv ue du e +∞
--<=-≥≥=-
=-⎰
⎰
三、(10分)设两个随机变量,X Y 相互独立,且它们都服从于均
值为0,方差为0.5的正态分布,求X Y -的数学期望与方差。
解:根据已知条件,可知(0,1)X Y N -
2
2x E X Y dx +∞
--∞
-==
⎰
()()()()22
2
2
()1
2()1E X Y D X Y E X Y D X Y E X Y E X Y π
⎡⎤-=-+-=⎣⎦
⎡⎤⇒-=-+-=-⎣⎦
四、(10分)已知正常男性血液中每毫升白细胞数平均是7300,标准差是700,试估计每毫升血液中白细胞数在5200——9400之间的概率。
解:设每毫升血液中白细胞数为X , 则7300,700X EX σ== 由切比雪夫不等式,得
()()2
2
8520094002100121009X
P X P X EX σ<<=-<≥-
=
五、(14分) 123
12(,),0,1,2, 0 <;
!
6(,)(),0,,,,,,x X Y n
n e X f x x x y
Y f y x y X X X Y Y Y X Y θ
θθθλλλλ
-==<+∞=
-<< 设总体具有密度函数且总体具有密度函数;及为分别来自于总体和总体的样本。
求
(1)θ的极大似然估计ˆ
θ; (2)λ的矩估计ˆ
λ;
(3)ˆλ的方差。
解: (1)
()111
1
11
1!!
ln ()ln ln(!)
1ln ()01ˆi
i x
n
n
x n i i i i n n
i i i i n i i n i i L e
e x x L n x x d L n x d X X n θ
θ
θθθθθθθθθθ--======∑==⇒=-+-⇒=-+=⇒==∏∏
∑∑∑∑
(2)
2
3
6()()2
ˆ2Y y EY yf y dy y dy Y
Y λ
λ
λλλ
+∞
-∞==-=
=⇒=⎰
⎰
(3)
12
2
14ˆ()(2)4()4()ˆ ()20
5n i i D D Y D Y D Y DY
n n DY D n
λλλλ
======
∴=∑
六、(6分)
假设某次考试的成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分,问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程。
解:假设该次考试的学生成绩为X ,0.05α=,则
2
(,)X N μσ 。
提出检验假设01:70,:70H H μμ=≠
由于2
σ
未知,选择统计量X t =
拒绝域为{}2(1) 2.0301t t n t α⎧⎫>-=>⎨⎬⎩⎭
得 1.4 2.0301t =
=<
所以接受原假设,可以认为全体考生的平均成绩为70分。
