导航原理之捷联惯导系统-姿态算法(矩阵)
§3.9捷联式惯导系统介绍

G G dωie G dr 对上式求导,假定地球旋转角速度是常矢量, = 0且 = ve ,可得 dt dt e G K dv e G G d 2r K K G = + ωie × ve + ωie × [ωie × r ] 2 dt i dt i
而
K G G d 2r = f +G dt 2 i
G G G G G dv e K K G = f − ωie × ve − ωie × [ωie × r ] + G dt i
b 标系 Oe X iYi Z i 的角速度 ωib ,上角标 b 表示该角速度在 b 坐标系上的投 b 进行姿态矩阵 Cbi 计算。由于姿态矩阵 Cbi 中的元素是 影。利用 ωib
OX bYb Z b 相对 OX iYi Z i 的航向角、横滚角、俯仰角的三角函数构成,
所以当求得了姿态矩阵 Cbi 的即时值,便可进行加速度计信息的坐标 变换和提取姿态角的大小。 这三项功能实际上就代替了平台式惯性导 航系统中的稳定平台的功能, 这样计算机中的这三项功能也就是所谓
哥氏校正
fb
比力测量值 的分解
fi
∑
∑
速度v e和 位置的估 计值
i
导航计算
Cbi
固连于载体 的陀螺
ω
b ib
速度和位置的初始估计值 姿态计算
姿态的初始估值
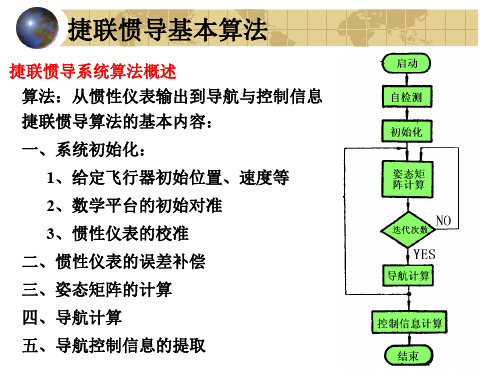
图 捷联式惯导系统——惯性坐标系机械编排
3、当地地理坐标系的机械编排
在这种机械编排中,地理坐标系表示的地速是 vet ,它相对于地理 坐标系的变化率可通过其在惯性坐标系下的变化率表示 G G dv e dv e G G G = − [ wie + wet ] × ve dt t dt i G G G G G G dv e dve 用 ,得 = f − ωie × ve + g1 替代 dt t dt i G G dv e G G G K = f − [2 wie + wet ] × ve + g1 dt t 表示在选定的导航坐标系(地理坐标系)中,有
捷联惯导系统算法.ppt
cos
b Ebz
注意事项:当 θ= 90 度时,方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度,所以:
CbE
b ib
E iE
C
E b
或四元数微分方程:
q(t)
(
b ib
b iE
)q(t)
注意事项: 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小,计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量:陀螺仪数字脉冲输出,每个脉冲代表一个角增量
一个采样周期内,陀螺输出脉冲数对应的角增量为:
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述:
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序:
Ψ →θ →γ
车载捷联惯导系统基本原理
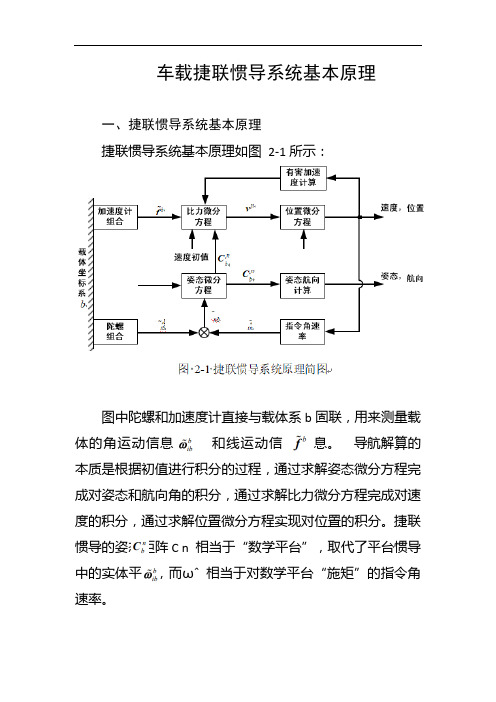
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示:图中陀螺和加速度计直接与载体系b固联,用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程,通过求解姿态微分方程完成对姿态和航向角的积分,通过求解比力微分方程完成对速度的积分,通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”,取代了平台惯导中的实体平台,而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程(一)姿态微分方程在捷联惯导系统中,导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示,相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为:在欧拉角微分方程式(2.2-7)中,当俯仰角θ趋于90º时,cosθ趋于0,tanθ趋于无穷,方程存在奇异性,所以这种方法不能在全姿态范围内正常工作;姿态矩阵微分方程式(2.2-1)可全姿态工作,但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组,计算量大;四元数微分方程式(2.2-6)同样可以全姿态工作,且更新算法只需求解4个未知量的线性微分方程组,计算量小,算法简单,是较实用的工程算法。
(二)速度微分方程速度微分方程即比力方程,是惯性导航解算的基本关系式:三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息,实际上就是求解三个微分方程的过程,相应存在姿态更新算法、速度更新算法和位置更新算法。
(一)姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为:在车辆行驶过程中,一般不存在高频大机动环境,并且车载导航系统往往不工作在纯惯性导航方式,而是利用里程仪或零速条件进行组合导航,所以算法误差的影响有限,常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源,其中器件误差和初值误差又是影响导航结果的主要因素。
捷联惯导系统

作业思考题
1、简要说明捷联惯导系统的基本组成和原理。 2、什么是数学平台?它有什么作用?
惯性导航系统
第四十四讲 捷联惯导系统 力学编排方程(一)
捷联式惯导系统(SINS)
加速度计
fb
数学平台
姿态矩阵 Cbp
f p 导航 速度、位置
计算机 姿态、航向
姿态矩阵计算
陀螺
ibb
pbb
b ip
姿态航向
-
C11 C21 C31
Cep 1 Cep T
C12 C13 1 C11 C21
C22
C23
C12
C22
C32 C33 C13 C23
C11 C22C33 C23C32 C21 C13C32 C12C33 C31 C12C23 C22C13
C31
C32
C33
位置矩阵微分方程组
Cep 0 f 0,0,0
1
p p epx epy
g g egx egy
R VeggxVeggy
VeppxVeppy
三、位置速率方程
11
p p epx epy
g g egx egy
RN RE
捷联惯导的发展
1、1950年起,德雷珀实验室捷联系统得到成熟的探索; 2、1969年,在“阿波罗-13”宇宙飞船,备份捷联惯导系统; 3、20世纪80~90年代,波音757/767、A310民机以及F-20战 斗机上使用激光陀螺惯导系统,精度达到1.85km/h的量级; 4、20世纪90年代,美国军用捷联式惯导系统已占有90% 。光 纤陀螺的捷联航姿系统已用于战斗机的机载武器系统中及波 音777飞机上。 5、国内由90年代挠性捷联惯导到现在激光捷联惯导、光纤陀 螺捷联航姿系统。
车载捷联惯导系统定位测姿算法研究

第15卷第l期2007年2月中国惯性技术学报JoumalofChineseInertialTcchnologyVbl.15No.1Feb.2007文章编号:1005-6734(2007)01一0024-04车载捷联惯导系统定位测姿算法研究陈允芳1,叶泽田2,钟若飞3(1.山东科技大学地球信息科学与工程学院,青岛266510;2.中国测绘科学研究院,北京100039;3.首都师范大学,北京100037)摘要:GPs/INs组合精确测定平台的位置和姿态是移动测图系统中的重要模块。
对陀螺仪和加速度计所测角速度和比力进行两次积分得载体姿态、速度和位置即sINs力学机械编排。
目前该过程大多在地理坐标系进行。
这里详细推导了地球坐标系中完整的解算过程,以四元数姿态矩阵更新及重力计算为核心,由IMu原始观测值解算出了载体位置、速度和姿态等参数,可快速高效与GPs输出的位置速度信息进行组合滤波处理,可据此编程进行工程应用数据处理。
关键词:捷联惯导系统;姿态矩阵;坐标转换;力学编排;四元数中图分类号:u666.1文献标识码:APositioningandorientationcomputationonVehicle-borneSINSanddiscussofcalculationerrorcHENYun.‰91,YEze-tian2,zHONGRuo.fei3(1.Geo·info衄ationScience&EngineeringCollege,ShandongUniverSi哆ofScienceaIldTbchnology,Qingdao266510,China;2.SurveyingaTldMappingScienceResearchInStituteofChina,Beijing100039,China;3.C印italNomlalUniverSi劬Beijing100037,China)Abstract:GPSandINSintegratedtoaccuratelydeteminingpositionaIldattitudeofnatI‘oofisVitalmoduleinmobilemappingSystem.Specincforcc行omspeedometer蚰d舭glerate矗om留roareinte铲atedtwicerespectiVelytoachievean沁de,veloc时aIldpositionn锄elySINSmechaIlization.Currentlythistookplacedingeogr印hiccoordinate,whiIeheredemonstratedindetailmewholemechaJlizationineanll-centclrcdearth-fixedcoordinate,mostlyquatemiona钍itudematrixupdating锄dgravit)rcaIculation.Ultimatelyvehiclenavigationpar锄eterssuchaSattitude,veIocity锄dpositionwercgahed丘omIMUorigin“0bservations.Mathematicsplatfo眦isfomlcdinSrNStocarryoutsuⅣeyingaJldcalculatingpreciselythenavigationmoVementpar锄cterS.Theresultsarcpronetointe黟atewitllsimilarpammeters疔omGPStofilterprocessing.Pro可锄minghercbyc锄pmcessdatainengineeringapplicationKeywords:SINS;attitudematrix;coordinatetransfomation;mechanization;quatemion随着惯性技术与卫星导航定位技术的发展,由GPS/INs不同程度组合而成的定位定姿传感器已成为移动测图系统中确定载体轨迹和平台姿态的重要工具,其中GPs多用于定位而INS则用于测姿。
捷联惯导结算原理

0 cos sin , Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角:
(5) 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结:1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系, 加速计的比 力信息直接投影在导航系中,可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出;而捷联式惯导用数学平台取代实体的物理平台,通过求
惯性导航_第5章
武汉大学测绘学院 卫星应用研究所
2.动态差模型
对于陀螺 的一个轴 ,其表达 式为
D1 D2 D3 D4 D5 D6 dx 2 x y z x y z
2 2 2 D 7 D D D10 D11 D12 x 8 y 9 z x y y z x z
姿态矩阵计算
迭代次数
NO
导航计算
控制信息计算
结束
武汉大学测绘学院 卫星应用研究所
一、系统的初始化
系统的初始化包括三项任务:
1.给定飞行器的初始位置和初始速度等初始信息。 2.数学平台的初始对准:确定姿态矩阵的初始 值,是在计算机中用对准程序来完成的。在物理概 念上就是把“ 数学平台” 的平台坐标系和导航坐标系 相重合,称其为对准。 3.惯性仪表的校准:对陀螺的刻度系数进行标 定,对陀螺的漂移进行标定。对加速度计标定刻度 系数。
式中
、 、 、 、 、 分别为 飞行器相 对惯 x y z x y z
性空 间沿陀螺 三个轴的 角速度 及角加速 度分量 (弧 度/S 、 弧度 /S )。D 4 为 刻度系数,D 4 x 为陀螺 的正常 输出值,其它 名项 为误 差项,对 应的系数 D l 至 D12 为动 态误差系 数。
b b 、 a 一—沿飞 行器 坐标 ib ib
系表 示的 陀螺及 加速度 计输 出的 原始测量 值;
b b 、aib 一—误 差 补 偿后 的 ib
陀螺 及加速度 计的输出 值;
b b 、 aib —— 由误差 模型 ib
给出 的陀 螺及加 速度计 的估 计 误 差 ( 包 括静 态 和 功 态 误 差项 )。
武汉大学测绘学院 卫星应用研究所
捷联惯导算法与组合导航原理讲义
捷联惯导算法与组合导航原理讲义严恭敏,翁浚编著西北工业大学2016-9前言近年来,惯性技术不论在军事上、工业上,还是在民用上,特别是消费电子产品领域,都获得了广泛的应用,大到潜艇、舰船、高铁、客机、导弹和人造卫星,小到医疗器械、电动独轮车、小型四旋翼无人机、空中鼠标和手机,都有惯性技术存在甚至大显身手的身影。
相应地,惯性技术的研究和开发也获得前所未有的蓬勃发展,越来越多的高校学生、爱好者和工程技术人员加入到惯性技术的研发队伍中来。
惯性技术涉及面广,涵盖元器件技术、测试设备和测试方法、系统集成技术和应用开发技术等方面,囿于篇幅和作者知识面限制,本书主要讨论捷联惯导系统算法方面的有关问题,包括姿态算法基本理论、捷联惯导更新算法与误差分析、组合导航卡尔曼滤波原理、捷联惯导系统的初始对准技术、组合导航系统建模以及算法仿真等内容。
希望读者参阅之后能够对捷联惯导算法有个系统而深入的理解,并能快速而有效地将基本算法应用于解决实际问题。
本书在编写和定稿过程中得到以下同行的热心支持,指出了不少错误之处或提出了许多宝贵的修改建议,深表谢意:西北工业大学自动化学院:梅春波、赵彦明、刘洋、沈彦超、肖迅、牟夏、郑江涛、刘士明、金竹、冯理成、赵雪华;航天科工第九总体设计部:王亚军;辽宁工程技术大学:丁伟;北京腾盛科技有限公司:刘兴华;东南大学:童金武;中国农业大学:包建华;南京航空航天大学:赵宣懿;武汉大学:董翠军;网友:Zoro;山东科技大学:王云鹏。
书中缺点和错误在所难免,望读者不吝批评指正.作者2016年9月目录第1章概述 (6)1.1捷联惯导算法简介 (6)1.2 Kalman滤波与组合导航原理简介 (7)第2章捷联惯导姿态解算基础 (10)2。
1反对称阵及其矩阵指数函数 (10)2。
1。
1 反对称阵 (10)2。
1.2 反对称阵的矩阵指数函数 (12)2。
2方向余弦阵与等效旋转矢量 (13)2.2.1 方向余弦阵 (13)2。
捷联惯导系统姿态解算模块的实现
目前,国内的飞行器采用的计算机大多是 冯·诺伊曼结构的通用型微处理器,这些通用型 微处理器的乘法用软件实现,常常需要若干个机 器周期才能完成,而且由于同时运行多个进程,使 数据处理速度较慢。并且采用这些微处理器的器 件体积大,功耗大,电路结构复杂,可靠性低,成本 高,无法更好地满足当代捷联惯性导航系统对小 型化、高精度、实时性的要求。
下,用四阶龙格一库塔法进行姿态解算,误差<0.005 3%;应用TMS320C6713B进行硬件电路设计,每次解算时间<
36肚s,能够满足捷联惯性导航系统对精度和速度的要求。
关键词:捷联系统;惯性导航;姿态解算;四元数
中图分类号:V448.22
文献标识码:A
Realization of attitude algorithm module in strapdown inertial guidance system
2.Graduate University oJ’Chinese Academy oJ’Sciences,Beijing 100039,China; 3.Daqing Vocational College,Daqing 163255,China;
4.School of Cornmunic’ation Engineering,Jilin University,Changc’hun 130012,Chi*la)
Abstract:A method to realize attitude algorithm module in strapdown inertial guidance is presented. Based on the digital signal processor and quaternions,an.attitude algorithm module in strapdown iner— tial guidance is designed.The working principle of trapdown inertial guidance,the attitude algorithm and the numerical method are introduced.The circuit and software of attitude algorithm are designed. The test results show that the relative error iS 1ess than 0.005 3%with 4 order Runge~Kutta when the increment is less than 5。;it can meet the demands of trapdown inertial guidance,when the algorithm time is less than 36 pts with TMS320C6713B. Key words:strapdown system;inertial guidance;attitude algorithm;quaternion
导航原理之捷联惯导系统-姿态算法(矩阵)
G0 GT
C C
G0 G0
G0
N E
G CGT0
GT
C I I TG IG
0
T
G G B G CBTT (CGT0 )1CB00 CBT0
Lecture 10 -- Algorithms for SINS 15
3.7 算例
某捷联惯导系统在 n 时刻, 其载体坐标系和惯性坐标系重合. 然 后从时刻 n 到时刻 n+1, 沿着载体三个轴的三个陀螺仪 X, Y, Z 的角增量输出分别为 0.002, 0.004 和 0.006 (rad); 请利用基于 Peano-Paker 解的一阶角增量算法计算时刻 n+1 载体和惯性坐 标系之间的方向余弦矩阵.
C(n) I3
0 z y z 0 x y 0.006 0.004 0 x 0.006 0 0.002 0.004 0.002 0 0
C(n 1) C(n)I 3
记
记初始时刻的地理坐标系为 G0 , 则有 G G CB 0 CB 0 B IB
B dt IB
0
T
其中
0 B IB z y z 0
0 z y
T 0
z 0 x
y x 0
j
k
i
R
载体的旋转导致 C 发生变化
S1
Lecture 10 -- Algorithms for SINS
8
2.2 方向余弦矩阵的导数
dj' dk' di' i dt i dt i dt i i' i j ' i k ' di' j i ' j j ' j k ' dj' dk' C so C j j j dt dt dt k i ' k j ' k k ' k di' k dj' k dk' dt dt dt 设载体坐标系相对于导航坐标系的角速度为 X Y Z T 表示在载体坐标系中 i' j' k ' di ' 则 i' x y z ( j ' z k ' y ) dt 1 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C C
R
也可用欧拉角、四元数等表示姿态
Lecture 10 -- Algorithms for SINS
4
1.3 SINS的示意框图
AX AY AZ
姿态信息 沿载体轴的 加速度输出 对加速度分量 进行坐标变换 沿地理坐标 系各轴的加 速度 导 航 计 算 位置 速度
显 示
GX GY GZ
C(n) I3
0 z y z 0 x y 0.006 0.004 0 x 0.006 0 0.002 0.004 0.002 0 0
C(n 1) C(n)I 3
C13 0 C 23 z C 33 y
x
y x C
0
C11 y C12 x C 21 y C 22 x C 31 y C 32 x
-- 斜
对称矩阵
C C --- 其解取决于 C(0) 和载体的转动角速度的变化规律
Lecture 10 -- Algorithms for SINS
3
1.2 姿态变换
z, 方位轴
加速度需要变换:
fE f bx f N C f by f f bz
x, 滚动轴 y, 俯仰轴
e
N
E
C 包含姿态信息.
j
k
i
R
载体的旋转导致 C 发生变化
S1
Lecture 10 -- Algorithms for SINS
8
2.2 方向余弦矩阵的导数
dj' dk' di' i dt i dt i dt i i' i j ' i k ' di' j i ' j j ' j k ' dj' dk' C so C j j j dt dt dt k i ' k j ' k k ' k di' k dj' k dk' dt dt dt 设载体坐标系相对于导航坐标系的角速度为 X Y Z T 表示在载体坐标系中 i' j' k ' di ' 则 i' x y z ( j ' z k ' y ) dt 1 0 0
C12 z C13 y C 22 z C 23 y C 32 z C 33 y C11 C 21 C 31 C12 C 22 C 32
C13 x C11 z C 23 x C 21 z C 33 x C 31 z z 0
记
记初始时刻的地理坐标系为 G0 , 则有 G G CB 0 CB 0 B IB
B dt IB
0
T
其中
0 B IB z y z 0
0 z y
T 0
z 0 x
y x 0
惯性元件
对地理坐 标系进行
修正 姿态
沿载体轴的 角速率输出
计算载体的 姿态信息 数学平台 计算机
Lecture 10 -- Algorithms for SINS
5
Outline
捷联惯导系统概述
姿态矩阵(DCM)微分方程的推导
方向余弦矩阵的求解: 角增量算法
Lecture 10 -- Algorithms for SINS
19
Lecture 10 -- Algorithms for SINS
16
3.7 算例
0.006 0.004 1 0 0 0 0 0.002 C(n 1) C(n)I 3 0 1 0 I 3 0.006 0 0 1 0.004 0.002 0
类似的
dj ' (k ' x i ' z ) dt
dk ' (i ' y j ' x ) dt
9
Lecture 10 -- Algorithms for SINS
2.3 方向余弦矩阵微分方程
则
i ( j ' z k ' y ) i (k ' x i ' z ) i (i ' y j ' x ) C j ( j ' z k ' y ) j (k ' x i ' z ) j (i ' y j ' x ) k ( j ' z k ' y ) k (k ' x i ' z ) k (i ' y j ' x )
Lecture 10 -- Algorithms for SINS
17
Summary
捷联惯导系统概述
方向余弦矩阵微分方程的推导
方向余弦矩阵的求解: 角增量算法
Lecture 10 -- Algorithms for SINS
18
End
Lecture 10 -- Algorithms for SINS
12
3.2*毕-卡解
0 IB (t ) dt G C (T ) C (0) e CB 0 (0) e
B T
G0 B
G0 B
sin 0 1 cos 0 2 C (0) I 2 0 0 ------ 毕-卡形式的解
6
2.1 方向余弦矩阵
z, 方位
C C
S2
x, 滚动 y, 俯仰
咋来的? 设 S1 为导航坐标系,其单 位坐标矢量为 i, j 和 k S2 为载体坐标系, 其单位坐标矢量 为 i’, j’ 和 k’
N
E
R
S1
Lecture 10 -- Algorithms for SINS
7
2.1 方向余弦矩阵
G G B CBT0 CB00 CBT0
G IG
VN R V E e cos R VE t an sin e R
B0
C
B0 BT
BT
C
G G CG 0 CG 0 G IG
G0 B0
ζ
G CBTT
C
x
G0 B
y x
0
T
where i i dt
(角增量)
i x, y, z
and denote
B ( t ) dt IB
则
C (T ) C (0) e 0
G0 B
0 x y z
2 2
2
(向量的模)
Lecture 10 -- Algorithms for SINS
G0 GT
C C
G0 G0
G0
N E
G CGT0
GT
C I I TG IG
0
T
G G B G CBTT (CGT0 )1CB00 CBT0
Lecture 10 -- Algorithms for SINS 15
3.7 算例
某捷联惯导系统在 n 时刻, 其载体坐标系和惯性坐标系重合. 然 后从时刻 n 到时刻 n+1, 沿着载体三个轴的三个陀螺仪 X, Y, Z 的角增量输出分别为 0.002, 0.004 和 0.006 (rad); 请利用基于 Peano-Paker 解的一阶角增量算法计算时刻 n+1 载体和惯性坐 标系之间的方向余弦矩阵.
方向余弦矩阵的求解: 角增量算法
Lecture 10 -- Algorithms for SINS
2
1.1*捷联惯导系统: 特点
陀螺和加速度计被直接“捆绑 (strapped)”到载体上 没有物理的平台 对陀螺仪的角速度输出进行 积分,获取载体的姿态信息.
滚动轴
E
方位轴
俯仰轴
N
加速度计的输出需要变换到导航坐标系中. 对导航坐标系中的加速度分量进行补偿并积分,获取载体的速 度和位置信息.
Lecture 10 -- Algorithms for SINS
10
Outline
捷联惯导系统概述
姿态矩阵(DCM)微分方程的推导
方向余弦矩阵的求解: 角增量算法
Lecture 10 -- Algorithms for SINS
11
3.1 方向余弦矩阵微分方程
G B G CB CB GB
G0 B
可记为: 近似计算:
order S C
G G CB 0 (T ) CB 0 (0) I S C 2
1 1
2 1
3
4
0
1 2
02 1 6 1 2
02 1 6 1 02 2 24
Lecture 10 -- Algorithms for SINS
13
3.3*角增量算法
order S C
1 1 2 1
3
4
