经典模型简化-及-测试题目
数学模型题集(二)
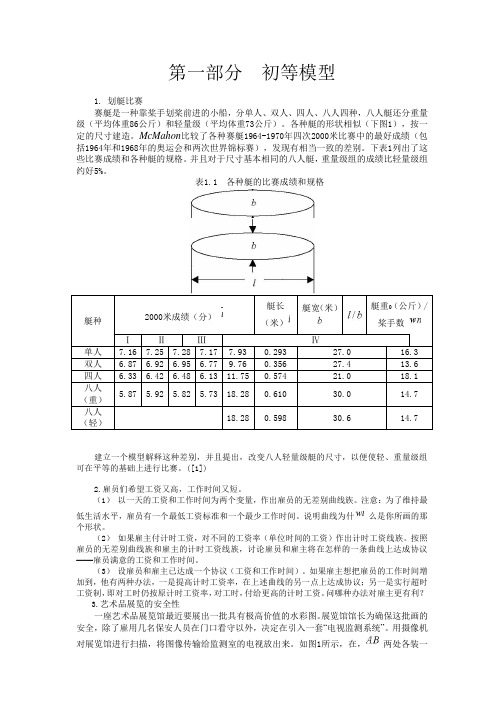
第一部分初等模型1. 划艇比赛赛艇是一种靠桨手划桨前进的小船,分单人、双人、四人、八人四种,八人艇还分重量级(平均体重86公斤)和轻量级(平均体重73公斤)。
各种艇的形状相似(下图1),按一定的尺寸建造。
McMahon比较了各种赛艇1964-1970年四次2000米比赛中的最好成绩(包括1964年和1968年的奥运会和两次世界锦标赛),发现有相当一致的差别。
下表1列出了这些比赛成绩和各种艇的规格。
并且对于尺寸基本相同的八人艇,重量级组的成绩比轻量级组约好5%。
表1.1 各种艇的比赛成绩和规格Ⅳ建立一个模型解释这种差别,并且提出,改变八人轻量级艇的尺寸,以便使轻、重量级组可在平等的基础上进行比赛。
([1])2.雇员们希望工资又高,工作时间又短。
(1)以一天的工资和工作时间为两个变量,作出雇员的无差别曲线族。
注意:为了维持最低生活水平,雇员有一个最低工资标准和一个最少工作时间。
说明曲线为什么是你所画的那个形状。
(2)如果雇主付计时工资,对不同的工资率(单位时间的工资)作出计时工资线族。
按照雇员的无差别曲线族和雇主的计时工资线族,讨论雇员和雇主将在怎样的一条曲线上达成协议——雇员满意的工资和工作时间。
(3)设雇员和雇主已达成一个协议(工资和工作时间)。
如果雇主想把雇员的工作时间增加到,他有两种办法,一是提高计时工资率,在上述曲线的另一点上达成协议;另一是实行超时工资制,即对工时仍按原计时工资率,对工时,付给更高的计时工资。
问哪种办法对雇主更有利?3.艺术品展览的安全性一座艺术品展览馆最近要展出一批具有极高价值的水彩图。
展览馆馆长为确保这批画的安全,除了雇用几名保安人员在门口看守以外,决定在引入一套“电视监测系统”。
用摄像机对展览馆进行扫描,将图像传输给监测室的电视放出来。
如图1所示,在,两处各装一台摄像机。
在展览馆的展墙上,每隔挂一幅画。
两个摄像机镜头的视角为,完成一次来回扫描。
但是,在监测室的工作人员只有的时间在观察电视画面。
数学建模能力测试题简单答案与提示

文乘以
1 1 的逆,就可以完成解密。 1 2
6. 12 个小球称 3 次,13 个小球也称 3 次,具体答案可以在网上找到。 7. 从第一行中间的 1 开始,按箭头方向数。
8. 参见《高等数学》下册第九章第十节的最小二乘法。 9. 在网上搜素聚类分析,可以查到。具体想法就是可以将每一个同学的身高和体重看做是 二维空间中的一个点,离得近的放到一起,远近用距离表示。 10. 自己发挥。
Q 先生:我知道你不知道这张牌
如果有单张的话,P 肯定就知道这牌了,既然 Q 知道 P 不知道是什么牌,那么 说明牌的花色肯定不是单张里面的,排除了刚刚出来的黑桃和草花 (第二步排除 的) 再一次排除黑桃和草花之后,所以现在的牌就有: 对于 Q 红桃:A Q 4 方块:A 5 对于 P
A:红桃、方块 Q: 红桃 5:方块 4:红桃
所以要求 x 4 必须是 55 3125 的整数倍,那么最小的应为 3125。 4 4 4 4 4 所以至少摘了 3125 个桃子,第五个猴子走后还剩下 ( x 4) 1024 5 5 5 5 5 但是其中有 4 个是借来的, 自然要减去, 所以第五个猴子走后实际上还剩下 1020 个。 4. 提示: (答案不唯一,只要合理就行)将 20,12,7,10,15,14 将际上可以理解为少 4 个,先借给它们 4 个再 分。虽然桃子多了 4 个,但每个猴子分得的桃子并不会增多,当然也不会减少。 每次刚好分为 5 堆,这样就容易算了。 设此堆桃子共有 x 个,则有 4 4 4 4 4 ( x 4) 整数 (最后剩下的桃子必须是整数个) 5 5 5 5 5
模型练习题

一、选择题1. 下列哪个是机器学习中的监督学习算法?A. 决策树B. 支持向量机C. 聚类算法D. 线性回归2. 下列哪个是深度学习中的卷积神经网络(CNN)常用的激活函数?A. ReLUB. SigmoidC. TanhD. Softmax3. 下列哪个是特征选择的方法?A. 特征提取B. 特征选择C. 特征工程D. 特征降维4. 下列哪个是Kmeans聚类算法的终止条件?A. 达到最大迭代次数B. 所有样本聚类中心不再变化C. 聚类中心距离小于阈值D. 聚类中心距离变化小于阈值5. 下列哪个是时间序列分析中的自回归模型?B. MA模型C. ARIMA模型D. LSTM模型二、填空题1. 机器学习中的“过拟合”是指模型在训练数据上表现良好,但在测试数据上表现较差的现象。
2. 下列哪个是神经网络中的全连接层?A. 卷积层B. 全连接层C. 池化层D. 展平层3. 下列哪个是支持向量机(SVM)中的核函数?A. 线性核B. 多项式核C. RBF核D. Sigmoid核4. 下列哪个是深度学习中的循环神经网络(RNN)?A. CNNB. RNNC. LSTMD. GRU5. 下列哪个是时间序列分析中的自回归移动平均模型?A. AR模型C. ARIMA模型D. LSTM模型三、简答题1. 简述决策树算法的原理。
2. 简述支持向量机(SVM)中的核函数的作用。
3. 简述深度学习中的卷积神经网络(CNN)的基本结构。
4. 简述时间序列分析中的自回归移动平均模型(ARIMA)的原理。
5. 简述特征选择在机器学习中的作用。
四、编程题1. 编写一个简单的决策树算法,实现分类任务。
2. 编写一个简单的支持向量机(SVM)算法,实现分类任务。
3. 编写一个简单的卷积神经网络(CNN)模型,实现图像分类任务。
4. 编写一个简单的循环神经网络(RNN)模型,实现序列预测任务。
5. 编写一个简单的自回归移动平均模型(ARIMA),实现时间序列预测任务。
大学生数学建模技能测试题

大学生数学建模技能测试题考虑现实世界问题(不要求解答):在一条新公共汽车路线上,要沿路设置公共汽车站且每个车站都需要遮雨棚。
公交公司希望这种服务既要满足顾客的需求同时又不能超过公交车的要求。
请问车站设置在什么位置,才能使尽可能多的人享受到这种服务?在设计一个简单的数学模型时,您认为以下的假定哪个最不重要?A.假设仅仅能建一个遮雨棚B.假设路是平直的C.假设晴天是雨天的两倍D.假设公共汽车运行的是半小时的时间表E.假设顾客不会走很远的路去乘车2考虑现实世界问题(不要求解答):沿一条新电车路线,安置电车站。
且每个车站都需要遮雨棚。
电车公司希望这种服务既要满足顾客的需求同时又不能超过电车的要求。
请问车站设置在什么位置,才能使尽可能多的人享受到这种服务?在设计一个简单的数学模型时,您认为以下的假定哪个最不重要?A.假设顾客不会走很远的路去乘电车B.假设电车运行的是20 分钟的时间表C.假设电车线是单轨道D.假设电车司机能从电车的前后都可以驾驶E.假设电车站可以设置在任何位置。
3考虑现实世界问题(不要求解答):一个步行者要穿过一条交通繁忙的马路,假设马路是一条直的单行机动车道。
在设计一个是否需要设置人行横道的简单数学模型时,您认为以下假定哪个最不重要?A 横穿马路将由行人通过按钮来控制B 交通流量是恒定的C 车流速度是常数并且等于限制速度D. 行人以恒定的速度通过马路E. 行人不会走很远路来由此穿过马路4考虑现实世界问题(不要求解答)自行车轮子的最佳尺寸是多少?以下哪个问题最能说明骑车的稳定性?A 轮子与脚蹬间有链条相连吗?B 骑车人有多高?C 自行车传动装置吗?D 能骑上去的最高路缘是多少?E. 地形情况怎样?5考虑现实世界问题(不要求解答)婴儿车轮子的最佳尺寸是多少?下面的哪一个陈述的问题最能表明小孩坐车感到平稳?A.婴儿车有三个轮子还是四个轮子?B.前后轮子之间的距离是多少?C.座位装有软垫吗?D.孩子有多大?E.是柏油碎石路面还是混泥土路面?6考虑现实世界问题(不要求解答)您希望将您的汽车倒入已停好的一排车中间的一个空车位。
数学建模经典习题集

第一部分 练习与思考题 第1章 建立数学模型 1.1 在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何?(稳定的椅子问题见姜启源《数学模型》第6页) 1.2 在商人们安全过河问题中,若商人和随从各四人,怎样才能安全过河呢?一般地,有n名商人带n名随从过河,船每次能渡k人过河,试讨论商人们能安全过河时,n与k应满足什么关系。(商人们安全过河问题见姜启源《数学模型》第7页) 1.3 人、狗、鸡、米均要过河,船需要人划,另外至多还能载一物,而当人不在时,狗要吃鸡,鸡要吃米。问人、狗、鸡、米怎样过河? 1.4 有3对夫妻过河,船至多载两人,条件是任一女子不能在其丈夫不在的情况下与其他的男子在一起。问怎样过河? 1.5 如果银行存款年利率为5.5%,问如果要求到2010年本利积累为100000元,那么在1990年应在银行存入多少元?而到2000年的本利积累为多少元? 1.6 某城市的Logistic模型为2610251251NNdtdN,如果不考虑该市的流动人口的影响以及非正常死亡。设该市1990年人口总数为8000000人,试求该市在未来的人口总数。当t时发生什么情况。 1.7 假设人口增长服从这样规律:时刻t的人口为)(tx,最大允许人口为mx,t到tt时间内人口数量与)(txxm成正比。试建立模型并求解,作出解的图形并与指数增长模型和阻滞增长模型的结果进行比较。 1.8 一昼夜有多少时刻互换长短针后仍表示一个时间?如何求出这些时间? 1.9 你在十层楼上欲乘电梯下楼,如果你想知道需要等待的时间,请问你需要有哪些信息?如果你不愿久等,则需要爬上或爬下几个楼层? 1.10 居民的用水来自一个由远处水库供水的水塔,水库的水来自降雨和流入的河流。水库的水可以通过河床的渗透和水面的蒸发流失。如果要你建立一个数学模型来预测任何时刻水塔的水位,你需要哪些信息? 第2章 初等模型 2.1 学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数: (1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者. (2)2.1节中的Q值方法. (3)d’Hondt方法: 将各宿舍的人数用正整数,2,1n ,3相除,其商数如下表: 1 2 3 4 5 … A B C 235 117.5 78.3 58.75 … 333 166.5 111 83.25 … 432 216 144 108 86.4 将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配席位.你能解释这种方法的道理吗。 如果委员会从10人增至15人,用以上3种方法再分配名额.将3种方法两次分配的结果列表比较. (4)你能提出其他的方法吗.用你的方法分配上面的名额. 2.2 在超市购物时你注意到大包装商品比小包装商品便宜这种想象了吗.比如洁银牙膏50克装的每支1.50元,120克装的每支3.00元,二者单位的重量的价格比是1.2:1,试用比例方法构造模型解释这个现象. (1)分析商品的价格C与商品重量W的关系.价格由生产成本、包装成本和其它成本等决定,这些成本中有的与重量W成正比,有的与表面积成正比,还有与W无关的因素。 (2)给出单位重量价格C与W的关系。画出它的简图,说明W越大C越小,但是随着W的增加C减小的程度变小。解释实际意义是什么。 2.3 一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用与测量,请你设计按照测量的长度估计鱼的重量的方法。假设鱼池中只有一种鲈鱼,并且得到了8条鱼的如下数据(胸围指鱼身的最大周长):
米哈游模型测试题

米哈游模型测试题
1、通用题
比较简单,一般是简单题,出题有三个角度
岗位选择
游戏经历
职业规划
比如职业规划的出题方式可能就是
你为什么想做游戏运营/用户研究/文案策划/交互策划/关卡战
斗策划/数值策划/系统策划呢?
为什么想加入米哈游呢?在准备的时候也要从这三个角度出发,以游戏经历为例,你要梳理3-5个自己的过往游戏经历,梳理的维度要包括游戏时长、等级、排位等。
说完了通用题,这里再主要讲一下专业题的出题思路和准备技巧。
2、专业题的出题点
一般集中在游戏类产品和岗位最关心的几个经典问题上。
比如:如何策划节日/假期活动?
如何进行社区运营?
如何进行数据分析?
如何看待游戏产品的作弊/反作弊?
当然,题目不会给的这么简单,而是非常的细节,题干一般分为场景+3-4个小问
请你回忆过去一年里某款游戏的节日活动
(1)描述你参加该活动的过程和体验
(2)分析该活动的优缺点及改进建议。
(3)如果你是活动运营,你会如何策划这场活动?
当然,这里是举例,真实的题目考察的会更加具体。
注意,这几个小问题之间的掌握程度一般是不同的,在写答案的时候就要把握重点
描述:写出过程和细节
分析:写出原因和联系
策划:追求创意,最好能给出一些新结构/新认知
这就需要大家有比较强的行业融入感,如果你选择的是运营岗位,那你肯定要找3-5个游戏从平台、运营、用户的角度完整拆解一下活动运营的所有过程、分析活动运营的前因后果并试着自己策划一场活动。
数学模型与实际问题模拟试题
数学模型与实际问题模拟试题一、问题描述某公司生产和销售某种产品,投入一定成本和人工后可获得一定利润。
假设每生产一件产品需要投入成本$C$元,并能卖出$P$元。
公司决定在每个季度生产数量为$x$件的产品。
此外,公司要为员工支付固定的季度工资$W$元。
为了最大化利润,公司应该制定何种生产策略,以确保获得最大的净利润?二、问题分析本问题涉及一个典型的经济决策问题,需要根据公司的成本、收入和工资等因素来确定最优的生产策略。
为了解决这一问题,我们首先需要建立数学模型,然后利用该模型进行实际问题的模拟,最终求解最优解。
三、建立数学模型假设每个季度公司生产$x$件产品,则成本为$C \cdot x$元,收入为$P \cdot x$元。
同时需要支付固定工资$W$元。
因此,净利润可表示为$P \cdot x - C \cdot x - W$元。
为了最大化净利润,我们可以通过求解下面的最优化问题来得到最优的生产策略:\[\max_{x} P \cdot x - C \cdot x - W\]其中,$x$为生产的产品数量。
四、模拟试题假设某公司的成本$C$为200元,产品的售价$P$为500元,季度工资$W$为5000元。
现在,我们通过模拟试题来求解最优的生产策略。
1. 使用数学模型,计算在给定成本、售价和工资情况下的最优生产数量$x$,并计算相应的净利润。
解答:由数学模型可知,要最大化净利润,我们需要求解下面的最优化问题:\[\max_{x} 500 \cdot x - 200 \cdot x - 5000\]对该问题进行求解,可以通过求导的方法来找到极值点。
对目标函数求导得到:\[\frac{d}{dx}(500 \cdot x - 200 \cdot x - 5000) = 300 - 200 = 100\]令导数等于零,得到极值点$x = \frac{5000}{100} = 50$因此,最优生产数量为50件产品。
高三板块模型题型练习题
高三板块模型题型练习题在高三阶段,各科目的模型题型成为了考试的重点,因为这些题型不仅考察了学生的知识掌握程度,还对学生的综合应用能力进行了考验。
本文将就高三板块模型题型进行一些练习题,帮助同学们更好地掌握这些题型。
一、数学板块:函数与解析几何1. 设函数 f(x) = x^2 - 3x + 2,求函数 f(x) 的极值点和最小值。
2. 已知直线 L :2x + y - 3 = 0 与抛物线 C :y^2 - 4x - 2y + 2 = 0 相切,求直线 L 的方程。
二、物理板块:力学和电磁学1. 牛顿第二定律 F = ma 描述了物体在受到合外力 F 作用时的运动情况。
若一个质量为 5 kg 的物体受到的合外力 F 是一个常量,该物体的初始速度为 2 m/s,经过 3 s 后的速度为 8 m/s,求合外力 F 的大小。
2. 在一个电路中,有两个电阻R1 = 3 Ω 和R2 = 4 Ω,这两个电阻并联,接入一个电动势为 12 V 的电源。
求电路总电流以及电路中通过R1 和 R2 的电流大小。
三、化学板块:元素周期表和化学键1. 元素周期表中第一周期只有两个元素,它们分别是氢和氦。
请回答以下两个问题:a) 氢的原子序数是多少?氦的原子序数是多少?b) 氢和氦的电子层排布分别是怎样的?2. 有一个分子式为 CH2O 的有机化合物,该化合物属于什么类别?它分子中有多少个氧原子?四、生物板块:遗传与进化1. 在一群蚂蚁的基因中,有一对基因 G1 和 G2 决定了蚂蚁的身体颜色,如果 G1 和 G2 均为红色基因,蚂蚁显红色。
如果 G1 和 G2 均为黑色基因,蚂蚁显黑色。
如果 G1 和 G2 不同,则呈现为混合色。
现有两只父蚂蚁,一只红色,一只黑色,请确定它们的子代会呈现出什么颜色?2. 自然选择理论是达尔文进化理论的核心内容之一。
请简要解释什么是自然选择,并举例说明。
五、英语板块:语法和阅读理解1. 下列句子中,找出含有定语从句的句子:a) I know a girl who loves playing basketball.b) The book on the table belongs to me.c) She is the woman I spoke to just now.2. 阅读理解Passage 1:It is common for people to feel tired at times. This kind of fatigue usually can be treated with rest or a few nights of good sleep. But when youfeel tired all the time or the tiredness is increasing over time, you should pay attention to it.According to a study, there are several factors that may lead to constant tiredness. These include poor sleep, unhealthy diet, lack of exercise, and mental health issues.Passage 2:Sleep is an important aspect of our daily lives, as it allows the body to rest and recover. According to experts, adults need an average of 7 to 9 hours of sleep each night to maintain good health. Lack of sleep can lead to various problems such as decreased concentration, memory loss, and increased risk of developing chronic conditions.Based on the information provided in the passages, answer the following questions:a) What are some factors that may contribute to constant tiredness?b) How many hours of sleep do adults need each night to maintain good health?以上就是高三板块模型题型的一些练习题,希望能够帮助同学们更好地掌握这些题型。
