福建省福州八中2008-2009学年高三第四次质量检查数学(文科)
度福州八中高三第四次质量检查(理)

2008-2009学年度福州八中高三第四次质量检查数学试卷(理科)考试时间:120分钟 试卷满分:150分一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,)1.设全集=U {1,2,3,4,5,7},集合=A {1,3,5,7},集合=B {3,5},则 ( ) A .U A B =⋃B .()U U A B =⋃ðC .)()(.B A U U U ⋃=D .()U U A B =⋃ð 2.已知抛物线y = 34 x 2,则它的焦点坐标是( )A .(0,316 )B .( 316,0)C .(13,0)D .(0, 13)3.已知两条直线1l :0=++c by ax ,2l :0=++p ny mx ,则bm an =是直线1l ∥2l 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知函数sin()y A x m ωϕ=++的最大值是4,最小值是0,最小正周期是2π,直线3x π=是其图象的一条对称轴,则下面各式中符合条件的解析式是( )A .4sin(4)6y x π=+ B .2sin(4)26y x π=++C .2sin(4)23y x π=++D .2sin(2)23y x π=++5.若函数22)(23--+=x x x x f 的一个正数零点附近的函数值用二分法计算,其参考数据如下:那么方程02223=--+x x x 的一个近似根(精确到0.1)为 ( )A . 1.5B . 1.4C . 1.3D . 1.26.如图,在正方体1111ABCD A B C D -中,M 为的棱1BB 的中点,则异面直线AM 与1BD所成角的余弦值是( )ABCD7.焦点为F (0,10),渐近线方程为4x±3y=0的双曲线的方程是 ( )A .16y 9x 22-=1 B .22916y x -=1C .226436y x -=1D .36y 64x 22-=1 8.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ( )A .9πB .10πC .11πD .12π9.已知点(2,0)A -、(3,0)B ,动点2(,)P x y PA PB x ⋅=满足,则点P 的轨迹是 ( )A .抛物线B .椭圆C .双曲线D . 圆10.给出下列命题:①若平面α内的直线l 垂直于平面β内的任意直线,则βα⊥;②若平面α内的任一直线都平行于平面β,则βα//;③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;④若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱.其中为假.命题的个数( )A .1B .2C .3D .411.设1232,2()log (1)2x e x f x x x -⎧⎪=⎨-≥⎪⎩<,,,则不等式f (x )>2的解集为 ( ) A .(1,2)⋃(3,+∞) B .(10,+∞)C .(1,2)⋃(10 ,+∞)D .(1,2)12.若直线1+=kx y 与圆0422=-+++my kx y x 交于N M ,两点,且N M ,关于直线0=-y x 对称, 动点P ()b a ,在不等式组20-+≥⎧⎪-≤⎨⎪≥⎩kx y kx my y 表示的平面区域内部及边界上运动,则21b w a -=-的取值范围是( )A .),2[+∞B .]2,(--∞C .]2,2[-D .),2[]2,(+∞⋃--∞二、填空题:(本大题共有4个小题,每小题4分,共计16分.) 13.不论m 取何值时,直线(m-1)x-y+2m+1=0恒过定点 . 14.222()3x x dx -=⎰ . 15.已知向量、的夹角为60°,且4,()(23)16a a b a b =+⋅-=,则在方向上的投影等于 . 16.给出下列命题:①函数f (x )=⎪⎭⎫⎝⎛-≠+-21121x x x 对称中心是(-2121-,); ②已知S n 是等差数列{a n }(n ∈N*)的前n 项和,若75S S >,则93S S >; ③函数f (x )=x |x |+px +q (x ∈R )为奇函数的充要条件是q =0; ④已知a ,b ,m 均是正数,且a<b ,则.a m a b m b+>+ 其中真命题的序号是_______(将所有真命题的序号都填上).三、解答题:( 本大题共有6个小题,共74分。
2008-2009学年福州八中高三毕业班第一次质量检查

2008-2009学年度福州八中高三毕业班第一次质量检查地理试卷考试时间:90分钟试卷满分:100分第I卷、单选题。
(60分)用实验模拟某一天气系统(见图):在塑料盒中间插一隔板,两侧分别注入同体积红色暖水(代表暖空气)与蓝色冷盐水(代表冷空气)。
读图,完成1〜3题。
1 .在向上抽出隔板后的数秒内,冷暖水之间()A .出现水平交界面,蓝色水在上C.出现倾斜交界面,蓝色水在上2.该实验模拟在天气系统是A .气旋B .锋3•该模拟实验存在的主要不足是①没能模拟出主导气流的运动方向③没能模拟出冷锋与暖锋A .①②③B .②③④B. 出现水平交界面,红色水在上D .出现倾斜交界面,红色水在上C •高气压D •低气压②没能模拟出成云致雨的天气现象④没能模拟出冷暖空气的密度差异C .①③④D .①②④4.与北美洲相比,下列气候类型中,亚洲缺少的是A .极地气候B .地中海气候C .热带雨林气候D.温带海洋性气候F图是某区域沿回归线的地形剖面示意图,读图回答5〜7题。
5.下列叙述正确的是70( )50*a 处气候类型为地中海气候A .为西澳大利亚寒流是全球规模最大的洋流B. 中国南方低山丘陵 D .西欧平原汨茱绘直申丸肚阻电曲烁琴井弔总耄田t 1迟R I ---------------- H —I 东冷囱蚪戾粋曲匕丸从松屿盅卅喑井專录書压10.甲大陆北端地处两大板块交界地带,这两大板块是6. B .C .D .流经 b 山脉由南极洲板块与美洲板块碰撞、挤压而成c 地处于世界最大的河流流域d 所在地形区为东非高原e 海域的洋流7. 8. 9. C .对沿岸有增温增湿作用 由高纬流向低纬e 海域与f 海域的温度(T )、盐度(S )相比 A . Te >Tf ; Se > Sf C . Te <Tf ; Se >SfTe > Tf ; Te < Tf ;F 图是 陆地自然景观类型分布与水热条件关系示意图Se < Sf Se < Sf”,读图回答8〜9题。
福建省福州八中高三数学第二次质量检查 文 新人教版

福建省福州八中2008—2009学年高三第二次质量检查数学试题(文科)考试时间:120分钟 试卷满分:150分注意事项:准考证号码填写说明:准考证号码共九位,每位都体现不同的分类,具体如下:一、选择题:每小题5分共60分,每小题仅有一个正确选项1 若集合}1,1{-=A ,}1|{==mx x B ,且A B A =⋃,则m 的值为( )A .1B .1-C .1或1-D .1或1-或0 2 要得到)42sin(3π+=x y 的图象只需将y=3sin2x 的图象( )A .向左平移4π个单位 B .向右平移4π个单位 C .向左平移8π个单位D .向右平移8π个单位3.已知函数)sin(ϕω+=x A y 在同一周期内,9π=x 时取得最大值21,π94=x 时取得最小值-21,则该函数解析式为 ( )A .)63sin(21π+=x yB .)63sin(21π+=x yC .)63sin(21π-=x yD .)63sin(21π-=x y4.已知等差数列{}n a 满足1231010a a a a ++++=,则有( )A .11010a a +>B .11010a a +<C .11010a a +=D .5151a = 5.数列2311,,,,,,n a a a a -的前n 项的和为( )A .11na a --B .111n a a +--C .211n a a+--D .以上均不正确6.某数列既成等差数列也成等比数列,那么该数列一定是( )A .公差为0的等差数列B .公比为1的等比数列C .常数数列1,1,1…D .以上都不对7.已知数列{ a n }的前n 项和为S n =4n 2 -n +2,则该数列的通项公式为( )级别代号 科类代号 教学班代号 行政班代号 行政班座号A . a n =8n +5(n ∈N*)B . a n =8n -5(n ∈N*)C . a n =8n +5(n ≥2)D . ⎪⎩⎪⎨⎧∈≥-==),2(58)1(5+n N n n n n a8.下列函数中,以π为周期的偶函数是 ( )A .|sin |x y =B .||sin x y =C .)32sin(π+=x yD .)2sin(π+=x y9.函数22cos y x =的一个单调增区间是 ( )A .π3π44⎛⎫⎪⎝⎭,B .ππ2⎛⎫ ⎪⎝⎭,C .ππ44⎛⎫- ⎪⎝⎭,D .π02⎛⎫ ⎪⎝⎭,10.某工厂六年来生产某种产品的情况是:前三年年产量的增长速度越来越快,后三年年产量保持不变,则该厂六年来这种产品的总产量...C 与时间t 的函数关系可用图象表示的是( )A. B. C.D.11.如果函数),,(,)(23R c b a c bx ax x x f ∈+++=在R 上不单调,则 ( )A .b a 32< B .b a 32≤ C .b a 32>D .b a 32≥12..偶函数))((R x x f ∈满足:0)1()4(==-f f ,且在区间[0,3]与),3[+∞上分别递减和递增,则不等式0)(3<x f x 的解集为 ( )A .),4()4,(+∞⋃--∞B .)4,1()1,4(⋃--C .)0,1()4,(-⋃--∞D .)4,1()0,1()4,(⋃-⋃--∞二、填空题:每小题4分共16分13.在等比数列{}n a 中, 若101,a a 是方程06232=--x x 的两根,则47a a ⋅=______.14.若函数f(χ)是偶函数,且当χ<0时,有f(χ)=cos3χ+sin2χ,则当χ>0时,f(χ)的表达式为 15.已知数列的12++=n n S n ,则12111098a a a a a ++++=_____________。
福建省福州市第八中学2016届高三数学第四次质量检测试题文

福州八中2015—2016学年高三毕业班第四次质量检查数学(文)试题考试时间:120分钟 试卷满分:150分参考公式:样本数据x 1,x 2, …,x n 的标准差 锥体体积公式s =13V Sh = 其中x 为样本平均数其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式V Sh =24S R =π,343V R =π其中S 为底面面积,h 为高其中R 为球的半径第Ⅰ卷(选择题 共60分)一、选择题:(每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求)1.已知()211i i z+=-(i 为虚数单位),则复数z =( )A.1i +B.1i -C.1i -+D.1i --2.已知集合A ={(x ,y )|x +y =0,x ,y ∈R },B ={(x ,y )|y =x 2,x ,y ∈R },则集合A ∩B 的元素个数是( ) A .0B .1C .2D .33. 若k ,-1,b 三个数成等差数列,则直线y =kx +b 必经过定点( )A .(1,-2)B .(1,2)C .(-1,2)D .(-1,-2)4. 设15<(15)b <(15)a<1,那么( )A .a a<a b<aB .a b <a a<aC .a a <a <a bD .a < a b <a a5. 某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .18+B .20+C .46+D .50+6. 函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示,则将y =f (x )的图象向右平移π6个单位后,得到的图象解析式为( )A .y =sin 2xB .y =cos 2xC .y =sin(2x +2π3)D .y =sin(2x -π6)7.下列叙述中正确的是( ) A .若a ,b ,c ∈R ,则“ax 2+bx +c ≥0”的充分条件是“b 2-4ac ≤0” B .若a ,b ,c ∈R ,则“ab 2≥cb 2”的充要条件是“a >c ”C .命题“对任意x ∈R ,有x 2≥0”的否定是“存在x ∈R ,有x 2≥0”D .命题“l 是一条直线,α,β是两个不同的平面,若//,//l l αβ则α∥β”为假命题8. 已知各项不为0的等差数列{a n }满足a 4-2a 27+3a 8=0,数列{b n }是等比数列,且b 7=a 7,则b 2b 8b 11等于( )A .1B .8C .4D .29. 下列四个图象可能是函数y =10ln|x +1|x +1图象的是()10.已知圆()()22:344C x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P ,使得90APB ∠=,则m 的最大值为( ) A .7 B.6 C.5D.411. 若x ,y 满足1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩且z=ax+2y 仅在点(1,0)处取得最小值,则实数a 的取值范围是( )A .(]4,0a ∈-B .[)0,2a ∈C .()4,2a ∈-D .()()4,00,2a ∈-U12.已知函数()2sin 2f x x =,将函数()y f x =的图像向左平移6π个单位,再往上平移1个单位,得到函数()y g x =的图像.对任意的a R ∈, ()y g x =在区间[,10]a a π+上零点个数的所有可能值为A .20B .21C .20或21D .21或22第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分 13.函数()f x =的定义域为________. 14. 设0<θ<π2,向量a =(sin 2θ,cos θ),b =(1,-cos θ),若a b ⊥r r ,则tan θ=________.15.在平面直角坐标系xOy 中,设A 是曲线C 1:y =ax 3+1(a >0)与曲线C 2:x 2+y 2=52的一个公共点,若C 1在A 处的切线与C 2在A 处的切线互相垂直,则实数a 的值是________.16. 对大于或等于2的正整数的幂运算有如下分解方式:22=1+3,32=1+3+5,42=1+3+5+7,…; 23=3+5,33=7+9+11,43=13+15+17+19,….根据上述分解规律,若m 2=1+3+5+…+11,p 3的分解中最小的正整数是21,则m +p=_____. 三、解答题:解答应写出文字说明,证明过程或演算步骤.17. 已知数列{a n }前n 项和为S n ,首项为a 1,且1,a n ,S n 成等差数列.(1)求数列{a n }的通项公式;(2)数列{b n }满足b n =(log 2a 2n +1)×(log 2a 2n +2),求证:1b 1+1b 2+1b 3+…+1b n <1418.已知函数()2sin()f x x ω=,其中常数0ω>.(1)令1ω=,判断函数()()()2F x f x f x π=+-的奇偶性并说明理由;(2) 已知在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若a =3,b =2,sin B =63,求F(x )+4cos(2A +π6) ,(x ∈[0,11π12])的取值范围.19.在三棱柱111-ABC A B C 中,侧棱1AA ⊥底面ABC ,,⊥AB BC D 为AC 的中点, 12A A AB ==,3BC =.(1)求证:1//AB 平面1BC D ; (2) 求四棱锥11-B AAC D 的体积.20.设(,),(,)A A B B A x y B x y 为平面直角坐标系上的两点,其中,,,A A B B x y x y ∈Z .令B A x x x ∆=-,B A y y y ∆=-,若x ∆+=3y ∆,且||||0x y ∆⋅∆≠,则称点B 为点A 的“相关点”,记作:()B A τ=.(Ⅰ)请问:点(0,0)的“相关点”有几个?判断这些点是否在同一个圆上,若在,写出圆的方程;若不在,说明理由;(Ⅱ)已知点(9,3),(5,3)H L ,若点M 满足(),()M H L M ττ==,求点M 的坐标;(Ⅲ)已知0P 0000(,)(,)x y x y ∈∈Z Z 为一个定点,点列{}i P 满足:1(),i i P P τ-=其中1,2,3,...,i n =,求0n P P 的最小值.21、设函数()x f x e ax =-,x R ∈.(Ⅰ)当2a =时,求曲线()f x 在点(0,(0))f 处的切线方程; (Ⅱ)在(Ⅰ)的条件下,求证:()0f x >; (Ⅲ)当1a >时,求函数()f x 在[0,]a 上的最大值.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分,解答时请写清题号. 22、(本小题满分10分)选修4-1:几何证明选讲如图,AB 是圆O 的直径,CD ⊥AB 于D ,且AD =2BD ,E 为AD 的中点,连接CE 并延长交圆O 于F .若CD =2,则求线段AB 与EF 的长度 .23、(本小题满分10分)选修4-4:坐标系与参数方程已知极坐标系的极点在平面直角坐标系的原点O 处,极轴与x 轴的正半轴重合,且长度单位相同.直线l 的极坐标方程为ρ=92sin ⎝ ⎛⎭⎪⎫θ+π4,点P (1+cosα,sin α),参数α∈[0,2π).(1)求点P 轨迹的直角坐标方程 (2)求点P 到直线l 距离的最小值.24、(本小题满分10分)选修4-5;不等式选讲 已知函数f (x )=|x -a |.(1)若不等式f (x )≤1的解集为{x |1≤x ≤3},求实数a 的值;(2)若a =2,且存在实数x,使得()(5)m f x f x ≥++成立,求实数m的取值范围.福州八中2015—2016学年高三毕业班第四次质量检查数学(文)试卷参考答案及评分标准一、选择题 CCADB DDBCA CC二、填空题 (13)()1,00,2⎡⎫-+∞⎪⎢⎣⎭U (14)12(15)4 (16)11 三、解答题17、 (1)解 ∵1,a n ,S n 成等差数列,∴2a n =S n +1,-----1分 当n =1时,2a 1=S 1+1,∴a 1=1,----------------2分 当n ≥2时,S n =2a n -1,S n -1=2a n -1-1,两式相减得a n =S n -S n -1=2a n -2a n -1,-------------3分∴a na n -1=2,-------------------------------------4分 ∴数列{a n }是首项为1,公比为2的等比数列,-------5分∴a n =1×2n -1=2n -1.------6分(2)证明 b n =(log 2a 2n +1)×(log 2a 2n +3)=log 222n +1-1×log 222n +3-1=4n (n +1),---7分1b n=1111114141n n n n ⎛⎫⎛⎫⨯=- ⎪ ⎪++⎝⎭⎝⎭,-----------8分 123*11111111111++++=4122311111()414n b b b b n n n N n ⎡⎤⎛⎫⎛⎫⎛⎫-+-+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦⎛⎫=-<∈ ⎪+⎝⎭L L即1b 1+1b 2+1b 3+…+1b n <14.--------12分 18、解:(1)ƒ(x )=2sin ,x()()()2sin 2sin 2sin cos 22F x f x f x x x x x ππ⎛⎫⎛⎫=+-=+-=- ⎪ ⎪⎝⎭⎝⎭-----1分0,,444444F F F F F F ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-=--≠-≠- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭----5分 所以,F (x )既不是奇函数也不是偶函数。
2008-2009学年福州八中高三第四次质量检查文
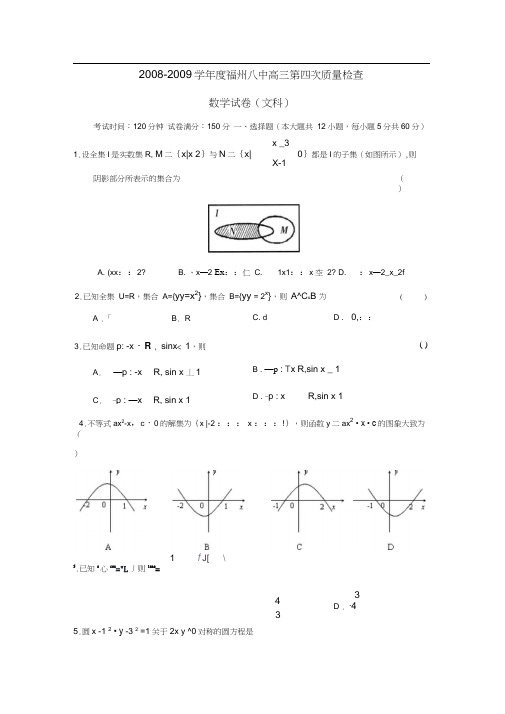
4 32008-2009学年度福州八中高三第四次质量检查数学试卷(文科)考试时间:120分钟 试卷满分:150分 一、选择题(本大题共 12小题,每小题5分共60分)x _31.设全集I 是实数集R, M 二{x|x 2}与N 二{x|0}都是I 的子集(如图所示),则X-1阴影部分所表示的集合为 ()A. (xx ::2? B . 、x —2 Ex ::仁 C . 1x1::x 空 2? D . :x —2_x_2f2.已知全集 U=R ,集合 A={yy=x 2},集合 B={yy = 2x },则 A^C u B 为()4.不等式ax 2-x ,c ・0的解集为{x |-2 ::: x :::!},则函数y 二ax 2 • x • c 的图象大致为()1f J[ \5.已知s 心cos="L 丿则tane=3 D . -45.圆x -1 2 • y -3 2 =1关于2x y ^0对称的圆方程是A .「B . R3.已知命题p: -x ・R , sinx < 1,则A . —p : -x R, sin x 丄1C ._p : —x R, sin x 1C . dD . 0,::( )B . —p : T x R,sin x _ 1 D . _p : xR,sin x 12 2A. (x +7 j +(y +1 j =1 2 2B . (x+7) +(y+2 $ =1圆x2 y2—2Rx—2Ry R2 =0在直角坐标系中的位置特征是那么几何体的侧面积为c. (x +6 2 +(y+1 ] =1 (x+6 j +(y+2 2 =16.7.A .圆心在直线y=x上C.圆心在直线y=-x上F列叙述正确的是函数B. 向量C. 数列B .圆心在直线y=x上,且与两坐标轴均相切D .圆心在直线y=-x上,且与两坐标轴均相切y=a x(a • 0,且a")的值域为实数集Ra = (1,1),则其模长为2玄满足a n ^2a n,则;a n[一定为等比数列D. 函数 2 2y = sin x - cos x的最小正周期是n8. 如图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,9. 椭圆=1的右焦点到直线. 3x的距离是10 .数列玄的a1 =1,a = n,a n ,b= a n 1,n 1 ,且a - b,则100A. —100B. 100 c .型9911.已知椭圆的中心在坐标原点,焦点在x轴上,且长轴长为12,离心率为-3,则椭圆的方程是2 2 2 2 2 2 2 2x y x y x y x yA. + =1B. + =1C. + =1D. + =1144 128 36 20 32 36 36 3212•某文具店出售羽毛球拍和羽毛球,球拍每副定价20元,羽毛球每只定价5元,该店制定了两种优惠方法:①买一副球拍赠送一只羽毛球;②按总价的92%付款。
微积分高考题

1.[福建省福州八中2008—2009学年度高三第四次质量检查数学(理科)第14题]222()3x x dx -=⎰ .2.[浙江省五校2009届高三第一次联考数学(理科)试题卷第11题]22sin x dx ππ-=⎰ ▲ .3.[浙江省嘉兴市2008学年高中学科基础测试数学(理科)试卷第14题]设函数()2f x ax b =+(a≠0),若⎰=20)(2)(x f dx x f ,x 0>0,则x 0= .4.[福建三所中学2009届高三期中联考试卷(理数)第6题]5.[济宁市育才中学2009届高三阶段性测试第11题]由曲线2y x =和直线()20,1,,0,1x x y t t ===∈所围成的图形(阴影部分)的面积的最小值为 ( ) A .14B .13C .12D .236.[天津蓟县2009届高三第一学期期中考试(理数)第12题]7、[广东省南海中学2009届高三12月统测数学(理科)试卷第5题]函数1,(10)()cos ,(0)2x x f x x x π+-≤<⎧⎪=⎨≤≤⎪⎩的图象与x 轴所围成的封闭图形的面积为( )A.32B. 1C. 2D.128.[济宁市育才中学2009届高三阶段性测试第6题]设函数2103()10x x f x x x⎧-≥⎪⎪=⎨⎪<⎪⎩,若()f a a >,则实数a 的取值范围是 ( )A .(,3)-∞-B .(,1)-∞-C .(1,)+∞D .(0,1)9.[福建省福州八中2008—2009学年度高三第四次质量检查数学(理科)第11题]设1232,2()log (1)2x e x f x x x -⎧⎪=⎨-≥⎪⎩<,,,则不等式f (x )>2的解集为 ( )A .(1,2)⋃(3,+∞)B .(10,+∞)C .(1,2)⋃(10 ,+∞)D .(1,2)10. [安徽凤阳中学2009届高三第四次月考数学试卷理科第4题] 设曲线x x y sin cos 1+=在点⎪⎭⎫⎝⎛1,2π处的切线与直线01=+-ay x 平行,则实数a 等于A.1-B.1C.2-D.211.[福建省政和二中2009届高三数学第四次月考试卷第10题]若函数))4(,4(,sin )(f x e x f x则此函数图象在点=处的切线的倾斜角为 ( ) π12、[2009届广东省六校第二次联考高三年级理科数学试卷第12题]已知函数32()(,)f x x ax b a b R =-++∈图像上任意一点处的切线的斜率都小于1, 则实数a 的取值范围是 . 13. [2009届广东省六校第二次联考高三年级理科数学试卷第6题]函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示,则函数)(x f 在),(b a 内有极小值点共有-------------------------------------( )A .1个B .2个C .3个D . 4个14、[广东省南海中学2009届高三12月统测数学(理科)试卷第6题]函数x x y cos 2+=在区间⎥⎦⎤⎢⎣⎡2,0π上取得最大值时x 的值为( ) A.0 B.6π C. 3π D. 2π 15.[山东省青岛市2007-2008学年度第一学期高三期末考试数学试题(理科)第4题]16.[福建省政和二中2009届高三数学第四次月考试卷第7题]设)(x f 是定义在R 上的一个函数,则函数)()()(x f x f x F --=在R 上一定是( ) A 奇函数 B 偶函数 C 既是奇函数又是偶函数 D 非奇非偶函数17、[辽宁省大连市第24中学2008~2009学年度上学期期中考试高三年级数学科试卷第8题]若定义在R 上的函数()f x 满足:对任意12,x x R ∈有()()()12121f x x f x f x +=++,则下列说法一定正确的是A.()f x 为奇函数B.()f x 为偶函数C.()1f x +为奇函数D.()1f x +为偶函数18.[2008学年广东省中山市一中高三年级第一次统测试题理科数学第7题]偶函数()()f x x R ∈满足:(4)(1)0f f -==,且在区间[0,3]与),3[+∞上分别递减和递增,则不等式()0xf x <的解集为A .),4()4,(+∞⋃--∞B .)4,1()1,4(⋃--C .)0,1()4,(-⋃--∞D .)4,1()0,1()4,(⋃-⋃--∞19.[2009届广东省六校第二次联考高三年级理科数学试卷第7题] 设奇函数()f x 在(0)+∞,上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集为---------------------------------------------------------( ) A .(10)(1)-+∞ ,, B .(1)(01)-∞- ,, C .(1)(1)-∞-+∞ ,, D .(10)(01)- ,,20、[辽宁省大连市第24中学2008~2009学年度上学期期中考试高三年级数学科试卷第5题]已知()f x 是实数集R 上的奇函数,且在区间(0,+∞)上单调递增,若102f ⎛⎫= ⎪⎝⎭, 三角形的内角A 满足()cos 0f A <,则A 的取值范围是 A.2,3ππ⎛⎫ ⎪⎝⎭ B.,32ππ⎛⎫ ⎪⎝⎭ C.2,33ππ⎛⎫ ⎪⎝⎭ D.2,323ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,21、[广东省南海中学2009届高三12月统测数学(理科)试卷第8题]定义在R 上的偶函数|4|2)(,]5,3[),2()()(--=∈+=x x f x x f x f x f 时当满足,则( ) A .)6(cos )6(sinππf f <B .)1(cos )1(sin f f >C .)32(sin )32(cos ππf f <D .)2(sin )2(cos f f >22.[2009年无锡市高三年级部分学校调研测试数学第10题]已知函数f (x )=log a | x |在(0,+∞)上单调递增,则f (-2) ▲ f (a +1).(填写“<”,“=”,“>”之一)23、[江苏海头高级中学2008~2009学年度高三数学模拟练习第2题]若关于x 的方程()233740tx t x +-+=的两个实根,αβ满足012αβ<<<<,实数t 的取值范围是 。
福建省福州八中2009届高三第四次质量检查(语文)
福建省福州八中09届高三数学第一次模拟考试(文)
某某八中2008—2009高三毕业班第一次模拟考试数学试题(文科)考试时间:120分钟 试卷满分:150分第Ⅰ卷 (选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,把答案填在答题卡相应的位置上. 1.若集合B A x x x B x x x A 则},0|{},|||{2≥+====( )A .[—1,0]B .[)+∞,0C .[)+∞,1D .(]1,-∞-2 ( )A . BC .D 3.设b 、c 表示两条直线,α、β表示两个平面,下列命题中的真命题是( )A .//c c α⎫⇒α⊥β⎬⊥β⎭B .////b c b c ⊂α⎫⇒α⎬⎭C .//c c α⎫⇒⊥β⎬α⊥β⎭D .////b b c c ⊂α⎫⇒⎬α⎭4.已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( )A .64B .100C .110D .120 5.已知53)4sin(-=+πx ,则x 2sin 的值等于( )俯视A .257-B .257C .2518-D .25186.如图,一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,则几何体的全面积是( ) A .324 B .334C .12D .8 7.“1=a ”是“函数()||f x x a =-在区间),1[+∞上为增函数”的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.已知y x y x y x 311,2lg 8lg 2lg ,0,0+=+>>则的最小值是( )A .2B .22C .4D .239.已知F 1、F 2是椭圆13422=+y x 的两个焦点,平面内一个动点M 满足|MF 1|-|MF 2|=2,则动点M 的轨迹是 ( )A .双曲线B .双曲线的一个分支C .两条射线D .一条射线10.已知圆22:()(2)4(0)C x a y a -+-=>及直线:30l x y -+=,当直线l 被圆C 截得的弦长为a 等于( )AB .2C 1D 111.设O 是△ABC 内部一点,且AOC AOB OB OC OA ∆∆-=+与则,2的面积之比为 ( )A .2B .21 C .1 D .5212.已知函数⎩⎨⎧=≠=)0(00(|||ln |)(x x x x f ,则方程0)()(2=-x f x f 的不相等的实根个数( ) A .5B .6C .7D .8第Ⅱ卷 (非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分. 13.已知点O 为坐标原点,点A 在x 轴上,正△OAB 的面积为3,其斜二测画法的直观图为B A O '''∆,则点B ′ 到边A O ''的距离 为.14.数列{}n a 的前n 项和242,n S n n =-+1210||||||a a a +++= .15.在可行域内任取一点,规则如流程图所示,则能 输出数对(x ,y )的概率是. 16.已知函数)(x f 的导数a x x f a x x a x f =-+='在若)(),)(1()(处取到极大值,则a 的取值X 围是.三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知向量:)0(),x sin 2,x sin x (cos n ),x cos 3,x cos x (sin m >ωωω-ω=ωω+ω=其中, 函数n m x f ⋅=)(,若)(x f 相邻两对称轴间的距离为.2π(1)求ω的值,并求)(x f 的最大值及相应x 的集合;(2)在△ABC 中,c b a ,,分别是A ,B ,C 所对的边,△ABC 的面积1)(,4,35===A f b S ,求边a 的长.ACDBPM Q18.(本小题满分12分)已知关于x 的一次函数n mx y +=(1)设集合P={-2,-1,1,2,3 }和Q={-2,3},分别从集合P 和Q 中随机取一个数作为m 和n ,求函数n mx y +=是增函数的概率; (2)实数n m ,满足条件 ,11;11;01≤≤-≤≤-≤-+n m n m求函数n mx y +=的图像经过一、二、三象限的概率.19.本小题满分12分.如图,在四棱锥ABCD P -中,底面ABCD 为菱形,60=∠BAD ,Q 为AD 的中点。
福州八中学年高三毕业班第四次质量检查.docx
福州八中2015—2016学年高三毕业班第四次质量检查数学(理)试题考试时间:120分钟 试卷满分:150分命题、校对:教务处 2015.12.14第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题意要求的.1.设全集{}1,2,3,4,5U =,集合{}{}2,3,4,1,2A B ==,则[()U A B =(A ){}2 (B ){}5(C ){}34,(D ){}2345,,,2.下列函数中,既是偶函数,又在区间()+∞,0内是减函数的是(A )xy )21(=(B )x y cos = (C )x y ln = (D )21x y -= 3.等差数列}{n a 中,211152=++a a a ,则=+-+-108642a a a a a (A )0 (B )7 (C )14 (D )21 4.“92>x ”是“3>x ”的(A )充分而不必要条件 (B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件5.已知0>a ,0>b 且b a ≠,设x =2ba +,b a y +=,4ab z =,则x ,y ,z 的大小关系是 (A )z x y >> (B )z y x >>(C )x z y >>(D )x y z >>6.已知数列}{n a 满足2121n n n a a a -+=+,且01=a ,则该数列的前100项的和等于(A )24(B )25 (C )74 (D )757.已知几何体的三视图如图所示,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是(A )38(B )328 (C )34 (D )3248.存在函数)(x f 满足:对任意R ∈x ,都有 (A )x x f 2sin )(sin =(B )x x f 2sin )(cos =(C )|1|)2(2-=-x x x f(D )1|)1(|2-=-x x f9.已知O 为△ABC 外接圆的圆心,3||=AB ,5||=AC ,则BC AO ⋅=(A )2(B )4(C )8(D )1610.若y mx z +=在平面区域⎪⎩⎪⎨⎧≤-+≥-≥-03,02,02y x x y y x 上取得最小值时的最优解不唯一,则z 的最大值是(A )3-(B )0(C )21 (D )23 11.关于函数x x x f cos sin )(=的性质的描述,不正确的是 (A )任意R ∈x ,)()π(x f x f =+ (B )任意R ∈x ,)2π()2π(x f x f -=+(C )不存在)2π,0(0∈x ,使0)(0=x f (D )不存在)2π,0(0∈x ,使21)(0>x f12.比较下列各组中两数的大小: ①2015201620162015<; ②2015201620162015>;③2015201620162015<;④2015201620162015>,其中正确结论的序号是(A )①③(B )②④(C )①④(D )②③第Ⅱ卷二、填空题:本大题4小题,每小题5分,共20分.把答案填在答题卡相应位置. 13.若31)4πtan(=-θ,则θtan =___________. 14.已知向量)1,3(=a ,)1,(-=+x b a .若b a //,则||b =___________.C 1B 1A 1CBA15.正三棱锥ABC P -内接于球O ,球心O 在底面ABC 上,且3=AB ,则球的表面积为___________.16.曲线14122=+y x 上的点到原点O 的距离最小值等于___________. 三、解答题:解答应写出文字说明、证明过程或演算步骤 17.(本小题满分12分)已知数列}{n a 的前n 项和n S ,满足n a S n n 22-=,2+=n n a b . (Ⅰ)求}{n a 的通项公式; (Ⅱ)记n n b c 2log =,数列}1{1+n n c c 的前n 项和为n T ,证明21<n T . 18.(本小题满分12分)ABC ∆中,c b a ,,分别是三个内角C B A ,,的对边,且A b B a c cos cos )2(=-.(Ⅰ)求B ;(Ⅱ)若6=BC ,AC 边上的中线BD 的长为7,求ABC ∆的面积. 19.(本小题满分12分)已知三棱柱111C B A ABC -,侧面⊥C C AA 11侧面11A ABB ,211===CA C A AA ,21==B A AB .(Ⅰ)求证:BC AA ⊥1;(Ⅱ)求二面角1A BC A --的正弦值. 20.(本小题满分12分)已知椭圆G 的焦点分别为)0,2(1-F ,)0,2(2F ,且经过点)2,2(-M ,直线2:+=ty x l 与椭圆G 交于A ,B 两点. Ⅰ)求椭圆G 的方程;(Ⅱ)求△AB F 1的面积的最大值. 21.(本小题满分12分)已知函数3)(e 2)(2+--=a x x f x ,R ∈a .(Ⅰ)若函数)(x f y =的图象在0=x 处的切线与x 轴平行,求a 的值; (Ⅱ)若0≥x 时,0)(≥x f 恒成立,求a 的取值范围. 注:e 是自然对数的底数.—————————— 新学期 新成绩 新目标 新方向 ——————————OFEDCBA请考生在第(22)、(23)、(24)三题中任选一题做答.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-1:几何证明选讲如图,梯形ABCD 内接于圆O ,BC AD //,过点C 作圆O 的切线,交BD的延长线于点F ,交AD 的延长线于点E .(Ⅰ)求证:BC DE AB ⋅=2;(Ⅱ)若9==BC BD ,6=AB ,求切线FC 的长.23.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,已知曲线C 的参数方程为2cos sin x y αα=⎧⎨=⎩,(α为参数).以直角坐标系原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为()πcos 224ρθ-=.(Ⅰ)求直线l 的直角坐标方程;(Ⅱ)点P 为曲线C 上的动点,求点P 到直线l 的距离的最大值.24.(本小题满分10分)选修4-5:不等式选讲设函数m x mx x f ++-=4)((0>m ). (Ⅰ)证明:4)(≥x f ;(Ⅱ)若5)2(>f ,求m 的取值范围.EDCBA福州八中2015—2016学年高三毕业班第四次质量检查数学(理)试卷参考答案及评分标准一、选择题 CDBBAC ACCDBD 二、填空题 13、2 14、102 15、π4. 16、3三、解答题17、解:(Ⅰ)因为n a S n n 22-=,所以)1(2211+-=++n a S n n ,从而22211--=++n n n a a a ,即221+=+n n a a .所以22422211=++=++=++n n n n n n a a a a b b . 又22111-==a S a ,所以21=a ,04211≠=+=a b ,所以}{n b 是首项为4,公比为2的等比数列,所以11224+-=⨯=n n nb ,从而221-=+n n a .…………………6分(Ⅱ)由(Ⅰ)得1+=n c n,所以2111)2)(1(111+-+=++=+n n n n c c n n ,从而212121)2111(...)4131()3121(<+-=+-+++-+-=n n n T n .……12分18、解:(Ⅰ)根据正弦定理,由(2)cos cos c a B b A -=, 可得A B B A C cos sin cos )sin sin 2(=-,整理得A B B A B C cos sin cos sin cos sin 2+=, 所以C BC sin cos sin 2=,因为0sin ≠C ,所以21cos =B , 又因为π),0(∈B ,所以3π=B .………………6分 (Ⅱ)如图,延长BD 至点E ,使得BD DE =,连接AE ,CE . 因为D 为AC 的中点,所以四边形ABCE 为平行四边形,所以3π2=∠BCE ,14=BE .在BCE ∆中,根据余弦定理,得3π2cos2222⋅⋅-+=CE BC CE BC BE , 即016062=-+CE CE,解得10=CE ,所以10==CE AB .所以ABC ∆的面积3153πsin 10621sin 21=⨯⨯⨯=⋅⋅=B BC AB S .……12分解法二:(Ⅰ)同解法一. (Ⅱ)因为BD 是AC 边上的中线,所以)(21BC BA BD +=,所以22)(41BC BA BD +=, 即BC BA BC BA BD ⋅++=24222.所以3πcos 626||74222⨯⨯⨯++=⨯BA BA ,即016062=-+BA BA ,解得10||=BA ,即10=AB .Oz yxC 1B 1A 1CBA所以ABC ∆的面积3153πsin 10621sin 21=⨯⨯⨯=⋅⋅=B BC AB S. 解法三:(Ⅰ)同解法一. (Ⅱ)设x AB =,=CD y DA =.在ABC ∆中,根据余弦定理,可得3πcos2222⋅⋅-+=BC AB BC AB AC , 即366422+-=x x y…①. 在BCD ∆中,根据余弦定理可得,yy y y DC BD BC DC BD BDC 141372672cos 2222222+=⨯-+=⋅-+=∠. 在ABD ∆中,同理可得,yx y y x y AD BD AB AD BD BDA 14497272cos 22222222+-=⨯-+=⋅-+=∠. 因为π=∠+∠BDA BDC ,所以BDA BDC ∠-=∠cos cos ,所以)49(13222+--=+x y y ,即62222-=x y…②. 由①②可得016062=-+x x ,所以10=x ,即10=AB .所以ABC ∆的面积3153πsin 10621sin 21=⨯⨯⨯=⋅⋅=B BC AB S .19、解:(Ⅰ)取1AA 中点O ,连接CO ,BO .1CA CA =,1AA CO ⊥∴,又∵1BA BA =,∴1AA BO ⊥,……3分 O CO BO = ,⊥∴1AA 平面BOC ,⊂BC 平面BOC ,BC AA ⊥∴1.……5分(Ⅱ)由(Ⅰ)1AA CO ⊥,又侧面⊥C C AA 11侧面11A A B B,侧面 C C AA 11侧面11A A B B =1AA ⊥∴CO 平面11A ABB ,而1AA BO ⊥,∴OA ,OB ,OC 两两垂直.如图,以O 为坐标原点,分别以OA ,OB ,OC 为x ,y ,z 轴建立空间直角坐标系O -xyz . 则有)0,1,2(),3,0,0(),0,1,0(),0,0,1(),0,0,1(),0,0,0(11--B C B A A O ,……7分设),,(1111z y x =n 是平面ABC 的一个法向量, ),,(2222z y x =n 是平面BC A 1的一个法向量,)3,1,0(),3,0,1(-=-=CB CA ,由⎪⎩⎪⎨⎧=⋅=⋅,0,011CB CA n n 即⎩⎨⎧=-=-,03,031111z y z x 解得⎩⎨⎧==,3,31111z y z x令11=z ,∴)1,3,3(1=n .又)3,0,1(),0,1,1(11==C A B A ,由⎪⎩⎪⎨⎧=⋅=⋅,0,01212C A B A n n 即⎩⎨⎧=+=+,03,02222z x y x 解得⎩⎨⎧=-=,3,32222z y z x令12-=z ,∴)1,3,3(2--=n .……10分设二面角1A BC A --为θ,则71|cos |2121=⋅⋅=n n n n θ, 高三数学(理)第四次质检试卷答案 第2页 共4页所以二面角1A BC A --的正弦值是734. ……12分20、解:(Ⅰ)设椭圆方程为)0(12222>>=+b a by a x ,则24232||||221=+=+=MF MF a ,所以22=a ,又因为2=c ,所以4222=-=c a b ,所以椭圆G 的方程为14822=+y x . ……5分 (Ⅱ)由⎪⎩⎪⎨⎧+==+,2,14822ty x y x 得044)2(22=-++ty y t ,032322>+=∆t 恒成立. 设),(11y x A ,),(22y x B ,则24221+-=+t t y y ,24221+-=t y y .△AB F 1的面积等于⋅≤+++⋅=++⋅=-+=-⋅⋅=∆2411112821284)(2||221222221221211t t t t y y y y y y c S AB F当且仅当11122+=+t t ,即0=t 时,等号成立,所以当0=t时,△AB F 1的面积的最大值等于24.……12分21、解:(Ⅰ))e (2)(a x x f x+-='.因为函数)(x f y =的图象在0=x 处的切线与x 轴平行,所以0)1(2)0(=+='a f , 解得1-=a ,经检验1-=a 符合题意.……5分 (Ⅱ)当0≥x 时,0)(≥x f 恒成立,等价于0)(min ≥x f .首先,必须0)0(≥f ,即0322≥+-a ,解得55≤≤-a .以下只研究]5,5[-∈a 的情况.)e (2)(a x x f x +-=',设)e (2)(a x x g x +-=,则当0≥x 时,0)1e (2)(≥-='x x g ,所以)e (2)(a x x g x +-=在),0[+∞内单调递增,且)1(2)0(a g +=.①当0)1(2≥+a ,即1-≥a 时,0)0()()(≥≥='g x g x f ,所以)(x f 在),0[+∞内单调递增,0)0()(≥≥f x f ,所以当51≤≤-a 时,在),0[+∞内单调递增.②当0)1(2<+a ,即1-<a 时,由)e (2)(a x x g x +-=在),0[+∞内单调递增,知存在唯一),0[0+∞∈x 使得0)(0=x g ,即a x x -=00e ,且当∈x ),0(0x 时,0)()(<='x g x f ,)(x f 在),0(0x 上单调递减, 当∈x ),(0+∞x 时,0)()(>='x g x f ,)(x f 在),(0+∞x 上单调递增,所以)(x f 的最小值为3)(e 2)(2000+--=a x x f x ,又a x x -=00e,所以3)e (e 2)(2000+-=x x x f )3e )(1e (00-+-=x x ,因此,要使当0≥x 时,0)(≥x f 恒成立,只需0)(0≥x f ,即03e 0≤-x 即可.解得3ln 00≤<x ,此时由a x x -=00e ,可得0e 0x x a -=.以下求出a 的取值范围.x x x h e )(-=,]3ln ,0(∈x , 得0e 1)(<-='x x h ,所以)(x h 在]3ln ,0(上单调递减,从而133ln -<≤-a高三数学(理)第四次质检试卷答案 第3页 共4页综上①②所述,a 的取值范围]5,33[ln-.……12分22、解:(Ⅰ)因为CF 与圆O 相切,所以DBC DCE ∠=∠,又BC DE //,所以DCB CDE ∠=∠,所以BCD CDE ∆∆~,可得DC DE BC DC =,所以BC DE DC ⋅=2, 又DC AB =,所以BC DE AB ⋅=2……………………………………5分(Ⅱ)DBC DCE ∠=∠,BFC ∠是公共角,所以BCF CDF ∆∆~,所以69===CD BC FC FB DF FC ,所以FD FC 326+=, 又FB FD FC ⋅=2)9(+⋅=FD FD ,所以554=FC .………………10分23、解:(Ⅰ)直线l 的极坐标方程可化为22sin 22cos 22=+θρθρ, 所以直线l 的直角坐标方程为04=-+y x . ……………5分 (Ⅱ)设点)sin ,cos 2(ααP ,则点P 到直线l 的距离为 24)sin(524sin cos 2-+=-+=ϕαααd (其中=ϕtan 2), 所以当1)sin(-=+ϕα时,点P 到直线l 的距离的最大值为22410+.…………………10分24、解:(Ⅰ)因为m >0,所以m mm x m x m x m x x f +=+--≥++-=4|)()4(|4)(,又因为4424=⋅≥+m m m m ,当且仅当2=m 时等号成立,所以4)(≥x f .………………………………………………5分(Ⅱ)|2||42|)2(m m f ++-=,当24<m ,即2>m 时,44)2(+-=m m f ,由5)2(>f ,解得2171+>m .当24≥m ,即20≤<m 时,m m f +=4)2(,由5)2(>f ,解得10<<m .综上,m 的取值范围是),2171()1,0(+∞+ .…………………………10分。
福建省福州市第八中学高三第四次质检——数学(理)(1)数学(理)
福建省福州市第八中学2015届高三第四次质检考试数学(理)试题考试时间:120分钟试卷满分:150分本试卷分第I卷(选择题)和第II卷(非选择题),第II卷第21题为选考题,其他题为必考题.本试卷满分150分.考试时间120分钟.参考公式:样本数据x1,x2,…,x n的标准差其中为样本平均数锥体体积公式V=Sh 其中S为底面面积,h为高柱体体积公式V=Sh其中S为底面面积,h为高球的表面积、体积公式,其中R为球的半径第Ⅰ卷(选择题共50分)一、选择题(本大题共10小题,每小题5分,共50分,在每个小题给出的四个选项中,只有一项是符合题目要求的.把正确选项涂在答题卡的相应位置上.)1.已知,,则()A.B.C.D.2.双曲线22221(0,0)x ya ba b-=>>的渐近线方程为,则此双曲线的离心率为()A.B.C.D.3.已知命题:≤0,则( )A.是假命题;:≤0B.是假命题;:>0C.是真命题;:≤0D.是真命题;:>04.设,下面四个不等式中,正确的是()①;②;③;④A.①和②B.①和③C.①和④D.②和④5. 已知为常数,则使得成立的一个充分而不必要条件是()A.B.C.D.6.已知点、、不在同一条直线上,点为该平面上一点,且,则( ) A.点P在线段AB上B.点P在线段AB的反向延长线上C.点P在线段AB的延长线上D.点P不在直线AB上7. 已知是圆:内一点,现有以为中点的弦所在直线和直线:,则()A.,且与圆相交B.,且与圆相交C.,且与圆相离D.,且与圆相离8.若平面区域220,20,(1)x y y y k x -+≥⎧⎪Ω-≤⎨⎪≥+⎩:的面积为3,则实数的值为 ( ) A. B . C . D .9. 已知函数),1(2)()(xf x f x f =满足当时,若在区间内,函数,有三个不同的零点,则实数的取值范围是( )A. B. C. D.10.已知抛物线,圆2222:()C x y p p +-=,直线,其中,直线与的四个交点按横坐标从小到大依次为,则的值为( )A .B .C .D .第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡相应位置.11. 已知两条直线1:(2)453++=-l m x y m ,互相垂直,则=_________.12. 已知则_________.13. 等差数列的前n 项和为, , ,当取最小值时, 等__________.14.若函数1,0,()(021,0xx a x f x a b x ⎧⎛⎫-≥⎪ ⎪=>⎨⎝⎭⎪-<⎩且2a ≠,0b >且1)b ≠的图象关于y 轴对称,则b a 8+的最小值为__________.15.设是已知平面上所有向量的集合,对于映射,记的象为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省福州八中2008—2009学年度高三第四次质量检查数学(文科)考试时间:120分钟 试卷满分:150分一、选择题(本大题共12小题,每小题5分共60分) 1.设全集I 是实数集R, 3{|2}{|0}1x M x x N x x -=>=≤-与都是I 的子集(如图所示), 则阴影部分所表示的集合为( )A .{}2x x <B .{}21x x -≤<C . {}12x x <≤D . {}22x x -≤≤2.已知全集U=R ,集合A={}2x y y =,集合B={}x y y 2=,则B C A U 为 ( )A .ΦB .RC . {}0D .[)+∞,0 3.已知命题:p x ∀∈R ,sin 1x ≤,则( )A . 1sin ,:≥∈∀⌝x R x pB .1sin ,:≥∈∃⌝x R x pC . 1sin ,:>∈∀⌝x R x pD .1sin ,:>∈∃⌝x R x p4.不等式02>+-c x ax 的解集为}12|{<<-x x ,则函数c x ax y ++=2的图象大致为( )AB C D 5.已知=⎪⎭⎫⎝⎛∈=+θππθθθtan ,,2,51cos sin 则( )A .43B .34C . -43D . -345.圆()()对称的圆方程是关于05213122=++=-+-y x y x ( )A .()()11722=+++y xB .()()12722=+++y xC .()()11622=+++y xD .()()12622=+++y x6.圆022222=+--+R Ry Rx y x 在直角坐标系中的位置特征是 ( ) A . 圆心在直线y=x 上 B .圆心在直线y=x 上, 且与两坐标轴均相切 C . 圆心在直线y=-x 上 D .圆心在直线y=-x 上, 且与两坐标轴均相切 7.下列叙述正确的是 ( ) A .函数)10(≠>=a a a y x ,且的值域为实数集R B .向量)1,1(=a ,则其模长为2C .数列{}{}n n n n a a a a 则满足,21=+一定为等比数列D .函数x x y 22cossin-=的最小正周期是π8.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为 ( )A .12π B .2C .4D .4π9.椭圆13422=+yx的右焦点到直线x y 3=的距离是 ( )A .21 B .23 C .1 D .310.数列{}()()=⊥+===+10011,,1,,,,1a b a n a b a n a a a n n n 则且的 ( )A .—100B .100C .99100 D .—9910011.已知椭圆的中心在坐标原点,焦点在x 轴上,且长轴长为12,离心率为31,则椭圆的方程是( )A .1442x+1282y=1 B .362x+202y=1 C .322x+362y=1 D .362x+322y=112.某文具店出售羽毛球拍和羽毛球,球拍每副定价20元,羽毛球每只定价5元,该店制定了两种优惠方法:①买一副球拍赠送一只羽毛球;②按总价的92%付款。
现某人计划购买4副球拍和30只羽毛球,两种方法中,更省钱的一种是 ( ) A .不能确定 B .①②同样省钱 C .②省钱 D .①省钱二、填空题(本大题共4小题,每小题4分共16分)13.b a ,的夹角为120,____________5,31=-==a 则14.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,,底面周长为3,则这个球的体积为 .15.若过点(3,0)的直线l 和圆C: 22(1)1x y -+=相切,则直线l 的斜率为_______.16.如图是)(x f y =的导数的图像,则正确的判断是(1))(x f 在)1,3(-上是增函数 (2)1-=x 是)(x f 的极小值点(3))(x f 在)4,2(上是减函数,在)2,1(-上是增函数 (4)2=x 是)(x f 的极小值点以上正确的序号为三、解答题(共六大题74分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)已知函数212cos2cos2sin )(2-+=x x x x f .(Ⅰ)若()的值求απαα,,0,42)(∈=f ;(Ⅱ)求函数)(x f 在⎥⎦⎤⎢⎣⎡-ππ,4上最大值和最小值.18.(本小题满分12分)已知平面向量a (1,)x =,b(23,)x x =+-()x R ∈.(Ⅰ)若a ⊥b,求x 的值; (Ⅱ)若a ∥b ,求|a -b|.19.(本小题满分12分)如图,已知矩形ABCD 中,AB=10,BC=6,将矩形沿对角线BD 把△ABD 折起,使A 移到1A 点,且1A 在平面BCD 上的射影O 恰好在CD上.(Ⅰ)求证:1BC A D ⊥;(Ⅱ)求证:平面1A BC ⊥平面1A BD ; (Ⅲ)求三棱锥1A BC D -的体积.20.(本小题满分12分)设函数3()f x ax bx c =++(0)a ≠为奇函数,其图象在x=1处的切线与直线670x y --=垂直,导函数'()f x 的最小值为12-. (I )求的值c b a ,,;(II )求函数()f x 的单调递增区间,并求函数()f x 在[1,3]-上的最大值和最小值. 21.(本小题满分12分){}()222,2,11≥+==-n a a a a n n n n 数列 (I )求数列{}n n a a 的通项公式; (II )求数列{}n n S n a 项和的前;(III ){}为递减数列求证数列若n nn b a n b ,12-=。
22.(本小题满分14分)已知椭圆中心在原点,焦点在x 轴上,一个顶点为A (0,-1),且其右焦点到直线x -y +22=0的距离为3.(I )求椭圆的方程;(II )是否存在斜率为k (k ≠0)的直线l ,使l 与已知椭圆交于不同的两点M 、N ,且|AN |=|AM |?若存在,求出k 的取值范围;若不存在,请说明理由.OA 1CBAD参考答案一、选择题:(本大题共12小题,每小题5分共60分) CDCCA BDABA DD 二、填空题:(本大题共4小题,每小题4分共16分) 13.7 14.43π 15.33±16.(2)(3)三、解答题:(共六大题74分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)解:(I )212cos 1sin 21)(-++=xx x f )cos (sin 21x x +=)4sin(22π+=x …2分由题意知 42)4sin(22)(=+=πααf ,即 21)4sin(=+πα …………3分∵),0(πα∈ 即 )45,4(4πππα∈+ ∴127654παππα=⇒=+…………6分 (II )∵ παπ≤≤-4即 4540ππα≤+≤ …………8分∴22)4()(max ==πf x f ,21)()(m i n-==πf x f …………12分18.(本小题满分12分)解:(Ⅰ)若a ⊥b ,则a ·b(1,)x =·(23,)x x +-1(23)()0x x x =⨯++-=.整理得2230x x --=,解得:1x =-或3x =.………………………4分(Ⅱ)若a ∥b,则有1()(23)0x x x ⨯--+=,即 (24)0x x +=.解得:0x =或2x =-.………………………………………………8分当0x =时,a (1,0)=,b(3,0)=;∴|a -b|=|(1,0)(3,0)-|=|(2,0)-|2==.………………10分当2x =-时,a (1,2)=-,b(1,2)=-;∴|a -b|=|(1,2)-(1,2)--|=|(2,4)-|==. ……12分19.(本小题满分12分)证明:(Ⅰ)∵ 1A 在平面BC D 上的射影O 在C D 上,∴ 1A O ⊥平面BC D ,又B C ⊂平面BC D ∴ 1BC A O ⊥……2分 又,,1O CO O A CO BC =⊥∴ B C ⊥平面1A C D ,又11A D A C D ⊂平面,∴ 1B C A D ⊥ …4分 (Ⅱ)∵ A B C D 为矩形 ,∴ 11A D A B ⊥由(Ⅰ)知B BC B A BC D A =⊥ 11,∴ 1A D ⊥平面1A BC ,又1A D ⊂平面1A B D ∴ 平面1A BC ⊥平面1A B D ……8分 (Ⅲ)∵ 1A D ⊥平面 1A BC ,∴ 11A D A C ⊥.…10分 ∵ 16,10A D C D ==, ∴ 18A C =, ∴ 1111(68)64832A B C D D A B C V V --==⋅⋅⋅⋅=. …12分20.(本小题满分12分)解: (Ⅰ)∵()f x 为奇函数,∴()()f x f x -=- 即33ax bx c ax bx c --+=---∴0c = …………1分 ∵2'()3f x ax b =+的最小值为12-,.12,0-=>∴b a …………3分又直线670x y --=的斜率为16因此,'(1)36f a b =+=- …………5分 ∴2a =,12b =-,0c =. …………6分 (Ⅱ)3()212f x x x =-.OA 1CBA D2'()6126(f x x x x =-=+-,列表如下:所以函数()f x 的单调增区间是(,-∞和)+∞. …………9分∵(1)10f -=,f =-(3)18f =∴()f x 在[1,3]-上的最大值是(3)18f =,最小值是f =-……12分21.(本小题满分12分)解:(I)∵()2221≥+=-n a a n n n分公差首项为为等差数列分31,1222122122211111 ==⎭⎬⎫⎩⎨⎧∴=-⇒+=∴---d a ,a a a a a nnn n nn nn nn因此,nn nn n a n ,n a 21)1(12⨯=∴=⨯-+=……4分(II )()()()()分分分两式相减得分82212227221212622222522122212221232221111113211321321+⨯-=⨯+-=∴⨯---=⨯-++++=-⨯+⨯-++⨯+⨯=⨯+⨯-++⨯+⨯+⨯=∴++++++-n n n n n nn n n n nn nn n n n S n n S :n n S n n S (III)021212>⋅-=-=nnn n n a n b∴112)1(12++⋅++=n n n n b ∴)12(222)1()12()12(221-++=⋅+⋅-⋅+=+n n n n n n n n b b nn …10分()()(){}分为递减数列即时当又12,102122,022,122212211222222n n n nn b b b b b n n n n n n n n n n n n n ∴<<∴>+>-+∴>-+≥-+=+--+++222222:(本小题满分14分)(I )解:由题意,设椭圆方程为:1222=+y ax (a >1), 则右焦点为F (12-a ,0),由已知32|2201|2=+--a ,解得:a =3∴椭圆方程为:1322=+yx…………5分(II )解:设存在满足条件的直线l ,其方程为y =kx +b (k ≠0)由 ⎪⎩⎪⎨⎧=++=1322y x bkx y 得:0336)13(222=-+++b bkx x k ① …………7分 设M (x 1,y 1)、N (x 2,y 2)是方程①的两根,则0121236)33)(13(1236222222>+-=-+-=∆b k b k b k ② …………9分由韦达定理得:136221+-=+k bk x x从而MN 的中点P 的坐标为(13,13322++-k b k bk) ……10分∵|AM |=|AN | ∴AP 是线段MN 的垂直平分线 ∴AP ⊥MN于是 ()1321,10133)1(132222+=-=-+---+k b k k bkkb, ………12分 代入②并整理得:(3k 2+1)(k 2-1)<0,∴-1<k <1故满足条件的直线l 存在,其斜率k 的范围为-1<k <1且k ≠0. ………14分。
