(九年级数学)锐角三角函数(五)应用举例(2)_
新人教版九年级数学下册《锐角三角函数应用举例——坡度问题》教学设计

教学难点
利用坡度和坡角等条件,解决有关的实际问题。对于坡度 i 表示成 1∶m 的形 式学生易疏忽,教学中应着重强调,引起学生的重视。 一.引入 山坡陡峭程度、梯子倾斜度描述。 二、新授。
教学过程
1.坡度的概念,坡度与坡角的关系。
(1) h :铅垂高度。 (2) l :水平长度。
(3)坡角 :坡面与水平面的夹角。
(4)坡度(坡比):坡面的铅垂高度 h 和水平长度 l 的比。 记作: i ,即: i h tan
l
注意:
i h 1 1 tan llm h
显然,坡度 i 越大,坡角 就越大,坡面就越陡。
练习:
1、如图是一个拦水大坝的横断图,AD∥BC.,
(1)如果斜坡 AB=10m,大坝高为 8m,则 斜坡 AB 的坡度为________
锐角三角函数应用举例
——坡度问题教学设计
知识与技能:巩固用三角函数有关知识解决问题,学会解决坡度问题。 过程与方法:掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与 教学目标 坡度有关的实际问题。 情感、态度与价值观:培养学生用数学的意识,渗透数形结合的数学思想和 方法。
教学重点 理解坡度和坡角的概念。
练习提高 下图是一座人行天桥的示意图,其高是 8m,原 坡面的倾斜角为 45°现在要降低坡度,使新坡 面的倾斜角为 30°,若新坡角前需留 3m 的人行 道,问原距底 A 点 10 m 的建筑物是否需要拆除? 请说明理由. 课堂小结 学习了本堂课,回答下列问题: 1.有哪些量可以反映斜坡的陡峭程度?如何反映? 2.坡度是角度吗?坡度指的是什么? 3.坡度与坡角有什么关系? 课后作业 1.课本 77 页练习 2 2.课本 79 页第 9 题
的高度为 米.
第7章 锐角三角函数(小结与思考)(单元复习课件)九年级数学下册课件(苏科版)

° − ° ==_________________.
° − °
6.已知tanα=1.237,cosβ=0.9205,sinγ=0.6436(α,β,γ均为锐角),则
α,β,γ的大小顺序为__________.(提示:利用函数值的大小与特殊角的
β<γ<α
函数值的大小关系比较)
边、角之间的关系:sinA= ,cosA= ,tanA=
解直角三角形
已知一锐角、一边:一锐角、一直角边或一斜边
基本类型
已知两边:一直角边,一斜边或者两条直角边
与仰角、俯角有关的实际问题
简单应用
与方向角有关的实际问题
与坡角有关的实际问题
与生活有关的其他实际问题
知识回顾
特殊角的锐角三角函数值:
cosA=sinB=sin(90°-∠A)
tanA ·tanB =1
解直角三角形
知识框架
定义
由直角三角形的边、角中的已知元素,求出所有边、角中的
未知元素的过程,叫做解直角三角形.
三边之间的关系:a2+b2=c2 (勾股定理)
第7章 锐角
三角函数
依据
锐角之间的关系: ∠A+ ∠B=90°(直角三角形的两个锐角互余)
A. 40°
B. 30°
C. 20°
D. 10°
巩固练习
3. (2023·山东)计算:| − | + ° − =
4. 已知2cosθ=1,则θ=
60 °.
60
5. 已知α是锐角,tanα=2cos30°,则α=______°.
1 .
巩固练习
6.如图,在△ABC中,∠C=90°,点D在AC上,已知∠BDC=45°,
九年级(下)数学教案:锐角三角函数的简单应用(全3课时)
主备人用案人授课时间年月日总第课时课题7.6锐角三角函数的简单应用(1)课型新授教学目标1.进一步掌握解直角三角形的方法,比较熟练的应用解直角三角形的知识解决与仰角、2.俯角有关的实际问题,培养学生把实际问题转化为数学问题的能力。
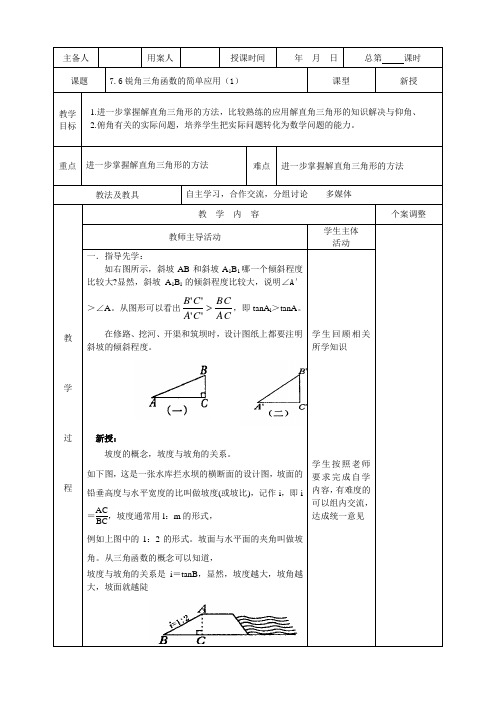
重点进一步掌握解直角三角形的方法难点进一步掌握解直角三角形的方法教法及教具自主学习,合作交流,分组讨论多媒体教学过程教学内容个案调整教师主导活动学生主体活动一.指导先学:如右图所示,斜坡AB和斜坡A1B1哪一个倾斜程度比较大?显然,斜坡A1B l的倾斜程度比较大,说明∠A′>∠A。
从图形可以看出ACBCCACB'''',即tanA l>tanA。
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度。
新授:坡度的概念,坡度与坡角的关系。
如下图,这是一张水库拦水坝的横断面的设计图,坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,例如上图中的1:2的形式。
坡面与水平面的夹角叫做坡角。
从三角函数的概念可以知道,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡学生回顾相关所学知识学生按照老师要求完成自学内容,有难度的可以组内交流,达成统一意见教学过程教学内容个案调整教师主导活动学生主体活动四.检测巩固:如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角。
和坝底宽AD。
(i=CE:ED,单位米,结果保留根号)2.如图,单摆的摆长AB为90cm,当它摆动到∠BAB'的位置时,∠BAB'=30°。
问这时摆球B'较最低点B升高了多少?五.小结反思:通过本节课的学习,你有何收获?你还存在什么疑惑?学生独立完成,有难度的可以组内交流,教师巡视,指导学生分组讨论交流,总结归纳,教师补充板书设计7.6锐角三角函数的简单应用(1)坡度的概念,坡度与坡角的关系。
坡面的铅垂高度与水平宽度的比叫做坡度(或坡比),记作i,即i=ACBC,坡度通常用l:m的形式,坡度与坡角的关系是i=tanB,显然,坡度越大,坡角越大,坡面就越陡布置作业补充习题教学札记教学过程教学内容个案调整教师主导活动学生主体活动1、摩天轮启动多长时间后,小明离地面的高度将首次到达10m?2、小明将有多长时间连续保持在离地面20m以上的空中?三.释疑拓展:如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离(精确到l米)。
第二十八章 锐角三角函数(单元总结)-2021学年九年级数学下册(人教版)(解析版)
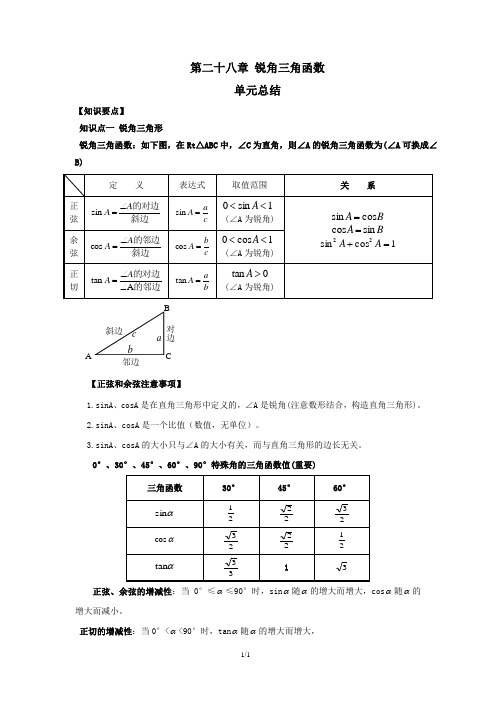
第二十八章 锐角三角函数单元总结【知识要点】 知识点一 锐角三角形锐角三角函数:如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)【正弦和余弦注意事项】1.sinA 、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA 、cosA 是一个比值(数值,无单位)。
3.sinA 、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,对边邻边C知识点二 解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形. 直角三角形五元素之间的关系: 1. 勾股定理()2. ∠A+∠B=90°3. sin A==4. cos A= =5.tan A= =【考查题型】考查题型一 正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为( )A .43B .34C .35D .45【答案】D 【分析】过C 作CD AB ⊥于D ,首先根据勾股定理求出AC ,然后在Rt ACD ∆中即可求出sin BAC ∠的值.【详解】如图,过C 作CD AB ⊥于D ,则=90ADC ∠︒,∴AC =222234=+=+AC AD CD =5. ∴4sin 5CD BAC AC ∠==. 故选D . 【点睛】本题考查了勾股定理的运用以及锐角三角函数,正确作出辅助线是解题的关键.变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C =∠,10AB =,8AC =,则sin A 等于( )A .35B .45C .34D .43【答案】A 【解析】分析:先根据勾股定理求得BC=6,再由正弦函数的定义求解可得. 详解:在Rt △ABC 中,∵AB=10、AC=8, ∴2222=108=6AB AC --,∴sinA=63105BC AB ==. 故选:A .点睛:本题主要考查锐角三角函数的定义,解题的关键是掌握勾股定理及正弦函数的定义.变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt△ABC中,∠C=90°,sin A=45,AC=6cm,则BC的长度为()A.6cm B.7cm C.8cm D.9cm 【答案】C【详解】已知sinA=45BCAB=,设BC=4x,AB=5x,又因AC2+BC2=AB2,即62+(4x)2=(5x)2,解得:x=2或x=﹣2(舍),所以BC=4x=8cm,故答案选C.考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC等于()A 5B25C5D.23【答案】B【详解】由格点可得∠ABC所在的直角三角形的两条直角边为2,4,222425+=∴cos∠25525=.故选B .变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠=,AB 6=,1cosA 3=,则AC 等于( ) A .18 B .2C .12D .118【答案】B 【分析】根据三角函数的定义,在直角三角形ABC 中,cosA =ACAB,即可求得AC 的长. 【详解】解:∵在△ABC 中,∠C =90°,∴cosA =ACAB , ∵cosA =13,AB =6,∴AC =123AB =,故答案选:B . 【点睛】本题考查了解直角三角形中三角函数的应用,解题的关键是要熟练掌握直角三角形中边角之间的关系.变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M (5,2),那么cosα的值是( )A 5B .23C 25D 5【答案】D 【分析】如图,作MH⊥x轴于H.利用勾股定理求出OM,即可解决问题.【详解】解:如图,作MH⊥x轴于H.∵M(5,2),∴OH=5,MH=2,∴OM=22(5)2+=3,∴cosα=5 OHOM=,故选:D.【点睛】本题考查解直角三角形的应用,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为()A.12B.1 C3D3【答案】B【分析】连接BC,由网格求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可求出所求. 【详解】 如图,连接BC ,由网格可得AB=BC=5,AC=10,即AB 2+BC 2=AC 2, ∴△ABC 为等腰直角三角形, ∴∠BAC=45°, 则tan ∠BAC=1, 故选B .【点睛】本题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为( ).A .2B .3C .2D .1【答案】A 【解析】分析:本题考查等腰直角三角形的性质及解直角三角形.解题的关键是作辅助线,构造直角三角形,运用三角函数的定义建立关系式然后求解. 解析:如图,作DE ⊥AB 于E .∵tan ∠DBA==,∴BE=5DE .∵△ABC 为等腰直角三角形,∴∠A=45°,∴AE=DE .∴BE=5AE ,又∵AC=6,∴AB=6,∴AE+BE=AE+5AE=6,∴AE=,∴在等腰直角△ADE中,由勾股定理,得AD=,AE=2.故选A.变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡的倾斜角是∠BAC,若2tan5BAC∠=,则此斜坡的水平距离AC为()A.75m B.50m C.30m D.12m 【答案】A【分析】根据BC的长度和tan BAC∠的值计算出AC的长度即可解答.【详解】解:因为2tan5BCBACAC=∠=,又BC=30,所以,3025AC=,解得:AC=75m,所以,故选A.【点睛】本题考查了正切三角函数,熟练掌握是解题的关键.考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A.(32,12) B.(-32,-12)C.(312) D.(-123【答案】B 【详解】∵点(-sin60°,cos60°)即为点(312),∴点(-sin60°,cos60°)关于y 3,12).变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A.cos40°=sin50°B.tan15°•tan75°=1C.sin225°+cos225°=1 D.sin60°=2sin30°【答案】D【详解】试题分析:选项A,sin40°=sin(90°﹣50°)=cos50°,式子正确;选项Btan15°•tan75°=tan15°•cot15°=1,式子正确;选项C,sin225°+cos225°=1正确;选项D,sin60°=3,sin30°=12,则sin60°=2sin30°错误.故答案选D.变式4-2.(2018·河北唐山市·九年级期末)如果△ABC中,sin A=cos B=22,则下列最确切的结论是()A.△ABC是直角三角形B.△ABC是等腰三角形C.△ABC是等腰直角三角形D.△ABC是锐角三角形【答案】C【解析】因为sin A=cos B 2,所以∠A=∠B=45°,所以△ABC是等腰直角三角形. 故选C.考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt△ABC中,∠C =90°,sinA=45,则cosB的值等于( )A.35B.45C.34D5【答案】B 【解析】在Rt△ABC中,∠C=90°,∠A+∠B=90°,则cos B=sin A=45.故选B.点睛:本题考查了互余两角三角函数的关系.在直角三角形中,互为余角的两角的互余函数变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA= 12,那么sinA 的值是( )A .2B .2C .3D .12【答案】B 【分析】利用同角三角函数间的基本关系求出sinA 的值即可. 【详解】:∵Rt △ABC 中,cosA=12 ,∴ =2, 故选B . 【点睛】本题考查了同角三角函数的关系,以及特殊角的三角函数值,熟练掌握同角三角函数的关系是解题的关键.变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠=,如果4cosA 5=,那么tanA 的值是( ) A .35B .53C .34D .43【答案】C 【分析】本题可以利用锐角三角函数的定义求解. 【详解】解:∵在Rt △ABC 中,∠C=90°,∴cosA=b c ,tanA=ab ,a 2+b 2=c 2. ∵cosA=45,设b=4x ,则c=5x ,a=3x .∴tanA=a b =3344x x =. 故选C.【点睛】利用锐角三角函数的定义,通过设参数的方法求三角函数值.考查题型六 解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为( )A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα【答案】B【分析】在两个直角三角形中,分别求出AB 、AD 即可解决问题;【详解】在Rt △ABC 中,AB=AC sin α, 在Rt △ACD 中,AD=AC sin β, ∴AB :AD=AC sin α:AC sin β=sin sin βα, 故选B .【点睛】 本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题. 变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为( )A .10B .15C .6D .10 【答案】D【分析】过点A 作AD BC ⊥,垂足为D ,在Rt ACD ∆中可求出AD ,CD 的长,在Rt ABD ∆中,利用勾股定理可求出AB 的长,再利用正弦的定义可求出sinB 的值.【详解】解:过点A 作AD BC ⊥,垂足为D ,如图所示.在Rt ACD ∆中,1CD CA cosC ⋅==,2215AD AD CD ∴=-=;在Rt ABD ∆中,315BD CB CD AD =﹣=,=,22BD AD 26AB ∴=+=,AD 10sin AB B ∴==. 故选:D .【点睛】考查了解直角三角形以及勾股定理,通过解直角三角形及勾股定理,求出AD ,AB 的长是解题的关键.变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为( )A.11米B.(36﹣153)米C.153米D.(36﹣103)米【答案】D【分析】分析题意可得:过点A作AE⊥BD,交BD于点E;可构造Rt△ABE,利用已知条件可求BE;而乙楼高AC=ED=BD﹣BE.【详解】解:过点A作AE⊥BD,交BD于点E,在Rt△ABE中,AE=30米,∠BAE=30°,∴BE=30×tan30°=103(米),∴AC=ED=BD﹣BE=(36﹣103)(米).∴甲楼高为(36﹣103)米.故选D.【点睛】此题主要考查三角函数的应用,解题的关键是熟知特殊角的三角函数值.考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,2≈1.4)【答案】云梯需要继续上升的高度BC 约为9米.【分析】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,在Rt ABD ∆中,求得AD 的长;在Rt ACD ∆中,求得CD 的长,根据BC=CD-BD 即可求得BC 的长.【详解】过点A 作AM EF ⊥于点M ,AD BC ⊥于点D ,∵CN EF ⊥ ,∴90AMN MND ADN ∠=∠=∠=︒,∴四边形AMND 为矩形.∴ 2.5DN AM ==米.∴10.5 2.58BD BN DN =-=-=(米),由题意可知,45BAD ∠=︒,65CAD ∠=︒,∵AD BC ⊥,∴90ADB ∠=︒,在Rt ABD ∆中,tan BD BAD AD ∠=, ∴88tan tan45BD AD BAD ===∠︒(米). 在Rt ACD ∆中,tan CD CAD AD∠=, ∴tan 8tan658 2.116.8CD AD CAD =⋅∠=︒≈⨯=(米).∴16.888.89BC CD BD =-≈-=≈(米).答:云梯需要继续上升的高度BC 约为9米.【点睛】本题考查解直角三角形﹣仰角俯角问题,添加辅助线,构造直角三角形,建立直角三角形模型是解决问题的关键.变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC 的高度,从距离楼底C 处603米的点D (点D 与楼底C 在同一水平面上)出发,沿斜面坡度为i=1:3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).【答案】153+【分析】如图作BN ⊥CD 于N ,BM ⊥AC 于M ,先在RT △BDN 中求出线段BN ,在RT △ABM 中求出AM ,再证明四边形CMBN 是矩形,得CM=BN 即可解决问题.【详解】如图作BN ⊥CD 于N ,BM ⊥AC 于M .在RT △BDN 中,BD=30,BN :ND=13,∴BN=15,DN=153,∵∠C=∠CMB=∠CNB=90°,∴四边形CMBN是矩形,∴CM=BM=15,BM=CN=603153453-=,在RT△ABM中,tan∠ABM=43 AMBM=,∴AM=603,∴AC=AM+CM=15603+.【点睛】构造适当的直角三角形,并应用锐角的三角函数,正确理解坡比的概念.变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)【答案】高、低杠间的水平距离CH 的长为151cm .【解析】分析:利用锐角三角函数,在Rt △ACE 和Rt △DBF 中,分别求出AE 、BF 的长.计算出EF .通过矩形CEFH 得到CH 的长.详解:在Rt △ACE 中,∵tan ∠CAE=CE AE, ∴AE=()15515521tan tan82.47.5CE cm CAE =≈≈∠︒ 在Rt △DBF 中,∵tan ∠DBF=DF BF, ∴BF=()23423440tan tan80.3 5.85DF cm DBF =≈=∠︒. ∵EF=EA+AB+BF≈21+90+40=151(cm )∵CE ⊥EF ,CH ⊥DF ,DF ⊥EF∴四边形CEFH 是矩形,∴CH=EF=151(cm ).答:高、低杠间的水平距离CH 的长为151cm .点睛:本题考查了锐角三角函数解直角三角形.题目难度不大,注意精确度.。
初三锐角三角函数知识点总结、典型例题附带部分答案、练习(精选)
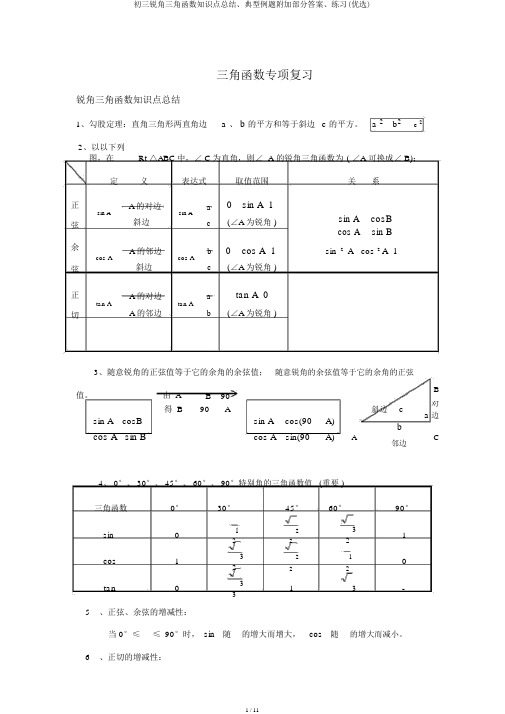
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边 a 、 b 的平方和等于斜边 c 的平方。
a 2 b 2c 22、以以下列图,在Rt △ABC 中,∠ C 为直角,则∠ A 的锐角三角函数为 ( ∠A 可换成∠ B):定 义 表达式取值范围关系正A 的对边 a 0 sin A 1sin A 斜边sin A(∠A 为锐角 )sin A cosB 弦ccos Asin B余A 的邻边 b 0 cos A 1sin 2 A cos 2 A 1cos A 斜边cos A(∠A 为锐角 )弦c正A 的对边atan A 0tan Atan A(∠A 为锐角 )切A 的邻边b3、随意锐角的正弦值等于它的余角的余弦值; 随意锐角的余弦值等于它的余角的正弦值。
由 A B 90 B得 B90A斜边c对a 边sin A cosBsin Acos(90A)bcos A sin Bcos A sin(90A)AC邻边4、 0°、 30°、 45°、 60°、 90°特别角的三角函数值 (重要 )三角函数0° 30°45°60°90°sin0 1 2 3 1 222cos13 2 1 02 22tan0 3 13-35 、正弦、余弦的增减性:当 0°≤≤ 90°时, sin 随 的增大而增大, cos 随的增大而减小。
6 、正切的增减性:当 0° < <90°时, tan随的增大而增大,7、解直角三角形的定义:已知边和角(两个,此中必有一边)→全部未知的边和角。
依照:①边的关系:a2b2c2;②角的关系:A+B=90°;③边角关系:三角函数的定义。
( 注意:尽量防范使用中间数据和除法)8、应用举例:(1)仰角:视野在水平线上方的角;俯角:视野在水平线下方的角。
锐角三角函数课件

余弦函数
1
定义和公式
余弦函数描述直角三角形中的比例关系,其定义和公式为cos(x) = 邻边/斜边。
2
图像和性质
余弦函数的图像呈现波浪形状,具有周期性、振幅和相位差等性质。
3
应用举例
余弦函数在几何、物理、工程等领域有广泛的应用,如研究周期性现象和计算机 图形学。
正切函数
定义和公式 图像和性质 应用举例
和差化积公式
三角函数的和差化积公式可 以将两个三角函数的和、差 表达为一个三角函数的乘积。
倍角公式
三角函数的倍角公式用于计 算两倍角的三角函数值。
总结
特点和应用
锐角三角函数具有周期性、对称性和广泛的 应用,为解决实际问题提供了重要的数学工 具。
实际生活中的应用举例
锐角三角函数在摄影、测量、物理仿真等实 际生活中有广泛的应用。
ห้องสมุดไป่ตู้
扩展和推广
锐角三角函数的研究和应用正在不断扩展和 推广,涉及到更多领域和复杂情况。
未来发展和研究方向
锐角三角函数的未来发展将涉及到更多领域 的交叉研究和深入探索。
正切函数用来描述直角三角形中的比例关系, 其定义和公式为tan(x) = 对边/邻边。
正切函数的图像呈现周期性、无界和渐近线等 特点,其图像在某些范围内会无限逼近无穷。
正切函数在物理、工程、电子等领域中常用于 信号处理和电路分析等方面。
三角函数的关系式
基本关系式
正弦、余弦和正切函数之间 有一系列关系式,如sin²θ + cos²θ = 1等。
特点
锐角三角函数的值域在特 定区间内,具有周期性和 对称性等特点。
正弦函数
定义和公式
正弦函数用来描述直角三角形 中的比例关系,其定义和公式 为sin(x) = 对边/斜边。
初三锐角三角函数教案(3篇)
课时安排:2课时教学目标:1. 知识与技能:(1)理解锐角三角函数的概念,掌握正弦、余弦、正切的基本定义。
(2)能运用锐角三角函数解决实际问题。
(3)熟练掌握30°、45°、60°角的正弦、余弦、正切值。
2. 过程与方法:(1)通过观察、比较、分析等活动,探究锐角三角函数的性质。
(2)通过小组合作,培养合作探究能力。
3. 情感态度与价值观:(1)激发学生对数学的兴趣,培养学生数学思维。
(2)培养学生严谨、求实的科学态度。
教学重点:1. 锐角三角函数的概念。
2. 30°、45°、60°角的正弦、余弦、正切值。
教学难点:1. 理解锐角三角函数的概念。
2. 运用锐角三角函数解决实际问题。
教学准备:1. 多媒体课件。
2. 练习题。
教学过程:一、导入1. 回顾直角三角形中锐角的概念。
2. 引入锐角三角函数的概念。
二、新课讲授1. 正弦、余弦、正切的概念:(1)正弦:锐角的对边与斜边的比值。
(2)余弦:锐角的邻边与斜边的比值。
(3)正切:锐角的对边与邻边的比值。
2. 30°、45°、60°角的正弦、余弦、正切值:(1)正弦:sin30°=1/2,sin45°=√2/2,sin60°=√3/2。
(2)余弦:cos30°=√3/2,cos45°=√2/2,cos60°=1/2。
(3)正切:tan30°=1/√3,tan45°=1,tan60°=√3。
三、课堂练习1. 填空题:(1)在直角三角形ABC中,∠C=90°,AB=5,BC=3,则sinA=________,cosA=________,tanA=________。
(2)在直角三角形ABC中,∠C=90°,AC=2,BC=√2,则sinB=________,cosB=________,tanB=________。
数学:28.1锐角三角函数(2)课件(人教新课标九年级下)
例题示范
3 例2 如图,在Rt△ABC中,∠C=90°,BC=6,sinA= 5 ,求 cosA、tanB的值.
B
解:∵
BC sin A AB
A
6
BC 5 AB 6 10 sin A 3
又
C
AC AB 2 BC 2 10 2 62 8
AC 4 AC 4 cos A , tan B AB 5 BC 3
2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余 弦值和正切值有什么变化? 解:设各边长分别为a、b、c,∠A的三个三角函数分别为
a b a sin A , cos A , tan A c c b
则扩大2倍后三边分别为2a、2b、2c
B
2a a sin A 2c c 2b b cos A 2c c 2a a tan A 2b b
2、sinA、 cosA、tanA是一个比值(数值)。
3、sinA、 cosA 、tanA的大小只与∠A的大小 有关,而与直角三角形的边长无关。
课后作业
课时作业本 P76—P83
独立完成作业的良好习惯,
是成长过程中的良师益友。
中考语录
中考是一场跳高比赛,取胜关 键在于你起跳时对大地用力多少!
结束寄语
试一试:
下图中∠ACB=90°,CD⊥AB,垂足为D。指出∠A和∠B 的对边、邻边。 B D (1) tanA =
(BC )
= CD (AD) AC
A
C
(2) tanB=
(AC )
BC
= CD ( BD)
试一试:
如图,在Rt△ABC中,锐角A的邻边和斜边同时 扩大100倍,tanA的值( C ) A.扩大100倍 B.缩小100倍 C.不变 D.不能确定
锐角三角函数应用举例
如图所示,直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E 在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是_____如图所示△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值、正切值。
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.(1)求点C的坐标;(2)若点D在反比例函数y=(k>0)的图象上,求反比例函数的解析式.13一副直角三角板如图放置,点C 在FD 的延长线上,AB ∥CF ,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD 的长。
4.盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224m 到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.(取1.73,结果精确到0.1m)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是450,然后:沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是600,求两海岛间的距离AB.如图,海中有一灯塔P,它的周围8海里内有暗礁.海伦以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。
九年义务教育 九年级(下册)数学 《锐角三角函数》--司马义.苏来曼
C B ACBCBA新课标人教版初中数学九年级下册第28章《锐角三角函数》新疆巴州库尔勒市和什力克乡中学 司马义.苏来曼第一课时 课题:第28章 锐角三角函数28.1锐角三角函数(1) ——正弦【学习目标】⑴: 经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
⑵: 能根据正弦概念正确进行计算 【学习重点】理解正弦(sinA )概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实. 【学习难点】当直角三角形的锐角固定时,,它的对边与斜边的比值是固定值的事实。
【导学过程】 一、自学提纲:1、如图在Rt △ABC 中,∠C=90°,∠A=30°,BC=10m ,•求AB2、如图在Rt △ABC 中,∠C=90°,∠A=30°,AB=20m ,•求BC二、合作交流:问题: 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,•在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m ,那么需要准备多长的水管?思考1:如果使出水口的高度为50m ,那么需要准备多长的水管? ; 如果使出水口的高度为a m ,那么需要准备多长的水管? ;结论:直角三角形中,30°角的对边与斜边的比值思考2:在Rt △ABC 中,∠C=90°,∠A=45°,∠A 对边与斜边的比值是一个定值吗?•斜边c对边abC B (2)1353CB A(1)34CB A如果是,是多少?结论:直角三角形中,45°角的对边与斜边的比值三、教师点拨:从上面这两个问题的结论中可知,•在一个Rt △ABC 中,∠C=90°,当∠A=30°时,∠A 的对边与斜边的比都等于12,是一个固定值;•当∠A=45°时,∠A 的对边与斜边的比也是一个固定值.这就引发我们产生这样一个疑问:当∠A 取其他一定度数的锐角时,•它的对边与斜边的比是否也是一个固定值?探究:任意画Rt △ABC 和Rt △A ′B ′C ′,使得∠C=∠C ′=90°, ∠A=∠A ′=a ,那么''''BC B C AB A B 与有什么关系.你能解释一下吗?结论:这就是说,在直角三角形中,当锐角A 的度数一定时,不管三角形的大小如何,•∠A 的对边与斜边的比 正弦函数概念:规定:在Rt △BC 中,∠C=90,∠A 的对边记作a ,∠B 的对边记作b ,∠C 的对边记作c .在Rt △BC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A 的正弦, 记作sinA ,即sinA= =a c . sinA =A aA c∠=∠的对边的斜边 例如,当∠A=30°时,我们有sinA=sin30°=;当∠A=45°时,我们有sinA=sin45°= . 四、学生展示:例1 如图,在Rt △ABC 中,∠C=90°,求sinA 和sinB 的值.随堂练习 (1): 做课本第79页练习.随堂练习 (2):1.三角形在正方形网格纸中的位置如图所示,则sin α的值是﹙ ﹚A .43 B .34 C .53 D .542.如图,在直角△ABC 中,∠C =90o,若AB =5,AC =4,则sinA =( )A .35B .45C .34D .433. 在△ABC 中,∠C=90°,BC=2,sinA=23,则边AC 的长是( )A .13B .3C .43D . 54.如图,已知点P 的坐标是(a ,b ),则sin α等于( )A .a bB .ba CD五、课堂小结:在直角三角形中,当锐角A 的度数一定时,不管三角形的大小如何,∠A •的对边与斜边的比都是 .在Rt △ABC 中,∠C=90°,我们把锐角A 的对边与斜边的比叫做∠A •的 ,•记作 ,六、作业设置:课本 第85页 习题28.1复习巩固第1题、第2题.(只做与正弦函数有关的部分)七、自我反思:本节课我的收获: 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(九年级数学)锐角三角函数(五)——应用举例(2)
第 周 星期 班别_______ 姓名_________ 学号_____
一、学习目标:
1.认识坡度、坡角的概念。
2.会解与梯形有关的实际问题。
二、新课学习
1、小知识:
(1)如图19.4.5,坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡
比).记作i,即i=lh. 坡度通常写成1∶m的形式,如i=1∶6.
(2)坡面与水平面的夹角叫做坡角,记作a,有i=lh=tan a
显然,坡度越大,坡角a就越 ,坡面就越 .
2、试一试
(1)如图,已知Rt△DCF中,DC=4,CF=2,则
斜坡CD的坡度i= .
(2)如图,斜坡AB的坡度i=1:2.5,水平宽度AC=20,
求:∠A和BC
解:
3、例题学习:
(1)某人沿坡角为30°的斜坡前进1000米,那么他在水平方向前进了多少米?在垂直方向升高了几米?我
们说这个斜坡的坡度i是多少?
解:依题意得:在Rt△ABC中,AB=_______, ∠A=_____
答:他在水平方向前进______米;在垂直方向升高了_____米;这个斜坡的坡度i是______
(2)一个小球由地面沿着i=1: 3的坡面向上前进了10米,此时,小球距离地面的高
度是多少?
解:
三、课堂练习
1、如图,一段路基的横断面是梯形,高为4.2米,上底的宽是12.51米,路基的坡面与地面的倾角分别是32°
和28°.求路基下底的宽.(精确到0.1米)
解:作DE⊥AB,CF⊥AB,垂足分别为E、F. 由题意可知:
DE=CF= , CD=EF= .
答: 路基下底的宽约为_________米.
2、如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角a和坝底宽AD.
(i=CE∶ED,单位米,结果保留根号)
解:
答:坡角a为 ,坝底宽为 米
3、水库大坝的横断面为梯形ABCD,坝顶宽6.2米,坝高23.5米,斜坡AB的坡度
i1=1∶3,斜坡CD的坡度i2=1∶2.5.求:
(1)斜坡AB与坝底AD的长度;(精确到0.1米)
(2)斜坡CD的坡角α.(精确到1°)
解:作BEAD,CFAD,垂足分别为E、F
4、 如图,一铁路路基的横断面为等腰梯形ABCD,根据图示数据计算路基下底宽AD(精确到0.1米)和坡角.
5、某路基横断面为等腰梯形,根据图示数据,求:下底BC;坡角;修筑长4千米的公路需要的立方数
