车桥耦合程序应用
车桥耦合程序

车桥耦合程序车桥耦合是现代车辆仿真技术中的重要部分,它是指汽车底盘参数和发动机参数之间的相互作用,也可以说是车辆运动学和动力学之间的耦合。
车桥耦合程序是通过计算机模拟车辆的运动和驱动系统的动力学行为,通过数值算法计算出车辆的运行状态和行驶性能的技术。
这种技术在汽车制造工业中具有重要意义,可以用来模拟车辆运动、提高车辆性能和优化设计。
汽车模型是道路机动车辆行驶过程的基础,而车桥耦合程序则是汽车模型的核心算法。
车桥耦合程序涉及到的方面非常广泛,包括车轮轨迹、车辆动力学、路面反力、转向控制、仿真时间和路面摩擦等。
车轮轨迹是车桥耦合程序的重要之一。
它是指在不同的路况条件下汽车车轮的运动轨迹,也是汽车运动学和动力学之间的关键。
车轮轨迹的计算可以被建模为一个动态方程,其中考虑了路面变形、车轮滑动、制动和反作用力等因素。
通过计算车轮轨迹,可以提高汽车的操控性能和安全性。
车辆动力学考虑了汽车在运动过程中所产生的力和动力学参数,包括车辆加速度、转向力和制动力等。
这些方程式对汽车运动进行了描述,其中包括汽车加速度、上坡和下坡行驶、加速过程中发动机转速变化等。
通过对汽车动力学的建模,可以对汽车的加速性能和制动性能进行预测和优化。
路面反力是汽车在行驶过程中产生的力。
这些力与路面的摩擦力、路面的侧面接触力和反射力等因素有关。
关于这些力学特征和其影响的研究,可以为汽车行驶性能的优化提供重要的参考。
转向控制是汽车行驶过程中的重要因素。
通过计算车轮的横向变位、角度变化和转向力等参数,可以精确描述车辆的操控性。
转向控制的建模涉及到运动学和动力学的多学科研究。
如果不掌握严谨的转向控制技术,容易导致车辆的失控和不稳定,影响驾驶者的安全。
仿真时间是车桥耦合程序的关键因素之一。
它与模拟器硬件和软件、仿真车辆的计算性能等多个因素相关。
为了提高仿真精度和有效性,需要通过多项技术手段来优化和改善仿真时间。
路面摩擦是汽车行驶过程中最为常见的路况条件之一。
MSC软件应用于铁路桥梁车桥耦合动力响应分析

第1 5卷 增刊
2 0 年 9月 06
文 章 编号 :0 60 7 f0 6S 一3 10 10 —8 12 0 ) l0 9 —4
计 算 机 辅 助 工 程
COM PUTER DED AI ENGI NEERn、 J G
Vo . 5 S p 1 1 u pl S p 2 0 e .0 6
图 5 MS d ms 的 车 桥 整体 模 型 CA a 中
分别以 20k g ~ 2 mh之间共 8 5 rh 4 0k / a 种车速进
行仿真计算 ,计算结果可以给出各种车速条件下动 车、 拖车的最大车体振动加速度 、舒适度 、 脱轨系
数 、横向轮轨力和轮重减载率.同时给出桥梁跨 中 截面的最大竖 、横 向动挠度及振动加速度等计算结 果 ,以下就车速 30 m h的工况分别说明. 0 / k
转向架和车体模型构造好 以后 ,就可以进行单
车装配 ,根据 实际的车辆定距进行单车装配. C 3 I E 列车为动力分散型 , 节车为一个动力单元 , 节为 4 8
一
个最小编组 ,单车模 型构造好以后 ,设置各节车
之问的连接 , 进行列车编组 . 节 的编组如图 1 8 所示.
IE 高速列车为例 ,应用 MS C3 C软件进行车桥耦合
m,高低不平顺幅值 7 9 m, 向不平顺幅值 5 . 5m 轨 . 5
22 轮轨模 型 .
车轮踏面采用 L M磨耗型踏面 , 钢轨为中国T 0 6
钢轨 ,轮轨问摩擦系数 O . . 3
3 桥 梁模 型的建立
应用 MS a a 按照京沪铁路客运专线 3 CP tn r 2m 简支梁桥的实际尺寸建立桥梁 的三维有限元模型, 墩高 2 墩身尺寸为 6 × 3 0m, . 8 . m、壁厚 0 3 .m 5 的矩形空心墩 ,墩梁 问支座采用主从约束方程来处 理; 单元采用 8结点 空 间等参单元 ; 考虑 到 MS C A a s的计算效率问题 ,该模型共建 5跨 ,总共 dm 7 9 个结点 , 8 个单元. 1 9 4 4 5 模型如图 2 所示.
公路车-桥耦合振动的理论和应用研究进展

公路车-桥耦合振动的理论和应用研究进展
公路车-桥耦合振动的理论和应用研究进展
作者:邓露;何维;俞扬;王维
作者机构:湖南大学风工程与桥梁工程湖南省重点实验室,湖南长沙410082;湖南大学土木工程学院,湖南长沙410082;湖南大学土木工程学院,湖南长沙410082;湖南大学土木工程学院,湖南长沙410082 来源:中国公路学报
ISSN:1001-7372
年:2018
卷:031
期:007
页码:38-54
页数:17
中图分类:U441.2
正文语种:chi
关键词:桥梁工程;公路桥梁;综述;车-桥耦合;冲击系数;振动控制;疲劳寿命;损伤识别;行车舒适性;桥梁动态称重;移动荷载识别摘要:为了推动公路车-桥耦合振动理论的发展和仿真技术的广泛应用,从公路车-桥耦合振动理论研究和应用研究2个方面系统性梳理了公路车-桥耦合振动相关领域的学术研究现况、既有研究成果、发展前景、存在的问题和对策.理论研究方面,系统总结了车-桥耦合振动研究中车-桥、桥梁、路面不平整度等参数的数学模型和车-桥耦合时变系统动力学方程的数值解法.基于调研和分析发现,经过国内外学者长期的努力,车-桥系统数值模型已经可以越来越真实地模拟实际车辆、桥梁以及路面不平整度等其他条件因素.在未来的研究中应持续改进有限元建模技术和优化数值算法,以进一步提高车-桥耦合振动仿真分析的精度和效率,扩展其应用范围.应用研究方面,以桥梁动力冲击系数、桥梁疲劳分析、桥梁结构损伤识别、桥梁振动控制、桥上行车舒适性以及桥上车辆荷载动态识别。
车桥耦合

1.车-桥耦合动力相互作用的研究现状目前各国主要针对地铁、公路、轻轨等交通系统开展振动的研究工作,面对高架路的振动研究近于空白。
由于高架桥跟其他桥梁有相似和共同的地方,国内外对于其他桥梁上行车舒适度研究相对较多,因此可以很好的借鉴到高架桥上。
车桥桥梁振动问题的研究一直得到国内外学者的普遍关注。
随着计算机和有限元方法的发展,车辆振动分析的现代理论以考虑更加接近真实的三维空间车辆模型和桥梁理想化为多质量的有限元或有线条模型并考虑车桥耦合振动为主要特点,同时还要计及路面不平顺度这一随机因素的影响。
故车辆桥梁系统动力响应的研究有待于进一步的深入和完善。
在此基础上,方能对行车舒适度进行深入研究。
古典理论最初提出了将列车简化为移动常量力[1]或者移动质量作用于桥梁上。
之后,Michaltsos[2]等将列车模拟为移动的质量块,采用级数的方法研究了均匀截面简支梁在移动质量块作用下的动力响应。
Garinei[3]等研究了高速移动的简谐荷载作用下简支梁的动力特性等。
随着数学、力学、电子计算机的应用以及有限元技术的发展,人们可以建立比较真实的车辆和桥梁的空间计算模型,从而更精确地模拟车桥空间模型以及它们之间的耦合振动,并考虑引起激励的轨道不平顺、车辆加速和减速等复杂因素。
车桥耦合振动的研究从而有了飞速的进步。
美国Chu[4,5]等最早采用多刚体多自由度的复杂车辆模型,认为车辆由车体、转向架构架、轮对等刚体组成,各刚体在空间具有6个自由度。
Green和Cebon[6]提出了在频域内利用模态脉冲响应函数和模态激扰力求解分离的车桥系统方程的方法。
Walter[7]等采用Ritz能量法得到了拱桥在高速列车作用下的动力响应的闭合解,讨论了荷载分布情况、列车速度等因素的影响。
在国内,夏禾教授及其课题组在车-桥耦合振动方面进行了大量的研究。
夏禾[8]等在桥梁模型中引进了模态综合技术,用振型叠加法来计算桥梁的反应,仅考虑少数一些振型就可以获得满意的精度;张楠[9,10]通过理论计算与现场试验研究了高速列车与桥梁的动力相互作用,模拟了中华之星列车高速通过秦沈客运专线24m双线预应力混凝土简支箱梁桥的全过程,计算了列车-桥梁的动力响应,并与现场实测结果进行了对比。
车桥耦合动力仿真分析的应用
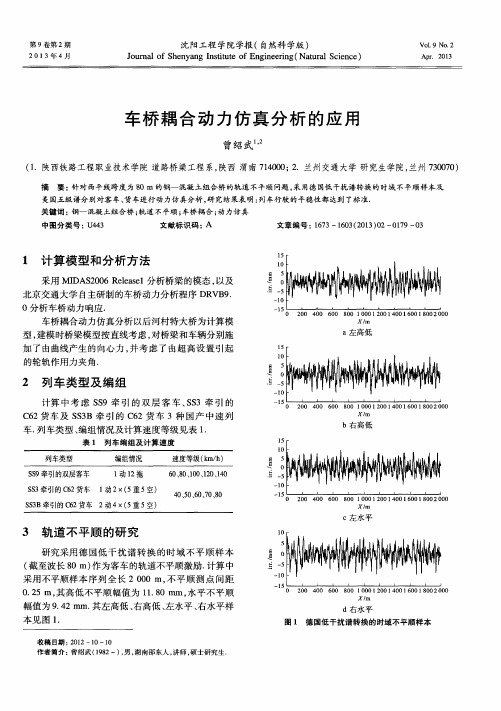
C左 水 平
3 轨 道 不 平顺 的研 究
研 究 采用 德 国低 干 扰 谱 转 换 的 时 域 不 平 顺 样 本 ( 截 至波 长 8 0 m) 作 为客 车 的轨道 不平顺 激 励 . 计 算 中 采用 不平顺 样 本 序 列 全 长 2 0 0 0 i n , 不 平 顺 测 点 间距
摘 要: 针对 西平线跨度为 8 0 m 的钢一混凝 土组合桥 的轨道 不平顺问题 , 采 用德 国低干扰谱转换 的时域不平顺样 本及
美国五级谱 分别对客 车、 货车进行动力仿真分析 , 研 究结果表明 : 列 车行驶 的平稳性都 达到 了标 准.
关键词 : 钢一 混凝土组合桥 ; 轨道 不平顺 ; 车桥耦合 ; 动力仿 真
根据给定 的 S S 9牵 引 的 双 层 客 车 、 S S 3牵 引 的 C 6 2货车及 S S 3 B牵 引的 C 6 2货 车共计 3种 车辆 的参 数, 以德 国低 干扰 谱转 换 的时域 轨 道 不 平顺 样 本 和美 国五 级谱转 换 的时域 轨 道 不平 顺 样本 作 为 系 统激 励 ,
中 图分 类 号 : U 4 4 3 文 献标 识 码 : A 文 章 编 号 :1 6 7 3—1 6 0 3 ( 2 0 1 3 ) 0 2— 0 1 S 2 0 0 6 R e l e a s e 1 分析桥梁的模态 , 以及 北京 交 通大 学 自主研制 的车桥动 力分 析程 序 D R VB 9 .
0分 析车 桥动 力响 应 .
猢 伽
车桥耦 合 动力仿 真分 析 以后 河 村特 大桥 为计算 模 型, 建 模时桥 梁模 型按 直线 考虑 , 对 桥梁 和车辆 分别 施 加 了由 曲线 产生 的向心 力 , 并 考 虑 了 由超 高设 置 引 起 的轮 轨作用 力 夹角 .
MATLAB在车桥耦合振动问题中的应用研究

mb b C ( +t y l
.
Vy )tbta0 cyy 争 b a0十1 -1 )} hl - 七YY +2 -2 ( 一 ( 十
据 以上编程思想 , 结合 M T A A L B的语法 , 编制 了基于 O E D
量和阻尼 的影响。作为移动荷载的车辆采用二分之一 车模 型 ,
j2y b 0)0 (( +a t =
() 5
简化为两系 的弹簧一阻尼 一质量系统 ,"为车体质量 ,b 1b 1 1 J 为车 体的点头刚度 ,"为构架质量与轮对质量之和 , 1 1 1 k 为轮对一侧
收稿日期 :0 7 0 — 0 2o—83 作者简介 : 丽( 93 )女 , 李 1 7一 , 工程师 , 专业 : 公路与桥梁。
二系垂 向刚度 , C 为转 向架一侧二 系垂 向阻尼 , 为车辆通过 v
桥梁时的速度伪 ~恒量) 。 根据欧拉 一贝努利梁假设 , 桥梁系统
的振动方程为 :
技术改造决策更加科学 、 改造技术方案更加经济合理 、 铁路提
速更加安全可靠 , 具有重要的社会意义 、 经济 价值 和广泛 的应
数值求解方法相 比较 , 在保证精度 的前提下 , 缩短 了计算所 需
的时 间 。
1 系统 的建模
6l ) f y. ,f ( { 6= 其他 ≤ .({。 f < 半 ; f0- ( f1 … … )…其他 . :¨ - =‘ . l - 6 1
【 0
…
( 3 )
由对车辆系统的受力分析可知 :
( 广西桂通公路工程监理咨询有限责任公 司, 广西 南 宁 5 02 ) 3 0 3
摘要 : 动荷栽质量的影响给荷栽 一 梁 系统的振动方程的 求解与研 究带来很 大的 困难。本文利用 MA L B对二分之一车模型作用 移 桥 TA 下简支粱的车桥耦合振动方程进行研究 , 以一座 大跨斜拉桥 为例, 究了汽车以各种速度通过桥 梁时斜拉桥 的动力响应。 实践证 明 : 研 基 于 MAT AB内部函数 OD L E求解 系统运动方程组 的二 次开发 函数 ,较好地 解决了车桥耦合振动 问题 的数 值求解 ,在 保证精 度的前提 下, 缩短 了计算所需的时间。 关键词: MAT A 耦 合; L B; 移动荷栽 中图分类号 : 4 7 0 6 文献标识码 : A 文章 编号 : 7 — 4  ̄(0 7 1 — o 2-3 1 2 5 5 2 0 ) 0 2 . 6 0 0
车桥耦合振动分析软件
第1章系统概述 (1)1.1系统特点 (1)1.2软件功能 (1)1.2.1车辆子系统 (2)1.2.2激励模型 (2)1.2.3桥梁/轨道子系统 (3)1.2.4求解方法 (3)1.2.5后处理 (3)1.3计算流程 (4)第2章软件安装与运行方式 (6)2.1软件安装 (6)2.2运行方式 (6)第3章前处理所需文本文件定义 (8)3.1输入文件概述 (8)3.2桥梁/轨道子结构:Modal_Substructure_Bridge.dat (9)3.2.1第一行控制参数 (9)3.2.2第二行后的节点坐标参数 (10)3.2.3轨道节点编号 (10)3.2.4集中阻尼和非线性弹簧单元定义 (10)3.2.5与仿真计算同步输出桥梁响应的节点个数 (11)3.2.6桥梁/轨道结构模态信息 (11)3.2.7后处理考察节点位移和应力/内力定义 (13)3.3车辆子结构:Modal_Substructure_Vehicletypes.dat (13)3.3.1第一行控制参数 (13)3.3.2第二行控制参数 (14)3.3.3第二行后的节点坐标参数 (14)3.3.4车轮节点编号 (14)3.3.5车轮静载、轮轨/路面耦合类型 (16)3.3.6车轮刚度、阻尼和质量等参数定义 (16)3.3.7集中阻尼和非线性弹簧单元定义 (16)3.3.8与仿真计算同步输出车辆响应的节点个数 (17)3.3.9车辆结构模态信息 (17)3.3.10其他车辆的定义 (17)3.4集中阻尼和非线性弹簧:NonlinearSpringParameters.dat (18)3.4.1第一行控制参数 (18)3.4.2其后依次定义每个单元的相关参数: (18)3.5轨道/车道位置:Rails_Location.dat (19)3.5.1第一行控制参数 (19)3.5.2第二行控制参数 (19)3.5.3每条轨道的关键点定义 (19)3.6车队编组及运行组织:VehicleOrginazition.dat (21)3.6.1第一行控制参数 (21)3.6.2车队编组定义 (22)3.6.3车队运行参数定义 (22)3.7路面不平顺:Irregularity.dat (23)3.7.1第一、三、五行提示参数 (23)3.4.1第二、四、六行控制参数 (23)3.4.2第六行后的不平顺样本 (24)3.8求解参数:SolutionParameters.dat (24)第4章后处理二进制文件存储格式 (26)4.1Modal_Substructure_Bridge_ANSYS (26)4.2Modal_Substructure_Bridge_ANSYS_postprocess.bin (26)4.3Res_DisResults_Bridge.bin (26)4.4Res_AccResults_Bridge.bin (27)4.5Res_Modal_Coordinate_Results_Bridge.bin (27)4.6Res_BridgeResponseBulkDate_disacc.bin (27)4.7Res_BridgeResponseBulkDate_dis_static.bin (28)4.8Res_BridgeResponseBulkDate_stress.bin (28)4.9Res_BridgeResponseBulkDate_stress_static.bin (28)4.10Res_AccResults_Vehicles.bin (29)4.11Res_DisResults_Vehicles.bin (29)4.12Res_ReductionRation_Vehicles.bin (29)4.13Res_DerailmentFactor_Vehicles.bin (30)4.1418.Res_WheelsetirregDisVehilces.bin (30)车桥耦合振动分析软件操作手册第1章系统概述车桥耦合振动分析软件VBC(Vehicle-Bridge Coupling)采用Intel Visual Fortran 2013语言编制而成,为Windows控制台程序,目前为3.1版本,可在32位或64位操作系统上运行。
基于等参映射与改进折半法的公路车桥耦合分析系统
基于等参映射与改进折半法的公路车桥耦合分析系统作者:赵越黄平明刘修平韩万水毛旺涛来源:《湖南大学学报·自然科学版》2020年第11期摘要:针对传统全耦合车桥耦合分析计算量大、效率低的问题,基于等参映射及改进折半法建立公路车桥耦合分析系统. 采用ANSYS建立桥梁有限元模型,利用MATLAB建立多種精细化车辆动力分析模型,采用全过程迭代法分别求解桥梁子系统与车辆子系统. 为实现车轮荷载快速自动加载,引入四边形等参映射和改进折半查找法确定车桥接触点的插值系数和加载位置. 基于弹簧-质量模型过简支梁算例及某大跨悬索桥行车试验,将该分析系统与经典数值分析方法、实测数据以及传统的时间步迭代方法进行对比. 研究结果表明,所建立的车桥耦合分析系统具有较好的分析精度和计算效率,迭代过程收敛速度较快,可为高流量、高随机车辆荷载下桥梁结构空间响应分析提供参考.关键词:桥梁;车桥耦合分析;有限元模型;全过程迭代;改进折半查找;等参映射中图分类号:U445.446 文献标志码:AHighway Vehicle-bridge Interaction Analysis System Based onIsoparametric Mapping and Improved Binary SearchZHAO Yue,HUANG Pingming†,LIU Xiuping,HAN Wanshui,MAO Wangtao(School of Highway,Chang’an University,Xi’an 710064,China)Abstract:To reduce the computing work and improve the efficiency of vehicle-bridge coupling analysis when using traditional fully coupled method, a high efficiency highway vehicle-bridge interaction analysis system was established based on improved binary search and isoparametric mapping. The finite element model of the bridge was simulated using ANSYS, the multiple refineddynamic vehicles were modeled in MATLAB, and the inter-history iteration method was used to analyze the bridge subsystem and vehicle subsystem separately. The quadrilateral isoparametric mapping and improved binary search method were introduced for quick determination of interpolation coefficient and loading position of vehicle-bridge contact point to realize the quick automatic loading of wheel load. Based on the spring-mass model passing through a simply supported beam and a running test of a long-span suspension bridge, the proposed analysis system was compared with the classical numerical analysis method, measured data and traditional time step iteration method. The results show that the proposed analysis system exhibits a good computing efficiency and accuracy and rapid convergence, which can provide a reference for the bridge spatial response analysis under large and highly random traffic flow.Key words:bridge;vehicle-bridge interaction analysis;finite element model;inter-history iteration;improved binary search;isoparametric mapping车桥间的耦合作用不仅会影响到桥梁结构的安全性和适用性,还会影响行车安全和舒适性. 近年来,桥梁结构形式的多样化、汽车速度和载重的不断加大使得车桥之间的相互作用愈发复杂和不确定,车桥耦合振动问题受到了国内外学者的广泛关注[1-4].车桥耦合振动的分析方法主要包括3种:解析法、试验研究法和数值模拟法[5]. 解析法虽然是理论推导,比较严谨,但当桥梁几何特征和材料特性有限制条件时,在方程建立过程中不可避免地要对实际条件进行简化,而且有些复杂方程无法得到解析解,所以解析法在实际工程中运用有一定的局限性[6]. 试验法虽然能客观且综合地反映桥梁在车辆动载作用下的实际工作情况,但由于人力、物力消耗较大且操作难度高,实现起来并不经济. 目前数值模拟凭借易实现、低成本等特点已成为车桥耦合振动的主要分析手段. 早期的数值模拟法大多是基于Visual C++或Visual Fortran的自主研发分析系统[7-8],以自编的程序计算桥梁系统的响应. 随着各种大型通用商业有限元分析软件的开发,其前处理模块中,桥梁上、下部结构和附属结构等均可选用不同的单元类型来模拟,在求解过程中也能兼顾结构的几何非线性和材料非线性,以此为基础的各种数值方法[9-13]成为模拟分析车桥耦合振动问题的行之有效的工具.基于数值方法进行车桥耦合分析系统编制主要包括基于模态叠加法及基于全耦合理论两种[14].相比于后者,模态叠加法简单实用,但结构高阶模态的提取较难,分析结果的精度易受影响[15]. 基于全耦合方法的车桥耦合分析物理意义明确,分析精度相对较高,但由于车辆对桥梁结构每一时步的加载求解均需借助复杂的迭代过程,故分析效率相对较低,尤其是在分析高流量、高随机车流作用下大跨径桥梁的结构动力响应问题时,将面临较高的時间成本问题[16],因此提高车桥耦合分析运算效率已成为当前国内外学者的一个研究方向[17]. 例如张楠等[18]提出了基于全过程迭代的车桥耦合动力分析方法,可通过人为干预促进计算收敛,相比传统的时间步迭代方法,总求解次数大幅减少. 李岩等[19]提出了一种维度时变的随机车流与桥梁耦合振动分析方法,使得振动方程单步的求解维度降低,既保持了整体法计算稳定的特点,又有效提高了计算效率. Chen等[20]则通过将随机车流等效为移动荷载列的方法,达到了降低计算成本的目的. 总体来看,车桥耦合分析系统可以从桥梁模型、荷载模型以及计算方法上进行优化.本文以优化确定车桥接触点的插值系数和加载位置为出发点,引入了四边形等参映射和改进折半查找法提高公路车桥耦合分析系统的计算效率. 首先,采用MATLAB语言建立公路桥梁典型车辆动力分析模型,基于ANSYS建立桥梁有限元模型;其次,采用全过程迭代法分别求解得到桥梁和车辆的运动状态,通过程序间的接口调用施加车桥间作用力,期间引入四边形等参映射和改进折半查找法并控制时步输出结果以提高车桥耦合运算效率;最后通过经典数值算例和实桥应用对比验证所建立的分析系统的准确性和实用性.1 基于等参映射与改进折半法的车桥耦合分析系统建立1.1 车辆模型汽车车辆一般由车体、车轮等构件以及连接这些构件的减震系统、悬挂系统组成,根据车桥耦合振动分析的需要对车辆模型进行简化,将车辆模拟为刚体的组合,刚体之间通过轴质量块、弹簧元件和阻尼元件相互连接,不同车型所对应的车辆动力分析模型不同. 根据课题组前期研究成果,目前公路常见车辆按照车辆轴数、轮数、轴距、轴重等数据可划分为5大类,17个车型[21-23]. 采用MATLAB语言,针对17种车型分别建立相应的车辆动力分析模型.在车辆动力分析模型建立过程中,车辆被划分为不同的刚体部件,如车体、车轮等. 空间内单一刚体具有3个方向的平动和3个方向的转动自由度. 在车辆匀速直线前进时,刚体部件沿着车辆前进方向的振动对桥梁的竖向及横向振动影响不大,因此各刚体沿车体运动方向的自由度可忽略,此时车体具有5个自由度:竖向、横向、点头、侧滚和摇头,每个车轮具有横向和竖向2个自由度,拖挂式车型不考虑横移和摇头这2个自由度,每个车体具有浮沉、点头及侧滚3个自由度,每个车轮只有竖移一个自由度.图1以三轴车(双后轴)为例,给出了相应的动力分析模型立面及侧面图. 其中,K i1.2 车桥运动方程及求解策略车桥耦合系统的动力方程可表示为:式中:Mv、Cv、Kv分别为车辆系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Mb、Cb、Kb分别为桥梁系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Zv、Zb分别为车辆、桥梁系统的位移向量;Fv、Fb分别为车辆、桥梁系统的荷载向量.在车辆运行过程中,假设车轮始终与桥面接触,桥梁振动引起的桥梁竖向位移将引起车辆减震系统、悬挂系统的变形,且路面粗糙度也是车桥耦合体系的主要激励源之一,因此车桥系统之间的相互作用力既是车辆和桥梁系统运动状态Zv、Zb的函数,也是路面粗糙度Ra的函数,则车桥耦合系统的运动方程可进一步表示为:联立式(1)与(2),对车辆与桥梁两个子系统建立耦合关系. 采用全过程迭代法分别求解桥梁子系统和车辆子系统,主要迭代过程通过MATLAB编制相应运算程序予以实现,期间由基于ANSYS的桥梁有限元模型及相应分析过程提供响应输出,具体流程如图2所示,收敛准则定义为‖F iv ‖<0.1. 全过程迭代法每一步均为全时程计算,具有思路清晰明确、易于操作、计算准确、占用内存少等优点.1.3 基于等参映射的接触点荷载分配目前桥梁结构桥面模拟有限元模型多为梁格模型、实体或板壳单元模型,车轮荷载一般简化为集中力并分配至相邻4个节点,如图3所示. 在二维平面内四边形荷载分担方式与位移插值函数一致. 当车轮荷载作用于某一位置(x,y)时,相应的等参映射关系如图4所示.坐标映射关系为:式中:x、y是车轮荷载与桥面接触点坐标;xi、yi分别为四边形单元的第i个节点的横、纵位置;ξ、η为x、y映射到母单元的值;ξi、ηi分别为母单元的第i个节点的横、纵位置,是已知量;Ni(ξ,η)为等参映射点(ξ,η)的函数[24];函数值Ni为四边形单元的第i个节点的荷载分配系数.双线性方程组(3)的未知量ξ和η可通过牛顿迭代法[25]求解,进而计算出分配系数Ni,实现车轮荷载的自动加载. 迭代过程为:1.4 基于改进折半法的快速加载为实现车轮荷载的快速自动加载,需定位临近4个节点的位置信息,折半查找法作为一种在有序数组中查找某一特定元素的搜索算法,通过不断将查找范围减半提高搜索效率,本文将折半法查找确定值的思想扩展到查找车轮作用区间范围上. 折半查找的前提条件是必须将搜索目标范围排成有序数列,虽然折半查找效率高,但排序本身又增加了一定工作量. 桥梁结构模型的特点决定了同一计算过程中,主梁节点一经确定便不再改动,因此全部计算过程仅需一次排序,后续所有车轮作用范围的确定均可直接使用,从全局角度考虑可有效提高查找效率.基于数值方法进行车桥耦合分析系统编制主要包括基于模态叠加法及基于全耦合理论两种[14].相比于后者,模态叠加法简单实用,但结构高阶模态的提取较难,分析结果的精度易受影响[15]. 基于全耦合方法的车桥耦合分析物理意义明确,分析精度相对较高,但由于车辆对桥梁结构每一时步的加载求解均需借助复杂的迭代过程,故分析效率相对较低,尤其是在分析高流量、高随机车流作用下大跨径桥梁的结构动力响应问题时,将面临较高的时间成本问题[16],因此提高车桥耦合分析运算效率已成为当前国内外学者的一个研究方向[17]. 例如张楠等[18]提出了基于全过程迭代的车桥耦合动力分析方法,可通过人为干预促进计算收敛,相比传统的时间步迭代方法,总求解次数大幅减少. 李岩等[19]提出了一种维度时变的随机车流与桥梁耦合振动分析方法,使得振动方程单步的求解维度降低,既保持了整体法计算稳定的特点,又有效提高了计算效率. Chen等[20]则通过将随机车流等效为移动荷载列的方法,达到了降低计算成本的目的. 总体来看,车桥耦合分析系统可以从桥梁模型、荷载模型以及计算方法上进行优化.本文以優化确定车桥接触点的插值系数和加载位置为出发点,引入了四边形等参映射和改进折半查找法提高公路车桥耦合分析系统的计算效率. 首先,采用MATLAB语言建立公路桥梁典型车辆动力分析模型,基于ANSYS建立桥梁有限元模型;其次,采用全过程迭代法分别求解得到桥梁和车辆的运动状态,通过程序间的接口调用施加车桥间作用力,期间引入四边形等参映射和改进折半查找法并控制时步输出结果以提高车桥耦合运算效率;最后通过经典数值算例和实桥应用对比验证所建立的分析系统的准确性和实用性.1 基于等参映射与改进折半法的车桥耦合分析系统建立1.1 车辆模型汽车车辆一般由车体、车轮等构件以及连接这些构件的减震系统、悬挂系统组成,根据车桥耦合振动分析的需要对车辆模型进行简化,将车辆模拟为刚体的组合,刚体之间通过轴质量块、弹簧元件和阻尼元件相互连接,不同车型所对应的车辆动力分析模型不同. 根据课题组前期研究成果,目前公路常见车辆按照车辆轴数、轮数、轴距、轴重等数据可划分为5大类,17个车型[21-23]. 采用MATLAB语言,针对17种车型分别建立相应的车辆动力分析模型.在车辆动力分析模型建立过程中,车辆被划分为不同的刚体部件,如车体、车轮等. 空间内单一刚体具有3个方向的平动和3个方向的转动自由度. 在车辆匀速直线前进时,刚体部件沿着车辆前进方向的振动对桥梁的竖向及横向振动影响不大,因此各刚体沿车体运动方向的自由度可忽略,此时车体具有5个自由度:竖向、横向、点头、侧滚和摇头,每个车轮具有横向和竖向2个自由度,拖挂式车型不考虑横移和摇头这2个自由度,每个车体具有浮沉、点头及侧滚3个自由度,每个车轮只有竖移一个自由度.图1以三轴车(双后轴)为例,给出了相应的动力分析模型立面及侧面图. 其中,K i1.2 车桥运动方程及求解策略车桥耦合系统的动力方程可表示为:式中:Mv、Cv、Kv分别为车辆系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Mb、Cb、Kb分别为桥梁系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Zv、Zb分别为车辆、桥梁系统的位移向量;Fv、Fb分别为车辆、桥梁系统的荷载向量.在车辆运行过程中,假设车轮始终与桥面接触,桥梁振动引起的桥梁竖向位移将引起车辆减震系统、悬挂系统的变形,且路面粗糙度也是车桥耦合体系的主要激励源之一,因此车桥系统之间的相互作用力既是车辆和桥梁系统运动状态Zv、Zb的函数,也是路面粗糙度Ra的函数,则车桥耦合系统的运动方程可进一步表示为:联立式(1)与(2),对车辆与桥梁两个子系统建立耦合关系. 采用全过程迭代法分别求解桥梁子系统和车辆子系统,主要迭代过程通过MATLAB编制相应运算程序予以实现,期间由基于ANSYS的桥梁有限元模型及相应分析过程提供响应输出,具体流程如图2所示,收敛准则定义为‖F iv ‖<0.1. 全过程迭代法每一步均为全时程计算,具有思路清晰明确、易于操作、计算准确、占用内存少等优点.1.3 基于等参映射的接触点荷载分配目前桥梁结构桥面模拟有限元模型多为梁格模型、实体或板壳单元模型,车轮荷载一般简化为集中力并分配至相邻4个节点,如图3所示. 在二维平面内四边形荷载分担方式与位移插值函数一致. 当车轮荷载作用于某一位置(x,y)时,相应的等参映射关系如图4所示.坐标映射关系为:式中:x、y是车轮荷载与桥面接触点坐标;xi、yi分别为四边形单元的第i个节点的横、纵位置;ξ、η为x、y映射到母单元的值;ξi、ηi分别为母单元的第i个节点的横、纵位置,是已知量;Ni(ξ,η)为等参映射点(ξ,η)的函数[24];函数值Ni为四边形单元的第i个节点的荷载分配系数.双线性方程组(3)的未知量ξ和η可通过牛顿迭代法[25]求解,进而计算出分配系数Ni,实现车轮荷载的自动加载. 迭代过程为:1.4 基于改进折半法的快速加载为实现车轮荷载的快速自动加载,需定位临近4个节点的位置信息,折半查找法作为一种在有序数组中查找某一特定元素的搜索算法,通过不断将查找范围减半提高搜索效率,本文将折半法查找确定值的思想扩展到查找车轮作用区间范围上. 折半查找的前提条件是必须将搜索目标范围排成有序数列,虽然折半查找效率高,但排序本身又增加了一定工作量. 桥梁结构模型的特点决定了同一计算过程中,主梁节点一经确定便不再改动,因此全部计算过程仅需一次排序,后续所有车轮作用范围的确定均可直接使用,从全局角度考虑可有效提高查找效率.基于数值方法进行车桥耦合分析系统编制主要包括基于模态叠加法及基于全耦合理论两种[14].相比于后者,模态叠加法简单实用,但结构高阶模态的提取较难,分析结果的精度易受影响[15]. 基于全耦合方法的车桥耦合分析物理意义明确,分析精度相对较高,但由于车辆对桥梁结构每一时步的加载求解均需借助复杂的迭代过程,故分析效率相对较低,尤其是在分析高流量、高随机车流作用下大跨径桥梁的结构动力响应问题时,将面临较高的时间成本问题[16],因此提高车桥耦合分析运算效率已成为当前国内外学者的一个研究方向[17]. 例如张楠等[18]提出了基于全过程迭代的车桥耦合动力分析方法,可通过人为干预促进计算收敛,相比传统的时间步迭代方法,总求解次数大幅减少. 李岩等[19]提出了一种维度时变的随机车流与桥梁耦合振动分析方法,使得振动方程单步的求解维度降低,既保持了整体法计算稳定的特点,又有效提高了计算效率. Chen等[20]则通过将随机车流等效为移动荷载列的方法,达到了降低计算成本的目的. 总体来看,车桥耦合分析系统可以从桥梁模型、荷载模型以及计算方法上进行优化.本文以优化确定车桥接触点的插值系数和加载位置为出发点,引入了四边形等参映射和改进折半查找法提高公路车桥耦合分析系统的计算效率. 首先,采用MATLAB语言建立公路桥梁典型车辆动力分析模型,基于ANSYS建立桥梁有限元模型;其次,采用全过程迭代法分别求解得到桥梁和车辆的运动状态,通过程序间的接口调用施加车桥间作用力,期间引入四边形等参映射和改进折半查找法并控制时步输出结果以提高车桥耦合运算效率;最后通过经典数值算例和实桥应用对比验证所建立的分析系统的准确性和实用性.1 基于等参映射与改进折半法的车桥耦合分析系統建立1.1 车辆模型汽车车辆一般由车体、车轮等构件以及连接这些构件的减震系统、悬挂系统组成,根据车桥耦合振动分析的需要对车辆模型进行简化,将车辆模拟为刚体的组合,刚体之间通过轴质量块、弹簧元件和阻尼元件相互连接,不同车型所对应的车辆动力分析模型不同. 根据课题组前期研究成果,目前公路常见车辆按照车辆轴数、轮数、轴距、轴重等数据可划分为5大类,17个车型[21-23]. 采用MATLAB语言,针对17种车型分别建立相应的车辆动力分析模型.在车辆动力分析模型建立过程中,车辆被划分为不同的刚体部件,如车体、车轮等. 空间内单一刚体具有3个方向的平动和3个方向的转动自由度. 在车辆匀速直线前进时,刚体部件沿着车辆前进方向的振动对桥梁的竖向及横向振动影响不大,因此各刚体沿车体运动方向的自由度可忽略,此时车体具有5个自由度:竖向、横向、点头、侧滚和摇头,每个车轮具有横向和竖向2个自由度,拖挂式车型不考虑横移和摇头这2个自由度,每个车体具有浮沉、点头及侧滚3个自由度,每个车轮只有竖移一个自由度.图1以三轴车(双后轴)为例,给出了相应的动力分析模型立面及侧面图. 其中,K i1.2 车桥运动方程及求解策略车桥耦合系统的动力方程可表示为:式中:Mv、Cv、Kv分别为车辆系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Mb、Cb、Kb分别为桥梁系统的总体质量矩阵、总体阻尼矩阵及总体刚度矩阵;Zv、Zb分别为车辆、桥梁系统的位移向量;Fv、Fb分别为车辆、桥梁系统的荷载向量.在车辆运行过程中,假设车轮始终与桥面接触,桥梁振动引起的桥梁竖向位移将引起车辆减震系统、悬挂系统的变形,且路面粗糙度也是车桥耦合体系的主要激励源之一,因此车桥系统之间的相互作用力既是车辆和桥梁系统运动状态Zv、Zb的函数,也是路面粗糙度Ra的函数,则车桥耦合系统的运动方程可进一步表示为:联立式(1)与(2),对车辆与桥梁两个子系统建立耦合关系. 采用全过程迭代法分别求解桥梁子系统和车辆子系统,主要迭代过程通过MATLAB编制相应运算程序予以实现,期间由基于ANSYS的桥梁有限元模型及相应分析过程提供响应输出,具体流程如图2所示,收敛准则定义为‖F iv ‖<0.1. 全过程迭代法每一步均为全时程计算,具有思路清晰明确、易于操作、计算准确、占用内存少等优点.1.3 基于等参映射的接触点荷载分配目前桥梁结构桥面模拟有限元模型多为梁格模型、实体或板壳单元模型,车轮荷载一般简化为集中力并分配至相邻4个节点,如图3所示. 在二维平面内四边形荷载分担方式与位移插值函数一致. 当车轮荷载作用于某一位置(x,y)时,相应的等参映射关系如图4所示.坐标映射关系为:式中:x、y是车轮荷载与桥面接触点坐标;xi、yi分别为四边形单元的第i个节点的横、纵位置;ξ、η为x、y映射到母单元的值;ξi、ηi分别为母单元的第i个节点的横、纵位置,是已知量;Ni(ξ,η)为等参映射点(ξ,η)的函数[24];函数值Ni为四边形单元的第i个节点的荷载分配系数.双线性方程组(3)的未知量ξ和η可通过牛顿迭代法[25]求解,进而计算出分配系数Ni,实现车轮荷载的自动加载. 迭代过程为:1.4 基于改进折半法的快速加载为实现车轮荷载的快速自动加载,需定位临近4个节点的位置信息,折半查找法作为一种在有序数组中查找某一特定元素的搜索算法,通过不断将查找范围减半提高搜索效率,本文将折半法查找确定值的思想扩展到查找车轮作用区间范围上. 折半查找的前提条件是必须将搜索目标范围排成有序数列,虽然折半查找效率高,但排序本身又增加了一定工作量. 桥梁结构模型的特点决定了同一计算过程中,主梁节点一经确定便不再改动,因此全部计算过程仅需一次排序,后续所有车轮作用范围的确定均可直接使用,从全局角度考虑可有效提高查找效率.基于数值方法进行车桥耦合分析系统编制主要包括基于模态叠加法及基于全耦合理论两种[14].相比于后者,模态叠加法简单实用,但结构高阶模态的提取较难,分析结果的精度易受影响[15]. 基于全耦合方法的车桥耦合分析物理意义明確,分析精度相对较高,但由于车辆对桥梁结构每一时步的加载求解均需借助复杂的迭代过程,故分析效率相对较低,尤其是在分析高流量、高随机车流作用下大跨径桥梁的结构动力响应问题时,将面临较高的时间成本问题[16],因此提高车桥耦合分析运算效率已成为当前国内外学者的一个研究方向[17]. 例如张楠等[18]提出了基于全过程迭代的车桥耦合动力分析方法,可通过人为干预促进计算收敛,相比传统的时间步迭代方法,总求解次数大幅减少. 李岩等[19]提出了一种维度时变的随机车流与桥梁耦合振动分析方法,使得振动方程单步的求解维度降低,既保持了整体法计算稳定的特点,又有效提高了计算效率. Chen等[20]则通过将随机车流等效为移动荷载列的方法,达到了降低计算成本的目的. 总体来看,车桥耦合分析系统可以从桥梁模型、荷载模型以及计算方法上进行优化.本文以优化确定车桥接触点的插值系数和加载位置为出发点,引入了四边形等参映射和改进折半查找法提高公路车桥耦合分析系统的计算效率. 首先,采用MATLAB语言建立公路桥梁典型车辆动力分析模型,基于ANSYS建立桥梁有限元模型;其次,采用全过程迭代法分别求解得到桥梁和车辆的运动状态,通过程序间的接口调用施加车桥间作用力,期间引入四边形等参映射和改进折半查找法并控制时步输出结果以提高车桥耦合运算效率;最后通过经典数值算例和实桥应用对比验证所建立的分析系统的准确性和实用性.。
浅谈ANSYS中车桥耦合振动的实现方法与应用
浅谈ANSYS中车桥耦合的实现方法与应用作者:黄江广安区交通运输局摘要:弹簧移动质量的振动问题可通过大型通用结构有限元软件ANSYS进行分析解决,解决方法有三种,分别为:位移耦合法、生死单元法和位移接触法。
这三种方法各有优势与适用范围,本文对相关方法的具体情况作出简要介绍,并采用简单算例通过位移接触法进行应用介绍,阐述了车桥耦合振动仿真模拟的一般步骤,有利于读者了解这方面的内容。
关键词:位移耦合生死单元位移接触1前言车桥耦合振动问题是桥梁振动理论中的一项难题,随着大型通用有限元软件的开发,车桥振动模型在逐步得到精确化模拟,根据不同的车桥模型应有不同的模拟方法。
以下结合大型通用结构有限元软件ANSYS将三种模拟方法及应用作简要介绍。
2方法介绍位移耦合法位移耦合法的思路是仅创建一个质量单元模拟移动质量,根据移动速度对移动质量施加不同的水平约束位移,将移动质量与所移动到位置处的节点竖向位移耦合。
采用位移耦合法时赢注意以下几点:①因移动质量与梁上节点耦合,因此移动质量只能从梁上一个节点移动到下一节点,而从一个节点移动到下一节点为一个荷载步。
在一个荷载步中若设置多个子步,当KBC=0时会造成还没有移动到下一节点时就耦合自由度,也就是耦合位置不对;当KBC=1时,虽然在第一子步到达下一节点位置,即耦合位置正确,但中间收敛结果所产生的速度和加速度会对计算造成“污染”,因此无论KBC 如何设置,宜将NSUBST设置为1。
②阻尼问题。
ANSYS完全法瞬态动力分析不能设置模态阻尼比,但可用质量阻尼系数α和刚度阻尼系数β等效(Rayleigh阻尼假定),但正是因为Rayleigh 阻尼假定会造成ANSYS计算时产生“虚假”阻尼(α×质量矩阵),而理论推到中没有此项。
因此考虑阻尼进行结果对比时可仅考虑刚度阻尼。
③采用CP命令耦合自由度时,因自由度为线性耦合,不适合大变形情况。
如打开大变形,ANSYS计算的梁体位移、速度和加速度正确,但移动质量位移和加速度虽然趋势基本一致,但数值均存在很大误差或数值不正确,且误差随速度增大而增大。
钢—混组合梁桥车桥耦合振动分析及局部疲劳研究
钢—混组合梁桥车桥耦合振动分析及局部疲劳研究钢—混组合梁桥车桥耦合振动分析及局部疲劳研究摘要:随着城市交通的发展和交通运输的日益繁忙,钢—混组合梁桥作为重要的城市交通枢纽,承担着巨大的交通压力。
然而,在长期的运营过程中,钢—混组合梁桥常常会遭受车辆荷载带来的振动和局部疲劳问题,这对桥梁的安全可靠性提出了挑战。
本文通过对钢—混组合梁桥车桥耦合振动以及局部疲劳的研究,旨在为提高桥梁的耐久性和减少维修成本提供理论支持。
1.引言钢—混组合梁桥是一种采用钢结构和混凝土结构相结合的桥梁形式。
其结构特点为钢负责承受水平荷载和高弯矩力,混凝土负责承受垂直荷载和低弯矩力。
这种桥型结构是传统混凝土桥和钢桥的结合,兼具了两种材料的优点。
然而,由于车辆荷载的作用,桥梁会产生振动,从而引发局部疲劳破坏。
因此,针对钢—混组合梁桥车桥耦合振动以及局部疲劳进行研究具有重要的现实意义。
2.车桥耦合振动分析车桥耦合振动是指运行车辆的振动会导致桥梁结构的振动,并且车桥振动与桥梁振动相互影响。
车桥耦合振动可以通过数学模型进行分析和预测。
通过建立动力学方程、运用傅里叶变换等方法,可以解决车桥耦合振动的问题。
实际工程中,可以利用有限元软件对桥梁进行车桥耦合振动分析,并可以预测车桥振动对桥梁结构的影响。
3.局部疲劳研究桥梁的局部疲劳指的是在特定的应力范围下,桥梁结构发生疲劳破坏的现象。
在钢—混组合梁桥中,常常会出现焊缝和连接件等局部部位的疲劳损伤。
局部疲劳的研究需要利用疲劳试验、应力分析等方法,以确定桥梁在不同工况下的局部疲劳特性。
通过分析局部断裂机理,可以提出针对性的改进措施,增强桥梁结构的抗疲劳能力。
4.耐久性改进措施为了提高钢—混组合梁桥的耐久性和减少局部疲劳破坏,可以采取以下措施:4.1 结构优化设计:通过优化桥梁的几何形状和剖面尺寸,减小悬臂长度和跨距,以降低桥梁的自振频率,从而减少车桥耦合振动。
4.2 车辆配置优化:调整交通流量和车辆速度,减少车辆对桥梁的荷载作用,降低桥梁的振动响应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实测频谱图(一)
1.5 1
振幅比值
0.5 0 0.00 -0.5 -1 -1.5 桥轴向距离(m) 20.00 40.00 60.00 80.00 100.00 120.00 140.00
实测竖向一阶振型曲线
6 4
振幅比值
2 0 0.00 -2 -4 桥轴向距离(m)
20.00
40.00
60.00
赣龙铁路福建龙岩吊钟岩大桥动力检测
1、工程概述 吊钟岩特大桥(GDK251+355.54)位于上杭境内吊钟岩低山区。桥址 跨越低山及深切沟谷和319国道。吊钟岩特大桥主桥为1-140m上承式钢筋 混凝土拱桥。
2、自振特性测试与结果 吊钟岩特大桥的自振特性采用脉动法测试。自振测点 的布置中,沿跨径方向平分12等间距,共布置13个自振测 点。
加速度(m/s2)
0 0.2 0.0 -0.2 0.6 0.3 0.0 -0.3 -0.6 0 0
10
20
30
40
50
10
20
30
40
50
10
20
30
40
50
时 间(s)
C截面(跨中)竖向加速度实测结果(m/s2)
车次 下行 上行 上行 下行 上行 上行 车速km/h 10 20 20 20 30 30 竖向 最小 -0.146 -0.335 -0.283 -0.251 -0.246 -0.276 最大 0.103 0.201 0.197 0.227 0.190 0.142
吊钟岩特大桥频谱图
.50 .38 .25 .13 .00 1.00 .75 .50 .25 .00 .0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 Hz
F1=1 0 . 16 Hz F1=1 8 . 07 Hz 竖向 1 F2=2 8 . 61 Hz
横向 1 F2=1 6 . 50 Hz
80.00
100.00
120.00
140.00
实测竖向二阶振型曲线
1.4 1.2 1 0.8 0.6 0.4 0.2 0 0.00 20.00 40.00 60.00 80.00 100.00 120.00 140.00
振幅比值
桥轴向距离(m)
实测横向一阶振型曲线
1.5 1
振幅比值
0.5 0 0.00 -0.5 -1 -1.5 桥轴向距离(m)
车桥耦合程序应用
研究生:任硕 jinan168777@
桥梁检测车:日本的桥梁检查设备中,桥体结构的近距离 检查有以下方式:当桥下有检查通道时可运用高空作业车完 成2 年一遍的全面检查。使用高架桥、桥梁折臂检查作业车, 既可以用于检查,也可用于维修作业,桥上设置有人行道, 使用轮胎自行式桥梁检查车。
桥跨结构实测频率及阻尼比
振型 横向一阶 横向二阶 竖向一阶 频率(Hz) 1.016 1.650 1.807 阻尼比 0.010 0.006 0.007
竖向二阶
2.867
0.003
横向、竖向基频分别为1.016、1.807 Hz,参照《铁路桥梁检定规范》 中所规定简支梁的限定:
L/100=100/140=0.714 Hz,可以认为该桥的横向刚度较好。 实测桥跨结构的阻尼为0.003~0.010之间,属于小阻尼振动,符合桥跨结 构的实际情况。
0.0
-0.4 0 10 20 30 40 50 60
时 间(s)
30km/h上行8~9#柱跨中竖、横、纵向动位移曲线
C截面(跨中截面)动位移横向振幅测试结果(mm)
车次 上行 上行 下行 上行 下行 上行 速度 km/h 20 30 30 40 40 50 横向 最小 -0.37 -0.90 -0.70 -0.87 -1.45 -1.78 最大 0.34 0.93 0.70 0.70 1.52 2.09
Min
Max
-0.38
-0.146
Hale Waihona Puke 0.1030.391
4、动位移振幅测试结果与分析 各测试截面的实测位移时程曲线。桥跨结构的实测动位 移振幅的最大、最小值。
行车(上行30km/h)吊钟岩大桥(8~9#墩跨中)
1
0
-1
动位移(mm)
0.4
0
10
20
30
40
50
60
0.0
-0.4 0.4 0 10 20 30 40 50 60
应变 (uε)
40
测点B-1A
0
-40
20
0
10
20
30
40
50
测点B-2A
应变 (uε)
0
-20
-40 0 10 20 30 40 50
时 间(s)
40km/h上行B(L/4)截面动应变时程曲线
从动力系数结果可见,在行车工况下, A截面的应力冲击系数介于1.00~1.24之间; B截面的应力冲击系数介于1.01~1.12之间; C截面的应力冲击系数介于1.01~1.32之间; D截面的应力冲击系数介于1.01~1.61。 说明行车对桥跨桥跨结构的冲击作用较为明显,同时11#立 柱底部(D截面)的冲击作用要强于拱肋截面(A、B、C截 面)。实桥试验时,线路道碴尚未振捣密实,因而实测冲 击作用偏大,符合实际情况。
上行
上行 min max
55
58
-1.49
-1.64 -1.78 -0.37
1.83
1.49 0.34 2.09
根据《铁路桥梁检定规范》中规定,参照对预应力钢筋混凝土简支梁, 实测跨中横向最大振幅(单峰值,mm)应满足下式的规定:
Amax L / 16.5
其中L为跨度(m)。因此[A]=8.48mm。吊钟岩大桥的实测横向振幅均 小于相应简支梁的限值,可认为横向刚度较好。
行车(上行40km/h)吊钟岩大桥(拱 角)
应变 (uε)
30
测点A-1A
0
-30
-60 40 -10 0 10 20 30 40 50 60 70
应变 (uε)
测点A-1B
0
-40
-10
0
10
20
30
40
50
60
70
时 间(s)
40km/h上行A(拱脚)截面动应变时程曲线
行车(上行40km/h)吊钟岩大桥
下行
下行 上行 上行 下行 上行 下行 上行 上行
30
30 40 40 40 50 50 55 58
-0.209
-0.319 -0.245 -0.304 -0.352 -0.328 -0.380 -0.376 -0.362
0.234
0.164 0.247 0.170 0.391 0.250 0.353 0.226 0.227
20.00
40.00
60.00
80.00
100.00
120.00
140.00
实测横向二阶振型曲线
3、加速度测试结果 各测试截面的实测加速度时程曲线。桥跨结构各截面处实 测加速度结果分别对其最大值及最小值进行提取,跨中截面 处的加速度结果。行车(下行50km/h)吊钟岩大桥(8~9#墩跨中)
0.2 0.0 -0.2
