刘徽割圆术ppt
合集下载
数学家刘徽PPT优选版

• 算问题。 利用圆周率可以求圆的周长、面积;圆柱、圆锥的体积等。
长方形的宽就等于圆的半径(r),长方形的长就是圆周长(C)的一半。
• 刘徽提出的计圆算圆面周积率的公科学式方的法,推奠定导了:此后把千余圆年平来中均国圆分周成率计若算在干世份界上,的领可先以地位拼。 成一个近似的长方形。
《再隋去书 八·个律角历,志长又》变方论成历形了代十量的六制边宽引形商就。功章等注于,说圆"魏的陈留半王景径元(四年r()263,)刘徽长注方《九形章》的。长就是圆周长(C)的一半。 《长海方岛 形算的经宽》就长一等书于方中圆形,的刘半的徽径精(面心r)积选,编长是了方九a形个b的测,长量就那问是题圆圆,周这的长些(面题C目)积的的创一就造半是性。、:复杂圆性的和富半有代径表(性,r都)在的当时平为西方方乘所瞩以目。π, S=πr²。 他善于观察、善于发现,通过自己不懈的努力才有了今天到的成就。
背景资料链接
• 刘徽在数学上的贡献极多,在开方不尽的问题中提出"求徽数"的思想,这
方法与后来求无理根的近似值的方法一致,它不仅是圆周率精确计算的必 要条件,而且促进了十进小数的产生;在线性方程组解法中,他创造了比 直除法更简便的互乘相消法,与现今解法基本一致;并在中国数学史上第 一次提出了"不定方程问题";他还建立了等差级数前n项和公式;提出并定义 了许多数学概念:如幂(面积);方程(线性方程组);正负数等等.刘徽还提出了 许多公认正确的判断作为证明的前提.他的大多数推理、证明都合乎逻辑, 十分严谨,从而把《九章算术》及他自己提出的解法、公式建立在必然性 的基础之上。虽然刘徽没有写出自成体系的著作,但他注《九章算术》所 运用的数学知识,实际上已经形成了一个独具特色、包括概念和判断、并 以数学证明为其联系纽带的理论体系。
长方形的宽就等于圆的半径(r),长方形的长就是圆周长(C)的一半。
• 刘徽提出的计圆算圆面周积率的公科学式方的法,推奠定导了:此后把千余圆年平来中均国圆分周成率计若算在干世份界上,的领可先以地位拼。 成一个近似的长方形。
《再隋去书 八·个律角历,志长又》变方论成历形了代十量的六制边宽引形商就。功章等注于,说圆"魏的陈留半王景径元(四年r()263,)刘徽长注方《九形章》的。长就是圆周长(C)的一半。 《长海方岛 形算的经宽》就长一等书于方中圆形,的刘半的徽径精(面心r)积选,编长是了方九a形个b的测,长量就那问是题圆圆,周这的长些(面题C目)积的的创一就造半是性。、:复杂圆性的和富半有代径表(性,r都)在的当时平为西方方乘所瞩以目。π, S=πr²。 他善于观察、善于发现,通过自己不懈的努力才有了今天到的成就。
背景资料链接
• 刘徽在数学上的贡献极多,在开方不尽的问题中提出"求徽数"的思想,这
方法与后来求无理根的近似值的方法一致,它不仅是圆周率精确计算的必 要条件,而且促进了十进小数的产生;在线性方程组解法中,他创造了比 直除法更简便的互乘相消法,与现今解法基本一致;并在中国数学史上第 一次提出了"不定方程问题";他还建立了等差级数前n项和公式;提出并定义 了许多数学概念:如幂(面积);方程(线性方程组);正负数等等.刘徽还提出了 许多公认正确的判断作为证明的前提.他的大多数推理、证明都合乎逻辑, 十分严谨,从而把《九章算术》及他自己提出的解法、公式建立在必然性 的基础之上。虽然刘徽没有写出自成体系的著作,但他注《九章算术》所 运用的数学知识,实际上已经形成了一个独具特色、包括概念和判断、并 以数学证明为其联系纽带的理论体系。
北师大版数学六年级上册第1单元《圆周率的历史》ppt课件

落木学.科.网
论述“木叶”是诗人们笔下钟爱的形象。
赏析第二部分
1.古代的诗人们都在什么场合才用“木”字呢? ——秋风叶落的季节。
2.作者为什么要拿 “高树”和“高木”进行对比? ——“高树”则饱满,“高木”则空阔。“木” 仿佛本身就含有一个落叶的因素。
“木”的艺术特征之一——“木”被钟爱的第一个 原因。
原因。
论述为什么诗人钟爱“木叶”这一形象。
赏析第三部分
“木叶”是古代诗人们钟爱的意象,其实诗人们钟 爱的是“木”这一意象所暗示出来的“木”的全部的艺 术特征。
林庚先生认为,“木叶”之与“树叶”,不过是一 字之差,“木”与“树”在概念上原是相去无几的,然 而到了艺术形象的领域,这里的差别就几乎是一字千金。
春风又绿江南岸,明月何时照我还。
望月怀远,思念亲人,思念家乡, 暗含月圆人不圆的愁绪。
在我国古代的艺术殿堂中,诗歌始终象一颗璀 璨的明珠,放射出经久不衰、灿烂夺目的光彩。在 诗歌中有许多意象由于具有相对稳定的感情色彩, 诗人们往往用它们表现相似或相通的感情。如“折 柳”、“蟋蟀”等表示赠别的意象,常可见于赠别 类诗歌中。文中“木叶”如此。本课,我们了解了 “木”的两个艺术特征,领会了诗歌语言的暗示 性。
355
22 7
为 11,3
密率为 ,并且精确地算出圆周率在3.1415926和
3.1415927之间。 这一成就,使中国在圆周率的计 算方面在世界领先1000年。
电子计算机的出现带来了计算方面的革命, 的
小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后 12411亿位。
与同学交流阅读后的感觉,你又知道了哪些有关圆周率的知识? 收集其他有关圆周率的历史资料,在班上进行展示。
《圆周率的认识》圆PPT课件

3.14×20=62.8(厘米) 3.14×4×2=25.12(分米)
自主学习反馈
2、古代人们用来磨面的石碾的半径是1.2米, 估一估,绕石碾走一 圈大约是多少米?
3.14×1.2×2=7.536(米)
探究新知
探究一:
如何测量车轮的周长呢?用图片试一试看。
圆片向右滚动一周。
355
22 ,7
密率为 11,3 并且精确地算出圆周率在3.1415926和3.1415927
之间。
这一成就,使中国在圆周率的计算方面在世界领先1000 年。
电子计算机的出现带来了计算方面的革命, 的小数
点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后 12411亿位。
与同学交流阅读后的感觉,你又知道了哪些有关圆周率的知识? 收集其他有关圆周率的历史资料,在班上进行展示。
探究新知
探究三: 找3个大小不同的圆片,分别测量出周长和直径,做一 做,填一填。
观察上表,你能发现圆的周长与直径有什么关系吗? 圆的周长总是直径的3倍多一些。
探究新知
探究三: 找3个大小不同的圆片,分别测量出周长和直径,做一 做,填一填。
观察上表,你能发现圆的周长与直径有什么关系吗? 实际上,圆的周长除以直径的商是一个固定的数,我们把它叫 作圆周率,用字母π表示,计算时通常取3.14。
六年级上册
圆的周长
情境导入 人们很早就发现,轮子越大,滚一圈就越远。
你有什么发现?
车轮滚动一圈的长度就是它的周长。
本节目标
1、在观察、操作、测量等活动中,经历探索圆周率以及总结圆周长公式 的过程。 2、认识圆周率,理解并掌握圆的周长公式,能运用周长公式正确进行计 算。 3、体验数学与日常生活的密切联系,了解圆周率的探索历史,激发民族 自豪感。
刘徽割圆术求圆面积的过程

刘徽割圆术求圆面积的过程
刘徽首先从圆的内接正六边形开始割圆,然后将边数逐渐增加,照这样一直分割下去,等到不可割的时候,圆的内接正多边形就和圆合二为一了。
然后他将这个正多边形分割成以圆心为原点,以每条边为底的等腰三角形,这些等腰三角形的高和底相乘得出的结果,是它本身面积的两倍。
因此将他们全部相加便是圆的面积的两倍,而这些等腰三角形的底边之和便是圆的周长,因此圆的面积等于圆的周长的一半乘以半径。
割圆术
均速度为
y 16(2) 2 16(0) 2 32英尺 / 秒 t 20
例 2 求上例中岩石在时刻t=2的速度
y 16(2 h)2 16(2)2 t h
时间区间的长度h(秒) 该时间区间内的平均速 度∆y/∆t(英尺/秒)
1 0.1 0.01 0.001 0.0001 0.00001
实验表明一块致密的固体在地 球表面附近从静止状态自由落
下,下落的头t秒钟下落的英尺
数为
y 16t
2
例 1 (求平均速度) 一块岩石突然松动从峭壁顶 上掉下来,掉下来的头2秒岩石的平均速度是多少?
在任何给定的时间区间上岩石的平均 速度是所走过的距离∆y除以时间区间
的长度∆t。从t=0到t=2的头2秒下落平
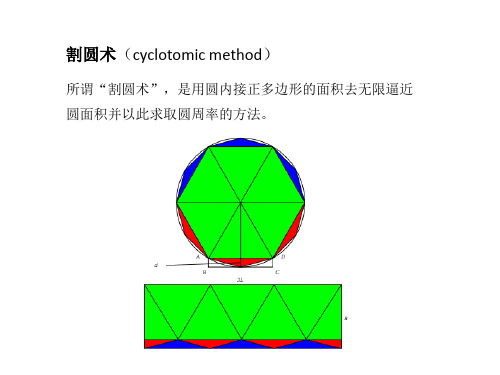
割圆术(cyclotomic method)
所谓“割圆术”,是用圆内接正多边形的面积去无限逼近 圆面积并以此求之上的。他 首先论证,将圆分割成多边形,分割来越细,多边形 的边数越多,多边形的面积就和圆面积没有差别了。
他说,将6边形一边的长度乘以圆半径,再乘3,得12
边形的面积。将12边形的一边长乘半径,再乘6,得 24边形面积。越割越细,多边形和圆面积的差越小。 如此割了再割,最后终于和圆合为一体,毫无差别了
正12边形面积 <正24边形面积< 正48边形面积<正96 边形面积……<内接6*2N边形面积<圆面积
按照这样的思路,刘徽把圆内接 正多边形的面积一直算到了正
80 65.6 64.16 64.016 64.0016 64.00016
例 2 求上例中岩石在时刻t=2的速度
y 16(2 h) 2 16(2) 2 t h 16(4 4h h 2 ) 64 h 64h 16h 2 64 16h h
y 16(2) 2 16(0) 2 32英尺 / 秒 t 20
例 2 求上例中岩石在时刻t=2的速度
y 16(2 h)2 16(2)2 t h
时间区间的长度h(秒) 该时间区间内的平均速 度∆y/∆t(英尺/秒)
1 0.1 0.01 0.001 0.0001 0.00001
实验表明一块致密的固体在地 球表面附近从静止状态自由落
下,下落的头t秒钟下落的英尺
数为
y 16t
2
例 1 (求平均速度) 一块岩石突然松动从峭壁顶 上掉下来,掉下来的头2秒岩石的平均速度是多少?
在任何给定的时间区间上岩石的平均 速度是所走过的距离∆y除以时间区间
的长度∆t。从t=0到t=2的头2秒下落平
割圆术(cyclotomic method)
所谓“割圆术”,是用圆内接正多边形的面积去无限逼近 圆面积并以此求之上的。他 首先论证,将圆分割成多边形,分割来越细,多边形 的边数越多,多边形的面积就和圆面积没有差别了。
他说,将6边形一边的长度乘以圆半径,再乘3,得12
边形的面积。将12边形的一边长乘半径,再乘6,得 24边形面积。越割越细,多边形和圆面积的差越小。 如此割了再割,最后终于和圆合为一体,毫无差别了
正12边形面积 <正24边形面积< 正48边形面积<正96 边形面积……<内接6*2N边形面积<圆面积
按照这样的思路,刘徽把圆内接 正多边形的面积一直算到了正
80 65.6 64.16 64.016 64.0016 64.00016
例 2 求上例中岩石在时刻t=2的速度
y 16(2 h) 2 16(2) 2 t h 16(4 4h h 2 ) 64 h 64h 16h 2 64 16h h
圆周率的认识PPT课件

独立阅读,想一想你知道了哪些有关圆周率的知识?
最早的圆周 率
阿基米德和圆周 率
刘以后
最早的解决方案是测量。人类的祖先在实 践中发现,不同粗细的圆木,用绳子绕上一 圈,绳子的长度总是圆木直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年 前的《周髀算经》。
刘徽用这种方法不断地“割圆”,一直算到圆内 接正192边形,得到圆周率的近似值是3.14.
我国南北朝时期的数学家祖冲之使用“缀 术”计算圆周率。可惜这种方法早已失传。 据专家推测,“缀术”类似“割圆术”,通 过对正24576边形周长的计算来推导。计算 相当繁杂,当时还没有算盘。
最后得出了 的两个分数形式的近似值:约率为 ,密
率为2 2 ,并且精3确5 5地算出圆周率在3.1415926和3.1415927
之间7 。
113
这一成就,使中国在圆周率的计算方面在世界领先1000 年。
电子计算机的出现带来了计算方面的革命, 的小数
点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后 12411亿位。
与同学交流阅读后的感觉,你又知道了哪些有关圆周率的 知识?
收集其他有关圆周率的历史资料,在班上进行展示。
个人观点供参考,欢迎讨论
用测量的方法计算圆周率,圆周率的精确程度取决 于测量的精确程度,而有许多实际困难限制了测量的 精度。
古希腊数学家阿基米德发现: 当正多边形的边数增加时,它的形状就越
来越接近圆。
223<圆周率<22
71
7
我国魏晋时期的数学家刘徽创造了用“割 圆术”求圆周率的方法,在数学史上占有重 要的地位。刘徽是怎样“割圆”的呢?
最早的圆周 率
阿基米德和圆周 率
刘以后
最早的解决方案是测量。人类的祖先在实 践中发现,不同粗细的圆木,用绳子绕上一 圈,绳子的长度总是圆木直径的3倍多一点。
在我国,现存有关圆周率的最早记载是2000多年 前的《周髀算经》。
刘徽用这种方法不断地“割圆”,一直算到圆内 接正192边形,得到圆周率的近似值是3.14.
我国南北朝时期的数学家祖冲之使用“缀 术”计算圆周率。可惜这种方法早已失传。 据专家推测,“缀术”类似“割圆术”,通 过对正24576边形周长的计算来推导。计算 相当繁杂,当时还没有算盘。
最后得出了 的两个分数形式的近似值:约率为 ,密
率为2 2 ,并且精3确5 5地算出圆周率在3.1415926和3.1415927
之间7 。
113
这一成就,使中国在圆周率的计算方面在世界领先1000 年。
电子计算机的出现带来了计算方面的革命, 的小数
点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后 12411亿位。
与同学交流阅读后的感觉,你又知道了哪些有关圆周率的 知识?
收集其他有关圆周率的历史资料,在班上进行展示。
个人观点供参考,欢迎讨论
用测量的方法计算圆周率,圆周率的精确程度取决 于测量的精确程度,而有许多实际困难限制了测量的 精度。
古希腊数学家阿基米德发现: 当正多边形的边数增加时,它的形状就越
来越接近圆。
223<圆周率<22
71
7
我国魏晋时期的数学家刘徽创造了用“割 圆术”求圆周率的方法,在数学史上占有重 要的地位。刘徽是怎样“割圆”的呢?
刘徽和祖冲之、祖暅父子在球体积计算方面的成就-课件(共20张PPT)
中图,小方盖差在等高处的截面面积等于r2 -a2 =h2.
右图,底边为r,高也是r的倒正四棱锥,在 等高处的截面面积也是h2.
根据祖暅原理可知:小方盖差和倒立正四棱 锥的体积相等。
谢谢欣赏!
用微笑告诉别人,今天的我,比昨天更强。瀑布跨过险峻陡壁时,才显得格外雄伟壮观。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。孤独是 每个强者必须经历的坎。有时候,坚持了你最不想干的事情之后,会得到你最想要的东西。生命太过短暂,今天放弃了明天不一定能得到。只有经历人生 的种种磨难,才能悟出人生的价值。没有比人更高的山,没有比脚更长的路学会坚强,做一只沙漠中永不哭泣的骆驼!一个人没有钱并不一定就穷,但没 有梦想那就穷定了。困难像弹簧,你强它就弱,你弱它就强。炫丽的彩虹,永远都在雨过天晴后。没有人能令你失望,除了你自己人生舞台的大幕随时都 可能拉开,关键是你愿意表演,还是选择躲避。能把在面前行走的机会抓住的人,十有八九都会成功。再长的路,一步步也能走完,再短的路,不迈开双 脚也无法到达。有志者自有千计万计,无志者只感千难万难。我成功因为我志在成功!再冷的石头,坐上三年也会暖。平凡的脚步也可以走完伟大的行程。 有福之人是那些抱有美好的企盼从而灵魂得到真正满足的人。如果我们都去做自己能力做得到的事,我们真会叫自己大吃一惊。只有不断找寻机会的人才 会及时把握机会。人之所以平凡,在于无法超越自己。无论才能知识多么卓著,如果缺乏热情,则无异纸上画饼充饥,无补于事。你可以选择这样的“三 心二意”:信心恒心决心;创意乐意。驾驭命运的舵是奋斗。不抱有一丝幻想,不放弃一点机会,不停止一日努力。如果一个人不知道他要驶向哪个码头, 那么任何风都不会是顺风。行动是理想最高贵的表达。你既然认准一条道路,何必去打听要走多久。勇气是控制恐惧心理,而不是心里毫无恐惧。不举步, 越不过栅栏;不迈腿,登不上高山。不知道明天干什么的人是不幸的!智者的梦再美,也不如愚人实干的脚印不要让安逸盗取我们的生命力。别人只能给 你指路,而不能帮你走路,自己的人生路,还需要自己走。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。后悔是一种耗费精神的情绪,后悔是 比损失更大的损失,比错误更大的错误,所以,不要后悔!复杂的事情要简单做,简单的事情要认真做,认真的事情要重复做,重复的事情要创造性地做。 只有那些能耐心把简单事做得完美的人,才能获得做好困难事的本领。生活就像在飙车,越快越刺激,相反,越慢越枯燥无味。人生的含义是什么,是奋 斗。奋斗的动力是什么,是成功。决不能放弃,世界上没有失败,只有放弃。未跌过未识做人,不会哭未算幸运。人生就像赛跑,不在乎你是否第一个到 达终点,而在乎你有没有跑完全程。累了,就要休息,休息好了之后,把所的都忘掉,重新开始!人生苦短,行走在人生路上,总会有许多得失和起落。 人生离不开选择,少不了抉择,但选是累人的,择是费人的。坦然接受生活给你的馈赠吧,不管是好的还是坏的。现在很痛苦,等过阵子回头看看,会发 现其实那都不算事。要先把手放开,才抓得住精彩旳未来。可以爱,可以恨,不可以漫不经心。我比别人知道得多,不过是我知道自己的无知。你若不想 做,会找一个或无数个借口;你若想做,会想一个或无数个办法。见时间的��
右图,底边为r,高也是r的倒正四棱锥,在 等高处的截面面积也是h2.
根据祖暅原理可知:小方盖差和倒立正四棱 锥的体积相等。
谢谢欣赏!
用微笑告诉别人,今天的我,比昨天更强。瀑布跨过险峻陡壁时,才显得格外雄伟壮观。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。孤独是 每个强者必须经历的坎。有时候,坚持了你最不想干的事情之后,会得到你最想要的东西。生命太过短暂,今天放弃了明天不一定能得到。只有经历人生 的种种磨难,才能悟出人生的价值。没有比人更高的山,没有比脚更长的路学会坚强,做一只沙漠中永不哭泣的骆驼!一个人没有钱并不一定就穷,但没 有梦想那就穷定了。困难像弹簧,你强它就弱,你弱它就强。炫丽的彩虹,永远都在雨过天晴后。没有人能令你失望,除了你自己人生舞台的大幕随时都 可能拉开,关键是你愿意表演,还是选择躲避。能把在面前行走的机会抓住的人,十有八九都会成功。再长的路,一步步也能走完,再短的路,不迈开双 脚也无法到达。有志者自有千计万计,无志者只感千难万难。我成功因为我志在成功!再冷的石头,坐上三年也会暖。平凡的脚步也可以走完伟大的行程。 有福之人是那些抱有美好的企盼从而灵魂得到真正满足的人。如果我们都去做自己能力做得到的事,我们真会叫自己大吃一惊。只有不断找寻机会的人才 会及时把握机会。人之所以平凡,在于无法超越自己。无论才能知识多么卓著,如果缺乏热情,则无异纸上画饼充饥,无补于事。你可以选择这样的“三 心二意”:信心恒心决心;创意乐意。驾驭命运的舵是奋斗。不抱有一丝幻想,不放弃一点机会,不停止一日努力。如果一个人不知道他要驶向哪个码头, 那么任何风都不会是顺风。行动是理想最高贵的表达。你既然认准一条道路,何必去打听要走多久。勇气是控制恐惧心理,而不是心里毫无恐惧。不举步, 越不过栅栏;不迈腿,登不上高山。不知道明天干什么的人是不幸的!智者的梦再美,也不如愚人实干的脚印不要让安逸盗取我们的生命力。别人只能给 你指路,而不能帮你走路,自己的人生路,还需要自己走。勤奋可以弥补聪明的不足,但聪明无法弥补懒惰的缺陷。后悔是一种耗费精神的情绪,后悔是 比损失更大的损失,比错误更大的错误,所以,不要后悔!复杂的事情要简单做,简单的事情要认真做,认真的事情要重复做,重复的事情要创造性地做。 只有那些能耐心把简单事做得完美的人,才能获得做好困难事的本领。生活就像在飙车,越快越刺激,相反,越慢越枯燥无味。人生的含义是什么,是奋 斗。奋斗的动力是什么,是成功。决不能放弃,世界上没有失败,只有放弃。未跌过未识做人,不会哭未算幸运。人生就像赛跑,不在乎你是否第一个到 达终点,而在乎你有没有跑完全程。累了,就要休息,休息好了之后,把所的都忘掉,重新开始!人生苦短,行走在人生路上,总会有许多得失和起落。 人生离不开选择,少不了抉择,但选是累人的,择是费人的。坦然接受生活给你的馈赠吧,不管是好的还是坏的。现在很痛苦,等过阵子回头看看,会发 现其实那都不算事。要先把手放开,才抓得住精彩旳未来。可以爱,可以恨,不可以漫不经心。我比别人知道得多,不过是我知道自己的无知。你若不想 做,会找一个或无数个借口;你若想做,会想一个或无数个办法。见时间的��
《微积分发展简史》PPT课件
主要内容
微积分的符号
微分学中的符号“dx”、“dy”等,系 由莱布尼茨首先使用。其中的d 源自拉丁语 中“差”(Differentia )的第一个字母。积 分符号“∫”亦由莱布尼茨所创,它是拉丁语 “总和”(Summa)的第一个字母s 的伸长 (和Σ有相同的意义)。
微积分发展史
微积分的萌芽
微积分的发展 微积分的建立 微积分的严格化
微积分的发展
4、费马求极大值和极小值方法 按费马的方法。设函数f(x)在点a处取极
值,费弓用“a+e”代替原来的未知量a,并使 f(a+e)与f(a)逼近,即:
f(a+e)~f(a) 这里所提到的“e”就是后来微积分学当
中的“ x ”
微积分的发展
5、巴罗的“微分三角形” 巴罗是牛顿的老师。是英国剑桥大学第一
出一条纵坐标为z的曲线,使其切线的斜率
为
.如果是在区间[a,b]上,由[0,b]
上的面积减去[0,a]上的面积,便得到
b
ydx zb za
a
微积分的严格化
自牛顿和莱布尼兹之后,微积分得到了 突飞猛进的发展,人们将微积分应用到自然 科学的各个方面,建立了不少以微积分方法 为主的分支学科,如常微分方程、偏微分方 程、积分方程、变分法等等形成了数学的三 大分支之一的“分析”。微积分应用于几何 开拓了微分几何,有了几何分析;应用于理 学上,就有了分析力学;于天文上就有了天 体力学等。但是微积分的基础是不牢固的, 尤其在适用无穷小概念上的随意与混乱,一 会儿说不是零,一会儿说是零,这引起了人 们对他们的理论的怀疑与批评。
主要内容
微积分的基本概念还包括函数、无穷 序列、无穷级数和连续等,运算方法主要 有符号运算技巧,该技巧与初等代数和数 学归纳法紧密相连。
六年级数学上册- 刘徽割圆术
刘徽割圆术
同学们:你们知道在古代,人们还没有推导出圆周长计算公式的时 候,他们是怎么计算圆的周长的吗?
请你试一试,完成下面的表格。
……
(3 )边形
( 6)边形
( 12)边形
圆
边长:5.1cm 边长:3cm
边长:1.6cm
半径:3cm
周长:15.3cm 周长:18cm
周长:19.2cm
周长:18.84cm
割圆计算的刘徽算法
l6 l12 l24 l48 S12 S24 S48
L
取 r l6 1 递推计算
l2n 2
S2n
n 2
ln
4 ln2
证明基于勾股定理
小
股
勾 勾小
股小
弦
弦
8
从先秦时期开始 “周三径一” 误差很大
正六边形的周长
其数值要比实际的圆 周长小得多
刘徽割圆术
正30பைடு நூலகம்2边形
π≈3.14和3.1416
这个结果是当时世界上圆周 率计算的最精确的数据。
刘徽割圆术
极限
无穷小分割
刘徽的割圆术,为圆周率研究工作奠定了坚实 可靠的理论基础,在人类历史上首次将极限和无穷小 分割引入数学证明,成为人类文明史中不朽的篇章。
谢谢!
我的发现: 1. 边长×边数=正多边形的周长。
2.画的正多边形边数越多,越接近圆,正多边形周长也越接近圆 的周长。 3. 如果这样一直画下去,就可以无限接近圆。
千古绝技
割圆术
刘徽割圆术
割之弥细,所失弥少。 割之又割,以至于不可割, 则与圆周合体而无所失矣。
刘徽割圆术
刘徽割圆术
不 断 分 割
……
同学们:你们知道在古代,人们还没有推导出圆周长计算公式的时 候,他们是怎么计算圆的周长的吗?
请你试一试,完成下面的表格。
……
(3 )边形
( 6)边形
( 12)边形
圆
边长:5.1cm 边长:3cm
边长:1.6cm
半径:3cm
周长:15.3cm 周长:18cm
周长:19.2cm
周长:18.84cm
割圆计算的刘徽算法
l6 l12 l24 l48 S12 S24 S48
L
取 r l6 1 递推计算
l2n 2
S2n
n 2
ln
4 ln2
证明基于勾股定理
小
股
勾 勾小
股小
弦
弦
8
从先秦时期开始 “周三径一” 误差很大
正六边形的周长
其数值要比实际的圆 周长小得多
刘徽割圆术
正30பைடு நூலகம்2边形
π≈3.14和3.1416
这个结果是当时世界上圆周 率计算的最精确的数据。
刘徽割圆术
极限
无穷小分割
刘徽的割圆术,为圆周率研究工作奠定了坚实 可靠的理论基础,在人类历史上首次将极限和无穷小 分割引入数学证明,成为人类文明史中不朽的篇章。
谢谢!
我的发现: 1. 边长×边数=正多边形的周长。
2.画的正多边形边数越多,越接近圆,正多边形周长也越接近圆 的周长。 3. 如果这样一直画下去,就可以无限接近圆。
千古绝技
割圆术
刘徽割圆术
割之弥细,所失弥少。 割之又割,以至于不可割, 则与圆周合体而无所失矣。
刘徽割圆术
刘徽割圆术
不 断 分 割
……
刘徽与割圆术
②在筹式演算理论方面 先给率以比较明确的定义,又以遍乘、通约、齐同等三种基本运算为基 础,建立了数与式运算的统一的理论基础,他还用“率”来定义中国古代数 学中的“方程”,即现代数学中线性方程组的增广矩阵。 学中的“方程”,即现代数学中线性方程组的增广矩阵。 ③在勾股理论方面 逐一论证了有关勾股定理与解勾股形的计算原理,建立了相似勾股形理 逐一论证了有关勾股定理与解勾股形的计算原理,建立了相似勾股形理 论,发展了勾股测量术,通过对“勾中容横”与“股中容直”之类的典型图 形的论析,形成了中国特色的相似理论。 ④在面积与体积理论方面 用出入相补、以盈补虚的原理及“割圆术”的极限方法提出了刘徽原理, 用出入相补、以盈补虚的原理及“割圆术”的极限方法提出了刘徽原理, 并解决了多种几何形、几何体的面积、体积计算问题。这些方面的理论价值 至今仍闪烁着余辉。
成就
刘徽的成就大致为两方面:
一是清理中国古代数学体系并奠定了它的理论基础。这方面集中体现在《九章算 是清理中国古代数学体系并奠定了它的理论基础。这方面集中体现在《
术注》 术注》中。它实已形成为一个比较完整的理论体系: ①在数系理论方面 用数的同类与异类阐述了通分、约分、四则运算,以及繁分数化简等的 用数的同类与异类阐述了通分、约分、四则运算,以及繁分数化简等的 运算法则;在开方术的注释中,他从开方不尽的意义出发,论述了无理方根 的存在,并引进了新数,创造了用十进分数无限逼近无理根的方法。
刘徽断言“割之弥细,所失弥少,割之又割,以至于不可割,则 与圆合体,而无所失矣”。其思想与古希腊穷竭法不谋而合。割 圆术在圆周率计算史上曾长期使用。1610年德国数学家柯伦用 圆术在圆周率计算史上曾长期使用。1610年德国数学家柯伦用 2^62边形将圆周率计算到小数点后35位。1630年格林贝尔格利 2^62边形将圆周率计算到小数点后35位。1630年格林贝尔格利 用改进的方法计算到小数点后39位,成为割圆术计算圆周率的最 用改进的方法计算到小数点后39位,成为割圆术计算圆周率的最 好结果。分析方法发明后逐渐取代了割圆术,但割圆术作为计算 圆周率最早的科学方法一直为人们所称道。
