上海高二数学复数实系数一元二次方程的解1
沪教版高中数学高二下册第十三章13.6.1实系数一元二次方程教案

沪教版高中数学高二下册第十三章13.6.1实系数一元二次方程教案13.6.1实系数一元二次方程教学目标:通过用比较的方法讨论在复数集内解实系数一元二次方程的问题,完整掌握实系数一元二次方程的解,完善实系数一元二次方程的基本理论。
会在复数集内对二次及简单的三次、四次多项式进行分解因式。
教学重点与难点:理解在复数范围内,实系数一元二次方程总有两个根,并掌握根的求法。
当时,实系数一元二次方程有两个共轭的虚根。
教学过程:动动手:试在复数集中解下列方程:想一想:1、以上方程的解在复数集中有几种不同的情况?2、是什么在影响方程的解?4、你能归纳出方程在复数集中解的不同情况吗?活动一小结:1、以上结论的使用条件__实系数一元二次方程。
2、实系数一元二次方程的根在复数集中共有三种不同情况:两个不等实根、两个相等实根和一对共轭虚根。
3、代数基本定理:在复数域里,任何一元n次方程至少严格证明。
有一个根。
据此退出,在复数范围里一元n次方程有且仅有n个根(k重根作k个根计)。
1797年高斯首先给出。
活动一的小结1、若关于x的一元二次方程有虚根,则实数k的取值范围是____________。
2、判断下列命题的真假:(1)在复数范围内,方程总有两个根。
(2)若是方程的一个根,则是方程的另一个根。
(3)若是方程的一个根,则这个方程的另一个根是。
活动二测一测,你掌握了吗?例1:在复数集中解下列一元二次方程:例2:在复数集中分解因式:活动三例题讲解本节课总结:1、实系数一元二次方程的根的三种情况,注意本结论的使用条件。
2、会对二次多项式、简单的高次多项式在复数集中进行分解因式。
3、遇到新问题时,善于联想、比较、类比、化归、归纳等方法,总能找到解决之路。
课后思考思考:若是实系数一元二次方程的一个根,求方程的另一个根及的值。
活动四总结。
【公开课教案】沪教版高中数学高二下册第十三章13.6 实系数一元二次方程- 实系数一元二次方程的解教案

实 系 数 一 元 二 次 方 程 的 解教学目标:1.学会求解判别式小于零的实系数一元二次方程,培养复杂问题简单化,陌生问题熟悉化的转化能力。
2.增强知识的类比能力,完善求解实系数一元二次方程的知识体系。
3.体验自主探究,合作交流的学习过程,增强独立解决问题的自信心。
教学重点:实系数一元二次方程求虚根 教学难点:克服由根求系数时实数运算的负迁移 教学过程:一. 引入1. 复习实系数一元二次方程在判别式大于等于零时的根的情况。
2. 实数集扩充到复数集主要解决了负实数没有平方根的矛盾,所以在复数集中,实系数一元二次方程20ax bx c ++=都会有根。
二、新课1、自主尝试--------------求解下列关于x 的一元二次方程222222(1)160(2)20(3)220(4)0(,,,0,40)(5)25(1)x x x x ax bx c a b c R a b ac x x -=+=++=++=∈≠-<=-2、合作交流(1)解决问题的基本途径---------配方法,找平方根≥±当a 0时,实数a 的平方根为当a<0时,实数a 的平方根为(2)当实系数一元二次方程的判别式小于零时,方程有两个虚根,1,212x x x =与互为共轭复数3、深化理解---------------求解关于x 的方程:2360()x x a a R -+=∈4、回顾总结>0=0<5、辨析提高221212221,21221,212(1)6130,(3)70()(4)0()3x x x x x x x x x x x x x k k R x x x x -+=+-+=-++=∈-=22已知1-2i 是关于x 的实系数方程x +mx+n=0的一个根,求另一个根 和系数m,n 的值(2)若方程x 的两个根是,求值:若方程的两个根是,求值:若方程的两个根是,且求实数k 的值.三.小结1.实系数一元二次方程一定有根,或为实根,或为虚根。
高二数学实系数一元二次方程1

例2、已知一元二次方程x2 mx n 0(m、n R),
试确定一组m、n 的值,使该方程分别有两个
不相等的实数根、两个相等的实数根、两个虚
数根,并解方程.
例3、在复数集中分解因式:
(1)x2 x 2; (2)2x2 4x 5
.
2、实系数一元二次方程中根与系数的关系:
13.6(1)实系数一元二次方程
上海市新中高级中学 陶志诚
一、复习 1、一元二次方程ax2 bx c 0(a、b、c R且a 0)
的求根公式 当 b2 4ac 0时,方程有两个实数根:x b b2 4ac
2a 2a
2、-1的平方根是: i
设问①:一元二次方程 x2 1 0在复数范围内有没有解?
b b2 4ac x
2a 2a
(2)当 b2 4ac 0时,原方程有两个相b2 4ac 0时,原方程有两个不相等的虚数根
x b 4ac b2 i 为一对共轭虚数根
2a 2a
例1、(1)在复数集中解方程:3x2 x 2 0
(2)在复数集中解关于x 的方程:
x2 ax 4 0(a R)
;单创:/News/Detail/2019-9-20/442424.htm
;
我也是服了!“ (9)“您就当浪子回头吧,兴许真考上了,您也是积德了。”我回复了微信,也不忘调侃地加了几个坏笑的表情。 (10)之后,因为工作的关系,我离开了那座城市,也与律师楼和老李少了很多的交集。 (11)青海茫崖的矿难,突然成为了这个国家的头条新闻。部分矿务局 领导受贿私自外包矿坑,私人小矿主违规野蛮开采,导致了一次灭顶的矿难。在矿难中死去的矿工遗孀,因为没有基本的合同和安全保险凭据,无法获得赔偿,更无人
高二数学实系数一元二次方程1

上海市新中高级中学 陶志诚
一、复习 1、一元二次方程ax2 bx c 0(a、b、c R且a 0)
的求根公式 当 b2 4ac 0时,方程有两个实数根:x b b2 4ac
2a 2a
2、-1的平方根是: i
设问①:一元二次方程 x2 1 0在复数范围内有没有解?
x2 ax 4 0(a R)
例2、已知一元二次方程x2 mx n 0(m、n R),
试确定一组m、n 的值,使该方程分别有两个
不相等的实数根、两个相等的实数根、两个虚
数根,并解方程.
例3、在复数集中分解因式:
(1)x2 x 2; (2)2x2 4x 5
.
2、实系数一元二次方程中根与系数的关系:
设问②:在复数范围内如何解一元二次方程x2 x 1 0?
二、新课
1、实系数一元二次方程在复数集C中解的情况:
设一元二次方程 ax2 bx c 0(a、b、c R且a 0)
原方程可变形为
x2
b a
x
c a
即
(x
b )2 2a
b2 4ac 4a2
(1)当 b2 4acBiblioteka 0时,原方程有两个不相等的实数根
实系数一元二次方程ax2 bx c 0(a、b、c R且a 0)
根与系数的关系: x1 x2
b a
,x1 x2
c a
例4、已知3i 2是关于x的方程 2x2 px q 0 的一个根,求实数p、q的值.
三、课堂练习 见课本P91练习13.6(1); P92练习13.6(2)T1.2.3.
四、课堂小结
五、课后作业 1.书面作业:练习册P55 习题13.6 A组 T1.2.3.4.5.
上海高二数学下册--02—复数的方根与实系数一元二次方程
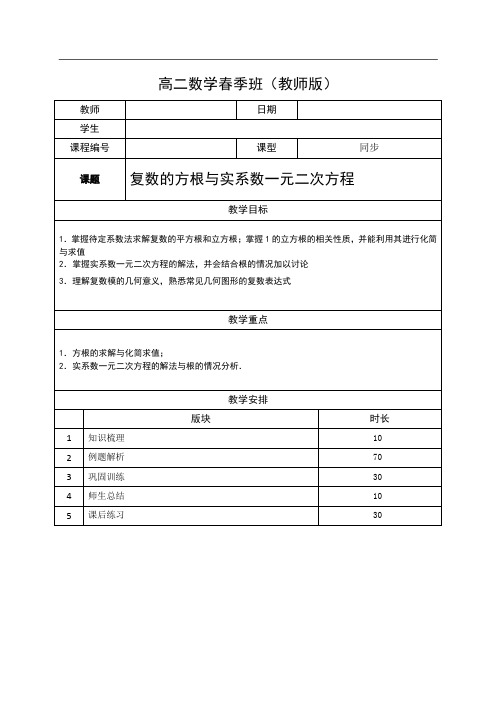
高二数学春季班(教师版)一、复数的平方根与立方根 1.复数的平方根的定义若复数1z ,2z 满足212z z =,则称1z 是2z 的平方根.2.复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等,把复数平方根问题转化为实数方程组来求. 3.复数的平方根的性质复数(0)z z ≠总有两个平方根1z ,2z ,且120z z +=(见图1). 4.复数的立方根的定义类似的,若复数1z ,2z 满足312z z =,则称1z 是2z 的立方根.5.1的立方根设复数12ω=-+,则21,,ωω都是1的立方根. 6.ω的性质 ①210ωω++=, ②31ω=,③212ωω==-. 可运用这些性质化简相关问题(见图2). 7.其他有用结论2(1)2i i -=-,2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式,那么(1)0∆>⇔方程有两个不相等的实根2b a-±;复数的方根与实系数一元二次方程知识梳理(2)0∆=⇔方程有两个相等的实根2b a-; (3)0∆<⇔,在(3)的情况下,方程的根与系数关系(韦达定理)仍然成立. 求解复数集上的方程的方法:(1)设(,)z x yi x y =+∈R 化归为实数方程来解决(化归思想).(2)把z 看成一个未知数(而不是实部和虚部两个未知数),用复数的性质来变形(整体思想). (3)对二次方程,直接用一元二次方程的求根公式(公式法).三、常见几何图形的复数表达式复数1z ,2z 为定值,且12z z ≠.(1)线段12Z Z 的中垂线方程:12||||z z z z -=-; (2)以1Z 为圆心,半径为r 的圆方程:1||z z r -=; (3)以1Z 、2Z 为焦点,长轴长为2(0)a a >的椭圆方程:12||||2z z z z a -+-=(其中12||2z z a -<); (4)以1Z 、2Z 为焦点,实轴长为2(0)a a >的双曲线方程:12||||||2z z z z a ---=(其中12||2z z a ->).1、复数的平方根与立方根 【例1】求4-及86i -的平方根.【难度】★【答案】4-的平方根为2i 或2i -;86i -的平方根为3i -或3i -+ 【例2】计算:(112112(1)22i i i ⎛⎫-+ ⎪⎝⎭;(2)50820028)i +-++⎝⎭. 【难度】★★【答案】(1)513;(2)247+【例3】记12ω=-,求1ωω+,221ωω+. 【难度】★★ 【答案】11ωω+=-,2211ωω+=-【例4】已知等比数列123,,,,n z z z z ,其中11z =,2z x yi =+,3z y xi =+(,,0x y x ∈>R ).(1)求,x y 的值; (2)试求使1230n z z z z ++++=的最小正整数n ;(3)对(2)中的正整数n ,求123n z z z z 的值.【难度】★★【答案】(1)12x y ⎧=⎪⎪⎨⎪=⎪⎩;(2)12n =;(3)1-.【巩固训练】1.复数34i +的平方根是 .例题解析【难度】★ 【答案】(2)i ±+2.计算:(11996= . (2)151512(1)(1)(1)i -+=-+ .【难度】★ 【答案】(1)12-;(2)03.已知ω满足等式210ωω++=.(1)计算4(1)ωω++;304050ωωω++;224(1)(1)ωωωω-+-+;(2)求证:对任意复数u ,有恒等式33233(1)()()3(1)u u u u ωω+++++=+; (3)计算:21n n ωω++,*n ∈N . 【难度】★★【答案】(1)1-;0;4;(2)略;(3)*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式:2223x x ++ 【难度】★【答案】22232x x x x ⎛++=-⎝⎭⎝⎭11222x x ⎛⎫⎛⎫-+=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=,求()41z z ++的值 【难度】★★【答案】由210z z ++=得,21102z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1.若虚数z 满足327z =,则32315z z z +++的值为 . 【难度】★★ 【答案】332.,,求的值.【难度】★★【答案】12ω=-时,原式=15-;12ω=-时,原式;3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ,求方程的解. 【难度】★【答案】920m ∆=- 当0∆>时,即920m <时,32x ±=;当0∆=时,即920m =时,32x =; 当0∆<时,即920m >时,32i x =.【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根,且2αβ∈R ,求βα的值.【难度】★★【答案】∵2αβ∈R ,∴2222ααβαββαβ=⇒=,即330αβ-=∴12αβ=-± 1≠ω13=ω32302ωωω+++【例9】已知12,x x 是实系数方程20x x p ++=的两个根,且满足12||3x x -=,求实数p 的值. 【难度】★★ 【答案】14p ∆=-, (1)当0∆≥时,即14p ≤时,12,x x 是实根,∴12||3x x -==,即32p =⇒=-; (2)当0∆<时,即14p >时,12,x x 是共轭虚根,设1(,)x a bi a b =+∈R ,则2x a bi =-, ∴123|||2|2||32x x bi b b -===⇒=±,由1221x x a +==-,得12a =-.从而21215||2p x x x ===.综上,2p =-或52.【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根,求||||αβ+的值. 【难度】★★【答案】212m ∆=-,(1)当0∆≥时,即m ≥m ≤-30αβ=>,∴||||||||m αβαβ+=+=; (2)当0∆<时,即m -<<||||2||αβα+===.【例11】已知复数12,z z 满足1||2z =,2||1z =,12||2z z -=,求12z z . 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=, ∴12121z z z z ⋅+⋅=, ∴122211211z zz z z z z z ⋅⋅+⋅⋅=, ∴122141z zz z +=. 令12z t z =,则141t t+=,∴240t t -+=,∴122t =±,即12122z i z =±.【例12】(1)方程20()x px k p -+=∈R 有一个根为12i +,求实数k 的值; (2)方程240x x k -+=有一个根为12i +,求k 的值. 【难度】★【答案】(1)由题意:另一个根为12i -,∴(12)(12)5k i i =+-=; (2)由题意2(12)4(12)074i i k k i +-++=⇒=+.【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根,且一个根的模是2,求实数a 、b 的值. 【难度】★★【答案】设()t t ∈R 是方程的一实根,则2(2)()i 0t at a bt b -++-=.则220,0t at a bt b ⎧-+=⎨-=⎩.(1)当0b =时,此方程为220x ax a -+=. ①有实根,0∆≥即1a ≥或0a ≤.当根为2时,440a a -+=.得43a =. 当根为2-时,440a a ++=.得45a =-.②有一对共轭虚根即01a <<.模为2,即有4a =(舍).(2)当0b ≠时,则1t =,此时1a =.又因为模为2,所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1.下列命题在复数集中是否正确?为什么?(1)若,,a b c ∈R ,0a ≠,且240b ac -≥,则方程20ax bx c ++=有两个实数根;(2)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则12b x x a +=-,12cx x a=; (3)若,,a b c ∈R ,0a ≠,且12,x x 是方程20ax bx c ++=的两个根,则221212||()x x x x -=-;(4)若,,a b c ∈R ,0a ≠,且α是方程20ax bx c ++=的根,则α也是方程的根. 【难度】★★ 【答案】(1)、(2)、(4)正确,(3)不正确2.若12,x x 为方程270x x -+=的两个根,则212||x x -= .【难度】★★ 【答案】273.已知,0x y ≠且,求20092009()(x y x y x y+++的值. 【难度】★★【答案】14.关于x 的方程222(31)10x m x m --++=的两根为αβ、,且||||3αβ+=,求实数m 的值. 【难度】★★【答案】53m =-或2m =5.设αβ、为方程220x x t ++=,(t ∈R )的两个根,()||||f t αβ=+, (1)求()f t 的解析式;(2)证明关于t 的方程()f t m =,当2m >时恰有两个不等的根,且两根之和为定值. 【难度】★★【答案】(1)0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩...(2)证明:函数()y f t =的图像关于直线12t =对称(证略) 当(1,)t ∈+∞时,()f t 为增函数,且()(2,)f t ∈+∞;022=++y xy x当(,0)t ∈-∞时,()f t 为减函数,且()(2,)f t ∈+∞.所以当2m >,方程()f t m =在区间(1,)+∞上有唯一解1t ,在区间(,0)-∞上也有唯一解2t , 则121212t t +=⨯=.4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中,1z ,2z ,m 都是复数,且21241620z z i -=+,设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值. 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=.∴2121|(4)|74m z z --=,即|(45)|7m i -+=, 这表明复数m 在以(4,5)C 为圆心,7为半径的圆周上,∴max ||7m =min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<.【例14】已知22016220160122016(1)x x a a x a x a x ++=++++,试求0362016a a a a ++++的值。
沪教版高中数学高二下册第十三章13.6 实系数一元二次方程 课件(2)

59.不要让追求之舟停泊在幻想的港湾,而应扬起奋斗的风帆,驶向现实生活的大海。 7、虚弱的人会游说各地的不幸,而坚强的人只会在沉默中变得更强。 15.这个世界本就邋遢,所以没有什么可怕。每个人都有无法发泄的苦涩,都有无力排解的抑郁,而生活在这里的我们,哪一个不是拼尽全力 ,甚至不择手段地活着。
8、生活是一个过程。您不必太在意结果。心态不好的人会看过去,心态好的人会看未来。放开过去的所有无助。 75.你看着天空,才发现从七岁起陪着你的那个天空,一直都在你的头顶。然后,你最后一次的想,会不会云层的上头,真的有那一个城堡。 却又突然间觉得自己的这个想法很可笑。你终于是明白,原来生活比你想象的是艰难很多。
问题3:
❖ 当实系数一元二次方程有一对共轭虚根 时,根与系数的关系还成立吗?
x
1
x
1
x2 x2
c a
b a
√
例4.3i-2是关于x的方程2x2+px+q=0 的一个根,求实数p、q的值.
问题4:根与方程的关系
❖知道方程,可以求根 ❖知道根,如何得到方程?
例5. 1+2i是实系数一元二次方 程的一个根,则这个方程可以 是?
98.哪怕此刻的生活有多糟糕,也总会有好转的一天。走过的生活并不完美,太完美的也就不是生活了!每人每天都在做一件事情:为了未来 而奋斗!固然结果不同,皆因我们平时的努力,每个今天我们都尽十分的努力,未来的成功就是必然!
高二数学下:13.6《实系数一元二次方程》教案(2)(沪教版)

13.6(2)实系数一元二次方程一、教学内容分析本节课是“实系数一元二次方程”的第二节课,上一节课主要讨论了实系数一元二次方程在复数集中解的情况.学生会在复数集中解实系数一元二次方程;会在复数范围内对二次三项式进行因式分解;能理解实系数一元二次方程有虚数根时的根与系数的关系,并会进行简单应用.本节课将通过练习巩固以上知识,并检验学生对以上知识的掌握程度.课本中的例题3是“实系数一元二次方程”这一节的重点和难点,本节课将引导学生进行重点探究.二、教学目标设计进一步掌握在复数集中解实系数一元二次方程和对二次三项式进行因式分解;掌握实系数一元二次方程有虚数根时的根与系数的关系及其应用.三、教学重点及难点对实系数一元二次方程有虚数根时的根与系数关系的灵活应用.四、教学用具准备电脑、实物投影仪五、教学流程设计六、教学过程设计课堂小结并布置作业复习旧知巩固练习例题精析课堂练习(一)复习旧知上一节课我们主要学习了哪些内容?我们一起来回顾一下.1.实系数一元二次方程20axbx c 在复数集C 中解的情况:(1)当240b ac 时,原方程有两个不相等的实数根242bb ac xa;(2)当240bac 时,原方程有两个相等的实数根2b xa;(3)当240bac 时,原方程有一对共轭虚根21422b ac bx i aa,22422b ac bx i a a.2、二次三项式2axbx c 在复数范围内分解因式:212()()axbx c a xx x x .3、实系数一元二次方程20axbx c 的韦达定理:12bx x a,12c x x a. 特别地,当240bac 时,12x x 和为一对共轭虚根,即21x x —,∴2121||x x x ,1212Re x x x .[说明]以上三点可以让学生回答,而第3点中的“2121||x x x ,1212Re x x x ”可以让学生在老师的引导下发现.(二)巩固练习1.已知1-i 是实系数一元二次方程20xpx q 的一个根,则p q = .2.若两个数之和为2,两个数之积为3,则这两个数分别为.3.在复数集中分解因式:2321xx = .4.若方程220()xax a R 有虚数根z ,则|z|= .参考答案:1. -4 2.12i 和12i3.12123()()3333x i x i 4.2(三)例题精析例1、已知方程210()xpx pR 的两根为1x 、2x ,若121x x ,求实数p 的值.分析:要求实数p 的值,即要利用已知条件121x x ,从而应考虑1x 、2x 为实根还是虚根,因此,应对0和0讨论.解:(见课本P92例3)[说明]对于△<0的情形,也可考虑设1(,)x a bi a bR ,则2x a bi ,由1221x x bi得12b,又由2221211||x x x a b,得32a,所以1223p x x a .设问①:若将题设中的“两根”改为“两虚根”,则如何作答?设问②:我们知道:当1x 、2x 为实数时,2212121212()()4x x x x x x x x ,而当1x 、2x 为虚数时,上式是否仍然成立?请说明理由.[说明]可以给点时间让学生思考和讨论.因为当z 为虚数时,22zz,所以当1x 、2x 为虚数时,上式不成立.可以适当修改为2221212121212|||()||()4|x x x x x x x x x x (*)该结论显然成立.设问③:大家尝试一下,能否利用上述结论(*)来解答本例?因为2222121212121()()44x x x x x x x x p,所以3p 或5p .[说明]在已知12x x 的值时,利用结论(*)可以避免对0与0的讨论.设问④:本例删除已知条件“121x x ”后,请用m 来表示12x x .将例1的“两根之差的绝对值”改为“两根的绝对值之和”,可以有以下例题. 例2、已知关于x 的方程222440xax aa ()a R 的两根为、,且3,求实数a 的值.解:2244(44)16(1)aaa a .当0,即1a 时,、为实数,且2244(2)0aa a ,所以23a,又1a,所以32a. 当0,即1a时,、为一对共轭虚数,所以23得294,所以94,所以29444a a 得72a 或12a ,因为1a,所以12a. 故32a或12a . [说明](1)前面有例1的分析与探讨,例题2可考虑让学生自己完成.(2)提醒学生注意:对0与0的讨论.(3)例2删除已知条件“3”后,也可用a 来表示.例3、已知关于x 的方程2(12)2(1)0axi x a i ()a R 有实数根,求实数a 的值.解:设x 0是原方程的两个根,则20(12)2(1)0axi x a i ,即20(2)(22)0axx a x a i ,所以20020220ax x a x a,解该方程组得0a或3a.[说明]补充例3主要是考虑到练习册第58页习题13.6 B 组第5题与例3属同一类问题,可以视情况选用.若时间允许,例3还可以考虑在求出a 的值后,解该方程.(四)课堂练习1.若、是方程270xx 的两个根,则2= .2.见课本P93练习13.6(2)T4.[说明]练习第1题可以直接用求根公式,也可以使用结论(*).其答案是27.(五)课堂小结本节课是在复习与巩固上节课主要内容“实系数一元二次方程解的情况和韦达定理”的基础上,通过例题1和例题2,进一步探讨实系数一元二次方程有虚数根时的韦达定理的应用,应灵活利用2121||c x x x a,1212Re b x x x a.注意分类讨论这一数学思想的应用,例题1和例题2都对0与0(即实根与虚根)进行了讨论,但合理利用以下等式:2221212121212|||()||()4|x x x x x x x x x x ,可以避免分类讨论.(六)课后作业1.书面作业:练习册P55 习题13.6 A 组 T6.8. P57 习题13.6 B 组 T4.5.2.思考题:(补充题及备选题)(1)若方程22810()xx a a R 有一个虚根的模为5,则实数a 的值为 . (2)已知关于x 的方程220()xx m m R 的两根为、,求. (3)已知关于x 的方程2(2)20()xki x ki kR 有实根,求实数k 的值,并解方程.参考答案:(1)9(2)2,0121,02,1m m m m mk时,原方程的两根为2,22i;(3)当22k时,原方程的两根为2,22i.当22[说明]补充的思考题,可作为学有余力的同学的能力训练题,也可作为教师的备选题.。
复数集内一元二次方程的解法

复数集内一元二次方程的解法 实系数一元二次方程复系数一元二次方程 ∆的作用 可以用来判断根的情况不能用来判断根的情况 求根公式 适用适用 韦达定理适用 适用 只有实系数一元n 次方程的虚根才成对共轭,1.判定下列方程根的情况,并解方程(1)022=++x x ,0722=++x x ,0452=+-x x(2)0122=+-x x 答:471i x ±=,05322=+-x x ,09222=+-x x 2.若关于x 的方程x 2+5x+m=0的两个虚数根x 1,x 2满足|x 1-x 2|=3,求实数m 的值.|x 1-x 2|=3,|(x 1-x 2)2|=9;则|(x 1+x 2)2-4x 1x 2|=9,即|25-4m|=9.3.已知实系数一元二次方程2x 2+rx +s=0的一个根为2i-3,求r ,s 的值.二、复系数一元二次方程虚根不一定成对,成对也不一定共轭。
1.求方程x 2-2ix-5=0的解.(当b 2-4ac ≥0时,方程的解都是实数吗?)求方程x 2-2ix-7=0的解 解方程:x 2-4ix+5=0; 解方程:0)2(25222=--++-i x x x x 答:i x x 5351,221-==(应用求根公式,不能用复数相等) 06)32(2=+++i x i x 答:i x x 3,221-=-=(b 2-4ac 为虚数,)2.解方程:x 2+(1+i )x +5i=0.251122=+++x x x x 答:4151,13,21i x x ±== 231122=+-+x x x x 答:4151,13,21i x x ±=-= 三、方程有实根或纯虚根的问题1.方程x 2+(m+2i )x+2+mi=0至少有一实根,求实数m 的值和这方程的解.2.已知方程x 2+mx+1+2i=0(m ∈C )有实根,求|m|的最小值.解方程关于x 的方程03)12(2=-+--i m x i x 有实数解,则实数m 满足的条件是( C )A .41-≥mB .41-≤mC .121=mD .121-=m R k ∈,方程04)3(2=++++k x i k x 一定有实根的充要条件是( D )A .4≥kB . 522-≤k 或522+≥kC .23±=kD .4-=k一元二次方程缺少常数项,必有零根(一个特殊的实根)设βα与是实系数一元二次方程0m x 2=++x 两个虚根,且3=-βα,求m 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实系数一元二次方程的解1
一、知识的梳理:
1、实系数一元二次方程()0,,,02≠∈=++a R c b a c bx ax
⇔>∆0方程有 ,=2,1x ;
⇔=∆0方程有 ,=2,1x ;
⇔<∆0方程有 ,=2,1x ;
2、实系数方程02=++c bx ax ,则=+21x x ,21x x = ,
二、例题讲解:
例1:在复数集中解方程;
⑴ 240x +=
⑵0322=+-x x
练习:
(1)01362=++x x (2)22540x x -+=
例2:方程),(02R b a b ax x ∈=++的一个根是i 31+
,求a,b 的值。
练习:已知方程042=+-k x x ()R k ∈有一个虚根1-2i ,求k 的值。
实系数一元二次方程的解综合练习
一、填空:
1、已知(为虚数单位)是一元二次方程
(均为实数)的一个根,则=__________.
2 、已知复数,则_______. 3、在复数范围内,方程210x x ++=的根是 .
4、设复数(2)117z i i -=+(i 为虚数单位),则z = .
5、已知复数24z i =+,21(1)
z w z +=-,则w = . 6、复数i
ai -+21(其中i 为虚数单位)为纯虚数,则实数=a _______. 7、已知点(1,1)(12)(21)(34)A B C D --、,、,、,,则向量AB 在CD 方向上的投影为 .
8、设为虚数单位,集合,集合,则____.
二、选择题:
1、若关于x 的一元二次实系数方程02=++q px x 有一个根为22-i (i 为虚数单位),则()
(A )⎪⎩⎪⎨⎧==2
22q p (B )⎪⎩⎪⎨⎧-=-=222q p (C )⎪⎩⎪⎨⎧==422q p (D )⎪⎩⎪⎨⎧=-=4
22q p 2、下面是关于复数21z i =-+的四个命题: ①2z =; ②22z i =; ③z 的共轭复数为1i +; ④z 的虚部为1-.
其中正确的命题……………………………………………………………………………( )
A .②③
B .①②
C .②④
D .③④
32i x =--i 20x ax b ++=,a b a b +i
i z +-=1)1(3
=z i {}i i,,1,1--=A ⎭⎬⎫⎩
⎨⎧-+-+-=i 1i 1i),i)(1(1,i ,1i 410B =B A
三、解答题:
1、已知复数z 是方程0222=++x x 的解,且0Im >z ,若i b z z
a +=+(其中a 、
b 为实数,i 为虚数单位,z Im 表示z 的虚部).求复数bi a w +=的模.。
