二次型与矩阵特征值的关系研究
5矩阵的特征值与二次型

第一节 向量的内积与正交向量组 第二节 方阵的特征值和特征向量 第三节 相似矩阵与矩阵的对角化 第四节 实对称矩阵的对角化 第五节 二次型及化二次型为标准型 第六节 正定二次型
§1
向量的内积与正交向量组
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
n阶方阵 可逆的充分必要条件是 的全部特征值都不 阶方阵A可逆的充分必要条件是 阶方阵 可逆的充分必要条件是A的全部特征值都不 为零. 为零 定理4 都是方阵A的对应于特征值 定理 设 都是方阵 的对应于特征值 的特 征向量,则它们的任何非零线性组合 征向量, 为不全为零的常数, 也是A的对应于 ( 为不全为零的常数, )也是 的对应于 返回 上一页 下一页 的特征向量. 特征值 的特征向量
定理5 方阵 与它的转置矩阵 方阵A与它的转置矩阵 定理 因而有相同的特征值. 因而有相同的特征值 证 由
有相同的特征多项式, 有相同的特征多项式,
因此, 与 有相同的特征多项式, 因此,A与 有相同的特征多项式,所以它们有相 同的特征值.证毕 证毕. 同的特征值 证毕
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
§2 方阵的特征值和特征向量
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
下一页
返回
上一页
特征值与特征向量二次型
,n
第五步
得到正交变换X=TY
T =(1 ,2 ,
,n )
正定二次型
定义 设有实二次型 f ( x ) x T Ax, 如果对任何x 0,
都有f ( x ) 0(显然f (0) 0), 则称f为正定二次型 , 并 称对称矩阵A是正定的; 如果对任何x 0, 都有f ( x ) 0, 则称f为负定二次型 , 并称对称矩阵 A是负定的.
i , j 1
例1 设A是3阶矩阵, 它的3个特征值为 1 1, 2 1, 3 2, 设B A 3 5 A 2 , 求 B ; A 5 E . 解 利用 A 1 2 n来计算 A .
, 令f ( x ) x3 5 x2 , 因为 1 , 2 , 3 是A的全部特征值 所以f ( i)(1 i 3)是f ( A) A3 5 A2 B的全部特征值故 . B f ( A) f ( 1) f ( 2 ) f ( 3 ) ( 4)( 6)( 12) 288.
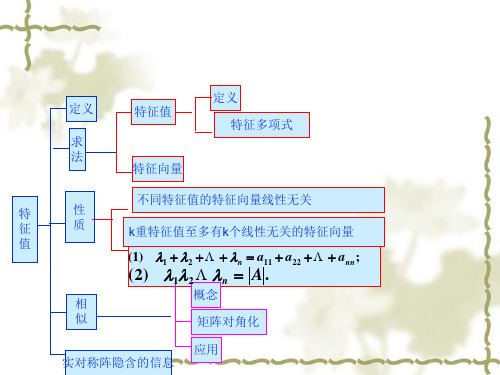
定义
求 法
定义 特征值 特征多项式 特征向量 不同特征值的特征向量线性无关 k重特征值至多有k个线性无关的特征向量
特 征 值
性 质
(1) 1 2 n a11 a22 ann ;
( 2) 12 n A .
概念 矩阵对角化 应用
相 似 实对称阵隐含的信息
( 2) 12 n A .
显然,如果矩阵A可逆,则A的特征值不等于0.
3. 设 是A (a ij ) nn的特征值, 则 (1)也是 AT的特征值; (2) k是 Ak的特征值( k 为任意自然数); ( )是
( A)的特征值.其中 ( ) a 0 a1 ( A) a 0E a1A a m Am.
3.2 实对称矩阵与实二次型

一、 实对称矩阵的特征值与特征向量
定理3.6: 实对称矩阵的特征值一定是实数。 实对称矩阵的特征值一定是实数。 定理
为其任一特征值, λ 证明: 实对称, 证明:设A实对称, = a + bi为其任一特征值, 对应的特征 向量为 α + iβ ,
于是有 A(α + iβ ) = ( a + bi )(α + iβ ) 展开, 展开, Aα = aα − bβ , Aβ = bα + a β
2 + a n1 x1 x n + a n 2 x 2 x n + a n 3 x 3 x n + L + a nn x n
+ LL
= x1 ( a11 x + a12 x 2 + a13 x 3 + L + a1 n x n )
+ x 2 ( a 21 x1 + a 22 x + a 23 x 3 + L + a 2 n x n )
= ( x1 ,
x2 , L,
a11 a 12 = ( x1 x2 L xn ) a1n
a12 L a1n x1 a22 L a2 n x2 为实数) M (其中 a ij 为实数) L L a2 n L ann xn
个标准正交的特征向量。 注:求正交矩阵 Q 的关键是求矩阵 的n个标准正交的特征向量。 求正交矩阵 的关键是求矩阵A的 个标准正交的特征向量
具体步骤) 实对称矩阵对角化的实现: 具体步骤 实对称矩阵对角化的实现: (具体步骤 1)求出 A 的全部特征值 ) 的全部特征值; 2)对于每一个λi ,求出其对应的线性无关的特征向量 ) 求出其对应的线性无关的特征向量, 从而得出矩阵 A 的 n 个线性无关的 特征向量η 1 , η 2 ,..., η n . 均为单根时, 3) 当 λ i 均为单根时,将
二次型定理

二次型定理二次型定理是线性代数中的重要定理之一,它将二次型与矩阵的特征值联系起来,通过特征值的求解,可以确定二次型的性质。
本文将详细介绍二次型定理的概念、证明过程及其应用。
一、二次型的定义在线性代数中,二次型是指由多个变量的平方和线性组合而成的函数。
设有n个实数变量x_1,x_2,...,x_n,记作x=(x_1,x_2,...,x_n)^T。
二次型可以表示为:f(x) = x^TAx其中,A是一个n\times n的实对称矩阵。
二、二次型的矩阵表示设A是一个n\times n的实对称矩阵,x=(x_1,x_2,...,x_n)^T,则f(x)=x^TAx可以写成矩阵形式:f(x)=\begin{pmatrix}x_1 & x_2 & \cdots & x_n\end{pmatrix}\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn}\end{pmatrix}\begin{pmatrix}x_1 \\x_2 \\\vdots \\x_n\end{pmatrix}整理得:f(x)=\sum_{i=1}^n\sum_{j=1}^na_{ij}x_ix_j将此式称为二次型的矩阵表示。
三、二次型定理二次型定理表明,任何一个二次型都可以通过正交变换转化为标准型。
具体来说,对于一个n\times n的实对称矩阵A,必存在一个正交矩阵P,使得:P^TAP = D其中,D是一个对角矩阵,其对角线上的元素称为二次型的主元或特征值。
进一步推广,在主元前面引入主元系数q_i,则有:P^TAP = q_1\lambda_1 + q_2\lambda_2 + ... + q_n\lambda_n其中,\lambda_1, \lambda_2, ..., \lambda_n是A的特征值,q_1, q_2, ..., q_n 是相应的特征向量。
矩阵的特征值和特征向量二次型

while 1
if isempty(e)
%若为空阵则为真
第17页,共58页。
return; end
d=e(1); f=sum(abs(e-d)<10*eps); %特征值d的代数重数 g=n-rank(A-d*eye(n)); %特征值d的几何重数 if f~=g y=0; return;
end
e(find(abs(e-d)<10*eps))=[ ]; end
(Trace)。 它 等 于 A的 主 对 角 元 素 的 和 。
第4页,共58页。
用Matlab计算特征值和特征向量的命令如下:
d=eig(A) 仅计算A的特征值(以向量形式d存放)
[V,D]=eig(A)
其中:D为由特征值构成的对角阵,V
为由特征向量作为列向量构成的矩阵
。且使 AV=VD 成立
定 理 2: 实 对 称 矩 阵 A正 定 的 充 分 必 要 条 件 是 A的 特 征 值 都 大 于 零 。
第34页,共58页。
1. 顺序主子式判断法 ⑴ 求二次型 F=X’AX 的矩阵 A 的各阶顺序
y=0;
return;
end e(find(abs(e-d)<10*eps))=[ ]; end
第16页,共58页。
function y=trigle(A)
%可对角化返回1,否则返回0。
y=1;c=size(A);
if c(1)~=c(2)
y=0;
return
end
e=eig(A);n=length(A);
矩阵的特征值和特征 向量二次型
第1页,共58页。
实验目的
1、学会用MATLAB软件求矩阵的特征值
特征值、特征向量与二次型

4、特征多项式性质 1)、若x是A的对应于λ的特征向量,则对于任意k ≠ 0, kx也是A的对应于λ的特征向量. 2)、设λ1, λ2是方阵A的两个不同特征值, p1, p2分别 是与之对应的特征向量,则p1+ p2不是A的特征向量 3)、方阵A的对应于λ的特征向量不是唯一的, 而是有 的对应于λ 无限多个. 4)、对于方阵A的对应于λ的所有特征向量, 其非零的 的对应于λ 非零的
3)、以这n个两两正交的单位特征向量为列向量构 成正交矩阵P,这时P-1AP = PTAP = Λ,其中对角方阵Λ 的元素排列顺序依次与P的列向量的排列顺序相对应 三、二次型及其标准形 1、实二次型及矩阵 含n个变量的二次齐次函数
f (x1, x2 ,L, xn )
= a x + 2a12x1x2 + 2a13x1x3 +L+ 2a1n x1xn 2 + a22 x2 + 2a23x2 x3 +L+ 2a2n x2 xn +L 2 + ann xn
Step1 计算A的特征多项式|A - λE|. Step2 令|A - λE| = 0得出A的所有不同的特征值. Step3 对于每个不同的特征值λ,求出齐次线性方程组 (A - λE)x = 0的所有非零解即得A的对应于λ的全部特 征向量. 更具体地说, 先求出(A - λE)x = 0的一个基础解系ξ1, ξ2,…, ξn-r,其所有非零的线性组合k1ξ1+ k2ξ2+…+ kn-rξn(只要k1, k2, …, kn-r不全为0)就是A的对应于λ的全部 k 0) A r( 特征向量, 其中R(A) = r.
线性组合 k x + k x +L+ k x 1 1 2 2 m m 也是A的对应于λ的特征向量. 的对应于λ
3.2 实对称矩阵与实二次型

两式相减, 并注意到 T A T A为一个数量, 有 b( T T 为实数。
定理3.7 : 实对称矩阵的属于不同特征值的特征向量正交。
T T T ( 1 , 1 , 1 ) , ( 1 , 2 , 4 ) , ( 1 , 3 , 9 ) , 对应的特征向量依次为 1 2 3
又 (1,1,3)T ,
(1)将 用1 , 2 , 3线性表示; (2)求An
( n N ).
ex4 : 设三阶矩阵 A的特征值为 1, 2,3, 求下列矩阵B的特征值:
( 1 )B A2 2 A I ,
1 2 ( 2) B A , 3
1
( 3) B A*
例5:已知1, 1 , -1是三阶实对称矩阵A的三个特征值,
1 (1,1,1)T , 2 (2, 2,1)T 是A的对应于1 2 1 的特征向量,
1 , 2的特征向量, 证明: 设A实对称矩阵, 1 , 2为属于不同特征值
于是 A1 11 , A 2 2 2 ,
2 A 1 1 2 1 ,
T T
1 A 2 2 1 2 ,
T T
T T T T T T T 2 A 1 ( 2 A 1 )T 1 A 2 1 A 2 , 1 2 2 1 ,
2
n
例1设
0 1 2 A 2 2 2 0 2 3
100 1 (2) A Q AQ 为对角阵 . (1)求正交矩阵 Q 使得
解:
1 2 ( 1 ) I A 2 2
0 2
2023数一线代大题二次型

2023数一线代大题二次型二次型是高中数学中的一个重要概念,也是线性代数中的重要内容。
在2023年的数一线代大题中,二次型也将成为一道重要的考点。
了解并掌握二次型的性质、特征和相关计算方法对于解答这道大题是至关重要的。
1. 二次型的定义与性质二次型是多元二次方程的总和,表达形式为:$f(x_1, x_2, \ldots, x_n) = a_{11}x_1^2 + a_{22}x_2^2 + \ldots +a_{nn}x_n^2 + 2a_{12}x_1x_2 + \ldots + 2a_{ij}x_ix_j + \ldots + 2a_{n-1,n}x_{n-1}x_n$其中,$a_{ij}$ 是实数系数,$x_1, x_2, \ldots, x_n$ 是变量。
二次型的计算可以通过矩阵的形式进行简化,可以用矩阵的方式表示为:$\mathbf{x}^\mathrm{T}\mathbf{A}\mathbf{x}$其中,$\mathbf{x}$ 是列向量,$\mathbf{A}$ 是一个$n \times n$ 的矩阵。
二次型的性质有一些重要的特点,其中包括:对称性:$f(x_1, x_2, \ldots, x_n) = f(x_2, x_1, \ldots, x_n)$,即二次型的各项次序可交换。
非负性:对于任意非零的向量$\mathbf{x}$,有$\mathbf{x}^\mathrm{T}\mathbf{A}\mathbf{x} > 0$ 或$\mathbf{x}^\mathrm{T}\mathbf{A}\mathbf{x} < 0$。
秩的性质:秩为 $r$ 的对称矩阵可以表示为 $r$ 个平方项相加的形式。
2. 二次型的标准形式与规范形式将二次型化为标准形式是研究二次型性质和进行计算的基础。
标准形式的表达式为:$f(x_1, x_2, \ldots, x_n) = \lambda_1y_1^2 + \lambda_2y_2^2 + \ldots + \lambda_ky_k^2$其中,$\lambda_1, \lambda_2, \ldots, \lambda_k$ 为二次型的特征值,$y_1, y_2, \ldots, y_k$ 为相应的特征向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次型与矩阵特征值的关系研究引言:
在线性代数中,二次型和矩阵特征值都是重要的概念。
二次型是一种与二次多
项式相关的函数,而矩阵特征值是矩阵在线性代数中的一个重要性质。
本文将探讨二次型与矩阵特征值之间的关系。
一、二次型的定义与性质
二次型是一种形如$Q(x)=x^TAx$的函数,其中$x$是一个$n$维列向量,$A$是
一个$n\times n$的实对称矩阵。
二次型具有以下性质:
1. 对于任意非零向量$x$,$Q(x)>0$,则称$Q(x)$为正定二次型;若$Q(x)<0$,则称$Q(x)$为负定二次型;若$Q(x)$既大于零又小于零,则称$Q(x)$为不定二次型。
2. 对于任意非零向量$x$,若存在非零向量$y$使得$Q(x+y)>Q(x)$,则称
$Q(x)$为正定二次型;若存在非零向量$y$使得$Q(x+y)<Q(x)$,则称$Q(x)$为负定
二次型;若存在非零向量$y$使得$Q(x+y)$既大于$Q(x)$又小于$Q(x)$,则称
$Q(x)$为不定二次型。
3. 二次型可以通过矩阵的特征值来判断其正定性。
若矩阵$A$的所有特征值均
大于零,则对应的二次型$Q(x)=x^TAx$为正定二次型;若矩阵$A$的所有特征值均小于零,则对应的二次型$Q(x)=x^TAx$为负定二次型;若矩阵$A$的特征值既有正值又有负值,则对应的二次型$Q(x)=x^TAx$为不定二次型。
二、矩阵特征值的定义与性质
矩阵特征值是一个矩阵在线性代数中的一个重要性质,它可以通过特征方程来
求解。
给定一个$n\times n$的矩阵$A$,如果存在一个非零向量$x$,使得
$Ax=\lambda x$,其中$\lambda$是一个标量,则称$\lambda$为矩阵$A$的特征值,$x$为对应的特征向量。
矩阵特征值具有以下性质:
1. 矩阵的特征值与其特征向量是一一对应的。
2. 矩阵的特征值的和等于其对角线上元素的和,即
$\sum_{i=1}^{n}\lambda_i=\sum_{i=1}^{n}a_{ii}$。
3. 矩阵的特征值的积等于其行列式的值,即$\prod_{i=1}^{n}\lambda_i=|A|$。
4. 矩阵的特征值可以用来判断矩阵的性质。
若矩阵$A$的所有特征值均大于零,则矩阵$A$为正定矩阵;若矩阵$A$的所有特征值均小于零,则矩阵$A$为负定矩阵;若矩阵$A$的特征值既有正值又有负值,则矩阵$A$为不定矩阵。
三、二次型与矩阵特征值的关系
根据前文所述的二次型与矩阵特征值的性质,我们可以得出二次型与矩阵特征
值之间的关系。
对于一个二次型$Q(x)=x^TAx$,如果矩阵$A$的所有特征值均大于零,则二次
型$Q(x)$为正定二次型;如果矩阵$A$的所有特征值均小于零,则二次型$Q(x)$为
负定二次型;如果矩阵$A$的特征值既有正值又有负值,则二次型$Q(x)$为不定二
次型。
这是因为矩阵的特征值可以看作是二次型的正定性、负定性或不定性的度量。
特征值大于零意味着矩阵在相应方向上的拉伸,使得二次型的值大于零;特征值小于零意味着矩阵在相应方向上的压缩,使得二次型的值小于零;特征值既有正值又有负值意味着矩阵在不同方向上的拉伸和压缩,使得二次型的值既大于零又小于零。
结论:
二次型与矩阵特征值之间存在着密切的关系。
矩阵的特征值可以用来判断二次
型的正定性、负定性或不定性。
特征值的正负与二次型的正定性、负定性或不定性是一致的。
因此,在研究二次型的性质时,可以借助矩阵特征值的信息来进行分析
和判断。
这种关系在实际应用中具有重要的意义,可以帮助我们更好地理解和应用线性代数的概念。
