黑体辐射强度与波长
黑体辐射实验
实验十 黑体辐射实验实验者:头铁的小甘引言:任何物体,只要温度大于绝对零度,就会向周围发生辐射,这称为温度辐射。
黑体是指能够完全吸收所有外来辐射的物体,处于热平衡时,黑体吸收的能量等 于辐射的能量,由于黑体具有最大的吸收本领,因而黑体也就具有最大的辐射本 领。
这种辐射是一种温度辐射,辐射的光谱分布只与辐射体的温度有关,而与辐 射方向及周围环境无关。
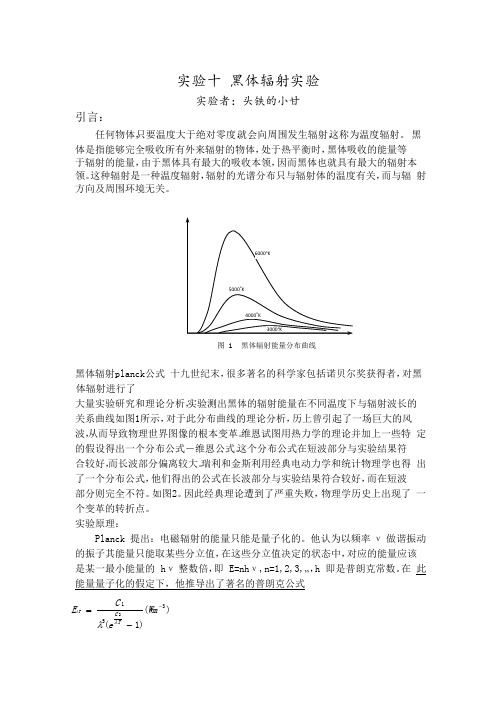
6000o K5000o K4000o K3000o K图 1 黑体辐射能量分布曲线黑体辐射 p lanck 公式 十九世纪末,很多著名的科学家包括诺贝尔奖获得者,对黑体辐射进行了大量实验研究和理论分析,实验测出黑体的辐射能量在不同温度下与辐射波长的 关系曲线如图 1 所示,对于此分布曲线的理论分析,历上曾引起了一场巨大的风 波,从而导致物理世界图像的根本变革。
维恩试图用热力学的理论并加上一些特 定的假设得出一个分布公式-维恩公式。
这个分布公式在短波部分与实验结果符 合较好,而长波部分偏离较大。
瑞利和金斯利用经典电动力学和统计物理学也得 出了一个分布公式,他们得出的公式在长波部分与实验结果符合较好,而在短波 部分则完全不符。
如图 2。
因此经典理论遭到了严重失败,物理学历史上出现了 一个变革的转折点。
实验原理:Planck 提出:电磁辐射的能量只能是量子化的。
他认为以频率ν做谐振动 的振子其能量只能取某些分立值,在这些分立值决定的状态中,对应的能量应该 是某一最小能量的 h ν整数倍,即 E=nh ν,n=1,2,3,…,h 即是普朗克常数。
在 此能量量子化的假定下,他推导出了著名的普朗克公式)()1(3512--=Wm eC E TC T λλλπ第一辐射常数C 1=8πhc =3.74×10-16(Wm 2),第二辐射常数C 2=1.4388×10-2(mK )。
它与实验结果符合得很好。
Planck 提出的能量量子假说具 有划时代的意义,标志了量子物理学的诞生。
原子物理论文 黑体辐射随波长的变化规律

黑体辐射随波长的变化规律研究要求和目标:1、根据普朗克公式,计算斯特潘常数及维恩常数。
2、以温度为参量,通过计算给出单色辐射本领随波长的变化规律。
研究准备背景知识:在19世纪开始的时候,天文学家赫谢耳(F.W.Herschel,1739—1822)发现了红外辐射的热效应。
他在实验中用灵敏温度计测试太阳光谱各部分的热效应,结果发现在红外光谱以外的区域温度升得最高,他认为在可见的红光之外还有不可见的辐射,这就是通常所指的热辐射。
以后物理学家们对于热物体发射的辐射感到有兴趣,为了研究谱线的可见光部分,使用了照像的方法,对于红外区域即热辐射部分用热电偶测量。
在实验发现的基础上,理论研究也活跃起来了,总结实验发现的经验规律也就相继地提出来了。
1859年德国物理学家基尔霍夫(G.R.Kirchhoff,1824—1887)得到如下结论:“在相同的温度下同一波长的辐射本领与吸收系数之比对于所有物体都是相同的,是一个取决于波长和温度的函数。
”如果这一函数用φ(λ,T)表示,物体的辐射本领,即从物体表面单位面积上所发射的波长在λ附近的单位波长间隔的辐射功率用e(λ,T)表示,物体的吸收系数,即物体在波长λ和λ+d λ范围内吸收的能量与入射能量的比率用a(λ,T)表示,则当物体处在辐射平衡时有e(λ,T)=φ(λ,T)a(λ,T)当物体的吸收系数a=1时,φ(λ、T)就是该物体的辐射本领。
绝对黑体:若以物体对什么光都吸收而无反射,我们就称这种物体为“绝对黑体”,简称“黑体”。
在1860年,基尔霍夫把a=1的理想物体定义为“绝对黑体”,这种黑体在任何情况下能够吸收射在它上面的一切热辐射,所以对绝对黑体的研究成为寻找基尔霍夫函数φ(λ,T)的关键。
事实上,当然不存在“绝对黑体”,不过有些物体可以近似地作为“黑体”来处理,例如一束光一旦从狭缝射入空腔后就很难再通过狭缝反射出来,这个空腔的开口就可以被看做是黑体。
1864年,英国物理学家丁铎尔用加热空腔充作黑体测定了单位表面积、单位时间内黑体辐射的总能量与黑体温度的关系。
黑体辐射的原理和应用

黑体辐射的原理和应用1. 黑体辐射的基本概念黑体是指具有完美吸收和辐射性能的物体,它能够吸收所有入射到其表面的辐射能量,而且能够以最高效率将能量辐射出去。
黑体辐射是指黑体表面上的电磁波辐射,它是由于黑体内部原子或分子的热运动而产生的,具有各种波长的辐射光谱。
黑体辐射的特点是它的辐射能量与波长之间的关系是确定的。
2. 黑体辐射的原理黑体辐射的原理可以用普朗克辐射定律来描述,该定律是由德国物理学家马克斯·普朗克在20世纪初提出的。
普朗克辐射定律表明,黑体辐射的能量密度与波长的关系符合普朗克分布函数。
该函数在不同波长范围内的峰值位置和强度有所不同,但都是由辐射体的温度所决定的。
当温度较低时,黑体辐射的能量主要集中在长波段;当温度较高时,能量则主要分布在短波段。
普朗克辐射定律的数学表达式如下:$$B(\\lambda,T)=\\frac{2hc^2}{\\lambda^5}\\frac{1}{e^{hc/\\lambda kT}-1}$$其中,$B(\\lambda,T)$表示波长为$\\lambda$的辐射能量密度,ℎ为普朗克常数,c为光速,k为玻尔兹曼常数,T为黑体的温度。
3. 黑体辐射的应用黑体辐射在许多领域都有广泛的应用。
以下列举了一些常见的应用领域:3.1 热辐射和能量转换黑体辐射是热辐射的基础,它在能量转换和传递过程中起着重要的作用。
例如,太阳光是由黑体辐射引起的,地球上的太阳能利用就是通过能源转换将太阳辐射的能量转换为电能或其他形式的能量。
3.2 红外线技术黑体辐射的波长范围覆盖了红外线区域,红外线技术利用了黑体辐射的特性。
红外线技术在军事、医学、安防等领域有广泛的应用,如红外线热成像、红外线测温、红外线通信等。
3.3 热辐射测量和光谱分析利用黑体辐射的特点,可以进行热辐射测量和光谱分析。
例如,利用红外光谱技术可以对物质的成分进行分析和检测,而红外辐射测温技术可以测量物体的温度。
4.1普朗克黑体辐射理论

19世纪末,经典物理学在各个领域都取得了很大的成功
力学
热学
电磁学
19世纪末页,牛顿定律在各个领域里都取得了很大的成功:在机械运动方面不用说,在分子物
理方面,成功地解释了温度、压强、气体的内能。在电磁学方面,建立了一个能推断一切电磁现
象的 Maxwell方程。另外还找到了力、电、光、声----等都遵循的规律---能量转化与守恒定律。 当时许多物理学家都陶醉在这些成绩之中,认为物理学已经发展到了尽头
能量
h=6.6310-34焦耳 . 秒。----普朗克常数
经典 量子
n为量子数,它只取正整数——能量量子化
E总 nh
3.能量量子化:微观粒子的能量是量子化的,或者说微观粒子的能量是分立 的.只能一份一份地按不连续方式辐射或吸收能量.
普朗克在1900年把“能量子”引入物理学,正确地破除了“能量连续变 化”的传统观念,成为新物理学思想的基石之一。
一方面,各种波长的辐度都有增加; 另一方面,辐射强度的极大值向波长较短的方向移动。
2.经验定律 (1)维恩位移定律:随着黑体温度升
高,所发射的辐射最强的波长变短, 即向光谱的紫色区移动。
(2)瑞利一金斯公式
3) 经典物理学所遇到的困难——解释实验曲线
1)维恩的半经验公式:
M 0
(T )
c1
5
c 2
相对论的问世
经典 力学
微观领域 高速领域
量子力学 相对论
思考与讨论1 在火炉旁边有什么感觉?
一、热辐射
任何温度下,宏观物体都要向外辐射电磁波。电磁波能量的多少, 以及电磁波按波长的分布都与温度有关,故称为热辐射。 辐射的能量及其波长的分布都随温度而变化。 热辐射的主要成分: 室温时 主要成分为波长较长的电磁波
8-2 黑体辐射基本定律

3. Eb 与I 的关系
黑体:
Eb I cosd
2
I cosd
2
I
2 0
2 cos sindd
0
θ
dθ
rsinθ
dA2
r
dA1
β dβ
I
漫射表面: E I cosd I 2
即当物体遵守兰贝特定律时,辐射力是任何方向上定向
辐射强度的倍。
THANKS
2
1
b
2
0
Eb d
1
0
E b
d
能量份额:
黑体辐射函数,可查表
Fb ( 0 T )
Eb(0 ) E b(0 )
0
Eb d f (T )
Eb
E b ( 1 2 ) E b ( Fb ( 0 2T ) F ) b ( 0 1T )
例: 一盏100W的白炽灯,发光时钨丝的温度可达2800K。如将灯 丝按黑体看待。试确定它发出的辐射能中可见光所占的百分数
增大, Eb 先增后减; Eb,max 对应的波长为 3)Tm升;高, m减小;
4) T升高, 可见光成分增加。
Planck定律的示图
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
二、维恩位移定律
求Eb,max 时的m.
mT 2897 .6 m K
三、斯蒂芬-玻尔兹曼定律(四次方定律)
解: 利用黑体辐射函数表:1T 0.38 2800 1064m K 2T 0.76 2800 2128m K
查表,得 Fb(01T ) 0.0007 0.07%
Fb (02T ) 0.088 8.8%
可见光占的总能量百分数:8.8-0.07=8.73% 即白炽灯发出的90%多的能量仅起到红外加热作用, 不起照明作用。
黑体的原理

黑体的原理黑体的原理是指黑体辐射的基本规律和相关理论。
黑体是一个理想化的物体,它能够完全吸收所有入射光线,并以最高效率辐射能量。
根据热力学理论,热辐射是物体在热平衡状态下发射出来的电磁波辐射。
黑体辐射不仅在理论物理研究中具有重要作用,也广泛应用于光学、电子学以及天文学等领域。
首先,黑体辐射的能谱分布。
根据普朗克辐射定律,黑体辐射的辐射能量与频率和温度有关。
公式表示为E(ν,T)= (2hν^3/c^2) * (1/(exp(hν/kT)-1)),其中E 表示单位面积单位时间内的辐射能量,ν是辐射频率,T是黑体的温度,h是普朗克常数,c是光速,k是玻尔兹曼常数。
该公式描述了黑体辐射的能量在不同频率下的分布,说明了辐射能量随温度的变化规律。
其次,黑体辐射的亮度和辐射通量。
亮度是指单位面积的黑体表面辐射能量,也称为辐射通量密度。
根据斯特凡-玻尔兹曼定律,黑体辐射的总辐射通量与温度的四次方成正比。
公式表示为j(T)=σT^4,其中j表示黑体的辐射通量密度,σ是斯特凡-玻尔兹曼常数。
这个定律说明了黑体辐射强度随温度的增加而增加,且远远大于其他物体的辐射强度。
另外,黑体辐射的波长峰值和温度之间的关系可以由维恩位移定律给出。
根据维恩位移定律,黑体辐射的波长峰值与其温度成反比。
公式表示为λ_max=T/b,其中λ_max表示波长峰值,T表示温度,b是维恩位移常数。
这个定律说明了黑体辐射的主要能量在短波长端,随着温度的升高,峰值向短波长方向移动。
最后,根据玻尔兹曼辐射定律,黑体辐射的辐射通量与频率的平方成正比。
公式表示为j(ν,T) = 4πB(ν,T),其中j(ν,T)表示单位面积单位时间内的辐射通量,B(ν,T)表示黑体辐射的亮度。
这个定律描述了黑体辐射能量在不同频率下的分布,在较高频率处辐射能量较高。
总结起来,黑体辐射的原理包括能谱分布、亮度和辐射通量、波长峰值和温度关系以及玻尔兹曼辐射定律。
这些规律和定律揭示了热辐射的特性和规律,为理解和研究热辐射提供了基础。
黑体辐射

式中:W0 为黑体总辐射通量密度,单位(W²cm-2);σ为斯忒藩-玻耳兹曼常量,(σ=(5.6697±0.0029)³10-2W²cm-2²k-4)式(2-7)为斯忒藩-玻耳兹曼定律,即黑体总辐射通量密度随温度的增加而迅速增大,它与温度的四次方成正比。
因此,温度只要有微小变化,就会引起辐射通量密度很大的变化,在用红外装置测定温度时,就是根据此定律作为理论依据的。
从图 2-10 中可以看到黑体辐射均有个极大值,它所对应的波长λmax,若对(2-6)式的 Wλ(λ,T)求波长的偏微分,并求极值,即可得到λmax。
?W? (?,T) ? 0??经整理可得:λmax²T=b(2 - 8)式中:λmax 为辐射通量密度的峰值波长;b 为常数,b=2897.8±0.4(μm²k)。
(2-9)式称为维恩位移定律,它说明随着温度的升高,辐射最大值对应的峰值波长向短波方向移动,表 2-4 给出不同温度时λmax 的数值。
表 2-4 不同温度时黑体辐射的峰值波长T(K) 273 300 310 1000 2000 3000 4000 5000 6000 7000λ maxμm 10.61 9.66 9.34 2.90 1.45 0.97 0.72 0.58 0.48 0.41上述讨论的是黑体辐射,自然界一般物体不是黑体,但在某一确定温度T 时,物体最强辐射所对应的波长λmax,也可以用维恩位移公式计算出近似值。
如:人体表面平均温度为37°(即 310K),其发射到空间的电磁辐射的峰值波长为外波段。
9.34即人体辐射的峰值波长位于热红二、地物的发射光谱特性任何地物当温度高于绝对温度OK 时,组成物质的原子、分子等微粒,在不停地做热运动,都有向周围空间辐射红外线和微波的能力。
通常地物发射电磁辐射的能力是以发射率作为衡量标准。
地物的发射率是以黑体辐射作为基准。
4-1 普朗克黑体辐射理论 (教学课件)-高中物理人教版(2019)选择性必修第三册

解析:在同一温度下,辐射强度最大的电磁波波长不是最大
的,也不是最小的,而是处在最大波长与最小波长之间,故选项
A错误,B正确;黑体辐射的强度与温度有关,温度越高,黑体辐
射的强度越大,则辐射强度的极大值也越大,故选项C正确;随
着温度的升高,黑体辐射强度的极大值向波长较短的方向移
动,故选项D正确。
三 能量子
典例剖析
小灯泡的功率P=1 W,设其发出的光向四周均匀辐射,平均波
长λ=10-6 m,求小灯泡每秒辐射的能量子数是多少?
(h=6.63×10-34 J·s)
答案:5×1018
解析:每秒小灯泡发出的能量为E=Pt=1 J
1个能量子的值为
ε=hν= =
.×- ××
上述变化都将反过来,故选项A、C、D正确,B错误。
学以致用
(多选)根据黑体辐射的实验规律,以下判断正确的是(
)
A.在同一温度下,波长越短的电磁波辐射强度越大
B.在同一温度下,辐射强度最大的电磁波波长不是最大的,
也不是最小的,而是处在最大波长与最小波长之间
C.温度越高,辐射强度的极大值就越大
D.温度越高,辐射强度最大的电磁波的波长越短
人称之为 普朗克常量 ,其值为h = 6.626 070 15×10-34 J·s。
3.普朗克的假设内容:微观粒子的能量是 量子化 的,或者
说微观粒子的能量是分立的。
微训练2下列能正确解释黑体辐射实验规律的是(
)
A.能量连续的经典理论
B.普朗克提出的能量量子化理论
C.能量连续的经典理论和普朗克提出的能量量子化理论都
D.黑体辐射电磁波的强度按波长的分布只与黑体温度有关
答案:AD
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑体辐射强度与波长
黑体辐射强度与波长之间的关系可以由普朗克定律和斯特藩-
玻尔兹曼定律描述。
普朗克定律表明,黑体辐射的辐射能量由频率(或波长)决定。
根据这个定律,黑体辐射强度与波长之间的关系可以表示为:
I(λ) = (2hc^2/λ^5) * [1/(e^(hc/λkT)-1)]
其中,I(λ)是波长为λ处的辐射强度,h是普朗克常数,c是光速,k是玻尔兹曼常数,T是黑体的绝对温度。
斯特藩-玻尔兹曼定律则描述了黑体的总辐射功率与温度之间
的关系。
根据这个定律,黑体辐射强度与波长之间的关系可以近似表示为:
I(λ) = σT^4/π
其中,I(λ)是波长为λ处的辐射强度,σ是斯特藩-玻尔兹曼常数,T是黑体的绝对温度。
这两个公式可以用来计算黑体辐射强度与波长之间的关系。
不过需要注意的是,普朗克定律适用于任意温度的黑体,而斯特藩-玻尔兹曼定律则适用于高温下的黑体。
