数据网格化和网格数据绘等值线图

合集下载

蓝马中简单zmap

蓝马中ZmapPlus是一个功能非常强的绘图软件，我们主要来用它绘制各种等值线图。

掌握ZmapPlus的关键是对MFD、ZGF的理解。

ZmapPlus7个主要文件的含义：（1）主文件（*.MFD）：存储各种绘图数据（Grid、Contours、Faults、Data等）；（2）绘图文件（*.ZGF）：存储所有的图片数据；（3）ASCII数据文件（*.DA T或*.dat）：各种绘图数据可以用ASCII数据输入；（4）参数文件（*. ZCLPARAMETER）：绘图过程中设置的参数；（5）格式文件（*.FMT）：ASCII数据转换成ZmapPlus格式时所用的格式文件；（6）颜色文件（*.TAB）：可以编辑或建立显示图片用的颜色文件；（7）宏旨令文件（*.ZCLMAC）：以批量作业绘制图片；一、建立MFD、ZGF文件1、设置文件路径启动ZmapPlus。

Openworks 2003 Command Menu：Applications——Z-mapPlus/Contouring Assistant，弹出图1。

图8-1Applications——Z—Map plus，弹出图2。

图8-22、设置路径Z—Map plus的主窗口——Directory Paths 弹出图8-3。

MFDs input path 1：/data2/lm_train_dz/mfd/；output path：/data2/lm_train_dz/mfd/。

这样所有文件的输入输出路径都要设置成相应的文件命名的文件夹。

图8-33、建立MFD、ZGF文件我们先在landmark进行构造解释，这样可以直接将解释成果输入到zmap中。

先作断层的polygon。

步骤：选择输出的层位。

单击工具栏中的Display Horizons图标，list选Top purple 层，Ok。

建一个map文件。

Maping——Maping File ——New，输入map文件名：mmmm，OK。

Surfer作图如何消除等值线中的负值

我们为了绘制等值线图需要网格化一个XYZ数据文件，虽然数据的Z值中并没有负值，例如某个地区的一次降水雨量值，不可能有负值，没下雨也就是雨量为0。

但是当我们做插值算法、生成网格文件后，在某些区域肯定会出现负值，对于一个插值算法而言，这非常正常。

但是到我们实际画出来的等值线以表示雨量的分布时，这显得非常不可思议：“雨量怎可出现负值？”下面的图，显示了江苏省2012年8月份双台风影响的雨量分布等值线，其中就有雨量为负值的区域。

如果强行修改最小等值线为0，则在负值区域将不会着色，呈现一片空白。

现在我们就来解决这个问题。

点击“网格|数学”菜单命令，显示网格数学对话框。

1、首先添加网格，你要选中要处理的网格.grd文件，它里面包含了负值。

我们期望消除这些负值。

2、然后修改参数，由于我们要处理的是Z值，雨量值，它位于C列，因此，在变量(Varible)一栏，将默认的A改成C。

3、数学表达式C=max(C,0)的含义是C值和0相比较，较大者存入C，这样一来，所有的负值将改为0。

这就达到了我们的目的。

4、选择好输出的文件名，点击“确认”，保存的新的.grd网格文件就是我们所需要的。

好了，在场景窗口中，点击“图形|新建|等值线图”，调入你刚才保存的.grd 文件。

看看第四张图，由于我们只是将已经生成的.grd网格文件做一些数学处理，所以还是要手工将最小等值线改成0，但是不会再出现空白区域了。

鼠标指向“数据范围”，也显示没有负值，最小值为0。

补充和更正：上面提到的变量C，我认真研究了一下，看来我有错误。

那个C，只是变量名称，和数据的C列，没有关系。

就是保留默认的A，表达式里不要写“C=”，只写“max(A,0)”，也是可以的。

但是，上面变量框里的变量名，和表达式里的变量名，却是要保持一致。

surfer插值

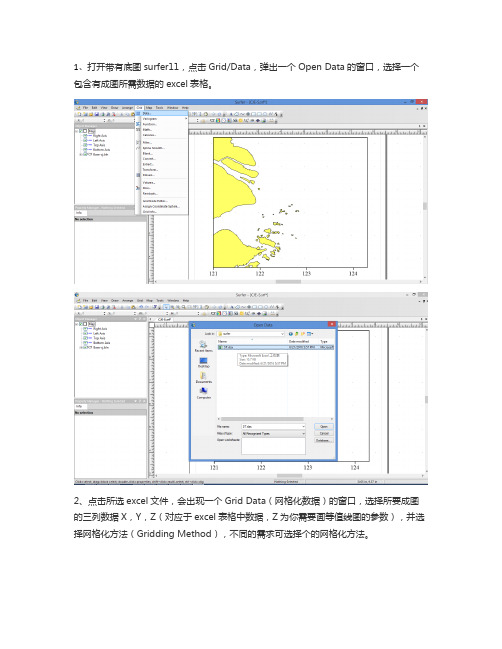
1、打开带有底图surfer11，点击Grid/Data，弹出一个Open Data的窗口，选择一个包含有成图所需数据的excel表格。

2、点击所选excel文件，会出现一个Grid Data（网格化数据）的窗口，选择所要成图的三列数据X，Y，Z（对应于excel表格中数据，Z为你需要画等值线图的参数），并选择网格化方法（Gridding Method），不同的需求可选择个的网格化方法。

3、选择存路径等，最后点击OK，就会输出一个grd文件并关闭Gridding Report, 得到插值的网格化grd.文件。

4、选择菜单栏Map/New/Contour Map，或者右击左边菜单栏里的Map/Add/Contour Layer，
5、找到上面的grd文件所在位置，点击打开，就得到所要的平面等值线图（未上色）。

如果等值线不够平滑，可以点击Contours...,在左下属性管理（Property Manager）选择General/Smoothing，进行None,Low,Medium,High四种不同程度地平滑
6、然后就是为等值线图上色；点击Contours...,在左下属性管理（Property Manager）选择Levels/Filled Contours/Fill Colors，勾选Fill Contours和Color Scale。

利用Mapgis成等值线图的方法

Mapgis成等值线图1、首先用surfer网格、白化、滤波、样条平滑所需要成图的数据，生成**.grd格式的文件。

2、用surfer打开**.grd格式文件，点击左上角“文件（F）”——另存为（A），在弹出的对话框中选择好保存的路径、文件名，在保存类型（T）项选择“GS Binary(*.grd)”保存。

3、打开Mapgis——空间分析——DTM分析——GDR模型——平面等值线绘制——在弹出的对框中选择刚刚另存为的文件打开——弹出的对话框中进行各项参数设置如下：132（1）红色框1中，根据自己需要进行选择，一般四个勾全选择，光滑度根据自己需要确定。

（2）红色框2中，一般选择原始数据范围，生成的比例尺就是1：1000的图，成图后可以根据自己需要进行调整。

（3）图框3中是最重要的，它的设置反应出做成图的美观程度，一般首先点击“等值线值”在弹出的对话框中设置，如下图右侧：（1）一般要“删除当前分段”（系统默认的等值线色阶），然后按照自己想分的色阶进行分别设置（每个起始、终止值及对应的颜色、步长都可以自己设置，设置好后点击“添加新分段”，系统就会按照设置好的步长进行颜色变化分段填充。

如果想设置多个色阶，第二个分段的起始值与第一个分段的终止值不能一样，必须要大些，应为这两个值也要对应颜色进行色阶分段填充）。

（2）如果要改变分段，可以选中分段后进行改正，但改正后必须“更新当前分段”。

（3）设置好后点距确认，推出此对话框。

4、此时可以在上图红色框3中进行“线参数”、“标记参数”的设置，还可以删除或添加等值线。

5、一切设置好后就可以点击确定，等值线图就完成了。

6、保存点、线、区文件。

7、打开Mapgis或者Section新建工程，添加刚刚保存的点、线、区文件即可。

注意：第3、4步中的设置很重要，因为到第5步后退出来就是做成的图，如果发现要改的地方，就没法再进去改参数，只能重新从第1步开始做。

（反正我没发现进入修改等值线参数的方法，如果谁知道请留言告诉我，谢谢！）。

Surfer作图如何消除等值线中的负值

但是当我们做插值算法、生成网格文件后，在某些区域肯定会出现负值，对于一个插值算法而言，这非常正常。

如果强行修改最小等值线为0，则在负值区域将不会着色，呈现一片空白。

现在我们就来解决这个问题。

点击“网格|数学”菜单命令，显示网格数学对话框。

1、首先添加网格，你要选中要处理的网格.grd文件，它里面包含了负值。

我们期望消除这些负值。

2、然后修改参数，由于我们要处理的是Z值，雨量值，它位于C列，因此，在变量(Varible)一栏，将默认的A改成C。

3、数学表达式C=max(C,0)的含义是C值和0相比较，较大者存入C，这样一来，所有的负值将改为0。

这就达到了我们的目的。

4、选择好输出的文件名，点击“确认”，保存的新的.grd网格文件就是我们所需要的。

好了，在场景窗口中，点击“图形|新建|等值线图”，调入你刚才保存的.grd 文件。

看看第四张图，由于我们只是将已经生成的.grd网格文件做一些数学处理，所以还是要手工将最小等值线改成0，但是不会再出现空白区域了。

鼠标指向“数据范围”，也显示没有负值，最小值为0。

补充和更正：上面提到的变量C，我认真研究了一下，看来我有错误。

那个C，只是变量名称，和数据的C列，没有关系。

就是保留默认的A，表达式里不要写“C=”，只写“max(A,0)”，也是可以的。

但是，上面变量框里的变量名，和表达式里的变量名，却是要保持一致。

一种采用插值网格化Kriging方法的等值线可视化技术

Kriging一、绪论等值线是地图制图和地形分析的重要工具之一，通过等值线可以直观地展示地面高程和地形特征，为地理信息系统、遥感技术、数值地形分析等提供有效支持。

而如何准确高效地获取等值线数据是等值线可视化技术研究的关键。

本文提出了一种采用插值网格化Kriging 方法的等值线可视化技术。

该技术通过插值方法将离散的高程数据转换为连续的表面，再利用网格化技术对得到的表面进行离散化处理，最终通过Kriging 方法计算等值线数据。

该方法具有计算速度快、插值精度高等优点，在地理信息系统和地形分析中具有广泛的应用前景。

二、插值网格化Kriging 方法的原理与步骤插值是将离散数据转化为连续的表面的过程。

网格化是将得到的表面离散化处理的过程。

Kriging 方法是一种基于统计学原理的空间插值方法。

下面将详细介绍插值网格化Kriging 方法的原理和步骤。

1. 插值将离散的高程数据转化为连续的表面需要插值方法。

常见的插值方法包括最近邻法、反距离权重法、三次样条插值法、Kriging 法等。

各种插值方法有其优缺点，但都能实现离散数据到连续表面的转换。

2. 网格化得到连续表面后，需要使用网格化方法将连续表面离散化处理。

网格化通常将表面分割成小的网格单元进行处理，每个网格单元可以代表一个等值线点。

网格化处理过程中需要考虑网格大小、网格分割方式等参数的选择。

3. Kriging 方法Kriging 方法是一种基于统计学原理的空间插值方法，旨在通过样本点之间的空间相关性进行插值。

Kriging 方法包括普通克里金(OK)和泛克里金(LK)等多种形式，不同的形式适用于不同的插值场景。

插值网格化Kriging 方法的具体实现步骤如下：( 1)原始数据采集：获取离散的高程数据；( 2)插值方法选择：从最近邻法、反距离权重法、三次样条插值法和Kriging 法中选择合适的插值方法；( 3) 表面生成：采用选定的插值方法将离散数据转化为连续的表面；(4)网格化处理：将得到的表面离散化处理，分割为一定数量的网格单元；( 5) Kriging 计算：使用OK 或LK 方法计算网格单元中等值线的值；( 6)等值线生成：根据Kriging 计算结果绘制等值线，可视化高程数据信息。

Surfer软件使用教程

Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 （以下简称Surfer）是一款画三维图（等值线，image map，3d surface）的软件，是美国Golden Software公司的系列绘图软件之一。

该软件简单易学，可以在几分钟内学会主要内容，且其自带的英文帮助文件（help菜单）是相当完美且容易阅读的，对如何使用Surfer，解释的很详细，只要学过英语的人都可以很快上手。

Surfer的主要功能是绘制等值线图（contour map），是具有插值功能的绘图软件，因此，即使你的数据是不等间距的，依然可以用它作图。

此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map，等形式的图形，其功能是比较强大的。

Surfer的安装比较简单（目前，只有Windows操作系统下的版本，最为常用的是8.0版本），只要按其提示缺省安装即可。

其安装软件的大小不到30M，一般的计算机硬件基本能够顺利使用该软件。

安装好Surfer以后，其环境界面如图3－1所示。

命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面·22·3.2 软件界面及命令菜单Surfer软件的界面非常友好，继承了Windows操作系统软件的特点。

从图3－1中可以看到，其最上方为命令菜单，在命令菜单的下方是命令菜单中的快捷工具栏（共两行），左侧的空白区域为目标管理窗口，用来更加方便的管理绘制的各个图形要素，右侧的空白区域为工作区，用来绘制图形，最右侧的一个竖条工具栏是绘图命令的快捷方式。

下面详细介绍各个命令菜单的主要内容。

3.2.1文件菜单（F）“文件菜单”如图3－2所示，主要是对文件进行操作，如文件的建立、加载、打印设置等。

图3-2 文件菜单新建—用来新建一个工作窗口，点击后即出现图3－1界面。

打开—打开一个已经存在的Surfer可以识别的文件。

地理坐标下网格化数据等值线处理具体步骤及编程方法

632022年2月下第04期总第376期信息技术与应用China Science & Technology Overview在研究地理坐标时需要对大量的数据进行处理，用计算机进行网格化数据处理，需要运用编程的方法对数据进行分析。

网格点的数据处理需要一些专业的功能，执行功能的专业软件有很多，如冲浪软件、GOLDEN 软件等。

但是，在运用专业的软件进行编程时需要处理大量的数据节点，并且对其进行进一步处理，目前的专业软件在执行这些功能价格昂贵，非常不方便，使用不到位还会引起侵权等纠纷。

本文分析了网格数据轮廓处理的原理和方法，并给出了用Microsoft C++5.0编写的源程序的相应功能。

1.等值线型数据网格化方法的研究地学和地球化学勘探中的网格划分通常包括3类：研究数据网格划分、轮廓数据网格划分和离散点数据网格划分[1]。

不同类型的数据必须采用不同的网格划分方法才能取得良好的效果。

对于研究数据，三次样条插值网格化方法有效；对于离散点类型数据，可以采用平方反比加权平均grid ding 方法或二次样条插值grid ding 方法[2]。

当前，等高线数据的网格化实用方法很少。

根据轮廓数据的特点，模拟了轮廓图中手动检索网格的方法和过程。

提出了一种分块存储等高线数据的网格方法，并在8个方向上查找和插值网格点。

主要的想法和过程如下。

1.1网格图幅条块划分根据网格地图范围的δx，δy 网格线距离，计算出N×M 网格线的网格数；然后，根据正确选择的r 插值搜索半径，将网格地图表拆分到的较小数据存储区域中的网格虚线数计算为LN×LM ：LN=R/ΔX IF (LN*XK.LT.RS) LN=R/ΔX+1LM=R/ΔYIF (LM*YK.LT.RS) LM=R/ΔY+1则数据存储小方块的宽度为XLN×YLM:XLN=LN×ΔX YLM=LM×ΔYMW=M/LM IF (MW*LM.LT.M) MW=M/LM+1NW=N/LNIF (NW*LN.LT.N) NW=N/LN+1注：*代表指针变量/代表注释标志1.2数据内插加密及坐标转换为了确保以下栅格点的八方位插值范围内的插值计算点和研究点的准确性，首先，必须在大约1mm 间隔（可以选择特定间隔）的数据点处沿每个轮廓插值并加密飞机轮廓的数字数据并且必须将网格地图范围内的数据点坐标转换并旋转到用户定义的网格地图坐标系，以便于后续步骤中的计算工作。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

不规则分布数据网格化和网格数据绘等值线图程序

严惠

芬

李长

法

(国家地震局地球物理勘探大队)提要

本丈介绍了用电子计算机绘制平面不规则分布教据的等值线图的数学方法私程序程序中采

用了

按距离加权平均法按方位取点加仪法趋势面残差叠加法及局部加权最小二乘法等多种

曲面

拟合

的方法将不规则分布的数据规则网化程序同时具有绘制居氏点和剖面线的功能文中着重讨论了为

提高计算速度和解的稳定性程序在实现这些计算过程中的一些具休处理方法如采用按条带搜索局

部进行拟合等手段最后结合应用实例甘各种方法的使用情况进行了讨论

等值线法广泛应用于表示各种自然现象如用于表示地形的等高线表示地下水位

深浅的等水位线表示降雨的等雨量线……这些等值线图一般是由实验观测或实地测

量获得的离散数据绘制的由于受各种条件的限制数据点的分布往往是不规则的密

度有时也不能满足制图的需要手工直接根据这些数据绘图或经过插道后绘图是一项繁

重的工作使用计算机绘制等值线图不仅能节约大量人力也缩短了成图周期目前数

据处理经常需要从等值线图上获取平面网格数据而数字化仪从图上得到的数据的分布是不规则的无法直接进行其他计算为满足数据处理和成图的要求我们编制了不规则分布数据网格化和网格数据绘等值线图程序下面分别讨论网格化和绘等值线图程序的数

学方法和

程序

一、网格化方法

专门介绍用曲面拟合的方法将不规则分布的离散数据化为规则数据的书及文

章

很

多,该方法的数学原理及公式的推导这里不多赘述仅给出程序中使用的计算公式及实

现过程中的一些具体处理方法1近点按距离加权平均法和按方位取点加权平均法

由这二种方法得到的曲面是通过数据点的前者仅考虑距网格点最近的N个数据点中原地理研完第四卷98年第期对其的影响即距网格点越近的数据点的值对网格点的值贡献越大后者弥补了前者参加计算的点有可能集中到网格点一侧的不足之处考虑了取点的方向性使得在网格点的不同方向上都有距离最近的点参加计算

。

A近点按距离加权平均法

设:网格点(XoYo)的值为2

数据点(XiYi)的值为iz数据点(XiiY)到网格点(X。Y。)的距离

d=亿(Xi一Xo)2

(Yi一Yo)

“i之z2……

权函数:

或.W

N习W121

则:Z。

二

习W

当di今

。

时

当id“。

时

B按方位取点加权平均法

如图A示:设网格点(i」)的值为Z(ij)以(i」)点为原点将平面分为四

个象限再将每个象限分成n等分这样整个平面划分为4n等分然后在每个等分角内

寻找一个距(i」)最近的点其值为iZ;它到i(j)的距离为rilo

则:Z(ij)=艺CilZi:11二1

4n梦*rj

’

其中:Ci

l二

K二4nnrL

L二1

L年K

些4n

叉

2加权.小二乘拟合法图A按照方位取点加权法的方位示意图

该方法与通常的最小二乘拟合法的不同之处是增加了与距离有关的权函数使靠近

网格点(x。y。)的数据点的权比远离(X。Y。)的数据点的权大设拟合函数为二次多项式

f(Xy)=e:+e,x+eay+e一x,+e

。

了:严忍芬李长法不规.Nl分布数据网格化和网格数据绘哥位线图程

序69

一~一...............

拟合值f(xiiy)与实测值iZ的误差

NQ=习

(

f(xiyi)一21)

“

i=1

其中:N为数据点的总个

数

Wi为权函数是数据点到网格点距离的函数

N兄记为习Wi记为

。

i二1

要使Q

、二*

。。Q

。

,`沙砚才网月匕.下几二r

二v

口、l

即求方程组,

二123、456

。

rC:兄W+C:公xiw+C。公Yiw+c.名X1Yiw+c。名Xi’W+c.名Yi`

{”习Z

{c,乙X`W+C,公X*’W+c:兄X`Y,W+C.习x`’Y,W十c。公x`’W

)+C。艺X`Y`’W”公X`z`

…C:习Y`W+C,公X`Y二W+C:公Y`’W+C`名x`Y`’W+c`乏x`’YW

}+C。￡Y,`W二习Y;z*W

}C1EX`Y`W+c,习x`’Y`W+c。习x`Y`’W十c`云x`’Y`’W十c.名x“Y

{W+C。云X1Yi吕W=习XIYIZIW

…el名xi:w+e,习x、.w+e,习xi,Y、w+e`公x;`Y、w+e。￡x*`w

{+C犯X;ZY;ZW=它X;22

;

…C,乙Y、ZW+C:习XY’W+C:公Y;’W+C一￡X;Y;`W+C。习X`’Y`’W

}+C。￡Yi`W=习Ys

名

娜臼产.

权函数W在程序中有4种方式供选用.令:di=(X三一X

。)’+(Yi一Y

)

则:W=

/(d

“

)

W=1

“)

’

)

W=EXp(一。di)/(di+.)

其中`是为防止滋出而

设的小

母甲n.中爪地理研完

…

第四冬1”5年第2期

a为权函数参量

解出C,C:C,C;

C。

则网

格

点值Z。二C、+CZX

。+C3Y。+C4X。Y。+C。X。、C。Y。

从权函数的表达式可以看出当d一。时尽管加了一个小量。防止溢出但舍入

截断误差仍然很大而且当d态程度大大增加解的稳定性差所以在程序中安排了当d<0lmm就直接取数据点的

值为网格值从计算过程上可以看出该方法兼有趋势面拟合和按距离加权方法的优点既考虑了

全部数据点的趋势变化又反映了局部特征但是每计算一个网格点的值要求解一个法

方程当数据点很多时计算量相当大所以程序在处理中可以将整个平面划分成几个大区在每个区内使用这种方法进行局部拟合在不影响计算精度的情况下减少了形

成法方程的计算时间但该方法仍未减少解方程组的次数在实际的数据处理中大多数情况下是采用下面的方法3趋势面拟合一残差加权叠加法

该方法首先使用全部数据点拟合一张趋势面计算出由该曲而得到的网格值再将趁势面与羚井改值灼残差用距离加权的方法求出网才各值二者之和为所求的网格值

越分面拟合的计算公式见加权最小二乘拟合法令权函数Wi二1即可。残差的分配

采用按距离加权平均法或按方位取点加权平均法从计算过程上分析可知该方法同样兼有趋势分析和按距离加权方法的优点而且仅需解一次方程组由于没有引进权函数该方程组的解比较稳定将残差按距离加权分配弥补了趋势分析造成的局部特征平滑的不足因而应用中该方法的效果比较理想!二面的讨论有一个共同的问题无论采用那种曲面拟合方法从拟合的精度和计

算

量两个方面考虑计算网格点的值时仅使用该点附近半径为R范围内的数据点但由于这些数据汽的分布是不规则的为搜寻这些附近点需要将全部数据点扫描一遍如果ii算球一个网洛点的值都将数据点扫描一遍那将浪费大量的机时程序中安排了先

将不规则分布的数据点进行单方向(如X方向)从小到大排序分段然后再按条带来搜百这些附近点的过程使得搜寻时间大大减少如果在R范围内参加计算的数据点

的点数少于规定值(如在第1种方法少于4第2种方法少于6)时程序能自动逐步地扩

大半径直到参加计算的点大于规定值为止

正如前而所述采用不同的拟合方法得到的结果是有差异的使用中要根据数据

点的分布精度数值的变化等情况杀顾计算精度和计算时间合理地选用拟合方法如对分布较卜勺匀数据精度较高的数据类型采用插值的方法计算效果比较好计算量也小对分布不均匀或数据的精度较低的数据类型采用拟合的方法得到的结果更合理对数据认的依梯度变化较大的数据类型采用趋势面一残差叠加法比较好这是因为参川加权平均分配的值是数据点的值减去拟合值后的残差值解比较稳定应该指

出由于各专业的要求不同数据的类型也各有特点不能仅从数学方法上来确定那一

种方法最合适只有在大量的数据处理过程中不断积累经验才能有效地应用这一数学