两相交圆的公共弦长
圆公共弦定理证明

圆公共弦定理证明圆的十八个定理1、圆心角定理:在同圆或等圆中,相等的圆心角所对弧相等,所对的弦相等,所对的弦的弦心距相等。
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形3、垂径定理:垂直弦的直径平分该弦,并且平分这条弦所对的两条弧。
推论1:①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧推论2:圆的两条平行弦所夹的弧相等4、切线之判定定理:经过半径的外端并且垂直于该半径的直线是圆的切线。
5、切线长定理:从圆外一点引圆的两条切线,他们的切线长相等,这一点与圆心的连线平分这两条切线的夹角。
6、公切线长定理:如果两圆有两条外公切线或两条内公切线,那么这两条外公切线长相等,两条内公切线长也相等。
如果他们相交,那么交点一定在两圆的连心线上。
7、相交弦定理:圆内两条弦相交,被交点分成的两条线段长的乘积相等。
8、切割线定理:从圆外一点向圆引一条切线和一条割线,则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。
9、割线长定理:从圆外一点向圆引两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。
10、切线的性质定理:圆的切线垂直于经过切点的半径推论1:经过圆心且垂直于切线的直线必经过切点推论2:经过切点且垂直于切线的直线必经过圆心11、弦切角定理:弦切角等于它所夹的弧对的圆周角推论:如果两个弦切角所夹的弧相等,那么这两个弦切角也相等12、定理:相交两圆的连心线垂直平分两圆的公共弦13、定理:把圆分成n(n≥3):(1)依次连结各分点所得的多边形是这个圆的内接正n边形2)经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形14、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆15、定理:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆16、定理:正n边形的半径和边心距把正n边形分成2n个全等的直角三角形17、定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
两两相交的圆的三公弦共点

两两相交的圆的三公弦共点1.引言1.1 概述在几何学中,圆是一种基本的几何图形,它具有许多独特的性质和特点。
当两个圆相交时,我们可以发现一些有趣的几何特征。
其中之一就是两两相交的圆的三公弦共点的性质。
所谓两两相交的圆,指的是存在两个圆,它们的边界相交于两个不同的点。
这种情况在几何中非常常见,许多几何问题和现实世界中的场景都与两个相交的圆有关。
当我们构造这两个圆的公切线时,我们会发现一条有趣的线段——三公弦。
三公弦是指通过两个相交圆的公共切点,并且与圆相交的线段。
这条线段有一个特殊的性质,即两两相交的圆的三公弦共点。
也就是说,不论两个相交的圆的位置如何变化,它们的三公弦都会交于同一个点。
对于这个特殊的现象,我们需要进行一定的证明来确保其正确性。
通过几何证明,我们可以得出结论:两两相交的圆的三公弦确实共点。
这个结论在几何学中具有重要的意义。
首先,它可以帮助我们解决一些与圆有关的问题,例如圆的切线构造、圆的内切和外切等。
其次,它也能够拓展我们的几何思维,让我们对圆的性质有更深入的理解。
在接下来的正文中,我们将探讨两两相交的圆的基本性质以及三公弦的定义和性质。
并通过几何证明,确认两两相交的圆的三公弦确实共点。
最后,我们将探讨这个结论的应用和意义,展示它在几何学中的重要作用。
1.2文章结构文章结构部分的内容应包括本文的主要内容和各个部分的简要介绍。
下面是一个可能的内容编写示例:在本文中,将探讨"两两相交的圆的三公弦共点"的现象和相关性质。
文章结构如下:第一部分:引言1.1 概述1.2 文章结构1.3 目的第二部分:正文2.1 两两相交的圆的基本性质2.2 三公弦的定义和性质第三部分:结论3.1 两两相交的圆的三公弦共点的证明3.2 应用和意义在正文部分,我们将首先介绍两两相交的圆的基本性质,包括相交的位置关系和相交点的性质。
随后,我们将详细讨论三公弦的定义和性质,探究这种特殊的弦与圆的关系。
人教版九年级数学下册第二十四章《圆》检测卷(含答案)
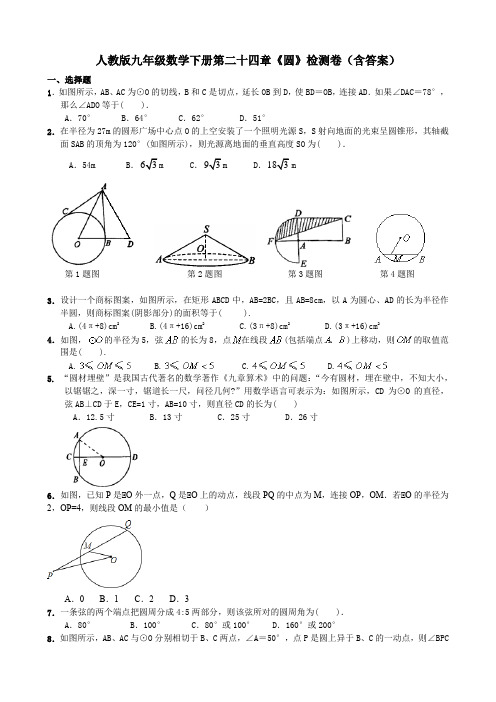
人教版九年级数学下册第二十四章《圆》检测卷(含答案)一、选择题 1.如图所示,AB 、AC 为⊙O 的切线,B 和C 是切点,延长OB 到D ,使BD =OB ,连接AD .如果∠DAC =78°, 那么∠ADO 等于( ).A .70°B .64°C .62°D .51°2.在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ,S 射向地面的光束呈圆锥形,其轴截面SAB 的顶角为120°(如图所示),则光源离地面的垂直高度SO 为( ). A .54m B ..m D .m第1题图 第2题图第3题图 第4题图3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm ,以A 为圆心、AD 的长为半径作半圆,则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm 2B.(4π+16)cm 2C.(3π+8)cm 2D.(3π+16)cm 24.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是( ). A. B. C. D. 5. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表示为:如图所示,CD 为⊙O 的直径,弦AB ⊥CD 于E ,CE=1寸,AB=10寸,则直径CD 的长为( )A .12.5寸B .13寸C .25寸D .26寸6.如图,已知P 是⊙O 外一点,Q 是⊙O 上的动点,线段PQ 的中点为M ,连接OP ,OM .若⊙O 的半径为2,OP=4,则线段OM 的最小值是( )A .0B .1C .2D .37.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为( ). A .80° B .100° C .80°或100° D .160°或200°的度数是( ).A .65°B .115°C .65°或115°D .130°或50°二、填空题 9.如下左图,是的内接三角形,,点P 在上移动(点P 不与点A 、C 重合),则的变化范围是__ ________.第9题图 第10题图10.如图所示,EB 、EC 是⊙O是两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,那么∠A 的度数是________________. 11.已知⊙O 1与⊙O 2的半径、分别是方程 的两实根,若⊙O 1与⊙O 2的圆心距=5.则⊙O 1与⊙O 2的位置关系是 __ __ .12.如图,AB 为⊙O 的直径,AB=AC ,BC 交⊙O 于点D ,AC 交⊙O 于点E ,⊙BAC=45°,给出以下五个结论:①⊙EBC=22.5°;②BD=DC ;③AE=2EC ;④劣弧是劣弧的2倍;⑤AE=BC ,其中正确的序号是 .13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______ ________. 14.已知正方形ABCD ,截去四个角成一正八边形,则这个正八边形EFGHIJLK 的边长为____ ____,面积为_____ ___.15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形,分别以它们的各顶点为圆心,以l 为半径画弧与两邻边相交,得到3条弧,4条弧,……1r 2r 2680x x -+=d(1)图(1)中3条弧的弧长的和为___ _____,图(2)中4条弧的弧长的和为_____ ___;(2)求图(m)中n条弧的弧长的和为____ ____(用n表示).16.如图所示,蒙古包可以近似地看做由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为9πm2,高为3.5m,外围高4 m的蒙古包,至少要____ ____m2的毛毡.三、解答题17. 如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.(1)证明:AF平分∠BAC;(2)证明:BF=FD.18.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:⊙A=⊙AEB;(2)连接OE,交CD于点F,OE⊙CD,求证:⊙ABE是等边三角形.19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.然后运用类似的思想提出了如下命题:③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:(1)请你从①②③三个命题中选择一个进行证明;(2)请你继续完成下面的探索;①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.参考答案一、选择题 1.【答案】B ;【解析】由AB 为⊙O 的切线,则AB ⊥OD .又BD =OB ,则AB 垂直平分OD ,AO =AD ,∠DAB =∠BAO .由AB 、AC 为⊙O 的切线,则∠CAO =∠BAO =∠DAB .所以,∠DAB =∠DAC =26°. ∠ADO =90°-26°=64°.本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.2.【答案】C ;【解析】圆锥的高、底面半径与母线组成直角三角形.由题意,SO ⊥AB 于O ,∴ ∠SOA =∠SOB =90°.又SA =SB ,∠ASB =120°,∴ ∠SAB =∠SBA =,设SO =x m ,则AS =2x m .∵ AO =27,由勾股定理,得(2x)2-x 2=272,解得(m).3.【答案】A.;【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系. ∵ 矩形ABCD 中,AB=2BC ,AB=8cm , ∴ AD=BC=4cm ,∠DAF=90°,,,又AF=AD=4cm , ∴,∴ .4.【答案】A ;【解析】OM 最长是半径5;最短是OM ⊥AB 时,此时OM=3,故选A. 5.【答案】D ;【解析】因为直径CD 垂直于弦AB ,所以可通过连接OA(或OB),求出半径即可. 根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”, 知(寸),在Rt △AOE 中,,即,解得OA=13,进而求得CD=26(寸).故选D. 6.【答案】B.【解析】设OP 与⊙O 交于点N ,连结MN ,OQ ,如图,⊙OP=4,ON=2, ⊙N 是OP 的中点, ⊙M 为PQ 的中点,⊙MN 为⊙POQ 的中位线,180120302=°-?°93x =⊙MN=OQ=×2=1,⊙点M 在以N 为圆心,1为半径的圆上,当点M 在ON 上时,OM 最小,最小值为1, ⊙线段OM 的最小值为1.故选B . 7.【答案】C ; 【解析】圆周角的顶点在劣弧上时,圆周角为;圆周角的顶点在优弧上时, 圆周角为.注意分情况讨论. 8.【答案】C ;【解析】连接OC 、OB ,则∠BOC =360°-90°-90°-50°=130°.点P 在优弧上时,∠BPC =∠BOC =65°;点P 在劣弧上时,∠BPC =180°-65°=115°. 主要应用了切线的性质定理、圆周角定理和多边形内角和定理.二、填空题 9.【答案】; 10.【答案】99°;【解析】由EB=EC ,∠E=46°知,∠ECB= 67°,从而∠BCD=180°-67°-32°=81°, 在⊙O 中,∠BCD 与∠A 互补,所以∠A=180°-81°=99°. 11.【答案】相交;【解析】求出方程 的两实根、分别是4、2,则-<<+,所以两圆相交.12.【答案】①①①;【解析】连接AD ,AB 是直径,则AD ⊙BC ,又⊙⊙ABC 是等腰三角形,故点D 是BC 的中点,即BD=CD ,故②正确; ⊙AD 是⊙BAC 的平分线,由圆周角定理知,⊙EBC=⊙DAC=⊙BAC=22.5°,故①正确;⊙⊙ABE=90°﹣⊙EBC ﹣⊙BAD=45°=2⊙CAD ,故④正确; ⊙⊙EBC=22.5°,2EC ≠BE ,AE=BE ,⊙AE ≠2CE ,③不正确; ⊙AE=BE ,BE 是直角边,BC 是斜边,肯定不等,故⑤错误. 综上所述,正确的结论是:①②④.13.【答案】7或3;【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,即另一圆半径为7或 3.5136010092⨯⨯=°°413608092⨯⨯=°°122680x x -+=1r 2r 1r 2r d 1r 2r14.【答案】; ;【解析】正方形ABCD 外接圆的直径就是它的对角线,由此求得正方形边长为a .如图所示,设正八边形的边长为x .在Rt △AEL 中,LE =x ,AE =AL,∴ ,, 即正八边形的边长为..15.【答案】(1)π; 2π; (2)(n-2)π;【解析】∵ n 边形内角和为(n-2)180°,前n 条弧的弧长的和为个以某定点为圆心,以1为半径的圆周长,∴ n 条弧的弧长的和为. 本题还有其他解法,比如:设各个扇形的圆心角依次为,,…,,则, ∴n 条弧长的和为.16.【答案】720π;【解析】∵ S =πr 2,∴ 9π=πr 2,∴ r =3.∴ h 1=4,∴ ,∴,.所求面积包括圆锥的侧面积和圆柱的侧面积,不包括底面积.1)a 22)a x 2x x a +=1)x a =1)a 2222241)]2)AEL S S S a x a a a =-=-=-=△正方形正八边形(2)1801(2)3602n n -=-121(2)(2)2n n ππ⨯⨯-=-1α2αn α12(2)180n n ααα+++=-…°1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-5l ==223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱2036720S ππ=⨯=总17.【答案与解析】(1)连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ,∴OF 垂直平分BC∴∴AF 平分∠BAC .(2)由(1)及题设条件可知∠1=∠2,∠4=∠3,∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18.【答案与解析】 证明:(1)⊙四边形ABCD 是⊙O 的内接四边形, ⊙⊙A+⊙BCD=180°, ⊙⊙DCE+⊙BCD=180°, ⊙⊙A=⊙DCE , ⊙DC=DE ,⊙⊙DCE=⊙AEB , ⊙⊙A=⊙AEB ;(2)⊙⊙A=⊙AEB , ⊙⊙ABE 是等腰三角形, ⊙EO ⊙CD , ⊙CF=DF ,⊙EO 是CD 的垂直平分线, ⊙ED=EC , ⊙DC=DE , ⊙DC=DE=EC ,⊙⊙DCE 是等边三角形, ⊙⊙AEB=60°,⊙⊙ABE 是等边三角形.19.【答案与解析】解:∵公共弦AB =120 ∴==a R 46120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=2BF FC =A BCDE FO12345HA BCD EFO 12H()∴=-⎛⎝ ⎫⎭⎪=-==r R a O o 442422222602606090,∠S S S R a r AmB AO B AO B弓形扇形=-=-=-229036012180036004244∆ππS S S R a r AnB AO B AO B弓形扇形=-=-=-1160360122400360036266∆ππ()∴=+=-+S S S AmB AnB 阴影弓形弓形4200360013π()[]∴-+两圆相交弧间阴影部分的面积为42003600132πcm .20. 【答案与解析】 (1)如选命题①. 证明:在图(1)中,∵ ∠BON =60°,∴ ∠1+∠2=60°. ∵ ∠3+∠2=60°,∴ ∠1=∠3. 又∵ BC =CA ,∠BCM =∠CAN =60°, ∴ △BCM ≌△CAN ,∴ BM =CM . 如选命题②.证明:在图(2)中,∵ ∠BON =90°,∴ ∠1+∠2=90°. ∵ ∠3+∠2=90°,∴ ∠1=∠3. 又∵ BC =CD ,∠BCM =∠CDN =90°, ∴ △BCM ≌△CDN ,∴ BM =CN . 如选命题③.证明:在图(3)中,∵ ∠BON =108°,∴ ∠1+∠2=108°. ∵ ∠2+∠3=108°,∴ ∠1=∠3. 又∵ BC =CD ,∠BCM =∠CDN =108°, ∴ △BCM ≌△CDN ,∴ BM =CN . (2)①答:当∠BON =时结论BM =CN 成立.②答:当∠BON =108°时.BM =CN 还成立. 证明:如图(4),连接BD 、CE 在△BCD 和△CDE 中,∵ BC =CD ,∠BCD =∠CDE =108°,CD =DE , ∴ △BCD ≌△CDE .∴ BD =CE ,∠BDC =∠CED ,∠DBC =∠ECD . ∵ ∠CDE =∠DEN =108°, ∴ ∠BDM =∠CEM .∵ ∠OBC+∠OCB =108°,∠OCB+∠OCD =108°. (2)180n n-°又∵∠DBC=∠ECD=36°,∴∠DBM=∠ECM.∴△BDM≌△CEN,∴ BM=CN.。
两圆公共弦所在直线方程与切线长相等.doc

两圆公共弦所在直线方程与切线长相等四川省筠连县中学邓敬过圆和圆交点的圆系方程:(为参数,且).当时,上式可化为过两圆公共弦所在直线方程:【实质】:将两圆方程相减可得两圆公共弦所在直线方程.下面介绍几个有关公共弦所在直线方程的重要结论,并举例运用,以加深学生对其该知识点的理解和掌握.1.若两圆相交,则方程为它们公共弦所在直线方程.【例1】:(新课标人教版A必修二,P133,习题4.2,A组9题)求圆与圆的公共弦长.【解析】:设两圆交于两点,将两圆方程相减可得公共弦所在直线方程:.再由再由弦长公式得:.当然,此题解法很多,该解法重点体现两圆公共弦所在直线方程的应用,其他解法在这里就不再遨述.同题型还有(新课标人教版A必修二,P144,复习参考题A组4题)求圆与圆的公共弦长.此题解答可参照例1.2.两圆外一动点P,向两相交圆所引切线长相等,则方程是P点的轨迹方程.【例2-1】:圆与圆外一动点P,向两圆所引切线长相等,则动点P的轨迹方程为【解析】:由切线长定理可知:所以P在两圆的公共弦所在直线上.即P点的轨迹为(P在两圆外).【例2-2】:已知和,在平面上找一点P,过P点引两圆切线并使他们的长都等于.【说明】:圆外一点,则向圆引切线长满足:.【解析】:如图所示,P点是两圆公共弦所在直线与以(或)为圆心,以(或)为半径的圆的交点.∴设,依题意可得:或∴P的坐标是或.【例2-3】:(新课标人教版A必修二,P144,复习参考题,A组6题),已知圆和圆关于直线对称,求直线方程.【解析】:由题意可知两圆相交,对称轴是两圆的中垂线.将两圆方程相减可得到其对称轴方程:.3.一动点P,向两相外切的圆所引切线长相等,则方程是P点的轨迹方程.【例3】:已知与相外切,两圆外一动点P,向两圆所引切线长相等,则P点的轨迹方程.【解析】:如图所示,,∴P点的轨迹方程仍为两圆方程之差,即为:.4.一动点P,向两相外离的圆所引切线长相等,则方程是P点的轨迹方程.两圆外离是将相交两圆的圆心距扩大所致,所以可以进行类比推理.【例4-1】:(07四川理15)、已知的方程是,的方程是,由动点向和所引的切线长相等,则动点的轨迹方程是【解析】::圆心,半径;:圆心,半径.两圆外离.动点的轨迹由两圆方程相减可得:.【例4-2】:(新课标人教版A必修二,P144,复习参考题A组7题)求与圆关于直线对称的圆的方程.【注意】:圆C和直线是相外离,所以对称后的两圆位置关系是外离,但是由于与已知圆共弦的圆不能唯一确定,所以通过类比此题不能用公共弦所在直线方程的思路来处理.【解析】:圆C圆心(),,设所求圆方程为,直线是两圆连心线的垂直平分线.∴∴所求圆的方程为.同类型的题还有(新课标人教版A必修二,P133,习题4.2,A组7题),求与圆C:关于直线L:对称的圆的方程.同学们可以参照例题4-2求解.。
两圆相交公共弦直线方程

两圆相交公共弦直线方程
公共弦方程
两个圆若是相交,则至多交于2点。
而将两圆的方程相减即是默认两条方程中有共同的解X、Y。
而减后的方程必定满足X、Y(就是两个交点),换句话说,就是两个交点所共同满足的直线方程。
而我们知道,平面内2点间有且只有1条直线,那么这条直线就是所求的公共弦。
相交两圆的公共弦所在的直线方程
若圆C1:(x-a1)^2+(y-b1)^2=r1^2或x2+y2+D1x+E1y+F1=0
圆C2:(x-a2)^2+(y-b2)^2=r2^2或x2+y2+D2x+E2y+F2=0
则过两圆交点的直线方程为:(x-a1)^2+(y-b1)^2-(x-a2)^2-(y-b2)^2=r1^2-r2^2或(D1-D2)x+(E1-E2)y+F1-F2=0 这是“两相交圆方程相减得公共弦方程”的变式
设两圆分别为
x^2+y^2+c1x+d1y+e1=0①
x^2+y^2+c2x+d2y+e2=0②
两式相减得
(x^2+y^2+c1x+d1y+e1)-(x^2+y^2+c2x+d2y+e2)=0③
这是一条直线的方程
(1)先证这条直线过两圆交点
设交点为(x0,y0)则满足①②
所以满足③
所以交点在直线③上
(2)由于过两交点的直线又且只有一条所以得证。
“相交两圆公共弦”问题的解法探究

彼得林奇英文语录-回复1. "Investing without research is like playing poker and never looking at the cards."2. "Everyone has the brainpower to make money in stocks. Not everyone has the stomach."3. "The stock market is filled with individuals who know the price of everything, but the value of nothing."4. "In the long run, it's not just how much money you make, but how much you keep that counts."5. "There's no shame in losing money on a stock. Everybody does it. What is shameful is to hold on to a stock, or worse, to buy more of it when the fundamentals are deteriorating."6. "The best stock to buy is the one you already own."7. "Spend at least as much time analyzing a stock as you would choosing a refrigerator."8. "Investing should be more like watching paint dry or watching grass grow. If you want excitement, take 800 and go to Las Vegas."9. "Don’t buy a stock just because everyone hates it, and don’t sella stock just because everyone loves it."10. "In this business, if you're good, you’re right six times out of ten. You’re never going to be right nine times out of ten."11. "Be patient and wait for the fat pitch."12. "If you're prepared to invest in a company, then you ought to be able to explain why in simple language that a fifth grader could understand, and quickly enough so the fifth grader won't get bored."13. "Investing should be more like watching paint dry or grass grow. If you want excitement, take 800 and go to Las Vegas."14. "Far more money has been lost by investors preparing for corrections or trying to anticipate corrections than has been lost in the corrections themselves."15. "Know what you own, and know why you own it."16. "A stock market decline is as routine as a January blizzard in Colorado."17. "The simpler it is, the better I like it."18. "The key to making money in stocks is not to get scared out of them."19. "An investment is simply a gamble in which you've managed to tilt the odds in your favor."20. "Investing is not a game where the guy with the 160 IQ beats the guy with 130 IQ."。
怎么求两圆的公共弦长

怎么求两圆的公共弦长
佚名
【期刊名称】《中学生数理化(高一版)》
【年(卷),期】2011(000)012
【摘要】求两圆x^2+y^2-10x—10y=0和x^2+y^2十6x+2y-40=0的公共弦的弦长.rn分析:我们可以通过两圆方程相减,求出两圆的公共弦所在的直线方程,把问题转化为求直线与圆相交弦的弦长.
【总页数】1页(P47-47)
【正文语种】中文
【中图分类】G633.65
【相关文献】
1.两圆锥曲线求交的图解方法
2.求两圆公共弦长问题的完整解法
3.求两圆锥相贯线另一途径
4.弦长公式在相交两圆中的运用
5.让“弦长”回归“任意两点间距离”的本质——探析弦长公式的误区及其在求“非弦”长度问题中的应用
因版权原因,仅展示原文概要,查看原文内容请购买。
两相交圆方程相减得公共弦方程

两相交圆方程相减得公共弦方程两相交圆方程相减得公共弦方程在代数几何中,我们经常遇到求解两个相交圆的公共特性的问题。
其中一个问题是求解两相交圆的公共弦方程。
本文将以深度和广度的方式探讨这个问题,并提供一个有价值的解决方案。
1. 了解圆的方程在开始解决问题之前,我们首先需要了解圆的方程。
一个圆可以由其圆心坐标和半径确定。
给定一个圆心坐标为(x0, y0)且半径为r的圆,其方程可以表示为:(x - x0)² + (y - y0)² = r²2. 两个相交圆的方程我们假设有两个相交的圆,其圆心分别为(x1, y1)和(x2, y2),半径分别为r1和r2。
我们需要求解这两个圆的公共弦方程。
为此,我们需要找到两个圆的交点坐标。
我们可以将两个圆的方程相减,得到一个含有交点坐标(x, y)的方程:(x - x1)² + (y - y1)² - ((x - x2)² + (y - y2)² = r1² - r2²展开上述方程,我们可以得到如下的表达式:x² - 2x1x + x1² + y² - 2y1y + y1² - (x² - 2x2x + x2² + y² - 2y2y + y2²) = r1² - r2²化简上述表达式,我们可以得到:-2x1x + x1² - 2y1y + y1² + 2x2x - x2² + 2y2y - y2² = r1² - r2²3. 公共弦方程的推导我们希望将上述方程进一步转化为公共弦方程的形式。
为此,我们需要找到公共弦的特征。
由于公共弦是两个圆的一个公共部分,我们可以将公共弦的两个端点表示为坐标(x, y)和(x', y')。
