图论课件第二章 树
离散数学-图论-树

二叉树
• 定义:二元有序树称为二叉树.
– 每个顶点最多有两个子顶点,一般称为左子顶 点和右子顶点. – 类似地,称每个顶点的左子树和右子树. – 每个顶点的出度都是0或2,称为二叉正则树.
二叉树的性质
• 定理:设有二叉树T, (1)第i层最多有2i个顶点; (2)若T高度为h,则T最多有2h11个顶点,最 少有h个顶点; (3)树叶个数出度为2的顶点个数1.
1 2
Huffman树与最优编码
• 若以符号为树叶,符号概率为树叶的权,利 用通过Huffman算法得到的二叉树对符号 编码,则可以保证i pili最小. • 例:对1,1,2,3,5,6,7,8构造Huffman树.
7 3 2 1 1 5 6
8
编码:设 A, B, C, D 的频率(即权值)分别为 17%, 25%, 38%, 20%, 试设计哈夫曼编码(最佳前缀码/最优编码)。
最优编码
• 构成消息的各符号的使用频率是不一样 的,显然常用符号编码短一些,罕用符号编 码长一点,可以使传输的二进制位数最少. • 最优编码问题:给定符号集{a1,a2,...,am}, ai 的出现概率是pi,编码长度为li,要使i pili最 小.
例:如果需传送的电文为 ‘A B A C C D A’,它只用到四种字符, 用两位二进制编码便可分辨。假设 A, B, C, D 的编码分别为 00, 01,10,11,则上述电文便为 ‘00010010101100’(共 14 位), 译码员按两位进行分组译码,便可恢复原来的电文。 数据的最小冗余编码问题 在编码过程通常要考虑两个问题 译码的惟一性问题
5 1 5 6 6
U 1
1 5 6 1 5 5 4 6 5 4 5 5
2
1.2树

v2 20
1
v7
4
9 16 17 v4
15 v3
3
v1 23 v6 28 v5 25 17 16
v2
1
v7
4
9
15 v3
3 v4
v1 23 v6 28 v5 25 17 16
v2
1
v7
4
9
15 v3
3 v4
v1 23 v6 28 v5 25 17
v2
1
v7
4
9 v3
3 v4
v1 23 v6 28 v5 25 17
(1) G不含圈 (2)G是连通图 (3)
q(G) p(G) 1
(4)图G=(V,E)是一个树
上述条件有两个成立,就推出其余条件成立。
树的性质: 1 在图中任意两点之间必有一条而 且只有一条通路。
树的性质: 1 在图中任意两点之间必有一条而 且只有一条通路。 2 在图中划去一条边,则图不连通。 树是边最少的连通图
去掉一条。在剩下的图中,重复以上步骤, 直到得到一个不含圈的连通图为止,这个图 便是最小支撑树。 例4 某六个城市之间的道路网如图4a 所示,要求沿着已知长度的道路联结六个城 市的电话线网,使得电话线的总长度最短。
v3
6
5
v5
4
v3
v5
3
v1
5
1
7
3 3
4
v6
v1
5
1
v6
4
v2
2
v4
v2
2
v4
图4a
树的性质: 1 在图中任意两点之间必有一条而 且只有一条通路。 2 在图中划去一条边,则图不连通。
3 在图中不相邻的两个顶点之间加 一条边,可得一个且仅得一个圈。
第2章 树

推论2.4.1 每一连通图 都包含一生成树。 每一连通图G都包含一生成树 都包含一生成树。 推论
证明:令 T 为G的极小 minimal)连通生成子图 极小( 极小 连通生成子图 (即 T 的任一真子图都不是G的连通生成子图) (由定义知,T 可在保持连通性 保持连通性的前提下,用逐步 保持连通性 从G中去边的办法求出( ∴所去的边一定在一圈中 边 (即非割边 非割边)(∴每步至少破坏一圈))。 由T的 非割边 定义知,ω(T) = 1 , ω(T - e) = 2 ∀ e ∈ E(T) 。 即 T 的每边为割边,故由定理2.4知T为树。
2.1.4 G为 林 ⇔ ε = ν - ω。 2.1.5 若林G 恰有2k个奇点 奇点,则G 中存在k条边不重 奇点 的路 1 ,P2 ,..,Pk ,使得E(G) = E(P1 )∪E(P2 )∪ ... ∪E(Pk )。 2.1.6 正整数序列 (d 1 ,d 2 ,...,d ν )是一 棵树的度序 ν 列,当且仅当
定理2.5 设 T 为G的一生成树,e为G中不属于 定理 T的边,则T+e 含唯一的圈。 证明: 若e为环(即1-圈),结论显然成立。 不然,由于T 无圈,T + e 中的每个圈(若存 在的话)都包含e 。又,C为 T + e 的一圈 ⇔ C - e 为T 中连接e的两个端点的路。但, 由定理2.1知,T中恰只有一条这样的路,因 此 T + e中包含唯一的圈。
⇔ 不含圈的图。 树(tree) ⇔ 连通无圈图。 叶 (leave) ⇔ 树中度为1的顶点。 例:六个顶点的树
称边e为图G的割边( cut edge) ⇔ ω(G-e) > ω(G) 。 (或即 ω(G-e) = ω(G) + 1 ) (称边e为图G的非割边 ⇔ ω(G-e) = ω(G) 。)
图论——树

森林
推论: 具有k个分支的森林有nk条边, 其中n是G的顶点数。
无向树的性质
定理2.2
证明
设T是n阶非平凡的无向树,则T中至少有两片树叶。
设T有x片树叶,由握手定理及定理2.1可知,
2(n 1) d (vi ) x 2(n x)
由上式解出x≥2。
例2.1
例2.1 画出6阶所有非同构的无向树。 解答 设Ti是6阶无向树。
唯一性(反证法)。 若路径不是唯一的,设Г1与Г2都是u到v的路径, 易知必存在由Г1和Г2上的边构成的回路, 这与G中无回路矛盾。
(2)(3)
如果G中任意两个顶点之间存在唯一的路径, 则G中无回路且m=n-1。 首先证明 G中无回路。 若G中存在长度大于2的圈, 则圈上任何两个顶点之间都存在两条不同的路径, 这也与已知矛盾。
说明
注意:T 不一定连通,也不一定不含回路。
生成树的存在条件
定理2.3 无向图G具有生成树当且仅当G连通。 证明 必要性,显然。 充分性(破圈法)。 若圈,任取一圈,随意地删除圈上的一条边,
若再有圈再删除圈上的一条边,直到最后无圈为止。 易知所得图无圈(当然无回路)、连通且为G的生成子图, 所以为G的生成树。
分支点—— 7个
高度—— 5
家族树
常将根树看成家族树,家族中成员之间的关系如下定义。 定义2.7 设T为一棵非平凡的根树, vi、vj∈V(T),若vi可达vj,则称vi为vj的祖先,vj为vi的后代。 若vi邻接到 vj(即 <vi,vj>∈E(T)), 则称vi 为 vj的父亲,而 vj为 vi 的儿子。 若vj、vk的父亲相同,则称vj与vk是兄弟。 定义2.8 设v为根树T中任意一顶点,称v及其后代的导出子图为 以v为根的根子树。
离散数学PPT课件 5树与生成树(ppt文档)
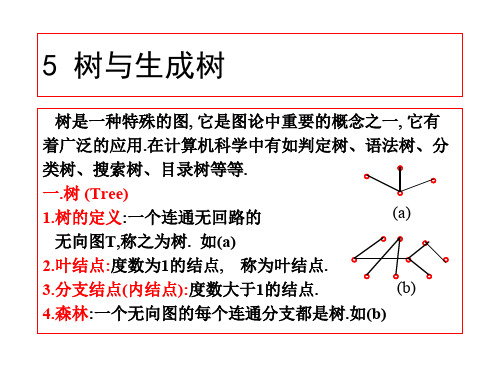
(b)
4.森林:一个无向图的每个连通分支都是树.如(b)
5.与树定义等价的几个命题
定理8-9.1给定图T,以下关于树的定义是等价的.
⑴无回路的连通图.
⑵无回路且e=v-1 其中e是T的边数,v是T的结点数.
⑶连通的且e=v-1.
⑷无回路但添加一条新边则得到一条仅有的回路.
⑸连通的,但删去任一条边,T便不连通.
v2 71
2 3 2
v3 51
v1 8 v8 7 v5 3 v4
4 2 v7 4
34 6 6 v6
Kruskal算法: 设G是有n个结点,m条边(m≥n-1)的连通图. S=Φ i=0 j=1
将所有边按照权升序排序: 43;1
⑹每对结点之间有一条且仅有一条路.
证明:⑴⑵:已知T是连通无回路图,通过不断地增加T中
的结点数,归纳证明.
当 v=2时, T如右图所示,e=1 显然e=v-1.
以后对T在保证连通又无回路的前提下每增加一个结点,
也增加一条边. 设最后T有v个结点e条边, 所以 e=v-1.
⑵⑶: 已知T是无回路的,且e=v-1.(推出T是连通的) 假设T不是连通的,设T有k个连通分支, T1,T2,...,Tk,(k≥2) 因为它的每个连通分支都是连通无回路的,所以都是树, 设Ti有结点数vi,边数ei, 所以边数 ei =vi-1 设T有v个结点,e条边. 所以
边 e78 e56 e35 e46 e67 e58 e12 e18
权4 4 5 6 6 7 7 8
v2
2 3
7 12
v3 51
v1 8 v8 7 v5 3 v4
图论 第二章 树

u
v
G2
7/39
G1
对于有n个点的图G,由(3)的假设知删去G中某边可得 两个具有同样性质的子图G1与G2。设Gi 的点数与边数分别为 ni 与mi(i =1,2)。显然n1< n,n2 < n。由归纳假设有 n1= m1+1,n2= m2+1
相加得
n1+n2= m1+ m2+2 同时有 n1+n2= n, m1+ m2= m-1 代入(*)式得:n = m+1。 (*)
若不然,则G+uv存在另一个圈C’,且C’与C都是图G添加边 uv后产生的,即这两个不同圈都含有uv边。因而在原图中有
两条不同的连接u 与 v 的路,矛盾。
u C’
v G+uv
10/39
(6)G 无圈,添加任一条边可得唯一的圈。
(1)G 是树
需证明G连通。 假设不连通,则存在两个 顶点u 与 v 之间不存在通路,因此增 加uv边不会在G+uv产生圈,矛盾!
凯莱生成树递推计数公式是他在1889年建立的。
24/39
(G )
(G) (G e) (G e)
证明 由于G的每一棵不包含e 的生成树也是 G-e 的生成 树。由此推知 ,τ(G-e) 就是G 的不包含 e 的生成树的棵 数。 类似, τ(G●e) 就是G 的包含 e 的生成树的棵数。从 而知结论成立。
(k 2)nk
14/39
§2.2树的中心和形心
定义1 设 G = (V, E) 是一连通图, v∈V,令 e(v) = max {d(u,v) | u∈V } 则称 e(v)为顶点 v 的离心率;又令 r(G) = min {e(v) | v∈V } 称 r(G) 为图 G 的半径。 比较图的直径与离心率的定义可知,图G 的直径是 G 的最大离心率;e(v) = r(G) 的点 v ,称为 G 的一个 中心点, G 中全体中心点的集合称为G 的中心。
图论 第二章 树(tree)
定义2.2.2 如果在图G中去掉一个顶点(自然同 时去掉与该顶点相关联的所有边)后图的分 支数增加,则称该顶点为G的割点。
定理2.2.1 当且仅当G的一条边e不包含在G 的 圈中时,e才是割边。
u x
e
v
Hale Waihona Puke yCG推论2.2.1 当且仅当连通图G的每一条边均为 割边时,G才是一棵树。
对割边有下面的等价命题:
推论2.1.3 设G的边数为q,顶点数为p,如果 G无圈且q=p-1,则G是一棵树。
推论2.1.4 在树中至少存在两个度为1的顶点。
关于树有下列的等价命题:
(1)G是一棵树 (2)G的任意两个顶点由唯一道路联结 (3)G是连通的,且q=p-1 (4)G是无圈的,且q=p-1 (5)G无圈,且若G的任意两个不邻接的顶点 联一条边e,则G+e中恰有一个圈。
A directed graph is Eulerian if it is connected and can be decomposed into arc-disjoint directed cycles.
An undirected graph is traversable if it is connected and at most two vertices in the graph are of odd degree
条包含G的所有边的闭链; ❖ (4)两个欧拉图的环和仍是欧拉图。
理定3.1.2和推论3.1.1反映了图的一 个重要性质,即图的连绘性。一个连 绘的图是指这个图可以用一笔画成而 没有重复的笔划。换句话说就是在这 个图中存在一条能过每条边的链。
3.3 哈密顿图
1856 年 hamilton 周游世界的游戏,十 二面体,有20个顶点,三十条边,十二 个面
图论中的树与森林
图论中的树与森林
在图论中,树和森林是两个重要的概念,它们是有机连通且无圈的图。
接下来将分别介绍树和森林的定义与性质。
1. 树
树是一种无圈的连通图,且任意两个顶点之间只有一条简单路径。
换句话说,树是一个极小连通图。
树有以下性质:
- 任意一棵树有n个顶点和n-1条边。
- 任意一棵树的任意两个顶点之间有唯一路径。
- 任意一棵树都是连通的,去掉任意一条边就不再连通。
- 任意一棵树没有回路。
- 任意一棵树中加入一条边都会形成回路。
- 一棵含有n个顶点的图是树当且仅当它有n-1条边且连通。
树是一种重要的数据结构,常用于解决树/图相关的问题,比如最小生成树、拓扑排序等算法。
2. 森林
森林是由若干棵不相交的树构成的连通图。
换句话说,森林是多个树的集合。
森林有以下性质:
- 森林中每个连通分支都是一棵树。
- 森林中各棵树之间没有边相连。
在实际问题中,森林通常用于表示一组有关系但不完全联通的数据
集合,比如多个家族的家谱关系等。
在计算机科学领域,树和森林被广泛运用于算法设计和数据结构中。
它们是图论中的重要概念,深入了解树和森林的性质有助于理解和解
决相关问题。
图论中的树与森林是一门深奥的数学学科,通过不断学
习和实践,我们可以更好地运用它们来解决实际问题。
图论及其应用--树与林
定理 设有完全m叉树,其树叶的数目为t,分支 数为i, 则(m-1)×i=t-1。
证明思路: m位选手,单淘汰赛,每局淘汰(m-1)位,
共比赛i局,最后剩1位选手。因此有:
(m-1)×i+1=t
定义 在根树中,一个结点的通路长度,就是从树 根到该结点的通路中的边数。分支点的通路长度称为 内部通路长度,树叶的通路长度称为外部通路长度。
定理2:任一棵树中至少存在两个叶。
证明: 因T连通则u∈T,deg(u)≥1。设T有k个一
度点,其它点均大于等于2,则 2e=∑deg(vi)≥k+2(v-k)=2v-k。 因e=v-1, 故2(v-1)≥2v-k,则k≥2。
2.2支撑树与支撑林
设F是图D的支撑子图,并且ω(F)=ω(D)。 若F是林,则称F为D的支撑林;若F是树, 则称F为D的支撑树。
例如:
a 19
b5
14 12
18
7
c
16 e 8
3
g
d
27
21
f
求最小生成树的克鲁斯卡尔(Kruskal)算法(避圈法): a)在G中选取最小权的边,记作e1,置i=1。 b)当i=n-1时结束,否则转c)。 c)设已选择边为e1,e2,……ei,此时无回路。在G 中选取不同于这i条边的边ei+1,该边使得{e1,…, ei+1}生成的子图中无回路,并ei+1是满足该条件中权 最小的一条边。
定理2.4 每个连通图都含支撑树。 推论2.4.1每个图都含支撑林或者支撑树。 推论2.4.2每个图均有ε≥ν- ω。 定理2.5设F是G的支撑林。若E(G)\E(F)
非空,则对其中的任何边e,F+e含有且 仅含有一条圈。
第二章 生成树
第二章树教学安排的说明章节题目:§2.1树的特性;§2.2割边与割点,§2.3生成树学时分配:共2课时本章教学目的与要求:会正确表述关于树的一些基本概念(如树、生成树、割边与割点),会用避圈法和破圈法找生成树,会用树的方法描述一些简单的实际问题.课 堂 教 学 方 案课程名称:§2.1树的特性;§2.2割边与割点;§2.3 生成树授课时数:2学时授课类型:理论课教学方法与手段:讲授法教学目的与要求:会正确表述关于树的一些基本概念(如树、生成树、割边与割点),会用避圈法和破圈法找生成树,会用树的方法描述一些简单的实际问题. 教学重点、难点:(1) 理解树的概念以及树的等价命题;(2) 掌握割边与割点的概念;(3) 理解生成树的定义;(4) 掌握找生成树的两种方法——避圈法和破圈法。
教学内容:树是图论中的一个重要概念。
树是一种极为简单而又非常重要的特殊图,它在计算机科学以及其它许多领域都有广泛的应用。
在1847年克希霍夫就用树的理论来研究电网络,1857年凯莱在计算有机化学中222n C H 的同分异构物数目时也用到了树的理论。
各类网络的主干网通常都是树的结构。
本节介绍树的基本知识,其中谈到的图都假定是简单图。
2.1 树的特性定义2.1.1 连通无圈的无向图称为无向树,简称为树(Undirected tree )。
记作T ,树中的悬挂点(或称T 中度数为1的顶点)又称为树叶(leave )(或叶顶点),其它顶点称为树枝(Branch Point 或内点(Inner Point))。
诸连通分支均为树的图称为森林(forest ),树是森林。
例1 图1中(a ),(b )为树,(c )为森林。
图1由于树无环也无重边(否则它有圈),因此树必定是简单图。
树还有等价命题:设T 是一个无向(,)n m 图,则以下关于T 的命题是等价的。
(1) T 是树;(2)T 无圈且1m n =-;(3) T 连通且1m n =-;(4)T 无圈,但增加任一新边,得到且仅得到一个圈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
•得x=8 •例8 设T为(n, m)树,T中有ni个度为i的点(1≦i≦k), 且有:∑ni=n.证明:
•证明:由m=n-1得:
•又由握手定理得:
•由上面两等式得:
13
•推论1 具有k个分支的森林有n-k条边。 •证明:设森林G的k个分支为Ti (1≦i≦k).对每个分支 ,使用定理3得:
•所以G-u至少有k+1条边。
15
•而当G是树时,边数恰为n-1. •所以n阶连通图G至少有n-1条边。 •所以,树也被称为最小连通图。 •定理5 任意树T的两个不邻接顶点之间添加一条边后, 可以得到唯一圈。 •证明:设u与v是树T的任意两个不邻接顶点,由定理2 知:有唯一路P连接u与v.于是P∪{u v}是一个圈。 •显然,由P的唯一性也就决定了P∪{u v}的唯一性。 •例9 设G是树且Δ≧k,则G至少有k个一度顶点。 •证明:若不然,设G有n个顶点,至多k-1个一度顶点 ,由于Δ≧k,于是,由握手定理得:
5
•2、树的应用 • 树是图论中应用最为广泛的一类图。在理论上,由 于树的简单结构,常常是图论理论研究的“试验田”。 在实际问题中,许多实际问题的图论模型就是树。 •例2 族谱图与树 • 要把一个家族的繁衍情况简洁直观表达出来,用点 表示家族中成员,成员x是成员y的儿女,把点x画在点 y的下方,并连线。如此得到的图,是一颗树,称为根 树。示意如下:
16
•所以,有:m (G)>n-1,与G是树矛盾! •例10 设G是森林且恰有2k个奇数顶点,则在G中有k条 边不重合的路P1, P2 ,…, Pk,使得:
•证明:对k作数学归纳。 •当k=1时,G只有两个奇数度顶点,此时,容易证明, G是一条路; •设当k=t时,结论成立。令k=t+1
17
• 在G中一个分支中取两个一度顶点u与v,令P是连 接该两个顶点的唯一路,则G-P是有2t个顶点的森林, 由归纳假设,它可以分解为t条边不重合的路之并,所 以G可以分解为t+1条边不重合的路之并。 •注:对图作某种形式的分解,是图论的一个研究对象, 它在网络结构分析中具有重要作用。
9
• 总之,树在图论研究和图论应用上都是十分典型 的特殊图。
•(二)、树的性质
•定理1 每棵非平凡树至少有两片树叶。 •证明 设P=v1v2…vk是非平凡树T中一条最长路,则 v1与vk在T中的邻接点只能有一个,否则,要么推出 P不是最长路,要么推出T中存在圈,这都是矛盾! 即说明v1与v2是树叶。 •定理2 图G是树当且仅当G中任意两点都被唯一的 路连接。 •证明:“必要性” •若不然,设P1与P2是连接u与v的两条不同的路。则
•所以:
•定理4 每个n阶连通图的边数至少为n-1. •证明:如果n阶连通图没有一度顶点,那么由握手定 理有:
14
•如果G有一度顶点。对顶点数作数学归纳。 •当n=1时,结论显然 •设当n=k时,结论成立。 •当n=k+1时,设u是G的一度顶点,则G-u为具有k个顶 点的连通图。 •若G-u有一度顶点,则由归纳假设,其边数至少k-1,于 是G的边数至少有k条; •若G-u没有一度顶点,则由握手定理:
7
• 该问题归结于在图中求所谓的最小生成树问题。 或称为赋权图中的最小连接问题。
•例4 化学中的分子结构与树 例如:C4H10的两种同分异构结构图模型为:
•h •h •h •h
•h •h •h •h •h
•h •h •h
ቤተ መጻሕፍቲ ባይዱ
•h •h
•h
•h •h •h •h
•h
8
•例5 电网络中独立回路与图的生成树 早在19世纪,图论还没有引起人们关注的时候,物理
10
•由这两条路的全部或部分将构成一个圈,这与G是 树相矛盾。 •“充分性” •首先,因G的任意两点均由唯一路相连,所以G是 连通的。 •其次,若G中存在圈,则在圈中任取点u与v,可得 到连接u与v的两条不同的路,与条件矛盾。 •定理3 设T是(n, m)树,则:
•证明:对n作数学归纳。
11
•当n=1时,等式显然成立; •设n=k时等式成立。考虑n=k+1的树T。 •由定理1 T中至少有两片树叶,设u是T中树叶,考 虑 ••T这1=就T证-u明,则了T定1为理k阶3。树,于是m(T1)=k-1, 得m(T)=k。 •例7 设T为12条边的树,其顶点度为1,2,5。如果T恰有 3个度为2的顶点,那么T有多少片树叶? •解:设T有x片树叶。 •由m=n-1得n=13. 于是由握手定理得:
图论课件第二章 树
2
•本次课主要内容
•(一)、树的概念与应用 •(二)、树的性质 •(三)、树的中心与形心
3
•(一)、树的概念与应用
•1、树的概念 •定义1 不含圈的图称为无圈图,树是连通的无圈图。 •例如:下面的图均是树
•树T1
•树T2
•树T3
•树T4
4
•定义2 称无圈图G为森林。 •注: (1)树与森林都是单图; •(2) 树与森林都是偶图。 •例1 画出所有不同构的6阶树。 •解:按树中存在的最长路进行枚举。6阶树中能够存在 的最长路最小值为2,最大值为5。
学 家克希荷夫就已经注意到电路中的独立回路与该电路中
的所 谓生成树的关系。即:如果电路是(n, m)图,则独立回路 •例6的通信网络中的组播树 • 个在数单为播m模-型n+中1.并,且数,据生包成通树过添网上络生沿成着树单外一的路G径的从一源条主边机向 •目标,主就机传递,但在组播模型中,组播源向某一组地址传递数 •据包可,以而得这到一一地独址立却回代路表。一个主机组。为了向所有接收者传 •递数据,一般采用组播分布树描述IP组播在网络里经过的路 •径。组播分布树有四种基本类型:泛洪法、有源树、有核树 •和Steiner树 。
•根树
6
• 实际上,根树是许多问题的模型,如社会结构, 计算机数据结构,数学中的公式结构,分类枚举表 示等。
•例3 道路的铺设与树 • 假设要在某地建造5个工厂,拟修筑道路连接这5处 。经勘探,其道路可按下图的无向边铺设。现在每条边 的长度已经测出并标记在图的对应边上,如果我们要求 铺设的道路总长度最短,这样既能节省费用 ,又能缩 短工期 ,如何铺设?
