河南省正阳县第二高级中学高三上学期文科数学周练(一) Word版含答案
河南省正阳县第二高级中学2021届高三数学上学期周练试题(一)理

河南省正阳县第二高级中学2021届高三数学上学期周练试题(一)理一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知全集U=R,集合A={x|x≥﹣1},集合B={x|y=lg(x﹣2)},则A∩(∁U B)=()A.[﹣1,2) B.[﹣1,2] C.[2,+∞)D.[﹣1,+∞)2.已知i是虚数单位,复数23zi-对应于复平面内一点(0,1),则|z|=()A.13 B.4 C.5 D.423.已知等比数列{n a}中,公比3571,642q a a a==,则4a=()A.1 B.2 C.4 D.84.设实数x,y满足约束条件140,0x yx yx y-≥⎧⎪+≤⎨⎪≥≥⎩,则目标函数z=x﹣3y的取值范围为()A.[﹣12,1] B.[﹣12,0] C.[﹣2,4] D.[1,4]5.某几何体的三视图如图所示,则该几何体的体积为()A.483π-B.883π-C.24﹣πD.24+π6.已知函数f(x)=sin(ωx+φ)(ω>0,2πϕ<)的零点构成一个公差为2π的等差数列,3(0)2f=-,则f(x)的一个单调递增区间是()A.5(,)1212ππ-B.(,)63ππ-C.5(,)1212ππ-D.7(,)1212ππ7.平面直角坐标系中,已知O为坐标原点,点A、B的坐标分别为(1,1)、(﹣3,3).若动点P满足OP OA OBλμ=+,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为()A.x﹣y=0 B.x+y=0 C.x+2y﹣3=0 D.(x+1)2+(y﹣2)2=58.已知双曲线与椭圆221925x y+=的焦点相同,且它们的离心率的乘积等于85,则此双曲线的方程为()A .221412x y -=B .221412y x -=C .221124x y -=D .221124y x -=9.运行如图所示的程序框图,输出i 和S 的值分别为( )A .2,15B .2,7C .3,15D .3,710.把8个相同的小球全部放入编号为1,2,3,4的四个盒中,则不同的放法数为( ) A .35 B .70 C .165 D .1860 11.已知函数ln ,0()2,0x x f x ax x >⎧=⎨+≤⎩(a ∈R ),若函数y=|f (x )|﹣a 有三个零点,则实数a的取值范围是( )A .a≥﹣2 B .a >2 C .0<a <1 D .1≤a<212.已知定义在(0,+∞)上的函数f (x )的导函数为f'(x ),满足x 2f'(x )+xf (x )=lnx ,f (e )=1e,则f (x )( ) A .有极大值,无极小值 B .有极小值,无极大值 C .既有极大值又有极小值 D .既无极大值也无极小值 二、填空题:13.(x ﹣2)5(1)x -的展开式中2x 项的系数为 .(用数字作答) 14.已知sin cos 11cos 22ααα=-,tan (α﹣β)=12,则tanβ= .15.设偶函数f (x )对任意x∈R,都有-1(3)()f x f x =+,且当x∈[-3,-2]时,f (x )=2x ,则f(113.5)的值是 .16.已知椭圆C :22221(0)x y a b a b+=>>的焦点为F 1,F 2,若点P 在椭圆上,且满足212.PO PF PF =(其中O 为坐标原点),则称点P 为“*”点,则椭圆上的“*”点有 个.三、解答题:(解答应写出文字说明,证明过程或演算步骤.)17.在△ABC中,已知内角A=60°,边23BC=.设内角B=x,△ABC的面积为y.(Ⅰ)求函数y=f(x)的解析式和定义域;(Ⅱ)当角B为何值时,△ABC的面积最大.18.如图,三棱柱ABC﹣A1B1C1中,AB=AC=CC1,平面BAC1⊥平面ACC1A1,∠ACC1=∠BAC1=60°,AC1∩A1C=O.(Ⅰ)求证:BO⊥平面AA1C1C;(Ⅱ)求二面角A﹣BC1﹣B1的余弦值.19.某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照分成9组,制成了如图所示的频率分布直方图.(Ⅰ)求直方图中m的值并估计居民月均用电量的中位数;(Ⅱ)从样本里月均用电量不低于700度的用户中随机抽取420.如图,椭圆C1:22221(0)x ya ba b+=>>(a>b>0)的离心率为32,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得121732SS=?请说明理由.21.已知函数21()ln2f x x x x x=+-的导函数为f'(x).(Ⅰ)判断f(x)的单调性;(Ⅱ)若关于x的方程f'(x)=m有两个实数根x1,x2(x1<x2),求证:2122x x<.[选修4-4:坐标系与参数方程]22.已知直线l的参数方程为31232xty⎧=--⎪⎪⎨⎪=⎪⎩(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为4sin()6πρθ=-.(Ⅰ)求圆C的直角坐标方程;(Ⅱ)设点为P(x,y)为直线l与圆C3x y+的取值范围.[选修4-5:不等式选讲23.已知不等式|2x﹣3|+x﹣6≥0的解集为M.(Ⅰ)求M;(Ⅱ)当a,b∈M时,证明:313a ab b+≥+.参考答案:1-6.BADCAC 7-12.CBCCBD对于第8题,可以分没有空盒37C ,一个空盒274C ,两个空盒2147C C ,三个空盒074C 讨论13.25 14.13 15.1516.4个17.y=0.5ABACsinA=(23x π-)2(0)3x π<< (II )B=60°时,△ABC的面积最大为18.(1)略(Ⅱ)-19. 解:(Ⅰ)1﹣100×(0.0004+0.0008+0.0021+0.0025+0.0006+0.0004+0.0002)=2m×100, ∴m=0.0015.居民月均用电量的中位数为408度. (Ⅱ)200户居民月均用电量在度的户数是4., 随机变量X 的分布列为:X 0 1 2 3 4P70495 224495 168495 32495 1495故数学期望为43. 20.解:(Ⅰ)故C 1,C 2的方程分别为2244x y +=,y=x 2﹣1. (Ⅱ)满足条件的直线存在,且有两条,其方程为32y x =± 21.解:(Ⅰ)f (x )在(0,+∞)上单调递增 …(Ⅱ)依题意,1122ln ln x x mx x m-=⎧⎨-=⎩,相减得2121ln x x x x -=,令21(1)x t t x =>,则有1ln 1t x t =-,2ln 1t t x t =-,欲证2122x x <成立,只需证222ln (ln )21(1)t t t t t <--成立,即证ln t <成立,令x =(x >1)21)3ln 0(1)x x x x -->>成立,再构造函数就可以了 22. 解:(Ⅰ)圆C的普通方程2220x y x ++-=(Ⅱ)取值范围是[﹣2,2]. … 23. 解:(Ⅰ)M={x|x≥3或x≤﹣3};(Ⅱ)平方展开即可。
河南省正阳县第二高级中学高三上学期文科数学周测

河南省正阳县第二高级中学2018-2019学年上期高三文科数学周测一一.选择题:1.已知集合A={1,2},B=2{|280}x Z x x ∈--<,则A B =( )A.{1}B.{1,2}C.{0,1,2}D.{0,1,3}2.已知平面向量(1,2),(2,3)a b x ==-,若a b ⊥,则x=_________A.4B.5.5C.4.5D.3.53.实数x,y 满足不等式组2421x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则目标函数z=3x+2y 的最大值是____________A.2B.6C.7D.54.在圆221x y +=内随机选取一点P(x,y),则|x|+|y|1≤的概率是( ) A.2π B. 1π C. 12π D. 32π5.已知2()ln f x x x =+,则不等式(21)()f x f x -≥的解集是( ) A.1(,][1,)3-∞+∞ B.1(,0)(0,][1,)3-∞+∞ C.1[,1]3 D.(0,1]6.当a=_____时,直线340x y a ++=将圆2244x y x y +=+分成1:3两部分A.-4B.-24C.-16D.-4或-247.在△ABC 中,A ,B ,C 的对边分别为a,b,c,若B=60°,a,c 分别为方程213400x x -+=的二根,则b=_______A.7B.5C.8D.68.若实数a,b,c 满足2520a b c ==,则211a b c+-的值为_________ A.1 B.0 C.2 D.49.若{}n a 为等差数列,255,2a a ==,则7a =( )A.1B.0C.2D.-110.已知椭圆22221(0)x y a b a b+=>>的左焦点为F ,若F 将长轴分成1:2两部分,则此椭圆的离心率等于( )13D. 1211.三棱锥A-BCD 的所有棱长均为1,AB ∥平面α,则三棱锥A-BCD 上的所有点在平面α内的射影构成的图形面积的最大值为 A.121412.已知曲线y =1ln 2y x =有公共点,且在公共点处有公共的切线,则正实数a 的值为 A.e B.1eC.1D.2e 二.填空题: 13.已知二次函数2()(21)1f x ax a x =+-+在区间3[,2]2-上的最大值为3,则正实数a 的值为( ) 14.在直棱柱111ABC A B C -中,14,3,5AA AB BC AC ====,则B 到面11AB C 的距离为()15.圆O 的半径为1,PA 、PB 为该圆的两条切线,A ,B 为切点则.PA PB 的最小值为( )16.已知周期为4的函数(1,1]()12,(1,3]x f x x x ⎧∈-⎪=⎨--∈⎪⎩,若3f(x)=x 恰好有5个实数解,则正实数m 的取值范围是( )三.解答题:17.在△ABC 中,a,b,c 分别是A ,B ,C 的对边,已知△ABC 的面积为23sin a A(1)求sinB.sinC (2)若6cosBcosC=1,a=3,求△ABC 的周长18. 已知命题P:直线x+3=2y 与抛物线2(0)y mx m =≠没有交点;已知命题q:方程22152x y m m+=-表示双曲线;若p q ∨为真,p q ∧为假,试求实数m 的取值范围.19.如图,三棱柱111C B A ABC -中,CB AC =,1AA AB =,0160=∠BAA(1)证明:C A AB 1⊥;(2)若平面⊥ABC 平面B B AA 11,2AB CB ==,求点A 到平面11BB C C 的距离.20. 已知12,F F 是椭圆22221(0)x y a b a b+=>>的左右焦点,O 为原点,(2,)5P -在椭圆上,线段1PF 与y 轴的交点N 满足12OP OF ON +=.(1)求椭圆的标准方程;(2)过椭圆右焦点2F 作直线l 交椭圆于A,B 两点,交y 轴于M 点,若1222,MA AF MB BF λλ==,求12λλ+.21. 已知函数()x x f ln =,()xg x e =. (1)求函数()x x f y -=的单调区间与极值;(2)求证:在函数()f x 和()g x 的公共定义域内,()()2g x f x ->恒成立.22. 在直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系。
河南省正阳县第二高级中学高一上学期数学周练(一) Wor

河南省正阳县第二高级中学2017-2018高一上期数学周练(一)一.选择题:1.在“①高一数学课本上的难题; ②所有的正三角形; ③方程220x +=的实数解;”中,能够形成集合的是_________A. ②B. ③C. ②③D. ①②③2.已知集合{2,0,2}A =-,B=2{|20}x x x --=,则____A B =A.∅B.{2}C.{0}D.{-2}3.设全集{1,2,3,4,5,6,7},{2,3,4,6},{1,4,5}U M N ===,则{1,5}等于________A.M NB. M NC.()U C M N D. ()U M C N 4.设A={|12}x x <<,B={|}x x a ≤,若A B ≠⊂,则实数a 的取值范围是________A.a ≥2B.a ≤1C. a ≥1D. a ≤25.满足1234{,,,}M a a a a ⊆,且12312{,,}{,}M a a a a a =的集合M 的个数是______A.3B.2C.1D.无穷多个6.已知集合{|212},{|21,}M x x N x x k k N +=-≤-≤==-∈,则M N 子集的个数是________________A.2B.1C.4D.8 7.11{|,},{|,}623n A x x m m Z B x x n Z ==+∈==-∈,1{|,}26p C x x p Z ==+∈,则A 、B 、C 的关系是___________A.A=B=CB.A B C ⊆=C.A B C ⊆⊆D.B C A ⊆⊆8.某班在全明星投票期间,对本班55位学生进行了调查,发现支持科比的有26人,支持詹姆斯的有23人,还有12人既不支持科比也不支持詹姆斯,则在该班中既支持科比又支持詹姆斯的人数为_______________A.5B.6C.35D.389.设I 为全集,1S ,2S ,3S 是I 的三个非空子集,且1S ∪2S ∪3S =I ,则下列结论正确的是___________:A.1()I C S ∩(2S ∪3S )=∅B.1S ⊆ 1()I C S ∩3()I C SC. 1()I C S ∩3()I C S =13()I C S SD.123()()I I S C S C S ⊆10.已知集合{|4A x x =<-或1}x >,M={|2121}x k x k -≤≤+,若M A ⊆,则实数k 的取值范围是_________________.1A k > B.52k <- C.1k >或52k <- D.512k -<< 11.设U R =,{|2A x x =≤-或5}x ≥,{|2}B x x =≤,{|23}C x a x a =-≤≤-, 若(())U C C A B C =,则实数a 的取值范围是_______________A.a>1B.a<1C.a>0D.a<012.已知集合123456789{,,,,,,,,,}A a a a a a a a a a a =,其中0(1,2,...1i a i >=,集合B={(,)|,,()}a b a A b A a b A ∈∈-∈,则集合B 的元素至多有___________个A.55B.45C.35D.65二.填空题:13.设集合A={-1,2},2{|20}B x x ax b =-+=,若,B B A ≠≠∅⊂,则a+b=____________ 14.已知2{,2},{,2},A a B a AB A B ===,则a=__________ 15.若集合2{1,3,},{1,}A x B x ==,{1,3,}A B x =,x Q ∈,则x 的值是______16.已知2{|430}A x x x =-+≥,{|}B x a x b =<<,,AB R A B ==∅,则 22a b +=_______________________三.解答题:17.已知集合2{4,21,},{5,1,9},{9}A a a B a a AB =--=--=,求a 的值18.集合{|35},{|223},A x x B x m x m B A =-≤≤=+<<-⊆,求m 的取值范围19.已知集合2{|60},{|1}A x x x B x m x m =--<=<-<①若AB A =,求实数m 的取值范围②若()RC A B ≠∅,求实数m 的取值范围20.222{|190},{|560}A x x ax a B x x x =-+-==-+=,2{|280}C x x x =+-= ①若AB A B =,求实数a 的值 ②若(),A B AC ≠∅⊂=∅,求a 的值21.已知集合2{|20}A x x x p =++=,若{|0}A x x >=∅,求实数p 的取值范围22.已知正整数集合222212341234{,,,},{,,,}A a a a a B a a a a ==,其中1234a a a a <<<,如果1414{,},10,A B a a a a A B =+=的所有元素之和为124,①求1a 和4a 的值 ②求集合A1-6.CBCABD 7-12.BBCCBB 13.0或者6 14. 0或者1 15.0 16.1017.-3注意集合元素的互异性18.(,4]-∞ 19.(1)1m ≥-(2).m<-1 20.(1)a=5(2)a=-221.0p ≥ 22.(1)141,9a a ==(2){1,3,5,9},{1,9,25,81}A B ==。
河南省正阳县第二高级中学高三上学期文科数学周练(四)
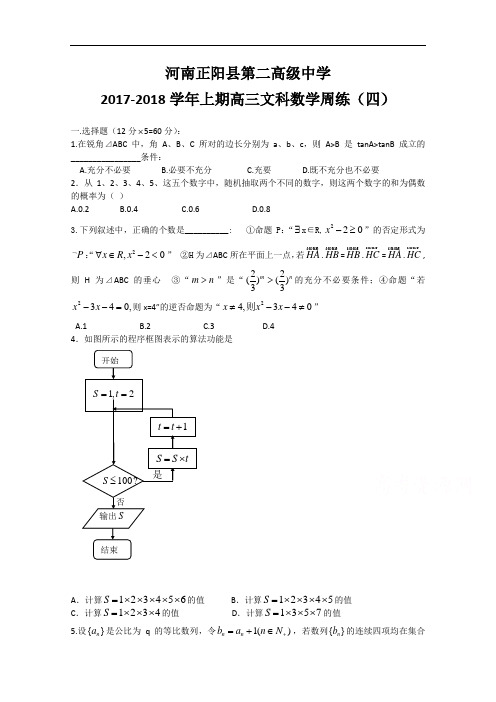
河南正阳县第二高级中学2017-2018学年上期高三文科数学周练(四)一.选择题(12分⨯5=60分):1.在锐角⊿ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c ,则A>B 是tanA>tanB 成立的________________条件:A.充分不必要B.必要不充分C.充要D.既不充分也不必要2.从1、2、3、4、5、这五个数字中,随机抽取两个不同的数字,则这两个数字的和为偶数的概率为( )A.0.2B.0.4C.0.6D.0.83.下列叙述中,正确的个数是__________: ①命题P :“∃x ∈R,220x -≥”的否定形式为P ⌝:“2,20x R x ∀∈-<” ②H 为⊿ABC 所在平面上一点,若HA .HB =HB .HC =HA .HC ,则H 为⊿ABC 的垂心 ③“m n >”是“22()()33m n >的充分不必要条件;④命题“若2340,x x --=则x=4”的逆否命题为“24,340x x x ≠--≠则”A.1B.2C.3D.4 4.如图所示的程序框图表示的算法功能是A .计算123456S =⨯⨯⨯⨯⨯的值B .计算12345S =⨯⨯⨯⨯的值C .计算1234S =⨯⨯⨯的值D .计算1357S =⨯⨯⨯的值5.设{}n a 是公比为q 的等比数列,令1()n n b a n N +=+∈,若数列{}n b 的连续四项均在集合{53,23,19,37,82}--中,则q=_________A.43-B.32-C.3223--或D.3443-或- 6. 复数i iz +=1(其中i 为虚数单位)的虚部是 ( )A.21-B.i 21C.21D.i 21-7. 在⊿ABC 中, 角A 、B 、C 所对的边长分别为a 、b 、c ,3C π=,若,OD aOE bOF =+且D 、E 、F 三点共线(该直线不经过O 点),则⊿ABC 周长的最小值是____________A.12 B.54 C.32 D.948.已知1122log (4)log (32)x y x y ++<+-,若x y λ-<恒成立,则λ的取值范围是_______A.(,10]-∞B.(,10)-∞C.[10,)+∞D.(10,)+∞9.已知函数2,0()2,0x x x x f x x ⎧-≤⎪=⎨->⎪⎩,则"()0"0"f x x ≤=是"的_______条件A.充分不必要B.必要不充分C.充要D.既不充分也不必要10.将函数sin y x x =+的图像向左平移m (m>0)个单位后得到一个偶函数的图像,则实数m 的最小值是____________ A.12π B. 6π C. 3π D.56π11.从2013年1月1号开始,铁道部对火车票大面积降价,但降价幅度引发了争议。
河南省正阳县第二高级中学2019届高三上学期(文科)数学周练含答案

河南省正阳县第二高级中学2018-2019学年上期高三文科数学周练十一.选择题:1.已知集合,则集合中元素的个数为( )A .1B .2C .3D .42.已知复数z 满足(i 是虚数单位),则z=( )A .3-iB .3+iC .-3-iD .-3+i3.在等差数列中,若,则=( )A .2B .-2C .-4 D.-64.某工厂生产A,B,C 三种不同型号的产品,产品的数量之比依次为3:4:7.现用分层抽样的方法抽出容量为n 的样本,样本中A 型号产品有15件,那么样本容量n 为( )A .50B .60C .70D .805.不等式组所表示的平面区域的面积为( )A .1B .2C .3 D.46.一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的体积为( )AB .C .D .7.设,是两个不重合的平面,m,n 是两条不重合的直线,则以下结论错误的是( )A .若∥,,则∥B .若m ∥,m ∥,,则m ∥nC .若∥,n ∥,则∥{|21,},{1,0,1,2,3,4}A x x k k Z B ==-∈=-A B (2)1z i i -=+{}n a 3272a a a -==-9a 143x y x y +≥⎧⎪≤⎨⎪≥⎩83αβαβm α⊆m βαβn αβ=,,m n m αα⊆⊆ββαβD .若m ∥,则⊥8.已知圆截直线x+y+2=0所得弦的长度为4,则实数a 的值为( )A .-2B .-4C .-6D .-89.阅读如图所示的程序框图,若输出的结果是63,则判断框内n 的值可为( )A .5B .6C .7D .810.如图,圆与两坐标轴分别切于A,B 两点,圆上一动点P 从A 开始沿圆周按逆时针方向匀速旋转回到A 点,则△OBP 的面积随时间变化的图像符合( )11.经过双曲线右焦点的直线与双曲线交于A,B 两点,若AB=4,则这样的直线的条数为( )A .4条B .3条C .2条D .1条12.若函数的图象在x=1处的切线与圆相切,则a+b 的最大值是( )A .4B .C .2 Dαm β⊥αβ22220x y x y a ++-+=2244x y -=1()ln (0,0)a a f x x a b b b+=-->>221x y +=二.填空题:13.已知函数,则f[f(-1)]= .14.平面向量,满足,与的夹角为60°,若,则实数m 的值为 .15.若命题是假命题,则实数a 的取值范围是 .16.在数列中,对任意正整数n 都有满足,则.三.解答题:17.在△ABC 中,角A,B ,C 的对边分别为a,b,c ,且满足bsinA=(2c+a)cos(A+C).(1)求角B 的大小;(2)求函数f(x)=2sin2x+sin(2x-B)的最大值.18.(本小题满分12分)如图1,在直角梯形ABCD 中,=90°,CD ∥AB ,AD=CD=2,AB=4.将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到如图2所示的几何体D —ABC.(1)求证:AD ⊥平面BCD ; (2)求点C 到平面ABD 的距离.2log ,0()4,0x x x f x x >⎧=⎨≤⎩a b 3,2a b ==a b ()a mb a -⊥2000,210x R ax x ∃∈++≤{}n a 123...31n n a a a a ++++=-22212...n aa a +++=ADC ∠19.在某次考试中,全部考生参加了“科目一”和“科目二”两个科目的考试,每科成绩分为A,B,C,D,E 五个等级.某考场考生的两颗考试成绩数据统计如图所示,其中“科目一”成绩为D 的考生恰有4人.(1)分别求该考场的考生中“科目一”和“科目二”成绩为A 的考生人数;(2)已知在该考场的考生中,恰有2人的两科成绩均为A ,在至少一科成绩为A 的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为A 的概率.20.(本小题满分12分)设椭圆的左、右焦点分别为,上顶点为A ,过点A 与垂直的直线交x 轴负半轴于点Q ,且恰是的中点,若过三点的圆恰好与直线相切.(1)求椭圆C 的方程;(2)若直线y=x+2与椭圆C 交于G,H 两点,在x 轴上是否存在点P(m,0),使得以PG,PH 为邻边的平行四边形是菱形.如果存在,求出m 的值;如果不存在,请说明理由.2222:1(0)x y C a b a b+=>>12,F F 2AF 1F 2QF 2,,A QF 3x =+21.已知函数,,F(x)=f(x)-g(x). (1)当m>0时,求函数f(x)的单调区间;(2)当m=-1时,试问过点(2,5)可作多少条直线与曲线y=F(x)相切?说明理由.22.已知函数,且的解集为[-3.3].(1)求m 的值;(2)若a>0,b>0,c>0,且,求证:.21()ln 2f x x m x =-21()22g x x x =-()2(0)f x m x m =-->(2)0f x +≥1112343m a b c ++=2349a b c ++≥参考答案:1-6.CADCBA 7-12.CBBABD 13.-2 14.3 15.a>1 16. 17.(1)120°(218.(1)略(219.(1)3,3 (2) 20.(1)(2)21.(1)上递减,上递增(2)有两条切线22.(1)m=3 (2)略912n -1622143x y +=27m =-)+∞。
河南省正阳县第二高级中学高二上学期文科数学周练 Word版含答案

河南省正阳县第二高级中学2019-2019学年上期高二文科数学周练(八)一.选择题(本题满分60分):1.下列各组数字中,能组成等比数列的是____:A.111,,369B.lg3,lg9,lg27C.6,8,10D.3,-2.在200米高的山顶上测量出该处与一塔顶和塔底的俯角分别为30°,60°,则塔高为_____:A.4003米 B. 米 C. 2003米 D.3.下列命题正确的个数是_____:①a>b,c>d ⇒a+c>b+d ②,a b a c b d d c >>⇒> ③ 22a b a b >⇔> ④11a b a b >⇔< A.1 B.2 C.3D.44.若a,b,c 成等比数列,则函数2y ax bx c =++的图象与x 轴交点的个数是__________:A.0B.1C.2D.0或25.在⊿ABC 中,已知角B=45°,3c b ==,则角A 的值是________: A. 15° B. 75° C. 105°D.75°或15°6.边长分别为5、7、8的三角形的最大角与最小角之和是____________:A. 90°B. 120°C.135°D.150°,7.若以3、5、x 为三边组成一个锐角三角形,那么x 的取值范围是____________:A. (2,8)B. (2,4)C.(4,8)D.(48. 等差数列{}n a 满足5628a a +=,则此数列前10项之和等于__________:A.140B.280C.168D.569.等比数列{}n a 的各项均为正数,且564718a a a a +=,则3132310log log ...log a a a +++=__A.12B.10C.1+ 3log 5D. 2+3log 510.使不等式210x a x ++≥对于一切实数x 恒成立的a 的取值范围是__________:A. [2,)-+∞B. (,2)-∞-C. [-2,2]D.[0,)+∞11.已知1既是2a 与2b 的等比中项,又是1a 与1b 的等差中项,则22a b a b ++的值为____:A.1或0.5B. 1或-0.5C. 1或13D.1或13-12.⊿ABC 的角A 、B 、C 所对的边分别为a,b,c,1),(cos ,sin )m n A A =-=u r r ,m n ⊥u r r ,且acosB+bcosA=csinC,则角A ,B 的大小分别为_____________:A. 30°,60°B. 120°,30°C. 60°,30°D.60°,60°二.填空题(本题满分20分):13.已知⊿ABC 的角A 、B 、C 依次成等差数列,若BC=6,AB=5,则此三角形的面积为_____14.在数列{}n a 中,11a =对任意的2n ≥,n N +∈都有223...n a a a n =,则35a a +=15不等式2121332x x x x ++>--的解集是________________; 16.已知下列函数:① 1y x x =+ ②2log log 2(02)x y x x x =+>≠且③ 2y= ④2y =其中最小值是2的函数的序号是___________三.解答题:17.(本题满分10分)在等差数列{}n a 中,158,2a a ==,若在每相邻两项间各插入一个数,使之成为新等差数列{}n b ,求数列{}n b 的前n 项和n S 的最大值18.(本题满分12分)⊿ABC 为等腰直角三角形,其中AB 为斜边,⊿ACD 为等边三角形,其中B 点与D 点位于AC 的两侧,BD 与AC 交于E 点,AB=2 ①求cos ∠CBE ②求AE 的长19. (本题满分12分)⊿ABC 的角A 、B 、C 所对的边分别为a,b,c,若222a bc c b +=+①求角A ②若a =22bc +的取值范围20.(本题满分12分)等差数列{}n a 的各项均为正数,13a =,前n 项和为n S ,数列{}n b 为等比数列,122332,32,120b b S b S ===,①求{}n a 和{}n b 的通项公式②求{}n n a b 的前n 项和n T21.(本题满分12分) 某货轮匀速行驶在相距300海里的甲、乙两地间运输货物,运输成本由燃料费用和其它费用组成。
河南省正阳县第二高级中学2019届高三上学期文科数学周练(十五) Word版含答案
河南省正阳县第二高级中学2018-2019学年上期高三文科数学周练(十五)一.选择题:1.设A ,B 是全集I={1,2,3,4}的子集,A={l ,2},则满足A ⊆B 的B 的个数是( ) A .5 B .4 C .3 D .22. 设1,x y R >-∈,,则“x+1>y”是“x+1>|y|”的( )A 、弃要条件B 、充分不必要条件C 、必要不充分条件D 、既不充分也不必要条件 3. 复数112ii--的虚部为( ) A .0.2 B .0.6 C .﹣0.2 D .﹣0.64. 已知()πα,0∈,22)3cos(-=+πα,则=α2tanA .33B .3-或33-C .33- D .3-5. 已知函数)(x f =bx ax +2是定义在[a a 2,1-]上的偶函数,那么b a +的值是 ( )A .31-B .31C .21D .21- 6. .运行如图所示的程序框图,若输出的结果为163,则判断框中应填入的条件是( )A .i >4?B .i <4?C .i >5?D .i <5?7. 若某几何体的三视图如图所示,则此几何体的体积是( )A .24B .40C .36D .488. 双曲线22221x y a b-=(a >0,b >0)的右焦点是抛物线y 2=8x 焦点F ,两曲线的一个公共点为P ,且|PF|=5,则此双曲线的离心率为( )A B C .2 D9. 己知直线ax+by ﹣6=0(a >0,b >0)被圆x 2+y 2﹣2x ﹣4y=0截得的弦长为ab 的最大值是( )A .9 B .4.5 C .4D .2.510. T 为常数,定义f T (x )=(),(),()f x f x TT f x T ≥⎧⎨<⎩,若f (x )=x ﹣lnx ,则f 3[f 2(e )]的值为.( )A .e ﹣lB .eC .3D .e+l11. 设向量a =(1,k ),b =(x ,y ),记a 与b 的夹角为θ.若对所有满足不等式|x ﹣2|≤y≤1的x ,y ,都有θ∈(0,2π),则实数k 的取值范围是( ) A .(﹣1,+∞) B .(﹣1,0)∪(0,+∞)C .(1,+∞)D .(﹣1,0)∪(1,+∞)12. 已知函数()g x 的图象与函数()()ln 1f x x a =+-的图象关于原点对称,且两个图象恰好有三个不同的交点,则实数a 的值为( ) A .1eB .1C .eD .2e 二.填空题:13. 已知点F 为抛物线2:4E y x =的焦点,点()2,A m 在抛物线E 上,则AF =___14. 已知棱长均为a 的正三棱柱ABC-A 1B 1C 1的六个顶点都在半径为6的球面上,则a 的值为 .15. 在平面直角坐标系xOy 中,已知圆()()22:434C x y -+-=,点A B 、在圆C 上,且AB =OA OB +的最小值是___________.16. 已知定义在R 上的函数()f x 是奇函数且满足()3-=2f x f x ⎛⎫⎪⎝⎭,()-2=-3f ,数列{}n a 满足11a =-,且21n n S an n=⨯+.(其中n S 为的{}n a 前n 项和),则()()56f a f a += .三.解答题:17. 设ABC 的三个内角A,B,C所对的边分别为a,b,c.平面向量()()()cos ,cosC ,c,,2b,0,m A n a p ===且()0m n p ⋅-=(1)求角A 的大小;(2)当x A ≤时,求函数()sin cos sin sin()6f x x x x x π=+-的值域.18. 已知单调递增的等比数列{}n a ,满足2a +3a +4a =28.且3a +2是2a ,4a 的等差中项。
河南省正阳县第二高级中学2019届高三上学期文科数学周测二 Word版含答案
河南省正阳县第二高级中学2018-2019学年上期高三文科数学周练(二)一.选择题:本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A ∩∁R B=( ) A .{1,5,7} B .{3,5,7} C .{1,3,9} D .{1,2,3} 2.已知复数a ii i--在复平面内对应的点在二、四象限的角平分线上,则实数a 的值为( ) A .﹣2 B .﹣1 C .0 D .23.若a ,b ,c ,d ∈R ,则“a+d=b+c”是“a ,b ,c ,d 依次成等差数列”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.函数f (x )=1+2log x 与g (x )=12x -+在同一直角坐标系下的图象大致是( )A .B .C .D .5.已知{}n a 是首项为1的等比数列,n S 是{a n }的前n 项和,且369S S =,则数列1{}na 的前5项和为( ) A .8532 B .3116 C .158 D .8526.阅读如图所示的程序框图,运行相应的程序,则程序运行后输出的结果为( )A .7B .9C .10D .117.将函数f (x )=cos (ωx+φ)(ω>0,﹣2π<φ<2π)图象上每一点的横坐标伸长为原来的2倍(纵坐标不变),再向右平移6π个单位长度得到y=cosx 的图象,则函数f (x )的单调递增区间为( )A .2[,]33k k ππππ-+(k ∈Z ) B .7[,]1212k k ππππ--(k ∈Z ) C .7[4,]33k k ππππ--(k ∈Z ) D .5[4,]33k k ππππ-+(k ∈Z )8.已知双曲线22221(0,0)x y a b a b-=>>的一个焦点为F (2,0),且双曲线的渐近线与圆22(2)3x y -+=相切,则双曲线的方程为( )A .221913x y -=B .221139x y -=C .2213x y -=D .2213y x -=9.一个空间几何体的三视图如图所示,则几何体的体积为( )A .2B .83C .3D .10310.设x ,y 满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩若目标函数z=ax+by (a >0,b >0)的值是最大值为12,则23b aab +的最小值为( ) A .256 B . 83 C . 113D .411.已知点M 是边长为2的正方形ABCD 的内切圆内(含边界)一动点,则.MA MB 的取值范围是( )A .[-1,0]B .[-1,2]C .[-1,3]D .[-1,4]12.已知函数f (x )=x+x a e -,g (x )=ln (x+2)﹣4a x e -,其中e 为自然对数的底数,若存在实数0x ,使f (0x )﹣g (0x )=3成立,则实数a 的值为( )A .﹣ln2﹣1B .﹣1+ln2C .﹣ln2D .ln2二、填空题:本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上.13.已知二项式1)nx的展开式中含有2x 的项是第3项,则n= .14.若正态变量ξ服从正态分布N (μ,σ2),则ξ在区间(μ﹣σ,μ+σ),(μ﹣2σ,μ+2σ),(μ﹣3σ,μ+3σ)内取值的概率分别是0.6826,0.9544,0.9973.已知某大型企业为10000名员工定制工作服,设员工的身高(单位:cm )服从正态分布N ,则适宜身高在177~182cm 范围内员工穿的服装大约要定制 套.(用数字作答) 15.已知等差数列{a n }的前n 项和为S n ,若a 1=1,S 3=﹣3,则2nnS 的最大值为 .16.已知四面体ABCD 的顶点都在同一个球的球面上,BD=4,且满足BC ⊥BD ,AC ⊥BC ,AD ⊥BD ,则该球的球面面积为 .三、解答题:17.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c (sin )b C C =. (Ⅰ)求角B 的大小;(Ⅱ)若b=2,求a+c 的取值范围.18.司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.(Ⅰ)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X ,若每次抽检的结果都相互独立,求X 的分布列和数学期望E (X ).参考公式与数据:,其中n=a+b+c+d .19.如图,在梯形ABCD 中,AB ∥DC ,AD=AB=BC=1,ADC ∠=60°,平面ACFE ⊥平面ABCD ,四边形ACFE 是矩形,AE=1,点M 在线段EF 上.(1)当FM :EM 为何值时,AM ∥平面BDF ?证明你的结论; (2)求二面角B ﹣EF ﹣D 的平面角的余弦值.20.已知椭圆的离心率e=2,左、右焦点分别为F 1、F 2,定点P (2,点F 2在线段PF 1的中垂线上.(Ⅰ)求椭圆C 的方程;(Ⅱ)设直线l :y=kx+m 与椭圆C 交于M 、N 两点,直线F 2M 、F 2N 的倾斜角分别为α、β且α+β=π,求证:直线l 过定点,并求该定点的坐标.21.已知函数f (x )=0.52x ﹣ax+(3﹣a )lnx ,a ∈R .(1)若曲线y=f (x )在点(1,f (1))处的切线与直线2x ﹣y+1=0垂直,求a 的值; (2)设f (x )有两个极值点1x ,2x 且1x <2x ,求证:f (1x )+f (2x )>﹣5.请考生在第(22)(23)题中任选一题作答22.已知曲线C1的参数方程为45cos55sinx ty t=+⎧⎨=+⎩(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).23.已知函数f(x)=|x+2|﹣|x﹣2|+m(m∈R).(Ⅰ)若m=1,求不等式f(x)≥0的解集;(Ⅱ)若方程f(x)=x有三个实根,求实数m的取值范围.AABC BBBD DACA13.n=8.14.1359 15.0.5 16.23π.17.(1)B=60°(2)a+c∈(2,4]解:(I)y=0.5ABACsinA=(23xπ-)2(0)3xπ<<(II)B=60°时,△ABC的面积最大为根据数表,计算28.257.879k=>,所以有99.5%的把握认为开车时使用手机与司机的性别有关;19.解:(1)略(220.解:(Ⅰ)椭圆方程为2212xy+=;(Ⅱ)直线MN过定点,该定点的坐标为(2,0).21.解:(1)94 a=(2)由题意,x1,x2为f′(x)=0的两根∴2<a<3,又∵x1+x2=a,x1x2=3﹣a,∴f(x1)+f(x2)=0.5(x12+x22)﹣a(x1+x2)+(3﹣a)lnx1x2,=f(x)=﹣0.5a2+a﹣3+(3﹣a)ln(3﹣a),设h(a)=﹣0.5a2+a﹣3+(3﹣a)ln(3﹣a),a∈(2,3),则h′(a)=﹣a﹣ln(3﹣a),∴h″(a)=﹣1+13a-=23aa-->0,故h′(a)在(2,3)递增,又h′(2)=﹣2<0,当a→3时,h′(a)→+∞,∴∃a0∈(2,3),当a∈(2,a0)时,h(a)递减,当a∈(a0,3)时,h(a)递增,∴h(a)min=h(a0)=﹣0.5a02+a0﹣3+(3﹣a0)ln(3﹣a0)>﹣0.5a02+a0﹣3+(3﹣a0)(﹣a0)=0.5a02﹣2a0﹣3=0.5(a0﹣2)2﹣5>﹣5.∴∀a∈(2,3),h(a)>﹣5,综上,f(x1)+f(x2)>﹣5.22.解:(Ⅰ)曲线C1的极坐标方程为ρ2﹣8ρcosθ﹣8ρsinθ+16=0.(Ⅱ)(2,)24ππ23.解:(Ⅰ)不等式f(x)≥0的解集为1[,)2-+∞(Ⅱ)﹣2<m<2.。
高三数学上学期周练二文 试题
正阳县第二高级中学2021-2021学年上期高三文科数学周练〔二〕创 作人:历恰面 日 期: 2020年1月1日一.选择题:本大题12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的.1.集合A={1,3,5,7,9},B={0,3,6,9,12},那么A∩∁R B=〔 〕 A .{1,5,7} B .{3,5,7}C .{1,3,9}D .{1,2,3}2.复数a ii i--在复平面内对应的点在二、四象限的角平分线上,那么实数a 的值是〔 〕 A .﹣2 B .﹣1 C .0D .23.假设a ,b ,c ,d∈R,那么“a+d=b+c〞是“a,b ,c ,d 依次成等差数列〞的〔 〕 A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件4.函数f 〔x 〕=1+2log x 与g 〔x 〕=12x -+在同一直角坐标系下的图象大致是〔 〕A .B .C .D .5.{}n a 是首项为1的等比数列,n S 是{a n }的前n 项和,且369S S =,那么数列1{}na 的前5项和为〔 〕 A .8532 B .3116 C .158 D .8526.阅读如下图的程序框图,运行相应的程序,那么程序运行后输出的结果为〔 〕A .7B .9C .10D .117.将函数f 〔x 〕=cos 〔ωx+φ〕〔ω>0,﹣2π<φ<2π〕图象上每一点的横坐标伸长为原来的2倍〔纵坐标不变〕,再向右平移6π个单位长度得到y=cosx 的图象,那么函数f 〔x 〕的单调递增区间为〔 〕A .2[,]33k k ππππ-+〔k∈Z〕 B .7[,]1212k k ππππ--〔k∈Z〕 C .7[4,]33k k ππππ--〔k∈Z〕 D .5[4,]33k k ππππ-+〔k∈Z〕 8.双曲线22221(0,0)x y a b a b -=>>的一个焦点为F 〔2,0〕,且双曲线的渐近线与圆22(2)3x y -+=相切,那么双曲线的方程为〔 〕A .221913x y -=B .221139x y -=C .2213x y -=D .2213y x -=9.一个空间几何体的三视图如下图,那么几何体的体积为〔 〕A .2B .83C .3D .10310.设x ,y 满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩假设目的函数z=ax+by 〔a >0,b >0〕的值是最大值为12,那么23b aab +的最小值为〔 〕 A .256B . 83C . 113D .411.点M 是边长为2的正方形ABCD 的内切圆内〔含边界〕一动点,那么.MA MB 的取值范围是〔 〕A .[-1,0]B .[-1,2]C .[-1,3]D .[-1,4]12.函数f 〔x 〕=x+x a e -,g 〔x 〕=ln 〔x+2〕﹣4a x e -,其中e 为自然对数的底数,假设存在实数0x ,使f 〔0x 〕﹣g 〔0x 〕=3成立,那么实数a 的值是〔 〕 A .﹣ln2﹣1 B .﹣1+ln2 C .﹣ln2 D .ln2二、填空题:本大题一一共4个小题,每一小题5分,一共20分,把正确答案填在题中横线上.13.二项式1)nx的展开式中含有2x 的项是第3项,那么n= .14.假设正态变量ξ服从正态分布N 〔μ,σ2〕,那么ξ在区间〔μ﹣σ,μ+σ〕,〔μ﹣2σ,μ+2σ〕,〔μ﹣3σ,μ+3σ〕内取值的概率分别是0.6826,0.9544,0.9973.某大型企业为10000名员工定制工作服,设员工的身高〔单位:cm 〕服从正态分布N ,那么适宜身高在177~182cm 范围内员工穿的服装大约要定制 套.〔用数字答题〕 15.等差数列{a n }的前n 项和为S n ,假设a 1=1,S 3=﹣3,那么2nnS 的最大值为 .16.四面体ABCD 的顶点都在同一个球的球面上,,BD=4,且满足BC ⊥BD ,AC ⊥BC ,AD ⊥BD ,那么该球的球面面积为 .三、解答题:17.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c (sin )b C C =. 〔Ⅰ〕求角B 的大小;〔Ⅱ〕假设b=2,求a+c 的取值范围.18.司机在开机动车时使用手机是违法行为,会存在严重的平安隐患,危及自己和别人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.〔Ⅰ〕完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;开车时使用手机开车时不使用手机合计男性司机人数女性司机人数合计〔Ⅱ〕以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,假设每次抽检的结果都互相HY,求X的分布列和数学期望E〔X〕.参考公式与数据:,其中n=a+b+c+d.P〔Χ2≥k0〕k0∠=60°,平面ACFE⊥平面ABCD,19.如图,在梯形ABCD中,AB∥DC,AD=AB=BC=1,ADC四边形ACFE是矩形,AE=1,点M在线段EF上.〔1〕当FM:EM为何值时,AM∥平面BDF?证明你的结论;〔2〕求二面角B﹣EF﹣D的平面角的余弦值.20.椭圆的离心率e=22,左、右焦点分别为F1、F2,定点P〔23,点F2在线段PF1的中垂线上.〔Ⅰ〕求椭圆C的方程;〔Ⅱ〕设直线l:y=kx+m与椭圆C交于M、N两点,直线F2M、F2N的倾斜角分别为α、β且α+β=π,求证:直线l过定点,并求该定点的坐标.21.函数f〔x〕=2x﹣ax+〔3﹣a〕lnx,a∈R.〔1〕假设曲线y=f〔x〕在点〔1,f〔1〕〕处的切线与直线2x﹣y+1=0垂直,求a的值;〔2〕设f〔x〕有两个极值点1x,2x且1x<2x,求证:f〔1x〕+f〔2x〕>﹣5.请考生在第〔22〕〔23〕题中任选一题答题22.曲线C1的参数方程为45cos55sinx ty t=+⎧⎨=+⎩〔t为参数〕.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.〔Ⅰ〕把C1的参数方程化为极坐标方程;〔Ⅱ〕求C1与C2交点的极坐标〔ρ≥0,0≤θ<2π〕.23.函数f〔x〕=|x+2|﹣|x﹣2|+m〔m∈R〕.〔Ⅰ〕假设m=1,求不等式f〔x〕≥0的解集;〔Ⅱ〕假设方程f〔x〕=x有三个实根,务实数m的取值范围.AABC BBBD DACA13. n= 8 .14. 1359 15. 16.23π.17.〔1〕B=60°〔2〕a+c∈〔2,4]解:〔I〕y=sinA=〔23xπ-〕2(0)3xπ<<〔II〕B=60°时,△ABC的面积最大为18.解:〔Ⅰ〕填写上2×2列联表,如下;开车时使用手机开车时不使用手机合计男性司机人数40 15 55 女性司机人数20 25 45 合计60 40 100 根据数表,计算28.257.879k=>,所以有99.5%的把握认为开车时使用手机与司机的性别有关;〔Ⅱ〕X的分布列为:X 0 1 2 3P2712554125361258125数学期望为EX=3×=.19.解:〔1〕略〔220.解:〔Ⅰ〕椭圆方程为2212xy+=;〔Ⅱ〕直线MN过定点,该定点的坐标为〔2,0〕.21.解:〔1〕94 a=〔2〕由题意,x1,x2为f′〔x〕=0的两根∴2<a<3,又∵x1+x2=a,x1x2=3﹣a,∴f〔x1〕+f〔x2〕=〔x12+x22〕﹣a〔x1+x2〕+〔3﹣a〕lnx1x2,=f〔x〕=﹣a2+a﹣3+〔3﹣a〕ln〔3﹣a〕,设h〔a〕=﹣a2+a﹣3+〔3﹣a〕ln〔3﹣a〕,a∈〔2,3〕,那么h′〔a〕=﹣a﹣ln〔3﹣a〕,∴h″〔a〕=﹣1+13a-=23aa-->0,故h′〔a〕在〔2,3〕递增,又h′〔2〕=﹣2<0,当a→3时,h′〔a〕→+∞,∴∃a0∈〔2,3〕,当a∈〔2,a0〕时,h〔a〕递减,当a∈〔a0,3〕时,h〔a〕递增,∴h〔a〕min=h〔a0〕=﹣a02+a0﹣3+〔3﹣a0〕ln〔3﹣a0〕>﹣a02+a0﹣3+〔3﹣a0〕〔﹣a0〕=a02﹣2a0﹣3=〔a0﹣2〕2﹣5>﹣5.∴∀a∈〔2,3〕,h〔a〕>﹣5,综上,f〔x1〕+f〔x2〕>﹣5.22.解:〔Ⅰ〕曲线C1的极坐标方程为ρ2﹣8ρcosθ﹣8ρsinθ+16=0.〔Ⅱ〕(2,)24ππ23.解:〔Ⅰ〕不等式f〔x〕≥0的解集为1[,)2-+∞〔Ⅱ〕﹣2<m<2.。
河南省正阳县第二高级中学高二上学期文科数学周练(二)
河南省正阳县第二高级中学2017-2018学年高二上期文科数学周练(二)一.选择题:1.给出下列说法:①命题“若α=30°,则sin α=12”的否命题是假命题;②命题p :∃x 0∈R ,使sin x 0>0.5,则﹁p :∀x ∈R ,sin x≤0.5;③“φ=π2+2kπ(k ∈Z)”是“函数y =sin(2x +φ)为偶函数”的充要条件;④命题p :“∃x ∈⎝⎛⎭⎫0,π2,使sin x +cos x =12”,命题q :“在△ABC 中,若sin A >sin B ,则A >B”,那么命题(﹁p)∧q 为真命题.其中正确的个数是( )A .1B .2C .3D .42.“2b ac =”是“a,b,c 成等比数列”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.已知数列{}lg n a 是等差数列,数列{}n a 的前n 项和为n S ,且2,57123=+=a a a S ,则=5a ( )A .21 B .21- C .2 D .2- 4. {|lg 0}A x x =>, {|21}xB x =>,则“x A ∈”是“x B ∈”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.已知n S 是等差数列{}n a 的前n 项和,12a =,145a a a +=,若32n S >,则n 的最小值为( )A .3 B .4 C .5 D .66.命题:“00x ∃>,使002()1x x a ->”,这个命题的否定是( )A .0x ∀>,使2()1x x a ->B .0x ∀>,使2()1xx a -≤C .0x ∀≤,使2()1x x a -≤D .0x ∀≤,使2()1x x a ->7. 数列1,3,5,7,9,--的一个通项公式为( ) A .21n a n =- B .(1)(12)n n a n =-- C .(1)(21)n n a n =-- D .(1)(21)n n a n =-+8. 在ABC ∆中,根据下列条件解三角形,其中有两个解的是( )A .010,45,60b A C === B .6,5,60a c B ===C .7,5,60a b A ===D .014,16,45a b A ===9. 在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,如果2b=a+c ,B=30°,△ABC 的面积是32,则 b=( )A .BCD .10. 若x ,y 满足约束条件4210x y y x x y +≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩,则1x y x +-的最小值为______. A. 43 B.13C.1D.0 11. 如果点P 在平面区域220,210,20x y x y x y -+≥⎧⎪-+≤⎨⎪+-≤⎩上,O 为坐标原点,则OP 最小值为( )ABC. D12.命题“关于x 的方程2230x x a -+=”有实根为假命题,则实数a 的取值范围是( ) A. 98a ≤ B.98a ≥ C. 98a > D. 98a <二.填空题:13.已知实数,x y 满足11y x x y y ≤⎧⎪+≤⎨⎪≥-⎩,则目标函数2z x y =-的最大值为__________.14.已知直线()200,0ax by a b -+=>>过点()1,1-,则12a b+的最小值为_________. 15.在ABC ∆中,角,,A B C 所对的边分别为,,a b c .若1,4a B π==,ABC ∆的面积2S =,则sin b B的值为_____________. 16. 在中,有等式:①csinC=bsinB ;②asinB=bsinA ;③sin()cos A B C +=;④sin sin sin b a c B A C+=+.其中恒成立的等式序号为_________.三.解答题:17.(本小题满分10分)已知命题p :函数f(x)=2ax 2-x -1(a≠0)在(0,1)内恰有一个零点;命题q :函数y =2a x -在(0,+∞)上是减函数.若p 且﹁q 为真命题,求实数a 的取值范围.18.(本小题满分12分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,满足sin sin sin sin a c A B b A C +-=-. (1)求角C ;(2)求a b c+的取值范围.19.(本小题满分12分)已知数列{}n a 的前n 项和n S 满足2()n S n n N +=∈(1)求数列{}n a 的前三项123,,a a a 并以此归纳出{}n a 的通项公式;(2)求数列11{}n n a a +的前n 项之和20.在ABC ∆中,c b a 、、为角C B A 、、所对的三边,已知222+c b a bc -=-.(1)求角A 的值;(2cos()cos A C B -+=ABC ∆的面积21.设数列{}n a 的前n 项和12n n S a a =-,且123,1,a a a +成等差数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)求数列⎭⎬⎫⎩⎨⎧n a n 的前n 项和n T22.设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足sinA+sinB=(cosA+cosB )sinC . (Ⅰ)求证:△ABC 为直角三角形;(Ⅱ)若,求△ABC 面积的最大值.1-6.CBAADB 7-12.BDAAAD 13.5 14.32+ 15. 16.②④ 17.(1,2] 18.(1)60°(2)(1,2) 19.(1)1231,3,5,21n a a a a n ====-(2)221n n +20.(1)120°(2)4 21.(1)2n n a =(2)222n n n T +=- 22.(1)用正弦定理和余弦定理将角化边得222a b c +=(2)用面积公式和基本不等式14。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省正阳县第二高级中学 2018届高三下学期文科数学周练(一)
一.选择题:
1.已知集合{|33},{|(4)0}A x x B x x x =-<<=-<,则A
B =( )
A .(0,3)
B .(3,4)-
C .(0,4)
D .()3,4 2. 已知i 为虚数单位,则复数2
1z i
=-+的虚部为( ) A 、1-
B 、i -
C 、1
D 、i
3.在△ABC 中,∠C=90°,)1,(k BA =,)3,2(=BC ,则k 的值是( ) A.5
B.-5
C.
32 D.32
- 4.口袋中有形状和大小完全相同的四个球,球的编号分别为1,2,3,4,若从袋中随机抽取两个球,则取出的两个球的编号之和不大于5的概率为() A. 1/3 B. 5/6 C. 1/6 D. 2/3
5.已知数列{}n a 是公差大于0的等差数列,且满足15244,5a a a a +==-则数列{}n a 的前10项和等于( )A. 23 B. 95 C .135 D. 138
6.点A (1,2)在抛物线2
y =2px 上,抛物线的焦点为F ,直线AF 与抛物线另一交点为B ,则|AB |= ( )
A .2
B .3
C .4
D .6
7. 执行如图所示的程序框图,如果输入3x =,则输出k 的值为 ( )
A.6
B. 10
C. 8
D.12
8.某四棱锥的三视图如图所示(单位:cm),则该四棱锥的 表面积是( )
A .2)7313(cm +
B .2)3412(cm +
C .2)7318(cm +
D .53239++
9.已知数列{}n a 的前n 项和为n S ,且满足213n n S a +=,则1321...n a a a -+++=()
A.2312n -
B.31n -
C.918
n - D.21918n --
10.已知函数⎩⎨⎧>+-≤-=0
,20,)(2
x x x x x x f ,方程0)(-)(2
=x bf x f ()10b ,∈则方程的根的个数是( )
A. 2
B. 3
C. 4
D. 5
11.在三棱锥P ABC -中
,,2AB BC AB BC PA PC ⊥====,AC 中点为M
,
cos PMB ∠ ) A 、
32
π
B 、2π
C 、6π
D
12.已知函数(
))
2016
2016log 20162x x f x x -=++-+,则关于x 的不等式
()()314f x f x ++>的解集为( )
A 、1,4⎛⎫-+∞ ⎪⎝⎭
B 、1,4⎛⎫-∞- ⎪⎝⎭
C 、()0,+∞
D 、(),0-∞
二.填空题:
13. 已知函数2
()ln f x x ax =-在点(2,(2))f 处的切线的斜率是3
2
-
,则a =________. 14. ,x y 满足条件3560231500x y x y y -+≥⎧⎪
+-≤⎨⎪≥⎩
,则2z x y =-的最小值是_________.
15.过双曲线22145
x y -=的左焦点1F ,作圆224x y +=的切线交双曲线右支于点P ,切点为T ,1PF 的中点为M ,则||||MO MT -=_____________.
16.已知直角△ABC 的两直角边AB ,AC 的边长分别为方程2
x -2(1
x +
0的
两根,且AB <AC ,斜边BC 上有异于端点B 、C 的两点E 、F ,且EF =1,设∠EAF =θ,则tanθ的取值范围为__________.
三.解答题:
17.已知()f x a b =⋅
,其中(2cos ,2)a x x =,(cos ,1)b x =,x R ∈.
(1)求()x f 的单调递增区间;
(2)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,()1f A =-
,a =
,且向量(3,sin )m B =与(2,sin )n C =共线,求边长b 和c 的值.
18. 某新产品即将上市,为了对新产品进行合理定价,在该地区的三家大商场各进行了两天试销售,得到如下数据:
78
(1)以三家商场分别的平均售价和平均销量为散点,求出售价与销量的回归直线方程
y bx a =+;
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该产品成本价为40元/件,为使该产品在销售上获得最大利润,该产品的单价应定为多少元(保留整数)?
()()
()
1
1
22211
n n i i i i i i n n i i i i x x y y x y nxy b x nx x x a y bx
====⎧
---⎪
⎪==⎪⎨--⎪⎪⎪=-⎩∑∑∑∑
19.如图甲,在矩形ABCD 中,F E ,分别是
BC AD ,的中点,3,22==AB AD ,将矩形
ABCD 沿EF 折起,如图乙,使平面⊥
CDEF 平面ABFE ,点M 是AD 的中点,点N 在AB 上运动.
(1)证明:CN EM ⊥;
(2)若三棱锥BFN C -的顶点都在体积为3
28π
的球面上,求三棱锥BFN C -的体积.
20. 在平面直角坐标系xOy 中,过椭圆)0(122
22>>=+b a b
y a x 的一个焦点作一直线交椭圆
于F E ,两点,线段EF 长的最大值与最小值分别是22,24.
(1)求椭圆的方程;(2)与圆1)1(2
2
=+-y x 相切的直线y=kx+t 与椭圆交于N M ,两点,若椭圆上一点C 满足λ=+,求实数λ的取值范围.
21. 已知函数f (x )=x alnx (a ∈R ). (1)讨论f (x )的单调区间;
(2)设g (x )=f (x )+2alnx ,且g (x )有两个极值点为x 1,x 2,其中x 1∈(0,]e ,求
g (x 1)-g (x 2)的最小值.
22.在直角坐标系xoy 中,曲线C 的参数方程为3cos sin x y θ
θ
=⎧⎨
=⎩(θ为参数),直线l 的参数方程
为41x a t y t =+⎧⎨=-⎩
(t 为参数).
(1)若a=-1,求C 与l 的交点坐标;(2)若C 上的点到l a .
23. 已知函数()|21|f x x =-.(1)求不等式()4f x <;(2)若函数()()(1)g x f x f x =+-的
最小值为a ,且(0,0)m n a m n +=>>,求2221
m n m n
+++的取值范围.
1-6.BAADBC 7-12.BDCDCA 13.1
2
14.-3 15.
16
2 17.(1)函数的单调递增区间为5
[,],36
k k k Z π
πππ+
+∈,(2)b=1.5,c=1 18.(1)y=-2.25x+270.25(2)当x 约等于80时,f(x)取得最大值
19.(1)略(2)2
3
20.(1)22184x y +=
(2)((0,2)
21.(1)当02a <≤时,f(x)的单调递增区间为(0,)+∞,无减区间;当a>2时,函数f(x)的递
增区间为(0,
),()22a a -++∞
,减区间为()22
a a -+ (2)121111111()()2()2()ln g x g x x x x x x -=--+,构造函数得其最小值为4
e
- 22.(1)2124
(3,0),(,)2525
-
(2)a=-16或8 23.(-1.5,2.5)(2
)7[,)2++∞。
