BB6_5几种常用的二次曲面与空间曲线PPT课件
九节二次曲面-PPT课件

z
o x
y
x y z 2 2 1 2 a b c
2
2
2
双叶双曲面
o x
y
实轴与 x 轴相合, 虚轴与 z轴相合.
与平面 y y y b )的交线为双曲线. 1( 1
2 x2 z2 y1 2 2 1 2 b 双曲线的中心都在 y a c 轴上. y y 1
2 2 实轴与 x 轴平行, ( 1 ) y b , 1
虚轴与 z 轴平行.
x2 y2 2 1 2 a 2 b 2 2 2 ( c k ) 2 (c k ) 2 c c z k | k |c 当k由0变到c时,椭圆由大变小, 最后缩成一点。
同理与平面 x=k 和 y=k 的交线也是椭圆. 椭圆截面的大小随平面位置的变化而变化.
椭球面的几种特殊情况:
虚轴与 x 轴平行.
2 2 ( 2 ) y b , 实轴与 z 轴平行, 1
,b ,0 ) 的直线. ( 3 ) y b , 截痕为一对相交于点 (0 1
x z 0 , a c y b ( 4 ) y b , 1
x z 0 . a c y b
( x 0 ) (3)用坐标面 yoz ,x=k 与曲面相截
均可得抛物线. 同理当 p 时可类似讨论. 0 ,q 0
椭圆抛物面的图形如下:
z o x y z
x
o
y
p 0 , q 0
p 0 , q 0
q 特殊地:当 p 时,方程变为
x y z 2p 2p
旋转而成的)
第九节 二次曲面 一、基本内容
二次曲面的定义: 三元二次方程所表示的曲面. 相应地平面被称为一次曲面. 讨论二次曲面性状的截痕法: 用坐标面和平行于坐标面的平面与曲面 相截,考察其交线(即截痕)的形状,然后 加以综合,从而了解曲面的全貌.
二次曲面

结束
与平面 z z1 ( z1 0) 的交线为椭圆.
2 x2 y 1 2 pz1 2qz1 z z 1
当 z1 变动时,这种椭 圆的中心都在 z 轴上.
与平面 z z1 ( z1 0) 不相交. (2)用坐标面 xoz ( y 0)与曲面相截
x 2 pz 截得抛物线 y 0
二次曲面
二次曲面的定义: 三元二次方程所表示的曲面称之为二次曲面. 相应地,平面被称为一次曲面. 讨论二次曲面的形状用所谓的截痕法:
用坐标面和平行于坐标面的平面与曲面相截,考 察其交线(即截痕)的形状,然后加以综合,从而了 解曲面的全貌.
以下用截痕法讨论几种特殊的二次曲面.
首页 上页 返回 下页 结束
首页
z1 ( | z1 | c )的交线为圆.
上页 返回 下页 结束
2 a2 2 2 x y 2 2 (c z1 ) . 截面上圆的方程 c z z 1
( 2) a b c ,
x2 y2 z2 2 2 1 球面 2 a a a
方程可写为 x 2 y 2 z 2 a 2 .
H ( x, y) 0
G( y, z ) 0
T ( x, z ) 0
二次曲面: 椭球面、抛物面、双曲面
首页 上页 返回 下页 结束
思考题3
x 4 y z 25 方程 表示怎样的曲线? x 3
2 2 2
首页
上页
返回
下页
结束
思考题3 解答
4 y 2 z 2 16 x 4 y z 25 . x 3 x 3
首页
上页
返回
二次曲面的分类PPT

y2 b2
2z
x2 a2
y2 b2
2z
Thank you!
x2 y2 (10 ) a 2 b 2 1 0;
(11)
x2 a2
y2 b2
1
0;
(13) x2 y2 0; a2 b2
(15)x2 a2 0;
(17)x2 0.
x2 (12) a2
y2 b2
0;
(14)x2 2 py 0;
(16)x2 a2 0;
二次曲面分类
胡努春
浙江师范大学数学系 course.zjnu/hnc
二次曲面方程的化简和分类 ( ) P:130 Th4.2.2; P:133 Th4.3.1
定理 适当选取坐标系,二次曲面的方程总可 以化成下列五个简化方程中的一个:
(1) a11x2 a22y2 a33z2 a44 0,a11a22a33 0; (2) a11y2 a22y2 2a34z 0,a11a22a34 0; (3) a11x2 a22y2 a44 0,a11a22 0; (4)a11x2 2a24y 0,a11a24 0; (5)a11x2 a44 0,a11 0.
由上述4个方程消去其中的参数x1,y1,z1所得的
方为 x2 2pyz
注:此方程的图形比原锥面多了整个y轴(原点除外), 类似对准线为双曲线的锥面图形在几何直观上是不完整的, 通过添上无穷远点可得到完整图形。(射影几何:椭圆,
双曲线,抛物线认为是同一类曲线)参见:尤承业《解析几何》P:275
x2 a2
定理 通过适当选取坐标系,二次曲面的方 程总可以写成下面十七种标准方程的一种形式:
6. 二 次 曲 面
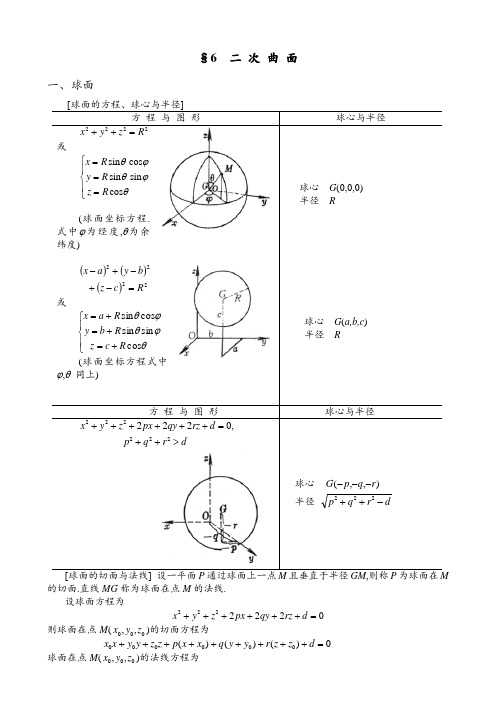
§6 二 次 曲 面一、 球面的切面.直线MG 称为球面在点M 的法线.设球面方程为x y z px qy rz d 2222220++++++=则球面在点M (x y z 000,,)的切面方程为x x y y z z p x x q y y r z z d 0000000+++++++++=()()() 球面在点M (x y z 000,,)的法线方程为x x x p y y y q z z z r-+=-+=-+000000 [两个球面的交角] 设两个球面S x y z p x q y r z d 12221111222++++++=0 S x y z p x q y r z d 22222222222++++++=0两个球面的交角是指它们在交点的两个切面的夹角,记作θ,则cos θ=++--++-++-22221212121212121212222222p p q q rr d d p q r d p q r d 因公式中不包含交点的坐标,所以在两个球面的交线上的各点的交角必相等.两个球面的正交条件为222012121212p p q q r r d d ++--=[球面束·两个球面的根面] 设S S S λλ120+=式中S 1和S 2如(1)式定义,λ为参数,则有)()(2)(2)(2))(1(21212121222=+++++++++++d d z r r y q q x p p z y x λλλλλ对λλ()≠-1的一个确定值,S λ表示一个球面,当λ取一切值()λ≠-1时,S λ所表示的球面的全体称为球面束.λ=-1时为一平面,称为两个球面S S 12,的根面,其方程为()()()222012121212()p p x q q y r r z d d -+-+-+-=根面与S 1和S 2的连心线垂直,束中任一球面λS 的中心在连心线上,且分连心线的比为λ.[球面汇·三个球面的根轴] 设S 1和S 2如(1)式定义,又设S x y z p x q y r z d 322233332220++++++=设 S S S S λμλμ1230++= 式中λμ,为二独立参数,则有()()()()()()12220222123123123123++++++++++++++++=λμλμλμλμλμx y z p p p x q q q y r r r z d d d对λμ,()λμ+≠-1的一对确定值,S λμ表示一个球面,当λμ,取一切值()λμ+≠-1时,S λμ所表示的球面的全体称为球面汇.三个球面中每对球面的根面分别为S S S S 122300-=-=,,和S S 210-=这三个平面交于一条直线,称为S S S 123,,的根轴.二、 椭球面三、双曲面a b c [双叶双曲面]x aybzc222222+-=-a=b时,为旋转双曲面]在Oxz平面上的曲线当a=b时,为旋转抛物面五、锥面与柱面当a=b时, 为圆锥面在Oxz平面上a b当a=b时,为圆柱面渐近锥面] 二次锥面 六、 一般二次曲面1. 二次曲面的一般性质上面所列举的椭球面、双曲面、抛物面等,它们的方程关于x,y,z 都是二次的.关于x,y,z 的一般二次方程的形式是ax by cz fyz gzx hxy px qy rz d 2222222220+++++++++= 它表示的曲面称为一般二次曲面.这里列举这些曲面的一些共同性质.[直线与二次曲面的交点] 一直线与一个二次曲面交于两点(实的,虚的,重合的).或者这直线全在曲面上,此时称它为二次曲面的直母线或母线.[平面与二次曲面的交线] 任一平面与一个二次曲面的交线为一个二次曲线.[二次曲面的直径平面与中心] 一个二次曲面的平行于已知方向的弦的中点在一个平面上,称为直径平面,它平分某一组平行弦.设已知方向的方向数为l ,m ,n ,则直径平面的方程为()()()()0=+++++++++++rn qm pl z cn fm gl y fn bm hl x gn hm al或改写为()()()ax hy gz p l hx by fz q m gx fy cz r n +++++++++++=0当l ,m ,n 变动时,这个方程表示一个平面把,由此二次曲面的直径平面组成一个平面把.把内任一平面都通过下列三个平面的交点:ax hy gz p hx by fz q gx fy cz r +++=+++=+++=000如果交点不在曲面上,则称它为二次曲面的中心,如果交点在曲面上,则称它为二次曲面的顶点.凡有中心的二次曲面称为有心二次曲面,其余的都称为无心二次曲面.[二次曲面的主平面与主轴] 如果直径平面垂直于被它所平分的弦,则称为主平面(对称平面),每个二次曲面至少有一个实主平面,非旋转二次曲面的任两主平面是互相垂直的,它们的交线为主轴.[二次曲面的切面与法线] 二次曲面在一点M (x y z 000,,)的切面方程为()()()()()()ax x by y cz z f y z z y g z x x z h x y y x p x x q y y r z z d 0000000000000+++++++++++++++=在点M 与二次曲面的切面垂直的直线称为曲面在点M 的法线,它的方程可写为x x ax hy gz p y y hx by fz q z z gx fy cz r-+++=-+++=-+++000000000000 [二次曲面的圆截面] 如果一个平面与一个二次曲面的交线为一个圆,则称该平面为曲面的圆截面.如果二次曲面不是球面,则通过空间中一点,二次曲面有六个圆截面;其中一般有两个实圆截面,四个虚圆截面;而且六个圆截面中有几个是重合的.2.二次曲面的不变量 由二次曲面的一般方程ax by cz fyz gzx hxy px qy rz d 2222222220+++++++++= (1)的系数组成的下列四个函数:222,,h g f ca bc ab J c b a I cf g f b h gh a D dr q p rc f g q f b h pg h a ---++=++===∆ 称为二次曲面的不变量,即经过坐标变换后,这些量是不变的.行列式∆称为二次方程(1)的判别式.。
5-6曲面与曲线5-7二次曲面

1
z
0
单叶双曲面图形
z
o
y
x
x2 a2
by22
cz22
1
双叶双曲面
o
y
x
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形?
(1)x2; (2)x2y24;
(3 )yx1 .
思考题解答
方程
平面解析几何中 空间解析几何中
x2 平行于y轴的直线平 行 于yo面 z的 平 面
(3)同理在 yoz面上的投影也为线段.
z
1 2,
x 0
| y| 3. 2
例 7 求抛物面 y2 z2 x与平面 x 2 y z 0
的截线在三个坐标面上的投影曲线方程.
解 截线方程为
y2 z2 x x2y z 0
如图,
( 1) 消 去 z得 投 影x25y24xyx0,
将 z z 1 , y 1 x 2 y 2代入
f(y1,z1)0
将 z z 1 , y 1 x 2 y 2代入 f(y1,z1)0
得方程 fx 2 y 2 ,z 0 ,
y坐 o 标 面 z 上 的 已 知 曲 线 f(y ,z ) 0 绕 z轴 旋
转 一 周 的 旋 转 曲 面 方 程 .
x2 y2 z( p与 q同号) 2p 2q
双曲抛物面(马鞍面) 用截痕法讨论:
设 p0,q0
z
图形如下:
o y
x
(三)双曲面
x2 a2
by22
cz22
1
单叶双曲面
(1)用坐标面 xo(zy0)与曲面相截
截得中心在原点 O(0,0,0)的椭圆.
《I二次曲面介绍》课件

二次曲面的切线和法平面
1
切线
切线方程式是确定点切线方向的关键工具,可以帮助我们理解二次曲面的基本特 征。
2
法平面
法平面相切于曲面上的点,并垂直于该点的切线,是描述曲面矢量值和方向的基 本方法。
3
应用
对于计算两个表面之间的夹角和反射光线,有着应用上的力量,也是了解曲面空 间特征的重要手段。
二次曲面的焦点和准线
《二次曲面介绍》PPT课 件
欢迎来到《二次曲面介绍》课程!二次曲面是数学中一个重要的概念,也具 有广泛应用。在此课程中,我们将深入了解二次曲面的分类、性质、公式和 应用,希望你享受这次学习!
什么是二次曲面?
定义
由二元二次方程$x^2+y^2+z^2+ax+by+cz+d=0$所确定的曲面称为一般二次曲面。
工程领域
2
对于数学知识结构的完备和优化起着重 要的推进作用。
在多种物理和工程应用中,二次曲面有
着广泛的实际用途。谷歌、苹果等大型IT
公司也在开发利用二次曲面技术的产品。
3
学术研究
二次曲面仍然是数学与物理学研究领域 的重要研究对象,对未来科学教育的贡 献巨大。
二次曲面的实践应用案例分析
医学成像
二次曲面在体绘制和定义了新 的医学成像方法。它可以为医 师提供三维数据,从而进行更 高质量的检查和诊断。
二次曲面的思考与总结
1 对数学的重要性
了解二次曲面的形式,有助于人们理解和应用数学知识,可以使数学这一抽象的学科更 加形象化、通透化。
2 对科学的启示
二次曲面的理论和应用研究有助于开拓科学领域的新思路,推动科学的不断发展和进步。
3 对未来的期许
曲面知识课件
z oy
椭圆锥面
x2 a2
y2 b2
z2
( a, b 为正数)
在平面 z t 上的截痕为椭圆
x2 (at)2
y2 (bt)2
1,
zt
z
z
o yy xx
在平面x=0 或y=0 上的截痕为过原点的两直线.
可以证明, 椭圆上任一点与原点的连线均在曲面上
内容小结
(1)空间曲面
三元方程 F(x, y , z) 0
则F(x,y,z)= 0 称为曲面S的方程(通常
称此方程为曲面的一般方程),
曲面 S 叫做方程 F(x,y,z) = 0的图形.
F(x, y, z) 0
z
S
oy x
例如:三元一次方程 Ax+By+Cz+D= 0 是空间平面 的方程. 平面又称为一次曲面.
曲面的参数方程
x x(u, v),
化简得 2x 6 y 2z 7 0
上例说明: 动点轨迹为线段 AB 的垂直平分面. 显然在此平面上的点的坐标都满足此方程, 不在此平面上的点的坐标不满足此方程.
曲面的一般方程
如果曲面 S 与方程 F(x, y, z) = 0 有下述关系: (1) 曲面 S 上的任意点的坐标都满足此方程; (2) 不在曲面 S 上的点的坐标不满足此方程,
椭圆抛物面
x2 y2 z ( p , q 同号) 2p 2q
特别,当 p = q 时为绕 z 轴的旋转抛物面.
z
y x
单叶双曲面
x2 a2
y2 b2
z2 c2
1
( a,b, c 为正数)
空间解析几何常见的曲面PPT学习教案
椭球面
x2 a2
y2 b2
z2 c2
1
与三个坐标面的交线
x2
xOy面
:
a
2
y2 b2
1
z 0
x2
xOz面
:
a
2
z2 c2
1
y 0
y2
yOz面
:
b2
z2 c2
1
x 0
椭球面的主截线(主椭圆)
z 椭球面
o
x
y
第6页/共68页
5.平截线:
z
x2 y2 z2 1
a2 b2 c2
用z = h截曲面 用y = m截曲面 用x = n截曲面
把方程的左边都化成两项正,一项负,则右边是1的就 表示单叶双曲面,而右边是-1的,就表示双叶双曲面.
2°绘图时要注意区分“实轴”和“虚轴”,并且保证对 坐标轴的标注要符合右手系的原则.
第38页/共68页
椭球面与双曲面都是中心二次曲面,它们的方程可以写成
统一的形式:Ax2 By2 Cz2 1, ABC 0.
,
;
(5)表示一个椭圆,两半轴长分别为
a
1
h2 c2
b 1 h2 c2
由于h是变化的,(5)表示一族椭圆,椭圆面可以看成 由一个椭圆变动而生成的,其在变动中始终保持所在 的平面与坐标面xoy平行.
第8页/共68页
椭球面的几种特殊情况:
(1) a b,
x2 a2
y2 a2
z2 c2
1
旋转椭球面
由椭圆
➢ 单叶双曲面 ➢ 双叶双曲面
➢ 抛物面
➢ 椭圆抛物面 ➢ 双曲抛物面
第2页/共68页
二次曲面的定义:
第讲二次曲面-精品
在一般情况下,如果曲面S与方程
F(x,y,z)0 有下面的关系:
(1)
(1)曲面S上任一点的坐标都满足方程(1);
(2)不在曲面S上的点的坐标都不,而曲面S就叫做方程(1)
的图形.
象在平面解析几何中把平面曲线当作动点轨迹一样,在空间
解析几何中,我们常把曲面看作一个动点按照某个规律运动而
第8讲---二次曲面
一、曲面的方程 二、常见的曲面的方程: 三、一般二次曲面
淮南矿业技师学院《应用数学》课件
学习目标
1.理解曲面及其方程的关系,知道球面、柱面和旋转曲 面的概念,掌握球面、以坐标轴为旋转轴、准线在坐标面 上的旋转曲面及以坐标轴为轴的圆柱面和圆锥面的方程及 其图形. 2.了解椭球面、椭圆抛物面等二次曲面的标准方程及其 图形.
淮南矿业技师学院《应用数学》课件
上面我们看到,不含z的方程x2+y2=R2在空间直 角坐标系中表示圆柱面,它的母线平行于z轴,它的准线 是xOy面上的圆x2+y2=R2.
一般地,只含x、y,而缺z的方程F(x,y)=0,在空 间直角坐标系中表示母线平行于z轴的柱面,其准线 是xOy面上的曲线C:F(x,y)=0.
给定 yoz 面上曲线 C: f(y,z)0
若点 M 1 (0 ,y 1 ,z1 ) C ,则有 f(y1,z1)0
z C
当绕 z 轴旋转时, 该点转到
M(x,y,z),则有 zz1 , x2y2y 1
故旋转曲面方程为
M(x,y,z)
M1(0,y1,z1)
o
y
x
f( x2y2,z)0
淮南矿业技师学院《应用数学》课件
例如,方程y2=2x表示母线平行于z轴的柱 面,它的准线是xOy面上的抛物线y2=2x ,该柱面叫做抛物柱面(如图所示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x2 a2
z2 c2
1
分别绕
x
轴和 z 轴旋转一周所生成的旋转曲面方程.
解:绕 x 轴旋转 所成曲面方程为
x2 a2
y2 z2 c2
1
绕 z 轴旋转所成曲面方程为
x2 y2 a2
z2 c2
1
x
y
z
这两种曲面都叫做旋转双曲面.
21
二、柱面
z
引例. 分析方程 x2 y2 R2
表示怎样的曲面 .
开口向下的旋转抛物面. 例3. 旋转椭球面
0
y
特点:母线C为椭圆,轴为椭圆的
x
对称轴. 例如:yoz面上的椭圆:
y2 a2
z2 b2
1
z
绕z轴旋转得旋转曲面方程:
x2 y2 a2
z2 b2
1
绕y轴旋转得旋转曲面方程:
x
y2 a2
x2 z2 b2
1
y
注:旋转曲面的重要特征是其两个变量的平方项系数相等. 19
例4. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为
的圆锥面方程. 解: 在yoz面上直线L 的方程为
z y cot
z L
绕z 轴旋转时,圆锥面的方程为
z x2 y2 cot
令 a cot
两边平方
x
M (0, y, z)
y
z2 a2( x2 y2 )
20
例5.
求坐标面
xoz
上的双曲线
M
解:在 xoy 面上, x2 y2 R2 表示圆C,
C
o
M1
y
在圆C上任取一点M1(x, y,0) , 过此点作 x
平行 z 轴的直线 l , 对任意 z , 点M (x, y, z)
l
的坐标也满足方程 x2 y2 R2
沿曲线C平行于 z 轴的一切直线所形成的曲面称为
圆柱面. 其上所有点的坐标都满足此方程, 故在空间
称它为空间曲线的 参数方程.
z
例如,圆柱螺旋线 的参数方程为
M
o
x a cos t y a sin t
令 t , b v
z vt
x x a cos y a sin
y
z b
当 2 时, 上升高度 h 2 b, 称为螺距 .
41
例1. 将下列曲线化为参数方程表示:
(1)
x2
y2
za
1 2
1 2
cos
t
42
2、空间曲线在坐标面上的投影
设空间曲线 C 的一般方程为 求其在 xoy 平面上的投影.
F(x, y, z) 0 G(x, y, z) 0
(1)
消去 z 得投影柱面 H (x, y) 0, (2)
满足(1)的数 x, y, z 中的 x, y 必满足(2)式。
给定 yoz 面上曲线 C: f ( y, z) 0
z
若点 M1(0, y1, z1) C, 则有 f ( y1, z1) 0
当绕 z 轴旋转时, 该点转到
M (x, y, z)
C
M1 (0, y1, z1 )
M (x, y, z) , 则有
o y
z z1, x2 y2 y1
x
故旋转曲面方程为
x2 y2 R2 表示圆柱面
22
定义2. 平行定直线并沿定曲线 C 移动的直线 l 形成
的轨迹叫做柱面. C 叫做准线, l 叫做母线.
• y2 2x表示抛物柱面,
z
母线平行于 z 轴;
准线为xoy 面上的抛物线.
•
x2 a2
y2 b2
1表示母线平行于
z 轴的椭圆柱面.
x
z
C
o
yl
z
• x y 0 表示母线平行于
表示为:
F(x, y) z 0
0
而 F (x, y) 0 在空间坐标系中表示柱面。
例如:抛物柱面 z 1 x2
z
(0,0,1)
在xoz平面上的准线L3
L3
L3 :
z 1 x2
y
0
x
y
39
三、几种常用的空间曲线
三元二次方程
Ax2 By2 Cz 2 Dxy Eyx Fzx Gx Hy Iz J 0
高等数学
第二十一讲
1
第五节
第六章
几种常用的二次曲面与空间曲线
一、旋转曲面 二、柱面 三、几种常用的空间曲线
2
一、旋转曲面
定义1. 一条平面曲线 绕其平面上一条定直线旋转 一周 所形成的曲面叫做旋转曲面. 该定直线称为旋转 轴.
例如 :
3
下面我们重点讨论母线在坐标面,轴是坐标轴的 旋转曲面.
建立yoz面上曲线C 绕 z 轴旋转所成曲面的方程:
o y
S : x2 z2 2 py
例如:将yoz平面上的抛物线C: y2 2 pz
x
绕z轴旋转一周所产生的抛物面为:
z
S : x2 y2 2 pz
z a(x2 y2)
问:此曲线若绕x轴旋转所得的是何图形?
0
y
18
例2: S : z 1 x2 y2
z
(0,0,1)
其图形顶点在z轴上(0,0,1)处,
1
2x 3z 6
(2)
z
x2
a2 x2 y2 y2 ax 0
解: (1) 根据第一方程引入参数 , 得所求为
x cost y sin t0 t 2z源自1 3(62
cos
t)
(2)
将第二方程变形为
(x
a 2
)2
y2
a2 4
, 故所求为
x
a 2
a 2
cos
t
y
a 2
sin
t
0 t 2
母线 平行于 x 轴;
准线 yoz 面上的曲线 l2. 方程 H (z, x) 0 表示柱面,
y x l1
x z l3
z l2 y
母线 平行于 y 轴;
x
准线 xoz 面上的曲线 l3.
y
38
注:柱面方程与坐标面上的曲线方程容易混淆, 在不同的坐标系中应该注意。
一般在xoy面上的曲线,在空间直角坐标系中应该
o
z 轴的平面.
(且 z 轴在平面上) x
y x
o y
37
一般地,在三维空间曲面图形的方程中缺少一个变量,
此方程表示柱面方程.其图形平行于所缺变量对应的数轴. 方程 F (x, y) 0 表示柱面, z
母线 平行于 z 轴;
准线 xoy 面上的曲线 l1. 方程 G( y, z) 0 表示柱面,
f ( x2 y2 , z) 0
17
同理:当曲线 C : f ( y, z) 0
绕 y 轴旋转时得旋转曲面方程: f ( y , x 2 z 2 ) 0
例1. 旋转抛物面
特点:母线C为抛物线,轴L为抛物线的对称轴。 z
例如:将yoz平面上的抛物线C: z2 2 py
绕 y 轴旋转一周所产生的抛物面为:
(二次项系数不全为 0 ) 的图形通常为二次曲面. 其基本类型有:
椭球面、抛物面、双曲面、锥面 适当选取直角坐标系可得它们的标准方程,下面仅 就几种常见标准型的特点进行介绍 . 研究二次曲面特性的基本方法: 截痕法
40
1、空间曲线的参数方程
将曲线C上的动点坐标x, y, z表示成参数t 的函数:
x x(t) y y(t) z z(t)
