驻波的能量分析_邓尚民
驻波实验报告实验原理

一、实验原理1. 驻波的形成驻波是两列振幅相等、频率相同、传播方向相反的波叠加形成的特殊波动现象。
当这两列波在空间相遇时,它们的振动方向相反,从而产生相互抵消的现象。
这种相互抵消的现象在空间上形成一系列稳定的波峰和波谷,称为驻波。
2. 驻波的特征(1)波节:驻波中振幅为零的点,称为波节。
波节在空间上固定不动,不会发生振动。
(2)波腹:驻波中振幅最大的点,称为波腹。
波腹在空间上固定不动,不会发生振动。
(3)波节间的距离:相邻波节之间的距离等于半个波长。
(4)波腹间的距离:相邻波腹之间的距离等于半个波长。
3. 驻波的形成条件(1)两列波振幅相等:只有当两列波的振幅相等时,它们在空间相遇才能形成稳定的驻波。
(2)两列波频率相同:只有当两列波的频率相同时,它们在空间相遇才能形成稳定的驻波。
(3)两列波传播方向相反:只有当两列波的传播方向相反时,它们在空间相遇才能形成稳定的驻波。
4. 驻波与波速的关系驻波的形成与波速有关。
当两列波在空间相遇时,它们的传播速度相同。
设波速为v,波长为λ,则频率f与波速v的关系为:v = fλ5. 驻波与弦线的关系在弦线上形成驻波时,弦线的长度应满足以下条件:(1)弦线长度为波长的整数倍:当弦线长度为波长的整数倍时,可以形成稳定的驻波。
(2)弦线两端固定:只有当弦线两端固定时,才能形成稳定的驻波。
6. 驻波实验原理驻波实验旨在验证驻波的形成条件、特征以及与波速、弦线的关系。
实验过程中,通过调节弦线长度、波源频率和张力,观察驻波的形成、变化和消失,从而验证驻波实验原理。
实验步骤如下:(1)搭建实验装置,包括弦线、波源、滑轮等。
(2)调节弦线长度,使其满足形成驻波的条件。
(3)调节波源频率,使其与弦线长度对应的波长匹配。
(4)观察驻波的形成、变化和消失,记录实验数据。
(5)分析实验数据,验证驻波实验原理。
通过驻波实验,我们可以了解驻波的形成条件、特征以及与波速、弦线的关系,为后续的物理学习和研究奠定基础。
驻波解析

原点描写合成驻波。由于绳很长,可不考虑反射。 绳上的波速设为u 。
解 设左端的振动为y1 =Acos t,则右端的振动 为 y2=Acos ( t + )。
设右行波的波动表达式(以绳的中心为坐标原点)
y1Acos(t[ux)1]
设左行波的波动表达式(以绳的中心为坐标原点)
dE k2dV A 22co 2(2 s πx)si2 nt dE p2dV A 22si2n 2 πxco 2st
(1) cos t = ±1 各质点的位移达到最大,dEk为零,
势能dEp不为零。波节处势能最大;在波腹处势 能最小。势能集中在波节附近。
波腹处势能始终为0
(2) cos t = 0 各质点都回到平衡位置,此时所有
反射波在B点的振动方程
tl y反 BAco2 s([T)]
反射波的表达式
y 反 A co 2 (T s t [ l) 2 (l x )]
y反
Acos2( t T
212x)
Acos2(t x)
T
(2)驻波的表达式为
yy入y反
Acos2(t x)Acos2(t x)
T
T
2Asin2xsin2t
x k
2
点O 到点B 之间的波节
x 0 ,,,3 ,2 ,5 , 3 ,7 ,4 ,9 ,5
22 2 2 2
波腹的坐标
sin 2π x 1 2π x(2k1)π x (2k 1)
2
4
x ,3 ,5 ,7 ,9 ,1 ,1,3 1 ,5 1,7 19
4444444 4 4 4
例题* 两人各执长为l 的绳的一端,以相同的角 频率和振幅在绳上激起振动,右端的 ]A co (t sx [l)]
10-5_驻波与电磁波.ppt

1
例 两相干波源相距30.5米,振幅相同,频率150Hz ,波速300m/s。如图所示,A波源的相位比B波源超前 /2。求A、B连线上干涉相长与相消点的坐标。 P B A 解 x X O 先考虑两波源之间的情况。任取一点P,坐标为x。 A、B两波源的振动在P点的相位差为: π 2 π 2 (BP AP ) ( ) ( r r ) p B A B A
A O B
P
2 π 2 π ( ) ( r r ) ( BP AP ) p B A B A 2 2 π π ( 30 . 5 ) 30 π 2
x
X
2 k π , k0 , 1 , 2 , 3 ,... 干涉相长 p ( 2 k 1 ) π , k0 , 1 , 2 , 3 ,... 干涉相消
由 t =0, y=0 , v<0 知: 2
2
4
-40 -20
y 4 co 4 s( t )( cm ) 0
o
x(cm)
22
(2) 向右传播的波动方程
(3)反射波的波动方程
x y 4 cos[ 4 ( t ) ]( cm ) 802
方法一: 入射波在B处的振动方程
x y 4 cos[ 4 ( t ) ] 0 反 80
2
240 y 4 cos[ 4 ( t ) ] 0 反 B 80 4 cos[ 4 t 12 ] 4 cos[ 4 t ] 0 0
与
y 4 c os 4 t[ ]进行比较,得 反 B
3.相邻两个波节之间的所有质元的振动相位都相同 ,即 它们是同步调的振动,只是每个质元振动的幅值不同. 4.在一个波长范围内的某个波节两侧的质元的 振动相位相反,即它们反步调振动。
驻波经典知识介绍

λ
的同频率谐振动。 的同频率谐振动。
三、驻波的特点
1.频率特点:由图及方程知,各质元以同一频率作简 1.频率特点:由图及方程知, 频率特点 谐振动。 谐振动。 2.振幅特点: 2.振幅特点 振幅特点: x (1)各点的振幅 有关, (1)各点的振幅 2Acos(2π λ ) 和位置 x 有关,振幅 大小按余弦规律随 x 变化 (2)波节 有些点始终静止, 波节: (2)波节:有些点始终静止,这些点称作波节
实际中驻波的形成 实际的驻波可由入射到媒质界面上的行波和它 的反射波叠加而成。 的反射波叠加而成。 1.波在固定端的反射 (如一端固定的弹性绳) 1.波在固定端的反射 如一端固定的弹性绳) 反射点是波节(和固定点情况吻合) 反射点是波节(和固定点情况吻合)。 2.波在自由端的反射 2.波在自由端的反射 反射点是波腹。 反射点是波腹。 问题 在两个介质分界面上将如何 ?
驻波的能量被“封闭” 驻波的能量被“封闭”在相邻波节和波腹间的 λ 的范围内,在此范围内有能量的反复流动, /4 的范围内,在此范围内有能量的反复流动,但能 量不能越过波腹和波节传播, 量不能越过波腹和波节传播,驻波没有单向的能量传 输。 形成驻波的两个行波的能流密度数值相等,方 形成驻波的两个行波的能流密度数值相等, 向相反,因此它们叠加而成的驻波能流密度为零, 向相反,因此它们叠加而成的驻波能流密度为零, 驻波不传播能量 ---“驻”字的第三层含义。 ---“ 字的第三层含义。
二 、驻波方程
设两列沿同一直线相向传播的同振幅相干波, 设两列沿同一直线相向传播的同振幅相干波, 取两波在空间某点引起振动,同时达到最大为起始时刻, 取两波在空间某点引起振动,同时达到最大为起始时刻, 该点为坐标原点. 该点为坐标原点. y1 u x 入射波 y 1 = A cos 2π t − x
驻波的平均能流密度

驻波的平均能流密度驻波是一种特殊的波形态,它是由两个同频率、同振幅、反向传播的波在介质中相遇而形成的。
驻波的能流密度是描述驻波能量传输特性的物理量,它在电磁学、声学等领域有着广泛的应用。
一、驻波简介1.1 定义驻波是由两个反向传播且频率相同、振幅相等的平面波在介质中相遇而形成的一种波动现象。
在介质中,两个平面波之间会产生干涉,使得某些点上的振动方向和大小发生变化,形成了固定位置上振幅不变但方向不断变化的节点和振幅最大但位置不断变化的腹部。
1.2 特点(1)驻波只存在于一定范围内,超出这个范围后就会消失;(2)驻波能量不会随着时间而传递,只会停留在某些位置上;(3)节点处能量密度为零,腹部处能量密度最大。
二、平均能流密度2.1 定义平均能流密度是指单位时间内穿过单位面积的能量,它是描述波动传输能量特性的物理量。
在驻波中,平均能流密度可以用来描述驻波的能量传输特性。
2.2 计算公式平均能流密度的计算公式为:$$\bar{S}=\frac{1}{T}\int_{0}^{T}S(t)dt=\frac{1}{2}\omegaA^{2}\rho v$$其中,$T$为周期,$S(t)$为瞬时能流密度,$\omega$为角频率,$A$为振幅,$\rho$为介质密度,$v$为波速。
2.3 物理意义平均能流密度反映了单位时间内通过单位面积的能量传输情况。
在驻波中,由于节点处能量密度为零,因此平均能流密度也为零;而在腹部处,由于振幅最大,因此平均能流密度也最大。
三、影响因素3.1 振幅振幅是指驻波中两个相向传播的波的振动幅度大小。
在给定介质和频率下,振幅越大,则腹部处的平均能流密度就越大。
3.2 频率频率是指两个相向传播的波在介质中的振动周期。
在给定介质和振幅下,频率越高,则腹部处的平均能流密度就越大。
3.3 波速波速是指驻波中两个相向传播的波在介质中传播的速度。
在给定介质和频率下,波速越大,则腹部处的平均能流密度就越大。
驻波-多普乐效应
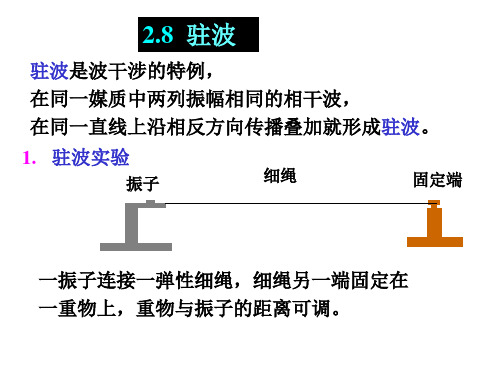
振幅
2Acos 2 x
波腹的位置 x k k 0, 1, 2, 3,
2
波节的位置 x (2k 1) k 0, 1, 2, 3,
4
相邻波腹(或波节)的距离
x x
k 1
k2
2
2
讨论 相位
y
2 A cos
2
t+1s 时刻
S● u
S●
u R
u
R
R
u
2. 波源不动,观测者以速度 υR 相对介质运动
0, 0
S
R
观测者所接收到的完整波的数目
等于在观测者前方(波源方向)长度等于u + υR
进一步的研究表明,当波在空间传播时, 在两种介质的分界面处究竟出现波节还是波腹, 这将决定于波的种类和两种介质的有关性质 以及入射角的大小。
讨论波动垂直入射的情况:
讨论波动垂直入射的情况: 如果是弹性波,把密度与波速的乘积较大的介质 称为波密媒质,乘积较小的介质称为波疏媒质 那么,当波从波疏媒质传播到波密媒质, 而在分界面处反射时,反射点出现波节(形成驻波时),
讨论 速度
y 2Acos 2 x cost
●
●
●
x 1
x 2
x 3
质点的速度
v y 2Acos 2 x sin t
t
讨论
●
●
●
xxx
1
2
3
y
2
2 Acos
x cost
v 2A cos 2 x sin t
能量
动能密度
驻波——精选推荐
驻波驻波(standing wave)频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
波在介质中传播时其波形不断向前推进,故称行波;上述两列波叠加后波形并不向前推进,故称驻波。
例如,如图所示,一弦线的一端与音叉一臂相连,另一端经支点O并跨过滑轮后与一重物相连。
音叉振动后在弦线上产生一自左向右传播的行波,传到支点O 后发生反射,弦线中产生一自右向左传播的反射波,当弦长接近1/2波长的整数倍时。
两列波叠加后弦线上各点的位移为(设音叉振动规律为u=Acosωt)u(x,t)=2Asin(x)sin(ωt )=A(x)sin(ωt),弦线上每个固定的点均作简谐运动,但不同点的振幅不同,由x值决定。
振幅为零的点称为波节,振幅最大处称为波腹。
波节两侧的振动相位相反。
相邻两波节或波腹间的距离都是半个波长。
在行波中能量随波的传播而不断向前传递,其平均能流密度不为零;但驻波的平均能流密度等于零,能量只能在波节与波腹间来回运行。
测量两相邻波节间的距离就可测定波长。
各种乐器,包括弦乐器、管乐器和打击乐器,都是由于产生驻波而发声。
为得到最强的驻波,弦或管内空气柱的长度L必须等于半波长的整数倍,即,k为整数,λ为波长。
因而弦或管中能存在的驻波波长为,相应的振动频率为,υ为波速。
k=1时,,称为基频,除基频外,还可存在频率为kn1的倍频。
入射波(推进波)与反射波相互干扰而形成的波形不再推进(仅波腹上、下振动,波节不移动)的波浪,称驻波。
驻波多发生在海岸陡壁或直立式水工建筑物前面。
紧靠陡壁附近的海水面随时间虽作周期性升降,海水呈往复流动,但并不向前传播,水面基本上是水平的,这就是由于受岸壁的限制使入射波与反射波相互干扰而形成的。
波面随时间作周期性的升降,每隔半个波长就有一个波面升降幅度为最大的断面,称为波腹;当波面升降的幅度为0时的断面,称为波节。
相邻两波节间的水平距离仍为半个波长,因此驻波的波面包含一系列的波腹和波节,腹节相间,波腹处的波面的高低虽有周期性变化,但此断面的水平位置是固定的,波节的位置也是固定的。
驻波-量子力学
波长=音速/频率驻波两个振幅、波长、周期皆相同的正弦波相向行进干涉而成的合成波。
此种波的波形无法前进,因此无法传播能量,故名之。
驻波通过时,每一个质点皆作简谐运动。
各质点振荡的幅度不相等,振幅为零的点称为节点或波节(Node),振幅最大的点位于两节点之间,称为腹点或波腹(Antinode)。
由于节点静止不动,所以波形没有传播。
能量以动能和势能的形式交换储存,亦传播不出去。
频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
波在介质中传播时其波形不断向前推进,故称行波;上述两列波叠加后波形并不向前推进,故称驻波引。
使用倍:由于波的行进当弦乐器的弦因振动发出声音时,振动频率最低者为例如X = 0 时,Y = 0,X = 180 时,Y = 0;若X 取值【180~360】,则我们可以看到,图像正好与原来的相反(在第四象限)。
这就是正弦波的图像了。
定义:统计热力学从粒子的微观性质及结构数据出发,以粒子遵循的力学定律为理论基础;用统计的方法推求大量粒子运动的统计平均结果,以得出平衡系统各种宏观性质的值.研究对象:大量粒子构成的集合体.研究方法::统计力学的方法,应用几率规律和力学定律求出大量粒子运动的统计规律.优点:揭示了体系宏观现象的微观本质,可以从分子或原子的光谱数据直接计算体系平衡态的热力学性质.缺点:受对物质微观结构和运动规律认识程度的限制. 统计系统的分类与术语:①粒子(子):组成系统的分子,原子,离子等的统称. ②独立子系统:粒子间相互作用可忽略的系统. 如理想气体,完美晶体③相依子系统:粒子间相互作用不能忽略的系统. 如真实气体,液体④定域子系统(可辨粒子系统):粒子有固定的平衡位置,运动是定域的; 如固体. ⑤离域子系统(全同粒子系统):粒子处于混乱的运动中,无法分别,粒子彼此是等同的. 如:气体,液体。
驻波振动的频率与波长和原来的进行波相等
2.0(m)。
23
範例2
2 基音與諧音
弦線A的長度為 L,線密度為μ,張力為T,兩端固
定。另一弦線 B,線密度為2μ,張力為 3T,兩端
也固定。欲使 B 弦的基頻與 A 弦的第三諧音頻率
相同,則 B 弦長度應為
。【87日大】
24
兩端固定之弦的駐波頻率 f nv n F (n 1,2,3,4......):
30
(1) 弦長為 公尺。
(2)如下圖(b)所示,欲使中間的節點數再增加一個,
則振盪的頻率應調整為
赫茲。
(3)承(2),此時駐波的波長為 公尺。
31
(1)一端固定之弦的駐波頻率f nv n 44
圖(a)為第五諧音 圖(b)為第七諧音
3
(3)v f
f
v
200 2
300(Hz。 )
3
28
※速解法:附圖所示為第三諧音(n 3) f nv 3 200 300(Hz。 ) 2 21
29
範例4
4 一端為自由端的駐波
一根線密度為0.02 公斤/公尺之弦,弦一端固定於 一振盪器上,另一端接於一個質量可不計的環上, 環則套在一個細長且光滑的柱上。振盪器的振動頻 率為175赫茲時,弦的張力為98牛頓,可使弦產生 如下圖(a)所示的駐波,則
= n (n = 1,3,5,7,……)
4
駐波的波長:
= 4 ( n = 1,3,5,7,……) 。
n
(3)由v f,可得駐波的頻率:
f=v= v
4
= nv 4
驻波检测理论分析
驻波检测理论分析电压驻波比介绍电压驻波比(VSWR)为英文Voltage Standing Wave Ratio 的简写。
电压驻波比产生的原因主要是由于在系统或者电路中存在阻抗不匹配,在无线电通信中,由于天线与馈线的阻抗不匹配或天线与发信机的阻抗不匹配,高频能量就会产生反射折回,并与前进的部分干扰汇合发生驻波。
为了表示和测量天线系统中的驻波特性,也就是天线中正向波与反射波的情况,人们建立了“驻波比”(Standing Wave Ratio)这一概念,驻波比的全称是电压驻波比。
当两个阻抗数值一样时,即达到完全匹配,反射系数Γ等于0,驻波比为1。
这是一种理想的状况,实际上总存在反射,所以驻波比总是大于1 的。
理想的比例为1:1 ,即输入阻抗相等于传输线的特性阻抗, 但几乎不可能达到,如果当VSWR 1.25:1 时,反射功率大概为1.14 %,当VSWR 1.5:1 反射功率为4.06 %,当VSWR 1.75:1 时,反射功率为7.53 %,由这个数字我们可以知道, 驻波比越大, 反射功率越高。
在射频系统阻抗匹配中,特别要注意要使电压驻波比达到一定要求,在移动通信系统中,一般要求驻波比小于1.5,一样一般可以保证通信系统的良好工作。
同时,因为在宽带运用时频率范围很广,驻波比会随着频率而变,所以应使阻抗在宽范围内尽量匹配。
电压驻波比对系统性能的影响随着驻波比的恶化,有效传输的功率将会减少,这是由于理想的阻抗匹配(VSWR=1:1)可以使功率无损传输,而严重的阻抗失配(高VSWR)将导致传输到负载的功率减少。
高的VSWR可能引起多种系统问题,其中对VSWR最为敏感的器件是功率放大器,因为其输出功率较大可能达到200 瓦左右,导致很大的功率反射,从而造成无线电装置的工作范围缩小、发射信号使接收部分饱和。
更为严重的影响是损坏发射机并且击穿传输电介质。
同时由于天线上反射回的信号在功率放大器处再次反射,然后重新发射出去,导致了类似多径现象,因此高VSWR可能引起基站系统的遮蔽衰落VSWR 值很高也有可能会损坏天馈系统,反射波在天线和发射机之间来回反复时会丧失一部分能量而转化为热能损耗了,这一部分热量增加了馈线对热损耗的承受能力,会产生破坏作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第卷第期山东工程学院学报
驻波的
能量
分
析
邓
尚
民哀
玉
珍
基
础部
摘要本文从能贡密度出发分析了驻波的能1及其分布
规律
关链词
驻波能量密度
许多教材`’一3,在介绍驻波时只简单地指出驻波不传播能且对为什么不传播能量
及
能童在驻波中怎样分布没有进行详细的分析本文从能量密度出发讨论驻波的能量及
其分布规律
设有两个振幅均为A的相干波一个
沿x轴正方向传播另一个沿
x
轴
负方向传
播其波动方程分别为
:
l
`l(
y
一
AcosZ
兀
y:=
A
eos
Z
汀
根据(1)和l()式可得驻波方程
:
(奋一奇)
(奋
+
奇
)
,`
J
才
+夕2一
2,
一
(浮)
一
(
攀
)
波节
位
于
二
一士(2、+
1
)
聋
k
=
0
0一一k,人一,ùk
一十
一
X
波腹位于
此外入射波和反射波的能量密度’”分别为
:
、
、
一E一、·’2·(牙反一:5in’2·(手奇)一鲁〔卜一4
:
登)一鲁[,一`·(奋一奇(奋十奇
十
"
一
T
式中E一州’。’p是弹性介质的质量密度aJ是圆颇率体人和甲反的最大值均为E最
小值均为零都具有T/2的周期由(5)式和(5)式可见波节和波腹以及任意位
置
x
处
的能量密度均随时问呈周期性变化因为入射波和反射波是相干波所以彼此叠加
后
形成了稳定的能量分希根据波的叠加原理和能童守恒定律驻波的能量密度等于入射
波和反射波的能童密度之和:即
二
一附+甲_一
:「1
一
cos擎cos
粤
八仅L凡
I
(6)
收稿
R
期
1996
一03一
13
第期邓尚民等驻波的能皿分析
一一
上式表明驻波能最密度的数值在ZE和。之间变化是周期性地分布在整个空
间
且
随时问作周期性变化空间周期等于相邻波节或波腹间的距离义/2时问周期是
T/2
恰为入射波或反射波相应周期的二分之一因此驻波的能量密度具
有时间和空问对称
的双重周期性
即
砰(rx)~砰
T
还
l
+百x+
万
比
较(6)式和(5)式显见驻波与行波的能量密度不同这种差别造成
驻波的能量分
布
与行波截
然不同
当时问`一定时由(6)式可得驻波能量密度关于位丑坐标的一阶和二阶偏导
数
:
刁
W
4兀。4兀x4
兀
t
了,
吕一;乙slnes二wecos气二
口
万
人^I
(7)
刁
2
甲
4兀\2_4
兀
x
丁
/
`
“
os
万厂
~
4
兀
t
T
(
8
)
令(7)式等于零}当`,(,k+,)晋{时得一士·聋”=012,…时即在波节和波腹
处
能量密度甲取极值极大值或极小值是由能量密度的二阶导数
的符号决定的
把(3)式和(4)式分别代
入(8)式中得波节
处
二
一
f
丝
、
、
又
/
。
4
们
二
co
s
万
不
(9)
丝
、
又
/
”
4
兀
z
乙
“。
s
下
(
1
0
)
州
UZ一
入
过
,
一
口
波腹
处
(9
)式和(10)式表明在任意时刻波节和波腹处的二阶导数总是等值异号且以
相同
的周期T/2作周期性变化因此能量密度在波节处取极大值时波腹处
必
为极
小值
反
之亦然从而说明了其能量也具有与能量密度相同的变化和分布规
律
把(3)式和(4)式分别代
入(6)式可得波节处的能量密度
:
二
一
:(1
+
。。
s
擎
\
了
波腹处的能量密度
:
二
一
E
f
:
一
c
os
丝
z
\
T
在任意时刻且无论所考虑的波节和波腹是否相邻均有
碎
、
+甲:一
ZE
(
川
并且等于恒量这表明在极值点波节和波腹处流出和流入的能量的净值是不随时问变化
的这一规律不仅在于任一波节和波腹还存在于任意一对对应位置处设任一
波
节位于x.处某点。位于x.十△石任一波腹位于xZ处某点b位于二2十△x则
称
。
和b为一对对应位置分别利用(3)(4)和(6)式得a点处能童密
度
一一山东
工程学院学报
年
甲
O
兀
△
又
O
丝
」
点处的能量密度
一
汀△又O兀
〕
十
一
则
O
在形成驻波的介质中有无数对对应位置(11)和(1(11)`)式为结果完全相同体现了
在整个弹性介质中无数对此驻波从整体效果上看对应位置问流出和流入的能量的净值是不随时问变化的因
不存在能量的传播
参考文献
程守珠等编普通物理学(第一册)北
京:人民教育出版社
197
8
南京工学院等七所工科院校编物理学(下盼)北京:高
等教育
出版社
191
张三惹等编光学近代物理北京科学技术出版社1987
EnergyAnalysisonS
tandin找
W
ave
DengShangntinYuanYuzh
en
(DePartmentofBasieCourses)
AbstraetThisPaPeraeeording
toenergydensityanalysestheenergyanditsdist
ribu
tionofst
andin
g
w
aves
(IeywordsStandingwaveEnergydensi
t
y
