驻波的能量
4.波的干涉_驻波
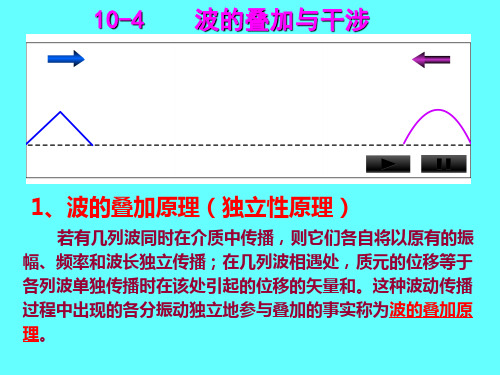
三、驻波能量:
⒈动能:
当各质点同时到达平衡位置时: 介质无形变,势能为零,此时驻波能量为动能。 波腹处动能最大,驻波能量集中在波腹附近。
⒉势能:
当各质点同时到达最大位移时: 动能为零,此时驻波能量为势能。 波节处形变最大,势能最大,能量集中在波节附近。
⒊结论:
动能、势能不断在波腹附近和波节附近间相互转 换,能量交替传递,无定向传播。
2 x 波腹位置: cos(2 ) 1 相邻两波腹距离 10 20 0 x x k , k 0,1,2 2 2
相邻两波节距离 x
各点相位:
y 2 A cos(2
x
) cos(2 t )
各质点作振幅为 2 A cos(2
cos(2
相位跃变(半波损失)
波 疏 介 质
波 密 介 质 较 大
u
较 小
u
当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失.
π
当波从波密介ቤተ መጻሕፍቲ ባይዱ垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
同一直线上沿相反方向传播时叠加而形成的一种特殊
的干涉现象.
驻波的形成
特征:
1、波形不移动。 2、各质点以不同的振幅在各自的平衡位置附近振动。
3、分段振动:振幅最大的点为波腹,
振幅为零的点为波节。
二、驻波方程:
沿X 轴正、负向传播的两列平面简谐波的波动方程为: x 在任意点 x 处叠加, y1 A cos 2 ( t ) 合位移: x y y1 y2 y 2 A cos 2 ( t ) x 2 A cos(2 ) cos(2 t ) ( 设初相 10 20 0)
驻波解析

原点描写合成驻波。由于绳很长,可不考虑反射。 绳上的波速设为u 。
解 设左端的振动为y1 =Acos t,则右端的振动 为 y2=Acos ( t + )。
设右行波的波动表达式(以绳的中心为坐标原点)
y1Acos(t[ux)1]
设左行波的波动表达式(以绳的中心为坐标原点)
dE k2dV A 22co 2(2 s πx)si2 nt dE p2dV A 22si2n 2 πxco 2st
(1) cos t = ±1 各质点的位移达到最大,dEk为零,
势能dEp不为零。波节处势能最大;在波腹处势 能最小。势能集中在波节附近。
波腹处势能始终为0
(2) cos t = 0 各质点都回到平衡位置,此时所有
反射波在B点的振动方程
tl y反 BAco2 s([T)]
反射波的表达式
y 反 A co 2 (T s t [ l) 2 (l x )]
y反
Acos2( t T
212x)
Acos2(t x)
T
(2)驻波的表达式为
yy入y反
Acos2(t x)Acos2(t x)
T
T
2Asin2xsin2t
x k
2
点O 到点B 之间的波节
x 0 ,,,3 ,2 ,5 , 3 ,7 ,4 ,9 ,5
22 2 2 2
波腹的坐标
sin 2π x 1 2π x(2k1)π x (2k 1)
2
4
x ,3 ,5 ,7 ,9 ,1 ,1,3 1 ,5 1,7 19
4444444 4 4 4
例题* 两人各执长为l 的绳的一端,以相同的角 频率和振幅在绳上激起振动,右端的 ]A co (t sx [l)]
高二物理竞赛课件:驻波的能量
须是波节,弦上形成驻波的条件(称为简正模式):
Ln
( n=1,2,3)
2
驻波波长和简正模频率:
2L , nu (基频, 二次谐频)
n
2L
返回 退出
*若弦的一端固定,一端自由,简正模:
Ln
24
(2n 1)u
4L
返回 退出
例 如图二胡弦长 l 0.3 m ,张力 T 9.4N . 密度 3.810 4 kg m . 求弦所发的声音的基频和谐频.
π] 3
(m)
为了在此弦线上形成驻波,并且在x= 0处为一
波节,此弦上还应有一简谐波,求其表达式。
解: 反向波:
y2
0.02 cos[2π( t 0.02
x) 20
]
合成波:
y y1 y2
0.04 cos[1 ( 2x π )]cos[1 ( 4πt π )]
2 20
3
2 0.02
x l 2 时,y1 = Acos t,
A c os t
l 2u
1
Acost
1
l
2u
返回 退出
x l 2 时,y2 = Acos t,
A c os t
l 2u
2
Acos(t
)
2
l
2u
右行波、左行波表达式:
y1
A cos
t
x u
l 2u
y2
A c os t
x u
l 2u
返回 退出
入射波与反射波 在反射点同相
波腹
光波:光密 到 光疏
固定端反射 半波反射
波疏 波密界面反射 光波:光疏 到 光密
入射波与反射波 在反射点反相
大学物理:Chapter 13-驻波

2
2
A驻 cos ( t )
A驻
2 Acos (2 x 2 1 ) 2
★ 说明:
(1) A驻 是 x 的周期函数,决定 x 处质点的振幅。
(2) (t ) 决定 x 处质点的振动状态。
(3) 各点作频率相同、振幅不同的谐振动。
(4) 方程中不含 (t x u) 项,非行波,没有波形的传播。
无半波损失时,应满足:
t kx0 0反 t kx0 0入
0反 0入 2kx0
有半波损失时,应满足:
t kx0 0反 t kx0 0入 0反 0入 2kx0
驻波在生活中的 应用
• 首先举几个生活中常见驻波的例子: • 以弦乐器的弦来说明。当拨动琴弦,产生一个波,遇到两
无半波损失时,
若入射波函数为:u入 ( x , t ) A cos(t kx) 则反射波函数一定为:u反 ( x , t ) A cos(t kx)
若入射波函数为:u入 ( x , t ) A cos(t kx 0 )
则反射波函数一定为:u反 ( x ,t ) A cos(t kx 0 )
解: (1)
y入
A cos
2
(
t T
x
)
入射波 O
反射波
P
波密 介质
x
y入O
A cos
2
t T
L = 5λ
波由O 传至P 再返回O ,引起O 点振动相位比 y入O 落后了:
2
2L
由半波损失引起的相位差
所以反射波在O点的振动方程为:
y反O
A cos[ 2
t T
(2
2L
)]
Acos[2 t (2 10 )] Acos[2 t 21 ]
电磁驻波中的能量与能流分布探讨

电磁驻波是电磁学中一个重要的研究课题。
它不仅可以提供精确的电磁场数据,而且可以用来探索电磁场中的能量和能量流分布。
首先,讨论电磁驻波中的能量分布。
电磁驻波中的能量主要来自电场和磁场,即电磁能量。
电场和磁场的能量密度分布可以用电磁能量密度的概念来解释。
它表明,电磁驻波中的能量密度分布是电磁功率的功率密度的函数。
电磁功率的功率密度可以用电功率和磁功率的功率密度的概念来解释。
其次,讨论电磁驻波中的能量流分布。
电磁驻波中的能量流是由电场和磁场的能量流决定的,它是一种电磁能流密度的概念。
电磁能流密度可以用电功率和磁功率的功率密度的概念来解释,电磁功率的功率密度是电磁能量的功率密度的函数。
因此,电磁驻波中的能量流分布与电磁能量的分布相关。
综上所述,电磁驻波中的能量主要来自电场和磁场,而电磁驻波中的能量流分布与电磁能量的分布相关。
电磁能量的功率密度可用电功率和磁功率的功率密度的概念来解释,而电磁能流密度可以用电磁功率的功率密度来解释。
因此,电磁驻波中的能量和能量流分布是电磁功率的功率密度的函数,可以反映电磁场的状态。
10-5 驻波

33
物理学
第十章 波动
20
1010-5
驻波
例题3 一平面简谐波某时刻波形如图所示, 例题 一平面简谐波某时刻波形如图所示,此波以波速 u沿x轴正方向传播,振幅为 ,频率为 。 轴正方向传播, 沿 轴正方向传播 振幅为A,频率为υ。
y
B D
x
点为x轴的坐标原点并以此 (1)若以图中 点为 轴的坐标原点并以此 )若以图中B点为 时刻为t=0时刻 写出此波的波函数。 时刻, 时刻为 时刻,写出此波的波函数。 点为反射点, (2)图中 点为反射点,且为一节点。若以 点为 )图中D点为反射点 且为一节点。若以D点为 X轴的坐标原点,并以此时刻为 时刻,写出此波 轴的坐标原点, 时刻, 轴的坐标原点 并以此时刻为t=0时刻 的入射波的波函数和反射波的波函数。 的入射波的波函数和反射波的波函数。
第十章 波动
18
1010-5
驻波
第十章 波动
19
1010-5
驻波
t x 例题2 如果入射波是y1 = A cos 2 π( + ) , T λ 处反射后形成驻波,反射点为波腹, 在 x = 0 处反射后形成驻波,反射点为波腹, 设反射后波的强度不变, 设反射后波的强度不变,则反射波的方程式为 y2 = Acos 2π(t / T x / λ) ,在 x = 2 λ 处质点 ______________________, 3 合振动的振幅等于______. 合振动的振幅等于 A
y = (2Acos
x ∈ (
2π
λ λ
λ
x) cos ωt = A′ cos ωt
2π
, ), cos x>0 4 4 λ
y = (2Acos
对于驻波能量的定量研究
对于驻波能量的定量研究驻波是一种特殊的波动现象,它由两个同频率但反向传播的波叠加而成。
驻波形成的条件是波的传播方向与波的反射方向一致,而反射方向的振幅与传播方向相反。
驻波在物理学中有着广泛的应用,比如在声学中,驻波能够形成声学共振,而在电磁学中,驻波可以形成共振腔。
对于驻波能量的定量研究,我们可以从驻波的能量分布和传播特性入手进行分析。
首先,我们需要研究驻波的能量分布。
在一维驻波中,驻波的能量密度与振幅的平方成正比。
对于一根被两端固定的弦,根据能量守恒定律,驻波的能量在弦的各个位置分布应该是均匀的。
但是,在一维驻波中,振幅和能量的分布并不均匀,而是呈现“波腹”和“波节”的分布规律。
波腹处能量密度最大,而波节处能量密度为零。
我们可以通过测量波腹和波节处的振幅来定量研究驻波的能量分布。
其次,我们可以通过传播特性来研究驻波的能量。
对于一维驻波,驻波的频率与波长有着特定的关系。
在一个封闭的管道中,当管道的长度等于波长的整数倍时,会产生共振现象,能量传递效果更为明显。
我们可以通过改变波长或改变驻波的条件来调节驻波的能量传输效果。
在三维空间中,驻波的能量分布和传播特性与一维驻波有所不同。
对于三维驻波,波场分布更为复杂,而且驻波的能量分布往往不再是均匀的,而是呈现出球面波的特点。
我们可以使用模拟方法或实验方法来研究三维驻波的能量分布和传播特性。
总的来说,驻波能量的定量研究需要结合能量分布和传播特性来进行分析。
通过测量振幅、频率和波长等参数,可以定量研究驻波能量在空间中的分布和传播特性。
驻波能量的定量研究对于理解波动现象以及在声学、电磁学等领域的应用具有重要意义。
驻波的能量特点
驻波的能量特点
驻波(Standing wave)是在一定空间范围内来回反射形成的波动模式。
它具有以下能量特点:
1. 能量局限:驻波的能量被局限在空间的特定区域内。
在驻波中,波峰和波谷形成固定的位置,能量在这些位置上来回传递,而在波节处能量几乎为零。
这导致能量在空间上被限制在驻波模式所占据的区域内。
2. 能量稳定:由于反射和干涉的作用,驻波中的能量处于稳定状态。
波峰和波谷之间的能量交换导致能量在区域内持续循环,而不会传播到其他区域。
这使得驻波的能量保持相对稳定,不会随时间推移而减弱或增强。
3. 最大与最小能量点:在一个驻波模式中,存在能量最大和能量最小的位置。
能量最大的位置位于波峰,而能量最小的位置位于波节。
这种分布使得驻波具有不同位置上能量密度的变化,形成特定的振动模式。
4. 振幅变化:驻波中的能量随着位置的变化而发生振幅的周期性变化。
在波峰处,振幅达到最大值;而在波节处,振幅几乎为零。
这种振幅变化形成了驻波模式的特征。
需要注意的是,驻波的能量特点与波长、频率等参数密切相关。
具体的能量分布和特性取决于驻波的模式和系统的几何形状。
驻波在许多领域中都有重要的应用,包括声学、光学和电磁学等。
1/ 1。
对于驻波能量的定量研究
玉林师范学院本科生毕业论文对于驻波能量的定量研究The Quantitative Study Of Standing Save Energy院系物理科学与工程技术学院专业物理学学生班级姓名学号指导教师单位物理科学与工程技术学院指导教师姓名指导教师职称对于驻波能量的定量研究物理学2008级1班指导教师摘要驻波是由两列振幅、频率相同,但传播方向相反的简谐波叠加而成的。
关于驻波的能量问题,在多数普通物理力教材中只作了简单介绍。
不过笔者认为,驻波是力学的重要组成部分,因此对这个问题的讨论,应该有一个定量的解析式分析,才能使之更富有普遍性和说服力。
本文通过“驻波是由两列振幅、频率相同,但传播方向相反的简谐波叠加而成”和“驻波方程”两个角度,首先阐明了弹性介质驻波形成的原理及其特点,导出了弹性介质中驻波质元的动能和势能的表达式,进一步导出了驻波能量的表达式,然后定量分析弹性介质中驻波的波节、波腹与波节(波腹)、波腹(波节)之间的能量分布及波节(波腹)、波腹(波节)之间能量的相互转换问题。
最后文章指出在驻波中没有引起能量的重新分布,但发生了能量的转换.并且在波节和波腹处,都没有能量的传递和通过,能量只能在相邻波节和波腹之间转换、流动。
关键词:驻波,波节,波腹,能量,转换和流动The quantitative study of Standing wave energyPhysics 2008-1 Zhou Shi- kunSupervisor Guan Xiao-rongAbstractStanding wave is by two columns of amplitude, frequency and same, but spread in the opposite direction of Jane harmonic a stack. In the energy of the wave problem about, in the most ordinary physical force only in the teaching material are introduced. But I think, as the in-depth discussions on this problem, should have a quantitative analytical analysis, can make it more rich universality and persuasive.This article through the standing wave by two columns amplitude frequency is same, but spread in the opposite direction of Jane harmonic superposition of standing wave equation into and two Angle, first expounded the elastic medium standing wave form the principle and features of the elastic medium are standing wave of mass yuan kinetic energy and potential formula, further derived and the expression of the standing wave energy, and quantitative analysis of the elastic medium standing wave wave quarter wave abdomen and wave festival (wave abdomen) wave abdomen (nodes) of energy between the distribution and wave festival (wave abdomen) wave abdomen (nodes) of energy conversion between each other last the article points out that in the standing wave did not cause the redistribution of energy, but happened the transfer of energy. And in the nodes and wave in the abdomen, all have no energy transfer and through, energy can only in adjacent nodes and wave abdomen convert between flow.Key words:standing wave;node;lop;energy;Conversion and flow目录1前言 (1)2驻波 (1)2.1驻波的形成 (1)2.2驻波方程 (2)2.3驻波振动的特点 (3)3驻波的能量 (5)3.1简谐波介质中质元的动能、势能、机械能 (5)3.2驻波介质中质元的动能、势能、机械能 (7)3.3简谐波的能流密度 (10)3.4驻波的能流密度 (10)3.5驻波在相邻波节(波腹)、波腹(波节)之间的能量 (12)3.6波在相邻波节(波腹)、波腹(波节)之间的动能 (13)3.7波在相邻波节(波腹)、波腹(波节)之间的势能 (14)4结论 (15)致谢 (16)参考文献 (16)玉林师范学院本科毕业生论文1前言对于驻波,大家都有所认识,它是一种常见的物理现象。
驻波能量分析
驻波能量分析摘要:驻波是由振幅、频率、和传播速度都相同的两列相干波,在同一直线沿相反方向传播时叠加而成的一种特殊形式的干涉现象。
但是它不同于行波,它不定向传播能量,只是在波腹和波节间转移。
本文以定量的方式来讨论驻波能量问题。
关键词:驻波能量定量解释不定向传播一、驻波的方程现在假设两个振幅、频率、和传播速度都相同、初相为零的两列简谐波,其波动方程分别为:y1=Α cos2π (νt− X/λ); (1)y2=Α cos2π (νt+ X/λ); (2)式中Α为波的振幅,ν为频率,λ为波长。
则其形成的驻波的波函数为:y=2Acos2πx/λcos2πνt; (3)上式表明驻波上各点做振幅为|2Acos2πx/λ|、频率为ν的简谐运动。
由驻波的波函数易得其波节位置为:x=±(2k+1)λ/4, k=0,1,2,⋯波腹位置为:x=±kλ/2, k=0,1,2,⋯二、驻波的动能、势能、总能量、能量密度下面我们以下图所示的棒为例,假设其为弹性均匀介质。
考察距棒x处一段长为dx的体积元。
该棒的密度为ρ,截面积为S,则该体积元体积为dV=Sdx,质量为dm=ρSdx。
当波传到了该体积元时,若它的左端发生了位移y,右端位移为y+dy,这表明它不仅发生了运动,而且还发生了被拉伸dy的形变,所以它应同时具有振动动能和弹性势能。
d W k=1/2(dm)υ; (4)由式(3),该体积元的振动速度为:υ=∂y/∂t=−2πν·2 Acos2π x/λ cos2πνt=−4πν Acos2π x/λ cos2πνt(5)所以sin22πνt; (6)d W k=1/2ρdV 16π2ν2A2cos22πxλ同时,体积元因形变而具有的弹性势能d W p=k(dy)2/2, 此处k为棒的劲度系数,而k与弹性模量E的关系为k=SE/dx。
于是弹性势能为:d W p=k(dy)2/2= SE/dx·(dy)2/2= SE·dx(dy/dx)2/2;又因为υ=E/ρ.所以上式为:d W p =1/2ρυ2(dy/dx)2;而此时dy/dx =∂y/∂x =−2π/λ·2A sin 2π x/λ cos 2πνt;所以d W p =1/2 ρdV 16π2ν2A 2sin 22πxλ cos 22πνt ; (7) 所以体积元的总能量为dW=d W k + d W p =8 ρdV π2ν2A 2(cos 22πxλsin 22πνt +sin 22πxλcos 22πνt); (8)其能量密度为: W =dWdV =8ρπ2ν2A 2(cos 22πxλ sin 22πνt +sin 22πxλcos 22πνt); (9)三、驻波能量在波节波腹间的变化①相邻波节、波腹之间的能量为W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx (2k+1)λ/42k λ/4=8S ρ π2ν2A 2[sin 22πνt ·(12x +λ8πsin 4π x/λ)|2k λ/4(2k+1)λ/4+ cos 22πνt ·(12x −λ8πsin 4π x/λ)|2k λ/4(2k+1)λ/4]=8S ρ π2ν2A 2·12·λ4(cos 22πνt +sin 22πνt)=8S ρ π2ν2A 2·12·λ4= S ρ π2ν2A 2λ (10) ②任意不相邻的波节与波腹之间的能量W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λ cos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx 2k+1 λ4+N λ22k λ/4=(2N+1) S ρ π2ν2A 2λ 其中N 为波节、波腹间隔的个数N= 0,±1,±2,±3,⋯ (11)③对应位置之间的能量W= dW= 8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λ cos 22πνt)dV =S8ρ π2ν2A 2(cos 22πx λ sin 22πνt +sin 22πx λcos 22πνt)dx 2k+1 λ4+N λ2+∆x 2k λ/4+∆x=(2N +1) S ρ π2ν2A 2λ 其中N 为波节、波腹间隔的个数N= 0,±1,±2,±3,⋯ (12)由上述三点可以得出这样一个结论:驻波的能量在任一波节及波腹间都保持不变,且在相对应的位置之间的能量之和也保持不变。
