地震波动方程(教学知识)
波动方程备课教案

波动方程备课教案一、教学目标本节课的主要目标是使学生了解波动方程的基本概念和性质,掌握波动方程的求解方法,并能够应用波动方程解决相关问题。
二、教学重点1. 波动方程的基本概念和性质;2. 波动方程的求解方法。
三、教学难点波动方程的求解方法。
四、教学准备1. 教师准备:- 精心设计的教案;- 讲解波动方程的相关概念和性质所需的教学材料;- 准备好的演示实验器材。
2. 学生准备:- 预习相关概念和性质。
五、教学过程导入:- 引入波动的概念,介绍波动现象在日常生活中的应用,如声波传播、地震波等。
一、波动方程的概念和性质- 讲解波动方程的定义和一维波动方程的形式;- 探讨波动方程的基本性质,如叠加原理和传播速度。
二、波动方程的求解方法1. 分离变量法- 介绍分离变量法的基本思想;- 通过具体例子,详细说明分离变量法的步骤。
2. 特征线法- 介绍特征线法的基本思想;- 通过实例,说明如何运用特征线法解决波动方程。
3. 傅里叶变换法- 介绍傅里叶变换法的基本原理;- 讲解如何使用傅里叶变换法求解波动方程。
三、教学实践与讨论- 利用实验装置演示波动方程的性质,将理论知识与实践相结合;- 引导学生探讨和解决波动方程的相关问题。
四、巩固与拓展- 出示一些练习题,让学生应用所学的方法来解决; - 鼓励学生思考波动方程的更广泛应用。
六、课堂总结- 总结本堂课的重点内容;- 强调学生需要掌握的知识和技能。
七、作业布置- 布置相关的练习题,让学生巩固和拓展所学内容。
八、板书设计波动方程的概念和性质波动方程的定义:一维波动方程的形式:波动方程的基本性质:- 叠加原理- 传播速度波动方程的求解方法1. 分离变量法步骤:...2. 特征线法步骤:...3. 傅里叶变换法基本原理:求解步骤:...九、教学反思通过本堂课的教学,学生对波动方程的概念和性质有了更深入的了解,并能够运用多种方法求解波动方程。
教学过程中,注重理论与实践的结合,通过演示实验和问题讨论,增强了学生的学习兴趣和实际应用能力。
4地震波动力学

地震波的动力学特征既可以用随时间而变化 的波形来描写,也可以用其频谱特性来表述。前 者是地震波的时间域表征,后者则是其频率域表 征。由于它们具有单值对应性,因此在任何一个 域内讨论地震波都是等效的。
地震子波的另一个属性是它具有确定的起始 时间和有限的能量,因此经过很短的一段时间即 衰减,衰减时间的长短称为地震子波的延续时间 长度,以后将会讨论到,它决定了地震勘探的分 辨能力,而且可以很容易地证明:地震子波的延 续时间长度同它的频谱的频带宽度成反比。
t
定义为视速度 。由图可见,地震波沿射线传播的真速度
V
*
V s / t
s
,
所以
V
*
因 x
cos
V c o s
(1.1.62)
式 中 为 地 震 波 射 线 与 其 自 身 的 地 表 投 影 的 夹 角 (出 射 角 = 9 0 ° -入 射 角 )。式( 1 .1 .6 2 )表 示 了 视 速 度 与 真 速 度 之 间的关系,称为视速度定理,可以看出,视速度总是大 于 真 速 度 。当
图1.1.22 惠更斯原理示意图
2.费马原理
费马原理表明,地震波沿射线传播的旅行 时和沿其它任何路径传播的旅行时相比为最小, 亦波是沿旅行时间最小的路径传播(最小时间 原理)的。
在时间场内,将时间相同的值连起来,组成等 时面,等时面与射线成正交关系。
3.视速度定理 图中 A、B 为两个检波器,间距为 x ,地震波沿射线 1 到 达 A 点的时间为 ,沿射线 2 到在 B 点的时间为 t t , x / t
0
时 ,V
*
V
,即 波 沿 观 测 方 向 传 播 ,其 视 时 ,V
地震概论第三章地震波讲义资料
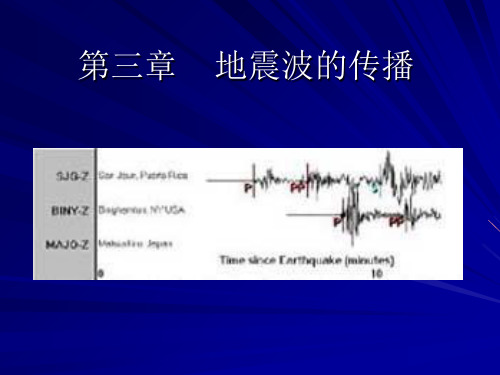
六、地震波与地球内部结构
体波之所以对地球内部结构比较敏感,是因为在地球 内部的不同部分,地震波传播速度不同 ,在不同部分的 分界面上发生的反射、折射和波型转换,既影响体波的 “行走时间”,又影 响体波的振幅和形状。
把面波的波长延伸到整个地球的尺度,我们还有一个 专用的名词:地球自由振荡。这时,地 球好像是一口铜 钟被大地震重重地敲击一下,余音缭绕,经久不绝。不同 形状、不同结构的 铜钟具有不同的音色;类似地,不同 形状、不同结构的星球也具有不同的自由振荡的形 式。 地震学家就像一位钢琴调音师那样,通过倾听地球 的“音乐”,辨认出地球内部的结构。
P波和S波的速度表达式
P波,速度Vp = V (K+ 3/4µ)/ρ 花岗岩: Vp = 5.5千米/秒; 水: Vp = 1. 5千米/秒 ρ为密度
S波,速度Vs=V µ/ρ 花岗岩: Vs =3.0 千米/秒; 水: Vs = 0 千米/秒
P波速度
花岗岩 水
5.5千米/秒 1.5千米/秒
S波速度 3.0千米/秒
复习
一、波动 波动方程 波速、波长、周期、波频率、初相位、简 谐波与复杂波
2、S波
S波:S波跑的比P波慢,它只可以在固体传 播。在S波传播时,质点的运动方向与S波 的传播方向互相垂直,介质中产生剪切应 力。由于流体不能承受剪切应力,因此S波 不能在液体和气体中传播。
P波和S波的速度由介质的密度和弹性常数 决定。
内部圈层
深度 km
地震波速度
纵波 横波
Vp
Vs
密度ρ g·cm-
3
压力 P
MPa
重力 g
m·s-2
温度t C
附注
0 5.6 3.4 2.6
第三章波动方程

拉普拉斯算子: 拉普拉斯算子: 1 ∂ 1 ∂ 1 ∂u ∂u ) + (sin α ∇ 2u = 2 ( r 2 r ∂r r ∂α ∂r r ⋅ sin α ∂α ∂u ∂ u ↓← = =0 ∂ α ∂β
2 1 ∂u ∂ 2 u 2 ∂u 2 ∂ u )= 2 + = 2 ( 2r +r 2 r ∂r r ∂r ∂r ∂r
13
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解 、
已知球面纵波传播波动方程如下: 已知球面纵波传播波动方程如下: ∂ 2ϕ − VP2 ∇ 2ϕ = 0 ∂t 2 此式是直角坐标系中的波动方程, 此式是直角坐标系中的波动方程,需转换到球 坐标系中, 坐标系中,即
为了定量地描述微观粒子的状态,量子力学中引入了 为了定量地描述微观粒子的状态, 波函数,并用ψ表示。一般来讲,波函数是空间和时间 波函数, 表示。一般来讲, 的函数,并且是复函数,即ψ=ψ(x,y,z,t)。 的函数,并且是复函数,
7
无限大、 3.1 无限大、均匀各向同性介质中的平面波
一、沿任意方向传播的平面波
如果使 t −
播的波,即向震源方向传播的波,称为聚会波。聚会波只存在于t 播的波,即向震源方向传播的波,称为聚会波。聚会波只存在于t为 负值的情况,这与实际不合,则该波是不存在的。 负值的情况,这与实际不合,则该波是不存在的。
16
因此,上式又可写为: 因此,上式又可写为:
ϕ=
ϕ
1 r ) = c1 ( t − r r VP
10
无限大、均匀各向同性介质中的波动方程的解有两组。 无限大、均匀各向同性介质中的波动方程的解有两组。 第一组解: 第一组解:当 V = V p = ( λ + 2 µ ) / ρ 时,
波动理论波动方程知识点总结

波动理论波动方程知识点总结波动方程是波动理论中的重要内容,研究波的传播和特性具有重要意义。
本文对波动方程的相关知识点进行总结,以帮助读者更好地理解和应用波动理论。
一、波动方程的基本概念波动方程是描述波的传播过程中波动量随时间和空间的变化关系的数学表达式。
一般形式为:∂²u/∂t² = v²∇²u其中,u表示波动量,t表示时间,v表示波速,∇²表示拉普拉斯算子。
二、波动方程的解法1. 分离变量法:将波动量u表示为时间和空间两个变量的乘积,将波动方程转化为两个偏微分方程,分别对时间和空间变量求解。
2. 化简为常微分方程:将波动方程应用于特定情境,通过适当的变换,将波动方程化简为常微分方程,再进行求解。
3. 利用傅里叶变换:将波动方程通过傅里叶变换或拉普拉斯变换转化为频域或复频域的代数方程,再进行求解。
三、波动方程的应用1. 声波传播:声波是由介质中的分子振动引起的机械波,通过波动方程可以描述声波在空气、水等介质中传播的特性,如声速、声强等。
2. 光波传播:光波是电磁波的一种,通过波动方程可以研究光的干涉、衍射、反射等现象,解释光的传播规律和光学器件的性质。
3. 地震波传播:地震波是地震过程中的弹性波,通过波动方程可以描述地震波在地球内部传播的规律,有助于地震监测和震害预测。
4. 电磁波传播:电磁波是由电场和磁场耦合产生的波动现象,在电磁学中应用波动方程可以研究电磁波在空间中传播的特性和应用于通信、雷达等领域。
5. 水波传播:水波是液体表面的波动现象,通过波动方程可以研究水波的传播和液面形态的变化,解释液体中的波浪、涌浪、潮汐等现象。
四、波动方程的性质和定解问题1. 唯一性:波动方程的解具有唯一性,即满足初值和边值问题的解是唯一的。
2. 叠加原理:波动方程具有线性叠加性质,一系统的波动解可以通过各个部分的波动解线性叠加而得到。
3. 边界条件:波动方程的求解需要给定适当的边界条件,例如固定端、自由端、吸收边界等,以确保解满足实际问题的物理要求。
地球物理勘探 1-5波动方程的解及地震波的特点解读

本章包括:
无限大、均匀各向同性介质中的平面波 无限大、均匀各向同性介质中的球面波 地震波的动力学特点 地震波的运动学特点
1
3 波动方程的解及地震波的特点
P波—波动方程 S波—波动方程 SV波 SH波
无限大、均匀各向同 性介质中的平面波
2
3 波动方程的解及地震波的特点
kx
)
将上式代入波的Navier方程
2
2U U ( ) grad F 2 t
整理简化,并令体力F=0,可得
2 A1 V 2 A1 0
A2 V 2 A2 0 A3 V 2 A3 0
10
无限大、均匀各向同性介质中的波动方程的解有两组。 第一组解:当 V V p ( 2 ) / 时,
9
二、沿X轴方向传播的平面波(即
k1 1 , k 2 0 , k 3 0 2i U A ex p x Vt d 2i x Vt u A1 ex p 2i x Vt v A2 ex p 2i x Vt w A3 ex p
4
3 波动方程的解及地震波的特点
地震波的运动特点 惠更斯-夫列涅尔原理 射线积分理论-克希霍夫积分
费马原理和波的射线 时间场和视速度定理
5
3 波动方程的解及地震波的特点
在均匀、各向同性、理想弹性介质中的弹性波方程为: 2U 2 U ( ) grad F 2 t 两边取分别散度和旋度,并且令
其位移方向与波的传播方向垂直,所以称为平面横波,也称为剪 切波,通常简称为S波。S波有两个质点振动方向:沿Z轴振动的S波分 量为垂直偏振剪切波,称为SV波,沿Y轴振动的S波为水平偏振剪切波, 11 称为SH波。
地球物理勘探 1-5波动方程的解及地震波的特点
r
dS
1 V
2 p
1( t )
再将特解带入左端项,则 有 :
19
lim
r 0 S
' C1 C1 1 r ' dS lim 2 C1 dS lim 2 ( C 1 r0 r0 r rV p Vp r S r
r 0 W r 0 S
将左端一、二项带回可得 : lim grad ndS
r 0 S
1 V
2 r 0 p
lim ( t )dW
W
1 V
2 p
1( t ) r
因为是纵波,只存在r方向的分量,即grad lim
r 0 S
, 则上式变为:
u0 v A2 exp[ i V i V ( x V s t )] ( x V s t )]
w A3 exp[
Байду номын сангаас
其位移方向与波的传播方向垂直,所以称为平面横波,也称为剪 切波,通常简称为S波。S波有两个质点振动方向:沿Z轴振动的S波分 量为垂直偏振剪切波,称为SV波,沿Y轴振动的S波为水平偏振剪切波, 11 称为SH波。
负值的情况,这与实际不合,则该波是不存在的。
16
因此,上式又可写为:
r
1
1 r
c1 ( t
r VP
)
该式是齐次方程的解,只反映了波的传播特点。当力位 函数不为零时,需求非齐次方程的解,即达朗贝尔解。
2 t 2 V p2 2 2 t 2 V p2 divgrad ( t )
0 ( t ) ( t ) 0
t0 0 t t t t
第三章波动方程培训课件
2 U ( )gr a F d 2 tU 2
两边分别取散度和旋度,并且令
V P 2(2)/
VS2 /
则可得纵波方程和横波方程
2t2 VP22
2t2 VS2
5
3 波动方程的解及地震波的特点
波动方程反映了物体波动过程的普遍规律。 波动方程的求解通常是和定解问题联系起来 考虑。波动方程的解就是波函数。
12
3.2 无限大、均匀各向同性介质中的球面波
2、坐标变换和球坐标下球面纵波的传播方程解
已知球面纵波传播波动方程如下:
2t2 VP220
此式是直角坐标系中的波动方程,需转换到球 坐标系中,即
x rsic nos y rs in s in(0 r ,0 ,0 2 ) z rcos
前面是平行的。
▪ k1,k2,k3 是平面的法线方向数。有 k12k2 2k3 21
▪ 取负号时,表示随时间t的增加,波沿k方向前进,即延 迟一个时间。
▪ 取正号时,表示随时间t的增加,波沿-k方向前进,即 提前一个时间
▪ 当K是任意矢量的,则平面法向量为任意方向的。即表 示沿任意方向传播的平面简谐波。
8
二、沿X轴方向传播的平面波(即
kx
)
U Aex 2 p ik1xk2yk3zV td AieA co sisin
k1 1 ,k 2
U A exp
u A 1 exp
0 ,k 3 0
2i
x
Vt
2i
x
Vt
d
v
A 2 exp
2i
x
Vt
w
A 3 exp
2i
u rer u rr r
地震勘探中波动方程的推导过程
地震勘探中波动方程的推导过程首先呢,咱们得从最基本的物理概念开始。
在地震勘探里,波的传播肯定是和介质的一些性质有关系的。
这里面就涉及到像弹性模量啊这些概念。
我知道这些听起来就有点头疼,但是没办法这就是基础嘛。
咱们得先有个大概的认识,就是波在不同的介质里传播速度是不一样的,为啥呢?就是因为介质的这些特性在捣鬼呢!然后呢,我们就开始建立一些简单的数学关系。
这里我觉得大家可以先想象一下一个很简单的情况,比如说一个质点在介质里受到力的作用开始振动。
这个振动就会引起周围质点跟着动起来,这就形成了波的传播啦。
不过呢,要把这个过程用数学式子表示出来可不容易哦。
我们通常会根据牛顿第二定律来建立方程。
这时候你可能会问,为啥是牛顿第二定律呢?哈这是因为波的传播本质上也是一种力学现象呀!根据这个定律,我们就可以把质点的受力和它的加速度联系起来。
这里我得说一句,这一步真的很关键哦!要是这一步没搞对,后面可就全乱套了。
接下来,我们还要考虑介质的弹性性质。
这部分我觉得可以更灵活一点去理解。
就是说不同的介质弹性不一样,那波在里面传播的方式和速度就会有差别。
咱们要把这个差别在方程里体现出来。
这时候可能就会用到一些关于弹性模量的知识。
当然啦,这些知识如果不是特别清楚也没关系,咱们只要知道大概怎么回事就行。
在推导的过程中,还会有一些假设和简化。
比如说,我们可能会假设介质是均匀的,这虽然和实际情况有点出入,但是这样做会让整个推导过程简单很多呢。
我刚开始学的时候也觉得这有点不合理,不过后来发现这是一种很有效的方法。
就像我们有时候为了算出一个大概的结果,会先忽略一些小的影响因素一样。
整个波动方程的推导过程就是这样啦。
刚开始可能会觉得麻烦,但习惯了就好了。
希望大家通过我的讲解能对地震勘探中的波动方程推导有个初步的了解!如果有什么不懂的地方,欢迎随时再研究研究或者找更多的资料看看呀。
2 地震学基础-2震级和烈度,地震波与波动方程
2.1 地球构造与板块运动
2.2 板内构造活动与板内地震
2.3 震源机制与地震类型
2.4 中国地震的背景与特点
2.5 地震灾害的破坏作用
2.6 地震震级与地震烈度
2.7 地震波与波动方程
§2.6
地震震级与地震烈度
2.6.1 地震震级 2.6.2 地震烈度
2.6.1 地震震级
骑自行车的人会摔倒,处不稳状 态的人会摔出几尺远,有抛起感
严重破坏——墙体龟裂, 0.51~0.70 局部倒塌,修复困难
地方出现裂缝、基岩上可能出现裂缝、 500 (354~707) 滑坡、坍方常见,砖烟囱出现倒塌
山崩和地震断裂出现,基岩上的拱桥 破坏,大多数烟囱从根部破坏 地震断裂延续很长,山崩常见,基岩 上的拱桥 地面剧烈变化,山河改观
现为扭转、局部破裂和倒塌;有的表现为结构本身的震动破坏、
物体的反应 桌上、架上摆放的小用具、书籍和挂饰等物品在地震时会 移动、坠落或翻到等等;
自然现象的变化
强烈地震时,自然环境有时也会发生变化,如山崩、地裂、 冒水、喷砂、地面变形、滑坡、陷落等,在海中的地震还易引 发海啸。
(3)地震烈度表
调整不同结构的烈度尺度,都不可能使不同尺子量出
的烈度值相统一。
现有烈度评定的精度是不高的,在极端情况下相差可达4
度之多,一般来说都会有1度之差的精度。 国际上的惯例是烈度只能为整数,而不出现小数,如8.5度, 7度半等;但在不少报告中,如我国和苏联,有时也出现这种 描述。
(6) 宏观烈度的地质效应
人们在感觉到一个上下颠簸的P波震动之后,会有一个短暂的停顿,然后会是 一个更加猛烈的水平摇动,持续的时间也相对长一些,大多数房屋在上下颠簸 变“酥”之后,便在水平摇晃中进一步毁坏倒塌,这就是地震S波的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 地震波动方程
现在,我们用前一章提出的应力和应变理论来建立和解在均匀全空间里弹性波传播的地震波动方程。
这章涉及矢量运算和复数,附录2对一些数学问题进行了复习。
3.1 运动方程(Equation of Motion )
前一章考虑了在静力平衡和不随时间变化情况下的应力、应变和位移场。
然而,因为地震波动是速度和加速度随时间变化的现象,因此,我们必须考虑动力学效应,为此,我们把牛顿定律(ma F =)用于连续介质。
3.1.1一维空间之振动方程式
质点面上由于应力差的存在而使质点产生振动。
如图1-3所示,考虑一薄棒向x 轴延伸,其位移量为u :
Fig3-1
则其作用力为“应力”X “其所在的质点面积”,所以其两边的作用力差为
()()()dxds x
x dx x ds ∂∂=
-+σ
σσ 惯量﹙inertia ﹚为
22t
u dxds ∂∂ρ
所以得出
x
t u ∂∂=∂∂σρ22 ……………………………………………………... (3-1)
其中ρ为密度﹙density ﹚,σ为应力﹙stress ﹚=x
u
E ∂∂。
3-1式表示,物体因介质中的应力梯度﹙stress gradient ﹚而得到加速度。
如果ρ与E
为常数,则3-1式可写为
2
22221t u
c x u ∂∂=∂∂ …………………………………………………… (3-2)
其中ρ
E
c =
运用分离变量法求解(3-2)式,设u=F(x)T(t),(3-2)式可以变为
T X c T X ''=
''2
1
设22ω-='
'=''T
T X X c 则可得:c
x i
t
i e
X e
T ωω±±∝∝,
考虑欧拉公式:)sin()cos(),sin()cos(t i t e t i t e
t i t
i ωωωωωω-=+=-
()
()
()
()
ct x c
i
ct x c
i
ct x c
i
ct x c
i
De
Ce
Be
Ae
u ---+-++++=ωωωω (3-3)
其中A,B,C,D 为根据初始条件和边界条件确定的常数。
考虑到ω可正可负,方程式的解具有()()ct x g ct x f u ++-=的形式,其中f 及g 为波的函数,以c 的波行速度向+x 与-x 方向传递。
我们可以采用如下程序模拟地震波的传播。
平面波在均匀介质里沿x 方向传播,
剪切波的齐次微分方程可表达为:
2
2
222x u t u ∂∂=∂∂β 这里u 是位移。
对100公里的波长和假定秒公里/4=β的情况,我们写出用有限差分法解这方程的计算机程序。
用长度间距公里1=dx ,时间间距1.0=dt 秒。
假
定在u (50公里)震源时间函数的形式为:
()()5sin 250t t u π= 0<t <5秒
用u (0公里)的应力自由边界条件和u (100公里)的固定边界条件。
用有限差分图解来近似二次导数:
2
1
1222dx
u u u x u i i i -++-=∂∂ 以4秒的间隔画出1-33秒的图。
M = moviein(101);
dx=1;dt=0.1;tlen=3;beta=4; %初始化变量,tlen为震源持续时间,beta为波传播的速度
u1=zeros(101,1);u2=u1;u3=u1;
%u1为前一个时刻的各点的位移,u2为当前时刻的位移,u3为下一个时刻的位移值,开始均假定为零
t=0;
jj=0;
while (t<=33) %模拟的最长时间为33秒
for ii=2:100
rhs=beta^2*(u2(ii+1)-2*u2(ii)+u2(ii-1))/dx^2; %方程的解
u3(ii)=dt^2*rhs+2*u2(ii)-u1(ii); %对时间求导数
end
%左边为自由边界条件,右边为固定边界条件
u3(1)=u3(2); %左边为自由边界条件
u3(101)=0.0; %右边为固定边界条件
%左右两边为自由边界条件
% u3(1)=u3(2); %左边为自由边界条件
% u3(101)=u3(100); %右边为自由边界条件
%左右两边为固定边界条件
% u3(1)=0.0; %左边为固定边界条件
% u3(101)=0.0; %右边为固定边界条件
if(t<=tlen)
u3(51)=(sin(pi*t/tlen)).^2; %地震震源时间函数
end
for ii=1:101
u1(ii)=u2(ii);u2(ii)=u3(ii); %时刻的更新
end
plot(u2); %绘制目前的波形图
ylim([-1.2 1.2]);
M(:,jj+1) = getframe; %获得当前的图像
t=t+dt; %时间延长
end
movie(M) %演示波形传播
3.1.2三维空间之振动方程式
推导三维空间之振动方程式的过程,与上节中所采用的一维空间讨论方式类似,如图3-2所表示,先探讨在x 方向之位移量u :
Fig3-2
在y-z 面上的作用力差为:()()[]dydz x dx x xx xx σσ-+ 在x-z 面上的作用力差为:()()[]
dxdz y dy y yx yx σσ-+ 在x-y 面上的作用力差为:()()[]dxdy z dz z zx zx σσ-+ 惯量为:
22t
u
dxdydz ∂∂ρ
得出
x zx yx xx f z
y x t u +∂∂+∂∂+∂∂=∂∂σσσρ22 ………………………………….. ﹙3-4﹚
其中σxx 、σyx 及σzx 分別为stress tensor 在xx ﹙x 面方向、x 力方向﹚,yx ﹙y 面方向、x 力方向﹚及zx ﹙z 面方向、x 力方向﹚方向的分量。
注意,在本讲义中有关stress tensor 的两个下标﹙indexes ﹚之定义,依序为面的方向与力的方向。
将σxx 、σyx 及σzx 与其对应的应变之关系代入3-4式可推导得出三维空间之振动方程式如下:
()x f u x
t u +∇+∂∂+=∂∂222μθ
μλρ …………………………………. ﹙3-5a ﹚
其中λ及μ为常数,而2
∇为Laplacian operator ,代表22
2
222z
y x ∂∂+∂∂+∂∂。
以相同的方法,可以得出在y 及z 方向的振动方程式,若其位移量分別为v 与w ,。
