东华大学物理振动波动部分习2题解答

合集下载

大学物理《普通物理学简明教程》振动、波动和光学习题精解概要

Aω
A1 φ0A2
π/4x
O
图10-17
解(1)如图10-17,两矢量间夹角为 ,所以合振动振幅
合振动初相
(2)合振动A再与第三个振动合成.根据振动叠加条件, 时合振动有极大值,即
(k=0,1,2…)
当时合振动有极小值,即
(k=0,1,2…)
10-19当两个同方向的简谐振动合成为一个振动时，其振动表式为：
3应用同一直线上两个简谐振动的合成规律时，要特别注意它们的相位差和合成的振幅的关系；同向时，合振幅最大，反向时，合振幅最小。
10.4思考题选答
1弹簧振子的无阻尼自由振动是简谐振动，同一弹簧振子在简谐驱动力持续作用下的稳态受迫振动也是简谐振动，这两种简谐运动有什么区别？
答：弹簧振子的无阻尼自由振动是在“无阻尼”，包括没有空气等外界施加的阻力和弹簧内部的塑性因素引起的阻力的情况下发生的，是一种理想情况。由于外界不能输入能量，所以弹簧振子的机械能守恒。这时振动的频率由弹簧振子自身的因素（）决定。
解：（1）根据振动方程可知：振幅，角率，初相，周期 =1秒；（2）分析质点运动情况：从t=0时刻起，；向轴负方向运动，直到 ,即为止；质点改变运动方向，向轴正方向运动到位置P点。最短时间间隔为：
(3) 处的时刻。
第11章机械波基础
答：从质量的意义上来说，质量表示物体的惯性，弹簧本身的质量计入时，系统的质量增大，更不易改变运动状态。对不断地周期性改变运动状态的弹簧振
子的简谐运动来说，其进程一定要变慢。这就是说，考虑弹簧的质量时，弹簧振子的振动周期将变大。
10.5习题解答
10-1质量为10g的小球与轻弹簧组成的系统，按的规律而振动，式中t以s为单位,试求:
式中t以s为单位。求各分振动的角频率和合振动的拍的周期。

大学物理[下册]波动习题课

将沿oy轴的负方向运动. 0 / 3
y
(
x,
t)
Acos[(t x ) u
0.1cos[500(t
0 ] x / 5000)

/
3]m
o
A/2 y
(2)在距原点7.5m处质点的运动方程.
y 0.1cos[500t 13 /12]m
t=0时该点的振动速度
15-5 波源作简谐运动,周期为0.02s,若该振动以100m.s-1的速度沿直线传播,设t=0时,波源处的质点经平衡位置向正方向运动,求:(1)距波源15.0m和5.0m处质点的运动方程和初相;(2)距波源分别为16.0m和 17.0m的两质点间的相位差.
解: (1)由题意知:T=0.02s,u=100m.s-1,可得
解: (1)已知波动方程为 y 0.20cos2.50t xm
与一般表达式 y Acos(t x / u) 0
比较,得 A 0.20m,u 2.5m s1, 0 0 / 2 1.25HZ u / 2.0m
(2)绳上的质点振动速度
15-9波动的能量与那些物理量有关?比较波动的能量与简谐运动的能量.
从波的能量密度公式可知 w A22 sin 2 t x / u
波动的能量不但与体积有关,且与,A,,u.
波动的能量与简谐运动的能量有显著的不同,在简谐运动系统中,动能和势能有/2的相位差,系统的机械能是守恒的.在波动中,动能和势能的变化是同相位的,对任何体积元来说,系统的机械能是不守恒的.
15-11波的干涉的产生条件是什么?若两波源所发出的波的振动方向相同,频率不同,则它们在空间叠加时,加强和减弱是否稳定?

大学物理《普通物理学简明教程》振动、波动和光学习题精解汇总

振动、波动和光学习题精解第10章机械振动10.1 要求1 了解简谐振动的能量；2 理解旋转矢量法、同方向和同频率简谐振动的合成的规律；3 掌握简谐振动的各物理量（ϕω,,A ）及各量间的关系、简谐振动的基本特征、建立简谐振动的微分方程、根据初始条件写出一维简谐振动方程、同方向和同频率简谐振动的合成。

10.2 内容摘要1 简谐振动运动学方程)cos(ϕω+=t A x特征量：振幅A ：决定振动的范围和能量；角频率ω：决定振动重复的快慢，频率ωπνπων21,2===T 周期；初相ϕ：决定起始的时刻的位置和速度。

2 振动的位相（ϕω+t ）简谐振动在t 时刻的位相；3 简谐振动动力学方程0222=+x dtx d ω 弹性力：kx F -=，Km T m K πω2,==； 4、简谐振动的能量 2222121)(21kA kx dt dx m E E E k p =+=+= 5、受迫振动：是在驱动力作用下的振动。

稳态的受迫振动的频率等于驱动力的频率。

当驱动力的频率等于系统的频率时，发生共振现象，振幅最大。

6、同方向、同频率简谐振动的合成)cos(111ϕω+=t A x ， )cos(222ϕω+=t A x)cos(21ϕω+=+=t A x x x其中， A =)cos(212212221ϕϕ-++A A A A ， 22112211cos cos sin sin arctan ϕϕϕϕϕA A A A ++= 相位差12ϕϕϕ-=∆起了相当重要的作用（1）两个谐振的频率相同时，合运动的振幅决定于它们的相位差：同向时（ 3,2,1,0,2=±=∆k k πϕ），合振动最大，为两者振幅之和；反向时合振动最小[ 3,2,1,0,)12(=+±=∆k k πφ]，为两者振幅之差；（2）两个谐振的频率不相同时，合运动会产生拍现象，拍的频率为两个谐振的频率之差。

大学物理知识点总结(振动及波动)

比较y0 和 y 。若y y0，则vo 0；若 y y0，则v0 0。
由图知：
对于1：
y

y0，则v 0
0。思考?
若传播方向相反
对于2 ： y y0，则 vo 0 。
时振动方向如何？
[例5]一列平面简谐波某时刻的波动曲线如图。
求：1）该波线上点A及B 处对应质元的振动相位。
E

Ek

Ep

1 2
kA2
动能势能相互转化
简谐振动的描述
一、描述简谐振动的物理量
① 振幅A：
A
x02

v
2 0
2
② 角频率： k
2
m
T
③ 相位( t + ) 和初相：
tg v0 x0
的确定！！
④相位差： (2t 2 ) (1t 1)
or 5
6
6

1 2
A且y0
v0 As
y0 0
0
in

。
1 5 2
6
A
③已知初位置的大小、正负以及初速度的大小。
[例3]已知某质点振动的初位置 y0 0.3A且v0 0.95A。由tg v0 的可能值. y0
由旋转矢量法知：
0 )
0

4
y Acos(500 t 2x )
A

4
o
y
200 4
2） x 100m y Acos(500 t 5 )
4
vy

dy dt

500A s in(500

大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)

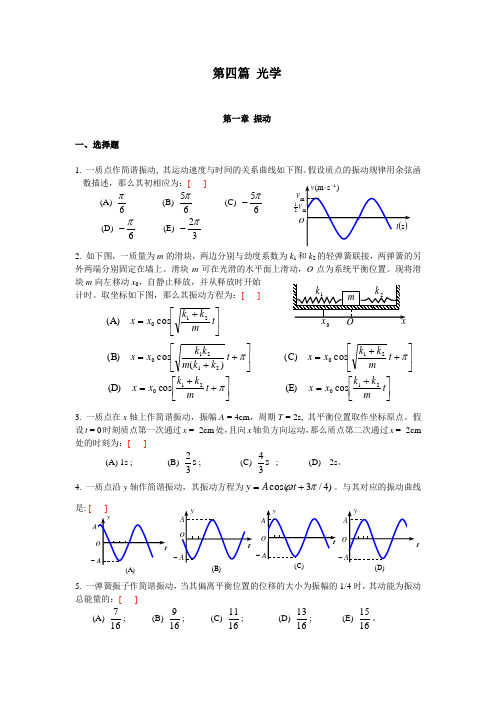
第四篇光学第一章振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。

假设质点的振动规律用余弦函数描述，那么其初相应为：[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图，一质量为m 的滑块，两边分别与劲度系数为k 1和k 2的轻弹簧联接，两弹簧的另外两端分别固定在墙上。

滑块m 可在光滑的水平面上滑动，O 点为系统平衡位置。

现将滑块m 向左移动x0，自静止释放，并从释放时开始计时。

取坐标如下图，那么其振动方程为：[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动，振幅A = 4cm ，周期T = 2s, 其平衡位置取作坐标原点。

假设t = 0时刻质点第一次通过x = -2cm 处，且向x 轴负方向运动，那么质点第二次通过x = -2cm 处的时刻为：[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。

4. 一质点沿y 轴作简谐振动，其振动方程为)4/3cos(πω+=t A y 。

与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的：[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。

(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线，假设这两个简谐振动可叠加，那么合成的余弦振动的初相为： [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ，0=t 时的初位移为0.04m, s -1，那么振幅A = ，初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动，经过0.5s 后，第二个振子才从正方向的端点开始运动，那么这两振动的相位差为。

大学物理振动与波题库及答案

大学物理振动与波1 一、选择题：（每题3分）1、把单摆摆球从平衡位置向位移正方向拉开，把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度使摆线与竖直方向成一微小角度q ，然后由静止放手任其振动，由静止放手任其振动，从放手时开始计时．从放手时开始计时．从放手时开始计时．若用余弦函数表示其运动方程，若用余弦函数表示其运动方程，若用余弦函数表示其运动方程，则该单摆振动的则该单摆振动的初相为(A) p ．(B) p /2．(C) 0 ．(D) q ．［2、两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x 1= A cos(w t + a )．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为(A) )π21cos(2++=a w t A x ．(B) )π21cos(2-+=a w t A x ．(C) )π23cos(2-+=a w t A x ．(D) )cos(2p ++=a w tA x ．［］3、一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T 1和T 2．将它们拿到月球上去，相应的周期分别为1T ¢和2T ¢．则有(A) 11T T >¢且22T T >¢．(B) 11T T <¢且22T T <¢．(C) 11T T =¢且22T T =¢．(D) 11T T =¢且22T T >¢．［］4、一弹簧振子，重物的质量为m ，弹簧的劲度系数为k ，该振子作振幅为A 的简谐振动．当重物通过平衡位置且向规定的正方向运动时，开始计时．则其振动方程为：(A) )21/(cos p +=t m k A x (B) )21/cos(p -=t m k A x (C) )π21/(cos +=t k m A x (D) )21/cos(p -=t k m A x (E) tm /k A x cos =［］5、一物体作简谐振动，振动方程为)41cos(p +=t A x w ．在t = T /4（T 为周期）时刻，物体的加速度为(A) 2221w A -．(B) 2221w A ．(C) 2321w A -．(D) 2321w A ．［］6、一质点作简谐振动，振动方程为)cos(f w +=t A x ，当时间t = T /2（T 为周期）时，质点的速度为(A) f w sin A -．(B) f w sin A ．(C) f w cos A -．(D) f w cos A ．［］7、一质点作简谐振动，周期为T ．当它由平衡位置向x 轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为(A) T /12．(B) T /8．(C) T /6．(D) T /4．［］8、两个同周期简谐振动曲线如图所示．x 1的相位比x 2的相位的相位(A) 落后p /2． (B) 超前p/2． (C) 落后p ． (D) 超前p ．［］9、一质点作简谐振动，已知振动频率为f ，则振动动能的变化频率是，则振动动能的变化频率是(A) 4f . (B) 2 f . . (C) f . (D) 2/f . (E) f /4 ［］ 10、一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的、一弹簧振子作简谐振动，当位移为振幅的一半时，其动能为总能量的 (A) 1/4. (B) 1/2. (C) 2/1. (D) 3/4. (E) 2/3. ［］11、一弹簧振子作简谐振动，当其偏离平衡位置的位移的大小为振幅的1/4时，其动能为振动总能量的为振动总能量的(A) 7/16. (B) 9/16. (C) 11/16. (D) 13/16. (E) 15/16. ［］12 一质点作简谐振动，已知振动周期为T ，则其振动动能变化的周期是，则其振动动能变化的周期是 (A) T /4． (B) 2/T ． (C) T ．(D) 2 T ． (E) 4T ．［］13、当质点以频率n 作简谐振动时，它的动能的变化频率为作简谐振动时，它的动能的变化频率为(A) 4 n ． (B) 2 n ． (C) n ． (D) n 21．［］14、图中所画的是两个简谐振动的振动曲线．图中所画的是两个简谐振动的振动曲线．若这两个简谐振动可叠加，若这两个简谐振动可叠加，若这两个简谐振动可叠加，则合成的余弦则合成的余弦振动的初相为振动的初相为(A) p 23． (B) p ．(C) p 21． (D) 0．［］15、若一平面简谐波的表达式为、若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则为正值常量，则 (A) 波速为C ． (B) 周期为1/B ．(C) 波长为波长为 2p /C ． (D) 角频率为2p /B ．［］16、下列函数f (x , t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量．其中哪个函数表示沿x 轴负向传播的行波？轴负向传播的行波？(A) )cos(),(bt ax A t x f +=． (B) )cos(),(bt ax A t x f -=．(C) bt ax A t x f cos cos ),(×=． (D) bt ax A t x f sin sin ),(×=．［］17、频率为、频率为 100 100 Hz Hz ，传播速度为300 300 m/s m/s 的平面简谐波，波线上距离小于波长的两点振动的相位差为p 31，则此两点相距，则此两点相距(A) 2.86 m ． (B) 2.19 m ．xtO x 1 x 2 xtO A/2 -Ax 1 x 2(C) 0.5 m ． (D) 0.25 m ．［］18、已知一平面简谐波的表达式为、已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则，则 (A) 波的频率为a ． (B) 波的传播速度为波的传播速度为 b/a ．(C) 波长为波长为 p / b ． (D) 波的周期为2p / a ．［］19、一平面简谐波的表达式为、一平面简谐波的表达式为 )3cos(1.0p +p -p =x t y (SI) ，t = = 00时的波形曲线如图所示，则如图所示，则 (A) O 点的振幅为点的振幅为--0.1 m． (B) 波长为3 m ． (C) a 、b 两点间相位差为p 21 ．(D) 波速为9 m/s ．［］20、机械波的表达式为y = 0.03cos6p (t + 0.01x ) (SI) ，则，则 (A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．轴正向传播．［］21、图为沿x 轴负方向传播的平面简谐波在t = = 00时刻的波形．若波的表达式以余弦函数表示，则O 点处质点振动的初相为点处质点振动的初相为(A) 0． (B) p 21．(C) p ． (D) p 23．［］22、一横波沿x 轴负方向传播，若t 时刻波形曲线如图所示，则在t + T /4时刻x 轴上的1、2、3三点的振动位移分别是三点的振动位移分别是 (A) A ，0，-A. (B) -A ，0，A. (C) 0，A ，0. (D) 0，-A ，0. ［］23一平面简谐波表达式为一平面简谐波表达式为 )2(sin 05.0x t y -p -= (SI)，则该波的频率则该波的频率 n (Hz)，波速u (m/s)及波线上各点振动的振幅及波线上各点振动的振幅 A (m)依次为依次为(A) 21，21，－0.05． (B) 21，1，－0.05．(C) 21，21，0.05． (D) 2，2，0.05．［］24、在下面几种说法中，正确的说法是：、在下面几种说法中，正确的说法是： (A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的．波源不动时，波源的振动周期与波动的周期在数值上是不同的． (B) 波源振动的速度与波速相同．波源振动的速度与波速相同．(C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后(按差值不大于p 计)．(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前．(按差值不大于p 计) ［］25、在简谐波传播过程中，沿传播方向相距为l 21（l 为波长）的两点的振动速度必定为波长）的两点的振动速度必定x (m ) O -0.1 0.1 ua by (m ) xyOuxyuA -A 123O(A) 大小相同，而方向相反．大小相同，而方向相反． (B) 大小和方向均相同．大小和方向均相同．(C) 大小不同，方向相同．大小不同，方向相同． (D) 大小不同，而方向相反．［］26、一平面简谐波沿x 轴负方向传播．已知 x = x 0处质点的振动方程为)cos(0f w +=t A y ．若波速为u ，则此波的表达式为，则此波的表达式为 (A) }]/)([cos{00f w +--=u x x t A y ． (B) }]/)([cos{00f w +--=u x x t A y ．(C) }]/)[(cos{00f w +--=u x x t A y ．(D) }]/)[(cos{00f w +-+=u x x t A y ．［］27、一平面简谐波，其振幅为A ，频率为n ．波沿x 轴正方向传播．设t = t 0时刻波形如图所示．则x = 0处质点的振动方程为处质点的振动方程为(A) ]21)(2cos[0p ++p =t t A y n ． (B) ]21)(2cos[0p +-p =t t A y n ．(C) ]21)(2cos[0p --p =t t A y n ．(D) ])(2cos[0p +-p =t t A y n ．［］28、一平面简谐波的表达式为、一平面简谐波的表达式为 )/(2c o s l n x t A y -p =．在t = 1 /n 时刻，x 1 = 3l /4与x 2 = l /4二点处质元速度之比是二点处质元速度之比是(A) -1． (B) 31． (C) 1． (D) 3 ［］29、在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4，则两列波的振幅之比是(A) A 1 / A 2 = 16． (B) A 1 / A 2 = 4． (C) A 1 / A 2 = 2． (D) A 1 / A 2 = 1 /4．［］30、如图所示，两列波长为l 的相干波在P 点相遇．波在S 1点振动的初相是f 1，S 1到P 点的距离是r 1；波在S 2点的初相是f 2，S 2到P 点的距离是r 2，以k 代表零或正、负整数，则P 点是干涉极大的条件为：点是干涉极大的条件为：(A) l k r r =-12． (B) p =-k 212f f ． (C) p =-p +-k r r 2/)(21212l f f ．(D) p =-p +-k r r 2/)(22112l f f ．［］31、沿着相反方向传播的两列相干波，其表达式为、沿着相反方向传播的两列相干波，其表达式为)/(2c o s 1l n x t A y -p = 和 )/(2c o s 2l n x t A y +p =．叠加后形成的驻波中，波节的位置坐标为叠加后形成的驻波中，波节的位置坐标为(A) l k x ±=． (B) l k x 21±=．(C) l )12(21+±=k x ． (D) 4/)12(l +±=k x ．xyt =t 0uOS 1S 2r 1r 2P其中的k = 0，1，2，3, …．…．［］32、有两列沿相反方向传播的相干波，其表达式为、有两列沿相反方向传播的相干波，其表达式为)/(2c o s 1l n x t A y -p = 和 )/(2c o s 2l n x t A y +p =．叠加后形成驻波，其波腹位置的坐标为：叠加后形成驻波，其波腹位置的坐标为：(A) x =±k l ． (B) l )12(21+±=k x ． (C) l kx 21±=． (D) 4/)12(l +±=k x ．其中的k = 0，1，2，3, …．…． [ ] 33某时刻驻波波形曲线如图所示，则a 、b 两点振动的相位差是的相位差是(A) 0 (B) p 21(C) p ． (D) 5p /4．［］34、沿着相反方向传播的两列相干波，其表达式为、沿着相反方向传播的两列相干波，其表达式为)/(2c o s 1l n x t A y -p = 和 )/(2c o s 2l n x t A y +p =．在叠加后形成的驻波中，各处简谐振动的振幅是在叠加后形成的驻波中，各处简谐振动的振幅是 (A) A ． (B) 2A ．(C) )/2cos(2l x A p ． (D) |)/2cos(2|l x A p ．［］ 35、在波长为l 的驻波中，两个相邻波腹之间的距离为的驻波中，两个相邻波腹之间的距离为 (A) l /4． (B) l /2．(C) 3l /4． (D) l ．［］36、在波长为l 的驻波中两个相邻波节之间的距离为的驻波中两个相邻波节之间的距离为 (A) l ． (B) 3l /4．(C) l /2． (D) l /4．［］37在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式是 )/(2c o s 0l n x t E E z -p =，则磁场强度波的表达式是：，则磁场强度波的表达式是： (A) )/(2cos /000l n m e x t E H y -p =． (B) )/(2cos /000l n m e x t E H z -p =．(C) )/(2cos /000l n m e x t E H y -p -=．(D) )/(2cos /000l n m e x t E H y +p -=．［］38、在真空中沿着z 轴负方向传播的平面电磁波，其磁场强度波的表达式为)/(cos 0c z t H H x +-=w ，则电场强度波的表达式为：，则电场强度波的表达式为： (A) )/(cos /000c z t H E y +=w e m ． (B) )/(cos /000c z t H E x +=w e m ．(C) )/(cos /000c z t H E y +-=w e m ．xyO 1l /2Aa bl -A(D) )/(cos /000c z t H E y --=w e m ．［］39、电磁波的电场强度E 、磁场强度、磁场强度 H 和传播速度和传播速度 u的关系是：的关系是： (A) 三者互相垂直，而E 和H 位相相差p 21．(B) 三者互相垂直，而且E 、H 、 u构成右旋直角坐标系．构成右旋直角坐标系． (C) 三者中E 和H 是同方向的，但都与是同方向的，但都与u垂直．垂直． (D) 三者中E 和H 可以是任意方向的，但都必须与可以是任意方向的，但都必须与u垂直．垂直．［］40、电磁波在自由空间传播时，电场强度E 和磁场强度H(A) 在垂直于传播方向的同一条直线上．在垂直于传播方向的同一条直线上． (B) 朝互相垂直的两个方向传播．朝互相垂直的两个方向传播． (C) 互相垂直，且都垂直于传播方向．互相垂直，且都垂直于传播方向．(D) 有相位差p 21．［］二、填空题：（每题4分）分）41、一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若t = 0时，时，(1) 振子在负的最大位移处，则初相为______________________； (2) 振子在平衡位置向正方向运动，则初相为________________；(3) 振子在位移为A /2处，且向负方向运动，则初相为______．42、三个简谐振动方程分别为 )21c o s (1p +=t A x w ，)67cos(2p +=t A x w 和)611cos(3p +=t A x w 画出它们的旋转矢量图，并在同一坐标上画出它们的振动曲线．画出它们的旋转矢量图，并在同一坐标上画出它们的振动曲线．43、一物体作余弦振动，振幅为15³10-2 m ，角频率为6p s -1，初相为0.5 p ，则，则振动方程为x = ________________________(SI)．44、一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点．已知周期为T ，振幅为A ．(1) 若t = 0时质点过x = 0处且朝x 轴正方向运动，则振动方程为轴正方向运动，则振动方程为 x =_____________________________．(2) 若t = 0时质点处于A x 21=处且向x 轴负方向运动，则振动方程为轴负方向运动，则振动方程为x =_____________________________．45、一弹簧振子，弹簧的劲度系数为k ，重物的质量为m ，则此系统的固有振动，则此系统的固有振动周期为______________________．46、在两个相同的弹簧下各悬一物体，两物体的质量比为4∶1，则二者作简谐振，则二者作简谐振动的周期之比为_______________________．47、一简谐振动的表达式为)3cos(f +=t A x ，已知，已知 t = 0时的初位移为0.04 m ，初速度为0.09 m/s ，则振幅A =_____________ ，初相f=________________．48、一质点作简谐振动，速度最大值v m = 5 cm/s ，振幅A = 2 cm ．若令速度具有．若令速度具有．若令速度具有正最大值的那一时刻为t = 0，则振动表达式为，则振动表达式为_________________________．49、两个简谐振动曲线如图所示，则两个简谐振动、两个简谐振动曲线如图所示，则两个简谐振动的频率之比n 1∶n 2=__________________，加速度最，加速度最大值之比a 1m ∶a 2m =__________________________，初始速率之比v 10∶v 20=____________________．50、有简谐振动方程为x = 1³10-2cos(p t +f )(SI)，初相分别为f 1 = p /2，f 2 = p ，f 3 = -p /2的三个振动．试在同一个坐标上画出上述三个振动曲线．出上述三个振动曲线．51、一简谐振动曲线如图所示，则由图可确定在t = 2s 时刻质点的位移为时刻质点的位移为 ____________________，速度为，速度为 __________________．52、已知两个简谐振动的振动曲线如图所示．两、已知两个简谐振动的振动曲线如图所示．两简谐振动的最大速率之比为_________________．53、一水平弹簧简谐振子的振动曲线如图所示．一水平弹簧简谐振子的振动曲线如图所示．当振子处在当振子处在位移为零、速度为位移为零、速度为--w A 、加速度为零和弹性力为零、加速度为零和弹性力为零的状态时，应对应于曲线上的________点．当振子处在位移的绝对值为A 、速度为零、加速度为、速度为零、加速度为--w 2A 和弹性力和弹性力为-kA 的状态时，应对应于曲线上的____________点．点．x (cm (cm))t (s)Ox (cm (cm) ) t (s)O 1 2 3 4 6 -6 x tO A-A ab c de fx 1 to xx 2-AA4 3 2 -1 1 t (s)ox (cm) x 1 x 2 1 -2 2 54、一简谐振动用余弦函数表示，其振动曲线如图所示，则此简谐振动的三个特征量为则此简谐振动的三个特征量为A =_____________；w =________________；f =_______________．55、已知两个简谐振动曲线如图所示．x 1的相位比x 2 的相位超前_______．56、两个简谐振动方程分别为、两个简谐振动方程分别为t A x w cos 1=，)31cos(2p +=t A x w在同一坐标上画出两者的x —t 曲线．曲线．xtO57、已知一简谐振动曲线如图所示，由图确定振子：、已知一简谐振动曲线如图所示，由图确定振子：(1) 在_____________s 时速度为零．时速度为零．(2) 在____________ s 时动能最大．时动能最大．(3) 在____________ s 时加速度取正的最大值．时加速度取正的最大值．58、已知三个简谐振动曲线如图所示，则振动方程分别为：别为：x 1 =______________________，x 2 = _____________________，x 3 =_______________________． 59、图中用旋转矢量法表示了一个简谐振动．旋转矢量的长度为0.04 m ，旋转角速度w = 4p rad/s ．此简谐振动以余弦函数表．此简谐振动以余弦函数表x (c (cm)m)t (s)105-101471013Ox (cm (cm))t (s)O 12x (cm )t (s)O x 1x 2x 3100-10123O x x 1 tx 2xOw示的振动方程为x =__________________________(SI)．60、一质点作简谐振动的角频率为w 、振幅为A ．当t = = 00时质点位于A x 21=处，且向x 正方向运动．试画出此振动的旋转矢量图．正方向运动．试画出此振动的旋转矢量图．61、两个同方向的简谐振动曲线如图所示．合振动的振幅、两个同方向的简谐振动曲线如图所示．合振动的振幅为_______________________________，合振动的振动方程，合振动的振动方程为________________________________．62、一平面简谐波．波速为6.0 m/s ，振动周期为0.1 s ，则波长为___________．在波的传播方向上，有两质点（其间距离小于波长）的振动相位差为5p /6，则此两质点相距___________．63、一个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示．试分别指出图中A ，B ，C 各质点在各质点在该时刻的运动方向．A _____________；B _____________ ；C ______________ ．64、一横波的表达式是一横波的表达式是 )30/01.0/(2sin 2x t y -p =其中x 和y 的单位是厘米、t 的单位是秒，此波的波长是_________cm ，波速是_____________m/s ． 65、已知平面简谐波的表达式为、已知平面简谐波的表达式为 )cos(Cx Bt A y -=式中A 、B 、C 为正值常量，为正值常量，此波的波长是_________，波速是_____________．在波传播方向上相距为d 的两的两点的振动相位差是____________________．66、一声波在空气中的波长是0.25 m ，传播速度是340 m/s ，当它进入另一介质时，，当它进入另一介质时，波长变成了0.37 m ，它在该介质中传播速度为______________．67、已知波源的振动周期为4.00³10-2 s ，波的传播速度为300 m/s ，波沿x 轴正轴正方向传播，则位于x 1 = 10.0 m 和x 2 = 16.0 m 的两质点振动相位差为__________．68、一平面简谐波沿x 轴正方向传播，波速轴正方向传播，波速 u = 100 m/s ，t = 0时刻的波形曲线如图所示．时刻的波形曲线如图所示．可知波长l = ____________；振幅A = __________；频率n = ____________．69、频率为500 Hz 的波，其波速为350 m/s ，相位差为2p /3 的两点间距离为的两点间距离为 ________________________．70、一平面简谐波沿x 轴正方向传播．已知x = 0处的振动方程为处的振动方程为 )cos(0f w +=t y ，波速为u ．坐标为x 1和x 2的两点的振动初相位分别记为f 1和f 2，则相位差f 1－f 2 =_________________．·x tO x 1(t ) x 2(t ) A 1 A 2-A 1 -A 2Txy u OA BCx (m (m))O 0.20.61.0-0.20.2y (m (m))71、已知一平面简谐波的波长l = 1 m ，振幅，振幅A = 0.1 m ，周期，周期T = 0.5 s ．选波的传播方向为x 轴正方向，并以振动初相为零的点为x 轴原点，则波动表达式为轴原点，则波动表达式为 y = _____________________________________(SI)．72、一横波的表达式是)4.0100(2sin 02.0p -p =t y (SI)，则振幅是________，波长是_________，频率是__________，波的传播速度是______________．77、已知一平面简谐波的表达式为、已知一平面简谐波的表达式为 )cos(bx at A -，（a 、b 均为正值常量），则波沿x 轴传播的速度为___________________．74、一简谐波的频率为、一简谐波的频率为 5³104 Hz ，波速为，波速为 1.5³103 m/s ．在传播路径上相距．在传播路径上相距 5³10-3 m 的两点之间的振动相位差为_______________．75、一简谐波沿BP 方向传播，它在B 点引起的振动方程为点引起的振动方程为 t A y p =2cos 11．另一简谐波沿CP 方向传播，它在C 点引起的振动方程为)2cos(22p +p =t A y ．P 点与B 点相距0.40 0.40 m m ，与C 点相距0.5 m （如图）．波速均为u = 0.20 m/s ．则两波．则两波在P 点的相位差为______________________．76、已知一平面简谐波的表达式为、已知一平面简谐波的表达式为 )cos(Ex Dt A y -=，式中A 、D 、E 为正值常量，则在传播方向上相距为a 的两点的相位差为______________．77、在简谐波的一条射线上，相距0.2 m 两点的振动相位差为p /6．又知振动周．又知振动周期为0.4 s ，则波长为_________________，波速为________________．78、一声纳装置向海水中发出超声波，其波的表达式为、一声纳装置向海水中发出超声波，其波的表达式为 )2201014.3cos(102.153x t y -´´=- (SI) 则此波的频率n = _________________ ，波长l = __________________，海水中海水中声速u = __________________．79、已知14℃时的空气中声速为340 m/s ．人可以听到频率为20 Hz 至20000 Hz 范围内的声波．可以引起听觉的声波在空气中波长的范围约为内的声波．可以引起听觉的声波在空气中波长的范围约为 ______________________________．80、一平面简谐波一平面简谐波（机械波）（机械波）（机械波）沿沿x 轴正方向传播，轴正方向传播，波动表达式为波动表达式为)21cos(2.0x t y p -p =(SI)，则x = -3 m 处媒质质点的振动加速度a 的表达式为________________________________________．P CB81、在同一媒质中两列频率相同的平面简谐波的强度之比I 1 / I 2 = 16，则这两列，则这两列，则这两列波的振幅之比是A 1 / A 2 = ____________________．82、两相干波源S 1和S 2的振动方程分别是)cos(1f w +=t A y 和)cos(2f w +=t A y . S 1距P 点3个波长，S 2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．83、两相干波源S 1和S 2的振动方程分别是t A y w cos 1=和)21cos(2p +=t A y w ．S 1距P 点3个波长，S 2距P 点21/4个波长．两波在P 点引起的两个振动的相位差点引起的两个振动的相位差是____________．84、两个相干点波源S 1和S 2，它们的振动方程分别是分别是)21cos(1p +=t A y w 和)21c o s (2p -=t A y w ．波从S 1传到P 点经过的路程等于2个波长，波从S 2传到P 点的路程等于7 / 2个波长．设两波波速相同，在传播过程中振幅不衰减，则两个波长．设两波波速相同，在传播过程中振幅不衰减，则两波传到P 点的振动的合振幅为__________________________．85、一弦上的驻波表达式为)90cos()cos(1.0t x y p p =(SI)．形成该驻波的两个反向传播的行波的波长为________________，频率为__________________．86、一弦上的驻波表达式为、一弦上的驻波表达式为 t x y 1500cos 15cos 100.22-´= (SI)．形成该驻波的两个反向传播的行波的波速为__________________．87、在弦线上有一驻波，其表达式为、在弦线上有一驻波，其表达式为 )2cos()/2cos(2t x A y n l p p =, 两个相邻波节之间的距离是_______________．88、频率为n = 5³107 Hz 的电磁波在真空中波长为_______________m ，在折射，在折射率为n = 1.5 的媒质中波长为的媒质中波长为______________m ．89、在电磁波传播的空间（或各向同性介质）中，任一点的E和H 的方向及波的方向及波传播方向之间的关系是：_____________________________________________ ____________________________________________________________．90、在真空中沿着x 轴正方向传播的平面电磁波，其电场强度波的表达式为轴正方向传播的平面电磁波，其电场强度波的表达式为)/(2cos 600c x t E y -p =n (SI)，则磁场强度波的表达式是，则磁场强度波的表达式是______________________________________________________． (真空介电常量真空介电常量 e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m 0 =4p ³10-7 H/m) 91、在真空中沿着x 轴负方向传播的平面电磁波，其电场强度的波的表达式为轴负方向传播的平面电磁波，其电场强度的波的表达式为 )/(2cos 800c x t E y +p =n (SI)，则磁场强度波的表达式是，则磁场强度波的表达式是________________________________________________________． (真空介电常量真空介电常量 e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m 0 =4p ³10-7 H/m) 92、在真空中沿着z 轴正方向传播的平面电磁波的磁场强度波的表达式为])/(cos[00.2p +-=c z t H x w (SI)，则它的电场强度波的表达式为，则它的电场强度波的表达式为____________________________________________________．（真空介电常量（真空介电常量 e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m 0 =4p ³10-7 H/m）93、在真空中沿着负z 方向传播的平面电磁波的磁场强度为方向传播的平面电磁波的磁场强度为)/(2cos 50.1l n z t H x +p = (SI)，则它的电场强度为E y = ____________________．（真空介电常量e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m0 =4p ³10-7 H/m ）94真空中一简谐平面电磁波的电场强度振幅为真空中一简谐平面电磁波的电场强度振幅为 E m = 1.20³10-2 V/m 该电磁波该电磁波的强度为_________________________．（真空介电常量（真空介电常量 e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m 0 =4p ³10-7 H/m ）95、在真空中沿着z 轴的正方向传播的平面电磁波，O 点处电场强度为点处电场强度为)6/2cos(900p +p =t E x n ，则O 点处磁场强度为___________________________．（真空介电常量（真空介电常量 e 0 = 8.85³10-12 F/m ，真空磁导率，真空磁导率 m 0 =4p ³10-7 H/m） 96、在地球上测得来自太阳的辐射的强度=S 1.4 kW/m 2．太阳到地球的距离约．太阳到地球的距离约为1.50³1011 m ．由此估算，太阳每秒钟辐射的总能量为__________________．97、在真空中沿着z 轴负方向传播的平面电磁波，O 点处电场强度为)312cos(300p +p =t E x n (SI)，则O 点处磁场强度点处磁场强度为_____________________________________．在图上表示出电场强度，磁场强度和传播速度之间的相互关系．度，磁场强度和传播速度之间的相互关系． 98、电磁波在真空中的传播速度是_________________(m/s)（写三位有效数字）．99、电磁波在媒质中传播速度的大小是由媒质的____________________决定的．决定的．100、电磁波的E 矢量与H矢量的方向互相____________，相位__________．三、计算题：（每题10分）分）101、一质点按如下规律沿x 轴作简谐振动：)328cos(1.0p +p =t x (SI)．求此振动的周期、振幅、初相、速度最大值和加速度最大值．求此振动的周期、振幅、初相、速度最大值和加速度最大值．102、一质量为0.20 kg 的质点作简谐振动，其振动方程为的质点作简谐振动，其振动方程为 )215c o s (6.0p -=t x (SI)．求：(1) 质点的初速度；质点的初速度；(2) 质点在正向最大位移一半处所受的力．质点在正向最大位移一半处所受的力．z yxO103、有一轻弹簧，当下端挂一个质量m 1 = 10 g 的物体而平衡时，伸长量为的物体而平衡时，伸长量为 4.9 cm ．用这个弹簧和质量m 2 = 16 g 的物体组成一弹簧振子．取平衡位置为原点，向上为的物体组成一弹簧振子．取平衡位置为原点，向上为x 轴的正方向．将m 2从平衡位置向下拉从平衡位置向下拉 2 cm 后，给予向上的初速度v 0 = 5 cm/s 并开始计时，试求m 2的振动周期和振动的数值表达式．的振动周期和振动的数值表达式．104、有一单摆，摆长为l = 100 cm ，开始观察时，开始观察时( t = 0 )，摆球正好过，摆球正好过 x 0 = -6 cm 处，并以v 0 = 20 cm/s 的速度沿的速度沿x 轴正向运动，若单摆运动近似看成简谐振动．试求轴正向运动，若单摆运动近似看成简谐振动．试求(1) 振动频率；振动频率； (2) 振幅和初相．振幅和初相．105、质量m = 10 g 的小球与轻弹簧组成的振动系统，按的小球与轻弹簧组成的振动系统，按)318cos(5.0p +p =t x 的规律作自由振动，式中t 以秒作单位，x 以厘米为单位，求以厘米为单位，求 (1) 振动的角频率、周期、振幅和初相；振动的角频率、周期、振幅和初相； (2) 振动的速度、加速度的数值表达式；振动的速度、加速度的数值表达式； (3) 振动的能量E ；(4) 平均动能和平均势能．平均动能和平均势能．106、一质量m = 0.25 kg 的物体，在弹簧的力作用下沿的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点. 弹簧的劲度系数k = 25 N²m -1． (1) 求振动的周期T 和角频率w ．(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v 0及初相f ．(3) 写出振动的数值表达式．写出振动的数值表达式．107、一质量为10 g 的物体作简谐振动，其振幅为2 cm ，频率为4 Hz ，t = 0时位移为时位移为－2 cm ，初速度为零．求，初速度为零．求 (1) 振动表达式；振动表达式；(2) t = (1/4) s 时物体所受的作用力．时物体所受的作用力．时物体所受的作用力．108、两个物体作同方向、同频率、同振幅的简谐振动．在振动过程中，每当第一个物体经过位移为2/A 的位置向平衡位置运动时，第二个物体也经过此位置，但向远离平衡位置的方向运动．试利用旋转矢量法求它们的相位差．位置的方向运动．试利用旋转矢量法求它们的相位差．109、一物体质量为0.25 kg ，在弹性力作用下作简谐振动，弹簧的劲度系数k = 25 N²m -1，如果起始振动时具有势能0.06 J 和动能0.02 J ，求，求 (1) 振幅；振幅； (2) 动能恰等于势能时的位移；动能恰等于势能时的位移；(3) 经过平衡位置时物体的速度．经过平衡位置时物体的速度．110、在一竖直轻弹簧下端悬挂质量m = 5 g 的小球，弹簧伸长的小球，弹簧伸长D l = 1 cm 而平衡．经推动后，该小球在竖直方向作振幅为A = 4 cm 的振动，求的振动，求(1) 小球的振动周期；小球的振动周期； (2) 振动能量．振动能量．111、一物体质量m = 2 kg ，受到的作用力为F = -8x (SI)．若该物体偏离坐标原点O 的最大位移为A = = 0.10 0.10 0.10 m m ，则物体动能的最大值为多少？为多少？112、一横波沿绳子传播，其波的表达式为 )2100cos(05.0x t y p -p = (SI) (1) 求此波的振幅、波速、频率和波长．求此波的振幅、波速、频率和波长． (2) 求绳子上各质点的最大振动速度和最大振动加速度．求绳子上各质点的最大振动速度和最大振动加速度．(3) 求x 1 = 0.2 m 处和x 2 = 0.7 m 处二质点振动的相位差．处二质点振动的相位差．113、一振幅为、一振幅为 10 10 cm cm ，波长为200 cm 的简谐横波,沿着一条很长的水平的绷紧弦从左向右行进，波速为向右行进，波速为 100 100 cm/scm/s ．取弦上一点为坐标原点，x 轴指向右方，在t = = 00时原点处质点从平衡位置开始向位移负方向运动．求以SI 单位表示的波动表达式（用余弦函数）及弦上任一点的最大振动速度．上任一点的最大振动速度．114、一振幅为一振幅为 10 cm ，波长为200 cm 的一维余弦波．沿x 轴正向传播，波速为波速为 100 cm/s ，在t = 0时原点处质点在平衡位置向正位移方向运动．求时原点处质点在平衡位置向正位移方向运动．求 (1) 原点处质点的振动方程．原点处质点的振动方程．(2) 在x = 150 cm 处质点的振动方程．处质点的振动方程．115、一简谐波沿x 轴负方向传播，波速为1 m/s ，在x 轴上某质点的振动频率为1 Hz 、振幅为0.01 0.01 mm ．t = = 00时该质点恰好在正向最大位移处．若以该质点的平衡位置为x 轴的原点．求此一维简谐波的表达式．点．求此一维简谐波的表达式．116、已知一平面简谐波的表达式为、已知一平面简谐波的表达式为 )37.0125cos(25.0x t y -= (SI) (1) 分别求x 1 = 10 m ，x 2 = 25 m 两点处质点的振动方程；两点处质点的振动方程；(2) 求x 1，x 2两点间的振动相位差；两点间的振动相位差；(3) 求x 1点在t = 4 s时的振动位移．时的振动位移．时的振动位移． 117、一横波方程为、一横波方程为 )(2cos x ut A y -p =l，式中A = 0.01 m ，l = 0.2 m ，u = 25 m/s ，求t = 0.1 s 时在时在x = 2 m 处质点振动的位移、速度、加速度．处质点振动的位移、速度、加速度．118、如图，一平面简谐波沿Ox 轴传播，波动表达式为])/(2c os [f l n +-p =x t A y (SI)，求，求(1) P 处质点的振动方程；处质点的振动方程；(2) 该质点的速度表达式与加速度表达式．该质点的速度表达式与加速度表达式．119、一平面简谐波，频率为300 Hz ，波速为340 m/s ，在截面面积为3.00³10-2 m 2的管内空气中传播，若在10 s 内通过截面的能量为2.70³10-2 J ，求，求(1) 通过截面的平均能流；通过截面的平均能流； (2) 波的平均能流密度；波的平均能流密度；(3) 波的平均能量密度．波的平均能量密度．120、一驻波中相邻两波节的距离为d = 5.00 cm ，质元的振动频率为，质元的振动频率为n =1.00³103 Hz ，求形成该驻波的两个相干行波的传播速度u 和波长l ．xFm OAxOPL。

大学物理--振动波动试题

振动、波动部分1．把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为 (A) ． (B) /2． (C) 0 ． (D) ．［］2．一劲度系数为k 的轻弹簧截成三等份，取出其中的两根，将它们并联，下面挂一质量为m 的物体，如图所示。

则振动系统的频率为(A) m k 32π1． (B) m k2π1． (C) m k 32π1． (D) m k62π1．［］3．一质点作简谐振动，振动方程为)cos(φω+=t A x ，当时间t = T/2（T 为周期）时，质点的速度为(A) φωsin A -． (B) φωsin A ．(C) φωcos A -． (D) φωcos A ．［］ 4．一质点作简谐振动．其运动速度与时间的曲线如图所示．若质点的振动规律用余弦函数描述，则其初相应为(A) /6． (B) 5 /6． (C) -5 /6． (D) - /6．(E) -2 /3．［］5．一弹簧振子作简谐振动，总能量为E1，如果简谐振动振幅增加为原来的两倍，重物的质量增为原来的四倍，则它的总能量E2变为(A) E1/4． (B) E1/2．(C) 2E1． (D) 4 E1 ．［］6．一质点作简谐振动，其振动方程为)cos(φω+=t A x ．在求质点的振动动能时，得出下面5个表达式：(1))(sin 21222φωω+t A m ． (2) )(cos 21222φωω+t A m ．(3))sin(212φω+t kA ． (4) )(cos 2122φω+t kA ．(5))(sin 22222φω+πt m A Tmvv21其中m 是质点的质量，k 是弹簧的劲度系数，T 是振动的周期．这些表达式中 (A) (1)，(4)是对的． (B) (2)，(4)是对的． (C) (1)，(5)是对的． (D) (3)，(5)是对的． (E) (2),(5)是对的 .［］7．机械波的表达式为y = 0.03cos6 (t + 0.01x ) (SI) ，则(A) 其振幅为3 m ． (B) 其周期为s 31．(C) 其波速为10 m/s ． (D) 波沿x 轴正向传播．［］8．一平面简谐波以速度u 沿x 轴正方向传播，在t = t ＇时波形曲线如图所示．则坐标原点O 的振动方程为 (A) ]2)(cos[π+'-=t t b u a y ． (B) ]2)(2cos[π-'-π=t t b u a y ． (C)]2)(cos[π+'+π=t t b u a y ． (D)]2)(cos[ππ-'-=t t b u a y ．［］9．如图所示，两列波长为的相干波在P 点相遇．波在S1点振动的初相是 1，S1到P 点的距离是r1；波在S2点的初相是 2，S2到P 点的距离是r2，以k 代表零或正、负整数，则P 点是干涉极大的条件为：(A) λk rr =-12． (B) π=-k 212φφ．(C) π=-π+-k r r 2/)(21212λφφ．（D ） π=-π+-k r r2/)(22112λφφ．［］10．两相干波源S1和S2相距 /4，（为波长），S1的相位比S2的相位超前π21，在S1，S2的连线上，S1外侧各点（例如P 点）两波引起的两谐振动的相位差是：(A) 0． (B) π21． (C) ． (D) π23．［］11．一弹簧振子作简谐振动，振幅为A ，周期为T ，其运动方程用余弦函数表示．若t = 0时，(1) 振子在负的最大位移处，则初相为______________________；(2) 振子在平衡位置向正方向运动，则初相为________________；(3) 振子在位移为A/2处，且向负方向运动，则初相为______．SS 1S 2Pλ/412．一物体作简谐振动，其振动方程为)2135cos(04.0π-π=t x (SI) ．(1) 此简谐振动的周期T =__________________；当t = 0.6 s 时，物体的速度v =__________________．13．一质点沿x 轴以 x = 0 为平衡位置作简谐振动，频率为 0.25 Hz ．t = 0时x = -0.37 cm 而速度等于零，则振幅是_____________________，振动的数值表达式为______________________________．14．一简谐振动的旋转矢量图如图所示，振幅矢量长2 cm ，则该简谐振动的初相为____________．振动方程为______________________________．15．一单摆的悬线长l = 1.5 m ，在顶端固定点的竖直下方0.45 m 处有一小钉，如图示．设摆动很小，则单摆的左右两方振幅之比A1/A2的近似值为_______________．16．图中所示为两个简谐振动的振动曲线．若以余弦函数表示这两个振动的合成结果，则合振动的方程为=+=21x x x __________(SI)17．已知波源的振动周期为4.00×10-2 s ，波的传播速度为300 m/s ，波沿x 轴正方向传播，则位于x1 = 10.0 m 和x2 = 16.0 m 的两质点振动相位差为__________．18．一平面简谐波沿x 轴负方向传播．已知 x = -1 m 处质点的振动方程为)c o s (φω+=t A y ，若波速为u ，则此波的表达式为__________．19．在同一媒质中两列频率相同的平面简谐波的强度之比I1 / I2 = 16，则这两列波的振幅之比是A1 / A2 = ____________________．20．两相干波源S1和S2的振动方程分别是)cos(1φω+=t A y 和)cos(2φω+=t A y .S1距P 点3个波长，S2距P 点 4.5个波长．设波传播过程中振幅不变，则两波同时传到P 点时的合振幅是________________．t0.45 m-21．一质量m = 0.25 kg 的物体，在弹簧的力作用下沿x 轴运动，平衡位置在原点. 弹簧的劲度系数k = 25 N ·m-1． (1) 求振动的周期T 和角频率．(2) 如果振幅A =15 cm ，t = 0时物体位于x = 7.5 cm 处，且物体沿x 轴反向运动，求初速v0及初相． (3) 写出振动的数值表达式．22．一物体作简谐振动，其速度最大值vm = 3×10-2 m/s ，其振幅A = 2×10-2 m ．若t = 0时，物体位于平衡位置且向x 轴的负方向运动. 求：(1) 振动周期T ； (2) 加速度的最大值am ；(3) 振动方程的数值式．23．质量m = 10 g 的小球与轻弹簧组成的振动系统，按)318cos(5.0π+π=t x 的规律作自由振动，式中t 以秒作单位，x 以厘米为单位，求(1) 振动的角频率、周期、振幅和初相； (2) 振动的速度、加速度的数值表达式； (3) 振动的能量E ；(4) 平均动能和平均势能．24．一简谐振动的振动曲线如图所示．求振动方程．25．在一竖直轻弹簧的下端悬挂一小球，弹簧被拉长l0 = 1.2 cm 而平衡．再经拉动后，该小球在竖直方向作振幅为A = 2 cm 的振动，试证此振动为简谐振动；选小球在正最大位移处开始计时，写出此振动的数值表达式．-26．一质点同时参与两个同方向的简谐振动，其振动方程分别为x1 =5×10-2cos(4t + /3) (SI) , x2 =3×10-2sin(4t - /6）(SI)画出两振动的旋转矢量图，并求合振动的振动方程．27．一简谐波沿x轴负方向传播，波速为1 m/s，在x轴上某质点的振动频率为1 Hz、振幅为0.01 m．t = 0时该质点恰好在正向最大位移处．若以该质点的平衡位置为x轴的原点．求此一维简谐波的表达式．28．已知一平面简谐波的表达式为)37.0125cos(25.0xty-=(SI)(1) 分别求x1 = 10 m，x2 = 25 m两点处质点的振动方程；(2) 求x1，x2两点间的振动相位差；(3) 求x1点在t = 4 s时的振动位移．29．一平面简谐波沿x轴正向传播，其振幅和角频率分别为A和，波速为u，设t = 0时的波形曲线如图所示．(1) 写出此波的表达式．(2) 求距O点分别为 / 8和3 / 8 两处质点的振动方程．(3) 求距O点分别为 / 8和3 / 8 两处质点在t = 0时的振动速度．x uOy30．如图所示，S1，S2为两平面简谐波相干波源．S2的相位比S1的相位超前 /4 ，波长 = 8.00 m，r1 = 12.0 m，r2 = 14.0 m，S1在P点引起的振动振幅为0.30 m，S2在P点引起的振动振幅为0.20 m，求P点的合振幅．31．设入射波的表达式为)(2cos1TtxAy+π=λ，在x = 0处发生反射，反射点为一固定端．设反射时无能量损失，求(1) 反射波的表达式；(2) 合成的驻波的表达式；(3) 波腹和波节的位置．P SS2。

东华理工大学物理练习试卷答案光的偏振

i0
1
2
二、填空题 6.使光强为I0的自然光依次垂直通过三块偏振片P1、P2和P3。相邻偏振片的偏振化方向成450角。则透过三块偏振片的光强I为 I0/8 . 7.如图所示，一束自然光入射到折射率分别为n1和n2的两种介质的交界面上，发生反射和折射。已知反射光是完全偏振光，那么折射角r的值为 π/2 - arctan n2/n. 1
14. （1）试求光在装满水的容器底部反射时的布儒斯特角。容器用冕牌玻璃制成，折射率为1.50，水的折射率为1.333。（2）今测得某釉质的起偏角i0=58 °，试求该釉质的折射率。解：（1）由布儒斯特定律可得
n2 1.50 i0 arctg arctg 48 n1 1.333
（2）
0 1 I0 I 5 I0 得 I 4I0 1 I0 2I0 I I 2
11.一束自然光垂直穿过两个叠放在一起的偏振片，若透射光强 I 为原入射光强I的1/4，则两偏振片的偏振化方向之间的夹角是多少？解：设通过第一个偏振片后的光强为I0
1 I0 I 2
4.两偏振片堆叠在一起，一束自然光垂直入射其上时没有光线通过。当其中一偏振片慢慢转动1800时透射光强度发生变化为[ B ] (A)光强单调增加； (B)光强先增加，后有减小至零； (C)光强先增加，后减小，再增加； (D)光强先增加，然后减小，再增加，再减小至零.
5.一束自然光自空气射向一块平板玻璃（如图），设入射角等于布儒斯特角i0 ，则在界面2的反射光[ B ] (A)是自然光； (B)是完全偏振光且光矢量的振动方向垂直入射面； (C)是完全偏振光且光矢量的振动方向平行入射面； (D)是部分偏振光.
16
证明：自然光通过P1后成为强度为 I0/2的线偏振光。设在t时刻， P1 与 P2的夹角为ωt， P2 与P3的夹角为 (90 °- ωt) 。由马吕斯定律可得

振动大学物理习题答案

，x

A12

A22
cos( t

tan 1
A1 ) A2
11-10 质量为 0.4kg 的质点同时参与相互垂直的两个谐振动：
x1

0.08 cos( 3
t

) 6
，
x2

0.06 cos( 3
t

) 3
求：（1）质点的轨迹方程；（2）质点在任一位置所受的力。
解：（1）设 x A1 cos( t 1 ) ， y A2 cos( t 2 ) ，消去 t 得
0.05sin 3

4 3
0.05 cos
0.06sin 4
0.06 cos
11.00 ， 84.8 1.48rad
4
4
（2）

3
1

2k
，3

2k

3 4
，k

0,1,2；

3
2

(2k
1)
，3

2k

5 4
，k
解：（1）由旋转矢量法知， 2 2 ， x 0.12 cos( t )
3
T2
3
（2） v d x 0.12 sin( t ) ， a d v 0.12 2 cos( t )
dt
3
dt
3
t 0.5s ， x 0.1039 m ， v 0.1885 m/s ， a 1.03m/s 2
dt2 m J / R2
（2）
k
，T 2 2 m J / R2

大学物理波动方程试题(附答案)

x
x
x
点处质点的振动速度 v 与时间 t 的关系曲线为： [ A ] v
ωA
Y
v
t (s )
1
u
P
0 0 .5
2
0
− ωA
1
2
A
0
t (s )
x
0
− ωA
v
0 .5
(A )
ωA
1
t (s )
2
(B)
v
0
1
(C )
(D )
π⎞ π⎞ ⎛ 2π ⎛ y P = Acos⎜ t − ⎟ = A cos⎜ π t − ⎟ 2⎠ 2⎠ ⎝ T ⎝
(SI)
φ O
2A / 2
A
y
又 λ = 200 m ，波动方程为
(2) 将 x ＝100m 代入上式，得该处的振动方程
5 ⎞ ⎛ y100 = A cos ⎜ 500πt + π ⎟ 4 ⎠ ⎝
ww
w. z
hi
na
nc
dy100 5 ⎞ ⎛ = −500πA sin⎜ 500πt + π ⎟ (SI) dt 4 ⎠ ⎝ 3 ⎞ ⎛ 将 x＝-100m 代入上式，得该处的振动方程 y −100 = A cos⎜ 500π t − π ⎟ 4 ⎠ ⎝ dy −100 3 ⎞ ⎛ = −500π A sin⎜ 500π t − π ⎟ (SI) 振动速度表达式为 v −100 = dt 4 ⎠ ⎝
《大学物理》AII 作业
No.2 波动方程
解：拉力恒定，则波速 u =
u T 恒定， λ = 。 ν 越大， λ 越小; 反之 ν 越小， λ 越大。 µ ν
na

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x） o s c
2 T
t
2 2 4 x 处振幅为： 2Acos 2 A c o s A. 3 3 3

u
Cu 2
B C
=Tu=

C
u
B C
2
相位差：
d u
B
d B C
Cd
解 :由题意知：沿 B P 方向传播的波，在 P 点引起的的振动方程为： y P 1 A1 c o （ 2 t 2 s BP u ）
2 2
r2 - r1

）
本题 2 0 = 1 0， r2 - r1 L 2 r A A1 A 2 2 A1 A 2 c o （ 2 s
2 2
L 2r

）
解 : 参看 P89 A A1 A 2 2 A1 A 2 c o （ 2 0 - 1 0 - 2 s
解 : 入射波在 O点引起的振动方程为： y1 0 A c o s 2 t T t T x . ） .
参看 P 9 1 .可得 y 2 A c o s 2 （参看 P 9 2，式（ 1 1 - 3 8 ）驻波方程为： y=（ 2Acos 2 2
2 6

所以选：B
解 :从图中可知：
0

2
或 0
3 2
所以选：D
解 : 参看 P 9 5。当波从波疏介质传播到波密介质，入射波在反射点反射时有相位的突变。 y要分析 P点的相位和传播方向考虑。
所以选：B
xl 解 : 波由 P点传到 x处的时间为： u （ x l） x点相位落后于 P 点： u x点振动的方程为：（ x l） y A co s t 0 u （ x l） A c o s [t ] 0 u
-
2 x 30 2 t
））]

2

2
0.01 ）
2 cos(
2 x 30
2 t 0.01
比较 P58式 (11-2) y 2 c o s [ ( t x u 2 0 .0 1 ) + 0）得：

u

2 30
，=
m ； u T u 2 3 0 u = 3 0 m u 30 s u
解 : 参看 P 3 1。图 1 0 2 3 由图得： M 2 = O M 1 + O M - 2 O M 1 O M c o s O 其中： M 1 1 0 3， O OM 20 解得： M 2 1 0 0， O M 2 1 0 O O M 1 + O M 2 O M O M 1M 9 0 1 2
.
-2 （
）。 2 0
2

2

2
2 20 = 2 k +
， k 0， 1， 2 ... ， 10 =
（ 2 ）据题意 20 - 10 - 2
r2 - r1

2

， r2 = r1
20 -

2
， 20 = 3 2

0 .3 7
338 m
s ） =17m
uT u

338 m （
s
） 2 （
125rad / S
解 : 已知： y 2 s in t / 0 . 0 1 - x / 3 0 ）（ 2 s in （ 2 s in [

2 2
-( +

2
+ +
2 t 0.01 2 x 30 +
2 2 2 0 2 2 2 2

6

2
解 : 已知： y 0 .0 2 5 c o （ 1 2 5 t - 0 . 3 7 x ） s 参看 P 5 8式（ 1 1 - 2 ） y=Acos[ t（ x u ） +0]
比较上两式得： =125rad/s

u
0 .3 7 ， u 2
u 3 a c o s [ （ t t ） + ] b 2 a cos[ u （ t t ） ] b 2
所以选：D
解 : 参看 P 68 弹性介质中简谐波的强度正比于振幅的二次方 A1
2 2
4，
A2
A1 A2
2
所以选：C
解 : 参看 P 66 （横波传播过程中，质元的动能和势能的时间关系式是相同的，两者不仅同相，而且大小总是相等的。动能达到最大值时势能也达到最大值。）
所以选：B
解（ 1） : k k k k T 2
1
1
1
2
， k = k 2m
k 2

， 2m k
k m

T 2
（ 2 ） k = k + k = 2 k T 2 ， m 2k 2k m

T 2
解 : x A c o （ t 0） s 由图知： A 6， T 4 2
L1 L2 Tu L1 L2

L1 L2

） ].
设与 P点振动状态相同的点的位置为 x. 则有： x + L 1 k ， L 1 + k ，（ k = 1 ， 2 ， . . . ） x
解 : 参看 P89 A A1 A 2 2 A1 A 2 c o （ 2 0 - 1 0 - 2 s
I A I 0 I 0 2 I 0 co（ - 2 ） = 4 I0 s 考虑 B点：

2
（ 2
3 4
）

2

3 2

所以选：D
I B I 0 I 0 2 I 0 co（） = 0 s
解 : 参看 P 92 在驻波中，同一分段上的各点有相同的振动相位
<<振动与波动>>习题解答
解 : 参看 P1 3 Ek = 1 2 m v ， x = A c o s （ t + 0），
2

2 T
2 f
v x A s in t + 0）（ Ek= 1 2
2
m A s in （ t + 0）
= A2 c o （ 2 t 2 s ） 0 .2 = A2 c o （ 2 t 5 ） s = A2 c o （ 2 t 4 ） s 相位差为： 0
解 :由图知：
1 0 .2 0 .8 m .
A 0 .2 m . uT v u
0 .4 A1 c o （ 2 t 2 s ） = A1 c o （ 2 t 4 ） s 0 .2 沿 CP方向传播的波，在 P点引起的振动方程为： y P2 CP A2 c o （ 2 t : 参看 P 8 9。叠加后波的强度为： I = I 1 + I 2 + 2 I 1I 2 c o s 20 10 2 考虑 A点： 3 r2 r1

2

2 4

2

3 2
2
所以选：B
解 :由题意得：（ A点处质元的振动动能在增大。 A点运动方向如图示。波向 x轴负方向运动。
所以选：B
解 : 参看 P 6 6， P 6 7 （质元的总机械能是随时间而变化的，它在零与最大值之间周期性变化。同时任一质元都在不断地接收和放出能量。

，T

2 3
初相
4 3
或-
解 :略
解 :同频率、同方向、不同振幅的振动合成两振动反相。合成的余弦振动的初相位为：或 2 2

3
解 :同频率、同方向、同振幅的振动合成由图可知：= 0 x
（ n+1） 1 （ n 1） k k1 n k1 k n k2 n+1） k （
所以选：C
解 : 参看 P 58 波函数： Y ( x , t ) = A c o s [ t （通过比较知 6 ， T 2 x u ) + 0） 1 3 s
3 2
20 = 2 k +
，（ k=0， 1， 2...）
解 : 参看 P92 相邻波腹之间的距离是：. 2

解 : y 2 A c o （ 2 x / ） o s t s c x

2
处质点的振动方程是：
2 1 y 2 A c o s [ （ - ） ] c o s t 2 2 A co（ - ） o s t 2 A co s t s c y 2 A s in t

2 4