Flute斯坦纳最小树构造算法
图的steiner最小树问题及其求解

图的steiner最小树问题及其求解
杨凌云
【期刊名称】《电脑知识与技术》
【年(卷),期】2009(005)025
【摘要】斯坦纳树问题是组合优化学科中的一个问题.属于NP-难问题,即无法在多项式时间内得到最优解.本文主要讨论了图的steiner最小树问题,并给出了近似算法,该算法是在破圈法的基础上进行了改进,并且引用了agent的思想.最后对算法进行了分析.
【总页数】2页(P7312-7313)
【作者】杨凌云
【作者单位】河南大学,计算机与信息工程学院,河南,开封,475001
【正文语种】中文
【中图分类】TP312
【相关文献】
1.图的Steiner最小树问题的降阶回溯算法 [J], 刘艳芳;宁爱兵;王英磊
2.图的Steiner最小树问题的混合遗传算法 [J], 赵礼峰;王小龙
3.欧氏Steiner最小树的Delaunay三角网混合智能求解方法 [J], 王家桢;马良;张惠珍
4.度约束欧氏Steiner最小树问题及其求解 [J], 张瑾;丁爱萍;马良
5.图的steiner最小树问题及其求解 [J], 杨凌云
因版权原因,仅展示原文概要,查看原文内容请购买。
最小生成树的算法

最小生成树是一种在图论中常见的问题,其目标是在给定一个加权连通图的情况下,寻找一棵包含所有顶点的树,使得这棵树的边的总权重最小。
常见的最小生成树算法有Kruskal算法和Prim算法。
Kruskal算法的基本思想是按照边的权重从小到大的顺序选择边,如果这条边连接的两个顶点不在同一棵树中,就将其添加到最小生成树中,否则就跳过这条边。
这个过程一直持续到添加了n-1条边为止。
Prim算法的基本思想是从一个顶点开始,每次选择一条连接已选顶点和未选顶点的权重最小的边,将其添加到最小生成树中,并将这条边的另一端点所在的连通块加入到已选顶点集合中。
这个过程一直持续到所有的顶点都被选中为止。
最小生成树MinimumSpanningTree
8
1、Prim算法
算法求精-初始化
将根r涂红加入红点集U,TE=φ。
对每个白点i (0≤i ≤n-1, i≠r ), i所关联的最短紫边(r,i)的 长度为G[r][i], 这n-1条最短紫边构成了初始的候选轻边集。
因为树边为空,故将T[0..n-2]全部用来存放候选轻边集。
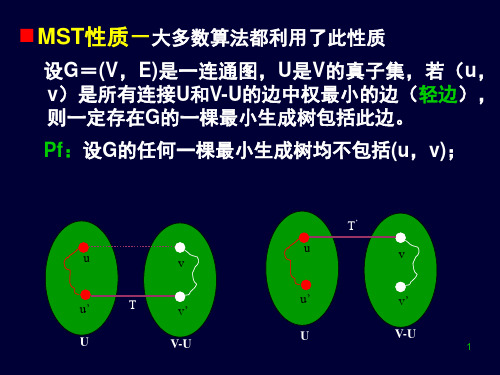
❖设V(G)={0,1,…,n-1}
❖算法的每一步均是在连接红、白点集的紫 边中选一轻边扩充到T(贪心),T从任意 一点r开始(r为根),直至U=V为止。 MST性质保证了贪心选择策略的正确性。
3
1、Prim算法
如何找轻边?
❖可能的紫边集
设红点集|U|=k, 白点集|V-U|=n-k,则可能的紫边 数为:k(n-k)。
//将(u,v)涂红加入树中,白点v加入红点集
ModifyCandidateSet(…);
//根据新红点v调整候选轻边集
}
}
算法终止时U=V,T=(V,TE)
6
1、Prim算法
实例
6 1
5
35 4
05
1
3
27 2
4
5
6
60 5
1
1
3
∞2
∞
4
5
0
151
3
2
5
2 4
4
5
0
151
3
2
5
2 4
4
5
0
151 2
int i, minpos, min=Infinity; for (i=k; i<n-1; i++) //遍历候选集找轻边
C语言实现最小生成树构造算法

C语⾔实现最⼩⽣成树构造算法最⼩⽣成树最⼩⽣成树(minimum spanning tree)是由n个顶点,n-1条边,将⼀个连通图连接起来,且使权值最⼩的结构。
最⼩⽣成树可以⽤Prim(普⾥姆)算法或kruskal(克鲁斯卡尔)算法求出。
我们将以下⾯的带权连通图为例讲解这两种算法的实现:注:由于测试输⼊数据较多,程序可以采⽤⽂件输⼊Prim(普⾥姆)算法时间复杂度:O(N^2)(N为顶点数)prim算法⼜称“加点法”,⽤于边数较多的带权⽆向连通图⽅法:每次找与之连线权值最⼩的顶点,将该点加⼊最⼩⽣成树集合中注意:相同权值任选其中⼀个即可,但是不允许出现闭合回路的情况。
代码部分通过以下步骤可以得到最⼩⽣成树:1.初始化:lowcost[i]:表⽰以i为终点的边的最⼩权值,当lowcost[i]=0表⽰i点加⼊了MST。
mst[i]:表⽰对应lowcost[i]的起点,当mst[i]=0表⽰起点i加⼊MST。
由于我们规定最开始的顶点是1,所以lowcost[1]=0,MST[1]=0。
即只需要对2~n进⾏初始化即可。
#define MAX 100#define MAXCOST 0x7fffffffint graph[MAX][MAX];void prim(int graph[][MAX], int n){int lowcost[MAX];int mst[MAX];int i, j, min, minid, sum = 0;for (i = 2; i <= n; i++){lowcost[i] = graph[1][i];//lowcost存放顶点1可达点的路径长度mst[i] = 1;//初始化以1位起始点}mst[1] = 0;2.查找最⼩权值及路径更新定义⼀个最⼩权值min和⼀个最⼩顶点ID minid,通过循环查找出min和minid,另外由于规定了某⼀顶点如果被连⼊,则lowcost[i]=0,所以不需要担⼼重复点问题。
1.6最小生成树及其算法

如果生成树T *的权 w(T * ) 是 G 的所有生成树的权中最 小者,则称 T * 是 G 的最小生成树,简称为最小树,即
w(T * ) min{w(T )},式中取遍 G 的所有生成树T .
T
介绍最小树的两种算法: Kruskal算法(或避圈法)和破圈法.
A. Kruskal算法(或避圈法)
b)广探法 例用广探法求出下图10的一棵生成树 步骤如下: i) 在点集V中任取一点u, 给u以标号0. ii) 令所有标号i的点集为 Vi,检查[Vi,V\Vi]中的边端点 是否均已标号. 对所有未标 号之点均标以i+1,记下这些 边. iii) 对标号i+1的点重复步 步骤ii),直到全部点得到 标号为止.
步 骤
u
L( b)
L( c)
L( d)
L( e)
L(f)
L( g)
e
V
T0
C(T 0)
1 2 3 4
a b e c
4 - - -
15 9 5 -
32 25
7 7 - -
28 28 28 (a, b) (a, e)
{a} {a, b} {a, b, e}
{(a, b)} {(a, b), (a, e)} {(a, b), (a, e), (c, e)}
(5)T T {e k }, k,t t 1, k k 1, 转( ) 3
例5.3 用Kruskal算法求下图的最小生成树。
解:将图的边按照权值从小到大进行排列,列 出下表
边 (a, b) (c, e) (a, e) (b, c) (d, g) (a, c)
3) 当第2)步不能继续执行时,则停止. 定理5.3 由Kruskal算法构作的任何生成树都是 最小树。
最小生成树算法详解

Kruskal算法应用案例
问题描述
最小生成树问题的求解算法除了Prim算法和Kruskal算法之外,还有基于动态规划的算法、基于回溯的算法、基于分治的算法等。
应用场景
例如,在计算几何中,可以通过基于动态规划的算法求解最小包围矩形、最小包围圆、最小包围球等问题;在数值计算中,可以通过基于回溯的算法求解一元高次方程的根等。
其他算法比较与择优
Kruskal算法
Prim算法
Boruvka算法
各算法优缺点比较
根据实际应用场景选择算法
03
Boruvka算法
时间复杂度为O(ElogE),其中E为边数,空间复杂度为O(E)。
各算法时间复杂度与空间复杂度比较
01
Kruskal算法
时间复杂度为O(ElogE),其中E为边数,空间复杂度为O(E)。
时间复杂度:Prim算法的时间复杂度为O(ElogE),其中E为边的数量。
Prim算法
总结词:Kruskal算法是另一种常用的最小生成树算法,其核心思想是通过将所有的边按照权值大小从小到大排序,然后依次选择每条边,如果这条边连接的两个顶点在已经生成的树中不构成环路,则将这条边加入到树中。详细描述:Kruskal算法的基本步骤如下将所有的边按照权值大小从小到大排序。初始化一颗空树作为生成的树的初始状态。从第一条边开始,遍历每条边,如果这条边连接的两个顶点在已经生成的树中不构成环路,则将这条边加入到树中。重复步骤3,直到所有的边都被遍历过。生成的树即为最小生成树。时间复杂度:Kruskal算法的时间复杂度为O(ElogE),其中E为边的数量。
详细描述:Prim算法的基本步骤如下
1. 从一个任意顶点开始,将该顶点加入到已经访问过的顶点集合中。
最小生成树的算法 -回复

最小生成树的算法-回复什么是最小生成树?最小生成树是图论中的一个重要概念,它是指在一个连通图中找到一个子图,该子图包含了图中所有的顶点,并且边的总权值最小。
最小生成树在许多实际应用中非常有用,如网络设计、电路布线以及城市规划等领域。
最小生成树的算法有哪些?最小生成树的算法包括Prim算法和Kruskal算法,它们是常用的解决最小生成树问题的两个经典方法。
下面将一步一步回答这两个算法。
Prim算法:Step 1: 初始化一个空的最小生成树集合T和一个顶点集合V。
Step 2: 选择一个起始顶点,并将其加入最小生成树集合T中。
Step 3: 从集合V中找到一个顶点,该顶点与T中的顶点相连且边的权值最小。
将这个顶点和边加入T中。
Step 4: 重复Step 3,直到集合V中的所有顶点都加入了最小生成树集合T。
Step 5: 最小生成树T即为所求。
Kruskal算法:Step 1: 初始化一个空的最小生成树集合T和一个边集合E。
Step 2: 对边集合E按照权值从小到大进行排序。
Step 3: 依次遍历边集合中的每条边,如果该边的两个顶点不在同一个连通分量中,则将该边加入最小生成树集合T,并将这两个顶点合并到同一个连通分量中。
Step 4: 重复Step 3,直到集合V中的所有顶点都加入了最小生成树集合T。
Step 5: 最小生成树T即为所求。
这两个算法的时间复杂度分别为O(ElogV)和O(ElogE),其中V为顶点数,E为边数。
Prim算法适用于稠密图,而Kruskal算法适用于稀疏图。
最小生成树算法的应用:最小生成树算法在实际应用中非常广泛。
例如,在网络设计中,最小生成树可以用来构建一个具有最小成本的网络,以便有效地传输数据;在电路布线中,最小生成树可以帮助设计最短线路,以减少布线的成本和功耗;在城市规划中,最小生成树可以帮助确定最佳的道路网络,以提高交通效率。
此外,最小生成树算法还可以用于建立物流路径、图像分割以及数据聚类等问题的解决。
§6.4 最小树

§6.4 最小树1、最小树及其性质支撑树T 的权(或长):∑'∈=E e e W T W )()(最小支撑树:G 中权最小的支撑树定理6.4.1 设T 是G 的支撑树, 则T 是G 的最小树当且仅当对任意边*T e ∈有)(max )()(e W e W e C e '=∈'其中e T e C +⊆)(为一个唯一的回路。
定理6.4.2 设T 是G 的支撑树, 则T 是G 的最小树当且仅当对任意边T e ∈有)(min )()(e W e W e e '=Ω∈'其中e T e +⊆Ω*)(为一个唯一割集。
定理6.4.3 设T 是G 的支撑树,则T 是G 的唯一最小树当且仅当对任意边T G e \∈,e 是C (e )中的唯一最大边。
定理6.4.4 设T 是G 的支撑树,则T 是G 的唯一最小树当且仅当对任意边T e ∈,e 是)(e Ω中的唯一最大边。
2、求最小树的Kruskal 算法(贪心算法或避圈法)基本思想:从图G 的m 条边中选取1-n 条权尽量小的边,并且使它们不构成回路。
理论基础:定理6.4.1具体步骤:首先选出一条权最小的边,再从剩下的边中选出一条权最小的, 并且与前面已经选出的边不构成回路。
如此选下去,直到选出1-n 条边为止。
第1步 开始把边按权的大小由小到大排列起来,即m a a a ,...,,21置 φ=S ,0=i ,1=j 。
第2步 若1||-==n i S ,则停。
这时T S G =][即为所求;否则, 转向第3步。
第3步 若}]{[j a S G Y 不构成回路,则置j i a e =+1,}{1+=i e S S Y ,1+=i i ,1+=j j ,转向第2步;否则,置1+=j j ,转向第2步。
例:求图6.4.1的最小树T 。
解:83221)(=+++=T w3、求最小树的破圈法具体步骤:任意选出图G 的一条回路,从中去掉一条权最大的边。
