基本初等函数总结表格
初等基本函数知识点总结

初等基本函数知识点总结函数是数学中最基本的概念之一,它在数学的各个分支中都有着重要的应用。
初等基本函数是指在初等数学范围内常见的基本函数,包括常数函数、一次函数、二次函数、指数函数、对数函数、幂函数、三角函数等。
本文将对这些初等基本函数的概念、性质等进行总结和介绍。
一、常数函数常数函数的定义是f(x) = c (c为常数)。
这里的c就是常数函数的函数值,它是一个常数,和x的取值无关。
在坐标系中,常数函数的图象是一条水平的直线,它的斜率为0。
常数函数的性质有:1. 常数函数的图象是一条水平的直线。
2. 常数函数的定义域是全体实数集R,值域为{c}。
3. 常数函数的导数为0,即f'(x) = 0。
4. 常数函数是一个一一对应的函数。
5. 常数函数是奇函数,偶函数,周期函数,增函数,减函数等的特殊情况。
二、一次函数一次函数的定义是f(x) = kx + b (k和b为常数,k≠0)。
在坐标系中,一次函数的图象是一条通过点P(k,b)的直线,它的斜率为k,截距为b。
一次函数的性质有:1. 一次函数的图象是一条直线,斜率k决定了直线的倾斜程度,截距b决定了直线与y轴的交点位置。
2. 一次函数的定义域是全体实数集R,值域是一切实数集R。
3. 一次函数的导数为k,即f'(x) = k。
4. 当k>0时,一次函数是增函数;当k<0时,一次函数是减函数;当k=0时,一次函数是常数函数。
5. 一次函数是一个奇函数,因为f(-x) = -kx + b = -f(x)。
三、二次函数二次函数的定义是f(x) = ax^2 + bx + c (a、b和c为常数,a≠0)。
二次函数的图象是一个开口向上或者向下的抛物线,它的开口方向由a的正负决定。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
二次函数的性质有:1. 二次函数的图象是一个抛物线,它关于y轴对称,对称轴方程为x = -b/2a。
高中基本初等函数完全归纳总结版

初等函数1、基本初等函数及图形基本初等函数为以下五类函数:(1) 幂函数 μx y =,μ是常数;1.当u 为正整数时,函数的定义域为区间),(+∞-∞∈x ,他们的图形都经过原点,并当u>1时在原点处与X 轴相切。
且u 为奇数时,图形关于原点对称;u 为偶数时图形关于Y 轴对称;2.当u 为负整数时。
函数的定义域为除去x=0的所有实数。
3.当u 为正有理数m/n 时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞+∞)。
函数的图形均经过原点和(1 ,1).如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m,n 均为奇数时,跟原点对称.4.当u 为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数.(2) 指数函数 xa y =(a 是常数且01a a >≠,),),(+∞-∞∈x ;1. 当a>1时函数为单调增,当a<1时函数为单调减.2. 不论x 为何值,y 总是正的,图形在x 轴上方.3. 当x=0时,y=1,所以他的图形通过(0,1)点.(3) 对数函数x y alog =(a是常数且01a a >≠,),(0,)x ∈+∞;(4) 三角函数正弦函数 x y sin =,),(+∞-∞∈x ,]1,1[-∈y ,余弦函数 x y cos =,),(+∞-∞∈x ,]1,1[-∈y ,1. 他的图形为于y 轴的右方.并通过点(1,0)2. 当a>1时在区间(0,1),y 的值为负.图形位于x 的下方,在区间(1, +∞),y 值为正,图形位于x 轴上方.在定义域是单调增函数.a<1在实用中很少用到/正切函数 x y tan =,2ππ+≠k x ,k Z ∈,),(+∞-∞∈y ,余切函数 x y cot =,πk x ≠,k Z ∈,),(+∞-∞∈y ;(5) 反三角函数反正弦函数 x y arcsin =, ]1,1[-∈x ,]2,2[ππ-∈y ,反余弦函数 x y arccos =,]1,1[-∈x ,],0[π∈y ,反正切函数 x y arctan =,),(+∞-∞∈x ,)2,2(ππ-∈y ,反余切函数 x y cot arc =,),(+∞-∞∈x ,),0(π∈y .选校网专业大全历年分数线上万张大学图片大学视频院校库(按ctrl 点击打开)。
基本初等函数

基本初等函数包括以下几种:(1)常数函数y = c(c 为常数)(2)幂函数y = x^a(a 为非0 常数)(3)指数函数y = a^x(a>0, a≠1)(4)对数函数y =log(a) x(a>0, a≠1)(5)三角函数:主要有以下6 个:正弦函数y =sin x余弦函数y =cos x正切函数y =tan x余切函数y =cot x正割函数y =sec x余割函数y =csc x此外,还有正矢、余矢等罕用的三角函数。
(6)反三角函数:主要有以下6 个:反正弦函数y = arcsin x反余弦函数y = arccos x反正切函数y = arctan x反余切函数y = arccot x反正割函数y = arcsec x反余割函数y = arccsc x初等函数是由基本初等函数经过有限次的有理运算和复合而成的函数。
基本初等函数和初等函数在其定义区间内均为连续函数幂函数简介形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
当a取非零的有理数时是比较容易理解的,而对于a取无理数时,初学者则不大容易理解了。
因此,在初等函数里,我们不要求掌握指数为无理数的问题,只需接受它作为一个已知事实即可,因为这涉及到实数连续统的极为深刻的知识。
特性对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:首先我们知道如果a=p/q,且p/q为既约分数(即p、q互质),q和p都是整数,则x^(p/q)=q 次根号下(x的p次方),如果q是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。
当指数a是负整数时,设a=-k,则y=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞)。
因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:排除了为0与负数两种可能,即对于x>0,则a可以是任意实数;排除了为0这种可能,即对于x<0或x>0的所有实数,q不能是偶数;排除了为负数这种可能,即对于x为大于或等于0的所有实数,a就不能是负数。
六大基本初等函数图像及其性质
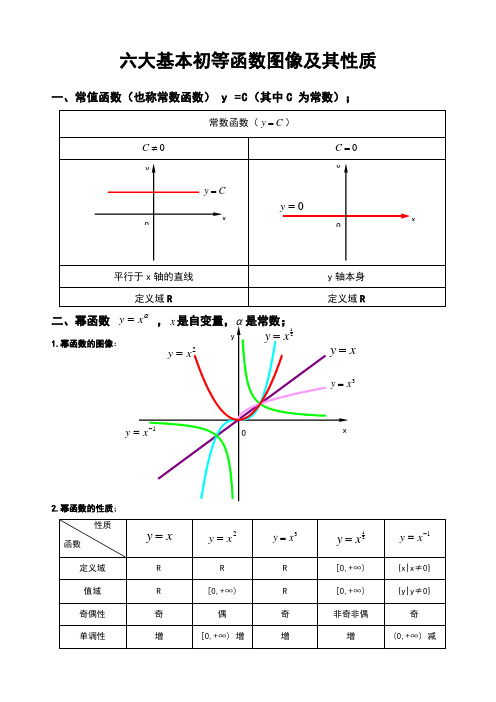
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);二、幂函数 αy =1.幂函数的图像:2.幂函数的性质;3y1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.指数函数的性质;1(1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
.当1>a 时,a 值越大,x a y =的图像越靠近y 轴;.当10<<a 时,a 值越大,xa y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)n m n m a a a -=÷(3)()()mn nmnm aaa ==xf x xxx g ⎪⎫⎛=1)((4)()n n n b a ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。
六种基本初等函数(elementaryfunction)
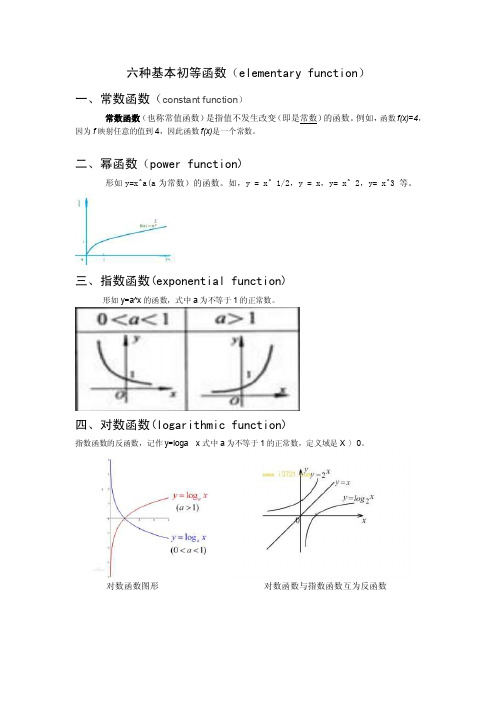
六种基本初等函数(elementary function)
一、常数函数(constant function)
因为f映射任意的值到4,因此函数f(x)是一个常数。
二、幂函数(power function)
形如y=x^a(a为常数)的函数。
如,y = x^ 1/2,y = x,y= x^ 2,y= x^3 等。
三、指数函数(exponential function)
形如y=a^x的函数,式中a为不等于1的正常数。
四、对数函数(logarithmic function)
指数函数的反函数,记作y=loga x式中a为不等于1的正常数,定义域是X〉0。
对数函数图形对数函数与指数函数互为反函数
五、三角函数(trigonometric function)
即正弦函数y=sinx ,余弦函数y=cosx ,正切函数y=tanx,余切函数y=cotx ,正割函数y=secx,余割函数y=cscx。
六、反三角函数(inverse trigonometic function)
反正弦函数y = arcsin x,为y=sin x的反函数反余弦函数y = arccos x,为y=cos x 的反函数
反正切函数y = arctan x,为y=tan x 的反函数反余切函数y = arccot x ,为y=cot x的反函数
反正割函数y = arcsec x ,为y=sec x的反函数反余割函数y = arccsc x ,为y=csc x的反函数七、定义域,值域和单调性。
高中基本初等函数总结归纳.doc

第二章基本初等函数(I)£2.13指数函数【2.1.1】指数与指数幂的运算(1)根式的概念① 如果,n./?e N + ,那么x 叫做的n 次方根.当n 是奇数时,《的次方根用符号&表示;当是偶数时,正数的正的n 次方根用符号 表示,负的n 次方根用符号-表示;0的n 次方根是0;负数6T 没有n 次方根.② 式子叫做根式,这里n 叫做根指数,6?叫做被开方数.当/2为奇数时,为任 意实数;当/?为偶数吋,tz>0.③ 根式的性质:(‘)当n 为奇数时,= a ;当/?.为偶数时,(2)分数指数幂的概念① 正数的正分数桁数幂的意义是0的正分 数指数幂等于0.- 2 1 - / 1② 正数的负分数指数幂的意义是:“"=(一广=彳(一广0/〉0,爪,託乂,且 a V aZ2>1). 0的负分数指数¥没有意义.注意口诀:底数取倒数,指数取相反数. (3)分数指数幂的运算性质① W = a r+s (a>0,r,sE R)(§)(</)、-a rs {a >0, r,5G R)③(ab)r= a r b r(a 〉0,b 〉0,re R)【2.1.2】指数函数及其性质指数函数y z y = a xy = a xyJ = 1J = 1(04)(0,1)0 X 0Xy/a" =| a \=a —a (^/>0) (tz<0)K2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①苦¥ = ;7(6/〉0,且《矣1),则叫做以tz为底7V的对数,id作x = log u/V,其屮0叫做底数,2V叫做真数.②负数和零没有对数.③对数式与指数式的互化:x二log, N^a x => 0,6/1, > 0).(2)几个重要的对数恒等式log w 1 = 0, log w 6Z = 1, \og a a h = b .(3)常用对数与自然对数常用对数:IgN,即log m7V;自然对数:\nN,即log^yV (其中£> = 2.71828…).(4)对数的运算性质如果〉0,7V〉0,那么M①加法:log w M + log^ N = log rt{MN)②减法:log n M - log^ N = \og a—n⑤ log h M n=-\og a M(b^^nER)⑥ 换庖公式(l blog; TV lQgz? N (b〉0,且/?弇1)1 log/, “【2.2.2】对数函数及其性质(5)对数函数(6)设函数y = /(幻的定义域为A,值域为C,从式子y = /(x)中解出X,得式子义二炉(>,)•如果对于y在C屮的任何一个位,通过式子x = x在A屮都科唯一确定的值和它对应,那么式子x = ^(y)表示x是y的函数,函数x = 叫做函数j = ,(x)的反函数,记作又二/—1。
基本初等函数总结

解 :因为-1<log������ < 1, 所以 当 故
1 a>1 时 ,y=logax 为增函数 ,有 ������ 3 3 a> , 结合a>1,故 a> ; 2 2 2 3 2 3 1 log������ ������
=
2 −1<log������ 3
2 3
< 1=logaa. <
1 ������ 2 3
专题二 指数函数、对数函数、幂函数的图象和性质的应用 指数函数、对数函数、幂函数是重要的基本初等函数.它们的图 象与性质始终是高考考查的重点.由于指数函数 y=ax(a>0,a≠1,x∈R),对数函数y=logax(a>0,a≠1,x>0)的图象与性质 都与a的取值有密切的联系,幂函数y=xα的图象与性质与α的取值有 关,因此,在a,α的值不确定时,要对它们进行分类讨论,利用图象可以 很快捷、直观地解决比较大小、求根等计算问题.
知识建构
综合应用
真题放送
专题一
专题二
专题三
专题四
(5)作 y=f(|x|)的图象时,可先将 y=f(x)(x≥0)的部分作出,再利用偶 函数的图象关于 y 轴对称,作出 x< 0 时 f(x)的图象. 例如,先画出 y=l og 1 ������(x>0)的图象 C1,再作出 C1 关于 y 轴对称的
∴x>2,∴f(x)的定义域为(2,+∞).
答案:C
知识建构
综合应用
真题放送
1
2
3
4
5
6
7
8
9
10
11
12
2(北京高考)下列函数中,定义域是R且为增函数的是 ( ) A.y=e-x B.y=x3 C.y=ln x D.y=|x| 解析:A项,函数y=e-x为R上的减函数; B项,函数y=x3为R上的增函数; C项,函数y=ln x为(0,+∞)上的增函数; D项,函数y=|x|在(-∞,0]上为减函数,在(0,+∞)上为增函数.故只有 B项符合题意,应选B. 答案:B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数总结表格
1. 常数函数:
- 定义:常数函数是一个恒定的值,不随自变量的变化而变化。
- 表达式:f(x) = c,其中c为常数。
- 特点:图像是一条水平直线,斜率为0。
2. 幂函数:
- 定义:幂函数是自变量以某个常数为指数的函数。
- 表达式:f(x) = x^n,其中n为实数。
- 特点:
- 当n为正数时,图像从原点出发,并随着x增大而增大,斜率逐渐变大;
- 当n为负数时,图像从正无穷大或负无穷大出发,并随着x增大而逐渐趋近于0;
- 当n为偶数时,图像关于y轴对称;
- 当n为奇数时,图像关于原点对称。
3. 指数函数:
- 定义:指数函数是以一个正常数为底数,自变量为指数的函数。
- 表达式:f(x) = a^x,其中a为正常数且不等于1。
- 特点:
- 当a大于1时,图像从原点出发,并随着x增大而变大,斜率逐渐变大;
- 当0 < a < 1时,图像从正无穷大出发,并随着x增大而逐渐趋近于0;
- 当a等于1时,图像是一条水平直线,斜率为0。
4. 对数函数:
- 定义:对数函数是指以一个正常数为底数,自变量为函数值的指数的函数。
- 表达式:f(x) = logₐ(x),其中a为一个正常数且不等于1,x为正实数。
- 特点:与指数函数为互逆函数,反映了指数运算的逆运算关系。
5. 三角函数:
- 正弦函数:
- 定义:正弦函数是一个周期性函数,描述了单位圆上的y 坐标值。
- 表达式:f(x) = sin(x),其中x为弧度。
- 特点:
- 周期为2π;
- 在x为0、π、2π等整数倍时,达到最大值1;
- 在x为π/2、3π/2等奇数倍时,达到最小值-1;
- 在x为π、2π等偶数倍时,取0。
- 余弦函数:
- 定义:余弦函数是一个周期性函数,描述了单位圆上的x 坐标值。
- 表达式:f(x) = cos(x),其中x为弧度。
- 特点:
- 周期为2π;
- 在x为0、2π等整数倍时,达到最大值1;
- 在x为π/2、3π/2等奇数倍时,取0;
- 在x为π、2π等偶数倍时,达到最小值-1。
- 正切函数:
- 定义:正切函数是一个周期性函数,描述了单位圆上的斜率值。
- 表达式:f(x) = tan(x),其中x为弧度,x不等于π/2 + kπ,k为整数。
- 特点:
- 周期为π;
- 在x为π/4、5π/4等奇数倍时,达到最大值1;
- 在x为3π/4、7π/4等奇数倍时,达到最小值-1;
6. 反三角函数:
- 反正弦函数:
- 定义:反正弦函数是正弦函数的反函数,用于求解一个角的正弦值。
- 表达式:f(x) = sin^(-1)(x),定义域为[-1, 1],值域为[-π/2, π/2]。
- 反余弦函数:
- 定义:反余弦函数是余弦函数的反函数,用于求解一个
角的余弦值。
- 表达式:f(x) = cos^(-1)(x),定义域为[-1, 1],值域为[0, π]。
- 反正切函数:
- 定义:反正切函数是正切函数的反函数,用于求解一个角的正切值。
- 表达式:f(x) = tan^(-1)(x),定义域为实数集,值域为[-π/2, π/2]。
通过以上的表格,我们可以看到基本初等函数的表达式、特点以及定义域与值域。
这些函数在数学和物理中都有广泛的运用,深入理解它们的特点对我们的学习和应用非常重要。
