管道热边界层理论的研究
第四章 边界层理论基础 边界层理论由普朗特1904年 ( Prantdl)提出,用于处理高 Re 数的流动问题。边界层理

y u0 u0
u0
x=0
u0 x
壁面附近速度梯度较大的流体层称为边界层。边界 层外,速度梯度接近于零的区称为外流区或主流区。
二、边界层的形成过程
层流边界层和湍流边界层
y 层流边界层 过 湍流边界层
在板前缘附近,边界层 内流速较低,为层流边界 层;而后逐渐过渡为湍流 u0
u0 u0
渡 区
u0
湍流 核心
在距壁面前缘 x 处,取 y
u0
一微元控制体
2
dV=δdx(1)
将动量守恒原理应用 δ
于微元控制体dV,得
ΣF d(mu) dθ
1
0
dx
x 方向:
ΣFx
d (mux ) dθ
(1)
3 δ dδ
4 x
一、边界层积分动量方程的推导
1-2截面:流入
δ
m1 ρuxdy(1)
0
δ
J1
ρu
2 x
dy(1)
边界层外为理想流体的势流,可用 Bernolli方程 描述。在流动的同一水平高度上,有
p ρu02 常数
2
dp dx
ρu0
du0 dx
0
u0
dp 0
dx
边界层内:p y 0
y p1
p3 δ
0
dp 0 dx
p2
p4
x
二、普朗特边界层方程的解
ux
ux x
uy
ux y
ν 2ux y 2
流函数
O(1)
(4)y :在边界层的范围内,y 由 0→δ,y O(δ)
(5)uy:由连续性方程
ux uy 0 x y
ux O(1) , x
流体力学与传热:12边界层理论

边界层内粘性 这一薄层内速度
平板上u=0 力不可忽略
梯度 vx 很大 y
边界层外边界 U99%
边界层名义厚度 外边界上流速达到U99%的 点到物面的法向距离。
根据速度分布的特点,可将流场分为两个区域:
一、边界层
这一薄层内速度梯度 vx 很大。 y
边界层内的流动是有旋流动
z
1 2
( v y x
vx y
离,近似认为y=δ,Vx=U。
具有Blasius相似解:
vx f ' () df / d
U
y U x
(12-18)
将上式代入边界层方程,有
2 f ''' ff '' 0
(12-20)
f满足的是三阶非线性常微分方程
边界条件为:
η=0, f=0, f′=0 η→∞, f′=1
非线性的微分方程,得不到解析解。
Rekp
(Ux
)kp
Uxkp
5 105
层流边界层转为湍流边界层转捩点的位置坐标
xkp
5105
U
(12-1)
§12-2 边界层基本微分方程
粘性不可压缩流体,不计质量力,定常流过 小曲率物体,物体表面可近似当作平面。
取物面法线为y轴。在大Re数情况下的边界 层流动有下面两个主要性质:
1) 边界层厚度较物体特征长度小得多,即
边界层: 在固体壁面附近,显著地受到粘性 影响的这一薄层。
从边界层厚度很小这个前提出发,Prandtl率先 建立了边界层内粘性流体运动的简化方程,开创 了近代流体力学的一个分支——边界层理论。
均匀来流绕一薄平板流动,微型批托管测得 沿平板垂直方向的速度分布如下图:
边界层理论在流体力学中的应用

边界层理论在流体力学中的应用引言流体力学研究的是流体在受力作用下的运动规律和性质。
在理论研究和工程应用中,边界层理论是流体力学的一个重要组成部分。
边界层理论描述了流体在靠近壁面的区域内,流动速度、压力、温度等物理量的变化规律。
本文将介绍边界层理论在流体力学中的应用,包括边界层的定义、边界层分析的方法以及边界层理论在实际工程中的应用案例。
1. 边界层的定义边界层是指流体靠近壁面的区域,其性质与远离壁面的流体存在明显差异。
一般来说,边界层的厚度相对较小,但对流体运动和传热传质过程有着重要影响。
边界层理论的研究对象主要是属于牛顿流体的不可压缩流体情况。
2. 边界层分析的方法边界层分析是研究边界层的关键方法之一,常用的方法包括速度边界层分析和能量边界层分析。
2.1 速度边界层分析速度边界层分析主要考虑流体在边界层内的速度分布情况。
一般来说,边界层靠近壁面时流速接近零,随着距离壁面的增加逐渐增大。
根据速度剖面的特征,可以将边界层划分为无滑移层、过渡层和主层三个区域。
•无滑移层:靠近壁面的区域,流体速度接近壁面速度,可以视为无滑移状态。
•过渡层:在无滑移层之上的区域,流体速度逐渐增大,但流体分子之间还存在相对滑移。
•主层:在过渡层之上的区域,流体速度增大趋势基本保持不变。
2.2 能量边界层分析能量边界层分析主要研究流体在边界层内的温度和压力变化情况。
在无滑移层内,温度和压力基本保持不变;在过渡层和主层内,存在温度和压力的变化。
3. 边界层理论在实际工程中的应用案例边界层理论在实际工程中有着广泛的应用,下面将介绍一些典型的案例。
3.1 汽车空气动力学研究汽车行驶时会与周围空气发生相互作用,而边界层理论可以帮助研究汽车在高速行驶时的空气动力学特性。
通过分析边界层的速度和压力分布,可以优化汽车外形和设计,减小空气阻力,提高燃油经济性。
3.2 航空气动力学研究在航空工程中,边界层理论被广泛应用于飞机机翼和机身的设计和改进。
流体动力学中的边界层理论应用研究

流体动力学中的边界层理论应用研究引言:流体动力学是物理学的一个重要分支,研究液体和气体的运动和行为。
在流体动力学中,边界层理论是一项基础而重要的研究领域。
边界层是指流体靠近固体表面时,由于黏性作用而发生变化的区域。
边界层的研究对于理解和解释无数实际问题具有重要意义,如空气动力学、水流、汽车运动和航空等领域的设计与优化都离不开边界层理论的应用研究。
本文将带领读者了解边界层理论的几个重要定律,并介绍其在实验中的应用。
一、边界层理论的几个重要定律:1. 力学能量定理:力学能量定理是流体动力学的基础定律之一,它指出了流体的能量在各个点之间的相互转换关系。
在边界层理论中,力学能量定理可以用来解释边界层内部流体的能量变化和分布情况。
通过实验观测和数值模拟,研究人员可以得出边界层的压力、速度和温度分布等重要参数,进而对流体的运动和行为进行分析和预测。
2. 缓变流动方程:缓变流动方程是边界层理论的重要数学方程,描述了在缓变流动情况下流体的运动规律。
在实验中可以通过精密的测量装置和仪器来观测流体在不同位置和时间的速度、压力和温度等变化,并将其与缓变流动方程进行对比和验证。
通过实验的数据分析和处理,可以得出边界层的分布和特性等相关结果。
3. 涡量定理:涡量定理是边界层理论中的一个重要概念,涡量是指流体在旋转过程中产生的旋转量。
边界层中的涡量对流体运动和动力学行为有重要影响。
实验中可以通过使用仪器观测流体中的旋转速度和旋转方向等参数,进而分析和评价边界层的旋转特性,并寻求相应的物理解释。
二、实验准备和过程:在进行流体动力学中边界层理论的实验时,我们需要准备以下材料和仪器:1. 流体实验设备:根据实验的需要,可以选择不同类型和性质的流体用于研究。
例如,可以使用空气、水或其他液体作为流体介质。
2. 测量仪器和传感器:实验中需要使用精密的测量仪器和传感器来观测流体的速度、压力和温度等参数。
比如,在边界层实验中可以使用热导传感器、压力传感器和激光多普勒测速仪等设备。
边界层理论(Boundary layer theory)--西安交大

)之外的流体速度就形成:润湿→附着→内摩擦力→减速→梯度
边界层内:沿板面法向的速度梯度很边界层外:不存在速度梯度或速度梯度
流体在平板上流动时的边界层:
流动边界层:存在着较大速度梯度的流体层区域,即流速降为主体流速的99%以内的区域。
边界层厚度:边界层外缘与壁面间的垂直距离。
层流边界层:在平板的前段,边界层内的流型为层流。
湍流边界层:离平板前沿一段距离后,边界层内的流
直管内:流体须经一定的距离才能形成稳定的边界层。
由于总流量不变,中心流速增加。
边界层占据整个管截面。
与物体的长度相比,边界层的厚度很小;边界层内沿边界层厚度的速度变化非常急边界层沿着流体流动的方向逐渐增厚;
边界层中各截面上的压强等于同一截面上在边界层内粘滞力和惯性力是同一数量级边界层内流体的流动存在层流和紊流两种
圆柱后部:猫眼
扩张管(上壁有抽吸)
B
S′
A
涡,这种旋涡具有一定的脱落频率,称为卡门涡街.
湍流产生的原因:
湍动强度
在模型实验中,模拟湍流,要求雷诺数和湍动强边界层的转变、分离以及热量和质量传递系数等
依微分方程的个数:零方程模型、一方
FLUENT软件在化学处理领域主要可应用 于:
燃烧 干燥 过滤 传热和传质 材料处理 混合 反应 分离 蒸馏 喷射控制 成型 焚化 测量/控制 聚合 沉淀 通风
。
边界层理论在工程流体力学中的应用

边界层理论在工程流体力学中的应用工程流体力学是研究流体在工程领域中运动和相互作用的学科。
边界层理论作为工程流体力学中重要的理论工具,在实际工程应用中起着关键的作用。
本文将介绍边界层理论在工程流体力学中的应用,并探讨其在不同工程领域的优势和挑战。
边界层是流体流动中离开壁面一段距离处的区域,其厚度与壁面形状、流体性质等相关。
边界层理论描述了在稳定流动的情况下,流体在边界处的运动特性。
在工程流体力学中,边界层理论应用广泛,例如在飞机、汽车、输油管道等领域。
首先,在空气动力学领域,边界层理论的应用十分重要。
飞机在空中运动时,与空气产生相对运动,会形成空气流动的边界层。
通过边界层理论,可以分析空气流动的速度分布、压力分布等参数,这些参数对于飞机设计和性能优化至关重要。
例如,可以通过调整飞机表面的纹理来改变空气流动的特性,以减少飞行阻力,提高飞机的燃油效率。
其次,在液体输送管道设计中,边界层理论也发挥着重要作用。
在输油管道中,流体与管道壁面之间的摩擦力对管道流体的输送有很大影响。
通过边界层理论,可以确定管道内流体的摩擦系数,从而确定管道的流量和输油能力。
边界层理论的应用还可以帮助设计高效的管道减阻器,减少管道中的压降,并降低能耗。
此外,边界层理论在汽车工程中也有广泛应用。
汽车行驶时,空气流经车身表面形成边界层,对车辆的气动性能产生影响。
通过边界层理论,可以研究车辆表面压力分布,评估气动阻力和升力。
这些数据对于改善汽车的稳定性、减少燃油消耗具有重要意义。
同时,边界层理论还应用于车身表面流场控制研究,通过改变车身表面形状和纹理,减少气动噪音和气动振动。
然而,边界层理论在工程流体力学中的应用也面临一些挑战。
首先,实际工程中流体流动往往涉及复杂的流动模式和边界条件,需要进一步的数值模拟和实验验证。
其次,边界层理论中的假设和简化有时难以准确描述实际情况,需要结合实验和经验进行修正。
此外,边界层理论需要考虑流体的非定常性和湍流特性,这对于流动的稳定性和控制具有挑战。
边界层理论
y 0
h
λ:流体导热系数
t
t y
y 0
∂t/∂y: 贴壁流体层的温度梯度 注意与导热问题第三类边界条件的区别
SJTU-OYH
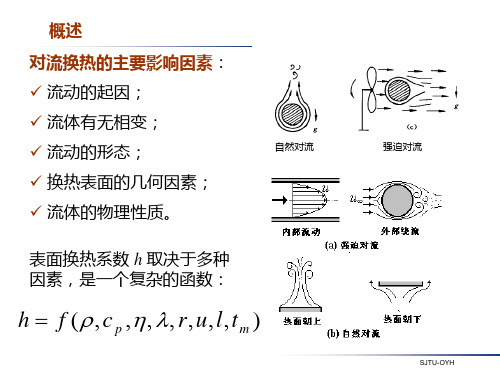
对流传热问题的数学描述 假设: 流体为连续介质,流动为二维; 流体为不可压缩牛顿流体; 常物性、无内热源; 忽略粘性耗散热;
忽略辐射换热。 四个未知量:u, v, p, t。
x<xc, Re<Rec 层流 x>xc, Re>Rec 湍流
层流底层(粘性底层):紧靠壁面处,粘性力占主导地位,使 粘附于壁的一极薄层仍然会保持层流特征。层流底层内具有最 大的速度梯度。 SJTU-OYH
4-2边界层型对流传热问题的数学描述 波尔豪森热边界层的概念: 实验发现:流体对流换热时温 度梯度主要存在于近壁面的薄 层,主流区温度梯度几乎为零。
4-2边界层型对流传热问题的数学描述 波尔豪森热边界层的概念: 与边界层内速度分布一样,热边界 层内的温度分布也与流动形态密切 相关。 层流:温度呈抛物线分布 湍流:温度呈幂函数分布
y y w ,t w ,l
hw,t hw,l
u ' v' + =0 x' y '
u ' u ' p ' 1 2u ' 2u ' u ' +v' =- Eu 2 2 x' y ' x' Re x' y '
欧拉数 雷诺数 普朗特数 贝克莱数 努谢尔数
2 Eu p /( u )
v v v p 2v 2v ( u v ) Fy ( 2 2 ) x y y x y
工程流体力学中的边界层理论与应用分析

工程流体力学中的边界层理论与应用分析工程流体力学是研究流体在工程中的力学性质和运动规律的学科,对于工程流体力学的研究,边界层理论与应用分析是一个重要的方向。
边界层是指在流体与固体表面接触处形成的一层流体,其性质和流动规律与远离固体表面的自由流体存在差异。
边界层理论主要研究边界层内的速度剖面、压力分布等参数。
边界层可以分为无粘和粘性边界层,其中粘性边界层是指存在粘性阻力的情况。
边界层理论在工程流体力学中的应用非常广泛,下面将从不同的领域介绍边界层理论的应用分析。
在空气动力学领域中,边界层理论被广泛用于研究飞行器表面的阻力和升力。
通过分析边界层内的速度剖面和压力分布,可以确定表面阻力的大小和性质,从而设计出形状合理的飞行器,并进行飞行性能的预测和优化。
在船舶工程中,边界层理论可以用于研究船体表面的水动力性能。
由于船体往往是复杂的几何形状,通过边界层理论可以对船体表面的粘性阻力进行分析和计算,为减少阻力、提高速度和降低耗能提供指导。
在地下水力学中,边界层理论可以用于研究地下水的渗流过程。
地下水与地下土壤之间的边界层对渗流的速度分布和水力梯度有重要影响,通过边界层理论的分析,可以更好地理解和预测地下水的渗流行为,为地下水资源的管理和利用提供科学依据。
在石油工程领域中,边界层理论被应用于油井开采过程中的油水两相流动研究。
边界层理论可以用于分析油井壁面上的粘性阻力和表面张力对油水两相流动的影响,从而指导油井的生产优化和多相流模拟。
此外,边界层理论还可以应用于工程中的热传导和传热问题、湍流流动和紊流的研究、污染物输运和混合过程的分析等。
总之,边界层理论与应用分析在工程流体力学中起着重要的作用。
通过对边界层内的速度剖面、压力分布等参数的研究,可以更准确地描述流体在工程中的行为并进行性能分析。
边界层的研究和应用将为工程设计、优化和控制提供重要的理论依据和实践指导。
