平行四边形相关知识梳理与常考题型

平行四边形相关知识梳理与常考题型总结
1.平行四边形的定义:(1)定义:两组对边分别平行的四边形是平行四边形;
(2)表示:平行四边形用符号“□”来表示。
2.平行四边形性质:(1)边:两组对边分别平行且相等;
(3)对角线:对角线互相平分。
3.平行四边形的判别方法:
①两组对边分别平行的四边形是平行四边形
②对角线互相平分的四边形是平行四边形
③一组对边平行且相等的四边形是平行四边形
④两组对边分别相等的四边形是平行四边形
⑤两组对角分别相等的四边形是平行四边形
4、三角形中位线——构造平行四边形
(1) 定义:连结三角形两边中点的线段叫做三角形的中位线.
(2)三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半.
三角形中位线定理的作用:①位置关系:可以证明两条直线平行.
②数量关系:可以证明线段的倍分关系.
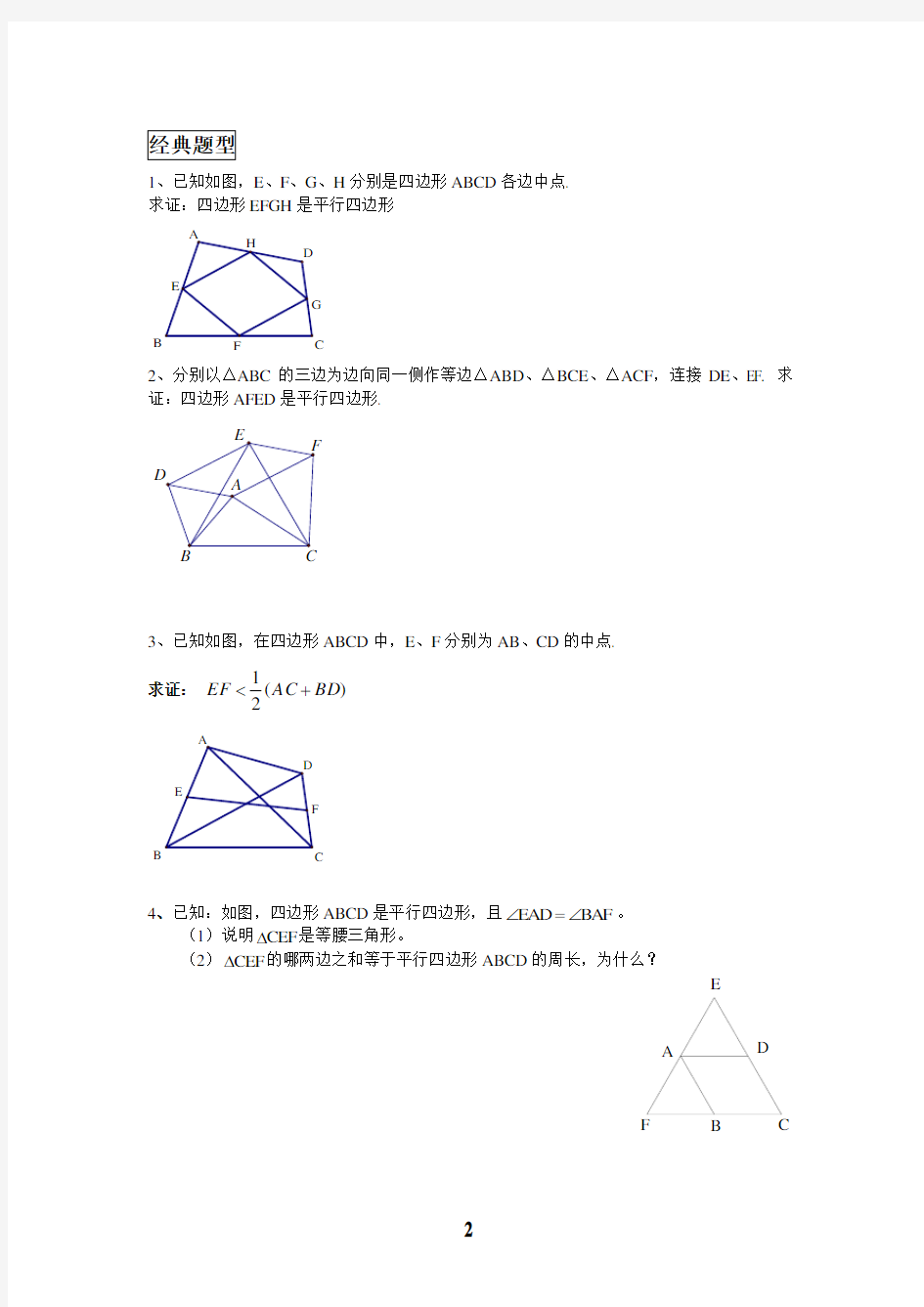
1、已知如图,E 、F 、G 、H 分别是四边形ABCD
各边中点. 求证:四边形EFGH 是平行四边形
2、分别以△ABC 的三边为边向同一侧作等边△ABD 、△BCE 、△ACF ,连接DE 、EF. 求证:四边形AFED 是平行四边形.
3
、已知如图,在四边形ABCD 中,E 、F 分别为AB 、CD 的中点.
求证:
4、已知:如图,四边形
(1)说明?CEF (2)?CEF
B
B
)
(2
1
BD AC EF +<
5.(黄冈市中考题)如图所示,平行四边形ABCD 中,G 、H 是对角线BD 上两点,且DG =BH ,DF =BE.
求证:四边形EHFG 是平行四边形
.
6 已知:如图,在平行四边形ABCD中,AB=2BC,E,F在直线BC上,且BE=BC =CF.求证:AF⊥DE.
7.(江西省中考题)已知:如图,平行四边形ABCD 中,AE ⊥BC ,CF ⊥BD ,垂足分别为E 、F ,G 、H 分别是AD 、BC 的中点,GH 交BD 于点O.
求证:GH 与EF 互相平分
.
8.(河南省中考题)已知:如图,平行四边形ABCD 中,对角线AC 的平行线MN 分别交DA 、DC 延长线于点M 、N ,交AB 、BC 于点P 、Q.
求证:MQ =NP.
1.已知:如图,平行四边形ABCD 中,AB =2BC ,E 为AB 中点,DF ⊥BC ,垂足F. 求证:∠AED =∠EFB.
E F
B C
2.如图,在平行四边形ABCD中,BC=2AB,M为AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.
作业
1.如下图所示,ABCD是平行四边形,以AD、BC为边在形外作等边三角形ADE和CBF,连结BD、EF,且它们相交于O,求证:EO=FO,DO=BO.
2.如图所示,∠EDA是平行四边形ABCD的外角,DF平分∠EDA与BA延长线交于F,FD 延长线与BC延长线交于G.求证:BF=BG.
3.如图所示,平行四边形ABCD中,作AF⊥BC于F,交BD于E,若DE=2AB.求证:∠ABD=2∠EBC.
取G 为DE 中点,连接AG.
在RT△ADE中,AG为斜边上的中线。
∴DE/2 = AG = EG = DG = AB
∴∠ABE = ∠AGE ,∠ADE=∠GAD
∴∠ABE = ∠AGE = ∠ADE+∠GAD=2∠ADE = 2∠CBD
证明:∵ABCD平行四边形AF⊥BC
∴∠EAD=90°
取DE中点M,则AM=MD=ED(直角三角形斜边上中线等于斜边一半)
∵DE=2AB
∴AB=AM=MD
∠ADM=∠DAM
∠ABD=∠AMB
∵∠AMB=∠ADM+∠DAM=2∠ADM
∴∠ABD=2∠ADM
∵∠ADM=∠DBC
∴∠ABD=2∠DBC
4.如图所示,平行四边形ABCD中,以BC、CD为边向内作等边三角形BCE和CDF.求证:△AEF为等边三角形.
5.如图所示,在△ABC中,BD平分∠B,DE∥BC交AB于E,EF∥AC交BC于F,求证:BE=FC
6.如图所示,平行四边形ABCD中,E是AB的中点,F是CD中点,分别延长BA和DC到
G、H,使AG=CH,连结GF、EH,求证:GF∥EH
7.如图所示,平行四边形ABCD中,E、F分别在AD、BC上,且AE=CF,AF与BE相交于G,CE与DF相交于H.求证:EF与GH互相平分
(1)在△ABC和△DBE中
AB=AD
∠ABC=∠EBC-∠EAB,∠DBE=∠DBA-∠EBA 因为∠EBC=∠DBE=60°
所以∠ABC=∠DBE
BC=BE
因此△ABC≌△DBE,DE=AC。
△ACF是等边三角形,所以AF=AC=DE
在△ABC和△FEC中
AC=FC
∠ACB=∠ECB-∠ECA
∠FCE=∠FCA-∠ECA
因为∠ECB=∠FCA=60°
所以∠ACB=∠FCE
BC=EC
因此△ABC≌△FEC,EF=AB
因为△ABD是等边三角形,所以AD=AB=EF
四边形ADFE两组对边分别相等,是平行四边形
平行四边形典型例题精编版
平行四边形典型例题 1 如图,□ABCD的对角线AC、BD 相交于点O,则图中全等三角形有() A .2 对 B .3对 C .4 对 D .5对 17如图,□ABCD中,∠ B、∠ C的平分线交于点O ,BO 和CD 的延长线交于求证:BO=OE. 例3】如图,在ABCD中,AE⊥ BC于E ,AF⊥DC 于F ,∠ ADC=60°,BE=2,CF=1, 求△ DEC 的面积. 解】在中,,、 在Rt △ABE 中,, 在△ 中,
例 4】已知:如图, D 是等腰△ ABC 的底边 BC 上一点, DE//AC , DF//AB 求证: DE+DF=A .B , ,从而可以利用平行四边形的定义和性质,等腰 三角 形的判定和性质来证. 解】∵ , ∴四边形 是平行四边形. ∴. ∵ ,∴ . ∵ ,∴ 说明:证明一条线段等于另外两条线段的和常采用的方法是: 分为两段,证明这两段分别等于另两条线段. 于 ,求证: 分析】 分析】由于 把三条线段中较长的线段 例 5】如图, 已知: 中, 相交于 点, 于 ,
解】因为四边形是平行四边形,所以,又因为、交于点, 所以. 又因为, 所以 从而例6】已知:如图,AB//DC ,AC、BD交于O,且 AC=BD。 求证:OD=OC. 证明:过B 作交DC延长线于E,则 于是△≌△ ∵ ,, E
∵, ∴∴ 说明:本题条件中有“夹在两条平行线之间的相等且相交的线 段 时用不上,为此通过作平行线,由“夹在两条平行线间的平行线B BE ,得到等腰△ BDE ,使问题得解. 例 7】如图, □ABCD 的对角线 AC 的垂直平分线与边 AD 、BC 分别交于 E 、F , 例 8】如图所示, □ABCD 中,各内角的平分线分别相交于点 E 、 F 、 G 、 H , 证明:四边形 EFGH 是矩形。 例 9】如图所示,已知矩形 ABCD 的对角线 AC 、BD 交于点 O ,过顶点 C ,作 BD 的垂线与∠ BAD 的平分线相交于点 E ,交 BD 于 G ,证明: AC=CE 。 求证:四边形 AFCE 是菱形. 解:略。 置交错而 A 由 AC 平移到 E
平行四边形综合性质及经典例题
一对一个性化辅导教案
平行四边形的性质与判定 平行四边形及其性质(一) 一、 教学目标: 1. 理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质. 2. 会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证. 3. 培养学生发现问题、解决问题的能力及逻辑推理能力. 二、 重点、难点 1. 重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用. 2. 难点:运用平行四边形的性质进行有关的论证和计算. 三、 课堂引入 1.我们一起来观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象 平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗 你能总结出平行四边形的定义吗 (1)定义:两组对边分别平行的四边形是平行四边形. (2)表示:平行四边形用符号“ ”来表示. 如图,在四边形ABCD 中,AB∥DC,AD∥BC,那么四边形ABCD 是平行四边形.平行四边形ABCD 记作“ ABCD”,读作“平行四边形ABCD”. ①∵AB ?50?360?360?180行 四边形的面积计算 六、随堂练习 1.在平行四边形中,周长等于48, ① 已知一边长12,求各边的长 ② 已知AB=2BC ,求各边的长 ③ 已知对角线AC 、BD 交于点O ,△AOD 与△AOB 的周长的差是10,求各边的长 2.如图,ABCD 中,AE⊥BD,∠EAD=60°,AE=2cm ,AC+BD=14cm ,则△OBC 的周长是____ ___cm .
3.ABCD 一内角的平分线与边相交并把这条边分成cm 5,cm 7的两条线段,则ABCD 的周长是__ ___cm . 七、课后练习 1.判断对错 (1)在ABCD 中,AC 交BD 于O ,则AO=OB=OC=OD . ( ) (2)平行四边形两条对角线的交点到一组对边的距离相等. ( ) (3)平行四边形的两组对边分别平行且相等. ( ) (4)平行四边形是轴对称图形. ( ) 2.在 ABCD 中,AC =6、BD =4,则AB 的范围是_ ____ __. 3.在平行四边形ABCD 中,已知AB 、BC 、CD 三条边的长度分别为(x+3),(x-4)和16,则这个四边形的周长是 . 4.公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB =15cm ,AD =12cm ,AC ⊥BC ,求小路BC ,CD ,OC 的长,并算出绿地的面积. (一) 平行四边形的判定 一、教学目标: 1.在探索平行四边形的判别条件中,理解并掌握用边、对角线来判定平行四边形的方法. 2.会综合运用平行四边形的判定方法和性质来解决问题. 3.培养用类比、逆向联想及运动的思维方法来研究问题. 二、重点、难点 重点:平行四边形的判定方法及应用. 难点:平行四边形的判定定理与性质定理的灵活应用. 四、课堂引入 1.欣赏图片、提出问题. 展示图片,提出问题,在刚才演示的图片中,有哪些是平行四边形你是怎样判断的 2.【探究】:小明的父亲手中有一些木条,他想通过适当的测量、割剪,钉制一个平行四边形框架,你能帮他想出一些办法来吗
平行四边形经典题型
1.平行四边形的性质: ①平行四边形两组对边相等。 ②平行四边形两组对角相等。 ③平行四边形对角线互分平分。 2.平行四边形判定: 定理1、一组对边平行且相等的四边形是平行四边形 定理2、两组对边分别相等的四边形是平行四边形。 定理3、对角线互相平分的四边形是平行四边形。 定理4、两组对角分别相等的四边形是平行四边形。 3.三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。 4.逆定理1:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是 三角形的中位线。 逆定理2:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
第四节:中心对称图形 课堂练习 1.下列图形中,既是中心对称图形,又是轴对称图形的是() A.正三角形 B.平行四边形 C.等腰直角三角形 D.正六边形 2.下列图形中,不是中心对称图形的是() 3.下列图形中,既是轴对称图形又是中心对称图形的是(). 4.下三图是由三个相同的小正方形拼成的图形,请你再添加一个同样大小的小正方形,使 所得的新图形分别为下列A,B,C题要求的图形,请画出示意图. (1)是中心对称图形,但不是轴对称图形; (2)是轴对称图形,但不是中心对称图形; (3)既是中心对称图形,又是轴对称图形. 第五节:平行四边形的判定 例题讲解 例1:判断下列说法的正误,如果错误请画出反例图 ①一组对边平行,另一组对边相等的四边形是平行四边形。 ( ) ②一组对边相等,另一组对边平行的四边形是平行四边形. ( ) ③一组对边平行,一组对角相等的四边形是平行四边形.( ) ④一组对边平行且相等的四边形是平行四边形. ( ) ⑤两组邻角互补的四边形是平行四边形。( ) ⑥相邻两个角都互补的四边形是平行四边形。 ( ) ⑦对角互补的四边形是平行四边形 ( ) ⑧一条对角线分四边形为两个全等三角形,这个四边形是平行四边形 ( ) ⑨两条对角线相等的四边形是平行四边形 ( )例2:如图所示,平行四边形ABCD中,M、N分别为AD、BC的中点,连结AN、DN、BM、CM,且AN、BM交于点P,CM、DN交于点Q.四边形MGNP是平行四边形吗为什么
(完整word版)平行四边形知识点及典型例题
一、知识点讲解: 1.平行四边形的性质: 四边形ABCD 是平行四边形?????? ????. 54321)邻角互补()对角线互相平分;()两组对角分别相等; ()两组对边分别相等;()两组对边分别平行;( 2.平行四边形的判定: . 3. 矩形的性质: 因为四边形ABCD 是矩形??? ? ??.3; 2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所( (4)是轴对称图形,它有两条对称轴. 4矩形的判定: (1)有一个角是直角的平行四边形; (2)有三个角是直角的四边形; (3)对角线相等的平行四边形; (4)对角线相等且互相平分的四边形. ?四边形ABCD 是矩形. 两对角线相交成60°时得等边三角形。 5. 菱形的性质: 因为ABCD 是菱形??? ? ??.321角)对角线垂直且平分对()四个边都相等; (有通性;)具有平行四边形的所( 6. 菱形的判定: ?? ? ?? +边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321?四边形ABCD 是菱形. 菱形中有一个角等于60°时,较短对角线等于边长; 菱形中,若较短对角线等于边长,则有等边三角形; 菱形中,两对角线把菱形分成4个全等的直角三角形,每个直角三角形的斜边是菱形的边,两直角边分别是两对角线的一半。 菱形的面积等于两对角线长积的一半。 A B D O C A B D O C A D B C A D B C O C D B A O C D B A O
C D A B A B C D O 7.正方形的性质: 四边形ABCD是正方形? ? ? ? ? ? . 3 2 1 分对角 )对角线相等垂直且平 ( 角都是直角; )四个边都相等,四个 ( 有通性; )具有平行四边形的所 ( 8. 正方形的判定: ? ? ? ? ? ? ? ? ? + + + + + + 对角线互相垂直 矩形 ) ( 一组邻边等 矩形 ) ( 对角线相等 )菱形 ( 一个直角 )菱形 ( 一个直角 一组邻边等 )平行四边形 ( 5 4 3 2 1 ?四边形ABCD是正方形. 9. 1.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三 遍的一半。 2.由矩形的性质得到直角三角形的一个性质:直角三角形斜边上的中线等于 斜边的一半。 二、例题 例1:如图1,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F. 求证: ∠BAE =∠DCF. 例2如图2,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD 于F. 求证:BE = CF. 例3.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的 中点.求证:四边形DFGE是平行四边形. 例4如图7, ABCD的对角线AC的垂直平分线与边AD,BC分 别相交于点E,F. 求证:四边形AFCE是菱形. (图1) E F O A B C D E F (图2) 图7 A B C D E F O
平行四边形经典题型(培优提高)
中心对称与平行四边形的判定 知识归纳 1.中心对称图形的定义:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与 原图形重合,那么就说这个图形是中心对称图形,这个点就是它的对称中心. 分析:一个图形;围绕一点旋转1800;重合. 2.思考:中心对称与中心对称图形有什么区别和联系? 1)区别: 中心对称是指两个全等图形之间的位置关系,成中心对称的两个图形中,其中一个图形上所有点关于对称中心的对称点都在另一个图形上,反之,另一个图形上所有点关于对称中心的对称点都在这;而中心对称图形是指一个图形本身成中心对称,中心对称图形上所有点关于对称中心的对称点都在这个图形本身上. 2)联系: 如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形;一个中心对称图形也可以看成是关于中心对称的两个图形. 3.中心对称图性质 1)中心对称图形的对称点所连线段都经过对称中心,而且被对称中心所平分. 2)中心对称图形的两个部分是全等的. 注:常见的中心对称图形有:矩形,菱形,正方形,平行四边形,圆,边数为偶数的正多边形,某些规则图形等. 正偶边形是中心对称图形 正奇边形不是中心对称图形如:正三角形不是中心对称图形、等腰梯形不是中心对称图形 4.平行四边形的性质: ①平行四边形两组对边相等。 ②平行四边形两组对角相等。 ③平行四边形对角线互分平分。 5.平行四边形判定: 定理1、一组对边平行且相等的四边形是平行四边形 定理2、两组对边分别相等的四边形是平行四边形。 定理3、对角线互相平分的四边形是平行四边形。 定理4、两组对角分别相等的四边形是平行四边形。
6.三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半。 7.逆定理1:在三角形内,与三角形的两边相交,平行且等于三角形第三边一半的线段是 三角形的中位线。 逆定理2:在三角形内,经过三角形一边的中点,且与另一边平行的线段,是三角形的中位线。
必用平行四边形知识点及典型例题
平行四边形知识点及典型例题 一、知识点讲解:. 定义:两组对边分别平行的四边形是平行四边形. 1.平行四边形的性质: 四边形ABCD 是平行四边形?????? ????. 54321)邻角互补()对角线互相平分;()两组对角分别相等; ()两组对边分别相等;()两组对边分别平行;( 2.平行四边形的判定: . 3. 矩形的性质: 因为四边形ABCD 是矩形??? ? ??.3; 2;1)对角线相等()四个角都是直角(有通性)具有平行四边形的所( (4)是轴对称图形,它有两条对称轴. 4矩形的判定: (1)有一个角是直角的平行四边形; (2)有三个角是直角的四边形; (3)对角线相等的平行四边形; (4)对角线相等且互相平分的四边形. ?四边形ABCD 是矩形. 两对角线相交成60°时得等边三角形。 5. 菱形的性质: 因为ABCD 是菱形??? ? ??.321角)对角线垂直且平分对()四个边都相等; (有通性;)具有平行四边形的所( 6. 菱形的判定: ?? ? ?? +边形)对角线垂直的平行四()四个边都相等(一组邻边等)平行四边形(321?四边形ABCD 是菱形. 菱形中有一个角等于60°时,较短对角线等于边长; 菱形中,若较短对角线等于边长,则有等边三角形; 菱形中,两对角线把菱形分成4个全等的直角三角形,每个直角三角形的斜边是菱形的边,两直角边分别是两对角线的一半。 菱形的面积等于两对角线长积的一半。 A B D O C A B D O C A D B C A D B C O C D B A O C D B A O
C D A B A B C D O 7.正方形的性质: 四边形ABCD 是正方形??? ? ??.321分对角)对角线相等垂直且平(角都是直角; )四个边都相等,四个(有通性;)具有平行四边形的所( 8. 正方形的判定: ???? ? ? ? ?? ++++++对角线互相垂直矩形)(一组邻边等 矩形)(对角线相等)菱形(一个直角)菱形(一个直角一组邻边等)平行四边形(54321?四边形ABCD 是正方形. 9. 三角形中位线 (1)定义:连接三角形两边中点的线段叫做三角形的中位线.每个三角形都有三条中位线. (2)三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半. 10. 直角三角形特殊性质 (1)斜边上的中线等于斜边的一半。 (2)300所对的直角边等于斜边的一半。 (3)射影定理,勾股定理,面积不变定理 特殊的、平行四边形知识点 学生记住
平行四边形 经典例题
平行四边形 一、 基础知识平行四边形 二、1、三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。 2、由矩形的性质得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半。 三、例题 例1、如图1,平行四边形ABCD 中,AE ⊥BD ,CF ⊥BD ,垂足分别为E 、F. 求证:∠BAE =∠DCF. 例2、如图2,矩形ABCD 中,AC 与BD 交于O 点,BE ⊥AC 于E ,CF ⊥BD 于F. 求证:BE = CF. 例3、已知:如图3,在梯形ABCD 中,AD ∥BC ,AB = DC ,点E 、F 分别在AB 、CD 上,且BE = 2EA , CF = 2FD. 求证:∠BEC =∠CFB. (图1) B O A B C D E F (图2)
例4、如图6,E 、F 分别是 ABCD 的AD 、BC 边上的点,且AE = CF. (1 △ ABE ≌△CDF ; (2)若 、N 分别是BE 、DF 的中点,连结MF 、EN ,试判断四边形MFNE 是怎样的四 边形,并证明你的结论. 例5、如图7 的对角线AC 的垂直平分线与边AD ,BC 分别相交于点E ,F.,求证:四边形AFCE 是菱形. 例6、如图8,四边形ABCD 是平行四边形,O 是它的中心,E 、F 是对角线AC 上的点. (1)如果 ,则△DEC ≌△BFA (请你填上一个能使结论成立的一个条件); (2)证明你的结论. 例7、如图9,已知在梯形ABCD 中,AD ∥BC ,AB = DC ,对角线AC 和BD 相交于点O ,E 是BC 边上一个动点(点E 不与B 、C 两点重合),EF ∥BD 交AC 于点F ,EG ∥AC 交BD 于点C. (1)求证:四边形EFOG 的周长等于2OB ; (2)请你将上述题目的条件“梯形ABCD 中,AD ∥BC ,AB = DC”改为另一种四边形,其他条件不变,使得结论,“四边形EFOG 的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证、不必证明. 例8、有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图13(1)、(2)上),并给予合理的解释. A D B C E F (图6) M N 备用图(1) 备用图(2) B C B
平行四边形典型例题
平行四边形典型例题 【例1】如图,□ABCD的对角线AC、BD相交于点O,则图中全等三角形有() A.2对 B.3对 C.4对 D.5对 【分析】由平行四边形的对边平行、对角线互相平分,可得全等三角形有:△ABD和△CDE, △ADC和△CBA ,△AOD 和△BOC 、△AOB 和△COD . 【答案】C 【例2】如图,□ABCD中,∠B、∠C的平分线交于点O ,BO 和CD 的延长线交于E ,求证:BO=OE . 【分析】证线段相等,可证线段所在三角形全等.可证△COE ≌△COB .已知OC 为公共边,∠OCE=∠OCB,又易证∠E=∠EBC.问题得证. 【证明】在□ABCD中,∵AB//CD, ∴, 又∵(角平分线定义). ∴, 又∵, ∴△≌△ ∴. 说明:证线段相等通常有两种方法:(1)在同一三角形中证三角形等腰;(2)不在同一三角形则证两三角形全等.本题也可根据等腰三角形“三线合一”性质证明结论.
【例3】如图,在ABCD中,AE⊥BC于E ,AF⊥DC 于F ,∠ADC=60°,BE=2,CF=1,求△DEC 的面积. 【解】在中,,、. 在Rt △ABE 中,,. ∴,. ∴. 在△中,. ∴. 故. 【例4】已知:如图,D 是等腰△ABC 的底边BC 上一点,DE//AC ,DF//AB .求证:DE+DF=AB. 【分析】由于,,从而可以利用平行四边形的定义和性质,等腰三角形的判定和性质来证. 【解】∵, ∴四边形是平行四边形. ∴. ∵,∴.
∵,∴. ∴. ∴. 说明:证明一条线段等于另外两条线段的和常采用的方法是:把三条线段中较长的线段分为两段,证明这两段分别等于另两条线段. 【例5】如图,已知:中,、相交于点,于, 于,求证:. 【分析】 【解】因为四边形是平行四边形, 所以,. 又因为、交于点, 所以. 又因为,, 所以.
平行四边形知识点总结及对应例题.
平行四边形、矩形、菱形、正方形知识点总结 定义:两组对边分别平行的四边形是平行四边形 平行四边形的性质: (1):平行四边形对边相等(即:AB=CD,AD=BC); (2):平行四边形对边平行(即:AB//CD,AD//BC); (3):平行四边形对角相等(即:∠A=∠C,∠B=∠D); (4):平行四边形对角线互相平分(即:O A=OC,OB=OD); 判定方法:1. 两组对边分别平行的四边形是平行四边形(定义判定法); 2. 一组对边平行且相等的四边形是平行四边形; 3. 两组对边分别相等的四边形是平行四边形; 4. 对角线互相平分的四边形是平行四边形; 5.两组对角分别相等的四边形是平行四边形; 考点1 特殊的平行四边形的性质与判定 1.矩形的定义、性质与判定 (1)矩形的定义:有一个角是直角的平行四边形是矩形。 (2)矩形的性质:矩形的对角线_________;矩形的四个角都是________角。矩形具有________的一切性质。矩形是轴对称图形,对称轴有_____________条,矩形也是中心对称图形,对称中心为_____________的交点。矩形被对角线分成了____________个等腰三角形。 (3)矩形的判定 有一个是直角的平行四边形是矩形;有三个角是_____________的四边形是矩形;对角线_____的平行四边形是矩形。 温馨提示:矩形的对角线是矩形比较常用的性质,当对角线的夹角中,有一个角为60度时,则构成一个等边三角形;在判定矩形时,要注意利用定义或对角线来判定时,必须先证明此四边形为平行四边形,然后再请一个角为直角或对角线相等。很多同学容易忽视这个问题。 2.菱形的定义、性质与判定 (1)菱形的定义:有一组邻边相等的平行四边形是菱形。 (2)菱形的性质 菱形的_______都相等;菱形的对角线互相_______,并且每一条对角线______一组对角;菱形也具有平行四边形的一切性质。菱形即是轴对称图形,对称轴有____条。 (3)菱形的面积
(完整版)平行四边形经典练习题
挑战自我: 1、 (2010年眉山市).如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ ABC 的度数为( ) A .90° B .60° C .45° D .30° 2、(2010福建龙岩中考)下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( ) A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 3.(2010年北京顺义)若一个正多边形的一个内角是120°,则这个正多边形的边数是( ) A .9 B .8 C .6 D .4 4、(2010年福建福州中考)如图4,在□ABCD 中,对角线AC 、BD 相交于点O ,若AC=14,BD=8,AB=10,则△OAB 的周长为 。 5、(2010年宁德市)如图,在□ABCD 中,AE =EB ,AF =2,则FC 等于_____. 6题 6、 (2010年滨州)如图,平行四边形ABCD 中, ∠ABC=60°,E 、F 分别在CD 、BC 的延长线上,AE ∥BD,EF ⊥BC,DF=2,则EF 的长为 7、 (2010年福建晋江)如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形是平行四边形,并予以证明.(写出一种即可)关系:①∥,②,③,④. 已知:在四边形中, , ;求证:四边形是平行四边形. 8、(2010年宁波市)如图1,有一张菱形纸片ABCD ,8=AC ,6=BD 。 (1)请沿着AC 剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四 边形,在图2中用实数画出你所拼成的平行四边形;若沿着BD 剪开, F E D C B A ABCD AD BC CD AB =C A ∠=∠?=∠+∠180C B ABCD ABCD D A B C A B C D 第5题图 F A E B C D
平行四边形知识点与经典例题
第十八章平行四边形 18.1.1 平行四边形的性质 第一课时平行四边形的边、角特征 知识点梳理 1、有两组对边分别平行的四边形叫做平行四边形,平行四边形ABCD记作□ABCD。 2、平行四边形的对边相等,对角相等,邻角互补。 3、两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条直线之间的距离。知识点训练 1.(3分)如图,两对边平行的纸条,随意交叉叠放在一起,转动其中一,重合的部分构成一个四边形,这个四边形是________. 2.(3分)如图,在□ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,那么图中共有平行四边形( ) A.6个B.7个C.8个D.9个 3.(3分)在□ABCD中,AB=6 cm,BC=8 cm,则□ABCD的周长为cm. 4.(3分)用40 cm长的绳子围成一个平行四边形,使其相邻两边的长度比为3∶2,则较长的边的长度为cm. 5.(4分)在□ABCD中,若∠A∶∠B=1∶5,则∠D=;若∠A+∠C=140°,则∠D=. 6.(4分)(2014·)如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是. 7.(4分)如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为( ) A.53°B.37°C.47°D.123°
8.(8分)(2013·)如图所示,已知在平行四边形ABCD中,BE=DF. 求证:AE=CF. 9.(4分)如图,点E,F分别是□ABCD中AD,AB边上的任意一点,若△EBC的面积为10 cm2,则△DCF的面积为。 10.(4分)如图,梯形ABCD中,AD∥BC,记△ABO的面积为S1,△COD的面积为S2,则S1,S2的大小关系是( ) A.S1>S2 B.S1=S2 C.S1<S2 D.无法比较 11.在□ABCD中,∠A∶∠B∶∠C∶∠D的值可能是( ) A.1∶2∶3∶4 B.1∶2∶2∶1 C.2∶2∶1∶1 D.2∶1∶2∶1 12.如图,将平行四边形ABCD折叠,使顶点D恰落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC;②MN=AM,下列说确的是( ) A.①②都对B.①②都错C.①对②错D.①错② 13.如图,在□ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF =60°,则□ABCD的周长为__.
平行四边形的判定典型例题
《平行四边形的判定》典型例题 例1如图,△DAB、△EBC、△FAC都是等边三角形,试说明四边形AFED 是平行四边形. 例2如图,E、F分别是ABCD边AD和BC上的点,并且AE=CF,AF和BE 相交于G,CE和DF相交于H、EF与GH是否互相平分,请说明理由. 例3如图,在平行四边形ABCD中,A1、A2、A3、A4和B1、B2、B3、B4分别是AB和DC的五等分点,C1、C2和D1、D2分别是AD和BC的三等分点,若四边形C1A4D2B1的面积为1,求S平行四边形ABCD. 例4已知:如图,E,F分别为ABCD的边CD,AB上一点,AE∥CF,BE,CF分别交CF,AE于H,G. 求证:EG=FH.
例5如图,已知:四边形ABCD中,AE⊥BD,CF⊥BD,E,F为垂足,且AE=CF,∠BAC=DCA. 求证:四边形ABCD是平行四边形.
参考答案 例1分析要证四边形AFED是平行四边形,应观察:两组对边是否相等、两组对角是否相等,或一组对边是否平行且相等、对角线是否相互平分.但在本题中没有对角线,也没有明显的对角之间的关系,因此可以先考虑去证明四边形AFED的对边是否相等. 事实上,AD=AB=BD,EF是否能等于这三条边中的一条呢可以看到 ,∴EF=AB=BD.同理DE=AC=AF,因此,所要证的四边形AFED是平行四边形. 证明,∴, 且,∴,∴ 又,同理.∴AFED是平行四边形. 例2分析若EF、GH互相平分,那么四边形EGFH应是平行四边形.观察已知条件,可以证明四边形EGFH是平行四边形. 证明是平行四边形,∴ 又,∴,且 ∴四边形AECF是平行四边形,∴,∴ 又四边形EDFB是平行四边形,∴,∴ 在四边形GEHF中,, ∴四边形GEHF是平行四边形,∴EF和GH互相平分. 说明:本题中多次使用了平行四边形的性质:对边平行且相等以及平行四边形的判断方法:对边平行且相等的四边形是平行四边形.通过解题应熟悉平行四边形的性质及判别. 例3 分析平行四边形ABCD被和分别成15个相等的小平行四边形。 而是4个小平行四边形面积的一半,是2个小平行四边形面积的一半。
平行四边形(知识点、经典例题、常考题型练习)
平行四边形(一) 【知识梳理】 1、平行四边形: 平行四边形的定义决定了它有以下几个基本性质: (1)平行四边形对角相等; (2)平行四边形对边相等; (3)平行四边形对角线互相平分。 除了定义以外,平行四边形还有以下几种判定方法: (1)两组对角分别相等的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)对角线互相平分的四边形是平行四边形; (4)一组对边平行且相等的四边形是平行四边形。 2、特殊平行四边形: 一、矩形 (1)有一角是直角的平行四边形是矩形 (2)矩形的四个角都是直角; (3)矩形的对角线相等。 (4)矩形判定定理1:有三个角是直角的四边形是矩形 (5)矩形判定定理2:对角线相等的平行四边形是矩形 二、菱形 (1)把一组邻边相等的平行四边形叫做菱形. (2)定理1:菱形的四条边都相等 (3)菱形的对角线互相垂直,并且每条对角线平分一组对角. (4)菱形的面积等于菱形的对角线相乘除以2 (5)菱形判定定理1:四边都相等的四边形是菱形 (6)菱形判定定理2:对角线互相垂直的平行四边形是菱形。 三、正方形 (1)有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形(2)性质:①四个角都是直角,四条边相等 ②对角线相等,并且互相垂直平分,每条对角线平分一组对角(3)判定:①一组邻边相等的矩形是正方形 ②有一个角是直角的菱形是正方形
平行四边形 矩形 菱形 正 方 形 等腰梯形 直角梯形 梯形 四边形 知识结构如下图 (1)弄清定义及四边形之间关系图1: (2)四边形之间关系图2: 2、几种特殊的四边形的性质和判定: 3、一些定理和推论: 三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半。 推论:夹在两平行线间的平行线段相等。 推论:直角三角形斜边上的中线等于斜边的一半; 推论:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。 【例题精讲】 填空题: 四边形 正方形
平行四边形知识点及练习题含答案
平行四边形知识点及练习题含答案 一、解答题 1.如图,在Rt ABC ?中,090BAC ∠=,D 是BC 的中点,E 是AD 的中点,过点A 作//BC AF 交BE 的延长线于点F (1)求证:四边形ADCF 是菱形 (2)若4,5AC AB ==,求菱形ADCF 的面积 2.在四边形ABCD 中,AD ∥BC ,AB=8cm ,AD=16cm ,BC=22cm ,∠ABC=90°.点P 从点A 出发,以1cm/s 的速度向点D 运动,点Q 从点C 同时出发,以3cm/s 的速度向点B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t 秒. (1)当t= 时,四边形ABQP 成为矩形? (2)当t= 时,以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形? (3)四边形PBQD 是否能成为菱形?若能,求出t 的值;若不能,请说明理由,并探究如何改变Q 点的速度(匀速运动),使四边形PBQD 在某一时刻为菱形,求点Q 的速度. 3.综合与探究 (1)如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF BE =.CE 和CF 之间有怎样的关系.请说明理由. (2)如图2,在正方形ABCD 中,E 是AB 上一点,G 是AD 上一点,如果45GCE ∠=?,请你利用(1)的结论证明:GE BE CD =+. (3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3在直角梯形ABCD 中,//()AD BC BC AD >,90B ∠=?,12AB BC ==,E 是AB 上一点,且45DCE ∠=?,4BE =,求DE 的长.
《平行四边形》知识点归纳和题型归类
平行四边形知识点归纳和题型归类【知识网络】 【要点梳理】 要点一、平行四边形 1.定义:的四边形叫做平行四边形. 2.性质:(1); (2); (3); (4)中心对称图形. 3.面积: 4.判定:边:(1)的四边形是平行四边形; (2)的四边形是平行四边形; (3)的四边形是平行四边形. 角:(4)的四边形是平行四边形; 对角线:的四边形是平行四边形. 要点诠释:平行线的性质: (1)平行线间的距离都; (2)等底等高的平行四边形面积 . 要点二、矩形 1.定义:的平行四边形叫做矩形. 2.性质:(1)边:; (2)角:; (3)对角线:; (4)是中心对称图形,也是轴对称图形. 3.面积: 4.判定:(1) 的平行四边形是矩形. (2)的平行四边形是矩形. (3)的四边形是矩形. 要点诠释:由矩形得直角三角形的性质: (1)直角三角形斜边上的中线等于斜边的; (2)直角三角形中,30度角所对应的直角边等于斜边的. 高 底 平行四边形 ? = S 宽 =长 矩形 ? S
要点三、菱形 1. 定义: 的平行四边形叫做菱形. 2.性质:(1)边: ; (2)角: ; (3)对角线: ; (4)是中心对称图形,也是轴对称图形. 3.面积: 4.判定:(1) 的平行四边形是菱形; (2) 的平行四边形是菱形; (3) 的四边形是菱形. 要点四、正方形 1. 定义:四条边都 ,四个角都是 的 形叫做正方形. 2.性质:((1)边: ; (2)角: ; (3)对角线: ; (4)是中心对称图形,也是轴对称图形. (5) 两条对角线把正方形分成四个全等的等腰直角三角形; 3.面积:=S 正方形边长×边长= 1 2 ×对角线×对角线 4.判定:(1) 的菱形是正方形; (2) 的矩形是正方形; (3) 的菱形是正方形; (4) 的矩形是正方形; (5)对角线互相垂直平分且相等的四边形是正方形; (6)四条边都相等,四个角都是直角的四边形是正方形. 中点四边形(拓展) 原四边形 一般四边形 矩形 菱形 正方形 图示 顺次连接 各边中点 所得的四 边形 平行四边形 菱形 矩形 正方形 2 对角线 对角线高= =底菱形??S M G F E D C B A C D E F M G B A B E A C G M F D A F G M B D E C
平行四边形知识点分类归纳练习题汇编
初二下数学第18章平行四边形期中复习卷 班级: 姓名: 座号: 平行四边形的性质 1、平行四边形定义: 的四边形是平行四边形. 表示方法:用 “□” 表示平行四边形,例如:平行四边形ABCD 记作 □ ABCD ,读作“平行四边形ABCD ”. 2、平行四边形的性质: (1)角:平行四边形的对角_________; (2)边:平行四边形两组对边 ; (3)对角线:平行四边形的对角线_________; (4)面积:①S ==?底高ah ;②平行四边形的对角线将平行四边形分成4个面积相等的三角形. 练习题: 1 . 已知一个平行四边形两邻边的长分别为6和8,那么它的周长为_____. 2.如图,□ABCD 中,BC=BD ,∠C=70°,则∠ADB 的度数是______,∠A 的度数是_____. 3. 如图,平行四边形ABCD 的对角线交于点O,且AB=5,△OCD 的周长为23,则平行四边形A BCD 的两条对角线的和是_____. 平行四边形的判定 平行四边形的判定方法:(5种方法) 边: (1) 定义:两组对边 的四边形是平行四边形 (2) 两组对边 的四边形是平行四边形 (3)一组对边 的四边形是平行四边形角: 角: (4) 两组对角 的四边形是平行四边形。 对角线: (5) 对角线 的四边形是平行四边形。 练习: 1. 点A 、B 、C 、D 在同一平面内,从①AB//CD ;②AB =CD ;③BC//AD ;④BC =AD 四个条件中任意选两个,不能使四边形ABCD 是平行四边形的选法有( ) A .①② B .②③ C . ①③ D . ③④ 2、如图,在平面直角坐标系中,点A 、B 、C 的坐标分别是A (-2,5),B (-3,-1),C (1,-1),在第一象限内找一点D ,使四边形ABCD 是平行四边形,那么点D 的坐标是
初三数学-平行四边形经典例题讲解(3套)
初三数学 经典例题(附带详细答案) 1.如图,E F 、是平行四边形ABCD 对角线AC 上两点,BE DF ∥, 求证:AF CE =. 【答案】证明:平行四边形ABCD 中,AD BC ∥,AD BC =, ACB CAD ∴∠=∠. 又BE DF ∥, BEC DFA ∴∠=∠, BEC DFA ∴△≌△, ∴CE AF = 2.如图,四边形ABCD 中,AB ∥CD ,∠B=∠D ,, 求四边形ABCD 的周长. 【答案】 解法一: ∵ ∴ 又∵ ∴ ∴∥即得是平行四边形 ∴ ∴四边形的周长 解法二: 3 ,6==AB BC AB CD ∥?=∠+∠180C B B D ∠=∠?=∠+∠180D C AD BC ABCD 36AB CD BC AD ====,ABCD 183262=?+?=A D C B D C A B E F
连接 ∵ ∴ 又∵ ∴≌ ∴ ∴四边形的周长 解法三: 连接 ∵ ∴ 又∵ ∴ ∴∥即是平行四边形 ∴ ∴四边形的周长 3.(在四边形ABCD 中,∠D =60°,∠B 比∠A 大20°,∠C 是∠A 的2倍, 求∠A ,∠B ,∠C 的大小. 【关键词】多边形的内角和 【答案】设x A =∠(度),则20+=∠x B ,x C 2=∠. 根据四边形内角和定理得,360602)20(=++++x x x . 解得,70=x . AC AB CD ∥DCA BAC ∠=∠B D AC CA ∠=∠=,ABC △CDA △36AB CD BC AD ====,ABCD 183262=?+?=BD AB CD ∥CDB ABD ∠=∠ABC CDA ∠=∠ADB CBD ∠=∠AD BC ABCD 36AB CD BC AD ====,ABCD 183262=?+?=A D C B A D C B
平行四边形典型例题
平行四边形典型例题 1.已知如图12-1-19,所示□ABCD的对角线AC、BD相交于点O,OE上AD于E,OF⊥BC于F. 求证:四边形AECF是平行四边形 错证:在△AOE和△COF中 ∵OE⊥AD,OF⊥BC ∴∠AEO=∠CFO=90° ∵四边形ABCD为平行四边形 ∴OA=OC,AD∥BC ∴∠EAC=∠ACF ) ∴△AOE≌△COF(AAS)∴OF=OE ∴四边形AECF是平行四边形 错误分析:上面证明由OF=OE,OA=OC不能说明EF与AC互相平分,因为原题设中没有说明E、O、F三点共线,因此先证E、O、F三点共线. 正确证明:在△AOE和△COF中 ∵OE⊥AD OF⊥BC ∴∠AEO=∠CFO=90° ∵四边形ABCD为平行四边形 ∴OA=OC,AD∥BC ∴∠EAC=∠ACF ∴△AOE≌△COF(AAS)∴OF=OE 又∵AD∥BC,OE⊥AD,OF⊥BC ∴E、O、F三点共线 ( ∴四边形AECF是平行四边形
2.如图12-1-22所示,现有一块等腰直角三角形的铁板,通过切割焊接成一个含有45°角的平行四边形,请你设计一种最简单的方案,并证明你的方案确实得到的是一个符合条件的平行四边形. 分析:运用三角形全等,平行四边形的识别方法来解答,在证明时不要忽略证明F,E,D共线. 解:取AC、BC的中点E、D连结ED,则沿ED切割下来,如图使点E不变,点C与点A重合,再焊接上去最简单. 证明:在Rt△ABC中∵AC=BC ∴∠B=45° 又∵E、D分别为AC、BC的中点 ∴EC=DC ∴∠CED=∠CDE=45° ∴∠AEF=∠CED=45°∴∠AEF+∠AED=∠CED+∠AED=180° ∴F、E、D在一条直线上∵∠EAF=∠C=90°∴AF∥CD — 又∵AF=CD=DB ∴四边形AFDB是平行四边形,且∠B=45° 3.如图12-1-23,在□ABCD的对角线上取两点E、F,且BF=DE,请至少用两种不同的方法证明四边形AECF 是平行四边形,并指出哪种方法最简便. 分析:可证两组对边分别相等,也可证对角线互相平分. 证明方法(一) 在△ABF和△CDE中,AB=CD,BF=DE,∠ABF=∠CDE. ∴△ABF≌△CDE ∴AF=CE 同理可证AE=CF,故四边形AECF是平行四边形 方法(二) 连AC交BD于O %
平行四边形典型例题
创作编号: GB8878185555334563BT9125XW 创作者:凤呜大王* 平行四边形典型例题 1.已知如图12-1-19,所示□ABCD的对角线AC、BD相交于点O,OE 上AD于E,OF⊥BC于F. 求证:四边形AECF是平行四边形 错证:在△AOE和△COF中 ∵OE⊥AD,OF⊥BC ∴∠AEO=∠CFO=90° ∵四边形ABCD为平行四边形 ∴OA=OC,AD∥BC ∴∠EAC=∠ACF ∴△AOE≌△COF(AAS)∴OF=OE ∴四边形AECF是平行四边形 错误分析:上面证明由OF=OE,OA=OC不能说明EF与AC互相平分,因为原题设中没有说明E、O、F三点共线,因此先证E、O、F三点共线. 正确证明:在△AOE和△COF中 ∵OE⊥AD OF⊥BC ∴∠AEO=∠CFO=90° ∵四边形ABCD为平行四边形
∴OA=OC,AD∥BC ∴∠EAC=∠ACF ∴△AOE≌△COF(AAS)∴OF=OE 又∵AD∥BC,OE⊥AD,OF⊥BC ∴E、O、F三点共线 ∴四边形AECF是平行四边形 2.如图12-1-22所示,现有一块等腰直角三角形的铁板,通过切割焊接成一个含有45°角的平行四边形,请你设计一种最简单的方案,并证明你的方案确实得到的是一个符合条件的平行四边形. 分析:运用三角形全等,平行四边形的识别方法来解答,在证明时不要忽略证明F,E,D共线. 解:取AC、BC的中点E、D连结ED,则沿ED切割下来,如图使点E不变,点C 与点A重合,再焊接上去最简单. 证明:在Rt△ABC中∵AC=BC ∴∠B=45° 又∵E、D分别为AC、BC的中点 ∴EC=DC ∴∠CED=∠CDE=45° ∴∠AEF=∠CED=45°∴∠AEF+∠AED=∠CED+∠AED=180° ∴F、E、D在一条直线上∵∠EAF=∠C=90°∴AF∥CD 又∵AF=CD=DB ∴四边形AFDB是平行四边形,且∠B=45° 3.如图12-1-23,在□ABCD的对角线上取两点E、F,且BF=DE,请至少用两种不同的方法证明四边形AECF是平行四边形,并指出哪种方法最简便. 分析:可证两组对边分别相等,也可证对角线互相平分.
平行四边形证明典型题
平行四边形证明题 1.已知:在矩形ABCD 中,AE ⊥BD 于E ,∠DAE=3∠BAE ,求:∠EAC 的度数。 2.已知:直角梯形ABCD 中,BC=CD=a 且∠BCD=60?,E 、F 分别为梯形的腰AB 、DC 的中点,求:EF 的长。 3、已知:在等腰梯形ABCD 中,AB ∥DC ,AD=BC ,E 、F 分别为AD 、BC 的中点,BD 平分∠ABC 交EF 于G ,EG=18,GF=10求:等腰梯形ABCD 的周长。 4、已知:梯形ABCD 中,AB ∥CD ,以AD ,AC 为邻边作平行四边形ACED , DC 延长线交BE 于F ,求证:F 是BE 的中点。 5、已知:梯形ABCD 中,AB ∥CD ,AC ⊥CB ,AC 平分∠A ,又∠B=60?,梯形的周长是20cm, 求:AB 的长。 _B _ C _ A _ B _ A _ B _ E
6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ,垂足分别是E 、F 、G 、H ,求证:EF ∥GH 。 7、已知:梯形ABCD 的对角线的交点为E ,若在平行边的一边BC 的延长线上取一点F ,使S ABC ?=S EBF ?,求证:DF ∥AC 。 8、在正方形ABCD 中,直线EF 平行于对角线AC ,与 边AB 、BC 的交点为E 、F ,在DA 的延长线上取一点G ,使AG=AD ,若EG 与DF 的交点为H ,求证:AH 与正方形的边长相等。 9、若以直角三角形ABC 的边AB 为边,在三角形ABC 的外部作正方形ABDE ,AF 是BC 边的高,延长FA 使AG=BC ,求证:BG=CD 。 _ A _ B _B _ C _B _ F _ B _ C _ F
