供应链-实验三-重力法选址问题
重心法选址实验报告心得

重心法选址实验报告心得引言重心法选址是一种常用的选址方法,通过计算不同位置的客流量、货流量和人口密度,以及考虑到竞争对手的影响,来确定最佳选址位置。
本次实验旨在通过使用重心法选址模型,选择最佳的开设新餐厅的位置。
实验内容我们组选择了一家连锁餐厅在某城市开设新分店的选址问题。
根据实验要求,我们收集了城市的客流量数据、货流量数据和人口密度数据,并与竞争餐厅的位置进行对比。
然后,我们使用重心法选址模型,计算不同位置的综合指标,并最终确定最佳选址位置。
实验过程数据收集在实验前,我们首先收集了相关的数据。
通过城市交通部门的统计数据,我们获得了客流量和货流量的数据。
此外,我们还使用了人口普查数据,获取了每个区域的人口密度。
数据处理和分析在收集到数据后,我们进行了数据处理和分析的工作。
首先,我们将客流量和货流量数据进行归一化处理,以便与人口密度数据进行对比。
然后,我们计算了每个位置的综合指标,包括客流量综合指标、货流量综合指标和人口密度综合指标。
重心法选址模型在完成数据处理和分析后,我们将使用重心法选址模型来确定最佳选址位置。
重心法选址模型通过计算不同位置质量中心的距离,来决定最佳选址位置。
我们将计算每个位置的质量中心,并选择离质量中心最近的位置作为最佳选址位置。
结果分析和讨论通过运行重心法选址模型,我们确定了最佳选址位置。
我们将最佳位置与竞争对手的位置进行对比,并进行了结果分析和讨论。
我们发现最佳选址位置在市中心附近,客流量和货流量较高,并且与竞争对手的位置相距一定距离,有着一定的市场优势。
心得体会本次实验让我对重心法选址有了更深入的理解。
重心法选址是一种简单而有效的选址方法,通过考虑多个因素来选择最佳的位置。
实验过程中,我学会了如何收集和处理相关数据,并运用重心法选址模型来确定最佳选址位置。
这个过程给我带来了很大的启示,不仅对选址问题有了更深入的认识,还提高了我的数据分析和决策能力。
另外,通过与竞争对手的位置进行对比,我也意识到竞争对手的位置对于选址决策的重要性。
重心法选址实训报告

一、实训背景与目的随着我国经济的快速发展,物流行业的重要性日益凸显。
仓库作为物流体系中的关键环节,其选址是否合理直接影响到物流成本和效率。
为了提高学生对仓库选址问题的认识,培养其解决实际问题的能力,本次实训以重心法选址为主题,通过模拟实际场景,让学生掌握重心法的基本原理和操作步骤。
二、实训内容与过程1. 实训准备实训前,首先由指导老师向学生介绍仓库选址的背景和重要性,讲解重心法的基本原理。
随后,学生根据实训要求,分组讨论,确定实训的具体场景和目标。
2. 实训场景设定本次实训场景设定为一家大型企业,需要在全国范围内选址建设一个新的仓库。
已知需求点的坐标、货物需求量以及运输成本。
3. 重心法原理讲解指导老师详细讲解了重心法的原理,包括以下步骤:(1)确定各需求点的坐标和货物需求量;(2)计算各需求点到候选仓库位置的运输成本;(3)利用重心公式计算最优仓库位置坐标;(4)根据计算结果,确定最优仓库位置。
4. 实训操作学生按照以下步骤进行实训操作:(1)分组讨论,确定候选仓库位置;(2)根据需求点坐标和货物需求量,计算各需求点到候选仓库位置的运输成本;(3)利用重心公式计算最优仓库位置坐标;(4)分析计算结果,评估最优仓库位置。
5. 实训总结实训结束后,各小组汇报实训成果,指导老师对学生的表现进行点评和总结。
三、实训成果与体会1. 实训成果通过本次实训,学生掌握了重心法选址的基本原理和操作步骤,能够运用所学知识解决实际仓库选址问题。
以下为部分小组的实训成果:- 小组一:根据需求点坐标和货物需求量,计算各需求点到候选仓库位置的运输成本,利用重心公式计算最优仓库位置坐标,确定最优仓库位置为(X=110,Y=150)。
- 小组二:在分析各候选仓库位置的基础上,综合考虑运输成本、交通便利程度等因素,确定最优仓库位置为(X=120,Y=160)。
2. 实训体会本次实训让学生深刻认识到仓库选址的重要性,以及重心法在解决实际问题中的应用价值。
关于配送中心重心法选址的研究

关于配送中心重心法选址的研究一、本文概述随着电子商务和物流行业的快速发展,配送中心作为物流网络中的关键节点,其选址问题日益受到业界的关注。
合理的配送中心选址不仅能够降低物流成本,提高物流效率,还能有效地优化供应链的整体性能。
重心法作为一种经典的设施选址方法,在配送中心选址中具有广泛的应用。
本文旨在对重心法在配送中心选址中的应用进行深入的研究和探讨。
本文首先介绍了配送中心选址的重要性,以及重心法的基本原理和计算方法。
在此基础上,通过文献综述的方式,对国内外关于重心法在配送中心选址中的研究进行了梳理和评价。
随后,结合具体案例,详细阐述了重心法在配送中心选址中的实际应用过程,包括数据收集、处理、模型构建和求解等步骤。
本文总结了重心法在配送中心选址中的优势与不足,并提出了相应的改进策略和建议。
本文的研究对于提高配送中心选址的科学性和合理性具有重要的理论意义和实践价值。
通过深入研究重心法在配送中心选址中的应用,不仅可以为企业提供更加科学和有效的选址决策支持,还能为物流行业的健康发展提供有力的理论支撑和实践指导。
二、文献综述配送中心选址问题是物流管理和供应链优化中的核心问题之一。
重心法作为一种经典的选址方法,在理论和实践层面均得到了广泛的研究和应用。
本文旨在对重心法在配送中心选址中的应用进行深入研究,通过对现有文献的梳理和评价,为后续的实证研究提供理论基础。
在文献综述部分,首先回顾了重心法的发展历程和基本原理。
重心法起源于物理学中的重心概念,后被引入到运筹学和物流管理中,用于解决多目标、多约束的选址问题。
该方法通过构建数学模型,将配送中心的选址问题转化为求解成本最小化或效率最大化的问题。
本文梳理了国内外学者在重心法选址研究方面的主要成果。
国内外学者在重心法的基础上进行了大量的改进和创新,如引入不同的成本函数、考虑多层次的约束条件、结合其他优化算法等。
这些研究不仅丰富了重心法的理论体系,也提高了其在实际应用中的效果。
基于重心法的配送中心选址问题研究
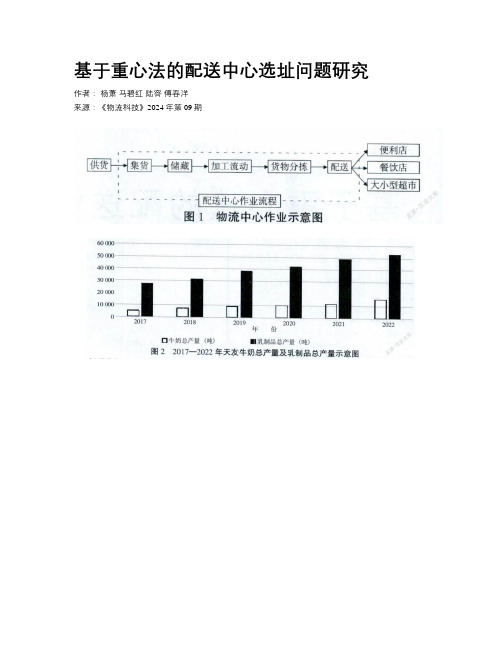
基于重心法的配送中心选址问题研究作者:杨萧马碧红陆容傅春洋来源:《物流科技》2024年第09期摘要:采用重心模型法對重庆天友乳业公司的物流配送中心选址进行分析,以得到物流配送中心的优化选址结果。
通过选择合适的初始位置和迭代优化的方式,最终得出结论:重庆市沙坪坝区白杨沟东南一千米左右为模型最佳地址(106.562 0,29.525 0),即配送中心经纬度。
基于经济分析方法,建立天友乳业物流配送中心优选模型的相关做法,希望为相关企业在物流网络空间规划和选择上提供更多参考。
关键词:配送中心选址;重心模型法;天友乳业中图分类号:F252.14 文献标志码:A DOI:10.13714/ki.1002-3100.2024.09.004Abstract: This paper analyzes the location of logistics distribution center of Chongqing Tianyou Dairy Company by using the center of gravity model. By choosing the suitable initial location and the way of iterative optimization, the conclusion is drawn: Baiyanggou in Shapingba District of Chongqing is the best address of the model(106.562 0,29.525 0), which is the longitude and latitude of the distribution center. Based on the economic analysis method, this paper establishes the optimization model of Tianyou dairy logistics distribution center, hoping to provide more reference for the related enterprises in the logistics network spatial planning and selection.Key words: location of distribution center; center of gravity model; Tianyou Dairy0 引言当前,随着社会经济的发展,传统消费模式焕然一新,尤其是客户消费场景、形式等的巨变,更是有目共睹。
基于重力p-median模型的支线机场物资供应中心选址

式中 h = 1ꎬ2ꎬ3ꎬꎬf - 1ꎬf + 1ꎬꎬq ꎮ
(1)
选择对偶生成法生成 Voronoi 图ꎬ步骤为:
步骤 1:在图上利用机场位置点构建 Delaunay 三角网ꎬ对各三角形进行编号ꎬ并记录其构成的三个机场
点ꎻ步骤 2:利用三点画圆找到各三角形的外接圆圆心ꎬ计算坐标ꎻ步骤 3:遍历三角形链表ꎬ将相邻三角形外
果表明该模型的改进具有实际意义ꎮ Wang 等 [14] 建立配送中心的选址模型ꎬ并运用改进的免疫优化算法解
决配送中心选址问题ꎮ
配送中心的选址涉及到很多错综复杂的因素ꎬ相关研究往往只能解决小区域范围的选址ꎬ具有局限性ꎻ
并且选址往往只是选择一个物流中心ꎬ考虑的因素相对较少ꎬ并不能解决多个机场物资供应的问题ꎮ 本文从
the location model was simulated. Simulation results show that based on the application of p ̄median model in the exampleꎬ
an ideal airport material center selection can be achieved. The model exhibits excellent practicability and operability.
于重力 p ̄median 模型从备选点中选取合适的机场位置ꎬ采用改进的免疫优化算法进行求解ꎬ确定符合目标
约束的选址位置ꎮ
2.1 选址备选点位置确定
由于重心法求解时精度不够ꎬ因此首先采用 Voronoi 确定备选点初始位置ꎮ 采用 Voronoi 图对机场群进
行不同区域划分ꎬ并求出不同区域的备选位置ꎮ Voronoi 图由一组连接两相邻点直线的垂直平分线组成的连
仓库选址问题方法介绍

1.根据成本因素的评价方法本节只介绍几种既简便又实用的方法,以便在短时间内就能得到初步的结论。
对于需要精确分析的,可再由计算机计算。
常用的方法有盈亏平衡法、重心法、数值分析法等。
以下通过实例分别介绍。
(1)盈亏点平衡法这是工程经济和财务管理中的基本方法,在选址评价中可用于确定特定产量规模下,成为最低的设施选址方案。
它建立在产量、成本、预测销售收入的基础之上。
例1.某公司有三个不同仓库建设方案,由于各长治有不同的征地费、建设费,工资、原材料等成本费用也各不相同,从而有不同的仓储成本。
三个厂址的仓储成本如下表所示,式决定不同仓储规模下最优的选址。
表1 三个不同仓库建设方案的仓储成本解:设C T表示总成本,C F表示固定储存费用,C V表示单件可变储存费用。
根据题意列出三个备选方案的成本函数,并绘制成本函数曲线。
C TA=C FA+C V A=600000+40XC TB=C FB+C VB=1200000+20XC TC=C FC+C VC=1800000+10X先求A\B方案的交点物流量,再求B\C两方案的交点物流量,就可以决定不同物流规模下的最有选址。
1)在M点A\B方案物流成本相同,该店物流量为Q M,则Q M=( C FB- C FA)/( C V A- C VB)=300002)在N点B\C两方案物流成本相同。
该店物流量为Q N,则Q N=( C FC- C FB)/( C VB- C VC)=600003)如按物流成本两低为标准,当物流量低于30000件时选A方案,物流量在30000到60000之间时选B方案,物流量大于60000件时选C方案。
(2)单一选址地点的重心法重心法是将物流系统的资源点与需求点看成是分布在某一平面范围内的物体系统,各自远点与需求点的物流量可分别看成是物体的重量,物体系统的重心将作为仓库地质的最佳位置,具体过程如下:设在某计划区域内,有n个资源点和需求点,各点的资源量货需求量为w j(j=1,2,3….n),它们各自的坐标为(x i,y j)(j=1,2,3…n)。
重心法选址——精选推荐
2单设施重心法选址2.1实验目的掌握单设施重心法选址的原理,能够计算简单选址题目中待选设施的位置; 掌握单设施重心选址的算法流程,能够设计类似题目的算法流程,并编写程序。
2.2实验过程(1)单设施重心法选址的原理重心法选址模型示意图如图2-1所示。
图2-1 单设施重心法选址选址示意图求解目标:C-总成本最低其中:f i -序号为i 的点的运输费率;V i -序号为i 的点的产量或者销量;d i -序号为i 的点到待选设施点的相对距离。
待选设施位置的计算公式:其中:X c -重心的X 坐标;Y c -重心的Y 坐标;X i -第i 个地点X 坐标;Y i -第i 个地点Y 坐标;i i ni i d V f MinC ∑==1∑∑===n i i i i n i i i i i c d V f dx V f X 11)/()/(∑∑===n i i i i n i i i i i c d V f d y V f Y 11)/()/()()(22y i c ix c d d Y d X i --+=XY(2)算法流程图,如图2-2所示。
图2-2 算法流程图2.3实验结果(1)单设施重心法选址程序参数设定及其求解界面如图2-3所示。
图2-3 单设施重心法选址程序参数设定及其求解界面(2)参数设定及其求解界面变量声明部分(代码)Private Sub Command1_Click()If Text1.Text = "" ThenMsgBox "X-横坐标不允许为空"Text1.SetFocusExit SubElseIf IsNumeric(Text1.Text) = False ThenMsgBox "X-横坐标必须为数值型数据!"Text1.Text = ""Text1.SetFocusExit SubEnd IfIf Text2.Text = "" ThenMsgBox "Y-纵坐标不允许为空"Text2.SetFocusExit SubElseIf IsNumeric(Text2.Text) = False ThenMsgBox "Y-纵坐标必须为数值型数据!"Text2.Text = ""Text2.SetFocusExit SubEnd IfIf Text3.Text = "" ThenMsgBox "产量或销量不允许为空"Text3.SetFocusExit SubElseIf IsNumeric(Text3.Text) = False ThenMsgBox "产量或销量应为数值型数据!"Text3.Text = ""Text3.SetFocusExit SubElseIf Val(Text3.Text) < 0 ThenMsgBox "产量或销量应为正数,否则无实际意义!" Text3.Text = ""Text3.SetFocusExit SubEnd IfIf Text4.Text = "" ThenMsgBox "运输费率不允许为空"Text4.SetFocusExit SubElseIf IsNumeric(Text4.Text) = False ThenMsgBox "运输费率应为数值型数据!"Text4.Text = ""Text4.SetFocusExit SubElseIf Val(Text4.Text) < 0 ThenMsgBox "运输费率应为正数,否则无实际意义!" Text4.Text = ""Text4.SetFocusExit SubEnd IfIf Text5.Text = "" ThenMsgBox "X0-横坐标不允许为空"Text5.SetFocusExit SubElseIf IsNumeric(Text5.Text) = False ThenMsgBox "X0-横坐标必须为数值型数据!"Text5.Text = ""Text5.SetFocusExit SubEnd IfIf Text6.Text = "" ThenMsgBox "Y0-纵坐标不允许为空"Text6.SetFocusExit SubElseIf IsNumeric(Text6.Text) = False ThenMsgBox "Y0-纵坐标必须为数值型数据!"Text6.Text = ""Text6.SetFocusExit SubEnd IfIf Text7.Text = "" ThenMsgBox "精度不允许为空"Text7.SetFocusExit SubElseIf IsNumeric(Text7.Text) = False ThenMsgBox "精度应为数值型数据!"Text7.Text = ""Text7.SetFocusExit SubElseIf Val(Text7.Text) < 0 ThenMsgBox "精度应为正数,否则无实际意义!"Text7.Text = ""Text7.SetFocusExit SubEnd IfFor i = 1 To List1.ListCountIf Text1.Text = Val(List1.List(i - 1)) And Text2.Text = Val(List2.List(i - 1)) ThenMsgBox "与第" & i & "输入坐标值相同,请重新输入"Text1.Text = ""Text2.Text = ""Text3.Text = ""Text4.Text = ""Text1.SetFocusExit SubEnd IfNext iList1.AddItem Text1.TextList2.AddItem Text2.TextList3.AddItem Text3.TextList4.AddItem Text4.TextText1.Text = ""Text2.Text = ""Text3.Text = ""Text4.Text = ""Text1.SetFocusIf List1.ListCount >= 2 ThenCommand2.Enabled = TrueEnd IfEnd SubPrivate Sub Command2_Click()Xc = Val(Text5.Text)Yc = Val(Text6.Text)JD = Val(Text7.Text)Dim SumCO As DoubleDim SumCN As DoubleDim Sum1 As DoubleDim Sum2 As DoubleDim Sum3 As DoubleFor j = 1 To 10000SumCO = 0SumCN = 0Sum1 = 0Sum2 = 0Sum3 = 0For i = 1 To List1.ListCountdi = Sqr((Xc - Val(List1.List(i - 1))) ^ 2 + (Yc - Val(List2.List(i - 1))) ^ 2) '距离公式SumCO = SumCO + Val(List3.List(i - 1)) * Val(List4.List(i - 1)) * diSum1 = Sum1 + (Val(List1.List(i - 1)) * Val(List3.List(i - 1)) * Val(List4.List(i - 1))) / diSum2 = Sum2 + (Val(List2.List(i - 1)) * Val(List3.List(i - 1)) * Val(List4.List(i - 1))) / diSum3 = Sum3 + (Val(List3.List(i - 1)) * Val(List4.List(i - 1))) / diNext iXc = Sum1 / Sum3Yc = Sum2 / Sum3For i = 1 To List1.ListCountdi = Sqr((Xc - Val(List1.List(i - 1))) ^ 2 + (Yc - Val(List2.List(i - 1))) ^ 2)SumCN = SumCN + Val(List3.List(i - 1)) * Val(List4.List(i - 1)) * diNext iIf (SumCO - SumCN) <= JD ThenText8.Text = XcText9.Text = YcText10.Text = SumCNText11.Text = jExit ForEnd IfNext jEnd SubPrivate Sub List1_Click()For i = 1 To List1.ListCountIf List1.Selected(i - 1) = True Thenh = InputBox("请输入要改的参数:", "参数修正")If h <> "" And IsNumeric(h) = True ThenList1.List(i - 1) = hElse: MsgBox "输入的数据必须为数值型数据"End IfEnd IfNext iEnd SubPrivate Sub List2_Click()For i = 1 To List2.ListCountIf List2.Selected(i - 1) = True Thenh = InputBox("请输入要改的参数:", "参数修正")If h <> "" And IsNumeric(h) = True ThenList2.List(i - 1) = hElse: MsgBox "输入的数据必须为数值型数据"End IfEnd IfNext iEnd SubPrivate Sub List3_Click()For i = 1 To List3.ListCountIf List3.Selected(i - 1) = True Thenh = InputBox("请输入要改的参数:", "参数修正")If h <> "" And IsNumeric(h) = True And Val(h) > 0 Then List3.List(i - 1) = hElse: MsgBox "输入的数据必须为数值型数据"End IfEnd IfNext iEnd SubPrivate Sub List4_Click()For i = 1 To List4.ListCountIf List4.Selected(i - 1) = True Thenh = InputBox("请输入要改的参数:", "参数修正")If h <> "" And IsNumeric(h) = True And Val(h) > 0 Then List4.List(i - 1) = hElse: MsgBox "输入的数据必须为数值型数据"End IfEnd IfNext iEnd Sub(3) 单设施重心法选址程序求解结果如图2-4所示。
基于简化的节约算法和重力法的RDC选址模型构建
基于简化的节约算法和重力法的RDC选址模型构建
董宇轩
【期刊名称】《电子制作》
【年(卷),期】2014(0)15
【摘要】配送是物流的职能之一,配送中心是物流过程的重要设施,在物流迅猛发展的同时,物流服务网络日趋扩大与复杂,物流企业都尽可能地加大服务网络的覆盖范围,从而赢得客户。
区域配送中心在其中扮演了越来越重要的角色。
本文以从仓库到区域配送中心的运输成本最小为目标,基于简化的节约算法将某企业的仓库分为若干区域,再将重力法进行简化来构建解决区域配送中心选址问题的模型。
【总页数】1页(P82-82)
【作者】董宇轩
【作者单位】南京农业大学工学院管理工程系 210000
【正文语种】中文
【相关文献】
1.基于集合覆盖模型的RDC选址问题研究 [J], 康怀飞
2.基于组合优化模型的RDC选址研究 [J], 温丹苹
3.基于运输模型的RDC选址问题研究 [J], 潘晓勇; 巫江; 张晨; 张泉伟; 赖冬
4.基于运输模型的RDC选址问题研究 [J], 潘晓勇; 巫江; 张晨; 张泉伟; 赖冬
5.基于集合覆盖模型与层次分析法的RDC选址研究——以三福百货公司为例 [J], 欧阳浩星
因版权原因,仅展示原文概要,查看原文内容请购买。
供应链-实验三-重力法选址问题
沈阳师范大学科信软件学院实验报告
实验题目:重力法选址问题
实验时间:2015.00.00
姓名:叶春艳
学号:
专业年级:
注意:n d 由公式()()22n n n y y x x d -+-=
得到,而x ,y 为决策变量,所以在插入函数
时关于x ,y 的量必须加“$$”符号,如x 在Excel 中的量“B16”必须写为“$B $16”。
2) 设置参数。
如下:
3) 求解。
注意本例目标函数为非线性,所以选择求解方法时要选择“非线性”,如下:
实验指导与数据处理:
1、 解释重力选址模型的含义。
答:模型的基本形式是确定的,在应用时只要根据实际情况对变量,参数进行改变就可以用来解决实际问题。
它对地区间的运输联系作出比较合理的解释,通过对地区间相互作用的分析来研究客货流的分布情况。
2、 完成实验内容中的所有操作,求出合适的实施位置以及成本。
3、 根据求的的设施位置获得新的位置
∑∑==='k
n n n n k n n
n n n d F D d x F D x 11和
∑∑==='k
n n n n k
n n n
n n d F D d y F D y 11
看看新的设施位置()y x '',是否与算出的设施位置()y x ,几乎相同,若相同则停止,否则设()y x ,=()y x '
',再次获得新位置,直到两次求得结果几乎相同。
答:结果如下:
分析讨论:
成绩实验教师评语
签名:
日期:。
供应链管理中的物流中心位置选址方法与优化模型
供应链管理中的物流中心位置选址方法与优化模型物流中心位置选址是供应链管理中的重要环节之一,它对企业的运营效率、成本控制和客户服务质量等方面起着关键作用。
合理选择物流中心的位置,能够使货物运输更加高效,提高物流服务响应速度,降低运输成本。
本文将介绍物流中心位置选址的方法和优化模型,帮助企业在供应链管理中做出明智的决策。
一、物流中心位置选址方法1. 区位因素法:区位因素法是一种常用的物流中心位置选址方法。
该方法按照地理位置、市场规模、运输季节、交通状况等因素来评估潜在物流中心的优劣。
选址者可以利用地理信息系统(GIS)技术进行数据分析,综合考虑各种因素,以找到最佳的物流中心位置。
2. 近邻优势法:近邻优势法是基于供应链网络的观点而提出的。
该方法认为,物流中心应该接近供应商和客户,以减少运输距离和时间成本,提高供应链效率。
通过分析供应商和客户的分布情况,选址者可以确定物流中心的合理范围,然后在范围内进行具体的选址。
3. 交通流分析法:交通流分析法是利用交通流量数据来评估物流中心选址的方法。
选址者可以查询交通监测数据或者进行交通流量调查,分析不同地段的交通状况,并对可能的运输路径进行评估。
根据交通流量的密集程度和物流需求的匹配程度,选址者可以确定最佳的物流中心位置。
4. 成本效益分析法:成本效益分析法是一种以成本为主要考虑因素的选址方法。
通过对不同物流中心位置的成本估算和效益分析,选址者可以找到最经济、最具竞争力的位置。
这种方法通常需要综合考虑人力资源、土地租金、设备投资、运输成本等多个因素。
二、物流中心位置优化模型除了上述的物流中心位置选址方法,还有一些经济学模型和优化方法可以帮助企业做出优化的决策:1. 最小总成本模型:最小总成本模型是一种通过协调各个物流环节的成本,找到最优位置的模型。
该模型考虑了生产、运输、仓储和分销等不同环节的成本,并通过数学优化算法寻找使总成本最小的物流中心位置。
2. 服务水平模型:服务水平模型是以客户服务水平为目标的物流中心位置选择方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
Байду номын сангаас实验题目:重力法选址问题
实验时间:2015.00.00
姓名:叶春艳
学号:
专业年级:
实验三重力法选址问题
一、实验目的及要求:
1、深入理解单设施重力法选址问题;
2、根据给定的供应源和市场的位置及之间的运输成本和运输量完成单设施的选择。
二、实验设备环境及要求:
连接到互联网的电脑。
二、实验内容与步骤:
1、重力选址模型
总的运输成本为
其中, 表示设施与供应源或市场n之间的距离。
:某一市场与供应源n的坐标位置。
:设施与市场供应源n之间一单位产品每英里的运输成本。
:设施与市场供应源n之间的运输数量。
决策变量x,y:设施的坐标位置。
2、利用上述模型根据SA公司的供应源和市场的地点,运输数量和运输成本应用Excel计算设施的具体点。
和
看看新的设施位置 是否与算出的设施位置 几乎相同,若相同则停止,否则设 = 再次获得新位置,直到两次求得结果几乎相同。
答:结果如下:
分析讨论:
实验教师评语
签名:
日期:
成绩
1)在Excel上建立线性规划模型,如下:
注意: 由公式 得到,而x,y为决策变量,所以在插入函数时关于x,y的量必须加“$$”符号,如x在Excel中的量“B16”必须写为“$B$16”。
2)设置参数。如下:
3)求解。注意本例目标函数为非线性,所以选择求解方法时要选择“非线性”,如下:
实验指导与数据处理:
1、解释重力选址模型的含义。
答:模型的基本形式是确定的,在应用时只要根据实际情况对变量,参数进行改变就可以用来解决实际问题。它对地区间的运输联系作出比较合理的解释,通过对地区间相互作用的分析来研究客货流的分布情况。
2、完成实验内容中的所有操作,求出合适的实施位置以及成本。
3、根据求的的设施位置获得新的位置
