高中导数放缩常用公式及证明
常用导数放缩法

一:消参放缩(适合含参)1.已知函数f(x)=e x-ln(x+m).(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明f(x)>0.解:(1)f′(x)=1e xx m -+.由x=0是f(x)的极值点得f′(0)=0,所以m=1.于是f(x)=e x-ln(x+1),定义域为(-1,+∞),f′(x)=1e1 xx-+.函数f′(x)=1e1xx-+在(-1,+∞)单调递增,且f′(0)=0.因此当x∈(-1,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0.所以f(x)在(-1,0)单调递减,在(0,+∞)单调递增.(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时,f(x)>0.当m=2时,函数f′(x)=1e2xx-+在(-2,+∞)单调递增.又f′(-1)<0,f′(0)>0,故f′(x)=0在(-2,+∞)有唯一实根x0,且x0∈(-1,0).当x∈(-2,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0,从而当x=x0时,f(x)取得最小值.由f′(x0)=0得0e x=01 2x+,ln(x0+2)=-x0,故f(x)≥f(x0)=01 2x++x0=212xx(+)+>0.综上,当m≤2时,f(x)>0.2.已知函数f(x)=m e x-ln x-1.(Ⅰ)当m =1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)当m ≥1时,证明:f(x)>1.【答案】(Ⅰ)y =(e -1)x(Ⅱ)当m ≥1时,f (x)= m e x-ln x -1≥e x-ln x -1.(放缩)要证明f (x)>1,只需证明e x-ln x -2>0.3.知函数1()ln(1)(1)nf x a xx=+--,其中*x∈N,a为常数.(Ⅱ)当1a =时,证明:对任意的正整数n ,当2n ≥时,有()1f x x -≤. 当1a =时,1()ln(1)(1)nf x x x =+--.当2x ≥时,对任意的正整数n ,恒有11(1)nx -≤,故只需证明1ln(1)1x x +--≤.令()1(1ln(1))2ln(1)h x x x x x =--+-=---,[)2x ∈+∞,,则12()111x h x x x -'=-=--,当2x ≥时,()0h x '≥,故()h x 在[)2+∞,上单调递增,因此当2x ≥时,()(2)0h x h =≥,即1ln(1)1x x +--≤成立. 故当2x ≥时,有1ln(1)1(1)nx x x +---≤.即()1f x x -≤.二:构造放缩(适合f(x)或其变式的N 项和有关)4.设函数()()2ln 1f x x b x =++.(1)若x =1时,函数()f x 取最小值,求实数b 的值;(2)若函数()f x 在定义域上是单调函数,求实数b 的取值范围;(3)若1b =-,证明对任意正整数n ,不等式33311......31211)1(n <k f nk ++++∑=都成立解:(1)由x + 1>0得x > – 1∴f(x)的定义域为( - 1,+ ∞),对x ∈ ( - 1,+ ∞),都有f(x)≥f(1),∴f(1)是函数f(x)的最小值,故有f /(1) = 0,,022,12)(/=+∴++=bx b x x f 解得b= - 4. 经检验合题意;(2)∵,12212)(2/+++=++=x b x x x b x x f 又函数f(x)在定义域上是单调函数,∴f /(x) ≥0或f /(x)≤0在( - 1,+ ∞)上恒成立.若f /(x) ≥0,∵x + 1>0,∴2x 2+2x+b ≥0在( - 1,+ ∞)上恒成立,即b ≥-2x 2-2x =21)21(22++x 恒成立,由此得b ≥21; 若f /(x) ≤0, ∵x + 1>0, ∴2x 2+2x+b ≤0,即b ≤- (2x 2+2x)恒成立,因-(2x 2+2x) 在( - 1,+ ∞)上没有最小值,∴不存在实数b 使f(x) ≤0恒成立.综上所述,实数b 的取值范围是⎪⎭⎫⎢⎣⎡+∞,21. (3)当b= - 1时,函数f(x) = x 2- ln(x+1),令函数h(x)=f(x) – x 3= x 2– ln(x+1) – x 3,则h /(x) = - 3x 2 +2x - 1)1(31123+-+-=+x x x x ,∴当[)+∞∈,0x 时,h /(x)<0所以函数h(x)在[)+∞∈,0x 上是单调递减.又h(0)=0,∴当()+∞∈,0x 时,恒有h(x) <h(0)=0,[ 即x 2– ln(x+1) <x 3恒成立.故当()+∞∈,0x 时,有f(x) <x 3..∵()1,0,,k N k +∈∴∈+∞取,1k x =则有311(),f k k < ∴33311 (312)11)1(n <k f nk ++++∑=,故结论成立。
导数大题中最常用的放缩大法

导数大题中最常用的放缩大法相信不少读者在做高考导数解答题时都有这样的感悟,将复杂的函数求导,再对导函数求导,再求导,然后就没有然后了......如果懂得了最常见的放缩,如:人教版课本中常用的结论⑴sin ,(0,)x x x π<∈,变形即为sin 1x x<,其几何意义为sin ,(0,)y x x π=∈上的的点与原点连线斜率小于1.⑵1x e x >+⑶ln(1)x x >+⑷ln ,0x x x e x <<>.将这些不等式简单变形如下: exx ex e x e x x x x x 1ln ,,1,1ln 11-≥≥+≥-≤≤-那么很多问题将迎刃而解。
例析:(2018年广州一模)x e x x f x x ax x f 2)(,0,1ln )(⋅≤>++=若对任意的设恒成立,求a 的取值范围。
放缩法:由可得:1+≥x e x 2)1(ln 1ln 2)1(ln )1(ln 1ln ln 22=+-++≥+-=+-=+-+x x x x x x e x x xe x x e x x x x高考中最常见的放缩法可总结如下,供大家参考。
第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥-> (放缩成类反比例函数)1ln 1x x≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+, ()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x +<<+第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x=-,ln y x x =. 拓展阅读:为何高考中总是考这些超越函数呢?和x e x ln 因为高考命题专家是大学老师,他们站在高观点下看高中数学,一览无遗。
导数中放缩法(切线放缩、对数均值不等式)

导数中放缩法(切线放缩、对数均值不等式)导数证明中的常用放缩在导数证明中,常用的放缩方法有切线放缩、对数放缩、指数放缩、指对放缩和三角函数放缩等。
其中,常用的放缩公式包括对数放缩和指数放缩。
一、常用放缩公式1.对数放缩对数放缩常常可以将一个函数放缩成一次函数或双撇函数,常用的对数放缩公式包括:lnx≤x-1,lnx<x,ln(1+x)≤xlnxx-1/x,x>1lnxx/2,0<x<1lnx≤x^2-x,ln(1+x)≤x-x^2/2,-1<x<∞ln(1+x)≥x/(1+x),ln(1+x)>x/2,x>02.指数放缩指数放缩常常可以将一个函数放缩成一次函数或二次函数,常用的指数放缩公式包括:ex≥x+1,ex>x,ex≥ex,x≤0ex<1-x,ex<1-x+x^2/2,x<0ex≥1+x+x^2,ex≥1+x+x^2+x^3,x>03.指对放缩指对放缩常常可以将一个函数的导数放缩成一个常数,常用的指对放缩公式包括:ex-lnx≥(x+1)-(x-1)/2,x>04.三角函数放缩三角函数放缩常常可以将一个函数放缩成一个三角函数或二次函数,常用的三角函数放缩公式包括:XXX<x<tanx,sinx≥x-x^2,-1≤x≤1cosx≤1-sin^2x,-1≤x≤1二、经典例题以函数f(x)=lnx+ax^2+(2a+1)x为例,讨论其单调性和当a<0时的最大值。
1) 解f(x)的定义域为(0,∞),求导得f'(x)=1/x+2ax+2a+1.当a≥-1/2时,f'(x)>0,因此f(x)在(0,∞)上单调递增;当a<-1/2时,f'(x)<0,因此f(x)在(0,∞)上单调递减。
2) 当a0,因此g(x)在(0,∞)上单调递增,且有g(x)≤g(1)=ln1-2/3=-2/3.又因为f(x)可以表示为f(x)=g(x)+(2a+1)x+ax^2+2/3x,因此有f(x)≤g(1)+(2a+1)x+ax^2+2/3x=-2/3+(2a+1)x+ax^2+2/3x=2/3x+ax^2+(2a+1)x-2/3.当2/3x+ax^2+(2a+1)x-2/3取到最大值时,有x=-(2a+1)/(2a),此时f(x)的最大值为-2/3+(2a+1)^2/(4a)-a(2a+1)^2/(4a)=-3/4a。
导数中放缩法(切线放缩、对数均值不等式)
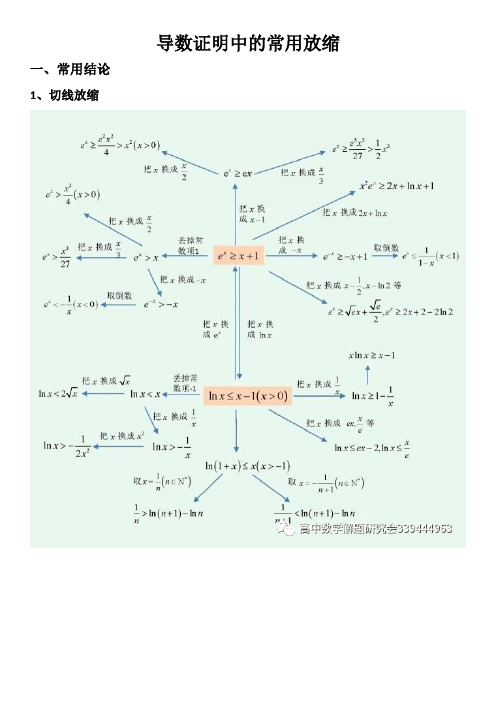
导数证明中的常用放缩一、常用结论1、切线放缩2、其它对数放缩(对数均值不等式)3、常用放缩公式:(考试时需给出证明过程)第一组:对数放缩(放缩成一次函数)ln 1x x ≤-,ln x x <,()ln 1x x +≤ (放缩成双撇函数)()11ln 12x x x x ⎛⎫<-> ⎪⎝⎭,()11ln 012x x x x ⎛⎫>-<< ⎪⎝⎭, )ln 1x x<>,)ln 01x x ><<, (放缩成二次函数)2ln x x x ≤-,()()21ln 1102x x x x +≤--<<,()()21ln 102x x x x +≥-> (放缩成类反比例函数)1ln 1x x≥-,()()21ln 11x x x x ->>+,()()21ln 011x x x x -<<<+,()ln 11x x x +≥+,()()2ln 101x x x x +>>+,()()2ln 101x x x x+<<+ 第二组:指数放缩(放缩成一次函数)1x e x ≥+,x e x >,x e ex ≥, (放缩成类反比例函数)()101x e x x ≤≤-,()10x e x x<-<, (放缩成二次函数)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩()()ln 112x e x x x -≥+--=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥-,22111cos 1sin 22x x x -≤≤-. 第五组:以直线1y x =-为切线的函数ln y x =,11x y e -=-,2y x x =-,11y x=-,ln y x x =.二、基础练习:练习题组一练习题组二:二、经典例题:母题 (2017·全国Ⅲ)已知函数f (x )=ln x +ax 2+(2a +1)x .(1)讨论f (x )的单调性;(2)当a <0时,证明f (x )≤-34a-2.(1)解 f (x )的定义域为(0,+∞),f ′(x )=1x +2ax +2a +1=(x +1)(2ax +1)x. 若a ≥0,则当x ∈(0,+∞)时,f ′(x )>0,故f (x )在(0,+∞)上单调递增.若a <0,则当x ∈⎝⎛⎭⎫0,-12a 时,f ′(x )>0; 当x ∈⎝⎛⎭⎫-12a ,+∞时,f ′(x )<0. 故f (x )在⎝⎛⎭⎫0,-12a 上单调递增,在⎝⎛⎭⎫-12a ,+∞上单调递减. (2)证明 由(1)知,当a <0时,f (x )在x =-12a 处取得最大值,最大值为f ⎝⎛⎭⎫-12a =ln ⎝⎛⎭⎫-12a -1-14a, 所以f (x )≤-34a -2等价于ln ⎝⎛⎭⎫-12a -1-14a ≤-34a-2, 即ln ⎝⎛⎭⎫-12a +12a+1≤0. 设g (x )=ln x -x +1,则g ′(x )=1x-1. 当x ∈(0,1)时,g ′(x )>0;当x ∈(1,+∞)时,g ′(x )<0.所以g (x )在(0,1)上单调递增,在(1,+∞)上单调递减.故当x =1时,g (x )取得最大值,最大值为g (1)=0.所以当x >0时,g (x )≤0.从而当a <0时,ln ⎝⎛⎭⎫-12a +12a +1≤0,即f (x )≤-34a-2. [子题1] 设函数f (x )=ln x -x +1.证明:当x ∈(1,+∞)时,1<x -1ln x<x . 证明 f ′(x )=1x -1=1-x x,x >0, 当x >1时,f ′(x )<0,f (x )单调递减,当0<x <1时,f ′(x )>0,f (x )单调递增,∴f (x )=ln x -x +1≤f (1)=0,∴ln x ≤x -1,∴当x >1时,ln x <x -1,①且ln 1x <1x-1,② 由①得,1<x -1ln x ,由②得,-ln x <1-x x, ∴ln x >x -1x ,∴x >x -1ln x, 综上所述,当x >1时,1<x -1ln x<x . [子题2] 已知函数f (x )=e x -x 2.求证:当x >0时,e x +(2-e )x -1x≥ln x +1. 证明 设g (x )=f (x )-(e -2)x -1=e x -x 2-(e -2)x -1(x >0),则g ′(x )=e x -2x -(e -2),设m (x )=e x -2x -(e -2)(x >0),则m ′(x )=e x -2,易得g ′(x )在(0,ln 2)上单调递减,在(ln 2,+∞)上单调递增,又g ′(0)=3-e>0,g ′(1)=0,由0<ln 2<1,则g ′(ln 2)<0,所以存在x 0∈(0,ln 2),使得g ′(x 0)=0,所以当x ∈(0,x 0)∪(1,+∞)时,g ′(x )>0;当x ∈(x 0,1)时,g ′(x )<0.故g (x )在(0,x 0)上单调递增,在(x 0,1)上单调递减,在(1,+∞)上单调递增,又g (0)=g (1)=0,所以g (x )=e x -x 2-(e -2)x -1≥0,故当x >0时,e x +(2-e )x -1x≥x . 又由母题可得ln x ≤x -1,即x ≥ln x +1,故e x +(2-e )x -1x≥ln x +1. 规律方法 利用导数证明不等式f (x )>g (x )的基本方法(1)若f (x )与g (x )的最值易求出,可直接转化为证明f (x )min >g (x )max .(2)若f (x )与g (x )的最值不易求出,可构造函数h (x )=f (x )-g (x ),然后根据函数h (x )的单调性或最值,证明h (x )>0.(3)通过题目中已有的或常用的不等式进行证明.(4)利用赋值法证明与正整数有关的不等式.跟踪演练1.(2018·全国Ⅰ)已知函数f (x )=a e x -ln x -1.(1)设x =2是f (x )的极值点,求a ,并求f (x )的单调区间;(2)证明:当a ≥1e时,f (x )≥0. (1)解 f (x )的定义域为(0,+∞),f ′(x )=a e x -1x. 由题设知,f ′(2)=0,所以a =12e 2. 从而f (x )=12e 2e x -ln x -1,f ′(x )=12e 2e x -1x. 当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )的单调递增区间为(2,+∞),单调递减区间为(0,2).(2)证明 当a ≥1e 时,f (x )≥e x e-ln x -1. 设g (x )=e x e-ln x -1(x ∈(0,+∞)), 则g ′(x )=e x e -1x. 当0<x <1时,g ′(x )<0;当x >1时,g ′(x )>0.所以x =1是g (x )的最小值点.故当x >0时,g (x )≥g (1)=0.因此,当a ≥1e时,f (x )≥0. 2.(2020·北京市陈经纶中学模拟)已知函数f (x )=ln x -1x-ax .若1<a <2,求证:f (x )<-1. 证明 f (x )的定义域为(0,+∞),为了证明f (x )<-1,即ln x -1x-ax <-1, 只需证明ln x -1-ax 2<-x ,即ln x <ax 2-x +1,令m (x )=ln x -x +1(x >0),则m ′(x )=1x-1, 令m ′(x )>0,得0<x <1;令m ′(x )<0,得x >1,所以m (x )在(0,1)上单调递增,在(1,+∞)上单调递减,所以m (x )max =m (1)=0,即ln x -x +1≤0,则ln x ≤x -1.令n (x )=ax 2-2x +2,因为1<a <2,所以Δ=4-8a <0,所以n (x )>0恒成立,即ax 2-2x +2>0,所以ax 2-x +1>x -1.综上所述,ln x <ax 2-x +1,即当1<a <2时,f (x )<-1.(2017年全国新课标1·理·21)已知()()22x x f x ae a e x =+--.(1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围.解析:(1)()()()()2'221211x x x x f x ae a e e ae =+--=+-若0a ≤,则()'0f x <恒成立,所以()f x 在R 上递减;若0a >,令()'0f x =,得11,ln x e x a a ==. 当1ln x a <时,()'0f x <,所以()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减; 当1lnx a >时,()'0f x >,所以()f x 在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. 综上,当0a ≤时,()f x 在R 上递减;当0a >时,()f x 在1,ln a ⎛⎫-∞ ⎪⎝⎭上递减,在1ln ,a ⎛⎫+∞ ⎪⎝⎭上递增. (2)()f x 有两个零点,必须满足()min 0f x <,即0a >,且()min 111ln1ln 0f x f a a a ⎛⎫==--< ⎪⎝⎭. 构造函数()1ln g x x x =--,0x >. 易得()1'10g x x =--<,所以()1ln g x x x =--单调递减. 又因为()10g =,所以()11111ln 01101g g a a a a a ⎛⎫--<⇔<⇔>⇔<< ⎪⎝⎭. 下面只要证明当01a <<时,()f x 有两个零点即可,为此我们先证明当0x >时,ln x x >. 事实上,构造函数()ln h x x x =-,易得()1'1h x x=-,∴()()min 11h x h ==,所以()0h x >,即ln x x >. 当01a <<时,()()22222110a ea e a a f e e e++---=++=>, ()2333333ln 121ln 11ln 10a f a a a a a a a a -⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+----=---> ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭, 其中11ln a -<,31ln ln a a a ->,所以()f x 在11,ln a ⎛⎫- ⎪⎝⎭和13ln ,ln a a a -⎛⎫ ⎪⎝⎭上各有一个零点. 故a 的取值范围是()0,1.注意:取点过程用到了常用放缩技巧。
第十讲 导数放缩和数列 教师版

(放缩成双撇函数)()11ln 12x x x x <−>⎛⎫ ⎪⎝⎭,()11ln 012x x x x >−<<⎛⎫⎪⎝⎭,)ln 1x x<>,)ln 01x x ><<,(放缩成二次函数)2l n x x x ≤−,()()21ln 1102x x xx +≤−−<<,()()21ln 102x x xx +≥−>(放缩成类反比例函数)1ln 1x x≥−,()()21ln 11x x x x −>>+,()()21ln 011x x x x −<<<+,()ln 11x x x+≥+,()()2ln 101x x x x+>>+,()()2ln 101x x x x+<<+第二组:指数放缩一次:1x e x ≥+,x e x >,x e ex ≥,类反比例:()101x e x x ≤≤−,()10x e x x <−<,二次:(泰勒)()21102x e x x x ≥++>,2311126x e x x x ≥+++, 第三组:指对放缩(双切线) ()()ln 112x e x x x −≥+−−=第四组:三角函数放缩()sin tan 0x x x x <<>,21sin 2x x x ≥−,22111cos 1sin 22x x x −≤≤−.第五组:以直线1y x =−为切线的函数ln y x =,11x y e−=−,2y x x =−,11y x=−,ln y x x =.3.放缩的思路二、课堂练习例1.已知函数()1x f x e x =−−. (1)证明()0f x ;(2)设m 为整数,且对于任意正整数n ,2111(1)(1)(1)222n m ++⋯+<求m 的最小值.【答案】【解答】解:(1)()1x f x e '=−,当0x >时,()0f x '>,函数单调递增,当0x <时,()0f x '<,函数单调递减, 故当0x =时,函数取得最小值(0)0f =, 所以()0f x ;(2)由(1)知,当0x >时1x e x >+, 所以(1)x ln x >+,令12n x =,则可得11(1)22n n ln +<, 从而2211(1)111111122(1)(1)(1)111222222212n n n nln ln ln −++++⋯++<++⋯+==−<−, 故2111(1)(1)(1)222n e ++⋯+<,而23111(1)(1)(1)2222+++>,故m 的最小值为3.变式1.已知函数()1f x elnx x =−+. (1)讨论()f x 的单调性; (2)证明:*(1)2((123)n n e n N ln n +>∈⨯⨯⨯⋯⨯,且2)n .【答案】【解答】解:(1)函数()f x 的定义域为(0,)+∞,()1e e xf x x x−'=−=. 在(0,)e 上,()0f x '>,在(,)e +∞上,()0f x '<.()f x ∴在(0,)e 上单调递增,在(,)e +∞上单调递减. (2)由(1)知()f x f (e )1=,11elnx x ∴−+,即xlnxe,当且仅当x e =时取等号. 从而11ln e<,22ln e <,33ln e <,⋯,n lnn e <,∴123123nln ln ln lnn e+++⋯++++⋯+<,∴(1)(123)2n n ln n e+⨯⨯⨯⋯⨯<, ∴(1)2(123)n n e ln n +>⨯⨯⨯⋯⨯.例2.已知()x f x e =,()1(g x x e =+为自然对数的底数). (1)求证:()()f x g x 恒成立;(2)设m 是正整数,对任意正整数n ,2111(1)(1)(1)333n m ++⋯+<,求m 的最小值.【答案】【解答】解:(1)令()()()1x h x f x g x e x =−=−−,()1x h x e '=−,()0h x '=,则0x =,当0x <,()0h x '<;0x >时,()0g x '>,所以()h x 在(0,)+∞单调递减,在(,0)−∞单调递增,所以()()00h x h ==最小值,即()0h x 恒成立; 所以()()f x g x ;(2)由(1)令13n x =,可知131013nn e <+<,由不等式性质得2211(1)3311111111111[1()]33333332322111(1)(1)(1)2333n n n n n e e e e ee e −++⋯+−−++⋯+<⋯===<=.所以m 的最小值为2.变式1.已知函数()1f x xlnx x =−+,()x g x e ax =−,a R ∈. (Ⅰ)求()f x 的最小值;(Ⅱ)若()1g x 在R 上恒成立,求a 的值;(Ⅲ)求证:2111(1)(1)(1)1222n ln ln ln ++++⋯++<.【答案】【解答】解:()()I f x lnx '=,∴当01x <<时,()0f x '<,1x >时,()0f x '>,()f x ∴在(0,1)上单调递减,在(1,)+∞上单调递增, ∴当1x =时,()f x 取得最小值f (1)0=;()II 由()1x g x e ax =−恒成立可得1x ax e +恒成立, 设()x h x e =,则()x h x e '=,故(0)1h '=,(0)1h =,∴函数()y h x =在(0,1)处的切线方程为1y x =+, 1x x e ∴+恒成立. 1a ∴=;()III 由()II 可知,1x x e +恒成立,两边取对数得(1)ln x x +,令1(12ix i ==,2,3)n ⋯累加得2211(1)111111122(1)(1)(1)111222222212n n n n ln ln ln −++++⋯++++⋯+==−<−,所以原不等式成立.例3.已知实数0a >,函数()1(x f x e ax e =−−是自然对数的底数) (1)求函数()f x 的单调区间及最小值. (2)若()0f x 对任意x R ∈恒成立,求a 的值. (3)证明:*1111(1)()23ln n n N n+++⋯+>+∈. 【答案】【解答】解:(1)()f x 的定义域为R ,()x f x e a '=−, 令f ‘()0x >得,x lna >,令f ’ ()0x <的,x lna <,()f x ∴的单调减区间为(,)lna −∞,增区间为(0,)+∞, ()()1min f x f lna a alna ∴==−−.(2))()0f x 等价于()0min f x ,∴由(1)得10a alna −−,设g (a )1a alna =−−,则g ‘(a )lna =−, 令g ’(a )0=得1a =,g ∴(a )在(0,1)上为增函数,(1,)+∞为减函数, g ∴(a )max g =(1)0=, g ∴(a )g (1)0=, g ∴(a )0=,1a ∴=;(3)由(2)可知,当1a =时,()0f x ,即10x e x −−, 1x e x ∴+,两边取对数得(1)x ln x +,当且仅当0x =时取等号,∴令1x n =得111(1)()n ln ln n n n+>+=, 111234123411()()()()()(1)23123123n n ln ln ln ln ln ln n n n n++∴+++⋯+>+++⋯+=⨯⨯⨯⋯⨯=+. 变式1.已知函数()(1)x f x e ln x =−+ (1)求函数()f x 的最小值;(2)证明:()()111*321,ne e e e ln n n N e +++⋯++∈为常数.【答案】【解答】解:(1)由题意知,()f x 的定义域为:1x >−; 对()f x 求导:1()1x f x e x '=−+ 对()f x '求导有:21()0(1)x f x e x ''=+>+,所以()f x '为(1,)−+∞上单调增函数;令()0f x '=,则有0x =;所以,当(1,0)x ∈−时,()0f x '<,()f x 在(1,0)−上单调递减; 当(0,)x ∈+∞时,()0f x '>,()f x 在(0,)+∞上单调递增; 故()f x 的最小值为(0)1f =.(2)由(1)知当0x =时,()f x 取得最小值,即()1f x(1)1x e ln x ∴−+,即(1)1x e ln x ++取1x n=,则11(1)1(1)1n e ln ln n lnn n ++=+−+于是211e ln ln −+;12321e ln ln −+; 13431eln ln −+;⋯1(1)1neln n lnn +−+;累加得:11132(1)ne e e e ln n +++⋯++,*()n N ∈故得证.例4.已知函数()(1)f x ln x =+(1)设()y g x =是函数()f x 在(0,0)处的切线,证明:()()f x g x (2)证明:2*22221111(1)(1)(1)(1)()123e n N n+++⋯+<∈ 【答案】【解答】解:(1)1()1f x x'=+,则(0)1f '=,又(0)0f =,所以()g x x = 证明()()(1)f x g x ln x x ⇔+,令()(1)h x ln x x =+−,则1()111xh x x x'=−=−++, 所以()h x 在(1,0)−上单调递增,在(0,)+∞上单调递减, 故()(0)0h x h =,所以(1)ln x x +.(2)由(1)知(1)ln x x +对任意的1x >−恒成立. 取1x =,则(11)1ln +<;212x =,则2211(1)22ln +<;⋯;2211(1)ln n n +<; 则22221111(11)(1)(1)122ln ln ln n n ++++⋯++<++⋯+, 又因为22111111112221223(1)n n n n++⋯+<+++⋯+=−<⨯⨯−, 所以2211(11)(1)(1)22ln ln ln n ++++⋯++<, 即2211(11)(1)(1)22ln n ++⋯+<, 所以2222111(1)(1)(1)12e n++⋯+<. 变式1.已知函数()f x x lnx =−. (1)求()f x 的最小值;(2)设m 为整数,且对于任意正整数n ,222111(1)(1)(1)23m n +⨯+⨯⋯⨯+<,求m 的最小值. 【答案】【解答】解::(1)11()1x f x x x−'=−=, 当(0,1)x ∈时,()0f x '<,故()f x 在(0,1)单调递减; 当(1,)x ∈+∞时,()0f x '>,()f x 在(1,)+∞单调递增; 故()f x f (1)1=,故()f x 的最小值为1. (2)由(1)可得,()1f x x lnx =−即1lnx x −, 所以222114422(1)4(21)(21)2121ln k k k k k k k +=<=−−+−+,*k N ∈,2n , 则222111222222222(1)(1)(1)223355*********ln ln ln ln n n n n ++++⋯++<−+−+⋯+−=−<<−++, 即222111(1)(1)(1)223ln ln n ++⋯+<, 所以222111(1)(1)(1)223n ++⋯+<. 又因为222111(1)(1)(1)123n++⋯+>,故对任意正整数n ,222111(1)(1)(1)23m n++⋯+<的整数m 的最小值为2. 例5.已知函数()f x xlnx kx =+,k R ∈.(1)求()y f x =在点(1,f (1))处的切线方程; (2)若不等式2()f x x x +恒成立,求k 的取值范围; (3)求证:当*n N ∈时,不等式2212(41)21ni n nln i n =−−>+∑成立.【答案】【解答】解:(1)函数()y f x =的定义域为(0,)+∞,()1f x lnx k '=++,f '(1)1k =+,f (1)k =,∴函数()y f x =在点(1,f (1))处的切线方程为(1)(1)y k k x −=+−, 即(1)1y k x =+−;(2)设()1g x lnx x k =−+−,1()1g x x'=−, (0,1)x ∈,()0g x '>,()g x 单调递增, (1,)x ∈+∞,()0g x '<,()g x 单调递减, 不等式2()f x x x +恒成立,且0x >,10lnx x k ∴−+−,()max g x g ∴=(1)20k =−即可,故2k ,(3)由(2)可知:当2k =时,1lnx x −恒成立, 令2141x i =−,由于*i N ∈,21041i >−. 故,221114141lni i <−−−,整理得:221(41)141ln i i −>−−, 变形得::21(41)1(21)(21)ln i i i −>−+−,即:2111(41)1()22121ln i i i −>−−−+1i =,2,3⋯⋯,n 时,有1312ln >−1(1)3−’ 1512ln >−1(1)3− ⋯⋯⋯⋯21(41)12ln n −>−11()2121n n −−+两边同时相加得:21112222(41)(1)2212121ni n n nln i n n n n =−−>−−=>+++∑, 所以不等式在*n N ∈上恒成立.变式1.已知函数()(1)(1)1f x ln x k x =−−−+. (1)求函数()f x 的极值点;(2)若()0f x 恒成立,求k 的取值范围; (3)证明:*22341(62460(1)22ln ln ln lnn n n N n n n −+++⋯+<∈−+,1)n > 【答案】【解答】解:(1)()f x 的定义域为(1,)+∞,1()1f x k x '=−−, 若0k ,则()0f x '>,()f x 在(1,)+∞单增,所以()f x 无极值点; 若0k >,令()0f x '=,得11x k=+, 当1(1,1)x k ∈+时,()0f x '>,()f x 在1(1,1)k +单增,当1(1,)x k ∈++∞时,()0f x '<,()f x 在1(1,)k++∞单减,所以()f x 有极大值点11x k=+,无极小值点; (2)由(1)知当0k 时,()f x 在(1,)+∞单增,又f (2)10k =−>,所以()0f x 不成立; 当0k >时,1()(1)max f x f lnk k=+=−,若()0f x 恒成立,只需1()(1)0max f x f lnk k=+=−,解得1k ,所以k 的取值范围是[1,)+∞;(3)由(2)知,当1k =时,1(1)lnx x x <−>,∴221111(,1)(1)(1)(1)1lnn n n N n n n n n n n n n −<==−∈>−−++,∴2234111111111(,1)62460(1)233412122ln ln ln lnn n n N n n n n n n n −+++⋯⋯+<−+−+⋯⋯+−=−=∈>−+++.例6.已知函数()2f x x lnx m =−−,()1g x mx =−,m R ∈. (1)若1m =,求函数()()()h x f x g x =−的最小值; (2)求证:*2222222123111111(1)(1)()1232323ln ln ln lnn n N n n n+++⋯++++⋯+−+++⋯+∈. 【答案】【解答】解:(1)当1m =时,()(0)h x x lnx x =−>,则11()1x h x x x−'=−=, 令()0h x '>,解得1x >;令()0h x '<,解得01x <<;∴函数()h x 在(0,1)上递减,在(1,)+∞上递增, ()min h x h ∴=(1)1=;(2)证明:由(1)可知,1x lnx −,即1lnx x −,当且仅当1x =时取等号,所以2211lnxx x x−, ∴222222212113111111,,,,()1222333ln ln lnnn N ln n n n −<−<−⋯⋯−∈, ∴2222222123111111111232233ln ln ln lnn n n n +++⋯⋯+−+−+−+⋯⋯+−, ∴*2222222123111111(1)(1)()1232323ln ln ln lnn n N n n n+++⋯++++⋯+−+++⋯+∈. 变式1.已知函数1()lnxf x x+=. (1)如果当1x 时,不等式()1af x x +恒成立,求实数a 的取值范围; (2)求证:222*211221211112()n n n N eee⨯+⨯++++⋯+<+∈;【答案】【解答】解:(1)不等式()1a f x x +,转化为(1)(1)x lnx a x++, 令(1)(1)()x lnx g x x++=,只需()min a g x 即可,2()x lnx g x x −'=,y x lnx =−,110y x'=−,y 在[1,)+∞递增,()h x h (1)10=>, 所以()0g x '>,()g x 在[1,)+∞递增, 所以()min g x g =(1)2=, 所以2a ;(2)令2a =,由(1)得121lnxxx ++,11x lnx x −+,即11x x e x −+,令211x n=+,代入则212121111111(2)(1)1n e n n n n n n +<+<+=+−−− 故22221122121111111111112221nn n n n ne e e ⨯+⨯++++⋯++++−+⋯+−=+−<+−. 故原式成立.例7.已知函数()sin f x a x blnx x =+−.(1)当0a =,1b =时,证明:()1f x −; (2)当6b π=时,若()f x 在(0,)3π上为增函数,求a 的取值范围; (3)*n N ∀∈,试比较2111(1)(1)(1)444n ++⋯+与13e 的大小,并进行证明.【答案】【解答】(1)证明:当0a =,1b =时,()f x lnx x =−,所以1()xf x x−'=, 令()0f x '>,得01x <<;令()0f x '<,得1x >, 所以()f x 在(0,1)上单调递增,在(1,)+∞上单调递减, 所以()min f x f =(1)1=−, 故()1f x −; (2)解:当6b π=时,()cos 16f x a x xπ'=+−,所以cos 106a x xπ+−在(0,)3π上恒成立,即66cos x ax xπ−在(0,)3π上恒成立,令6()6cos x h x x x π−=,(0,)3x π∈,显然当(0,)6x π∈时,()0h x <;当(6x π∈,)3π时,()0h x >,而当(6x π∈,)3π时,22cos sin (6)()06x x x x h x x cos xππ+−'=>,所以()h x 在(6π,)3π上单调递增, 所以()()13h x h π<=,所以1a ,即a 的取值范围是[1,)+∞;(3)132111(1)(1)(1)444n e ++⋯+<,证明:由(1)知(1)ln x x +< (0)x >, 令14x x =,得11(1)44x x ln +<, 所以11(1)44ln +<,2211(1)44ln +<,⋯,11(1)44n n ln +<,所以22111111(1)(1)(1)444444n n ln ln ln ++++⋯++<++⋯⋯+,即221111111111[(1)(1)(1)]4444443343n n n ln ++⋯+<++⋯⋯+=−⨯<,所以132111(1)(1)(1)444n e ++⋯+<.变式1.已知函数2()(21)(1)f x lnx ax a x a =+−+++. (1)若对1x ∀>,都有()0f x >恒成立,求a 的取值范围;(2)证明:22222(1)(2)(3)()n n n n n n e n +++⋯+>对任意正整数n 均成立,其中e 为自然对数的底数. 【答案】【解答】(1)解:212(21)1(21)(1)()2(21)ax a x ax x f x ax a x x x−++−−'=+−+==.1x >,10x ∴−>,故:①当0a 时,()0f x ',()f x 在(1,)+∞上单调递减, 而f (1)0=,()0f x ∴<,不符合题意; ②当12a时,即112a,()f x 在(1,)+∞上单调递增, 而()f x f >(1)0=,∴符合题意; ③当102a <<,1(1,)2x a∈时,()0f x '<,()f x 在1(1,)2a 上单调递减, 而f (1)0=,∴此时()0f x <,不符合题意, 综上所述,a 的取值范围为1[,)2+∞.(2)证明:要证明22222(1)(2)(3)()n n n n n n e n +++⋯+>,等价于证明2222222212n n n k n nn n n n ++++⋯⋯>, 等价于证明222222221212n n n k n n ln ln ln ln n n n n ++++++⋯++⋯+>.由(1)可得1(1)[1(1)]2lnx x x >−−−在(1,)+∞恒成立.令21kx n =+,1k =,2,3,⋯,n ,则221k n,∴2224221(1)22k k k k ln n n n n n +>−−, ∴222222222212121122n n n k n n n ln ln ln ln n n n n n n n ++++++⋯+++⋯++⋯+>−⨯=, ∴222222221212n n n k n n ln ln ln ln n n n n ++++++⋯++⋯+>成立,∴22222(1)(2)(3)()n n n n n n e n +++⋯+>成立.例8.已知函数()(1)f x x lnx =+,曲线()y f x =在1x =处的切线方程为y ax b =+. (Ⅰ)求a ,b 的值;(Ⅱ)求证:1x >时,()f x ax b >+;(Ⅲ)求证:2227(2)23(2,*)1632ln ln ln n n n N n n −++⋯++>∈−. 【答案】【解答】解:(Ⅰ)函数()f x 的定义域为(0,)+∞,1()x f x lnx x+'=+, f '(1)2=,⋯⋯⋯⋯⋯⋯⋯⋯(2分) 又因为f (1)0=,⋯⋯⋯⋯⋯⋯⋯⋯(3分) 所以该切线方程为2(1)y x =−,即2a =,2b =−. (Ⅱ)设()(1)22F x x lnx x =+−+, 则1()1F x lnx x'=+−, 设1()1g x lnx x=+−,(1)x ,g (1)0= 则21()x g x x−'=, 当(1,)+∞,()0g x '>,又g (1)0=,故()0g x >.所以()0F x '>,即()F x 在区间(1,)+∞单调递增,所以()F x F >(1)0= 所以1x >,()f x ax b >+.(Ⅲ)由(Ⅱ)可知,(1)2(1)x lnx x +>−.令22(2,*)x n n n N =−∈,则222(1)(2)2(3)n ln n n −−>−,因为222(2)2113111ln n n n n n −>=−−−−+,所以2n ,*n N ∈时,2227(2)111111111111321116332446211212ln ln ln n n n n n n n n n−++⋯+>−+−+−+⋯+−+−=+−−>−⋯−−−++ 即2227(2)23(2,*)1632ln ln ln n n n N n n −++⋯++>∈−. 变式8.已知函数1()(1)f x alnx a x x=−+−(1)当1a <−时,讨论()f x 的单调性 (2)当1a =时,若1()1g x x x=−−−,证明:当1x >时,()g x 的图象恒在()f x 的图象上方(3)证明:2*2222321(234(1)ln ln lnn n n n N n n −−++⋯+<∈+,2)n【答案】【解答】解:(1)函数1()(1)f x alnx a x x=−+−, 0x ∴>,2221(1)1()(1)a a x ax f x a x x x −+++'=−++=,1a <−,由()0f x '>,得[(1)1](1)0a x x −+−−>,当2a =−时,由()0f x '>,得1x ≠,增区间为(−∞,1],[1,)+∞,无减区间; 当12a −<<−时,由()0f x '>得,11x a >−+或1x <,增区间为(0,1],1[1a −+,)+∞,减区间为[1,1]1a −+; 当2a >−时,由()0f x '>得,11x a <−+或1x >,增区间为(0,1]1a −+,[1,)+∞,减区间为1[1a −+,1]. 证明:(2)1a =时,1()2f x lnx x x =−−,1()1g x x x=−−−, 设()()()1F x f x g x lnx x =−=−+,11()1xF x x x−'=−=, 当(0,1)x ∈时,()0F x '>,当(1,)x ∈+∞时,()0F x '<()F x F ∴(1)0=,即()()f x g x <恒成立, ()g x ∴的图象恒在()f x 图象的上方. (3)由(2)知10lnx x −+(0)x >, 设()1K x lnx x =−+,则11()1x K x x x−'=−=. 当(0,1)x ∈时,()0k x '>,()k x ∴为单调递增函数; 当(1,)x ∈∞时,()0k x '<,()k x ∴为单调递减函数;1x ∴=为()k x 的极大值点,()k x k ∴(1)0=. 即10lnx x −+,1lnx x ∴−.由上知1lnx x −,又0x >,∴11lnx x x−. n N +∈,2n ,令2x n =,得22211lnn n n−,∴2211(1)2lnn n n −,∴222222231111(111)23223ln ln lnn n n++⋯+−+−+⋯+− 2221111[1()]223n n=−−++⋯+1111[1()]22334(1)n n n <−−++⋯+⨯⨯+ 1111111[1()]223341n n n =−−−+−+⋯+−+ 111[1()]221n n =−−−+ 2*21(4(1)n n n N n −−=∈+,2)n ∴2*2222321(234(1)ln ln lnn n n n N n n −−++⋯+<∈+,2)n 三、课后练习1.若函数211()(1)(1)22f x aln x x a x =++−+−. (1)讨论函数()f x 的单调性;(2)若()0f x 在(1,)−+∞上恒成立,求实数a 的取值范围; (3)求证:对任意的正整数n 都有,11111234n ln ln ln lnn n−+++⋯+>. 【答案】【解答】解:(1)(1)()11a x x a f x x a x x +−'=+−=+−. 若0a ,则当(1,0)x ∈−时,()0f x '<,()f x 单调递减;当(0,)x ∈+∞时,()0f x '>,()f x 单调递增;若01a <<,则当(1,1)x a ∈−−或(0,)x ∈+∞时,()0f x '>,()f x 单调递增;当(1,0)x a ∈−时,()0f x '<,()f x 单调递减;若1a =,则()0f x '恒成立,当且仅当0x =时取等号,所以()f x 在(1,)−+∞单调递增; 若1a >,则当(1,0)x ∈−或(1,)x a ∈−+∞时,()0f x '>,()f x 单调递增;当(0,1)x a ∈−时,()0f x '<,()f x 单调递减; (2)11(0)0022f a a =−−⇒−<, 所以当(1,0)x ∈−时,()0f x '<,()f x 单调递减;当(0,)x ∈+∞时,()0f x '>,()f x 单调递增;当0x =时,()f x 取最小值(0)0f ;所以(a ∈−∞,1]2−.(3)当12a =−时,2211111111()(1)(1)02222(1)1f x ln x x x ln x x x x x =−++++−⇔=−+++对任意(1,)x ∈−+∞恒成立,当且仅当0x =时取等号. 所以对任意的正整数n ,111(1)1ln n n n >−++,所以1111111111112312231n ln ln ln n n n n n−++⋯+>−+−+⋯++=−=−. 2.已知函数()(1)(1)f x lnx x ax a =+−−−. (Ⅰ)当0a =时,求()f x 的最大值;(Ⅱ)若对1x ∀>,都有()0f x >恒成立,求a 的取值范围;(Ⅲ)证明:22222(1)(2)(3)()n n n n n n e n +++⋯⋯+>对任意正整数n 均成立,其中e 为自然对数的底数. 【答案】【解答】(1)解:当0a =时,()1f x lnx x =+−,(0)x >, 11()1xf x x x−'=−=. 可得(0,1)∈时,()0f x '>,(1,)x ∈+∞时,()0f x '<,()f x ∴在(0,1)递增,在(1,)+∞递减, ()f x ∴的最大值为f (1)0=;(2)解:212(21)1(21)(1)()(1)(1)ax a x ax x f x ax a x a x x x−++−−'=+−−+−==. .110x x >∴−>故:①当0a 时,()0f x ',()f x 在(1,)+∞单调递减,而f (1)0=,()0f x ∴<,不符合题意, ②当102a时,112a,()f x 在(1,)+∞单调递增,在(而f (1)0=, ()0f x ∴>,不符合题意,③当1002a <<时,1(1,)2a ∈时,()0f x ',()f x 在1(1,)2a 单调递减,而f (1)0=,∴此时()0f x <,不符合题意,综上所述:a 的取值范围1[2,)+∞(3)证明:要证明22222(1)(2)(3)()n n n n n n e n +++⋯⋯+>.等价于证明2222222212n n n k n nn n n n++++⋯⋯>, 等价于证明222222221212n n n k n n ln ln ln ln n n n n ++++++⋯++⋯>.由(2)可得1(1)[1(1)]2lnx x x >−−−在(1,)+∞恒成立.令21kx n =+,1k =,2,3,n ⋯.则221k n2224221(1)22k k k k ln n n nn n∴+>−−. 222222222212121122n n n k n n n ln ln ln ln n n n n n n n ++++++⋯+∴++⋯++⋯>−⨯=. ∴.222222221212n n n k n n ln ln ln ln n n n n ++++++⋯++⋯>.成立.22222(1)(2)(3)()n n n n n n e n ∴+++⋯⋯+>.成立.3.已知函数()()f x x ln x a =−+的最小值为0,其中0a >. (1)求a 的值;(2)若对任意的[0x ∈,)+∞,有2()f x kx 成立,求实数k 的范围;(3)证明:*12(21)2()21ni ln n n N i =−+<∈−∑(注12222:2)213521ni i n ==+++⋯−−∑【答案】【解答】解:(1)函数的定义域为(,)a −+∞.由()0f x '=得:1x a a =−>−又由()0f x '得:1x a −()f x ∴在(,1)a a −−单调递减,在[1a −,)+∞单调递增 (())(1)01min f x f a a ∴=−=⇒=(2)设2()()(0)g x kx x In x a x =−++,则()0g x 在[0,)+∞恒成立 ()0(0)(*)min g x g ⇔=注意到g (1)1200k In k =−+⇒> 又(221)()1x kx k g x x +−'=+①当1210()2k k −<<时,由()0g x '得122kx k−.()g x 在12[0,]2k k −单减,12(,)2k k−+∞单增,这与(*)式矛盾; ②当12k时 ()0g x '在[0,)+∞恒成立()(0)0g x g ∴=符合(*) ∴12k⋯⋯(8分) 证明:(3)由(2)知:令12k =得:21(1)2x In x x −+令2(1,2,,)21x i n i ==⋯−得:222[(21)(21)]21(21)In i In i i i −+−−<⋯−− 当1i =时,2232x In =⇒−<; 当2i 时,2211(21)2321i i i <−⋯⋯−−−(11分)从而2121[(21)(21)]23122121i In i In i In i n =−++−<−+−<−−∑. 4.已知函数()1f x x lnx =−−. (1)求函数()f x 的最小值;(2)当*n N ∈时,求证:①11n ln n n+>;②1111231ne n +++⋯+>+.(e 为自然对数的底)【答案】【解答】解:(1)函数()1f x x lnx =−−.(0,)x ∴∈+∞,11()1x f x x x−'=−=, 当(0,1)x ∈时,()0f x '<,()f x 是减函数, 当(1,)x ∈+∞时,()0f x '>,()f x 是增函数, ()min f x f ∴=(1)0=.证明:(2)①由(1)得()10f x x lnx =−−, 当且仅当1x =时取等号,1x lnx ∴−,令*11()n x n N n +=>∈,得11n lnn n+>, ∴11n lnn n +>.②11n lnn n+>, 1112311(1)2312n ln ln ln ln n n n+∴+++⋯+>++⋯+=+, ∴1111231nen +++⋯+>+.5.已知函数()f x x lnx =−. (1)求()f x 的最小值;(2)证明:对于任意正整数n ,222111(1)(1)(1)23e n+⨯+⨯⋯⨯+<. 【答案】【解答】解:(1)11()1x f x x x−'=−=, 当(0,1)x ∈时,()0f x '<,故()f x 在(0,1)单调递减; 当(1,)x ∈+∞时,()0f x '>,()f x 在(1,)+∞单调递增; 故()f x f (1)1=,故()f x 的最小值为1. (2)由(1)可得,()1f x x lnx =−即1lnx x −, 所以2211111(1)(1)1ln k k k k k k+<=−−−,*k N ∈,2n , 则222111111111(1)(1)(1)111232231ln ln ln n n n n ++++⋯++<−+−+⋯+−=−<−, 即222111(1)(1)(1)123ln n ++⋯+<, 所以222111(1)(1)(1)23ln e n ++⋯+<. 6.已知定义在(0,)+∞上的函数()f x 过点(1,0),其导函数为2()1f x x x'=−+,设23()(1)22x g x k x lnx =−+−++.(1)求()f x 的解析式;(2)是否存在实数k ,使得对任意的(0,)x ∈+∞不等式()()0f x g x +>恒成立?若存在,求出k 的取值范围,若不存在,请说明理由; (3)求证:2!(1)(2elnn n n n <+=,3,4)⋯ 【答案】 【解答】解:(1)2()1f x x x'=−+ 2()2(2x f x lnx x C C ∴=−++为常数)又()f x 过(1,0)f ∴(1)1102C =++=,解得32C =− 故23()222x f x lnx x =−+− (2)假设存在实数k ,使得对任意的(0,)x ∈+∞不等式()()0f x g x +>恒成立 由(1)知()()0f x g x +>, 0kx lnx −>,即lnxk x>令()lnx t x x =,则21()lnxt x x −'=,由()0t x '=解得x e =当0x e <<时()0t x '>,()t x 为增函数 当x e >时()0t x '>,()t x 为减函数 1e∴=,1k e ∴>,故k 的取值范围为1(e,)+∞.证明:(3)由(2)知,当0x >时,1lnxx e, ∴当2n =,3,4⋯时1lnn n e<,即elnn n < 22eln ∴<,33eln <,44eln <,⋯,elnn n <,2!(1)(2elnn n n n ∴<+=,3,4)⋯.7.已知函数2()1f x ax bx =++在3x =处的切线方程为58y x =−. (1)求函数()f x 的解析式;(2)若关于x 的方程()x f x ke =恰有两个不同的实根,求实数k 的值; (3)数列{}n a 满足12a f =(2),1()n n a f a +=,*n N ∈,证明: ①11n n a a +>> ②123201911112S a a a a =+++⋯+<. 【答案】【解答】(1)解:2()1f x ax bx =++,()2f x ax b '=+, 依题意,(3)5(3)7f f '=⎧⎨=⎩,即659310a b a b +=⎧⎨++=⎩,解得11a b =⎧⎨=−⎩,2()1f x x x ∴=−+;(2)解:方程()x f x ke =,即21x x x ke −+=, 得2(1)x k x x e −=−+, 记2()(1)x F x x x e −=−+,则22()(21)(1)(32)x x x F x x e x x e x x e −−−'=−−−+=−−+(1)(2)x x x e −=−−−.令()0F x '=,得11x =,22x =.∴当1x =−时,()F x 取极小值1e ,当2x =时,()F x 取极大值23e.可知当1k e=或23k e =时,它们有两个不同交点,因此方程()x f x ke =恰有两个不同的实根;(3)证明:①12a f =(2)3=,得1312a =>,又21()1n n n n a f a a a +==−+, ∴22121(1)0n n n n n a a a a a +−=−+=−>, 11n n a a +∴>>.②由211n n n a a a +=−+,得11(1)n n n a a a +−=−, 111111(1)1n n n n na a a a a +==−−−−,即111111n n n a a a +=−−−. ∴12320191223201920201111111111()()()111111S a a a a a a a a a a =+++⋯+=−+−+⋯+−−−−−−− 12020202011122111a a a =−=−<−−−. 8.已知函数()()f x ax ln x b =−+在点(1,1)处的切线与x 轴平行. (1)求实数a ,b 的值;(2)证明:22132(,2)()(1)nk n n n N n k f k n n =−−>∈−+∑.【答案】 【解答】解:(1)1()f x a x b'=−+,又由已知得f '(1)0=①f (1)1a lnb =−=② 由①,②解得:1a =,0b =(2)()k f k lnk −=,设212324,,(1)1n n n n n n n b lnn T a T T n n n −−−===−=+− 当2n 时有,2110,04n n n b lnn a −=>=> 设21()(2)4x h x lnx x −=−,则212()022x x h x x −'=−=>恒成立 即()h x 在[2,)+∞上是增函数, n n b a ∴>等价于221111n n h a b a b −−=(2)3204ln =−>,∴221114443223381(1)n n ln ln lnn n n n −−++⋯+>++⋯+=−+,∴22132(,2)()(1)nk n n n N n k f k n n =−−>∈−+∑. 9.已知函数2()1f x alnx x =−+. (Ⅰ)讨论()f x 的单调性; (Ⅱ)求证:22223(1)(21)(2)234(1)ln ln lnn n n n n n −+++⋯+<+. 【答案】【解答】(本小题满分12分)解:(Ⅰ)()f x 的定义域为(0,)+∞,22()2a a x f x x x x−'=−=.①当0a 时,()0f x ',()f x 在(0,)+∞上单调递减;(2分) ②当0a >时,由()0f x '<解得x >;由()0f x '>解得0x << 所以()f x在上单调递增,在)+∞上单调递减. (Ⅱ)证明:由(Ⅰ)得当2a =时,()max f x f =(1)21110ln =−+=, 即2210lnx x −+当且仅当1x =时等号成立.所以2210(2)lnn n n −+<,21(2)2n lnn n −<, 2211111111(1)[1]()(2)22(1)221lnn n n n n n n n <−<−=−−++, 所以22223111111111111()()2322233412221ln ln lnn n n n n n n −−++⋯+<−−+−+⋯+−=−−++, (11分) 即22223(1)(21)234(1)ln ln lnn n n n n −+++⋯+<+. 10.已知关于x 的函数()(1)f x ln x =+. (Ⅰ)当0x >时,证明:(1)1xln x x +>+; (Ⅱ)求证:1112()332313ni ln n n n=+−<−−∑. 【答案】【解答】(Ⅰ)证明:令1x t +=,(1)t >. 只需证明:1t lnt t −>,即证明110lnt t−+>,(1)t >. 令1()10g t lnt t=−+>,(1)t >.21()0t g t t−'=>,()g t ∴在(0,+∞单调递增. ()g t g ∴>(1)0=,即(1)1xln x x +>+; (Ⅱ)证明由(Ⅰ)可得(1)1x ln x x +>+,令1x n =,可得11(1)1ln n n<++.1111233123131n n nln lm ln lm n n n n n n ++++⋯+<++⋯+=+++− 111121111()()3231332313nni i n n n n n n n ==+−=++−−−−−∑∑ 11111(1)2332313n n n =+++⋯+++−−−(1)111)23n++⋯+ 111123n n n=++⋯+++ ∴1112()332313n i ln n n n=+−<−−∑. 11.已知函数1()12a f x ax a lnx x−=++−−,a R ∈. ()I 若1a =−,求函数()f x 的单调区间;(Ⅱ)若()0f x 在[1x ∈,)+∞上恒成立,求正数a 的取值范围; (Ⅲ)证明:*1111(1)()232(1)n ln n n N n n +++⋯+>++∈+. 【答案】【解答】解:()I 当1a =−时,2()3f x x lnx x=−−−−,则函数()f x 的定义域为{|0}x x >, 则2222(1)(2)()x x x x f x x x −−+−−+'==,则当(0,1)x ∈时,()0f x '>,则()f x 单调递增; 则当(1,)x ∈+∞时,()0f x '<,则()f x 单调递减;所以()f x 单调递增区间为(0,1),()f x 单调递减区间为(1,)+∞ (Ⅱ)因为1()12a f x ax a lnx x−=++−−,[1x ∈,)+∞,则f (1)0=,222211(1)1()(1)()a ax x a a af x a x x x x x x a −−−−−'=−−==−−.①当102a <<,时,此时11aa−>,当11ax a−<<,则()0f x '<,()f x 在[1,1]a a −上是减函数,所以在1(1,)a a −上存在0x ,使得0()f x f <(1)0<,()0f x 在[1,)+∞上不恒成立; ②当12a时,11aa−,()0f x '在[1,)+∞上成立,()f x 在[1,)+∞上是增函数,()f x f(1)0=,()0f x 在[1,)+∞上恒成立, 综上所述,所求a 的取值范围为1[,)2+∞;(Ⅲ)由(Ⅱ)知当12a 时,()0f x 在[1,)+∞上恒成立,1120(1)a ax a lnx x x−++−−, 令12a =,有11()2x lnx x−, 当1x >时,11()2x lnx x−>,令1k x k +=,有111111()[(1)(1)]2121k k k ln k k k k k ++<−=+−−++, 即111(1)()21ln k lnk k k +−<++,1k =,2,3,⋯,n ,将上述n 个不等式依次相加得:11111(1)()2232(1)ln n n n +<+++⋯+++,整理得1111(1)(1)232(1)n ln n n n n +++⋯+>+++. 12.已知函数()1f x x lnx =−−. (Ⅰ)求证:()0f x ;(Ⅱ)求证:*2111[(1)(1)(1)]1()222n ln n N ++⋯+<∈.【答案】【解答】证明:(Ⅰ)由题意知,()1f x x lnx =−−的定义域为(0,)+∞, 因为11()1x f x −'=−=,所以()f x 和()f x '的变化情况如下表所示:由表可知:()min f x f =(1)1110ln =−−=. 所以()()0min f x f x =.(Ⅱ)由(Ⅰ)可知:10x lnx −−>,(1)x ≠即1(1)lnx x x <−≠. 所以可得22111111(1),(1),,(1)222222n n ln ln ln +<+<⋯+<.将上述n 个式子相加可得:*21111111[(1)(1)(1)]11()2222422n n n ln n N ++⋯+<++⋯+=−<∈,所以结论得证,即*2111[(1)(1)(1)]1()222n ln n N ++⋯+<∈.。
导数放缩常用公式的证明

导数放缩常用公式的证明在微积分中,导数放缩是一种非常常见且有用的技巧,用于简化复杂函数的导数计算。
导数放缩常用公式包括常数倍法则、和差法则以及积的法则等。
在这篇文章中,我们将详细证明导数放缩常用公式的正确性。
常数倍法则首先,我们考虑导数常数倍法则的证明。
设f(f)是可微函数,f是常数,则有:$$ \\frac{d}{dx}(cf(x))=c\\frac{d}{dx}f(x) $$证明过程如下:根据导数的定义,我们有:$$ \\frac{df(c)}{dx}=\\lim_{h\\to 0}\\frac{f(c+h)-f(c)}{h} $$将f(f)替换为ff(f),得到:$$ \\begin{aligned} \\frac{df(cf)}{dx} & =\\lim_{h\\to0}\\frac{cf(c+h)-cf(c)}{h} \\\\ & =c\\lim_{h\\to0}\\frac{f(c+h)-f(c)}{h} \\\\ & =c\\frac{df}{dx} \\end{aligned} $$因此,常数倍法则得证。
和差法则接下来我们考虑导数和差法则的证明。
设f(f)和f(f)是可微函数,则有:$$ \\frac{d}{dx}(f(x)+g(x))=\\frac{d}{dx}f(x)+\\frac{d}{dx }g(x) $$证明过程如下:根据导数的定义,我们有:$$ \\begin{aligned} \\frac{d(f+g)}{dx} & =\\lim_{h\\to0}\\frac{(f+g)(x+h)-(f+g)(x)}{h} \\\\ & =\\lim_{h\\to0}\\frac{(f(x+h)-f(x))+(g(x+h)-g(x))}{h} \\\\ & =\\lim_{h\\to 0}\\frac{f(x+h)-f(x)}{h}+\\lim_{h\\to 0}\\frac{g(x+h)-g(x)}{h} \\\\ & =\\frac{df}{dx}+\\frac{dg}{dx} \\end{aligned} $$因此,和差法则得证。
常用导数放缩法

一:消参放缩(适合含参)1.已知函数f(x)=e x-ln(x+m).(1)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;(2)当m≤2时,证明f(x)>0.解:(1)f′(x)=1e xx m -+.由x=0是f(x)的极值点得f′(0)=0,所以m=1.于是f(x)=e x-ln(x+1),定义域为(-1,+∞),f′(x)=1e1 xx-+.函数f′(x)=1e1xx-+在(-1,+∞)单调递增,且f′(0)=0.因此当x∈(-1,0)时,f′(x)<0;当x∈(0,+∞)时,f′(x)>0.所以f(x)在(-1,0)单调递减,在(0,+∞)单调递增.(2)当m≤2,x∈(-m,+∞)时,ln(x+m)≤ln(x+2),故只需证明当m=2时,f(x)>0.当m=2时,函数f′(x)=1e2xx-+在(-2,+∞)单调递增.又f′(-1)<0,f′(0)>0,故f′(x)=0在(-2,+∞)有唯一实根x0,且x0∈(-1,0).当x∈(-2,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0,从而当x=x0时,f(x)取得最小值.由f′(x0)=0得0e x=01 2x+,ln(x0+2)=-x0,故f(x)≥f(x0)=01 2x++x0=212xx(+)+>0.综上,当m≤2时,f(x)>0.2.已知函数f(x)=m e x-ln x-1.(Ⅰ)当m =1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)当m ≥1时,证明:f(x)>1.【答案】(Ⅰ)y =(e -1)x(Ⅱ)当m ≥1时,f (x)= m e x-ln x -1≥e x-ln x -1.(放缩)要证明f (x)>1,只需证明e x-ln x -2>0.3.知函数1()ln(1)(1)nf x a xx=+--,其中*x∈N,a为常数.(Ⅱ)当1a =时,证明:对任意的正整数n ,当2n ≥时,有()1f x x -≤. 当1a =时,1()ln(1)(1)nf x x x =+--.当2x ≥时,对任意的正整数n ,恒有11(1)nx -≤,故只需证明1ln(1)1x x +--≤.令()1(1ln(1))2ln(1)h x x x x x =--+-=---,[)2x ∈+∞,,则12()111x h x x x -'=-=--,当2x ≥时,()0h x '≥,故()h x 在[)2+∞,上单调递增,因此当2x ≥时,()(2)0h x h =≥,即1ln(1)1x x +--≤成立. 故当2x ≥时,有1ln(1)1(1)nx x x +---≤.即()1f x x -≤.二:构造放缩(适合f(x)或其变式的N 项和有关)4.设函数()()2ln 1f x x b x =++.(1)若x =1时,函数()f x 取最小值,求实数b 的值;(2)若函数()f x 在定义域上是单调函数,求实数b 的取值范围;(3)若1b =-,证明对任意正整数n ,不等式33311......31211)1(n <k f nk ++++∑=都成立解:(1)由x + 1>0得x > – 1∴f(x)的定义域为( - 1,+ ∞),对x ∈ ( - 1,+ ∞),都有f(x)≥f(1),∴f(1)是函数f(x)的最小值,故有f /(1) = 0,,022,12)(/=+∴++=bx b x x f 解得b= - 4. 经检验合题意;(2)∵,12212)(2/+++=++=x b x x x b x x f 又函数f(x)在定义域上是单调函数,∴f /(x) ≥0或f /(x)≤0在( - 1,+ ∞)上恒成立.若f /(x) ≥0,∵x + 1>0,∴2x 2+2x+b ≥0在( - 1,+ ∞)上恒成立,即b ≥-2x 2-2x =21)21(22++x 恒成立,由此得b ≥21; 若f /(x) ≤0, ∵x + 1>0, ∴2x 2+2x+b ≤0,即b ≤- (2x 2+2x)恒成立,因-(2x 2+2x) 在( - 1,+ ∞)上没有最小值,∴不存在实数b 使f(x) ≤0恒成立.综上所述,实数b 的取值范围是⎪⎭⎫⎢⎣⎡+∞,21. (3)当b= - 1时,函数f(x) = x 2- ln(x+1),令函数h(x)=f(x) – x 3= x 2– ln(x+1) – x 3,则h /(x) = - 3x 2 +2x - 1)1(31123+-+-=+x x x x ,∴当[)+∞∈,0x 时,h /(x)<0所以函数h(x)在[)+∞∈,0x 上是单调递减.又h(0)=0,∴当()+∞∈,0x 时,恒有h(x) <h(0)=0,[ 即x 2– ln(x+1) <x 3恒成立.故当()+∞∈,0x 时,有f(x) <x 3..∵()1,0,,k N k +∈∴∈+∞取,1k x =则有311(),f k k < ∴33311 (312)11)1(n <k f nk ++++∑=,故结论成立。
导数放缩的常见形式

导数放缩的常见形式导数放缩是微积分中的一种常见技巧,通过对函数进行适当的变形,可以简化计算或者提供更多有关函数性质的信息。
下面是导数放缩的一些常见形式。
1.常数乘法和加法法则:对于函数f(x)和常数a、b,有以下关系:(a·f(x))'=a·f'(x)(f(x)+b)'=f'(x)这意味着导数函数遵循常数乘法和加法法则。
可以根据这个法则查找任何函数的导数。
2.乘法法则:对于两个函数f(x)和g(x),有以下关系:(f(x)·g(x))'=f'(x)·g(x)+f(x)·g'(x)乘法法则使我们能够通过计算原函数和导函数之间的乘积来计算复合函数的导数。
3.倒数法则:对于函数f(x),有以下关系:(1/f(x))'=-f'(x)/[f(x)]^2倒数法则允许我们通过计算原函数的导数来计算倒数函数的导数。
4.加法法则:对于函数f(x)和g(x),有以下关系:(f(x)+g(x))'=f'(x)+g'(x)加法法则使我们能够通过计算原函数的导数来计算两个函数之和的导数。
5.减法法则:对于函数f(x)和g(x),有以下关系:(f(x)-g(x))'=f'(x)-g'(x)减法法则允许我们通过计算原函数的导数来计算两个函数之差的导数。
6.链式法则:链式法则是导数放缩中最重要的法则之一,它适用于复合函数。
对于函数y=f(g(x)),有以下关系:dy/dx = f'(g(x))·g'(x)链式法则允许我们通过计算原函数和内部函数的导数来计算复合函数的导数。
7.平方函数的导数:对于函数f(x)=x^2,有以下关系:f'(x)=2x平方函数的导数是一个常见形式,计算平方函数的导数非常简单。
8.指数函数的导数:对于函数f(x)=a^x,有以下关系:f'(x) = ln(a)·a^x指数函数的导数是一个常见形式,计算指数函数的导数需要用到自然对数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中导数放缩常用公式及证明
在高中数学学习中,导数是一个重要的概念。
导数的定义和性质都是高中数学的基础知识。
导数的放缩是导数的一个重要应用,它可以让我们更加方便地进行计算和推导。
本文将介绍一些高中导数放缩常用公式及其证明。
一、导数放缩公式
1.和差法则
设函数f(x)和g(x)在点x0处可导,则有:
f(x) ± g(x)在x0处可导,且
(f(x) ± g(x))'|x0 = f'(x0) ± g'(x0)
证明:
对于f(x) + g(x),设h(x) = f(x) + g(x),则有:
h'(x0) = lim(x → x0) [h(x) - h(x0)] / (x - x0)
= lim(x → x0) [f(x) + g(x) - f(x0) - g(x0)] / (x - x0) = lim(x → x0) [f(x) - f(x0)] / (x - x0) + lim(x → x0) [g(x) - g(x0)] / (x - x0)
= f'(x0) + g'(x0)
同理可证f(x) - g(x)在x0处可导,且(f(x) - g(x))'|x0 = f'(x0) - g'(x0)。
2.积法则
设函数f(x)和g(x)在点x0处可导,则有:
f(x)g(x)在x0处可导,且
(f(x)g(x))'|x0 = f'(x0)g(x0) + f(x0)g'(x0)
证明:
对于f(x)g(x),设h(x) = f(x)g(x),则有:
h'(x0) = lim(x → x0) [h(x) - h(x0)] / (x - x0)
= lim(x → x0) [f(x)g(x) - f(x0)g(x0)] / (x - x0)
= lim(x → x0) [(f(x) - f(x0))g(x0) + f(x0)(g(x) - g(x0))] / (x - x0)
= lim(x → x0) [f(x) - f(x0)] / (x - x0) · g(x0) +
f(x0) · lim(x → x0) [g(x) - g(x0)] / (x - x0)
= f'(x0)g(x0) + f(x0)g'(x0)
3.商法则
设函数f(x)和g(x)在点x0处可导,且g(x0) ≠ 0,则有:
f(x) / g(x)在x0处可导,且
(f(x) / g(x))'|x0 = [f'(x0)g(x0) - f(x0)g'(x0)] / (g(x0))^2 证明:
对于f(x) / g(x),设h(x) = f(x) / g(x),则有:
h'(x0) = lim(x → x0) [h(x) - h(x0)] / (x - x0)
= lim(x → x0) [f(x) / g(x) - f(x0) / g(x0)] / (x - x0) = lim(x → x0) [(f(x)g(x0) - f(x0)g(x)) / (g(x)g(x0))] / (x - x0)
= lim(x → x0) [(f(x) - f(x0)) / (x - x0) · g(x0) - f(x0) / (x - x0) · (g(x) - g(x0))] / (g(x0))^2
= [f'(x0)g(x0) - f(x0)g'(x0)] / (g(x0))^2
二、导数放缩应用
1.最值问题
对于一元函数f(x),如果在区间[a, b]上可导,且在[a, b]的端点处导数存在,则在[a, b]上f(x)取得最大值或最小值时,导数为0。
证明:略。
2.曲线的拐点
对于一元函数f(x),如果在区间[a, b]上可导,且在[a, b]的端点处导数存在,则在[a, b]上f(x)的拐点满足f''(x) = 0或f''(x)不存在。
证明:略。
三、总结
导数放缩是高中数学中的一个重要应用,本文介绍了和差法则、积法则和商法则三个常用公式及其证明。
这些公式不仅可以方便地进行计算和推导,还可以应用到最值问题和曲线的拐点问题中。
在学习中,我们应该熟练掌握这些公式,并灵活运用。
