中考专题复习-----线段和差的最大值与最小值
初中几何中线段和差最大值最小值典型分析最全

初中几何中线段和(差)的最值问题一、两条线段和的最小值。
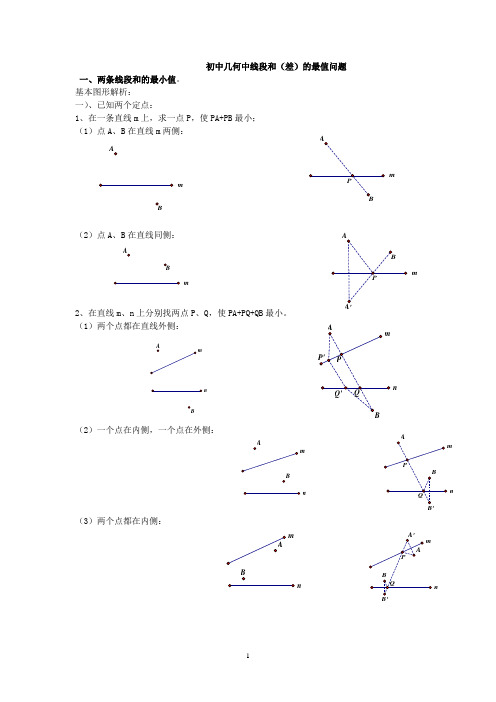
基本图形解析:(对称轴为:动点所在的直线上)一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
mmm mABm(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:nmnnmnnnm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:m nmnmnm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度mmmm恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:QQP练习题1.如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值为.Q2、如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为.3、如图,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC 边上一点.若AE=2,EM+CM的最小值为 .5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF 直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC 上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2(B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
(完整版)初中几何中线段和与差最值问题
三、其它非基本图形类线段和差最值问题
1、求线段的最大值与最小值需要将该条线段转化到一个三角形中,在该三角形中,其他两边是已知的,则所求线段的最大值为其他两线段之和,最小值为其他两线段之差。
点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)
1、两点在直线两侧:
2、两点在直线同侧:
(二)动点在圆上运动
点B在⊙O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B)
1、点与圆在直线两侧:
2、点与圆在直线同侧:
三)、已知A、B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点,使得PA+PQ+QB的值最小。(原理用平移知识解)
压轴题
1、如图,正比例函数 的图象与反比例函数 (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
2、如图,一元二次方程 的二根 , ( < )是抛物线 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求点D的坐标;
(2)过O,C,D三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段PO与PD之差的值最大?
若存在,请求出这个最大值和点P的坐标.若不存在,请说明理由.
初中几何中线段和差的最大值与最小值练习题(最全)教学文案
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
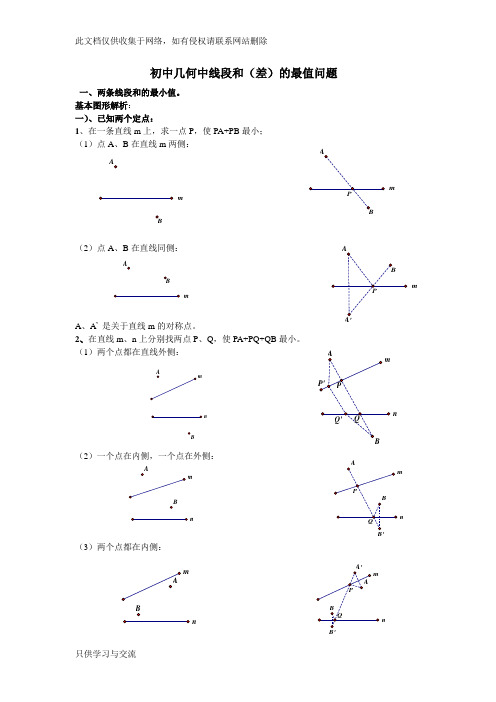
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mA Bmn mnnmnnnm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:mnm nm nm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR周长的最小值为.2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=52,∠BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .Q7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长; (3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
初中几何中线段和差的最大值与最小值练习题(最全)
初中几何中线段的最值问题一、两条线段和的最小值。
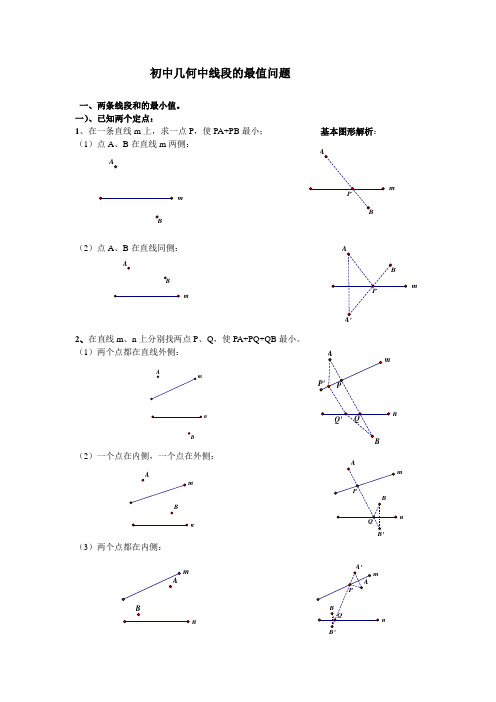
一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; 基本图形解析: (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mABmn mn nm nn nm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:mnm nm nm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .Q7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长; (3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
2020年中考备考专题复习课件:线段的和(差)最值问题(共18张PPT)

线段和(差)的最值问题
一、已知两个定点,一条直线,求 直线上一点,到两定点之和最小。
方法:作其中一点关于直 线的对称点 ,连接另一 点与对称点 ,与直线的 A 交点就是所要求的点。
基本图形 : FA+FB=F+FB`=AB` 此时,和最小
A
Bm
Bm F
B`
根据:两点间线段最短
5
BD
的最小值为4
5
B
C
5
E D
C
典型题解析
4.如图,△ABC为等边三角形,AB=2,若P为△ABC内一动点,
且满足∠PAB =∠ACP,则线段PB长度的最小值为___________.
C
解析:由∠PAB =∠ACP,且 ∠PAB+∠PAC=600,可得∠P=1200, 所以P应该是在AC所对的弧上运 动。由A、P、C三点确定辅助圆, 当B、P、O三点在一条直线上时, PB长度最小,根据两点间线段最 短。
解析:此题 A、C是两定点,点P在OB上为动点, 故可作C关于OB的对称点C`,连接AC`交OB于点P.
∵OA⊥OB, ∴∠AOB=900. ∵∠AOC=600, ∴∠BOC=300. ∴∠AOC`=300 ∴∠AOC=∠C`OC=600, ∠AOC`=1200 ∴OC⊥AC` ∴∠OAC`=300,AH=HC`.
y A
解析 :由PA-PB≤AB,故取等号时,差 最大,也就是当点P与点H重合时,差最 大。
∵A(-2,3) , B(3,1),
∴AB= 52 + 22 = 29 即:PA-PB长度最大为 29
y A
B
x
O
P
H
PO
B
数学人教版八年级上册中考几何复习专题——线段最值问题

《中考几何复习专题——线段最值问题》教学设计【教学目标】教学知识点:借助轴对称、平移、旋转等图形的变化,利用“两点之间线段,线段最短”,“三角形两边之和大于第三边,两边之差小于第三边”的原理解决线段和差最值的问题;感受临界状态和转化的数学思想.能力训练:在将实际问题抽象成基本数学模型的过程中,提高分析问题、解决问题的能力及渗透数学建模的思想.情感与价值观:通过有趣的问题提高学习数学的兴趣.在解决实际问题的过程中,体验数学学习的实用性,体现人人都学有所用的数学. 【教学重难点】重点: 线段和的最小值,线段差的最大值的基本模型.难点:利用平移和旋转解决三条线段和的最小值问题.【教学过程】一、复习线段和最小值,线段差最大值两个基本模型。
(1)“将军饮马问题”如图:A、B为直线同侧两定点,在直线上找一点P,使PA+PB最小。
学生回答解决方法:利用轴对称将同侧点转化为异侧,根据两点之间,线段最短找到点P 。
师生共同完成证明(任意另取一点P ’,借助三角形两边之和大于第三边P’完成证明)。
(2)如图:A 、B 为直线同侧两定点,在直线上找一点P ,使│PA —PB │最大。
点学生回答解决方法:师生共同完成证明(任意另取一点P ’,借助三角形两边之差小于第三边│P’A —P’B’ │>│PA-PB’ │,完成证明)。
二.练习强化如图,在正方形ABCD 中,AB=4,点E 为AB 上一点,BE=1A(1)在BD上找一点M,使EM+AM最小,求出最小值. (2)在BD上找一点M,使︱AM-EM ︱最大,求出最大值. (3)MN为BD上的一条动线段,MN= ,求EM+MN+NA 的最小值.(引出“造桥选址问题”)(4)在BD上找一点M,使AM+BM+CM最小,求出最小值. (引出“费马点”问题)三.造桥选址基本模型•A和B两地在一条河的两岸,现要在河上造一座桥MN。
桥造在何处可使从A到B的路程最短?(假定河的两岸是平行的直线,桥要与河垂直)学生先独立思考,再合作交流,教师给予”平移”动线段的提示共同解决问题。
初中几何中线段和差的最大值与最小值模型解析
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧: (2)点A 、B 在直线同侧: A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧: (4)台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.mnnm填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短. 二)一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、两点在直线两侧: 2、两点在直线同侧: (二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、点与圆在直线两侧:2、点与圆在直线同侧:(三)已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解)m(1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
中考复习专题系列----线段和、差的最值问题
《线段和差的最值问题》教学设计
1、公理:在连接两点的所有线中,______最短。
定
两点需异侧;
求
定
两点需同侧。
梳理思路:
四、教学反思
本次课是属于专题系列的归纳复习课,基本模型的探索过程采用微课的形式展示,作为课前导学,让学生细细体会“线段和、差的最值问题”三种基本模型的探索归纳,根据轴对称的性质,利用对称取点,转化成同侧、或异侧,对应基本模型,数形结合,使学生加深理解,初步形成“折化直”求最值。
把微课作为课前导学,为学生提供了反复学习的资源,学生学习不受时间、地域的限制,大大节约了课堂探究的时间,缓解学生压力,尤其是学困生,他们可以在微课学习后充分地思考、理解知识。
学生在微课的学习中提高归纳总结的能力,培养学生探索知识、分析问题、解决问题的能力,在学习过程中渗透数学建模的思想。
学案与微课同步,引导学生按部就班地开展学习本节内容。
学案中选取相应习题,设置知识应用,变式练习,巩固训练、知识延伸等环节,让学生快速地熟悉三种模型的结构,学会利用基本模型解决实际问题。
有课前的充分学习,课堂以“师徒互助”的学习小组模式进行。
学生兴致高昂,相互展示学习心得,尤其是“徒弟”,有充分地准备,有“师父”的帮助,都争抢着展现自己的成果,使得课堂紧凑、高效。
课堂中,教师精选了近几年相关中考题作为巩固提高练习,在综合图形中剖解出三种基本模型,分析问题并解决,紧扣中考,获得知识提升,突破中考的重难点。
此课可作为八年级上学期复习内容,亦可作为中考前专题复习,此种课前微课导学、师徒互助、小组展示交流的形式,学生甚是喜欢,有效地激发了学习数学的积极性,课堂效率大大提高,课后反馈效果理想。
中考压轴题分类专题二《线段和差的最值问题》
中考压轴题分类专题二——线段和差的最值问题基本题型:一、两线段和的最小值:已知两点A 、B 与直线l ,直线l 上有一动点P ,求PA +PB 的最小值。
求出A 点关于直线l 的对称点/A ,连接B A /交直线l 于点P ,则点P为所求最小值所取的点,()min /PB PA B A +=。
本题可转化为求ABP ∆的周长的最小值。
拓展:已知两点A 、B 与两直线1l 与2l , 动点P 在1l 上,动点Q 在2l 上,求AP +PQ +QB 的最小值。
求出A 点关于直线1l 的对称点/A ,再求出B 点关于直线2l 的对称点/B ,连接//B A 分别交直线1l 于点P、交直线2l 于点Q ,则P 、Q 为所求最小值所取的点,()min //QB PQ AP B A ++=。
本题可转化为求四边形APQB 的周长的最小值。
二、两线段差的最大值:已知两点A 、B 与直线l (AB 与l 不平行且在l 同侧),动点P 在l 上,求maxPBPA -。
连接AB 并延长交直线l 于点P ,则点P 为所求最大值时所取的点,maxPB PA AB -=。
yxOBA/PA所需知识点:一、 中点公式:已知两点()()2211y ,x Q ,y ,x P ,则线段PQ 的中点M 为⎪⎭⎫⎝⎛++222121y y ,x x 。
拓展:三角形的重心(三中线交点)公式:已知ABC ∆的顶点分别为()()()332211y ,x C ,y ,x B ,y ,x A ,则ABC ∆的重心G 为⎪⎭⎫⎝⎛++++3,3321321y y y x x x 。
二、 直线的斜率:直线的斜率是指直线与x 轴正方向所成角α的正切值。
00900<<α时,0t a n >=αk ;0018090<<α时,()0180t a n t a n 0<--==ααk 。
已知两点()()2211y ,x Q ,y ,x P ,则直线PQ 的斜率: 2121x x y y k PQ --=。
初中几何中线段和差最大值最小值练习题最全
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:m m BmABmn(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:(4)、台球两次碰壁模型nmnmnnnm变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点:(一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:(二)动点在圆上运动m nmnmnm点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:mmmm过A点作AC∥m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。
(2)点A、B在直线m同侧:练习题Q PQ1.如图,∠AOB =45°,P 是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值为.Q2、如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为.3、如图,在锐角三角形ABC中,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC 边上一点.若AE=2,EM+CM的最小值为 .5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.6、如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF 直线上的一点,则PA+PB的最小值为.7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N 分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC 上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2(B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC 绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F.(1)求经过A、B、C三点的抛物线的解析式;(2)当BE经过(1)中抛物线的顶点时,求CF的长;(3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ 的周长最小,求出P、Q两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x 轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边)基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大;(1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考专题------线段和(差)的最值问题 一、两条线段和的最小值。 基本图形解析: 一)、已知两个定点: 1、在一条直线m上,求一点P,使PA+PB最小; (1)点A、B在直线m两侧:
(2)点A、B在直线同侧: A、A’ 是关于直线m的对称点。 2、在直线m、n上分别找两点P、Q,使PA+PQ+QB最小。 (1)两个点都在直线外侧:
(2)一个点在内侧,一个点在外侧: (3)两个点都在内侧:
P mAB mA
B
mABP m
AB
A'
n mA
BQP
n
mA
BP'Q'
n mABQ
P
n
mA
BB'
QP n
mA
BB'
A'
n m
A
B(4)、台球两次碰壁模型 变式一:已知点A、B位于直线m,n 的内侧,在直线n、m分别上求点D、E点,使得围成的四边形ADEB周长最短.
填空:最短周长=________________ 变式二:已知点A位于直线m,n 的内侧, 在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.
二)、一个动点,一个定点: (一)动点在直线上运动: 点B在直线n上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B) 1、两点在直线两侧:
2、两点在直线同侧: m n
AP m n
AB
m nAP m
nAA'
B
mnAB
ED
m
nABA'
B'
mnAPQ
m
nA
A"
A'(二)动点在圆上运动 点B在⊙O上运动,在直线m上找一点P,使PA+PB最小(在图中画出点P和点B) 1、点与圆在直线两侧:
2、点与圆在直线同侧: 三)、已知A、B是两个定点,P、Q是直线m上的两个动点,P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点,使得PA+PQ+QB的值最小。(原理用平移知识解) (1)点A、B在直线m两侧:
过A点作AC∥m,且AC长等于PQ长,连接BC,交直线m于Q,Q向左平移PQ长,即为P点,此时P、Q即为所求的点。 (2)点A、B在直线m同侧:
mOAP'P m
OB
A
B'
mOAP m
OAB
A'
mAB
B'
E
QP
m
AB
QP
mABQP
m
A
BC
QP练习题 1.如图,∠AOB=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值为 .
2、 如图1,在锐角三角形ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值为 . 3、如图,在锐角三角形ABC中 ,AB=52,∠BAC=45,BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
4、如图4所示,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为 .
5、如图3,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=4,AB=5,BC=6,点P是AB上一个动点,当PC+PD的和最小时,PB的长为__________.
6、 如图4,等腰梯形ABCD中,AB=AD=CD=1,∠ABC=60°,P是上底,下底中点EF直线上的一点,则PA+PB的最小值为 .
Q 7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为 .
8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是
9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.
10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为 11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是
12、 如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为 .
13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 . 14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为 cm.(结果不取近似值).
15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则PA+PC的最小值是 .
16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )
(A)2 (B) (C)1 (D)2 解答题
1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1. (1)求反比例函数的解析式; (2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小. 2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6). (1)求此二次函数的解析式; (2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标; (3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
3、如图10,在平面直角坐标系中,点A的坐标为(1,) ,△AOB的面积是. (1)求点B的坐标; (2)求过点A、O、B的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的 坐标;若不存在,请说明理由; 4.如图,抛物线y=35x2-185x+3和y轴的交点为A,M为OA的中点,若有一动点P,自M点处出发,沿直线运动到x轴上的某点(设为点E),再沿直线运动到该抛物线对称轴上的某点(设为点F),最后又沿直线运动到点A,求使点P运动的总路程最短的点E,点F的坐标,并求出这个最短路程的长.
5.如图,已知在平面直角坐标系xOy中,直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于点E和F. (1)求经过A、B、C三点的抛物线的解析式; (2)当BE经过(1)中抛物线的顶点时,求CF的长; (3)在抛物线的对称轴上取两点P、Q(点Q在点P的上方),且PQ=1,要使四边形BCPQ的周长最小,求出P、Q两点的坐标.
6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a 为何值时,四边形ABDC的周长最短.
7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.
(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;
(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标. 二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析: 1、在一条直线m上,求一点P,使PA与PB的差最大; (1)点A、B在直线m同侧:
解析:延长AB交直线m于点P,根据三角形两边之差小于第三边,P’A—P’B<AB,而PA—PB=AB此时最大,因此点P为所求的点。 (2)点A、B在直线m异侧:
解析:过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’,PA-PB最大值为AB’ 练习题
1. 如图,抛物线y=-14x 2-x+2的顶点为A,与y 轴交于点B. (1)求点A、点B的坐标; (2)若点P是x轴上任意一点,求证:PA-PB≤AB; (3)当PA-PB最大时,求点P的坐标.
mBAmABm
A
BB'
PP'
mBAP'P
