31生活中的平移习题
第01讲 图形的平移(知识解读+达标检测)(原卷版)

第01讲图形的平移【题型1生活中的平移现象】【题型2图形的平移】【题型3利用平移的性质求面积】【题型4利用平移的性质求长度】【题型5利用平移的性质求角度】【题型6利用平移解决实际问题】【题型7平移作图】考点:平移1.定义:在平面内,将一个图形整体沿某一方向由一个位置平移到另一个位置,图形的这种移动,叫做平移变换,简称平移。
2.平移三要素:图形的原来位置、平移的方向、平移的距离。
3.平移的性质(1)对应点的连线平行(或共线)且相等(2)对应线段平行(或共线)且相等;(3)对应角相等,对应角两边分别平行,且方向一致。
4.平移作图的步骤和方法:平行线法、对应点连线法、全等图形法(1)找关键点;(2)过每个关键点作平移方向的平行线,截取与之相等的距离,标出对应点(3)连接对应点。
将原图形的各个特征点按规定的方向平移,得到相应的对称点,再将各对称点进行相应连接,即得到平移后的图形【题型1生活中的平移现象】【典例1】(2023秋•道里区校级期中)在下列实例中,属于平移过程的有()①时针运行的过程;②电梯上升的过程;③地球自转的过程;④小汽车在平直的公路行驶.A.1个B.2个C.3个D.4个【变式1-1】(2023春•林州市期末)下列运动属于平移的是()A.荡秋千的小朋友B.转动的电风扇叶片C.正在上升的电梯D.行驶的自行车后轮【变式1-2】(2023春•富川县期末)一个图形,经过平移后,改变的是()A.颜色B.形状C.大小D.位置【变式1-3】(2023春•呼伦贝尔期末)在下列现象中,属于平移的是()A.小亮荡秋千运动B.升降电梯由一楼升到八楼C.时针的运行过程D.卫星绕地球运动【题型2图形的平移】【典例2】(2023春•罗山县期末)如图所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是()A.B.C.D.【变式2-1】(2023春•启东市期末)“水是生命之源,滋润着世间万物”国家节水标志由水滴,手掌和地球变形而成.寓意:像对待掌上明珠一样,珍惜每一滴水!以下通过平移节水标志得到的图形是()A.B.C.D.【变式2-2】(2023春•扎赉特旗期末)如图,将图中的冰墩墩通过平移可得到图为()A.B.C.D.【变式2-3】(2023春•琼海期末)如图所示的各组图形中,表示平移关系的是()A.B.C.D.【题型3利用平移的性质求面积】【典例3】(2023春•惠城区校级期中)如图,长为50m,宽为30m的长方形地块上,有纵横交错的几条小路,宽均为1m,其它部分均种植草坪,则种植草坪的面积为()A.1344m2B.1421m2C.1431m2D.1341m2【变式3-1】(2023春•凉山州期末)如图在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m),则空白部分表示的草地面积是()A.70m2B.60m2C.48m2D.18m2【变式3-2】(2023春•南陵县期末)如图,小红家楼梯长3m,高2m,宽1m,若想铺上地毯,则所需地毯的面积()A.2m2B.3m2C.5m2D.6m2【变式3-3】(2023秋•滨州期中)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF 的位置,平移距离为7,AB=13,DO=6,则图中阴影部分的面积为()A.70B.48C.84D.96【题型4利用平移的性质求长度】【典例4】(2022秋•芝罘区期末)如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.22cm C.20cm D.24cm【变式4-1】(2022秋•桓台县期末)如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上).若BF=10cm,EC=4cm,则平移距离为()A.3cm B.4cm C.6cm D.10cm【变式4-2】(2023春•南山区期末)如图,将直角△ABC沿边AC的方向平移到△DEF的位置,连结BE,若CD=6,AF=14,则BE的长为()A.4B.6C.8D.12【变式4-3】(2023春•唐县期末)如图,直角三角形ABC的周长为22,在其内部有5个小直角三角形,这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形的周长为()A.11B.22C.33D.44【题型5利用平移的性质求角度】【典例5】(2023春•霸州市期末)如图,点B,C在直线l上,直线l外有一点A,连接AB,AC,∠BAC=45°,∠ACB是钝角,将三角形ABC沿着直线l向右平移得到三角形A1B1C1,连接AB1,在平移过程中,当∠AB1A1=2∠CAB1时,∠CAB1的度数是()A.15°B.30°C.15°或45°D.30°或45°【变式5-1】(2023春•丰满区期末)将△ABC沿AB方向平移到△EFD的位置,若∠1=31°,∠2=57°,则∠D的度数为()A.91°B.90°C.92°D.105°【变式5-2】(2023春•凤翔县期中)如图,∠1=70°,∠2=160°直线a平移后得到直线b,则∠3=()A.20°B.30°C.40°D.50°【变式5-3】(2023春•遂川县期末)如图(1),将一副直角三角板两斜边摆放在同一直线上,且点A,D重合,固定含45°角的三角板ABC,将含角的三角板DEF从图(1)的位置,沿射线BA平移至图(2)的位置,则平移过程中,根据两个三角板的摆放位置,下列钝角:100°,105°,120°,135°,150°,165°,170°,沿三角板的边缘能直接画出的有()A.1个B.2个C.3个D.4个【题型6利用平移解决实际问题】【典例6】(2023春•南宁月考)如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.(1)比较两条线路的长短:粗线①细线②;(填“>”、“<”或“=”)(2)如果这段路程长4.7千米,小丽坐出租车从体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.7元,小丽身上有10元钱,够不够坐出租车从体育馆到少年宫呢?说明理由.【变式6-1】(2022秋•路北区期末)如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).(1)用含字母x的式子表示:草坪的长a=米,宽b=米;(2)请求出草坪的周长;(3)当小路的宽为1米时,草坪的周长是多少?【变式6-2】(2022春•婺城区校级期中)如图是某一长方形闲置空地,宽为3a米,长为b 米,为了美化环境,准备在这个长方形空地的四个顶点处分别修建一个半径为a米的扇形花圃(阴影部分),然后在花圃内种花,中间修一条长b米,宽a米的甬路,剩余部分种草.(提示:π取3)(1)甬路的面积为平方米;种花的面积为平方米.(2)当a=2,b=10时,请计算该长方形场地上种草的面积.(3)在(2)的条件下,种花的费用为每平方米30元,种草的费用为每平方米20元,甬路的费用为每平方米10元.那么美化这块空地共需要资金多少元?【变式6-3】(2023春•莱州市期末)如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.(1)用含a、b的代数式表示草坪(阴影)面积并化简.(2)若a=10,b=5,计算草坪的造价.【题型7平移作图】【典例7】(2022秋•蚌山区期末)已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).(1)在图中画出平移后的△A1B1C1;(2)直接写出△A1B1C1各顶点的坐标.A1;B1;C1;(3)求出△ABC的面积.【变式7-1】(2023秋•崇左期中)如图,在平面直角坐标系中,点A(﹣1,4),B(﹣2,1),C(﹣4,1),将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1,点A、B、C的对应点分别为点A1、B1、C1.(1)在图上画出△A1B1C1,并写出点A1,B1,C1的坐标;(2)设点P(m,n)为△ABC内一点,经过平移后,请写出点P在△A1B1C1内的对应点P1的坐标.【变式7-2】(2023秋•铜陵期中)如图,在正方形网格中有一个格点三角形ABC(△ABC 的各顶点都在格点上).(1)画出△ABC中AB边上的高CD;(2)将△ABC先向上平移3格,再向右平移4格,画出平移后的△A′B′C′;(3)在图中画出一个锐角格点三角形ABP,使得其面积等于△ABC的面积,并回答满足条件的点P有多少个.【变式7-3】(2023秋•蚌山区期中)如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(3,1),C(0,2),将△ABC先向左平移2个单位,再向上平移3个单位得到△A'B'C'.(1)在图中画出平移后的△A'B'C';(2)求△ABC的面积.一.选择题(共10小题)1.(2023春•高邮市期中)下列图形中,不能通过其中一个四边形平移得到的是()A.B.C.D.2.(2023秋•长汀县期中)小芳和小明在手工课上各自制作楼梯模型,他们用的材料如图,则()A.一样多B.小明多C.小芳多D.不能确定3.(2022春•当涂县期末)下列生活现象中,属于平移现象的是()A.急刹车时汽车在地面滑行B.足球在草地上跳动C.投影片的文字经投影转换到屏幕上D.钟摆的摆动4.(2023秋•金安区校级月考)将点P(﹣3,2)先向右平移2个单位,再向下平移4个单位,得到的点的坐标为()A.(﹣1,﹣4)B.(﹣1,﹣2)C.(﹣5,﹣4)D.(﹣5,﹣2)5.(2022•陵水县二模)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A.48B.96C.84D.42 6.(2022•定海区校级模拟)如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为()A.3B.4C.5D.6 7.(2022春•甘井子区校级期末)线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是()A.(5,﹣7)B.(4,3)C.(﹣5,10)D.(﹣3,7)8.(2022春•古城区期末)如图,图1与图2中的三角形相比,图2中的三角形发生的变化是()A.向左平移3个单位长度B.向左平移1个单位长度C.向上平移3个单位长度D.向下平移1个单位长度9.(2022春•淮南期末)线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C (2,﹣1),则点B(1,1)的对应点D的坐标为()A.(﹣1,﹣3)B.(5,3)C.(5,﹣3)D.(0,3)10.(2022春•曲靖期末)如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为()A.5050m2B.5000m2C.4900m2D.4998m2二.填空题(共6小题)11.(2021•鞍山)如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为.12.(2022春•兴庆区期末)将点A(﹣2,﹣3)先向右平移3个单位长度再向上平移2个单位长度得到点B,则点B所在象限是第象限.13.(2020春•德州期末)某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为.14.(2022春•清河县期末)如图,把边长为3cm的正方形ABCD先向右平移1cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为.15.(2022春•连平县校级期末)如图,长方形ABCD的边AB=6,BC=8,则图中五个小长方形的周长之和为.16.(2023春•康巴什期末)如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是.三.解答题(共3小题)17.(2022春•饶平县校级月考)宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?18.(2022秋•大祥区期末)如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.19.(2022春•上海期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.;(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC=S四边形ABDC?若存在这样一点,(2)在y轴上是否存在一点P,连接PA,PB,使S△P AB求出点P的坐标;若不存在,试说明理由;(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①的值不变,②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.。
关于平移的练习题三年级

关于平移的练习题三年级一、物体的平移平移是指物体沿着平行方向移动,保持原来形状和大小不变。
在平移中,物体的每一点都按照同样的距离和方向同时移动。
三年级的小朋友们在学习数学时,也会接触到一些关于平移的练习题,通过解答练习题来加深对平移的理解和掌握。
以下是一些三年级平移的练习题,帮助同学们在数学学习中更好地掌握平移的概念和方法。
二、练习题一1. 小明画了一个正方形,边长为5个单位长度。
他将这个正方形向右平移3个单位长度,向下平移4个单位长度,求平移后正方形的边长和周长。
解析:正方形的边长为5个单位长度,向右平移3个单位长度,向下平移4个单位长度。
即平移后正方形的边长仍为5个单位长度。
平移后正方形的周长为4个相等的边长之和,即4 * 5 = 20个单位长度。
2. 小红画了一个长方形,长为6个单位长度,宽为4个单位长度。
她将这个长方形向左平移2个单位长度,向上平移3个单位长度,求平移后长方形的长、宽和周长。
解析:长方形的长为6个单位长度,宽为4个单位长度。
向左平移2个单位长度,向上平移3个单位长度。
平移后长方形的长仍为6个单位长度,宽仍为4个单位长度。
平移后长方形的周长为2倍长加2倍宽,即2 * 6 + 2 * 4 = 12 + 8 = 20个单位长度。
三、练习题二1. 小明画了一个圆形,半径为3个单位长度。
他将这个圆形向右平移5个单位长度,向上平移2个单位长度,求平移后圆形的半径和周长。
解析:圆形的半径为3个单位长度,向右平移5个单位长度,向上平移2个单位长度。
平移后圆形的半径仍为3个单位长度。
平移后圆形的周长为2倍半径乘以π,即2 * 3 * π = 6π个单位长度。
2. 小红画了一个三角形,底边长为8个单位长度,高度为5个单位长度。
她将这个三角形向左平移3个单位长度,向下平移4个单位长度,求平移后三角形的底边长、高度和面积。
解析:三角形的底边长为8个单位长度,高度为5个单位长度。
向左平移3个单位长度,向下平移4个单位长度。
第三章第1节《生活中的平移》练习题及答案
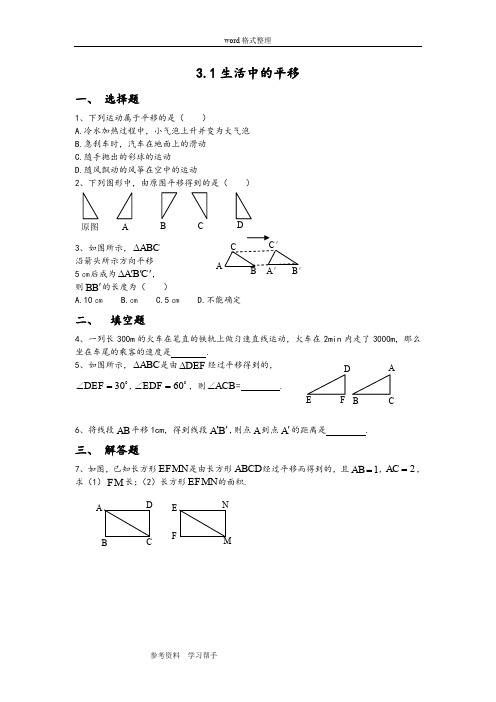
word 格式整理3.1生活中的平移一、 选择题1、下列运动属于平移的是( )A.冷水加热过程中,小气泡上升并变为大气泡B.急刹车时,汽车在地面上的滑动C.随手抛出的彩球的运动D.随风飘动的风筝在空中的运动2、下列图形中,由原图平移得到的是( )3、如图所示,ABC ∆沿箭头所示方向平移5㎝后成为C B A '''∆,则B B '的长度为()A.10㎝B.㎝C.5㎝D.不能确定二、 填空题4、一列长300m 的火车在笔直的铁轨上做匀速直线运动,火车在2min 内走了3000m ,那么坐在车尾的乘客的速度是 .5、如图所示,ABC ∆是由DEF ∆经过平移得到的, 30=∠DEF , 60=∠EDF ,则ACB ∠= .6、将线段AB 平移1cm ,得到线段B A '',则点A 到点A '的距离是 .三、 解答题7、如图,已知长方形EFMN 是由长方形ABCD 经过平移而得到的,且1=AB ,2=AC ,求(1)FM 长;(2)长方形EFMN 的面积.412±±232141412104.0412±±38、已知在ABC ∆中,13=AB cm,2=AC cm ,3=BC cm ,若将ABC ∆平移得到C B A '''∆,其中A 与A ',B 与B ',是对应顶点,则C B A '''∆是什么三角形?说明你的理由.四、 探究创新9、如图9已知Rt △ABC 中,∠C =90°,BC =4,AC =4,现将△ABC 沿CB 方向平移到A B C '''△的位置.若平移距离为2,求△ABC 与A B C '''△重叠部分的面积.答案一选择题1、B 2、D 3、C二填空题4、25m /s 5、90 6、1cm 三解答题 7、3=FM 长方形EFMN 的面积为38、C B A '''∆是直角三角形.理由:因为222AB BC AC =+,所以ABC ∆是直角三角形.再根据ABC ∆平移得到C B A '''∆,所以C B A '''∆也是直角三角形. 四探究创新9、重叠部分的面积为2 如有不对之处,请多包涵。
《生活中的平移》《简单的平移作图》测试题

_导 学 生
.
将 图形
:
0 0
,
,
.
A B
.
向右平 移
2
个单位
.
向右平 移 向左 平移 向左 平 移
、
8
8 2 14
个单位
c
D
.
个单位
个单位
、
, 7
, 7 \
|
.
、
l
三
解 答题 (
,
15
、
16
题 每题
10
分
,
17
题
11
分
.
共
4 1 4
分 )
,
14
如图
小船经 过平移
,
到 了新 的位
图4
钏 引 副 刻
3
,
9
.
R t △ 4 B C
,
沿 直 角边
D E F
B C
所 在
)
的 直 线 向右 平 移 错 误 的是
A B C
D
.
得 到 △
下 列 结 论 中 (
△ A 曰C
[
竺
=
A DE F
。
盐
图 3
.
D E E
=
9 0
.
A C
.
D F
E C
.
=
C F
10
△A B C
沿 某射线
X Y
的方 向平 移
2 5
.
5
12
. .
个圆 )
么 B CE
=
A
:
10
.
.
A
一
生活中的平移[上学期]
![生活中的平移[上学期]](https://img.taocdn.com/s3/m/7b5b6ca5bceb19e8b8f6bab4.png)
需要更完整的资源请到 新世纪教 育网 -
生活中的平移
对比一下,平移前后两图形之间有什么样的关系?
不变 整体:大小、形状 部分:对应点、对应线段、对应角
需要更完整的资源请到 新世纪教 育网 -
相等
生活中的平移
平移的性质:
在所画的相邻两个人脸图形中,找出三个对应点, 如何在一张半透明的纸上,画一排形状和大小如图 连接这些对应点,观察得出的线段,它们的位置、长短 中的人脸? 有什么关系?
A D B C A′ D′ B′ C′
( 11 把一个图形整体沿某一个方向移动,会得到一个新的图 )AA′∥BB′ ∥CC′ ∥DD′ 再作出连接一些其他对应 形,新图形与原图形的形状和大小完全相同。 =DD′ 点的线段,它们是否仍有上 (2)AA ′=BB′= CC ′ 2 新图形中的每一点,都是原图形中的某一点移动后得到 面的关系? 的,这两个点是对应点。连接各组对应点的线段平行且相等。 图形的这种移动,叫做平移变换,简称平移(translation)。
生活中的平移
卡农原来的意思是“规则”,在音乐上是指复调音 乐的一种写作技法。它的特点是:各个声部有规则地 互相模仿。也就是后面的声部按一定的时间距离依次 模仿前一声部的旋律。用卡农手法写成的乐曲叫做 “卡农曲”。我们平时经常听到的轮唱曲就是卡农曲 的一种。 冼星海作曲的《黄河大合唱》中的《保卫黄河》, 前半部分是齐唱,后半部分是二部轮唱,第二声部隔 开一小节模仿第一声部的旋律,两声部此起彼伏,前 呼后应,表现出一种浩浩荡荡的气势,生动地刻画了 活跃在万山丛中、出没在青纱帐里的抗日健儿的高昂 新世纪教 斗志和豪迈气概。需要更完整的资源请到 育网 -
B
C
E
F
2020-2021学年北师大版八年级数学下册《第3章图形的平移与旋转》知识点分类训练(附答案)

2021年北师大版八年级数学下册《第3章图形的平移与旋转》知识点分类训练(附答案)一.生活中的平移现象1.下面生活中的物体的运动情况可以看成平移的是(填写序号即可).①摆动的钟摆;②在笔直的公路上行驶的汽车;③随风摆动的旗帜;④摇动的大绳;⑤汽车玻璃上雨刷的运动.二.平移的性质2.如图,△ABC沿AC平移得到△A'B'C',A'B'交BC于点D,若AC=6,D是BC的中点,则C'C=.三.坐标与图形变化-平移3.如图,点A、B分别在x轴和y轴上,OA=1,OB=2,若将线段AB平移至A'B',则a+b 的值为.四.作图-平移变换4.如图,△ABC的三个顶点坐标分别为A(0,2),B(﹣3,1),C(﹣2,﹣2).(1)将△ABC向右平移3个单位,作出△A′B′C′;(2)写出△A′B′C′的面积;(3)在y轴上是否存在点P,使得△APC的面积与△ABC的面积相等,若存在,求出P 点的坐标;若不存在,说明理由.五.利用平移设计图案5.如图,下列图案中可以看成是由图案自身的一部分经平移后而得到的是()A.B.C.D.六.生活中的旋转现象6.分别以正方形的各边为直径向其内部作半圆得到的图形如图所示,将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是度.七.旋转的性质7.如图,Rt△ABC中,∠ACB=90°,∠B=30°,S△ABC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A'恰好落在AB上,A'B′与BC交于点D,则S△A′CD为()A.+1B.C.D.2﹣1八.旋转对称图形8.如图,三角形ABC中,∠BAC=150°,AB=6cm,三角形ABC逆时针方向旋转一定角度后,与三角形ADE重合,且点C恰好为AD中点.(1)指出旋转中心和图中所有相等的角;(2)求:AE的长度,请说明理由;(3)若是顺时针旋转,把三角形ABC旋转到与三角形ADE重合,则这个最小旋转角是多少.九.中心对称9.如图,点M为线段EF的中点,△AEC与△BFD成中心对称,试确定对称中心,并指出图中相等的线段和相等的角.十.中心对称图形10.不考虑颜色,对如图的对称性表述,正确的是()A.中心对称图形B.轴对称图形C.既是轴对称图形又是中心对称图形D.既不是轴对称图形又不是中心对称图形十一.关于原点对称的点的坐标11.平面直角坐标系中,点P(﹣2,3)与点Q(a,b)关于原点对称,则a+b=.十二.作图-旋转变换12.如图,在平面直角坐标系中,Rt△ABC的顶点坐标分别为A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1B1C1是由△ABC经过顺时针旋转变换得到的.(1)请写出旋转中心的坐标是,旋转角的大小是.(2)以(1)中的旋转中心为中心,画出△A1B1C1按顺时针方向旋转90°得到的△A2B2C2,并写出A2、B2、C2的坐标.十三.利用旋转设计图案13.如图是4×4的网格图.将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是()A.①B.②C.③D.④十四.几何变换的类型14.下列关于△ABC与△A'B'C'的几何变换中,配对正确的是()Ⅰ.轴对称;Ⅱ.中心对称;Ⅲ.旋转;Ⅳ.平移.A.①﹣Ⅰ,②﹣Ⅱ,③﹣Ⅲ,④﹣ⅣB.①﹣Ⅱ,②﹣Ⅰ,③﹣Ⅲ,④﹣ⅢC.①﹣Ⅱ,②﹣Ⅰ,③﹣Ⅲ,④﹣ⅣD.①﹣Ⅰ,②﹣Ⅱ,③﹣Ⅲ,④﹣Ⅲ参考答案一.生活中的平移现象1.解:①摆动的钟摆,属于旋转.②在笔直的公路上行驶的汽车,属于平移.③随风摆动的旗帜,不属于平移.④摇动的大绳,不属于平移.⑤汽车玻璃上雨刷的运动,属于旋转.故答案为:②二.平移的性质2.解:由平移的性质,可知,A′D∥AB,∵BD=CD,∴AA′=A′C=3,∴CC′=AA′=3,故答案为:3.三.坐标与图形变化-平移3.解:由作图可知,线段AB向右平移3个单位,再向下平移1个单位得到线段A′B′,∵A(﹣1,0),B(0,2),∴A′(2,﹣1),B′(3,1),∴a=﹣1,b=3,∴a+b=2,故答案为:2.四.作图-平移变换4.解:(1)如图,△A′B′C′即为所求作.(2)△A′B′C′的面积=××=5.(3)存在.设P(0,m),由题意,×|2﹣m|×2=5,解得m=7或﹣3,∴P(0,7)或(0,﹣3).五.利用平移设计图案5.解:A、是一个对称图形,不能由平移得到;B、是应该轴对称图形,不是平移;C、是平移;D、是中心对称图形,不是平移.故选:C.六.生活中的旋转现象6.解:图形可看作由一个基本图形每次旋转90°,旋转4次所组成,故最小旋转角为90°.故答案为:90.七.旋转的性质7.解:过C作CH⊥AB于H,∵∠ACB=90°,∠B=30°,∴∠A=60°,∴∠ACH=30°,∴AC=AB,∴CH=AC=AB,∵S△ABC=2,∴AB•CH=AB•AB=2,∴AB=4,∴AC=2,∵△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,∴CA=CA′=2,∠CA′B′=∠A=60°,∴△CAA′为等边三角形,∴∠ACA′=60°,∴∠BCA′=30°,∴∠A′DC=90°,在Rt△A′DC中,∵∠A′CD=30°,∴A′D=CA′=1,CD=A′D=,∴△A′CD的面积=×1×=.故选:C.八.旋转对称图形8.解:(1)旋转中心是点A,∠ACB=∠E,∠BAC=∠DAE,∠B=∠D;(2)由旋转的性质可知,AB=AD=6cm,AC=AE,∵AC=CD,∴AE=CD=AD=3(cm).(3)顺时针的最小旋转角=360°﹣∠BAC=210°.九.中心对称9.解:观察图形可知,A、E、M、F、B共线,∴旋转中心为M点,旋转角的度数为180°;根据旋转的性质可知,相等线段为:AC=BD,CE=DF,AE=BF,EM=FM,AM=BM,AF=BE,相等的角为:∠A=∠B,∠C=∠D,∠CEA=∠DFB.十.中心对称图形10.解:根据中心对称图形的概念和轴对称图形的概念可知:此图形是中心对称图形,不是轴对称图形,所以A选项正确.故选:A.十一.关于原点对称的点的坐标11.解:由点P(﹣2,3)与点Q(a,b)关于原点对称,得a=2,b=﹣3,则a+b=2+(﹣3)=﹣1,故答案为:﹣1.十二.作图-旋转变换12.解:(1)观察图象可知,旋转中心的坐标是O(0,0),旋转角为90°.故答案为:O(0,0),90°.(2)如图,△A2B2C2即为所求作.A2(1,﹣3),B2(3,1),C2(3,﹣3).十三.利用旋转设计图案13.解:如图,观察图象可知,把③涂灰,所有的灰色图形构成中心对称图形.故选:C.十四.几何变换的类型14.解:观察图象可知:①是中心对称,②是轴对称,③是旋转变换,④是平移变换.故选:B.。
生活中的平移(1)
昆明第十中学 谢晓玲
在公路上跑着的汽车,天上飞着的飞机.
在笔直的火车路上的火车
来来回回的开着
在工厂,产品
整齐地在传送带上 沿着生产线从一个
生产工位流向另一
个生产工位.
请同学们分析以上几种运
动现象你有什么发现?它们
之间有哪些共同的运动特征?
变化 不变
位置
根据上述分析,你能说说怎样 的图形运动称为平移吗?
C`
B
图中,对应点的连线AA`,BB`,CC`有怎样的位置关系?
图中每对对应线段之间有怎样的位置关系? 图中有哪些相等的线段、相等的角?
Y X A B` B
C
A`
C`
平移的性质:
经过平移,对应点所连的线段平行且相等; 对应线段平行且相等; 对应角相等.
Y X A B` C` A`
B
C
随堂练习一
你知道用三角板画平行线根据了什么数学原理?
a
理解 应用
你知道用三角板画平行线根据了什么数学原理?
a
理解 应用
你知道用三角板画平行线根据了什么数学原理?
a
理解 应用
你知道用三角板画平行线根据了什么数学原理?
b
a
探索 创新
今天我们学习图形平移对以后学习数学会 有什么用呢?
如图所示,一块蓝色正方形板,边长18cm, 上面
1、如图,∠DEF是∠ABC经过平移 得到的, ∠ABC=33°,求∠DEF的度 数.
A D
B
C
E
F
2、在下面的六幅图案中, (2)(3)(4)(5)(6)中的哪个图案可以通过 平移图案(1)得到?
3、将图中的小船向左移4格。翻开书本P61, 自己动手平移(不考虑颜色) 左移10格呢?
平移现象有哪些写10个
平移现象有哪些写10个
问题一:生活中有哪些平移现象和哪些平行现象
1、物体随升降电梯上,下移动
2、物体随自动扶梯斜向移动
3、轻轨列车在比直轨道上行驶
4、传送带
5、汽车在平直的公路上走,整个车在平移
6、急刹车中汽车在路面上的滑动
7、升旗杆上的旗
8、电梯上的人
9、传输带上的物品10、推拉门11、推拉窗
问题二:生活中平移现象有哪些
推拉门,重物升降木匠的推子,锯木头时木头在平移
问题三:日常生活中常见的平移现象有哪些
平移:电梯、平滑门窗、地铁、传送带升国旗
问题四:日常生活中常见的平移现象有哪些
电梯、
推拉门、窗户、传送带、
地铁、升国旗
根据平移的意义,在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移;根据旋转的意义,在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.在生活中平移现象有:电梯的运动、滑滑梯、升国旗等;
旋转现象有:钟表指针的运动、玩跷跷板、风车的运动等;
故答案为:电梯的运动、滑滑梯、升国旗,钟表指针的运动、玩跷跷板、风车的运动.
平移现象:(从大到小)宇宙的膨胀,无时间概念,无位置概念,可当做平移;地、月球围绕太阳公转,地球和月球是平移;人和移动的交通工具;人的器官和人体……实在太多,不胜枚举.\x0d旋转现象:(从大到小)地球自转、公转;游乐场的摩天轮,旋转木马;电风扇;陀螺……。
小学三年级数学平移练习题
小学三年级数学平移练习题一、实物平移练习在数学学习中,我们经常会遇到平移这个概念。
平移是指将一个物体按照规定的方向和距离移动,但保持原始形状和大小不变。
现在,我们来进行一些实物平移练习。
1. 平移练习题一将一本书从桌子的左边移动到右边,图示如下:(插入插图:桌子上有一本书,箭头表示移动方向和距离)请你用文字描述这个平移过程。
2.平移练习题二从教室的一侧,将右手向前伸出30厘米,再将左手向前伸出30厘米。
这个过程是一个平移操作,你能想象一下吗?请写下你的想法,并用手势模拟出这个平移过程。
二、图形平移练习除了实物平移,我们还可以进行图形平移练习。
下面是一些图形平移的练习题。
1. 平移练习题三给定一个三角形ABC,在坐标平面上,A(-2, 3),B(-1, 1),C(2, 2)。
请你将这个三角形向右平移3个单位,向下平移2个单位。
写出平移后的新坐标并画出新的三角形。
2. 平移练习题四给定一个矩形DEFG,在坐标平面上,D(1, 1),E(4, 1),F(4, 4),G(1, 4)。
请你将这个矩形向左平移2个单位,向上平移1个单位。
写出平移后的新坐标并画出新的矩形。
三、应用题练习除了简单的图形平移,我们还可以应用平移的概念解决一些实际问题。
下面是一些应用题练习。
1. 平移练习题五小明家离学校有7个街区,每个街区的距离相等。
他想知道他家和学校之间的距离是多少?请你用平移的概念解决这个问题,并写出解决的步骤和答案。
2. 平移练习题六小红想组织一个运动会,她找到两个场地,分别距离学校东边2公里和北边3公里处。
她想知道这两个场地之间的距离是多少?请你用平移的概念解决这个问题,并写出解决的步骤和答案。
总结:通过以上的练习题,我们对于小学三年级数学中的平移概念有了更深入的了解。
平移不仅仅局限于实物的位置移动,还可以应用到图形和实际问题中。
通过不断的练习和思考,我们的数学能力会不断提高。
希望大家能够善于运用平移的概念,解决更多有趣的问题。
二年级数学平移题讲解
二年级数学平移题讲解一、平移的概念基础题(5题)1. 下面物体的运动是平移的画“√”,不是平移的画“×”。
- 电梯的上下运动(√)- 解析:电梯沿着一个方向做直线运动,符合平移的定义,平移是指物体在平面内沿着某个方向移动,保持形状和大小不变。
- 风扇叶片的转动(×)- 解析:风扇叶片围绕中心点做圆周运动,不是直线运动,所以不是平移。
- 抽屉的推拉(√)- 解析:抽屉沿着轨道做直线的推拉运动,形状和大小不变,是平移。
- 钟摆的运动(×)- 解析:钟摆围绕一个固定点做圆弧摆动,不是直线运动,不是平移。
- 汽车在笔直公路上行驶(√)- 解析:汽车沿着笔直的公路做直线运动,车身的形状和大小不变,属于平移。
2. 哪些是平移现象?在括号里画“〇”。
- 国旗沿着旗杆上升(〇)- 解析:国旗沿着旗杆做直线上升运动,形状和大小不变,是平移现象。
- 拧开瓶盖(×)- 解析:拧开瓶盖时,瓶盖围绕瓶口做圆周运动,不是平移。
- 拉窗帘(〇)- 解析:拉窗帘时,窗帘沿着轨道做直线运动,是平移。
- 转动的方向盘(×)- 解析:方向盘围绕中心做圆周转动,不是平移。
3. 下面的图形通过平移能互相重合的有()组。
- (给出一些简单图形,如两个相同的三角形,一个在左边,一个在右边,且位置平行;还有两个相同的正方形,一个在上边,一个在下边,也是平行放置;另外有两个形状相同但方向不同的梯形)- 答案:2组。
- 解析:平移是不改变图形的形状、大小和方向的移动。
那两个平行放置的相同三角形和相同正方形,通过平移可以互相重合,而那两个梯形方向不同,不能通过平移互相重合。
4. 填空:平移是物体沿着(直线)运动,物体的(形状)、(大小)不变。
- 解析:这是平移的基本概念,平移就是物体在平面内沿着直线方向移动,在这个过程中物体本身的形状和大小不会发生改变。
5. 判断:只要物体在移动就是平移。
(×)- 解析:平移是物体沿着直线方向的移动,并且形状和大小不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
探索 创新
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
探索 创新
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
例练1 如图,把Rt△ABC沿BC的方向平移得Rt△DEF,
(1)过点D作DE∥AB且DE=AB, DF ∥AC且DF= AC
(2)连结EF
∴△DEF就是△ABC平移后的图形。
四、想一想,做一做
如图,将字母A按箭头所指的
方向平移3cm,作出平移后的图
形。
·
解:在字母A上找出5个关键 的点(如图所示),分别过
·
这5个点按箭头指向作5条长 · ·
3cm的线段,将所作线段 的另5个端点按原来的方式
·
·
连接,即可得到字母A平移Βιβλιοθήκη 后的图形。·· ··
五、练一练
将图中的字母N沿水平方向向右平移3cm, 作出平移后的图形。
3cm
更多方法
探索 创新
今天我们学习图形平移对以后学习数学会 有什么用呢?
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
探索 创新
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
探索 创新
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
探索 创新
如图所示,一块蓝色正方形板,边长18cm, 上面 横竖各两道红条,红条宽都是2cm,问蓝色部分 面积是多少?
已知AB=8, BE=5, DH=3,求图中阴影部分的面积.
解: 由平移图形得:
AD 3
S△ABC =S△DEF
8H
即 S阴影 + S△HEC
B
= S梯形ABEH+ S△HEC
5E
CF
∴ S阴影 = S梯形ABEH
∵ AB=8, BE=5, HE=DE-DH=AB-DH=8-3=5
∴ S阴影 = S梯形ABEH =
1 2
×5 ×(8 +5)=32.5
答:阴影部分的面积是32.5cm2.
考考你的观察力:
下面的五幅画中,(2)(3)(4)(5) 中的 哪个图案可以通过图案(1)得到?
(1)
(2)
(3)
(4) (5)
下面 2,3,4,5 幅图中那幅图 是由1平移得到的?
1
2
3
4
5
下列那幅图可以通过(1)平移而得?
(1)
A
C
D
E
⑶如果把移动前后的同一台电视机的屏幕 分别记为四边形ABCD和四边形EFGH (如下图),那么四边形ABCD和四边形 EFGH 的 形状、大小是否相同?
例题
如图,△ABE沿射线XY的方向平移一定距离后成为△CDF. 找出图中存在的平行且相等的线段和一组全等三角形.并 说明理由.
Y
C X
A
D
F
B
E
一、合作与交流
如图所示,经过平移,线段AB的端 点A移到了点D,你能作出线段AB平 移后的图形吗?
解: A
B
·D 1、连结AD
·E
2、过点B作BE平行 且等于AD 3、连结DE
∴线段DE就是线段AB平移后的图形
二、想一想,做一做
例1、经过平移,△ABC的顶点A移到了点D, 作出平移后的三角形。
A·
解:方法(一)
C
B
·D
E· ·F
1、过点C 、 B分别作线段CF、BE平行 且等于线段AD
2、连结DE、DF、EF
∴△DEF就是△ABC平移后的图形。
解:方法(二)
A
D
C
B
EF
