材料力学 沈玉凤10
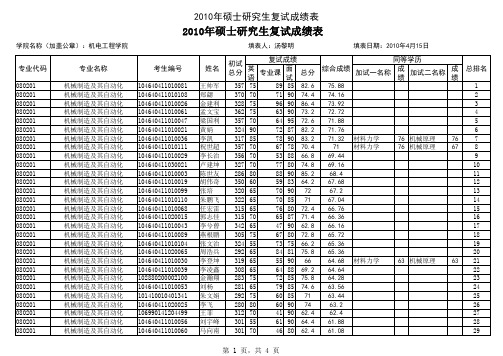
河南科技大学机电工程学院2010年研究生复试成绩
材料力学 材料力学
76 机械原理 76 机械原理
76 67
材料力学
63 机械原理
63
第 1 页,共 4 页
2010年硕士研究生复试成绩表
专业代码
080201 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080202 080203 080203 080203 080203 080203 080203 080203 080203
313 372 364 356 372 363 347 340 360 352 347 340 293 313 332 311 311 321 333 314 291 301 314 321 371 333 363 335 317 326 343 311 65 65 70 80 70 75 70 70 75 65 65 60 85 55 60 50 60 60 65 70 60 55 50 60 88 75 65 70 80 70 75 65 37 89 86 82 76 70 71 70 49 61 60 68 71 85 66 88 75 57 39 46 69 67 60 39 93 85 62 76 75 74 55 84 85 90 93 83 78 81 84 89 90 85 90 82 90 89 85 81 80 83 86 85 89 88 80 82 88 86 88 82 90 85 83 88 57.8 79.6 81 81.4 74 74.2 73.2 73.8 67.6 67.4 68 67.6 80.4 73.8 67.4 71.4 70 63.4 58.8 63.4 69.4 66.4 60 56 90 81.2 68.4 74.8 80 74.6 68.6 77.2 60.68 76.48 76.08 75.28 74.24 73.24 70.92 70.32 70.24 69.2 68.84 67.84 67.32 67.08 66.8 65.88 65.32 63.88 63.48 63.04 62.68 62.68 61.68 60.92 80.52 72.44 70.92 70.12 70.04 68.96 68.6 68.2 30 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 6 7 8
工程力学材料力学第四版(北京科技大学与东北大学)习题答案

(北京科技大学与东 北大学)
第 一意轴向拉伸和压缩
, 1-1 lfJ截 Illi法 求 下列各轩指 定的 lii fl'J 内 )J
2
f
2
F 2k N
I
(a 1
2
f
(bl
3P
11
(d 1
2kN P
2
2
(e 1
题 1 ) [fI
解
P
({)
P rlp|p
iE
『
e-
I Iz Il
F
5,
为 20 俐 , 许用应力 I δ]=50 Mpa . 试
根据吊钩螺纹部分的强主确定吊钩的阵 111 起重盐 1 解 P= 119kN
P
3m
B
P
E
题1-1 8 固
lIlí l - l ~ 罔
1 - 1 9 如入所示结构的 ABH 为钢轩,其帧故而积 -4.:::6 cm2 • 咛用阻力 ( σ 1=140 MPa ; BC
<.l
(bl
题 1-3 归
且ø 1 -4 因
1-4 : 桩杆起lli:机如 l 国所示,起lli:忏 AB 为钢管 , J[外径 。=2ûrnm , 内径 d= 1 8mrn;制绳
CB 的棋极而而积为 01cnEZe 己知l起重证
P=2脱lO N ,
试计fI起重机轩;归 钢丝绳的应 )J.
解 受力分析得
解
E = GPa . v = 0.3 17
1- 10: i主杆端部与的如1I相迹 , 其构应如罔 ,谊作用在连杆的轴向 jJ P=l28KN , 蝉挟处的内
径 d = 3.7cm , 螺栓材料的冉川剧
答案(10)---材料力学部分 (赵艳影) (1)

10.1一根直径为160mm 的圆形截面压杆,杆长为9m ,两端为固定端约束。
已知材料的弹性模量E =206Gpa, P =100,a =577Mpa ,b =3.74Mpa ,计算该压杆的临界载荷。
解:0.5μ=,404d i mm ==,0.59112.50.04p l i μλλ⨯===>,细长杆229222206100.16 3.225112.54cr cr E P A A MPa πππσλ⨯⨯⨯==⋅=⨯=10.2实心圆截面压杆的直径D =40mm ,长L =600mm ,两端铰支,材料为Q235钢,σp =200MPa ,σs =240MPa ,E=200Gpa ,a =304MPa ,b =1.12MPa ,压杆受到的最大工作压力为P max =40kN ,许用的安全系数为n st =10,试校核杆的稳定性。
解:160060404/L i μλ⨯===212304240100571112,..p E πλλσ-===≈21λλλ<<(属于中长杆)304112602368..cr a b MPaσλ=-=-⨯=2323684047444010max ./.cr st An n P σπ⋅⨯⨯===<⨯∴不安全10.3圆截面压杆直径为d =160mm ,长度为L 1=5m ,两端铰支,材料为Q235钢,σp =200MPa ,σs =240MPa ,E =200GPa ,a =304MPa ,b =1.12MPa ,许用的安全系数为n st =10,试确定压杆的最大工作压力。
解:212304240100571112,..p E πλλσ-=≈=≈,)(40,1mm i ==μ1125Li μλλ==>,所以该杆为大柔度杆222540()cr E P A kN πλ=⋅=254010cr st P n n P P==≥=254()p kN ≤10.4已知压杆BD 为20号槽钢,最小惯性半径为i =20.9mm ,A =32.837cm 2,材料为A3钢,λ1=100,λ2=62,a =304Mpa ,b=1.12,P =40kN ,稳定安全系数为n st =5,试校核BD 杆的稳定性。
工程力学--材料力学(北京科大、东北大学版)第4版第七章习题答案

第七章习题7-1 直径d=2cm的拉伸试件,当与杆轴成斜截面上的切应力时,杆表面上将出现滑移线。
求此时试件的拉力P。
7-2在拉杆的某一斜截面上,正应力为,切应力为。
试求最大正应力和最大切应力。
7-3 已知应力状态如图a、b、c所示,求指定斜截面ab上的应力,并画在单元体上。
7-4已知应力状态如图a、b、c所示,求指定斜截面ab上的应力,并画在单元体上。
7-5求图示各单元体的三个主应力,最大切应力和它们的作用面方位,并画在单元体图上。
7-6 已知一点为平面应力状态,过该点两平面上的应力如图所示,求及主应力、主方向和最大切应力。
7-7 一圆轴受力如图所示,已知固定端横截面上的最大弯曲应力为40MPa,最大扭转切应力为30 Mpa,因剪力而引起的最大切应力为6kPa.(1)用单元体画出在A、B、C、D各点处的应力状态;(2)求A点的主应力和最大切应力以及它们的作用面的方位。
7-8 求图示各应力状态的主应力、最大切应力以及它们的作用面的方位。
7-9 设地层为石灰岩,波松比,单位体积重。
试计算离地面400m深处的压应力。
7-10 图示一钢制圆截面轴,直径d=60mm,材料的弹性模量E=210Gpa。
波松比,用电测法测得A点与水平面成方向的线应变,求轴受的外力偶矩m。
7-11 列车通过钢桥时,在大梁侧表面某点测得x和y向的线应变,材料的弹性模量E=200Gpa,波松比,求该点x、y面的正应力和。
7-12 铸铁薄壁管如图所示,管的外直径D=200mm,壁厚t=15mm,内压p=4MPa,轴向压力P=200Kn,许用应力,波松比,试用第二强度理论校核该管的强度。
7-13 薄壁锅炉的平均直径为1250mm,最大内压为23个大气压(1大气压0.1MPa),在高温下工作,屈服点。
若安全系数为1.8,试按第三、第四强度理论设计锅炉的壁厚。
参考答案7-2解已知:解:7-3 (a)解已知:=0(b) 解已知:=0解(c) 解已知:解:7-4(a) 解已知:解:(b) 解已知:(c) 解已知:解:7-57-6 已知一点为平面应力状态,过该点两平面上的应力如图所示,求及主应力、主方向和最大切应力。
材料力学习题解hfut

6
w2 = A2 sinkx2 + B2 coskx 2 +
Fc x2 2F
当 x1 = 0,w1 = 0 → B1 = 0 当 x 2 = 0,w2 = 0 → B2 = 0 当 x1 = x2 = 或写成
l F ′ = − w2 ′ ,w1 = w2 = c ,w1 2 c
kl Fc l Fc A1sin 2 + 4 F = c kl Fc l Fc = A2 sin + c 2 4F kl Fc kl Fc A1 kcos 2 + 2 F = − A2 kcos 2 − 2 F
Fc F x1 − Fw1,M ( x 2 ) = c x 2 − Fw2 2 2
′′ + k 2 w1 = w1
式中,
Fc 2 F ′′ + k 2 w2 = c k 2 x2 k x1,w2 2F 2F k2 = F EI
Fc x1 2F
通解为
w1 = A1sinkx1 + B1coskx1 +
式中,
k12 =
以上二微分方程的通解为
F F 2 ,k 2 = EI 1 EI 2
w1 = A1sink1 x1 + B1cosk1 x1 + δ w2 = A2 sink 2 x 2 + B2 cosk 2 x 2 + δ
定未知常数的条件为
′=0 x1 = 0,w1 = 0,w1 x1 = l ′ = w2 ′ ,w1 = w2,w1 x2 = 0 x2 = l,w2 = δ
或简化成
sin
4k 2 EI kl kl kl kl [sin − (1 − )cos ] = 0 2 2 2 2 cl
工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析
![工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析](https://img.taocdn.com/s3/m/728e085302d276a201292e8a.png)
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a 所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN ,吊杆的尺寸如图b 所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
10材料力学河海大学期中试卷答案_Microsoft_Word_文档
2011--2012学年第二学期材料力学期中试卷(文天学院土木、水工、港航和机械专业)班级_________姓名___________学号______________得分________一、基本题1、试在图中标出低碳钢的比例极限σp 、弹性极限σe 、屈服极限σs 、破坏极限σb 、延伸率δ和弹性模量E 。
(6分)2、试画出以下不同截面圆轴受扭矩M x 作用时的切应力分布图。
(6分)σp实心圆截面 空心圆截面 薄壁圆截面3、图示悬臂梁,图(a )和(b )是正方形截面的两种不同放置形式。
试比较两种情况的容许荷载F 的大小(材料的容许应力为[σ] )。
(6分)解:由[]z Fl W ≤σ, 得[][]3()/6za W a F llσσ≤=,[][]3()/zb W a F ll σσ≤=所以[][]()()a b F F =4、作图示梁的弯矩图,并根据梁的弯矩和支撑条件,画出挠曲线大致形状。
(7分)解:作弯矩图如图所示 由0,0,Mw ''==挠曲线为直线,由A 端的边界条件,AB 为水平线;<0,>0M w '',挠曲线为上凸的曲线,C处的挠度为零:B 处挠度连续,C 处挠度和转角连续。
画出挠曲线如图所示M(a)z(b )二、计算题1、图示结构,AB 杆为刚性杆,A 端铰接于墙壁上,B 端受力F 的作用,C 、D 处分别由同材料、同面积的1、2两杆支撑,设1、2两杆的弹性模量为E ,横截面面积为A 。
求1、2两杆的内力。
(15分)解:平衡位置如图所示,变形协调几何条件:2△1=△2 伸长——拉力,缩短——压力 力与变形之间的物理条件:1212,F l F l E AE A∆=∆=代入几何条件,得补充方程:2F 1=F 2最后由平衡条件:120,23A M F l F l F l ∑=⨯+⨯=⨯ 解得:1236,55F F F F ==2、图示圆轴,直径d =100mm 。
材料力学 (10)_new
§2-1 轴向拉伸与压缩的概念
受力特征:杆受一对大小相等、方向相反的纵 向力,力的作用线与杆轴线重合
变形特征:沿轴线方向伸长或缩短,横 截面沿轴线平行移动
§2-2 轴向拉伸或压缩时的强度计算 ➢ 轴向拉伸或压缩的内力-轴力
NP
N P
例:求图示杆1-1、2-2、3-3截面上的轴力
➢ 轴向拉压杆的强度条件
1、极限应力、许用应力
⑴、极限应力(危险应力、失效应力):材料发生破坏或产生
过大变形而不能安全工作时的最小应力值。“σjx”(σu、σ0) ⑵、许用应力:构件安全工作时的最大应力。“[σ]”
jx (其中 n 为安全系数,值 > 1)
n
⑶、安全系数取值考虑的因素: (a)给构件足够的安全储备。 (b)理论与实际的差异。
N
d
N
根据对称性可得,径截面上内力处处相等
N FR 2
y
d F p(b d d)
2
π
p FR d
FR 0 d Fsin
FN
d
FN
π
( pb
d d )sin
pbd
0
2
N pbd
2
N 1 ( pbd ) pd A b 2 2
(2MPa)(200mm ) 40MPa 2(5mm)
例 已知:l, h, F(0 < x < l), AC为刚性梁, 斜撑杆
BD 的许用应力为 [ ].
试求:为使杆 BD 重量最轻, θ的最佳值.
斜撑杆
解:1. 斜撑杆受力分析
M A 0,
FN
Fx
hcos
FN,max
Fl
hcos
2. θ 最佳值的确定
工程力学材料力学(北京科大、东北大学版)第4版习题答案第二到九节
第二章习题2-1 一螺栓连接如图所示,已知P=200 kN, =2 cm,螺栓材料的许用切应力[τ]=80Mpa,试求螺栓的直径。
2-2 销钉式安全离合器如图所示,允许传递的外力偶距 m=10kN·cm,销钉材料的剪切强度极限=360 Mpa,轴的直径D=30mm,为保证m>30000 N·cm 时销钉被剪切断,求销钉的直径 d。
2-3 冲床的最大冲力为400 kN,冲头材料的许用应力[σ]=440 Mpa,被冲剪钢板的剪切强度极限=360 Mpa。
求在最大冲力作用下所能冲剪圆孔的最小直径D和钢板的最大厚度。
2-4 已知图示铆接钢板的厚度=10 mm,铆钉的直径为[τ]=140 Mpa,许用挤压应力[]=320 Mpa,P=24 kN,试做强度校核。
2-5 图示为测定剪切强度极限的试验装置。
若已经低碳钢试件的直径D=1 cm,剪断试件的外力P=50.2Kn,问材料的剪切强度极限为多少?2-6一减速机上齿轮与轴通过平键连接。
已知键受外力P=12 kN,所用平键的尺寸为b=28 mm,h=16 mm,l=60 mm,键的许用应力[τ]=87 Mpa,[]=100 Mpa。
试校核键的强度。
2-7图示连轴器,用四个螺栓连接,螺栓对称的安排在直径D=480 mm的圆周上。
这个连轴结传递的力偶矩m=24 kN·m,求螺栓的直径d需要多大?材料的许用切应力[τ]=80 Mpa。
(提示:由于对称,可假设个螺栓所受的剪力相等)2-8 图示夹剪,销子C的之间直径为0.6 cm,剪直径与销子直径相同的铜丝时,若力P=200 N,a=3 cm,b=15 cm,求铜丝与销子横截面上的平均切应力。
2-9 一冶炼厂使用的高压泵安全阀如图所示,要求当活塞下高压液体的压强达到p=3.4 Mpa时,使安全销沿1-1和2-2两截面剪断,从而使高压液体流出,以保证泵的安全。
已知活塞直径D=5.2cm,安全销采用15号钢,其剪切强度极限=320 Mpa,试确定安全销的直径d。
(完整版)北科大材料力学答案版.doc
(完整版)北科大材料力学答案版.doc自觉遵装守订考试线规则内,诚不信考得试,答绝不题作弊北京科技大学 2012--2013 学年第 2 学期工程力学 AII 试卷( A )院 (系) 班级学号姓名试卷卷面成绩占课平时成绩课程考程考占核成绩题号一二三四五六小计核成20%得分得分一、判断题(20分,每题2分,将“√”或者“X”填入题后括号内。
)1. 材料力学主要研究强度、刚度和稳定性问题。
(√)2. 矩形截面梁由剪力引起的剪应力在中性层为0,上下边缘处最大。
( X )3. 结构刚度越大 ,变形越小 ,也越不容易失稳。
(√)4. 塑性材料和脆性材料的失效破坏机理是一样的。
( X )5. 单位载荷法等能量方法可以直接用于求梁结构中的最大应力。
( X )6. 电测法的基本原理是将结构变形引起电阻丝长度变化,进而导致电阻等电学物理量的变化 ,由电学量的变化反推可得到结构的变形信息。
(√)7. 低碳钢扭转破坏试验后其断口平面与轴线垂直。
(√)8.测低碳钢的弹性模量与泊松比时在其上下表面各贴一个应变片,其主要考虑是得到双倍的应变值 ,因为越大的物理量测量精度一般越高。
( X )9. 铸铁试件的拉伸和扭转失效 ,主要原因都是最大剪应力超过了许用值。
( X )10. 对于主要受挤压的结构件,允许结构中出现部分的塑性变形。
(√)得分二、如图所示外伸梁,B为固定铰,C为移动铰,A端受集中力P=10 kN,B点受一集中力偶 M=40 kNm,HD 段受均布力 q=10 kN/m ,AB 、 BH、HC 和 CD 各段的长度均为 L=1 m,试作出梁的弯矩图和剪力图。
(20 分)qMA BDHPN B和C解:解除 B 点和 C 点约束,分别代之以约束反力 CN ,由M B 0,即PL M 2qL 2L N C 2LN C M PL 4qL245 kN (2 分)2L由M C 0,即3PL M N B2LN B M 3PL(2 分)35 kN2L2 分,一共 16 分,加上支反力 4 分,共计 20 分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
案例分析1:
把经过冷却的钢质实心球体,放人沸腾的热油锅
中,将引起钢球的爆裂,试分析原因。
案例分析2: 水管在寒冬低温条件下,由于管内水结冰引起体 积膨胀,而导致水管爆裂。由作用反作用定律可
知,水管与冰块所受的压力相等,试问为什么冰
不破裂,而水管发生爆裂。
案例分析3 中国古代:“火烧水滴法”开凿岩石 《后汉书》记载: 东汉武都太守虞诩遇到泉中大石塞流时: “乃使人烧石,以水灌之,石皆坼裂”
似乎比单向拉伸时更安全,但实验证明并非如此。
局限性
虽然考虑了
2 3
的影响,
它只与石料、混凝土等少数脆性材料的实验结果较符合;
,
混凝土、花岗岩受压时在 横向(ε1方向)开裂
但上述材料的脆断实验不支持本理论描写的 对材料强度的影响规律。
2 3
3. 最大切应力理论(第三强度理论) 材料发生塑性屈服的主要因素是 最大切应力; 无论处于什么应力状态,只要危险点处最大切应力达到 与材料性质有关的某一极限值,材料就发生屈服。
bL 1 3 Ljx by
2、强度准则:
[ L ] 1 3 [ y ]
M
3、莫尔强度理论的相当应力:
[ L ] 1 3 [ y ]
M
三、实用范围:
试用于破坏形式为屈服的构件及其拉压极限
强度不等的处于复杂应力状态的脆性材料的
§1
建立强度理论的基本思想
一、不同材料在同一环境及加载条件下对为失
效具有不同的抵抗能力。
例1 常温、静载条件下 低碳钢的拉伸破坏 低碳钢塑性屈服失效时光滑
表面出现45度角的滑移线;
表现为塑性屈服失效; 具有屈服极限
s
铸铁拉伸破坏
铸铁脆断失效时沿横截面断裂; 表现为脆性断裂失效; 具有抗拉强度极限
杆件基本变形下的强度条件
max
M max max [ ] W
FN ,max [ ] A
max [ ]
Fs S max [ ] bI z T max [ ] Wp
* z
max [ ]
max
max
满足
max [ ]
b
10、厚玻璃杯注入沸水而破裂,裂纹起始
强度理论的统一表达式:
相当应力
r [ ]
r ,1 1 [ ]
r ,2 1 ( 2 3 ) [ ]
r ,3 1 3 [ ]
无论材料处于什么应力状态,只要发生同一种破坏形 式,都是由于同一种因素引起。
2 1
σ2
σ
σ1 σ3
屈服准则:
vd v d jx
复杂应力状态的畸变能密度
单向应力状态下 屈服条件
1 ( 1 2 ) 2 ( 2 3 ) 2 ( 3 1 ) 2 s 2
强度条件
s 1 2 2 2 ( 1 2 ) ( 2 3 ) ( 3 1 ) 2 ns
适用范围: 材料的脆断
1 特别适用于拉伸型应力状态:
混合型应力状态中拉应力占主导 但
2 3 0
1 0, 3 0,
1 3
适用范围
铸铁拉伸 铸铁扭转
局限性:
1 只突出
1未考虑的 2 , 3
影响,
2、对没有拉应力的应力状态无法应用, 3、对塑性材料的破坏无法解释, 4 不能解释材料在三向均压下不发生断裂的事实;
σy σx
适用范围: 材料的脆断
要求材料在脆断前均服从胡克定律 铸铁在混合型应力状态中,压应力占主导引起的材料脆断
1 0
3 0
1 3
与实验结果也较符合;
局限性:
1、第一强度理论不能解释的问题,未能解决,
2、在二向或三向受拉时,
r 2 1 ( 2 3 ) r1 1
max [ ]
是否强度就没有问题了?
强度理论:
人们根据大量的破坏现象,通过判断推理、概 括,提出了种种关于破坏原因的假说,
找出引起破坏的主要因素, 经过实践检验,不断完善,在一定范围与实际相符 合,上升为理论。 为了建立复杂应力状态下的强度条件,而提出 的关于材料破坏原因的假设及计算方法。
σ2 σ1 σ3
σ
屈服准则:
max jx
复杂应力状态下的最大切应力
单向应力状态下 屈服条件 相应的强度条件:
max ( 1 3 ) / 2
jx
s
2
1 3
s
ns
低碳钢拉伸
低碳钢扭转
适用范围: 塑性屈服
此理论较满意地解释了塑性材料的屈服现象; 并能解释材料在三向均压下不发生塑性变形或断裂的事实。 偏于安全 常用于载荷往往较不稳定的机械、动力等行业
局限性:
1、未考虑
2
的影响,试验证实最大影响达15%。
2、不能解释三向均拉下可能发生断裂的现象,
此准则也称特雷斯卡(Tresca)屈服准则
4. 畸变能密度理论(第四强度理论) 材料发生塑性屈服的主要因素是 畸变能密度; 无论处于什么应力状态,只要危险点处畸变能密度达到 与材料性质有关的某一极限值,材料就发生屈服。
b
二、同一材料在不同环境及加载条件下也表现出对 失效的不同抵抗能力。
例2 常温静载条件下,带有环形深切槽的圆柱形低碳钢试件受拉
平断口 不再出现塑性变形; 切槽导致应力集中使根部附近出现两向和三向拉伸应力状态。 沿切槽根部发生脆断;
例3 常温静载条件下,圆柱形铸铁试件受压时
铸铁受压后形成鼓形,具有明显的塑性变形; 此时材料处于压缩型应力状态; 不再出现脆性断口,而出现塑性变形;
对塑性材料,此理论比第三强度理论更符合试验结果, 在工程中得到了广泛应用。
适用范围: 塑性屈服
它既突出了最大主剪应力对塑性屈服的作用,又适当考虑 了其它两个主剪应力的影响; 它与塑性较好材料的试验结果比第三强度理论符合得更好; 载荷较为稳定的土建行业,较多地采用第四强度理论。 此准则也称为米泽斯(Mises )屈服准则;
C:第三、第四强度理论只适用于塑性材料;
D:第三、第四强度理论适用于塑性流动破坏
5、
强度理论符合下图混凝土立方块的破坏。
A:第一强度理论;
B:第二强度理论;
C:第三强度理论; D:第四强度理论;
6、机轴材料为45号钢,工作时发生弯扭组合变形,
宜采用
强度理论进行强度校核?
A:第一、第二; B:第二、第三;
但此时的失效应力应通过能造成材料脆断的试验获得。
②脆性材料(如大理石) 在三向压缩应力状态下,呈塑性屈服失效状态; 应选用第三、第四强度理论; 但此时的失效应力应通过能造成材料屈服的试验获得。 ③脆性材料 在压缩型或混合型压应力占优的应力状态下, 像铸铁一类脆性材料均具有
bc b t 的性能,
例4 常温静载条件下,圆柱形大理石试件受轴向 压力和围压作用下
发生明显的塑性变形; 此时材料处于三向压缩应力状态下;
在简单试验的基础上已经建立的强度条件
根据常温静力拉伸和压缩试验,已建立起单向应力状态下的 弹性失效准则; 考虑安全系数后,其强度条件 根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性 失效准则; 考虑安全系数后,强度条件
s极限应力圆
s3
O
s2
s1
2、极限曲线:极限应力圆的包络线。
极限应力圆的包络线
近似包络线
二、莫尔强度理论:任意一点的应力圆若与极限 曲线相接触,则材料即将屈服或剪断。
M P [ y] O2 3
K
L
N o
O3
O1
1 [ L]
莫尔理论危险条件的推导
1、破坏判据:
1. 最大拉应力理论(第一强度理论)
材料发生断裂的主要因素是最大拉应力;
认为无论是什么应力状态,只要危险点处最大拉应力 达到与材料性质有关的某一极限值,材料就发生断裂
σ2
σ
σ1 σ3
脆断准则:
1 b
相应的强度条件:
1 t
t
b
nb
与铸铁,工具钢,工业陶瓷等多数脆性材料的实验结果较符合
单向应力状态下 断裂条件
jx b / E
b 1 [ 1 ( 2 3 )] E E
1 ( 2 3 ) b
相应的强度条件:
1 u( 2 3 ) t
b
nb
实验表明:
此理论对于一拉一压的二向应力 状态的脆性材料的断裂 较符合 铸铁受拉压比第一强度理论更接近实际情况。
9、危险点为二向拉伸应力状态的铸铁构件,采用
强度理论进行校核。Fra bibliotekA:只能用第一强度理论;
B:只能用第二; C:第一、第二均可以; D:用第四、第三;
7、工字形截面发生横力弯曲变形,剪力与弯矩均 不等于0,对a、b两点进行强度校核时,宜采用 比较合适。 A:σ≤|σ|; a B:τ≤|τ|; C:σ≤|σ|:τ≤|τ|; D:(σ2+4τ2)1/2≤|σ|;;
2. 最大伸长线应变理论(第二强度理论)
材料发生断裂的主要因素是最大伸长线应变; 无论处于什么应力状态,只要危险点处最大伸长线应变 达到与材料性质有关的某一极限值,材料就发生断裂
σ2 σ1 σ3
σ
脆断准则:
1 jx
复杂应力状态下最大线伸长应变
1 [ 1 ( 2 3 )] / E
rd f ( 1 , 2 , 3 )
