《三角形》三角形外角的性质及应用_题型归纳
初中数学知识归纳三角形的内角和与外角性质

初中数学知识归纳三角形的内角和与外角性质三角形是初中数学中重要的概念之一,在三角形的学习中,了解三角形的内角和与外角性质十分重要。
本文将对初中数学中与三角形的内角和与外角性质相关的知识进行归纳总结。
一、内角和的性质1. 三角形内角和定理三角形的内角和为180°。
这是三角形的基本性质,对于任意一个三角形而言,它的三个内角之和恒定为180°。
2. 等腰三角形的内角性质等腰三角形的两个底角(底边上的两个角)相等,而顶角等于两个底角之和的一半。
3. 直角三角形的内角性质直角三角形的两个锐角之和为90°。
4. 锐角三角形的内角性质锐角三角形的三个内角都是锐角。
5. 钝角三角形的内角性质钝角三角形的其中一个内角是钝角。
二、外角的性质1. 外角和内角的关系三角形的外角等于其对应的两个内角的和。
即一个三角形的外角与其非相邻的两个内角形成一条直线。
2. 三角形外角和的性质一个三角形的所有外角和等于360°。
三、实例应用1. 设某三角形的一个内角为60°,则其余两个内角的度数分别为多少度?根据三角形的内角和定理,三角形的内角和为180°。
已知一个内角为60°,设其余两个内角分别为x和y,则x + y + 60 = 180,整理得到x + y = 120。
因此,另外两个内角的度数分别为120°。
2. 若三角形的两个内角分别为30°和60°,求第三个内角的度数。
根据三角形的内角和定理,三角形的内角和为180°。
已知两个内角分别为30°和60°,设第三个内角的度数为x,则30 + 60 + x = 180,整理得到x = 90。
因此,第三个内角的度数为90°。
3. 在一个三角形中,一个内角为120°,另外两个内角是什么?根据三角形的内角和定理,三角形的内角和为180°。
课件《三角形的外角》优秀PPT课件 _人教版1

解:∵∠ADB=100°,∠C=80°, ∴∠DAC=∠ADB-∠C=100°-80°=20°. ∵∠BAD= ∠DAC,∴∠BAD= ×20°=10°. 在△ABD中,∠ABD=180°-∠ADB-∠BAD=180°100°-10°=70°, ∵BE平分∠ABC, ∴∠ABE= ∠ABC= ×70°=35°. ∴∠BED=∠BAD+∠ABE=10°+35°=45°.
【应用】(3)如图2,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.
∴∠DAE=90°-∠AED=90°-50°=40°. 如图,在△ABC中,∠B=24°,∠ACB=104°,AD⊥BC交BC的延长线于点D,AE平分∠BAC.
(1)求∠DAE的度数;
(2)∵AD⊥BC,∴∠D=90°,∴∠AED=90°-∠DAE, 在△ABE中,∠BAE=∠AED-∠B. 在△ACD中,∠ACB=∠CAD+∠D=∠DAE-∠CAE+90°, ∴∠CAE=∠DAE+90°-∠ACB. ∵AE平分∠BAC,∴∠BAE=∠CAE,∴90°-∠DAE∠B=∠DAE+90°-∠ACB,∴∠ACB=∠B+2∠DAE,即 ∠DAE= (∠ACB-∠B),∴∠DAE= (β-α).
(例3)如图,AB∥CD,DE交AC于点E,F为DC延长线上一点,下列结论:①∠A=∠ACF;
如图,AB∥CD,AD和BC相交于点O,∠A=25°,∠COD=80°,则∠C的度数是( )
(例2)如图,在△ABC中,∠ADB=100°,∠C=80°,∠BAD=∠DAC,BE平分∠ABC, 求∠BED的度数.
∴∠DAE= (β-α).
(1)若∠ABC=50°,∠ACB=80°,则∠A= 度,∠P=
三角形的外角性质定理

三角形的外角性质定理三角形是几何学中最基本的图形之一,它的性质及定理数不胜数。
本文将讨论三角形的外角性质定理,通过论述和推导,我们将揭示出这一性质的内涵和相关特点。
一、三角形的外角定义与性质我们首先来定义三角形的外角。
对于三角形ABC,若点D在边BC 的延长线上,且∠ADB为三角形ABC的外角,则称∠ADB为三角形ABC的外角,其性质如下:1. 外角定理三角形的外角等于其不相邻内角之和。
设∠ABC和∠ACB为三角形ABC的两个内角,∠ADB为该三角形的外角,根据外角定理,我们可以得到以下等式:∠ADB = ∠ABC + ∠ACB该等式表明,三角形的外角与其不相邻内角之和相等。
2. 外角大小三角形的外角是相邻内角的补角。
根据补角的概念,我们知道相邻的两个内角之和为180度。
因此,我们可以得到以下等式:∠ADB + ∠ABC = 180°∠ADB + ∠ACB = 180°这意味着三角形的外角与相邻的两个内角之和的和为180度。
3. 外角的性质三角形的外角可以大于、等于或小于360度。
当三角形的内角为锐角时,其外角为钝角;当内角为直角时,外角为直角;当内角为钝角时,外角为锐角。
这一性质与三角形的内角性质相对应,增加了我们对三角形的认识和理解。
二、外角性质定理的证明接下来,我们将证明外角性质定理。
我们可以通过以下步骤进行证明:1. 根据直角三角形的性质,证明直角三角形的外角等于90度。
2. 假设三角形ABC内角∠ABC + ∠ACB = α,三角形ABC外角∠ADB = β,通过对∠ADB进行角平分,我们得到角∠ADE = β/2。
3. 因为α + β/2 = α + (∠ADB/2) = 180度(直角三角形性质),所以有α + β/2 = 180度,从而推导出β = 2(180度 - α),即β = 360度 - 2α。
通过以上证明,我们可以得出结论:三角形的外角等于360度减去两个相邻内角的和的两倍。
三角形外角的性质及证明

探索与思考
A 41
2
6
B5
3C
2
B
∠1+∠2+∠3 就是△ABC的外角和。
A 1
C 3
∠1+∠2+∠3=
度
填空:与三角形的每个内角相邻的外角分别有 两 个,
这两个外角是 对顶角 ,他们的大小 相等
。
探索: 猜一猜 ∠1+∠2+∠3= 360 度
7.2.三2 角三角形形外外角角的的 性性质质及及证证明明
杜堂镇中学
学习目标 1、了解三角形的外角 2、探索并了解三角形的一个外角等于它不相邻 的两个内角的和; 3、学会运用简单的说理来计算三角形相关的角
重点和难点
重点:三角形的外角性质
难点:运用三角形外角性质进行有关计算时能准 确地表达推理的过程和方法。
2、作出△ABC的所有外角,并说出来。
2、找出三角形的外角
画一个三角形将它的所有外角画出来。
C
5
4
E A
3 6
12
A
7
8
E
9
B
D
B
C
外角
F
A
C
F B 外角
D
观察与思考 三角形的一边与另一边的延长线组 成的角,叫做三角形的外角.
B
想一想:
外角与相邻内角有什么特殊关系?
不相邻 1
内角
4
2
3
A 相邻内角 C
A
B
C
D
探索: (1)你能从理论上证明刚才的猜想吗?
A
B
C
D
∵∠ACD + ∠ACB=180 °, ∠A+ ∠B+ ∠ACB=180 ° ∴∠ACD= ∠A+ ∠B。
三角形外角性质的应用
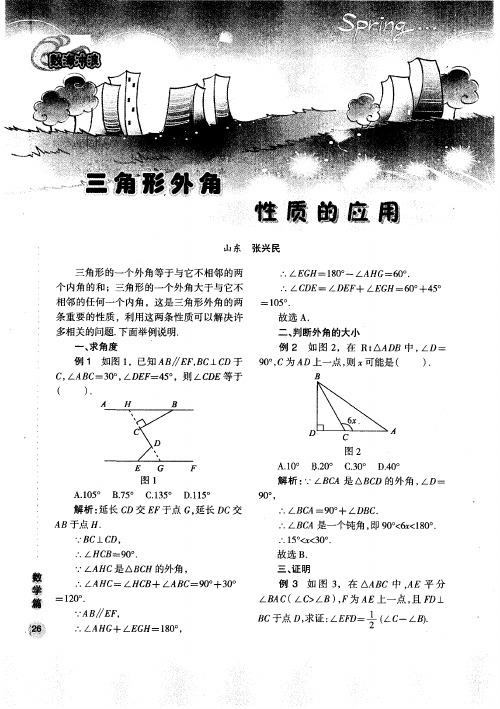
一
l/c)
1( C /B) L -_ . _
_
A
z
, ^ 、
,
,
・ 、
点评 : 本题在 证明过程 中 , 起关键作 用 的 是三角形外 角的性 质. 明时应 先理清思路 , 证
然后再 写证 明过程. 四、 探究
C
图6
例 4 如图 4 ,已知 A ∥C B D,探 究 1 ,
( ) .
A H B
图2
E G F
A.0 B.0 C3 。 1。 2。 .0
D. 。 4 0
图 l
A.0 。 B.5 C.3 。 1 5 7。 15 D. 1 。 1 5
解 析 :.LB A是 AB D的外 角 , ‘ ‘ C C LD=
9 。 0.
条重要 的性质 ,利用 这两条性质 可以解决许
多相 关的问题 . 下面举例说明.
一
: 15 . 0 。
故选 A . 二、 断外角 的大小 判 例 2 如图 2 ,在 Rt A B 中 , D= D A ) .
、
求角度
例 1 如图 1 ,已知 A ∥E ,C D于 9 。c为 A B FB 上C 0, D上一点 , 可能是 ( 则 C LA C 0, D =4。 , B =3。 5 ,则 LC E等于 D
+
A = A + A = 2 A .
图4
分析 : 为了利用已知条件 A ∥C , B D 我们
一
所 以 1 一
C + 3 LE A= 10. 一 C 8o
即 1 + 3 ( E C /E A) 10 , 一 A + _ C = 8。
故 1 + 3 一 2 8 。 =10 .
人教版八年级上册数学第11章 三角形 阶段题型专训 三角形内角和及内、外角关系应用的八种常见题型

应用:某零件如图②所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验 员量得∠BDC=145°时,就断定这个零件不合格.你能说出其中的道理吗?
解:如图,连接BC. 由上述结论得: 合格零件中∠BDC=∠A+∠ABD+∠ACD=143°, 又∵检验员量得∠BDC=145°≠143°,∴这个零件不合格.
2.如图,在△ABC中,点P是∠ABC,∠ACB的平分线的交点. (1)若∠A=80°,求∠BPC的度数.
解:∵BP,CP 分别为∠ABC,∠ACB 的平分线, ∴∠PBC+∠PCB=12(∠ABC+∠ACB)=12(180°-∠A)=12×(180° -80°)=50°. ∴∠BPC=180°-(∠PBC+∠PCB)=180°-50°=130°.
(2)求∠D的度数.
解:∵D 是外角∠ACH 与内角∠ABC 平分线的交点, ∴∠DCH=12∠ACH,∠DBC=12∠ABC, ∴∠D=∠DCH-∠DBC=12(∠ACH-∠ABC)=12∠A=30°.
8.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
【点拨】连接CG,利用转化思想,将求∠1+∠2+∠3+∠4+∠5+∠6+∠7的 和转化为求多边形DCGFE的内角和.
解:如图,连接CG. 在△COG和△AOB中,∠COG=∠AOB, ∴∠6+∠7=∠OCG+∠OGC. 在五边形CDEFG中,∠1+∠2+∠3+∠4+∠5+∠OCG+∠OGC=540°, ∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
三角形的外角和定理的应用
三角形的外角和定理的应用三角形是我们初中数学学习的重要内容之一,其中外角和定理是三角形的重要性质之一。
在本文中,我将详细介绍外角和定理的定义、性质以及应用,并通过实例来说明其在实际问题中的应用。
一、外角和定理的定义和性质在了解外角和定理的应用之前,我们首先需要了解外角和定理的定义和性质。
外角是指一个三角形的一个内角的补角。
具体来说,对于一个三角形ABC,如果我们将边AB和边BC延长,使其相交于一点D,那么∠ACD就是三角形ABC的外角。
同理,我们可以定义三角形的其他两个外角。
外角和定理是指三角形的三个外角之和等于360°。
换句话说,对于一个三角形ABC,我们可以得出以下等式:∠A + ∠B + ∠C = 360°。
二、外角和定理的应用外角和定理在数学的应用中具有广泛的应用,下面我将通过两个实例来说明其应用。
实例一:利用外角和定理解决几何问题假设有一个三角形ABC,其中∠A = 60°,∠B = 80°,我们需要求解∠C的度数。
根据外角和定理,我们知道∠A + ∠B + ∠C = 360°。
将已知的角度代入该等式,得到60° + 80° + ∠C = 360°。
通过简单计算,我们可以得出∠C = 220°。
实例二:应用外角和定理解决实际问题假设有一个三角形ABC,其中∠A = 50°,∠B = 70°,边AC的长度为10 cm,我们需要求解边BC的长度。
我们可以利用三角形的外角和定理,通过已知的角度和边长来求解未知的边长。
首先,我们可以利用三角形的内角和定理求解∠C的度数。
根据内角和定理,我们知道∠A + ∠B + ∠C = 180°。
将已知的角度代入该等式,得到50° + 70° + ∠C = 180°。
通过简单计算,我们可以得出∠C = 60°。
三角形外角的性质及证明复习过程
斜边AB上的高,∠BCD=35°,
求∠A与∠EBC的度数.
E
B
D
35°
A
C
此课件下载可自行编辑修改,仅供参考! 感谢您的支持,我们努力做得更好!谢谢
三角形外角的性质及证明
ቤተ መጻሕፍቲ ባይዱ
1、画一个△ABC。 2、指出它所有的内角。 3、延长线段BC至D,给∠ACD取名。
A
B
C
D
1、外角的概念:三角形的一边与另
一边的延长线所组成的角叫做三角形
的外角。
A
思考:
B
C
D
1、
△ABC有多少个外角?
2、作出△ABC的所有外角,并说出来。
判断下列∠1是哪个三角形的外角:
(3)求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
A
B
G
E
F
解:∵∠A+ ∠C= ∠EFA
∠B+ ∠D= ∠EGD
D
C
∠EGD + ∠EFA + ∠E = 180°
∴ ∠A+ ∠B+ ∠C+ ∠D+ ∠E= 180°
(4)如图,试计算∠BOC的度数.
A
90º D
110°
20º O B
30º
C
(5)如图,在直角△ABC中,CD是
注意:我们讲三角形的外角和时, 在三角形的每一个顶点处只取一个 外角。
例3.如图,已知∠1,∠2,∠3是△ABC 的外角,求证: ∠1+∠2+∠3=360°
A 1
3 B
C 2
(3)三角形三个外角和是 360°
练习:在△ ABC中, ∠A+ ∠B=100°, ∠C=4∠A, 求∠A,∠B及与∠C相邻的外角。
专题1.3 三角形的外角【十大题型】(学生版)
专题1.3三角形的外角【十大题型】【十大题型】【题型1三角形的外角】1【题型2三角形的外角性质(比较角的大小)】 (2)【题型3三角形的外角性质(求角)】 (3)【题型4三角形的外角性质(含角平分线)】 (4)【题型5三角形的外角性质(含垂直关系)】 (5)【题型6三角形的外角性质(含三角板)】 (6)【题型7三角形的外角性质(含平行线)】 (7)【题型8三角形的外角性质(折叠问题)】 (8)【题型9三角形的外角性质(内外角平分线模型)】 (9)【题型10三角形的外角性质(内外角平分线规律问题)】 (11)【知识点1三角形的外角】三角形外角的概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.【题型1三角形的外角】【例1】(2022•海沧区期末)如图,在△ABC中,点D,E分别是边AB,BC上的点,连接AE和DE,则下列是△BDE的外角的是()A.∠AED B.∠AEC C.∠ADE D.∠BAE【变式1-1】(2022•思明区校级期末)如图,四边形ABCD的对角线AC,BD交于点O,E是BC边上一点,连接AE,OE,则下列角中是△AEO的外角的是()A.∠AEB B.∠AOD C.∠OEC D.∠EOC【变式1-2】如图,有个三角形,∠1是的外角,∠ADB是的外角.【变式1-3】(2022•江北区校级月考)如图,在∠1、∠2、∠3和∠4这四个角中,属于△ABC外角的有()A.1个B.2个C.3个D.4个【知识点2三角形的外角性质】①三角形的外角和为360°;②三角形的一个外角等于和它不相邻的两个内角的和;③三角形的一个外角大于和它不相邻的任何一个内角.【题型2三角形的外角性质(比较角的大小)】【例2】(2022•通川区期末)如图,∠A、∠1、∠2的大小关系是()A.∠A>∠1>∠2B.∠2>∠1>∠A C.∠A>∠2>∠1D.∠2>∠A>∠1【变式2-1】(2022•临淄区期中)点P是△ABC内任意一点,则∠APC与∠B的大小关系是()A.∠APC>∠B B.∠APC=∠B C.∠APC<∠B D.不能确定【变式2-2】(2022春•兴隆县期末)如图所示,下列结论正确的是()A.∠1>∠B>∠2B.∠B>∠2>∠1C.∠2>∠1>∠B D.∠1>∠2>∠B【变式2-3】(2022•双流区期末)如图,在△ABC中,∠1是它的一个外角,E为边AC上一点,延长BC到D,连接DE.则下列结论正确的是()A.∠1>∠D B.∠D>∠2C.∠1=∠2+∠3D.∠3=∠A【题型3三角形的外角性质(求角)】【例3】(2022•石阡县模拟)如图,已知△ABC的外角∠CAD=120°,∠C=80°,则∠B的度数是()A.30°B.40°C.50°D.60°【变式3-1】(2022•梁子湖区期末)三角形中,三个内角的比为1:3:6,它的三个外角的比为()A.1:3:6B.6:3:1C.9:7:4D.3:5:2【变式3-2】(2022春•光明区期末)某零件的形状如图所示,按照要求∠B=20°,∠BCD=110°,∠D=30°,那么∠A的度数是()A.50°B.60°C.70°D.80°【变式3-3】(2022春•江阴市期中)小枣一笔画成了如图所示的图形,若∠A=60°,∠B=40°,∠C=30°,则∠D+∠E等于()A.100°B.110°C.120°D.130°【例4】(2022•沈阳模拟)如图,在Rt△ABC中,∠BAC=90°,AD平分∠BAC交BC边于点D,若∠C=26°,则∠ADB的度数是()A.61°B.64°C.71°D.109°【变式4-1】(2022春•宜兴市校级月考)如图,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M,若∠M=35°,则∠CFE=.【变式4-2】(2022春•邗江区期中)如图,∠ABD,∠ACD的角平分线交于点P,若∠A=50°,∠D=10°,则∠P的度数为()A.15°B.20°C.25°D.30°【变式4-3】(2022•武冈市期末)如图,已知P是三角形ABC内一点,∠BPC=120°,∠A=70°,BD是∠ABP的角平分线,CE是∠ACP的角平分线,BD与CE交于点F,则∠BFC等于()A.100°B.90°C.85°D.95°【例5】(2022•赤峰)如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为()A.65°B.70°C.75°D.85°【变式5-1】(2022春•鄂州校级期中)如图,BD,CE是△ABC的两条高,且交于点O,问:(1)∠1和∠2大小如何?(2)若∠A=50°,∠ABC=70°,求∠3和∠4度数.【变式5-2】(2022春•普陀区期末)如图,已知△ABC中,BD、CE分别是边AC、AB上的高,BD与CE交于O点,如果设∠BAC=n°,那么用含n的代数式表示∠BOC的度数是()A.45°+n°B.90°﹣n°C.90°+n°D.180°﹣n°【变式5-3】(2022春•腾冲县期末)已知:如图所示,∠ABC=66°,∠ACB=54°,BE是AC边上的高,CF 是AB边上的高,H是BE和CF的交点,求:∠ABE,∠ACF和∠BHC的度数.【例6】(2022春•宿城区期末)将一副直角三角板如图放置,∠A=30°,∠F=45°.若边AB经过点D,则∠EDB=°.【变式6-1】(2022•亭湖区校级一模)将一副三角尺按如图所示的方式摆放,则∠α的大小为()A.105°B.75°C.65°D.55°【变式6-2】(2022•丹东期末)如图所示,一副三角板叠放在一起,则图中∠α等于()A.105°B.115°C.120°D.135°【变式6-3】(2022•安徽二模)一副三角板如图放置,则∠1+∠2的度数为()A.30°B.45°C.60°D.75°【例7】(2022•沙湾区模拟)如图,直线a∥b,则∠1=()A.100°B.110°C.125°D.135°【变式7-1】(2022春•东西湖区校级月考)如图所示,l1∥l2,则下列式子中值为180°的是()A.α+β+γB.α+β﹣γC.β+γ﹣αD.α﹣β+γ【变式7-2】(2022•泸州)如图,直线a∥b,直线c分别交a,b于点A,C,点B在直线b上,AB⊥AC,若∠1=130°,则∠2的度数是()A.30°B.40°C.50°D.70°【变式7-3】(2022•细河区期末)如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.(1)求∠CBE的度数;(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.【例8】(2022•东城区校级期末)如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是()A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β【变式8-1】(2022•武昌区月考)如图,把△ABC纸片沿DE折叠,则()A.∠A=∠1+∠2B.2∠A=∠1+∠2C.3∠A=2∠1+∠2D.3∠A=2(∠1+∠2)【变式8-2】(2022春•宜兴市校级期末)如图,将△ABC的∠C折叠,使C点在AC边上,折痕为DE,则()A.∠BDC=∠DCE+90°B.∠BDC=2∠DCEC.∠BDC+∠DCE=180°D.∠BDC=3∠DCE【变式8-3】(2022春•长安区期末)如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.【题型9三角形的外角性质(内外角平分线模型)】【例9】(2022春•茌平区期末).如图,在ABC∠与ABC∠∠,ACB∠的平分线交于点O,D是ACF∆中,ABC平分线的交点,E是ABC∠的度数为()∠=︒,则D∆的两外角平分线的交点,若130BOCA.25︒B.30︒C.40︒D.50︒【变式9-1】(2022•中原区校级期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.【变式9-2】(2022•郏县期末)如图在△ABC中,BO,CO分别平分∠ABC,∠ACB,交于O,CE为外角∠ACD的平分线,BO的延长线交CE于点E,记∠BAC=∠1,∠BEC=∠2,则以下结论①∠1=2∠2,②∠BOC =3∠2,③∠BOC=90°+∠1,④∠BOC=90°+∠2正确的是()A.①②③B.①③④C.①④D.①②④【变式9-3】(2022春•江都区月考)如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=70°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.【题型10三角形的外角性质(内外角平分线规律问题)】【例10】(2022春•靖江市月考)如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+∠A=×180°+∠A.如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=×180°+∠A,∠BO2C=×180°+∠A.C=()根据以上阅读理解,你能猜想(n等分时,内部有n﹣1个点)(用n的代数式表示)∠BO n﹣1A.×180°+∠A B.×180°+∠AC.×180°+∠A D.×180°+∠A【变式10-1】(2022•曲靖期末)如图,在△ABC中,∠BAC=128°,P是△ABC的内角∠ABC的平分线BP1与外角∠ACE的平分线CP1的交点;P2是△BP1C的内角∠P1BC的平分线BP2与外角∠P1CE的平分线CP2的交点;P3是△BP2C的内角∠P2BC的平分线BP3与外角∠P2CE的平分线CP3的交点;依次这样下去,则∠P6的度数为()A.2°B.4°C.8°D.16°如图1,在△ABC中,点P是内角∠ABC和外角∠ACD的角平分线的交点,试猜想∠P与∠A之间的数量关系,并证明你的猜想.【迁移拓展】如图2,在△ABC中,点P是内角∠ABC和外角∠ACD的n等分线的交点,即∠PBC=∠ABC,∠PCD=∠ACD,试猜想∠P与∠A之间的数量关系,并证明你的猜想.【应用创新】已知,如图3,AD、BE相交于点C,∠ABC、∠CDE、∠ACE的角平分线交于点P,∠A=35°,∠E=25°,则∠BPD=.(1)如图1,△ABC,点O是∠ABC和∠ACB相邻的外角平分线的交点,若∠A=40°,请求出∠BOC的度数.【深入探究】(2)如图2,在四边形ABCD中,点O是∠BAC和∠ACD的角平分线的交点,若∠B+∠D=110°,请求出∠AOC的度数.【类比猜想】(3)如图3,在△ABC中,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,则∠BOC=(用α的代数式表示,直接写出结果,不需要写出解答过程).(4)如果BO,CO分别是△ABC的外角∠DBC,∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO=∠ECB则∠BOC=(用n、a的代数式表示,直接写出结果,不需要写出解答过程).。
第4章三角形证明题型解读1 三角形内角和定理及外角定理题型-2020-2021学年北师大版七数学
《三角形证明》题型解读1:三角形内角和定理及外角定理题型【知识梳理】1.三角形内角和定理①三角形的三个内角的和等于1800。
②证明过程---解题思路:把三角形三个内角,通过平行线性质,转化成一个平角。
如图,过△ABC 的顶点A 作DE//BC ,∵DE//BC ,∴∠B=∠DAB ,∠C=∠EAC ,∵∠DAB+∠BAC+∠EAC=180°, ∴∠B+∠BAC+∠C=180°,即三角形的三个内角和是180°.③拓展:n 边形内角和公式(n-2)×18002.三角形的外角①三角形外角的特征:顶点在三角形的一个顶点上;一条边是三角形的一边;另一条边是三角形另一边的延长线;如图2,∠1、∠2、∠3、∠4、∠5、∠6均是△ABC 的外角;由于这6个角中存在三组对顶角,所以一般说一个三角形的外角,是指它的三个外角。
②三角形的外角和定理:三角形的三个外角和等于360º如图2,∠1+∠3+∠5=∠2+∠4+∠6=360°; ③三角形的外角性质:三角形的任意一个外角等于和它不相邻的两个内角的和,注意:“不相邻”; 如图2,∠1=∠2=∠ACB+∠ABC 、∠3=∠4=∠BAC+∠ACB 、∠5=∠6=∠BAC+∠ABC.④三角形的外角大于和它不相邻的任意一个内角,注意:“不相邻”;⑤拓展:四边形的外角性质:如图,当∠A+∠C=180°时∠EDC=∠B【典型例题】 例1. 已知AB//CD ,求证:∠B=∠E+∠DE D C B AE D C B A E DC B A ∠∠°∠∠∠°∠∠∠∴∠=∠D+∠E (等量代换)21图2654321CB A【解析】:这是平行线中三大典型模型的“牛角模型”,未知外角性质定理时,我们的证明过程如下:当我们学习了外角性质定理时,证明过程就要简洁一些了。
证明:∵AB//CD (已知), ∴∠B=∠1(两直线平行,同位角相等),∵∠1=∠D+∠E (三角形外角性质),∴∠B=∠D+∠E (等量代换).例2.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”,如果一个“特征三角形”的“特征角”为100°,则这个“特征三角形”的最小内角的度数为____.【解析】:定义新运算题型,考查数学阅读理解能力,运用三角形的内角和定理即可解答。
