§5-2转动定律
合集下载
05--2、转动定律、转动能量

T=T’ …(5)
v v v aτ = β ×r
β+ r T m2 T’
T
m1
N r
T’
m1g - T= m1a….(1) T’r=Jβ…(2) β
1 2 J = mr …(3) 2
a+
m1g
m2g
a = rβ…(4) β
Jβ β T=T’= r 代入(1)式 代入 式: Jβ β m1g = m1a r Jβ β m1g = m1rβ β r m1gr β = 所以: 所以 m1r2+J 由(2)式: 式
v F // v r
v F v ⊥ F
转动定律说明了J 3)转动定律说明了J是物体转动惯性大小的量 因为: 度。因为: M一 时 ↑Lβ ↓ J ↓Lβ ↑ 定 J 越大的物体, 即J越大的物体,保持原来转动状态的性质就 越大的物体 越强,转动惯性就越大;反之, 越小 越小, 越强,转动惯性就越大;反之,J越小,越容 易改变状态,保持原有状态的能力越弱。 易改变状态,保持原有状态的能力越弱。或 者说转动惯性越小。 者说转动惯性越小。
基本步骤 (1)隔离法选择研究对象; )隔离法选择研究对象; (2)受力分析和运动情况分析; )受力分析和运动情况分析; (3)对质点用牛顿定理,对刚体用转动定理; )对质点用牛顿定理,对刚体用转动定理; (4)建立角量与线量的关系,求解方程; )建立角量与线量的关系,求解方程; (5)结果分析及讨论。 )结果分析及讨论。
r
r
T ' m3g T ' 1 v 2 a1 m
1
v mg 1
m2
m L 2g.T ' m 2 2 m L 3g.N THale Waihona Puke .T2 m 1 3v a2
大学物理 第5章刚体定轴转动

赵 承 均
转动平面 某质点所在的圆周平面,称为转动平面。
参考线
转心 矢径
转动平面内任一过转轴的直线,如选 x 轴。
某质点所在的轨迹圆的圆心,称为转心。 某质点对其转心的位矢,称为该质点的矢径。
第一篇
力学
重 大 数 理 学 院
显然:转动刚体内所有点有相同的角量,故用角量描述刚体 的转动更方便,只需确定转动平面内任一点的角量即可。 1.角坐标— 描写刚体转动位臵的物理量。 角坐标 转动平面内刚体上任一点 P 到转轴 O 点的连线与 参考线间的夹角 。
赵 承 均
第二类问题:已知J和力矩M:求出运动情况和 b及 F 。
第三类问题:已知运动情况和力矩M,求刚体转动惯量 J 。
第一篇
力学
重 大 数 理 学 院
第一类问题:已知运动情况和 J ,确定运动学和动力学的联 系 例 :长为 l,质量为 m 的细杆,初始时的角速 度为 ωo ,由于细杆与 桌面的摩擦,经过时间 t 后杆静止,求摩擦力 矩 Mf 。
Fi cos i Fi cos i mi ain mi ri 2 法向:
e i
第一篇
力学
重 大 数 理 学 院
由于法向力的作用线穿过转轴,其力矩为零。可在切向 方程两边乘以 ri ,得到:
Fi e ri sin i Fi i r i sin i mi ri 2
4.角加速度— 描写角速度变化快慢和方向的物理量。 ⑴ 平均角加速度 t
即:刚体的角速度变化与发生变化所用的时间之比。
赵 承 均
⑵ 角加速度 ①用平均角加速度代替变化的角加速度; ②令 t 0 取极限;
d d lim 2 t 0 t dt dt
§5.2-力矩---刚体绕定轴转动微分方程
F f m a i i
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
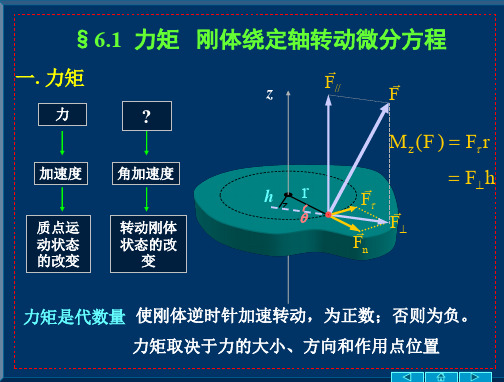
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
的切向加速度,质元沿
法向运动的科里奥里加
i
i
速度(定轴转动刚体没 有这种运动)
圆周轨迹切线投影
Fi fi miai
同乘以 ri
Fi ri fi ri miai ri miri2β ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
根据牛顿第二定律,第 i 个质元
外内
力 Fi
力 fi
miai
圆周轨迹切线投影
同乘以 ri
Fi fi miai Fi ri fi ri miai ri miri2β
ai=ri
对所有质元求和
Fi ri fi ri ( miri2 )β
§6.1 力矩
一. 力矩
力
?
加速度 角加速度
质点运 动状态 的改变
转动刚体 状态的改
变
刚体绕定轴转动微分方程
z
F//
F
hr
M z (F ) F r
F F Fn
Fh
力矩是代数量 使刚体逆时针加速转动,为正数;否则为负。 力矩取决于力的大小、方向和作用点位置
二. 刚体定轴转动微分方程
它在水平位置
求 它由此下摆 角时的 解 dm 质元 dm m dx
l
dm 重力矩 dM gdm x cos
O
ml
x
M
dM
1 2
mgl cos
gdm
重力对整个棒的合力矩等于重力全部 集中于质心所产生的力矩
转动定律 M
J J 1 ml2
3
大学物理第5章刚体的定轴转动

d ctdt
对上式两边积分得
d c td t
0 0
t
1 2 ct 2
2 2 600π π 3 rad s 由给定条件, c 2 t 300 2 75
d π 2 由角速度的定义,则任意 t 时刻的角速度可写为: d t 150
得到: 转子转数:
A M d E K
a b
动能定理
动量定理
A F ds E K
动能定理 角动量定理 角动量 守恒
t 0Fdt P
t
动量守恒
F 0, P 0
t 0 M z dt Lz
t
M 0, L 0
§5.1 刚体、刚体运动
一、一般运动 二、刚体的定轴转动 三、解决刚体动力学问题的一般方法
基本方法: 加
质点系运动定理 刚体特性 平动:动量定理
刚体定轴转动的 动能定理 角动量定理
F mac
可以解决刚体的一般运动(平动加转动)
一、一般运动
1. 刚体 特殊的质点系, 形状和体积不变化 —— 理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 2. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 z
刚体平面运动可看做刚体的平动与定轴转动的合成。 例如:车轮的滚动可以看成车轮随轮 轴的平动与绕轮轴的转动的组合。 描述刚体平面运动的自由度:3个
定点转动 刚体运动时,刚体上的一点固定不动,刚体绕过定点的一 瞬时转轴的转动,称作定点转动。
描述定点转动的自由度:3个
刚体的一般运动 质心的平动
+
绕质心的转动
z
描述刚体绕定轴转动的角量: 角坐标
大学物理 刚体的定轴转动

⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
5.1 刚体的运动的描述
•刚体(rigid body)
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时,它的角加速度与作用于刚体上的 合外力矩成正比,与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M=J 与 F ma地位相当 m反映质点的平动惯性,J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.
大学物理 第五章.

时,
刚体定轴转动的 角动量守恒定律
35
§5.4 刚体的角动量定理及守恒定律
例5.6:如图,质量为M,半径为R的转台,可绕通过中心竖直轴
转动,阻力忽略不计,质量为m的人站在台的边缘,人和台原来都 静止,如果人沿转台的边缘绕行了一周,问相对地面转台转过了多 少角度?
解:把人和转台看做一个系统
系统的角动量守恒 规定:逆时针转动为正方向,以 地面为参考系。 设人的角速度为ω,转台的角速度为Ω。
或
A = ∫ Mdθ = Mθ
42
例5.9:一质量为m,长为 l的匀质杆,两端用绳悬挂杆处于水平 状态,现突然将杆右端的悬线剪断,求(1)此瞬间另一根绳受到 的张力 ;(2)剪断绳子之后任一时刻杆的角速度 ω与转过角度 θ之 间的关系。 解: (1)首先考虑杆绕O点的的转动 根据转动定律: T O
匀变速运动
6
§5.1 刚体及其定轴转动描述
例5.1:一汽车发动机的转速在5s内由200r(转)/min均匀地增加 到3000r(转)/min。(1)求在这段时间内的初角速度、末角速 度和角加速度;(2)求这段时间内转过的角度;(3)发动机轴 上装有一半径为R=0.15m的飞轮,求轮边缘上一点在这第5s末的 切向加速度、法向加速度和总加速度。
24
§5.3 刚体转动的功和能
回顾: 质点 质量 牛顿运动定律
M = Jβ
刚体 转动惯量 转动定律
力做功
力矩做功
25
§5.3 刚体转动的功和能
一、力矩的功
轴
dθ dr α r
α
F 在转动平面内
ω
元功: dA = F • dr = F dr cos α = F ( rdθ ) cos α F ( r cos α )dθ = Mdθ
52--定轴转动定律
dt
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
Mdt d(J) 刚体定轴转动角动量定理微分形式
t
J
Mdt
t0
J00 d(J) J J00
刚体定轴转动角动量定理积分形式
4
L (miviri ) (miri2 ) ( miri 2 ) J
J miri 2 称为刚体对转轴的转动惯量
3
L J
于是有 M d(J) J d J
dt
dt
刚体定轴转动定理: M J
F ma
对 M d (J) 进行处理得到:
大小:M Fr sin
M
F
Or
d
Pr
z
F∥
or
F θ F⊥
转轴
转动平面 2
二、刚体定轴转动定理
在以角速度ω作定轴转动的刚体
内取一质点 mi ,则其对OZ轴
的角动量为:
o ri
v
P
Li miviri
对于整个刚体,各质点对定轴的角动量都具有相同的 方向。则定轴转动刚体的角动量就是对组成刚体的所 有质点的角动量求和。
刚体转动定律
1
一、作用于定轴刚体的外力矩
1 .力对固定点的矩
M
rF
2 .力对固定轴的矩
(1)力直于转轴
这种情况相当于质点绕固 定点O转动的情形。
(2)力与转轴不垂直 可以把力分解为平行于转轴
的分量和垂直于转轴的分量。
平行转轴的力不产生转动效果,
该力对转轴的 力矩 为零。 M r F
02-课件:5-2 转动惯量及惯性张量
―虹
ZZ
惯性矩、惯性积
□绕轴X、y和Z的质量惯性矩分别为
心=( y2 + z z)pdx = (y2 + z 2)dm
Iyy = J" (Z 2 + X 2 )Pd =肚(Z 2 + "枷
I
J=
3
+
y2
)pdv
=
JJJ m
(x2
+
y2
枫Q混m合矩(称为惯性积):
I xy
=
JJJvxy
Pdv
=
JJJm xydm
W\ Lz =
vyzPdv =
JJJm yzdmI zx=Fra bibliotekJJJ
zxpdv
=
JJJ zxdm
惯性张量和惯性矩阵 惯性张量与坐标系的原点和方位的选择有关。坐标轴平移或旋转
£ 后,惯性张量和惯性矩阵的各个元素会发生变化。设坐标系 C
I
£ 的原点设在刚体的质心,坐标系 刀的各轴与£ C —<•・
平行,根据平行轴理论,刚体相对于两坐标系的惯性矩和惯性
转动惯量及惯性张量
转动惯量的概念 物体质量为m ,半径为 r , F为切向力,N为扭矩
F = md dt
牛顿第二定律
(不考虑重力影响)。
B
门 、 。 dv d /
d
。 —— 虫 N
F
=
=
Fr
m——)=m=
mr
——
dt
r dt dt
N = Fr = mr2 =
迎 dt dt
转动惯量的概念
I = mr N 二=dIt
惯性张量
相对于给定的坐标系& ,可以用以上6个量组成一个矩阵勺 来表 示物体的质量分布特征,称为惯性张量。它可以被看成是对 — 个物体惯量的广义度量,和选取的坐标系有关。如果我们选取 坐标系的方位,使得各惯性积为零,则相对于这一坐标系,惯性 张 量是对角型。而此坐标系的各轴叫惯性主轴,相应的惯性矩叫 主惯性矩。
ZZ
惯性矩、惯性积
□绕轴X、y和Z的质量惯性矩分别为
心=( y2 + z z)pdx = (y2 + z 2)dm
Iyy = J" (Z 2 + X 2 )Pd =肚(Z 2 + "枷
I
J=
3
+
y2
)pdv
=
JJJ m
(x2
+
y2
枫Q混m合矩(称为惯性积):
I xy
=
JJJvxy
Pdv
=
JJJm xydm
W\ Lz =
vyzPdv =
JJJm yzdmI zx=Fra bibliotekJJJ
zxpdv
=
JJJ zxdm
惯性张量和惯性矩阵 惯性张量与坐标系的原点和方位的选择有关。坐标轴平移或旋转
£ 后,惯性张量和惯性矩阵的各个元素会发生变化。设坐标系 C
I
£ 的原点设在刚体的质心,坐标系 刀的各轴与£ C —<•・
平行,根据平行轴理论,刚体相对于两坐标系的惯性矩和惯性
转动惯量及惯性张量
转动惯量的概念 物体质量为m ,半径为 r , F为切向力,N为扭矩
F = md dt
牛顿第二定律
(不考虑重力影响)。
B
门 、 。 dv d /
d
。 —— 虫 N
F
=
=
Fr
m——)=m=
mr
——
dt
r dt dt
N = Fr = mr2 =
迎 dt dt
转动惯量的概念
I = mr N 二=dIt
惯性张量
相对于给定的坐标系& ,可以用以上6个量组成一个矩阵勺 来表 示物体的质量分布特征,称为惯性张量。它可以被看成是对 — 个物体惯量的广义度量,和选取的坐标系有关。如果我们选取 坐标系的方位,使得各惯性积为零,则相对于这一坐标系,惯性 张 量是对角型。而此坐标系的各轴叫惯性主轴,相应的惯性矩叫 主惯性矩。
2010大学物理学——5.刚体的转动
c a b
(2) 刚体的定轴转动
刚体上各点都绕同一转轴作不同半径 圆周运动, 的 圆周运动 , 且在相同时间内转过相 同的角度(角速度相同 角速度相同)。 同的角度 角速度相同 。
at v an
o
θ
v vv
s
S = Rθ v = Rω at = Rα 2 an = Rω
R
dθ ω = dt 2 α = dω = d θ 2 dt dt
= 6bt −12ct
2
Note:
角速度的矢量表示法: 角速度的矢量表示法:
ω
v
大小: 大小:ω 方向: 转轴 转轴, 方向://转轴 符合右手螺旋
ω
r⊥
v
v v
v v v 线速度: 线速度:v = ω × r
验证: 验证:
v r O
v v ω×r
大小: 大小: r⊥ ω 方向: 方向: 圆周切向
§5.5 转动中的功和能 (Rotational Work and Energy) 1.力矩的功 力矩的功
v F ⊥
F⊥t
ω
对于θ →θ +dθ,有
例5-8 已知:圆盘转动惯量J,初角速度ω0 已知:圆盘转动惯量 , 阻力矩M=-kω (k为正的常量 为正的常量) 阻力矩 为正的常量 所需的时间. 求:角速度从ω0变为ω0/2所需的时间 所需的时间 dω 转动定律: 解:转动定律: − kω = J dt t ω0 / 2 dω k → ∫ − dt = ∫ 0 ω0 J ω k ω /2 J ln 2 →− t = (ln ω) ω →t = J k [思考 思考] 思考
2
dm ∫
2
O
R
= mR
刚体的转动
J miri
i
例 如图
I m1r12 m2r22 m3r32
m2
可视为 质点
r1
m1
r2 r3
m3
转轴
•质量连续分布的物体
J rdm dm d 或 ds 或 dV
线积分
面积分
体积分
(记住:棒、圆盘和圆柱体的I)
例题 5-2
例题 5-3
例题 5-4
(4)以上三式联立,可得物体下落的加速度和速度:
a m g mM 2
V 2ah 4mgh 2m M
这时滑轮转动的角速度为 V 1 4mgh
R R 2m M
例题:质量M=1.1kg,半径=0.6m的匀质圆盘,可绕通过其
中心且垂直于盘面的水平光滑固定轴转动。圆盘边缘绕有
看成质点 水平飞行
刚体作平动,其上所有点的速度、加速度相等,运动 轨迹都相同,整个刚体可当作质点来处理,满足牛顿 定律。
转动 刚体运动时,如果刚体中所有质点都绕着一直线 作圆周运动,则这刚体的运动称为转动,这条直 线称为转轴。转轴固定的转动叫定轴转动。
转轴
地球仪转动
一般情况下,刚体十分复杂,同时存在平动和 转动;可以证明,刚体的一般运动可以当作由一平 动和一绕瞬时轴的转动组合而成。
F
ds
F
cos
ds
Ft rd
Md
The total work done during a finite angular displacement
is then
W 0 M d
(5-18)
In the special case of M is a constant
i
例 如图
I m1r12 m2r22 m3r32
m2
可视为 质点
r1
m1
r2 r3
m3
转轴
•质量连续分布的物体
J rdm dm d 或 ds 或 dV
线积分
面积分
体积分
(记住:棒、圆盘和圆柱体的I)
例题 5-2
例题 5-3
例题 5-4
(4)以上三式联立,可得物体下落的加速度和速度:
a m g mM 2
V 2ah 4mgh 2m M
这时滑轮转动的角速度为 V 1 4mgh
R R 2m M
例题:质量M=1.1kg,半径=0.6m的匀质圆盘,可绕通过其
中心且垂直于盘面的水平光滑固定轴转动。圆盘边缘绕有
看成质点 水平飞行
刚体作平动,其上所有点的速度、加速度相等,运动 轨迹都相同,整个刚体可当作质点来处理,满足牛顿 定律。
转动 刚体运动时,如果刚体中所有质点都绕着一直线 作圆周运动,则这刚体的运动称为转动,这条直 线称为转轴。转轴固定的转动叫定轴转动。
转轴
地球仪转动
一般情况下,刚体十分复杂,同时存在平动和 转动;可以证明,刚体的一般运动可以当作由一平 动和一绕瞬时轴的转动组合而成。
F
ds
F
cos
ds
Ft rd
Md
The total work done during a finite angular displacement
is then
W 0 M d
(5-18)
In the special case of M is a constant
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由长l 的轻杆连接的质点如图所示,求
(1)质点系对过A垂直于纸面的轴的转动惯量 (2)质点系对过B垂直于纸面的轴的转动惯量
2 2 2 3m( 2l ) (4m 5m )( 2l ) 解(1) J 2ml 32ml 2
(2)
4m 3m
2 2 2 J ml 3ml 4ml 5ml 2 m 13ml 2 A
答案D
2. 一轻绳跨过一具有水平光滑轴、质量为M的定滑 轮,绳的两端分别悬有质量为m1和m2的物体(m1< m2),如图所示.绳与轮之间无相对滑动.若某时刻 滑轮沿逆时针方向转动,则绳中的张力 (A) 处处相等. O (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断.
m1 m2
l l l
2m
B
l
5m
质量连续分布刚体的转动惯量
J m r r dm
2 j j 2 j
dm :质量元
对质量线分布的刚体:如 均匀细长棒 质量线密度
m L
dm dl
对质量面分布的刚体: 如 均匀圆盘
m 质量面密度 S
dm dS
例5 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 .
例3 一个飞轮的质量为69kg ,半径为0.25m,正在以每 分1000转的转速转动。现在要制动飞轮,要求在5.0秒 内使它均匀减速而最后停下来。摩擦系数为0.46。求 闸瓦对轮子的压力N为多大?(J = mR2 ) 解:飞轮制动时有角加速度
0
t
0
fr N
0 t 5s
O
l 2
dr O´
r
O
l 2
r
l
d r O´
解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质量元 dm dr dJ r 2dm r 2dr
1 3 J r dr l l 2 12 1 ml 2 12
l/2 2
r
如转轴过端点垂直于棒
1 2 J r dr ml 0 3
l 2
例6 一质量为 m 、半径为 R 的均匀圆盘,求通 过盘中心 O 并与盘面垂直的轴的转动惯量 .
解 设圆盘面密度为 , 在盘上取半径为 ,宽为 dr 的圆环 m π R2
r
圆环质量
d m 2 π rdr
2
R R
O
r dr
圆环对轴的转动惯量
dJ r dm 2 π r 3 dr
a R
mB g a mA mB mC 2 m A mB g T1 m A m B mC 2
( m A m C 2 )m B g T2 m A mB mC 2
如令mC
mA
T1
C
mC
T2
mB
0,可得
中学题目
m A mB g T1 T2 m A mB
M ij 0
j
z
O
m1
M
j
ej
( m r )α
2 j j
m j
m 2
定义转动惯量
转动定律
J m r
j
2 j j
M J
刚体定轴转动的角加速度与它所受的合外力矩成 正比 ,与刚体的转动惯量成反比 .
转动定律应用
M J
说明
(1) M J ,
与 M 方向相同
(2) 为瞬时关系
(3) 转动中 M J与平动中F ma 地位相同
(4) M 一定,J
动画
转动惯量是转动惯性大小的量度
例1 一根长为 l ,质量为 m 的均匀细直棒,可绕轴 O
在竖直平面内转动,初始时它在水平位置
求(1)初始时它的角加速度等于多少?
(2)它由此下摆 角时,它的角加速度又等于多少? 已知均匀棒对于通过其一端垂直于棒的轴的转动惯
M J
2 mgR J 3
1 J mR2 2
4 g 3R
圆盘作匀减速运动
0 t
4 g 3R
0 t
3 R t 0 4 g
3 R 答:经过 t 0 时间停止转动。 4 g
问它旋转几圈后停止转动?
2 2 0 3 R 2 0 2 8 g
§5-2
转动定律
一 力矩: 刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P, 且在转动平面内, r 为由点 O 到力的作用点 P 的径矢 .
M
M
O
Z 的力矩 F 对转轴
z
M Fr sin Fd
M r F
r
F
*
d
P
Fi 0 , Mi 0
mB g T2 mBa
T2R T1R M f J
a R
mB g M f R a mA mB mC / 2
m A ( m B g M f / R) T1 m A mB mC / 2
m B (m A mC 2) g M f R T2 m A mB mC 2
M rF sin
M rFt rmat mr 2
M
O
z
r
m
Ft
Fn
F
质量元受外力 F ,内力 F ij ej 2 Mej Mij m j rj
外力矩 内力矩
2)刚体
z
O
rj
Fej
m j
Fij
质量元受外力 F ,内力 F ij ej 2 Mej Mij m j rj
P
1.关于刚体对轴的转动惯量,下列说法中正确的是 (A)只取决于刚体的质量,与质量的空间分布 和轴的位置无关. (B)取决于刚体的质量和质量的空间分布, 与轴的位置无关. (C)取决于刚体的质量、质量的空间分布和 轴的位置. (D)只取决于转轴的位置,与刚体的质量和 质量的空间分布无关. 答案C
M 3 g cos 2l J
例2 质量为 m A 的物体 A 静止在光滑水平面上,和一 质量不计的绳索相连接,绳索跨过一半径为 R、质量 为 m C 的 圆柱形滑轮 C, 并系在另一质量为 m B 的物体 B 上. 滑轮与绳索间没有滑动, 且滑轮与轴承间的摩擦 力可略去不计. 问: (1) 两物体的线加速度 为多少?水平和竖直两段 绳索的张力各为多少? 已知 J 1 mR 2
转过的圈数
3 R 2 0 N 16 g 2π
四 平行轴定理
质量为 m 的刚体,如果对 其质心轴的转动惯量为 J C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量 C
d
m
O
J O J C md
2
1 圆盘对P 轴 2 2 J P mR mR 的转动惯量 2
R O m
转动 平面
变形, 对转动无贡献。 在定轴动问题中,如不加说明,所 指的力矩是指力在转动平面内的分力 对转轴的力矩。
r
2) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
M ji
d
ri
F ji i F
ij
rj
j
Mij M ji
二
转动定律 1)单个质点 m 与转 轴刚性连接
2
A
mA
C
mC
mB B
解(1)隔离物体分别对物体A、B 及滑轮作受力分析, 取坐标如图,运用牛顿第二定律 、转动定律列方程 .
N
mA
O
T1
mA g
x
T1
注意:T1 T2
mA
C
T2
T2
O
T1 mAa
mB g T2 mBa
T2R T1R J
mB
mB B m B g y
量为 J
解1
1 ml 2 3
转动定律
M J
l 2
O
mg
M l 3g M mg J 2 2l 1 J ml 2 3
(2)它由此下摆 角时,它的角加速度等于多少?
转动定律
M J
O
d
m
l
x
mg
C
1 解2 M mgd mg l cos 2
1 J ml 2 3
J m r
j
2 j j
物理意义:转动惯性的量度 .
转动惯性的计算方法
质量离散分布刚体的转动惯量
2 j j 2 11 j
J m r m r m r
2 2 2
2 j j 2
质量连续分布刚体的转动惯量
J m r r dm
j
dm
:质量元
例题4
r 宽度为dr的环带质量元 dr m dm 2rdr R 2 产生的阻力矩元 dMr r gdm (方向均向下)
dMr r gdm
dm 2rdr
Mr
R
0
2gr dr
2
r
2 2 3 gR mgR 3 3
dr
注意到阻力矩是负值,由刚体定轴转动定律
d F
: 力臂
F
Fi 0 , Mi 0
F
F
讨论 1) 力不在转动平面内
M r F r ( F1 F2 ) r F1 r F2
z
F1
F
F2
r F1 只能引起轴的
答案C
3.一轻绳绕在有水平轴的定滑轮上,滑轮的转动惯量 为J,绳下端挂一物体.物体所受重力为P,滑轮的角 加速度为b.若将物体去掉而以与P相等的力直接向下 拉绳子,滑轮的角加速度b将 (A) 不变. (B) 变小. (C) 变大. (D) 如何变化无法判断. F g F = mg
