第七章无穷级数38583

合集下载

高等数学第七章无穷级数.ppt

推论 (比较审敛法) 设
是两个正项级数,
且存在
对一切
有
则有
(1) 若强级数收敛 , 则弱级数
(常数 k > 0 ), 也收敛 ;
(2) 若弱级数发散 , 则强级数也发散 .
例1.
讨论
p
级数1
1 2p
1 3p
1 np
(常数
p
>
0)
的敛散性.
解: 1) 若 p 1, 因为对一切
1 n
而调和级数
知存在 N Z , 当n N 时, un1 1
un
收敛 , 由比较审敛法可知 un 收敛.
(2) 当 1 或时,必存在 N Z , uN 0,当n N
时
从而
un1 un un1 uN
因此
lim
n
un
uN
0,
所以级数发散.
说明: 当 lim un1 1 时,级数可能收敛也可能发散.
不存在 , 因此级数发散.
由定义, 讨论级数敛散性的方法 1. 先求部分和; 2. 求部分和的极限.
综合 1)、2)可知, q 1 时, 等比级数收敛 ;
q 1 时, 等比级数发散 .
利用此结论，可以直接判别某此级数的敛散性。例如：
例如：
公比 q 1 ,
2
q 1,
n1
(1) n1 2n1
3.按基本性质.
第三节正项级数
第七章
一、正项级数收敛的基本定理二、比较审敛法三、比值审敛法四、根值审敛法
一、正项级数收敛的基本定理
若 un 0, 则称 un 为正项级数 . n1
分析特点：部分和序列单调递增。
当

第7章无穷级数

1 lim S n lim 1 1 n n n 1
∴所给级数收敛，和为1
10 10
1 1 1 1 1 1 1 1 n 1 2 2 3 n n 1
单击此处编辑母版标题样式示例
1 n 4 n 级数收敛 n 1 2 5

23 23
单击此处编辑母版标题样式正项级数
• • • • • 单击此处编辑母版文本样式第二级若 u n 0 (n 1,2,3, ) ，则称级数 u n 为正项级数. 第三级 n 1 第四级第五级正项级数 u 收敛的充要条件是其部分和数列 S 有界.
• • • • • 单击此处编辑母版文本样式 1 讨论调和级数的敛散性. 第二级 n 1 n 第三级观察图中阴影部分，可以看出第四级第五级第一块矩形的面积 A1 1
1 第二块矩形的面积 A2 2 …… 1 第 n 块矩形的面积 An n
11 11
单击此处编辑母版标题样式示例
• • • • • 单击此处编辑母版文本样式 1 2 3 n n 1 例如 ( 1) 发散第二级 2 3 4 n1 第三级 2.必要条件但不充分. 第四级 1 1 1 例如 : 调和级数 1 第五级 2 3 n
有 lim un 0, 但级数是否收敛?
7.1.3 任意项级数的敛散性判别法
2 2
单击此处编辑母版标题样式
• • • • •
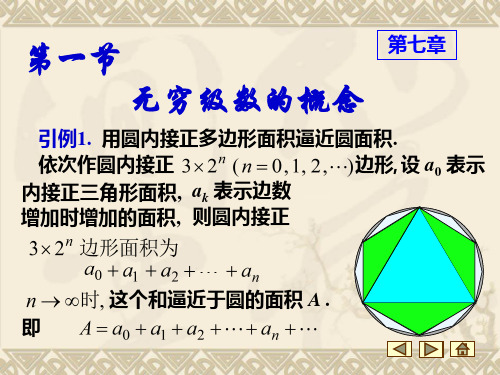
1. 计算半径为R圆的面积单击此处编辑母版文本样式第二级正六边形的面积 a1 第三级正十二边形的面积 a1 a2 第四级正 3 2 n 形的面积 a1 a2 an 第五级即 A a1 a2 an

高等数学无穷级数

第七章无穷级数10常数项级数概念及性质1、定义P264 ∑an=a1+a2+ +an+n=1∞an称为一般项或通项 Sn=u1+u2+ +un称为前n项部分和例1、1 =3+3+ +3+ =0.331010210n1+2+3+ +n+1-1+1-1+ +(-1)n-1+2、定义Sn=∑uKK=1nan=Sn+1-Sn如{Sn}收敛，则∑an收敛n=1∞3、几个重要极限等比级数（几何）∑aqn，当q<1 收敛，q≥1 发散；n=0∞P级数∑Pn=1∞1nP>1 收敛，P≤1 发散；∞1P=1当，∑ 又称调和级数。

n=1n4、级数性质 P266性质5是级数收敛的必要条件即∑an收敛→liman=0n=1n→∞∞例1、∑n=1∞n-11n-1 发散，∵ liman=lim=≠0 n→∞n→∞2n+122n+1 3n例2、∑ 发散，∵ lim=-1≠0 nnn→∞n-3n=1n-3∞3n例3、∑11 发散，但lim=0 n→∞nn=1n∞20正项级数判别法∑un∞n=1un≥0正项级数部分和数列{Sn}单调递增∴正项级数收敛部分和数列有上界1、比较判别法设Vn≥un，如∑Vn收敛，则∑un收敛n=1∞n=1∞∞∞ 如∑un发散，则∑Vn发散n=1n=1例、判别下列级数敛散性∞（1）∑n=114n+n2 （2）∑∞sin2n=1n2nπ 解（1）由于∞14n2+n≥14n2+n2=11⋅ 5n∵∑1发散，∴原级数发散 nn=1sin2（2）由于nπ∞1≤1，而∑收敛，∴原级数收敛 222n=1nnn比较判别法的极限形式如limun=A 则有n→∞Vn∞∞0<A<+∞时∑un，∑Vn，同时收敛，同时发散 n=1n=1A=0 如∑Vn 收敛，则∑un收敛n=1∞n=1∞∞∞A=+∞ 如∑un 收敛，则∑Vn收敛 n=1n=1判别下列级数敛散性例、∑lnn=1∞n+1 nlnn+1∞1=1 又∑发散，∴原级数发散 1n=1nn limn→∞1例、（1）∑ （2）∑(1-cos) nn=1n2+1+nn=1∞1∞ （3）∑lnn n=2n∞1解：（1）由limn→∞nn2+n+n=lim=1 21n→∞n+n+nn111-cos21（2）lim=lim= 1n→∞n→∞12n2n2∵ ∑∞12n=1n 收敛∴原级数收敛lnn1（3）∵ >nn∴∑例、P2712、比判别法∞(n≥3) ∵ ∑1 发散，nn=1∞lnn 发散 n=1n例7.7 7.8 设正项级数∑un的一般项满足n=1∞un+1lim=ρ n→∞un则当ρ<1时，级数收敛，ρ>1时发散，ρ=1不定3、根值法设∑un为正项级数，如limun=ρn=1∞n→∞则当ρ<1时，级数收敛，ρ>1时发散，ρ=1不定正项级数判别其敛散性的步骤：⎧≠0发散首先考察limun⎨ n→∞=0需进一步判别⎩①如un中含n!或n的乘积通常选用比值法；②如un是以n为指数幂的因子，通常用根值法，也可用比值法；③如un含形如nα（α可以不是整数）因子，通常用比较法；④利用级数性质判别其敛散性；⑤据定义判别级数敛散性，考察limSn是否存在，实际上考察{Sn}n→∞是否有上界。

第七章无穷级数

307第七章无穷级数【数学13AB 】2008考试内容 (本大纲为数学1，数学2-4需要根据大纲作部分增删)常数项级数的收敛与发散的概念收敛级数的和的概念级数的基本性质与收敛的必要条件几何级数与p 级数及其收敛性正项级数收敛性的判别法交错级数与莱布尼茨定理任意项级数的绝对收敛与条件收敛函数项级数的收敛域与和函数的概念幂级数及其收敛半径、收敛区间（指开区间）和收敛域幂级数的和函数幂级数在其收敛区间内的基本性质简单幂级数的和函数的求法初等函数的幂级数展开式函数的傅里叶（Fourier ）系数与傅里叶级数狄利克雷（Dirichlet ）定理函数在[－l ，l]上的傅里叶级数函数在[0，l]上的正弦级数和余弦级数2008考试要求1. 理解常数项级数收敛、发散以及收敛级数的和的概念，掌握级数的基本性质及收敛的必要条件。

2. 掌握几何级数与p 级数的收敛与发散的条件。

3. 掌握正项级数收敛性的比较判别法和比值判别法，会用根值判别法。

4. 掌握交错级数的莱布尼茨判别法。

5. 了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系。

6. 了觖函数项级数的收敛域及和函数的概念。

7. 理解幂级数收敛半径的概念，并掌握幂级数的收敛半径、收敛区间及收敛域的求法。

8.了解幂级数在其收敛区间内的基本性质（和函数的连续性、逐项求导和逐项积分），会求一些幂级数在收敛区间内的和函数，并会由此求出某些数项级数的和。

9. 了解函数展开为泰勒级数的充分必要条件。

10. 掌握,sin ,cos ,ln(1)(1)xe x x x x α++及的麦克劳林（Maclaurin ）展开式，会用它们将一些简单函数间接展开为幂级数。

11. 了解傅里叶级数的概念和狄利克雷收敛定理，会将定义在[0，l]上的函数展开为正弦级数与余弦级数，会写出傅里叶级数的和的表达式。

一、三基层面及其拓展1. 级数收敛充要条件：部分和存在且极值唯一，即：1lim n k n k S u ∞→∞==∑存在，称级数收敛。

无穷级数(全)

无穷级数1、无穷级数：表达式 +++++n u u u u 321 称为无穷级数,简称级数.记作∑∞=1n nu, 其中n u 称为级数的一般项.2、部分和: 级数∑∞=1n nu的前n 项和 ∑==nk kn uS 1称为级数∑∞=1n nu的部分和.3、收敛的定义: 如果级数∑∞=1n nu的部分和数列}{n S 有极限S ,即S S n n =∞→lim ,则称级数∑∞=1n nu收敛.S 称为级数∑∞=1n nu的和, 并写成： ++++=321u u u S ∑∞==1n nu.如果}{n S 没有极限, 则称级数∑∞=1n nu发散.4、常数项级数收敛的必要条件：若级数∑∞=1n nu收敛，则必有0lim =∞→n n u ，反之若0lim ≠∞→n n u ，则级数一定发散5常用级数敛散性判定方法： ①等比级数：∑∞=0n n aq ，当 1q < 收敛，且级数收敛于qa -111q ≥ 发散当然等比级数的敛散性也可以由等比级数的部分和数列来判断：若S 存在则收敛，反之则发散. ②P-级数：∑∞=1n P n 11p >收敛，1p ≤发散(p=1时为调和级数)；③常数级数：∑∞=0n C 当0≠C 时级数发散，0=C 时，级数收敛.6、级数收敛的性质以下假设∑∞=1n nu与∑∞=1n nv收敛于S 与T , 则①∑∑∞=∞==11n n n nu u λλ, (λ为常数). ②∑∑∑∞=∞=∞=±=±111)(n n n n n n nv u v u.③∑∞=1n nu收敛⇔对任意的非负整数m ,有∑∞+=1m n nu收敛.即: 在级数前面去掉或加上有限项不影响级数的敛散性. ④若S un n=∑∞=1,则将级数的项任意加括号后所成的级数S n n=∑∞=1σ. 反之不然.7、正项级数敛散性的判定方法： ①充要条件：部分和数列有界②比较法：对级数的缩放，利用已知的级数来判断未知级数的敛散性；适用于含有P(型)-级数、、多项式和正余弦的级数.其中P(型)-级数、对数、多项式主要是删减低次项和常数项，而正余弦主要是利用其小于1的性质.③比阶法：找到一个已知敛散性的级数，通过其与需求级数作商曲极限，来判断需求级数的敛散性.适用于P(型)-级数，等比级数、多项式等.定义如下：设∑∞=1n n u 与∑∞=1n n v 均为正项级数,若L v u nnn =∞→lim，则(1)当L=0时,若∑∞=1n nv收敛,则∑∞=1n nu也收敛；(2)当L=+∞时,若∑∞=1n nv发散,则∑∞=1n nu也发散.(3)当0<L<+∞时,∑∞=1n nv与∑∞=1n nu有相同敛散性.④比值法：通过对级数通向第n+1项与第n 项作商取极限来判断级数敛散性.不适用含有对数、多项式和正余弦的级数.定义如下：设∑∞=1n n u 为正项级数,若ρ=+∞→nn n u u 1lim,则(1)1<ρ时, 级数∑∞=1n nu收敛；(2) 1>ρ或+∞=ρ时, 级数∑∞=1n nu发散；(3)1=ρ时, 级数∑∞=1n nu可能收敛也可能发散.⑤其他常用方法(1)关于级数中带有多项式的分式方程的：ⅰ分子最高次≥分母最高次则级数一定发散； ⅱ分子最高次＜分母最高次，则用比阶法来判断. 设sn n V 1=（s 为分子最高项-分母最高项的差值） (2)关于级数中带有对数的：用比阶法题目中()c n U tn +=ln ，就设tn n V 1=作商取极限，需要用L ，hospital 定理8、交错级数的审敛法：（莱布尼茨定理) 设∑∞=--11)1(n n n u 为交错级数, 若满足(1) n n u u ≤+1, ,2,1=n ； (2) 0lim =∞→n n u , 则 ∑∞=--11)1(n n n u 收敛,9、任意项级数的绝对收敛和条件收敛 ①绝对收敛的级数∑∞=1n nu ：∑∞=1||n nu 收敛；②条件收敛的级数∑∞=1n n u：∑∞=1||n nu发散, 但∑∞=1n n u 收敛.③∑∞=1||n nu收敛 ⇒ ∑∞=1n n u 收敛. 反之不然.④此类级数多用比值法来判断绝对值级数是否发散 ⑤若任意项级数∑∞=1n nu条件收敛，则其所有正项或者负项构成的级数均为发散的.10、函数项级数①定义: 设 ),(,),(),(21x u x u x u n 是定义在I 上的函数,则++++=∑∞=)()()()(211x u x u x u x u nn n称为定义在区间I 上的(函数项)无穷级数.②收敛域(1) 收敛点I x ∈0—— ∑∞=10)(n nx u 收敛；(2) 发散点I x ∈0——∑∞=10)(n nx u 发散；(3) 收敛域D —— ∑∞=1)(n nx u 的所有收敛点的全体D ；(4) 发散域G ——∑∞=1)(n n x u 的所有发散点的全体G .（5）解题方法：已知级数∑∞=1)(n nx u，求其收敛域.ⅰ用比值法算出大致收敛域：）（的式子关于x 1Q x lim==+∞→nn n u u ρ，令）（x Q <1，算出x 收敛大范围（a ，b ），收敛半径R=2b-a （()∞++∞∞-∈可以为R R ,,） ⅱ将端点值带入级数∑∞=1)(n nx u中，算出∑∞=1)(n n a u 与∑∞=1)(n n b u 的敛散性，判断端点值是否可以取到，过程可以略过. ⅲ综上所述，写出级数∑∞=1)(n nx u的收敛域③和函数)(x S —— ∑∞==1)()(n nx u x S , D x ∈.解题方法：已知级数∑∞=1)(n nx u，求其和函数.ⅰ求出其收敛域；ⅱ将级数经过求导或者积分，得到一个等比级数 ⅲ用等比级数收敛公式qa -11算出和函数的导数或者原函数的表达式；ⅳ将求出的表达式积分或求导，写成)(x S 的形式，并注明收敛域.【注】已知级数∑∞=1)(n nx u，求∑∞=1n n V 的和ⅰ-ⅳ步骤同上ⅴ将n n V x u 与)(建立起联系，想当x 为何值时n n V x u =)(，然后将x 带入)(x S 中.11、函数项级数的展开式.(1) f (x ) = e x= ∑∞=0!n nn x , x ∈(-∞, +∞);(2) f (x ) = sin x = ∑∞=++-012!)12()1(n n n xn ,x ∈(-∞, + ∞);(3) f (x ) = cos x = ∑∞=-02!)2()1(n nn x n ,x ∈(-∞, + ∞);(4) 11()1n n f x x x ∞===-∑ ,x ∈(-1, 1);(5) 11()()1n n f x x x ∞===-+∑ ,x ∈(-1, 1);(6) f (x ) = ln (1 + x ) = ∑∞=+-11)1(n nn x n , x ∈(-1, 1]。

《数学分析》第七章无穷级数

第七章无穷级数一、本章知识脉络框图二、本章重点及难点无穷级数是数学分析的重要内容之一，它在研究函数的分析性质、函数逼近、近似计算和微分方程定性理论等领域起着非常重要的作用. 无穷级数的核心是收敛性理论，它的本质就是“无穷多项的和”，但不是从“有限项相加”到“无限项相加”的简单推广，两者有着本质的区别，例如，对于有限项求和而言，加法交换律、结合律以及加法和乘法的分配律总是成立，有限个连续函数的和也是连续函数，但这些规律和性质却不能直接搬到无穷级数上去. 这就要求人们要用一种新的数学思想来研究无穷级数.本章内容由数项级数、函数列与函数项级数、幂级数与傅里叶级数四部分组成，后两者氏特殊的函数项级数. 本章重点是各种级数的收敛性和一致收敛性的概念及其判别法，难点主要有以下几点：●数项级数收敛性判别方法；● 函数列与函数项级数一致收敛性判别法以及一致收敛的函数列与函数项级数的性质；● 幂级数的收敛半径以及和函数的性质，函数的幂级数展开； ● 将函数展成傅里叶级数的条件和方法.三、本章的基本知识要点（一）数项级数 1.级数的收敛性（1）级数收敛和发散的定义若数项级数∑∞=1n nu的部分和数列{}n S 收敛于S （即S S n n =∞→lim ），则称数项级数收敛，称S 为数项级数的和，记为∑∞==1n n u S 或.∑=n u S若{}n S 发散，则称级数∑∞=1n nu发散.（2）级数收敛的条件① 级数收敛的必要条件：级数∑∞=1n nu收敛.0lim =⇒∞→n n u② 级数收敛的柯西准则（充要条件）（10）级数∑∞=1n nu收敛⇔0>∀ε，+∈∃N N ，N n >∀，+∈∀N p ，有.21ε<++++++p n n n u u u（20）级数∑∞=1n nu发散⇔00>∃ε，+∈∀N N ，N n >∃0，+∈∃N p 0，使得.0210000ε≥++++++p n n n u u u（3）收敛级数的性质 ① 线性运算性质：若级数∑nu和∑nv都收敛，则对任意常数d c ,，级数()∑+n ndv cu也收敛，且().∑∑∑+=+n n n nv d u c dv cu② 级数的收敛性与前面有限项的值无关：去掉，增加或改变级数的有限项并不改变级数的敛散性.③ 在收敛级数的项中任意加括号，既不改变级数的收敛性，也不改变它的和. 2.正项级数收敛性的判别（1）（充要条件）正项级数∑nu收敛⇔部分和数列{}n S 有界（即+∈∃R M ，+∈∀N n ，有.M S n ≤）（2）(比较原则) 设∑nu和∑nv是两个正项级数，且+∈∃N N ，N n >∀，有n n v u ≤，则① ∑nv收敛⇒∑nu收敛； ②∑nu发散⇒∑nv发散.（3）(比较原则的极限形式) 设∑n u 和∑n v 是两个正项级数，l v u nnn =∞→lim，则① 当+∞<<l 0 时，级数∑nu和∑nv同敛态；② 当0=l 且级数∑nv收敛⇒∑nu收敛；③ 当+∞=l 且级数∑nv发散⇒∑nu发散.（4）(比式判别法或称达朗贝尔判别法) 设∑nu是正项级数，且+∈∃N N 0及常数)1,0(∈q .① 0N n >∀有q u u nn ≤+1⇒∑n u 收敛； ② 0N n >∀有11≥+nn u u ⇒∑n u 发散. （5）(比式判别法的极限形式) 设∑n u 是正项级数，且q u u nn n =+∞→1lim，则 ① 当1<q 时，级数∑nu收敛；② 当1>q 或+∞=q 时，级数∑nu发散.注当1=q 时不能用本法判别级数的敛散性.（6）(根式判别法或称柯西判别法) 设∑nu是正项级数，且+∈∃N N 0及正常数l .① 0N n >∀有1<≤l u n n ⇒∑nu收敛；② 0N n >∀有1≥n n u ⇒∑nu发散.（7）(根式判别法的极限形式) 设∑nu是正项级数，且l u n n =，则① 当1<l 时，级数∑nu收敛；② 当1>l 或+∞=l 时，级数∑nu发散.注当1=l 时不能用本法判别级数的敛散性.（8）(积分判别法) 设f 为],1[+∞上的非负减函数，则正项级数∑)(n f 与反常积分⎰+∞1)(dx x f 同时收敛或同时发散.3.一般项级数收敛性的判别（1）(交错级数的莱布尼茨判别法) 若交错级数∑+-n n u 1)1(（0>n u ）满足条件：数列{}n u 单调递减且趋于0，则∑+-n n u 1)1(收敛.（2）级数条件收敛和绝对收敛的定义 ① 若级数∑nu 收敛，则称级数∑nu绝对收敛;② 若级数∑nu收敛而∑nu发散，则称级数∑nu条件收敛.③ 绝对级数的级数一定收敛.（3）(阿贝尔判别法) 若{}n a 为单调有界数列，且级数∑nb收敛，则∑nn b a 也收敛.（4）(狄利克雷判别法) 若数列{}n a 单调递减，且0lim =∞→n n a ，又级数∑nb的部分和数列有界，则∑nn ba 收敛.（二）函数列与函数项级数 1.函数列及其一致收敛性（1）函数列的收敛域及极限函数① 设有一定义于同一数集E 上的函数列(){}x f n ，若对E x ∈0，数列(){}0x f n 收敛，则称0x 为函数列(){}x f n 的收敛点，若数列(){}0x f n 发散，则称0x 为函数列(){}x f n 的发散点，函数列(){}x f n 的所有收敛点的集合称为它的收敛域. 若E D x ⊂∈∀，数列(){}x f n 收敛，设)()(lim x f x f n n =∞→，则称)(x f 为函数列(){}x f n 的极限函数或称函数列(){}x f n 在D上点点收敛于函数)(x f ，记为.),()(lim D x x f x f n n ∈=∞→或)()(x f x f n → ),(∞→n .D x ∈② 函数列极限的N -ε定义：⇔∈=∞→D x x f x f n n ),()(lim 对每一固定的D x ∈，0>∀ε，恒存在正数),(x N N ε=（一般说来N 的值与ε和x 有关），使得当N n >时，总有.)()(ε<-x f x f n（2）函数列一致收敛的定义① 函数列(){}x f n 在D 上一致收敛于函数)(x f ⇔0>∀ε，+∈∃R N ，使得当Nn >时，对一切D x ∈，有.)()(ε<-x f x f n记为)()(x f x f n →→ ),(∞→n .D x ∈② 函数列(){}x f n 在D 上不一致收敛于函数)(x f ⇔00>∃ε，+∈∀R N ，总存在正整数N n >0与点D x ∈0，使得.)()(0000ε≥-x f x f n（3）函数列一致收敛的判别法① 利用函数列一致收敛的定义.② 柯西准则：)()(x f x f n →→ ),(∞→n .D x ∈⇔0>∀ε，+∈∃R N ，使得当N m n >,时，对一切D x ∈，都有.)()(ε<-x f x f m n③ 确界极限判别法：函数列(){}x f n 在D 上一致收敛于函数)(x f⇔.0)()(sup lim =-∈→∞x f x f n Dx n④ 优数列判别法：若+∈∃R N ，当N n >时，对一切D x ∈，有n n a x f x f ≤-)()(，且0lim =∞→n n a ，则函数列(){}x f n 在D 上一致收敛于)(x f .注数列}{n a 称为优数列.（4）一致收敛函数列的性质① 连续性：若函数列(){}x f n 在D 上一致收敛，且每一项都连续，则其极限函数)(x f 在D 上也连续，且D x ∈∀0，有).(lim lim )(lim lim 00x f x f n x x n n n x x →→∞→∞→=② 可积性：若函数列(){}x f n 在],[b a 上一致收敛于)(x f ，且每一项都连续，则)(x f 在],[b a 上也可积，且.d )(lim d )(lim d )(⎰⎰⎰→∞→∞==bab a ban n n n x x f x x f x x f③ 可微性：设函数列(){}x f n 在],[b a 上有定义，若],[0b a x ∈为(){}x f n 的收敛点，(){}x f n 的每一项在],[b a 上有连续的导数，且(){}x f n '在],[b a 上一致收敛，则(){}x f n 在],[b a 上一致收敛，其极限函数)(x f 在],[b a 上可导，且()).(d d lim )(lim d d )(d d x f x x f x x f x n n n n →∞→∞==2.函数项级数及其一致收敛性（1）函数项级数的收敛域及和函数设有一定义于同一数集E 上的函数列(){}x u n ，称++++)()()(21x u x u x u n ，.E x ∈为定义在E 上的函数项级数，记为∑∞=1)(n nx u或∑).(x u n 并称)()(1x u x S nk k n ∑==，E x ∈， ,2,1=为函数项级数∑)(x u n 的部分和数列. 若E x∈0，部分和数列)}({0x S n 收敛，则称0x 为函数项级数∑)(x u n的收敛点，若数列)}({0x Sn发散，则称0x 为函数项级数∑)(x u n 的发散点. 级数∑)(x u n的所有收敛点的集合称为它的收敛域. 若E D x ⊂∈∀，级数∑)(x u n的和数列(){}x S n 收敛于函数)(x S ，则称)(x S 为级数∑)(x u n的和函数，记为)()()()(21x S x u x u x u n =++++ ，.D x ∈注函数项级数的收敛性指的就是它的和函数列的收敛性.（2）函数项级数一致收敛的定义设(){}x S n 是函数项级数∑)(x u n的部分和数列，若(){}x S n在D 上一致收敛于函数)(x S ，则称函数项级数∑)(x u n 在D 上一致收敛于函数)(x S ，或称∑)(x u n 在D 上一致收敛，即0>∀ε，+∈∃R N ，N n >∀，D x ∈∀，有.)()(ε<-x S x S n（3）函数项级数一致收敛的判别法 ① 利用函数项级数一致收敛的定义. ② 柯西准则：函数项级数∑)(x u n在数集D 上一致收敛⇔0>∀ε，+∈∃RN ，使得当N n >时，对一切D x ∈和一切正整数p ，都有.)()(ε<-+x S x S n p n或.)()()(21ε<++++++x u x u x u p n n n注当1=p 时得到函数项级数一致收敛的必要条件：∑)(x u n在数集D 上一致收敛⇔函数列(){}x u n 在D 上一致收敛于零.③ 确界极限判别法：函数项级数∑)(x u n在D 上一致收敛于函数)(x S⇔.0)()(sup lim =-∈→∞x S x S n Dx n④ 优级数判别法：设函数项级数∑)(x u n定义在数集D 上，∑nM为收敛的正项级数，若对一切D x ∈，有n n M x u ≤)(，,,2,1 =n 则级数∑)(x u n在D 上一致收敛.⑤ 阿贝尔判别法：设（10）∑)(x u n在区间I 上一致收敛；（20）I x ∈∀,)}({x v n 是单调的；（30）)}({x v n 在I 上一致有界.则级数)()(x v x u nn∑在I 上一致收敛.⑥ 狄利克雷判别法：设（10）∑)(x u n的部分和数列在区间I 上一致有界；（20）I x ∈∀,)}({x v n 是单调的；（30）在I 上0)(→→x v n ).(∞→n则级数)()(x v x u nn∑在I 上一致收敛.（4）一致收敛函数项级数的性质 ① 连续性：若函数项级数∑)(x u n在区间],[b a 上一致收敛，且每一项都连续，则其和函数在],[b a 上也连续.② 逐项求积：若函数项级数∑)(x u n在区间],[b a 上一致收敛，且每一项都连续，则∑⎰⎰∑=.d )(d )(babannx x u x x u③ 逐项求导：若函数项级数∑)(x u n在],[b a 上每一项都有连续的导函数，],[0b a x∈为∑)(x u n的收敛点，且)(x u n∑'在],[b a 上一致收敛，则∑=)()(x u x S n在上可导，且可逐项求导，即().)(d d)(d d ∑∑=⎪⎭⎫ ⎝⎛x u xx u x n n （三）幂级数1.幂级数的一般形式：()∑∞=-0n nnx x a ；特殊形式：x an n n∑∞=0.2.阿贝尔定理：若幂级数x ann n∑∞=0在0≠=x x 收敛，则对满足不等式x x <的任何x ，幂级数x ann n∑∞=0收敛而且绝对收敛；若幂级数x a nn n ∑∞=0在x x =发散，则对满足不等式x x >的任何x ，幂级数x a n n n ∑∞=0发散.3.幂级数的收敛半径和收敛区间幂级数x ann n∑∞=0的收敛域是以原点为中心的区间，若以R 2表示区间的长度，则称R 为幂级数的收敛半径.（1）当0=R 时，幂级数x ann n∑∞=0仅在0=x 处收敛；（2）当∞=R 时，幂级数x ann n∑∞=0在),(+∞-∞上收敛；（3）当0>R 时，幂级数x ann n∑∞=0在),(R R +-内收敛；对一切满足不等式R x >的x ，幂级数x ann n∑∞=0都发散；在R x ±=处，可能收敛也可能发散.（4）()R R ,-称为幂级数x ann n∑∞=0的收敛区间.4.幂级数收敛半径定理：对于幂级数x a n n n ∑∞=0，若ρ=→∞n n n a lim ，或ρ=+∞→nn n a a 1lim ，则（1）当+∞<<ρ0时，幂级数x a n n n ∑∞=0的收敛半径是ρ1=R ；（2）当0=ρ时，幂级数x ann n∑∞=0的收敛半径是+∞=R ；（3）当+∞=ρ时，幂级数x ann n∑∞=0的收敛半径是0=R .5.幂级数的一致收敛性质（1）设幂级数x ann n∑∞=0的收敛半径为()0>R ，则在它的收敛区间()R R ,-内任意闭区间],[b a 上幂级数都一致收敛.（2）设幂级数x ann n∑∞=0的收敛半径为()0>R ，且在R x =（或R x -=）时收敛，则幂级数在],0[R （或]0,[R -）上一致收敛.6.幂级数的分析性质（1）幂级数x ann n∑∞=0的和函数是()R R ,-内的连续函数；若幂级数在收敛区间的左（右）端点上收敛，则其和函数也在这一端点上右（或左）连续.（2）幂级数x ann n∑∞=0与其逐项求导及逐项积分所得的幂级数具有相同的收敛区间.（3）设幂级数x ann n∑∞=0在收敛区间()R R ,-内的和函数为()x f ，()R R x ,-∈∀，则① ()x f 在x 可导，且()∑∞=-=11n n nxnax f ；② ()x f 在0与x 这个区间上可积，且()x n a t t f n n n x11d +∞=∑⎰+=. （4）记()x f 为幂级数x ann n∑∞=0在收敛区间()R R ,-内的和函数，则在()R R ,-内具有任意阶导数，求可逐项求导任意次，即() +++++='-x na x a x a a x f n n 1232132， () +-++⋅+=''-x a n n x a a x f n n 232)1(232， ()() +-++=+x a n n n a n x fn n n 12)1()1(!（5）记()x f 为幂级数x ann n∑∞=0在0=x 的某邻域内的和函数，则幂级数的系数与()x f 在0=x 处的各阶导数有如下关系： ()()() ,2,1,!0,00===n n fa f a n n7.幂级数的运算（1）若幂级数x ann n∑∞=0与x b nn n ∑∞=0在0=x 的某邻域内有相同的和函数，则称这两个幂级数在此邻域内相等.（2）幂级数x ann n∑∞=0与x b nn n ∑∞=0在0=x 的某邻域内相等 ,2,1,0,==⇒n b a n n（3）若幂级数x ann n∑∞=0与x b nn n ∑∞=0的收敛半径分别为a R 与b R ，则有x a x ann n nn n∑∑∞=∞==0λλ，a R x <.()x b a x b x ann n n nn n nn n∑∑∑∞=∞=∞=+=±0，R x <. x c x b x a n n n n n n n n n ∑∑∑∞=∞=∞==⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛000,R x <. 其中λ为常数，},m in{b a R R R =，kn nk k n ba c -=∑=.8. 泰勒级数（1）设()x f 在0x x =处存在任意阶的导数，则称()()()()()()()() +-++-''+-'+n n x x n x f x x x f x x x f x f 00200000!!2 为()x f 在0x 的泰勒级数，当00=x 时，称级数()()()()() +++''+'+x n f x f x f f nn !0!20002为函数的麦克劳林级数.（2）()x f 在0x 的泰勒级数收敛于()()0lim =⇔∞→x R x f n n ，其中()x R n 为()x f 在0x 的泰勒公式余项.（3）余项的形式 ① 皮亚诺型余项()()()nn x x o x R 0-=，()()x o x R n n =.② 拉格朗日型余项 ()()()()()101!1++-+=n n n x x n fx R ξ（ξ介于0x 与x 之间）()()()()10001)!1(++-+-+=n n x x n x x x fθ，10<<θ. ()()()()xn fx R n n n 11!1+++=ξ（ξ介于0与x 之间）()()x n x fn n 11)!1(+++=θ，10<<θ. ③ 柯西型余项()()()()()01!x x x n fx R n n n --=+ξξ（ξ介于0x 与x 之间）()()()()()100011!++---+=n n n x x n x x x fθθ，10<<θ.()()()()x x n fx R n n n ξξ-=+!1（ξ介于0与x 之间）()()()()xn x x x fn nn 10011!++--+=θθ，10<<θ.④ 积分型余项()()()()t t x t f n x R nx x n n d !101-=⎰+.()()()()t t x t f n x R nx n n d !101-=⎰+.（4）五个基本展开式① R ,!!21e 2∈+++++=x n x x x nx .② ()()R ,!121!5!3sin 12153∈+--+-+-=--x n x x x x x n n . ③ ()()R,!21!4!21cos 242∈+-+-+-=x n x x x x nn .④ ()()()()1,!11!21112<++--++-++=+x x n n x x x nααααααα.⑤ ()()(]1,1,1321ln 132-∈+-+-+-=+-x nx xx x x nn . 9. 函数的幂级数展开的方法（1）直接法先求出函数在0x x =处的各阶导数，其次估计余项，证明()0lim =→∞x R n n ，最后写出函数的展开式.（2）间接法利用基本展开式，经过四则运算或变量替换得到函数的幂级数展开式，或在收敛区间内用逐项求导或逐项积分求出函数的导数或原函数，再经逆运算得到函数的幂级数展开式（四）傅里叶级数1.三角函数系与三角级数（1）函数列 ,sin ,cos ,,2sin ,2cos ,sin ,cos ,1nx nx x x x x 统称为三角函数列或三角函数系.（2）三角函数系具有正交性，即在三角函数系中，任何两个不同的函数的乘积在[]ππ,-上的积分都等于零，而其中任何一个函数的平方在[]ππ,-上的积分都不等于零.（3）由三角函数系产生的形如()∑∞=++10sin cos 2n n n nx b nx a a 的级数称为三角级数. （4）若级数 ()∑∞=++102n n n b a a 收敛，则级数 ()∑∞=++10sin cos 2n n n nx b nx a a 在整个数轴上绝对收敛且一致收敛.2.以π2为周期的函数的傅里叶级数（1）傅里叶系数公式若在整个数轴上()()∑∞=++=10sin cos 2n n n nx b nx a a x f 且等式右边级数一致收敛，则有如下关系：()x nx x f a n d cos 1⎰-=πππ， ,2,1,0=n ， ()x x x f b n d sin 1⎰-=πππ， ,2,1=n .（2）以()x f 的傅里叶系数为系数的三角级数称为()x f 的傅里叶级数，记为()x f ～()∑∞=++10sin cos 2n n n nx b nx a a .（3）收敛定理：若以π2为周期的函数()x f 在[]ππ,-上按段光滑，则在没一点[]ππ,-∈x ，()x f 的傅里叶级数收敛于()x f 在点x 处的左、右极限的算术平均值，即()()()∑∞=++=-++10sin cos 2200n n n nx b nx a a x f x f ，其中n n b a ,为()x f 的傅里叶系数.（4）收敛定理的推论：若()x f 是以π2为周期的连续函数，且在[]ππ,-上按段光滑，则()x f 的傅里叶级数在()+∞∞-,上收敛于()x f .3.以l 2为周期的函数的傅里叶级数设()x f 是以l 2为周期的函数，级数∑∞=⎪⎭⎫ ⎝⎛++10sin cos 2n n n l x n b l x n a a ππ，其中()x l x n x f l a l l n d cos 1π⎰-=， ,2,1,0=n ，()x lx n x f l b l l n d sin 1π⎰-=， ,2,1=n ，称为函数()x f 的傅里叶级数，n n b a ,称为傅里叶系数.4.正弦级数与余弦级数（1）设()x f 是以l 2为周期的可积偶函数，或是定义在[]l l ,-上的可积偶函数，则()x f 可展成余弦级数()x f ～lx n a a n n πcos 210∑∞=+，其中 ()x lxn x f l a l n d cos 20π⎰=， ,2,1,0=n .（2）设()x f 是以l 2为周期的可积奇函数，或是定义在[]l l ,-上的可积奇函数，则()x f 可展成正弦级数()x f ～lxn b n n πsin1∑∞=，其中 ()x lxn x f l b l n d sin 20π⎰=， ,2,1=n . 5.贝塞尔不等式及其推论（1）贝塞尔不等式若函数()x f 在[]ππ,-上可积，则()()x x fb a a n nn d 1221222⎰∑-∞=≤++πππ，其中n n b a , 为()x f 的傅里叶系数.（2）推论1（黎曼-勒贝格定理）：若()x f 为可积函数，则()0d cos lim =⎰-∞→x nx x f n ππ，()0d sin lim =⎰-∞→x nx x f n ππ.（3）推论2：若()x f 为可积函数，则()0d 21cos lim 0=⎪⎭⎫ ⎝⎛+⎰∞→x x n x f n π，()0d 21sin lim 0=⎪⎭⎫ ⎝⎛+⎰∞→x x n x f n π. 5.傅里叶级数部分和的积分表达式若()x f 是以π2为周期的函数，且在[]ππ,-可积，则它的傅里叶级数部分和()x S n 可写成()()t t tn t x f x S n d 2sin221sin 1⎪⎭⎫ ⎝⎛++=⎰-πππ，当0=t 时，被积函数中的不定式有极限212sin221sin lim 0+=⎪⎭⎫ ⎝⎛+→n t tn t来确定.四、基本例题解题点击【例1】讨论下列级数的敛散性： 1.()∑∞=2ln ln 1n nn ； 2. ()∑-1na （1>a ）； 3. ∑nn n !； 4. ∑33n n .【提示】本题涉及到正项级数的几种常用的敛散性判别法，其中第三题困难之处在于寻找与()1-na 同阶无穷小，利用()1-a x 的泰勒展开式，将展开式中的x 替换为n1后即可知()1-na 与n1同阶. 【解】1. 当e 2>n 时，()21ln 1ln n n n <，而∑21n收敛，故()∑∞=2ln ln 1n n n 收敛. 2. 0ln 1lim 11lim 0>=-=-+→∞→a x a na x x nn ，而∑n 1发散，故()∑-1na 发散.3. 由于 1e 11lim lim 1<=⎪⎭⎫ ⎝⎛+=∞→+∞→nn n n n n n u u ，故∑n n n!收敛.4. 由于1313lim lim 3<==∞→∞→nn n n n n u ，故∑33n n 收敛. 【例2】设∑a n2与∑bn 2都收敛，证明下列级数也都收敛：1.∑n n b a ； 2. ()∑+2n n b a ; 及 3. ∑na n. 【证明】1.由()b a b a n n n n 2221+≤及∑a n 2和∑b n 2的收敛性可知∑n n b a 收敛. 2. 由()b b a a n b a n n n n n 2222++≤+及∑a n2和∑bn 2的收敛性与上小题的结果可知()∑+2n nb a收敛.3. 由⎪⎭⎫ ⎝⎛+≤a n n a n n 22121及∑a n 2与∑n21的收敛性可知∑n a n 收敛. 【例3】判断级数()nnn ln 1∑-的收敛性（中国地质大学2006年硕士研究生入学试题）. 【提示】考查交错级数收敛的判别法与级数的条件收敛性.【解】当e >x 时，0ln 1ln 2<-='⎪⎭⎫ ⎝⎛x xx x ，所以，当3≥n 时，n n ln 单调递减，且0ln lim =∞→n n n ，由交错级数的莱布尼茨判别法可知()nn n ln 1∑-收敛，但是()n n n n 1ln 1≥-，而∑n1发散，故()nn n ln 1∑-条件收敛. 【例4】证明下列级数收敛:1. nn n n n ∑∞=⎪⎭⎫ ⎝⎛+111cos ； 2.()∑∞=-12sin 1n nn n . 【证明】1. 设n n u n cos =，nn n v ⎪⎭⎫⎝⎛+=11.对于级数∑∞=1n n u ，由于⎭⎬⎫⎩⎨⎧n 1单调递减且01lim =∞→n n 及∑=nk k 1cos 有界，由狄利克雷判别法可知∑∞=1n nu收敛.又数列{}n v 单调递增有上界，根据阿贝尔判别法，原级数收敛.2. 由于22cos 1sin 2nn -=，故原级数收敛性证明可转化为下面两个级数的收敛性：()∑∞=-121n n n，()∑∞=+-1122cos 1n n nn .根据莱布尼茨判别法可知，级数()∑∞=-121n n n收敛.级数()()∑∑∞=+∞=+-=-11112cos 12122cos 1n n n n nn nn ，有数列⎭⎬⎫⎩⎨⎧n 1单调递减且01lim =∞→nn ，而()()∑∑=+=+-=-nk k nk k k k 11112cos 1cos 211cos 212cos 1 ()()()()1cos 112cos 12cos 13cos 5cos 1cos 3cos 1cos 211≤-++-++--+=+n n n . 由狄利雷判别法可知，级数()∑∞=+-1122cos 1n n nn 收敛. 因此级数()∑∞=-12sin 1n n nn收敛.【例5】讨论下列函数列在给定区间上的一致收敛性：1. ()x x x f nnn +=1，（1） []1,0∈x ；（2） []δ-∈1,0x ()10<<δ.2. ()nn n x x f ⎪⎭⎫⎝⎛+=1，[]1,0∈x .【解】1. （1）()()⎪⎩⎪⎨⎧=<≤==∞→.1,21,10,0lim x x x f x f n n 由于(){}x f n 中的每一项都在[]1,0上连续，而其极限函数()x f 在[]1,0上不连续，因此函数列(){}x f n 在[]1,0上不一致收敛.（2）因为 ()()0lim ==∞→x f x f n n，[]δ-∈1,0x . 又 ()()()()n nnn x n x x x x f x f δδδδ-+-=⎭⎬⎫⎩⎨⎧+=--≤≤-≤≤1111sup sup 1010. 所以，()()0sup lim 10=--≤≤∞→x f x f n x nδ，故函数列(){}x f n 在[]δ-1,0上一致收敛. 2. ()()e 1lim lim x nn n n n x x f x f =⎪⎭⎫ ⎝⎛+==∞→∞→，[]1,0∈x .又 ()()()0e 11<-⎪⎭⎫ ⎝⎛+='--x n n n x x f x f ，故()()x f x f n -在[]1,0上严格单调递减，即有()()0e 111≤-≤-⎪⎭⎫⎝⎛+-x f x f n n n .由此得 ()()()∞→→-⎪⎭⎫⎝⎛+≤--n n x f x f n n 0e 111. 故函数列(){}x f n 在[]1,0上一致收敛.【例6】证明函数列 ()()nn x nx x f -=1 ),2,1( =n 在闭区间]1,0[上收敛，但不一致收敛.【证明】]1,0[∈∀x ，显然有()()01lim lim =-=∞→∞→n n n n x nx x f . 即()()nn x nx x f -=1在闭区间]1,0[上收敛于零，但是由于()∞→→⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛n n n f nn e 1111，从而()00sup lim ]1,0[≠-∈∞→x f n x n，因此()x f n 在]1,0[上不一致收敛. 【例7】讨论下列函数项级数的一致收敛性： 1.()∑∞=++12n n nnn x x ，[]1,0∈x ；2.()∑∞=+-121n nxn ，()+∞∞-∈,x ；3.()∑∞=+-1cos 1n nxn ，.2,2⎥⎦⎤⎢⎣⎡-∈ππx 【解】1. 因为()n n n n nn x nx nn x x ⎪⎭⎫ ⎝⎛+⋅=+∑∑∞=∞=+11122，故设()n x x u n 2=，()nn n x x v ⎪⎭⎫⎝⎛+=1.由优级数判别法，易证()∑∞=1n n x u 在[]1,0上一致收敛.[]1,0∈∀x ，数列(){}x v n 单调递增，且()e e ≤≤x n x v ，[]1,0∈x ，+∈N n ，由阿贝尔判别法可知，原级数在[]1,0上一致收敛.2. 此级数为交错级数，由莱布尼茨判别法易证该级数在()+∞∞-,上收敛，设()x S n 与()x S 分别为级数()∑∞=+-121n nxn 的前n 项部分和与和函数，则()()01cos 11→<++≤-nx n x S x S n ()∞→n .由柯西准则可知()∑∞=+-121n nxn 在()+∞∞-,上一致收敛.3. 设()()nn x u 1-=，()x n x v n cos 1+=. 则级数()∑∞=1n n x u 的部分和数列在⎥⎦⎤⎢⎣⎡-2,2ππ上一致有界. 对⎥⎦⎤⎢⎣⎡-∈∀2,2ππx ，(){}x v n 单调递减且趋于零. 并且 []()01lim 0sup lim 2,2==-∞→-∈∞→nx v n n x n ππ，即(){}x v n 在⎥⎦⎤⎢⎣⎡-2,2ππ上一致收敛于零. 由狄利克雷判别法知，原级数在⎥⎦⎤⎢⎣⎡-2,2ππ上一致收敛.【例8】设()x x x u n n ln =，(]1,0∈x . 1. 讨论()∑∞=1n n x u 在(]1,0上的收敛性和一致收敛性.2. 计算()x x u n n d 11⎰∑⎪⎭⎫⎝⎛∞=.【解】1. ()∑∞=1n n x u 的部分和为()()()⎪⎩⎪⎨⎧=∈--=.1,0,1,0,1ln 1x x xxx x x S n n由此可知()∑∞=1n n x u 在(]1,0上收敛且和函数为()()⎪⎩⎪⎨⎧=∈-=.1,0,1,0,1ln x x xx x x S 又()())1(1ln 1lim 1ln lim lim 111S x xx x x S x x x≠-=+-=-=+→+→+→，即和函数()x S 在(]1,0上不连续，因此()∑∞=1n n x u 在(]1,0上不一致收敛.2. ()()1d 1ln d ln d 1ln d 1ln d 10101010101+-=--=-=⎪⎭⎫ ⎝⎛⎰⎰⎰⎰⎰∑∞=x x x x x x x x x x x x x x u n n.6111d 1d 121211011011π-=-=⎪⎭⎫ ⎝⎛-=-=∑∑⎰⎰∑∞=∞=-∞=-n n n n n n x n x x n x【知识扩展提示】利用极限函数或和函数的不连续性来证明函数列或函数项级数的不一致收敛性是一种非常简洁而又十分有效地办法.【例9】求下列幂级数的收敛半径和收敛域：1. ()x n nn n 111+∑⎪⎭⎫ ⎝⎛+； 2. x n nn211∑⎪⎭⎫⎝⎛+. 【解】1. 因为 ()e 11lim 11lim 11=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛++∞→+∞→n n n n n n n n ,所以幂级数的收敛半径是e1=R . 当e 1±=x 时，()nn n n n n n ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛+++e 11e 11111，由于数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛++111n n 严格单调递减且收敛于e （当∞→n 时），从而有e 111>⎪⎭⎫ ⎝⎛++n n ，即1e 111>⎪⎭⎫⎝⎛++n n ，所以有()0e 111lim 1≠⎪⎭⎫⎝⎛±⎪⎭⎫ ⎝⎛++∞→nn n n n ，由级数收敛的必要条件知，幂级数在e 1±=x 处发散，因此原幂级数的收敛域为.e 1,e 1⎪⎭⎫ ⎝⎛- 2. 【解法一】令y x =2，则原幂级数为y n nn∑⎪⎭⎫ ⎝⎛+11.由于111lim =⎪⎭⎫ ⎝⎛+∞→n nn n ，故幂级数的收敛半径为.1=R 当1±=y 时，因为 ()0e 111lim ≠=±⎪⎭⎫ ⎝⎛+∞→n nn n ，所以幂级数y n n n ∑⎪⎭⎫ ⎝⎛+11在1±=y 处发散，故y n nn∑⎪⎭⎫ ⎝⎛+11的收敛域为()1,1-，由()1,12-∈=y x 得 ()1,1-∈x ，即原幂级数的收敛域为()1,1-.【解法二】令()x n x u n nn 211⎪⎭⎫⎝⎛+=，则()()()()x x nx n x u x u nn n n n n n n 22221111111lim lim =+⎪⎭⎫ ⎝⎛++=++∞→+∞→，由正项级数收敛的比式判别法可知，当12<x 即()1,1-∈x 时原幂级数绝对收敛，当12>x 时幂级数发散，因此幂级数的收敛半径为1=R ，易证当1±=x 时幂级数发散，故原幂级数的收敛域为()1,1-.【知识扩展提示】求幂级数的收敛域一般分为两步：首先求收敛半径，其次考虑级数在端点处的敛散性. 对于缺少偶次项或奇次项的幂级数（如第2题）可以用变量替换或用正项级数收敛性判别法来确定收敛半径和收敛域.【例10】求∑∞=+11n nn x的收敛域与和函数.【解】由于111lim =+→∞n n n ，故收敛半径为1=R ，又∑∞=+111n n 发散，()∑∞=+-111n n n 收敛，因此幂级数的收敛域为[).1,1- 令()∑∞=+=11n nn x x f ，()()∑∞=++==111n n n xx xf x g ，则()xxx x g n n -=='∑∞=11，所以 ()()().1ln d 1d 00x x t ttt t g x g xx---=-='=⎰⎰ 从而当0≠x 时，()()()x x x x g x f ---==1ln 1，又显然有()00=f ，故 ()()[)()⎪⎩⎪⎨⎧=⋃-∈---=.0,0,1,00,1,1ln 1x x xx x f 【知识扩展提示】通常利用幂级数的四则运算性质、逐项求导性质及逐项积分性质来求幂级数的和函数【例11】求x sin 2在0=x 处的幂级数展开式.【解】因为 ()()∑∞=-=02!21cos n nnn xx ，R x ∈，所以()()()()()()∑∑∞=--∞=-=--=-=12121022!221!22121212cos 121sin n nn n n nn x n n x x x ，.R x ∈【例12】求函数()x x f 2=在ππ<<-x 上的傅里叶展开式，并计算∑∞=121n n.【解】补充定义()ππ2=f ，再把()x f 延拓为周期为π2的周期函数，则()x f 在R 上连续，且在[]ππ,-上按段光滑. 由收敛定理知，()x f 可以展成傅里叶级数，由于ππππ22032d 1==⎰-x x a .()nx nx x a nn 2241d cos 1-==⎰-πππ，,,2,1 =n0d sin 12==⎰-πππx nx x b n ， ,2,1=n .所以当ππ<<-x 时，()().cos 143122nx nx f n n ∑∞=-+=π当π=x 时，上面等式也成立，于是∑∞=+=1222143n nππ，故.61212π=∑∞=n n五、扩展例题解题点击【例1】利用柯西收敛准则证明： 1.()∑-nn 1收敛； 2.∑n 1发散.【证明】1. 0>∀ε，令ε11+=N ，则当N n >时，对+∈∀N p ，有（1）若p 为奇数，()pn n n p +-+++-+-112111ε<+<⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--+++⎪⎭⎫ ⎝⎛+-+-+=11111312111n p n p n n n n . （2）若p 为偶数，则()pn n n p +-+++-+-112111 ε<+<+-⎪⎪⎭⎫ ⎝⎛-+--+--⎪⎭⎫ ⎝⎛+-+-+=1111121312111n p n p n p n n n n . 所以，()∑-nn 1收敛.2. 取210=ε，0>∀N ，总存在正整数N n >0，00n p =，则000000021212121212111ε==++>+++++n n n n n n . 所以，∑n 1发散.【例2】讨论∑n1cos ln 的敛散性. 【提示】利用同阶无穷小.【解】由于 21cos 2sin limcos ln lim 020==-→→x x x xx x x ，所以 2111cosln lim 2=-→∞nn n ，又∑n21收敛，所以，∑n1cos ln 收敛. 【例3】证明：∑⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-n n11ln 1 收敛. 【证明】由nn n 111ln 11<⎪⎭⎫ ⎝⎛+<+，得 ()()nn n n n n n n n 23111111111ln 10<+++=+-<⎪⎭⎫ ⎝⎛+-<，而∑n231收敛，故∑⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+-n n 11ln 1 收敛. 【例4】设()x f 1在],[b a 上黎曼可积，令()()t t f x f xann d 1⎰=+， ,2,1=n 证明：(){}x f n在],[b a 上一致收敛于0（清华大学2003年硕士研究生入学试题）.【证明】由于()x f 1在],[b a 上黎曼可积，从而在],[b a 上有界，即存在0>M ，使得()M x f ≤1，从而有()()()a x M t t f x f xa -≤≤⎰d 12，()()()()22321d d a x M t a t M t t f x f xax a-=-≤≤⎰⎰，依次可推出()()()!11--≤-n a x M x f n n ，所以有()()()!11--≤-n a b M x f n n .易证正项级数()()∑---!11n a b n 收敛，由级数收敛的必要条件可知()()0!1lim 1=---∞→n ab n n ，故(){}x f n 在],[b a 上一致收敛于0.【例5】设t t nt t a n d sin sin 320⎰⋅=π，证明∑∞=11n na 发散（2009年首届中国大学生数学竞赛（数学专业）赛区试题）.【证明】213230320d sin sin d sin sin d sin sin I I t t ntt t t nt t t t nt t nn +=⋅+⋅=⋅⎰⎰⎰ππππ.2d d sin sin 2203301n t t n t t nt t I n πππ=<⋅=⎰⎰, 828d 2d sin sin 2332322n n t t t t t nt t I nn πππππππππ<⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛⋅<⋅=⎰⎰.因此，n a n π211>，由此得∑∞=11n na 发散. 【例6】设f 在0=x 的某邻域内有定义，()0f ''存在，证明：∑⎪⎭⎫⎝⎛n f 1绝对收敛的充要条件是()()000='=f f （南京大学2002年硕士研究生入学试题）.【证明】充分性. 由于()0f ''存在，故()()()()()02120lim 2lim lim 0020f x f x f x x f xx f x x x ''='-'='=→→→.从而，()()02111lim2f nn f n ''=∞→，而∑n21收敛，因此，∑⎪⎭⎫⎝⎛n f 1绝对收敛. 必要性. 由∑⎪⎭⎫ ⎝⎛n f 1绝对收敛可知，01lim =⎪⎭⎫ ⎝⎛∞→n f n ，又由于f 在0=x 处连续，故()00=f . 又()()()()x x f x f x f f x x 00lim 0lim 0→→=-='，从而有()01lim f n nf n '=⎪⎭⎫ ⎝⎛∞→，由于∑⎪⎭⎫⎝⎛n f 1绝对收敛，所以().00='f 【例7】设(){}x f n 是定义在],[b a 上的无穷次可微函数序列且逐点收敛，并在],[b a 上满足()M x f n ≤'.1. 证明：(){}x f n 在],[b a 上一致收敛；2. 设()()x f x f n n ∞→=lim ，问()x f 是否一定在],[b a 上处处可导，为什么（2009年首届中国大学生数学竞赛（数学专业）赛区试题）？【证明】1. 0>∀ε，将区间],[b a 分成K 等份，分点为()Ka b j a x j -+=，K j ,,2,1 =，使得ε<-Kab . 由于(){}x f n 在有限个点{}K j x j ,,2,1, =上收敛，因此N n m N >>∀>∃,0，使得()()ε<-j n j m x f x f 对每个K j ,2,1=都成立，于是，],[b a x ∈∀，设],[1+∈j j x x x ，则()()()()()()()()x f x f x f x f x f x f x f x f n j n j n j m j m m n m -+-+-≤-()()()()()()()εηξ12+<-'+-+-'=M x x f x f x f x x f j n j n j m j m. 因此，(){}x f n 在],[b a 上一致收敛.2. 不一定. 令()nx x f n 12+=在]1,1[-上满足题中条件，但是()()x x f x f n n==∞→lim 在]1,1[-上不能保证处处可导（在0=x 处就不可导）.【例8】证明：函数()∑=nnx x f 3sin 在()+∞∞-,上连续，且有连续的导函数.【证明】由于对()+∞∞-∈∀,x ，有nnnx 331sin ≤， ,2,1=n且级数∑n31收敛，故由优级数判别法知∑nnx 3sin 在()+∞∞-,上一致收敛.又n nxn nx 23cos sin ='⎪⎭⎫ ⎝⎛，而n n nx 221cos ≤，() ,2,1,,=+∞∞-∈n x ，由∑n21收敛知∑nnx 2cos 在()+∞∞-,上一致收敛. 又nnx 2cos () ,2,1=n 在()+∞∞-,上连续，从而由可积性定理知()x f 在()+∞∞-,上具有连续的导函数，从而()x f 也在()+∞∞-,上连续.【例9】将所有有理数排成一个数列{}n r ，试讨论函数()()∑-=2sng nn r x x f 的连续性（厦门大学2006年硕士研究生入学试题）.【解】因为()212sng nnn r x ≤-，且∑21n收敛，故由优级数判别法知()∑-2sng nn r x 在R 上一致收敛. R 0∈∀x ，当{}n r x ∉0时，通项()2sng nn r x -在0x x =处连续，由一致收敛函数项级数的和函数连续性定理知，()x f 在0x x =处连续. 当{}n k r r x ∈=0时，因为()()()2sng 2sng kk kn nn r x r x x f -+-=∑≠，右边第一项在k x x =处连续，第二项在k x x =处间断，因此()x f 在k x x =处不连续. 综上所述，()x f 在所有无理点处连续，在所有有理点处不连续.【例10】求下列级数的收敛域：1. ()()n x x n n 2111+++∑； 2. .113212nn n x x n ⎪⎭⎫⎝⎛+-++∑ 【解】1. 令x x y 21++=，则原级数为()y n n n ∑+11，易求得其收敛域为[]1,1-，即当1112≤++≤-x x 时，原级数收敛，解次不等式得01≤≤-x . 因此原级数的收敛域为[].0,1-2. 令x xy +-=11，则原级数为y nn n n ∑++2321. 由于3321lim 2=++∞→n n nn n，所以幂级数y n n n n ∑++2321的收敛半径为31，易求得其收敛域为⎥⎦⎤⎢⎣⎡-31,31，因此当311131≤+-≤-x x 时，原级数收敛，解不等式得 221≤≤x ，故原级数的收敛域为⎥⎦⎤⎢⎣⎡2,21. 【例11】设有幂级数x n nnn n ∑∞=⎪⎭⎫ ⎝⎛+1221，求1. 收敛半径与收敛域.2. 和函数在收敛域内的导函数.【解】1. 由于n n nn n n22n 21222n ≤+≤，且222lim 2lim 2==→∞→∞n n n n n n ，故2n 21lim 2n=+→∞n n n ，因此收敛半径为21=R . 当21±=x 时，级数∑∑∞=∞=⎪⎭⎫ ⎝⎛+⋅=⎪⎭⎫ ⎝⎛±⎪⎭⎫ ⎝⎛+12121212121n n n nn n n n n 收敛，故收敛域为.21,21⎥⎦⎤⎢⎣⎡- 2. 令()x n nx f n n n ∑∞=⎪⎭⎫ ⎝⎛+=1221，.21,21⎥⎦⎤⎢⎣⎡-∈x 因为 ()∑∞=-=-11ln n n n xx ，[).1,1-∈x故 ()()().21ln 11211121111xx x nx x x x n x f n nn n n---=+-=⎪⎭⎫⎝⎛+='∑∑∞=-∞= 【例12】求幂级数()∑∞=+11n nxn n 的收敛域及和函数.【解】由于 ()11lim =+→∞nn n n ，故()∑∞=+11n n x n n 的收敛半径为1=R ，又当1±=x 时，级数()()∑∞=±+111n nn n 发散，因此，()∑∞=+11n nxn n 的收敛域为()1,1-.令()()∑∞=-+=111n n xn n x f ，()1,1-∈x ，则由幂级数的逐项可积性，得()()()∑∑⎰⎰∞=∞=-+=+=11011d 1d n n n x n xx n t tn n t t f .()().1d 1d 1211101xx xt t n t tn n n n xnx n n-==+=+∑∑⎰⎰∑∞=∞=+∞= 所以， ()()22211211x x x x x x n n n --='⎪⎭⎫ ⎝⎛-=+∑∞=，()()()2221212x x x x x f -='⎪⎪⎭⎫ ⎝⎛--=，因此()()()21121x xx xf xn n n n-==+∑∞=. 【例13】求级数()∑∞=+1!1n n n的和. 【解】令()()x n n x f nn ∑∞=+=1!1，易求得该幂级数的收敛域为()+∞∞-,. 由幂级数的逐项求导和逐项积分性质，有()()()∑∑∞=∞==--=-='11e !11!1n x n n n x n x x n x x f . 故 ()()e x t e t x f x xt 11d 0-+==⎰. 从而有()().11!11==+∑∞=f n nn【知识扩展提示】利用幂级数求数项级数的和，要记住几个基本幂级数展开式.【例14】将下列函数在0=x 处展成幂级数： 1. ()t ttx f xd sin 0⎰=； 2. ()()x x f 22ln +=. 【解】1. 因为()()!121sin 120+-=+∞=∑n t t n n n，R t ∈，从而()()!121sin 20+-=∑∞=n t t t nn n ，于是()()()()()()∑∑⎰⎰∞=+∞=+⋅+-=+-==0120020!12121d !121d sin n n n n x n n xn n x t n t t t t x f ，R x ∈ 2. 因为()()nxx nn n ∑∞=--=+1111ln ，(]1,1-∈x ，所以。

第七章无穷级数2010

n=1 ∞
叫做级数的一般项一般项, 称上式为无穷级数，称上式为无穷级数，无穷级数其中第 n 项 un 叫做级数的一般项级数的前 n 项和
机动
目录
上页
下页
返回
结束
称为级数的部分和称为级数的部分和. 部分和为级数的和收敛 , 并称 S 为级数的和, 记作
则称无穷级数
则称无穷级数发散则称无穷级数发散 .
机动
目录
上页
下页
返回
结束
判别下列级数的敛散性: 例1. 判别下列级数的敛散性
解: (1)
2 4 n +1 3 Sn = ln + ln + ln +L+ ln 1 3 n 2
= (ln 2 − ln1) + (ln3 − ln 2) +L+ (ln(n +1) − ln n)
= ln(n +1) → ∞ ( n → ∞）
机动目录上页下页返回结束
两个重要级数：
1、等比级数
q <1 q ≥1
收敛， p > 1
2、p 级数
发散， p ≤ 1 发散。
特殊地，p=1时，调和级数
机动
目录
上页
下页
返回
结束
调和级数与 p 级数是两个常用的比较级数. 若存在 N ∈Z + , 对一切 n ≥ N ,
机动
目录
上页
下页
返回
∞ n−1 1
例如：∑(−1)
n=1
n
为条件收敛 .
为绝对收敛.
机动
目录
上页
下页
返回
结束
定理5. 定理绝对收敛的级数一定收敛 . 证: （不要求）设收敛 ,

第七章无穷级数资料

第七章无穷级数(无穷离散量之和的数学模型)无穷级数的理论在高等数学中占有重要地位。

它是与数列、极限密切相关的一个概念，它几乎与微积分同时诞生，牛顿就曾把二项式级数作为研究微积分的工具；为了解决微积分诞生时混乱的逻辑基础，拉格朗日也曾试图用无穷级数重建微积分理论，但由于当时对无穷级数认识的粗糙性，均未获成功。

无穷级数之所以难以捉摸是由于它与无穷（或无限）纠缠在一起。

随着运动和变量进入数学，无穷这个孪生鬼怪也同时降生，当时的数学家尽量避免无限，免得像阿基里斯追不上兔子一样困惑恼人。

直到19世纪中叶，才由大数学家Cauchy 揭开了无限的面纱，建立起无穷级数的严格理论。

所谓无穷级数就是无穷多个数或函数之和，它是研究无限离散量之和的数学模型，是人们认识客观事物间数量关系的一个很重要的数学工具，是数学分析的重要内容之一，是现代数学的重要方法已被广泛应用到了数学自身，以及自然科学和社会科学的各个领域。

它是高等数学中研究函数性质的一个重要工具，它可以表达一个函数（或数），也可以将一些复杂的量表示成简单量的无穷和，从而得到复杂量实用的近似计算公式。

我们将利用无限与有限的辩证关系，以极限为工具建立级数理论。

我们将级数分为两大类来研究，常数项级数（也简称为数项级数）和函数项级数，我们先介绍数项级数。

§1 常数项级数的概念与性质一、数项级数的概念1、实例已知线段AB ，设其长为S ，取A 1为AB 的中点，A 2为A 1B 的中点，…，依次取下去，A n 为A n-1B 的中点，则n 可无限增大，记各线段长度为,,,,,122111 n n n a A A a A A a AA ===- 则得各部分线段的长度数列,,,,21n a a a ，其中S a n n 21=. 将这无穷多个数依次用加号连接，得到的应是线段的总长度表达式++++=n a a a S 21.这里出现了无穷多个数依次相加的式子，在物理、化学等许多学科中，常能遇到这种无穷多个数或函数相加的情形，在数学上给出其定义，即2、定义1 设有数列}{n u ，则称式子++++n u u u 21为（常数项）无穷级数，简称为（数项）级数，其中依次叫做级数的第1项，第2项，…，un 又叫做级数的一般项或通项，利用通项级数可简记为∑∞=1n n u ，即++++=∑∞=n n n u u u u 211. (1) 例如+++++n 21814121——等比(或几何)级数， n n u 21=，即有 ∑=∞=121,21,,81,41,21n n n .++++n 21 ， n u n =，即有 ∑=++++=nn n n 121 .+-+-1111———波尔察诺级数， 1)1(+-=n n u ，即有 ∑-=+-+-∞=+11)1(1111n n .注我们只有有限多个数相加的定义，并没有无穷多个数相加的定义，因而上述定义只是形式上的定义，例如波尔察诺级数：设 +-+-+=11111x ，则 0)11()11(=+-+-= x ；1)11()11(1=-----= x ； 211)1111(1=⇒-=+-+--=x xx .没有一个确定的数值与之对应，这是数学的精确度不可靠，还是解法有问题？是Cauchy 指出以上解法犯了“墨守成规”的错误，即把“有限运算的结合律以及有限项相加总存在和”等观念照搬到无限项的运算中去了，这一论断澄清了当时对无限运算的糊涂观念。

无穷级数

第七讲无穷级数一、主要知识点（一）常数项级数1．数项级数的概念（1）无穷级数定义：121n n n u u u u ∞==++++∑ ．（2）敛散性定义：若S S n n =∞→lim (有限)，则级数∑∞=1n n u 收敛，其和为∑∞==1n nuS ．若n n S ∞→lim 不存在，则∑∞=1n n u 发散，没有和．2．数项级数的性质（1）级数∑∞=1n n u 与∑∞=1n n ku 有相同的敛散性)0(≠k ．（2）设级数∑∞=1n n u 及∑∞=1n n v ，则若S u n n =∑∞=1，σ=∑∞=1n n v ，则σ±=±∑∞=S v u n n n )(1；若∑∞=1n n u 收敛，∑∞=1n n v 发散，则)(1∑∞=±n n n v u 发散；若∑∞=1n n u ,∑∞=1n n v 均发散，则)(1∑∞=±n n n v u 敛散性不能确定．（3）在级数∑∞=1n n u 中添加、去掉或改变有限项不影响级数∑∞=1n n u 的敛散性．（4）设级数∑∞=1n n u 收敛，则对其各项任意加括号后所得新级数仍收敛于原级数的和．（5）级数∑∞=1n n u 收敛的必要条件：0lim =∞→n n u ．3．正项级数∑∞=1n n u )0(≥n u 判敛法（1）收敛的基本定理：正项级数∑∞=1n n u 收敛的充分必要条件是部分和数列}{n S 有上界．（2）比较判别法1：设级数∑∞=1n n u ,∑∞=1n n v 均为正项级数，若存在N ，当N n >时，有n n v u ≤≤0成立，则1）若级数∑∞=1n n v 收敛，则级数∑∞=1n n u 收敛．2）若级数∑∞=1n n u 发散，则级数∑∞=1n n v 发散．（3）比较法的极限形式2：设级数∑∞=1n n u ，∑∞=1n n v 均为正项级数，且limn n nu A v →∞=(0)n v ≠，则1）当+∞<<A 0，则级数∑∞=1n n u 与级数∑∞=1n n v 敛散性相同．2）当0=A ，若级数∑∞=1n n v 收敛，则级数∑∞=1n n u 收敛．3）当+∞=A ，若级数∑∞=1n n v 发散，则级数∑∞=1n n u 发散．常用作比较的级数：几何级数⎪⎩⎪⎨⎧-=∑∞=发散,10q aaqn n1||1||≥<q q ； -p 级数⎩⎨⎧=∑∞=发散收敛11n pn11≤>p p ；调和级数+++=∑∞=3121111n n是发散的．注意：若级数的分母、分子关于n 的最高次数分别为p 和q ，即1qpn n n αβ∞=++∑（其中,αβ为含n 的次数分别低于,p q 的多项式），则当1p q ->时级数收敛，当1p q -≤时级数发散．（4）比值判别法（达朗贝尔判别法）（适用于n u 中含有!n ,nn 及na 等因子）：设级数∑∞=1n n u (0≥n u )，若ρ=+∞→nn n u u 1lim，则11111n n n n u u ρρρ∞=∞=⎧>⎪⎪⎪<⎨⎪⎪=⎪⎩∑∑若，则级数发散若，则级数收敛若，方法失效．（5）根值判别法（柯西判别法）（适用于n u 含有以n 为指数幂的因子）：设级数∑∞=1n n u (0≥n u )，若ρ=∞→nnn u lim，则11111n n n n u u ρρρ∞=∞=⎧>⎪⎪⎪<⎨⎪⎪=⎪⎩∑∑若，则级数发散若，则级数收敛若，方法失效．注意：根值法，比值法条件是充分条件而非必要条件．（6）拉阿伯判别法：设级数∑∞=1n n u (0n u >)，若1lim (1)n n n u n u ρ→∞+-=，则11111n n n n u u ρρρ∞=∞=⎧>⎪⎪⎪<⎨⎪⎪=⎪⎩∑∑若，则级数收敛若，则级数发散若，方法失效．（7）柯西积分判别法：若函数()(0)f x x >是非负的不增函数，则级数1()n f n ∞=∑与广义积分1()f x dx +∞⎰同时收敛或同时发散．例如：级数11pn n∞=∑；21(l n )pn n n ∞=∑；21l n (l n )pn n n n ∞=∑与广义积分1pdx x+∞⎰；2(l n )pdx x x +∞⎰；2l n (l n)pdx x x x +∞⎰当1p >时同时收敛，当1p ≤时同时发散．4．一般项级数判敛法（1）交错级数)0()1(11≥-∑∞=-n n n n u u 莱布尼兹判敛法：若交错级数∑∞=--11)1(n n n u ，满足条件1）1,(1,2,)n n u u n +≤= ；2）0lim =∞→n n u ，则交错级数∑∞=--11)1(n n n u 收敛，且其和1u s ≤，余项1+≤n n u R ．注意：证明比较n u 与1+n u 大小的方法有三种：1）比值法：考查11<+nn u u ；2）差值法：考查01<-+n n u u ；3）由一般项n u 找出连续可导函数)(x f ，使)(n f u n =，考查导数0)(<'x f ，函数)(x f 就是单调减少，则有n n u u <+1．（2）亚伯耳判敛法：级数1nn n uv ∞=∑(其中,n n u v 为实数)满足条件1）级数1n n u ∞=∑收敛，2）{}n v 为单调有界数列，则级数1n n n u v ∞=∑收敛．（3）狄里克利判敛法：级数1nn n uv ∞=∑(其中,n n u v 为实数)满足条件1）部分和数列1nn ii S u==∑有界，2）当n →∞时，n v 为单调趋向于零，则级数1n n n u v ∞=∑收敛．（4）绝对收敛与条件收敛判别：绝对收敛：若级数∑∞=1||n n u 收敛，则称级数∑∞=1n n u 为绝对收敛．条件收敛：若级数∑∞=1||n n u 发散，而级数∑∞=1n n u 收敛，则称级数∑∞=1n n u 为条件收敛．若级数∑∞=1||n n u 收敛，则级数∑∞=1n n u 收敛，反之不一定成立．如∑∞=-1)1(n nn．注意：若用比值法（或根植法）判定级数∑∞=1||n n u 发散，则级数∑∞=1n n u 一定发散．（二）幂级数1．幂级数的收敛区间设幂级数∑∞=0n n n x a ，若1lim ||n n na a ρ+→∞=（或limn ρ→∞=，则收敛半径1,0,00,R ρρρρ⎧≠⎪⎪⎪=+∞=⎨⎪=+∞⎪⎪⎩当时当时当时．收敛区间[],R R -、(,)R R -、[,)R R -、(,]R R -四种情况之一．注意：若幂级数为∑∞=022n nn xa 或∑∞=++01212n n n x a （即缺少项的幂级数）时，应如何求收敛半径？2．幂级数的和函数（1）幂级数和函数的性质：设幂级数∑∞=0n n n x a 的和函数()S x 在区间收敛区间(,)R R -内连续、可导、可积，且可逐项求导、逐项积分，即11()(),(,)n n nn n n S x ax na xx R R ∞∞-==''==∈-∑∑，1(),(,)1x x nn n n n n a S x dx a x dx xx R R n ∞∞+====∈-+∑∑⎰⎰．（2）幂级数和函数的求法： 1）求出给定幂级数的收敛域；2）通过加、减、逐项积分或微分、变量代换（如：以x -代替x ，以2x 代替x ）等运算，将给定的幂级数化为常见函数展开式的形式，如：① 当所给的幂级数系数的分母出现!n 时，常常转化到xe 的展开式；② 当所给的幂级数系数出现)!2()1(n n-或1(1)(21)!n n +-+时，常常转化到x cos 或x sin 的展开式；③ 当系数是n 的多项式时，常常通过幂级数的加、减、逐项积分或微分运算，转化到等比级数xx n n -=∑∞=110，从而得到新的幂级数的和函数．3）对于得到的和函数再做相反的分析运算，便得原幂级数的和函数．3．函数的幂级数展开（1）泰勒级数：nn n x x n x f)(!)(000)(-∑∞=；（2）麦克劳林级数：()(0)!n nn fx n ∞=∑．（3）函数展开成幂级数1）展开式的唯一性：无论用什么方法将函数展为幂级数的展开式是唯一的； 2）展开的条件：函数在某点0x 的邻域内有任意阶导数；3）展开的方法：直接展开法与间接展开法．（4）直接展开法：利用泰勒级数nn n x x n x f)(!)(000)(-∑∞=，按下列步骤将函数)(x f 在点0x 展开．1）先求出函数)(x f 的各阶导数在0x x =处的值)(0x f ，0()f x '()00()()n f x fx ''再写出级数nn n x x n x f)(!)(000)(-∑∞=；2）写出拉格朗日余项)!1())(()(10)1(+-=++n x x fx R n n n ξ ，证明lim ()n n R x →∞是否趋于零，若lim ()0n n R x →∞=，则nn n x x n x fx f )(!)()(000)(-=∑∞=，即函数)(x f 在0x 处能展开成泰勒级数．3）求出收敛区间．（5）间接展开法：利用下面已知的6个函数的展开式，通过适当的变量代替，四则运算，复合及逐项积分、微分运算将一个函数展开成幂级数——间接展开法．常用的函数展开式1）23011,(1,1)1nnn x x x x x x x ∞==++++++=∈--∑；2）23011(1)(1),(1,1)1n nnnn x x x x x x x∞==-+-++-+=-∈-+∑ ；3）231111,(,)2!3!!!nxnn xe x x x x x n n ∞==++++++=∈-∞+∞∑；4）212135011sin (1)(1),(,)3!5!(21)!(21)!n n nnn xxx x x x x n n ++∞==-+-+-+=-∈-∞+∞++∑ ；5）2224011cos 1(1)(1),(,)2!4!(2)!(2)!nnnnn xxx x x x n n ∞==-+-+-+=-∈-∞+∞∑ ；6）1231111(1)ln(1)(1),(1,1]23nn nn n xxx x x x x nn-∞-=-+=-+-+-+=∈-∑；7）2(1)(1)(1)(1)1,2!!nn x x x x n ααααααα---++=+++++1(1)(1)1,(1,1)!nn n x x n ααα∞=--+=+∈-∑．（三）傅里叶级数1．周期函数的傅立叶级数（1）以2π为周期函数：设)(x f 在区间],[ππ-上是可积函数， ⎰-==πππ),2,1,0(,c o s )(1n n x d x x f a n ⎰-==πππ),2,1(,sin )(1n nxdx x f b n则称级数∑∞=++10)sin cos (2n n nnx b nx aa为函数)(x f 的傅里叶级数，称n n b a ,为傅里叶系数．（2）以2l 为周期函数：设)(x f 在区间],[l l -上是可积函数， ⎰-==l l n n dx l x n x f l a ),2,1,0(,cos )(1 π ⎰-==l ln n dx lx n x f lb ),2,1(,sin)(1 π则称级数∑∞=++10)sincos(2n n n lx n b lx n a a ππ为函数)(x f 的傅里叶级数，称n n b a ,为傅里叶系数．2．傅立叶级数收敛定理设函数)(x f 满足狄里克雷条件1）在区间],[l l -上连续或只有有限个第一类间断点； 2）在区间],[l l -上只有有限个极值点，则傅里叶级数∑∞=++10)sincos(2n n n lx n b lx n a a ππ在区间],[l l -上收敛，并且其和函数)(x f 有1）当x 为)(x f 连续点时，∑∞=++10)sincos(2n n n lx n b lx n a a ππ)(x f =；2）当x 为)(x f 间断点时，∑∞=++10)sincos(2n n n l x n b l x n a a ππ2)0()0(++-=x f x f ；3）当x 为)(x f 端点时，∑∞=++10)sincos (2n n n lx n b lx n a a ππ2)0()0(-++-=l f l f ．3．奇偶函数展开为傅立叶级数正弦级数：nx b n n sin 1∑∞=，其中⎰=ππsin )(2nxdx x f b n ，1,2,n = ；余弦级数：nx a a n n cos 210∑∞=+，其中⎰=ππcos )(2nxdx x f a n ，1,2,n = ．二．例题分析1．判别常数项级数敛散性例1．设∞=∞→n n a lim ，且0≠n a ，判别级数∑∞=+⎪⎪⎭⎫⎝⎛-1111n n na a 的敛散性．解：令111+-=n n n a a u ，则前n 项的部分和111322111)11()11()11(++-=-++-+-=n n nn a a a a a a a a S ，因为01lim1=+∞→n n a ，所以11lim a S n n =∞→，即原级数收敛且其和11a S =．例2．判别级数下列级数敛散性（1）∑∞=-1)cos1(n nπ；（2）11n ∞=∑（3）若级数)0(1≥∑∞=n n n a a 收敛，则级数∑∞=1n n na 收敛．解：（1）因为nn2sin2cos12ππ=-，所以将其与级数∑∑∞=∞==222212)2(2n n nn ππ比较，又因为 1)2(22s i n2lim222=∞→n nn ππ，所以级数nn 2sin221π∑∞=收敛，从而级数∑∞=-1)cos1(n nπ收敛．（2）将级数1n ∞=∑211n n∞=∑进行比较，即求极限222l i ml i m1(!)n n n n u nn n→∞→∞=，令22(!)n nny n =，则21ln 2ln 2ln !2[ln ln !]n y n n n n nn=-=-12[(l n l n 1)(l nl n 2)(l n l n)]nn nn n=-+-+-112l nni i n n==-∑，于是 1011l i m l n 2l i ml n 2l n l n 2nn n n i i y xdx n n→∞→∞==-=-=∑⎰，所以 2l i m n n y e →∞=，因此由级数∑∞=121n n收敛得到级数1n ∞=∑（3）由于)1(21122na na na n n n +≤⋅=，而且级数∑∞=1n n a 与级数∑∞=121n n均收敛，所以级数∑∞=1n n na 收敛．练习题：判别级数的敛散性（1）)0,0(1>>∑∞=s a na n sn ；当1<a 时，级数收敛，当1>a 时，级数发散，当1=a 时，级数为∑∞=11n sn，这是p 级数，当1>s 时收敛，当1≤s 时发散．（2）∑∞=1!3n nnnn ；（发散）（3）)0(111>+∑∞=a an n；（1>a 收敛，1≤a 发散）（4）∑∞=1233cosn nn n π；(收敛) （5）∑∞=+-+111)1(n n n n n．（收敛）例3．判别下列级数敛散性，若收敛是绝对收敛还是条件收敛？（1）1)1ln()1(1++-∑∞=n n n n；（2）1!(1)nnnn e n n∞=-∑；（3）当k 为何值时，级数221(1)(ln )nkn n n ∞=-∑收敛，是绝对收敛，还是条件收敛？解：（1）先考虑正项级数1)1ln(1++∑∞=n n n ．将级数1)1ln(1++∑∞=n n n 与级数111+∑∞=n n 进行比较，因为)2(,1)1l n (11>++<+n n n n ，由级数111+∑∞=n n 的发散，即可得级数1)1ln(1++∑∞=n n n 发散，但是交错级数1)1ln()1(1++-∑∞=n n n n，满足条件：1）ln(1)ln(1)1limlimlim0111n x x n x n x x →∞→+∞→+∞++===+++，2）n n u u <+1，证明之，令 1)1l n ()()(++===x x x f n f u n ，因为导数1ln(1)()0,(3)1x f x x x -+'=<≥+，所以函数)(x f 当3≥x 时，是单调减少的，从而 n n u u ≤+1，),4,3( =n ，于是，由莱布尼兹判别法知级数1)1ln()1(1++-∑∞=n n n n条件收敛．（2）先考虑正项级数1!nnn e n n∞=∑，因为111(1)!(1)1!(1)n n n nnnnen u e n e n u nn+++++==+，而1(1)ne n+<，所以11(1,2,)n nu u +> ，于是11n n u u u e ->>>= ，则lim 0n n u →∞≠，从而lim (1)0n n n u →∞-≠，故原级数1!(1)nnnn e n n∞=-∑发散．（3）当1k ≥时，22110ln ln kn nn n<≤，由级数221ln n n n∞=∑收敛得到级数221ln kn n n∞=∑收敛，所以当1k ≥时，级数221ln kn n n ∞=∑绝对收敛；当01k ≤<时，由于211ln k n nn>，由级数21n n∞=∑发散得到级数221ln kn n n∞=∑发散，由因为21ln n ku n n=单调减少，且21lim0ln kn n n→∞=，2莱布尼茨判别法知级数221(1)(ln )nkn n n ∞=-∑收敛，于是级数221(1)(ln )nkn n n ∞=-∑条件收敛；当0k <时，由于21lim0ln kn n n→∞=∞≠，则级数221(1)(ln )nkn n n ∞=-∑发散．练习题：判断下列级数的敛散性，若收敛则说明是绝对收敛还是条件收敛？（1）1ln (1)nn n n∞=-∑；（条件收敛）（2）11(1)(1)!n nn nn +∞=-+∑．（发散）例4．设1211211212345632313n u n n n=+-++-+++--- ，111123n v n n n=++++ ，求（1）1010u v ；（2）lim n n u →∞．解：因为1211211212345632313n u n n n=+-++-+++---11111111234532313n n n =++++++++-- 21212121[()()()()]33669933n n -++++++++111111111(1)2345323n n =++++++-++++ ，所以（1）10111111121330u =++++，10111111121330v =++++，于是10101u v =；（2）由于当n →∞时，1111ln 23n C n++++-→ （0.577216C ≈称欧拉常数），则有1111ln 23n C n nε++++=++ ，（其中n ε为无穷小）于是 111111111(1)2345323n u n n=++++++-++++ l n 3(l n )n n C n C n τε=++-++，（其中,n n τε为无穷小） 3lnn n n nτε=+-，故3lim lim [ln]ln 3n n n n n n u nτε→∞→∞=+-=．2．求幂级数收敛域、收敛区间例5．求下列幂级数的收敛域（1）nn x n n ∑∞=12)!2()!(；（2）nn n xn n 212)1(∑∞=-+；（3）∑∞=--1)21(2)1(n nnnx n；（4）∑∞=+⨯+1129)13(n nn n x ．解：（1）因为4121)12(1lim)!2()!()!22(])!1[(limlim221=++=++==∞→∞→+∞→n n n n n n a a n n nn n ρ，所以收敛半径为4=R ．当4=x 时，原级数为∑∞=124)!2()!(n nn n ，令nn n n b 4)!2()!(2=，因为112221>++=+n n b b nn ，则0211>=>>>-b b b n n ，所以0lim ≠∞→n n b ，因此级数发散；当4-=x 时，原级数为∑∞=-12)4()!2()!(n nn n ，由于0lim ≠∞→n n b ，所以0)1(lim ≠-∞→n nn b ，因此级数发散，于是级数nn x n n ∑∞=12)!2()!(收敛域为)4,4(-．（2）令t x =2，则nn n t n n 2)1(1∑∞=-+=nn t nn ∑∞=++112，因为 221121111lim22121lim1=+++++=+++++=∞→+∞→nnn n n n n n nn n ρ，所以级数nn t nn ∑∞=++112的收敛半径为12R '=，从而级数nn n xn n 212)1(∑∞=-+的收敛半径为21=R ，当21±=x 时，级数∑∑∞=∞=++=++1111)21(12n nn nnn n n 发散，因此原幂级数的收敛域为)21,21(-．（3）令t x =-21，则=--∑∞=1)21(2)1(n nnnx n∑∞=-12)1(n nnnt n，因为 2112lim212lim1=+=+=∞→+∞→nnn n nn n ρ，所以幂级数12(1)nnnn ∞=-∑的收敛半径为12R '=，从而原级数∑∞=--1)21(2)1(n nnnx n的收敛半径为21=R ，当21-=x 时，级数∑∑∞=∞==--111)21(2)1(n n nnnnn 发散；当21=x 时，级数∑∑∞=∞=-=-11)1()21(2)1(n nn nnnnn 收敛，因此幂级数1(1)nnnn ∞=-∑的收敛域为]21,21(-．又因为t x =-21，则212121≤-<-x ，从中解出10≤<x ，于是原级数∑∞=--1)21(2)1(n nnnx n的收敛域为]1,0(．（4）设nn n n x x u 9)13()(12++=，因为由比值法211232|13|919)1(|13|9|13|lim)()(lim)(+=+++==+++∞→+∞→x n x n x x u x u x n n n n n n n n ρ，所以，当1|13|91)(2<+=x x ρ，即3234<<-x 时，原级数绝对收敛；当1|13|91)(2<+=x x ρ，即34-<x 或32>x 时，原级数发散；又当34-=x 时，原级数为∑∞=-13n n发散；当32=x 时，原级数为∑∞=13n n发散，因此该幂级数的收敛域为)32,34(-．练习题：求下列幂级数的收敛半径及收敛域1．11(3(2))nnnn x n ∞=+-∑；（[,3)-） 2．12141-∞=∑n n nxn ；（)2,2(-）3．∑∞=-⨯--1215)2()1(n nnn n x ．(]52,52[,5+-=R )例6．设111123n u n=++++，求幂级数1nn nxu ∞=∑的收敛半径、收敛区间及收敛域．解：因为1111111123limlimlim11111231n n n n n nn u n u u u n ρ→∞→∞→∞++++++====+++++ ，所以收敛半径为1R =，收敛区间为收敛区间（－1,1）．当1x =-时，级数1(1)nn nu ∞=-∑为交错级数，且1111lim0,n nnn u u u →∞+=>，由莱布尼茨判别法知级数1(1)nn nu ∞=-∑收敛；当1x =时，由于2n u n <，即有112nu n>，所以级数11n nu ∞=∑，于是幂级数1nn nxu ∞=∑的收敛域为[1,1)-．3．幂级数的求和（1）求出给定幂级数的收敛域；（2）通过加、减、逐项积分或微分、变量代换（如：以x -代替x ，以2x 代替x ）等等运算，将给定的幂级数化为常见函数展开式的形式，如：① 当所给的幂级数系数的分母出现!n 时，常常转化到x e 的展开式；② 当所给的幂级数系数出现)!2()1(n n-或)!12()1(1---n n 时，常常转化到x cos 或x sin 的展开式；③ 当系数是n 的多项式时，常常通过幂级数的加、减、逐项积分或微分运算，转化到等比级数xx n n -=∑∞=110，从而得到新的幂级数的和函数；（3）对于得到的和函数再做相反的分析运算，便得原幂级数的和函数．例7．求下列幂级数的和函数（1）)1(21212-∞=∑-n n nxn ；（2）∑∞=+1)1(n nn n x；（3）20(2)!nn xn ∞=∑；（4）求nn x n n ∑∞=+1!1的和函数，并由此求nn n n 8!11∑∞=+之值．解：（1）先求收敛域因为2222211211212lim21)12(2212limlimx xn n xn xn u u n n nnn n nn n =-+=-+==∞→-+∞→+∞→ρ，当1212<=xρ，即2||<x 时，幂级数)1(21212-∞=∑-n n nxn 收敛；当1212>=xρ，即2||>x 时，幂级数)1(21212-∞=∑-n n nxn 发散；当2||±=x 时，幂级数∑∑∞=-∞=-=-1112122212n n n nn n 发散，因此该级数)1(21212-∞=∑-n n nxn 的收敛域为)2,2(-．再求其和函数，当0≠x 时=)(x S )1(21212-∞=∑-n n nxn 211()2n nn x-∞='=∑2112n nn x -∞='⎛⎫= ⎪⎝⎭∑ 2221112()212n n x x xx x ∞='⎛⎫'⎪⎛⎫==⋅ ⎪ ⎪⎝⎭ ⎪- ⎪⎝⎭∑ 222222(2)xx xx '+⎛⎫== ⎪--⎝⎭，)0(≠x 当0=x 时，21)0(=S ．于是该幂级数的和函数为⎪⎪⎩⎪⎪⎨⎧=≠-+=0,210,)2(2)(222x x x x x S ．（2）显然幂级数∑∞=+1)1(n nn n x的收敛区间为]1,1[-，求和函数)(x S ：当0=x 时，0)0(=S ；当0≠x 时，因为 ()1n 1n 1()(1)n nx xxS x n n n +∞∞=='⎛⎫'==⎪+⎝⎭∑∑，且 ()11n 1n111()()(1)1n n n n xxxS x xn n nx+∞∞∞-===''⎛⎫'''====⎪+-⎝⎭∑∑∑，两边积分得 ()01()l n (1)1x x S x d x x x'==---⎰，两边再积分一次得 0()l n (1)(1)l n (1)x x S x x d x x x x=--=---⎰，因此 )1l n ()11(1)(x xx S ---=，于是该幂级数的和函数为⎪⎩⎪⎨⎧=⋃-∈---=0,0)1,0()0,1(),1ln()11(1)(x x x xx S ．（3）级数的收敛域为(,)-∞+∞,令22421()1(2)!2!4!(2)!nnn xxxxs x n n ∞===+++++∑ ，两边求导，得213211()(21)!1!3!(21)!n n n xxxxs x n n --∞='==++++--∑于是有 234212()()1!2!3!4!(21)!(2)!n nx xxxxxs x s x n n -'+=++++++-而23421211!2!3!4!(21)!(2)!n nxx xxxxxe n n -=+++++++-所以()()xs x s x e '+= 这为一阶非齐次线性微分方程，可解得通解为1()2xxs x C ee -=+,由初始条件(0)1s =，得12C =,故 201()(2)!2nx xn xe en ∞-==+∑.（4）先求幂级数nn x n n ∑∞=+1!1的收敛域，因为0)!1(2lim1!)!1(2limlim1=++=+++==∞→∞→+∞→n n n n n n u u n n nn n ρ，所以收敛半径为+∞=R ，收敛区间为),(+∞-∞．再求和函数，因为该幂级数的系数带有!n ，所以它的和函数与指数函数x e 有关．于是 =)(x S nn xn n ∑∞=+1!11111(1)!!nnn n x xn n ∞∞===+-∑∑11111(1)!!n nn n x xx n n ∞∞-===+--∑∑1)1(1-+=-+=xxxe x e xe，),(+∞-∞∈x ，最后取8=x ，得118!nn n n ∞=+=∑198-e ．练习题：求下列幂级数的和函数（1）∑∞=+0)1(n n x n ；（)1,1(,)1(1)(2-∈-=x x x S ）（2）∑∞=+11n nx n n．（⎪⎩⎪⎨⎧=⋃-∈-+-=0,0)1,0()0,1(),1ln(111)(x x x x x x S ）例8．计算下列各题：（1）设幂级数0n n n a x ∞=∑的系数满足012,1,(1,2,)n n a na a n n -==+-= ，求此幂级数的和函数．（2）设12211,1,23,(1)n n n a a a a a n ++===+≥，求幂级数0n n n a x ∞=∑的收敛半径、收敛域及和函数．（3）求级数31()n n x ∞=∑中20x 的系数．解：（1）据题意知1(1)1n n n a a --=-，因此 120111111(1)(1)(1)1!!n n n a a a a nn n n n ---=-=-==-=- ，所以 11!n a n =+，于是为11()(1)!!nnnnnn n n n s x ax xx xn n ∞∞∞∞======+=+∑∑∑∑1||11x e x x=+<-．（2）因为2123n n n a a a ++=+为差分方程，则特征方程为 2230r r --=，其根为123,1r r ==-，所以11123(1)n n n a c c --=+-，由121,1a a ==得12121,31c c c c +=-=，求出1212c c ==，所以111(3(1))2n n n a --=+-．下面讨论级数11111(3(1))2nn n nn n n a x x ∞∞--===+-∑∑，因为 11111(1)33(1)3limlimlim 313(1)1()3nn n n n n n n n n n nu u ρ-+--→∞→∞→∞--++-====+-+-，所以幂级数12(1)nnnn ∞=-∑的收敛半径为12R '=，从而原级数1111(3(1))2n n nn x ∞--=+-∑的收敛半径为13R =，当13x =-时，级数11111(1)1(3(1))()[()]333nn n nnn n ∞∞--==-+--=-∑∑发散；当13x =时，级数111111(1)(3(1))()[]333nn n nnn n ∞∞--==-+-=-∑∑发散，因此幂级数1111(3(1))2n n nn x ∞--=+-∑的收敛域为11(,)33-．设111111111()(3(1))[(3)(1)]223n n nnn nn n n s x x x x ∞∞∞---====+-=+-∑∑∑131(1)61321(13)(1)xxx x xxx x -=+=-+-+，11(,)33x ∈-．（3）因为333311()()()11n n x x x xx∞===--∑，因为230111nnn xx x x x x∞===++++++-∑ ，该式两边两阶导数，得23223243(2)(1)(1)nx x n n x x =+⋅+⋅+++++- 0(2)(1)nn nn x ∞==++∑，于是31(2)(1)(1)2nn n n x x ∞=++=-∑，则3333311(2)(1)()()()112n n n n xn n x x xxx∞∞+==++===--∑∑，故级数31()n n x ∞=∑中20x 的系数为19181712⨯=．4．求数项级数的和方法：1）利用级数收敛的定义：先求出部分和n S ，再求其极限S S n n =∞→lim 为所求；2）引入相应的幂级数：① 找一个幂级数n n n x a ∑∞=1，使n nn u x a =0；② 求幂级数nn n x a ∑∞=1的收敛区间(,)R R -，若当0(,)x R R ∈-时，幂级数01nn n a x ∞=∑收敛，则∑∞=1n n u 也收敛；③ 求出幂级数n n n x a ∑∞=1的和函数)(x S ，再让x 在收敛区间内取个特定的值0x x =，即可求出其和．例9．求下列数项级数的和：（1）1n S ∞==∑；（2）∑∞==12n nnS ；（3）∑∞=12!n n n；（4）01(1)(21)!nn n n ∞=+-+∑．解：（1）因为)1()12(+-++-+=n n n n u n ，所以+-+-+-+-=+++=)]32()34[()]21()23[(21n n u u u S+--+-+++-+-+)]1()1[()]43()45[(n n n n)]1()12[(+-++-++n n n n)12(21+-++-=n n12121++++-=n n ．因此该级数的和∑∞=++-+=1)122(n n n n S 21lim -==∞→n n S ．（2）解：设幂级数nn x n ∑∞=1，只要求出幂级数n n x n ∑∞=1在点210=x 收敛，且其和即为数项级数∑∞==12n nnS 的和．显然级数n n x n ∑∞=1的收敛区间为)1,1(-，和函数1111()()nn nn n n S x nxx nxx x ∞∞∞-==='===∑∑∑211(1)n n x x x x x x x ∞=''⎛⎫⎛⎫===⎪ ⎪--⎝⎭⎝⎭∑．当21=x 时，∑∞==12)21(n nn S 2)211(212=-=，即所求的数项级数的和为221==∑∞=n nn S ．或用另一方法如下：该级数的部分和nn n S 223222132++++=，且1432223222121+++++=n n n S ，上两式相减得11322211))21(1(2122121212121++---=-++++=n nn nn n n S ，从而n n n nS 2))21(1(2--=，于是 2]2))21(1(2[lim lim =--==∞→∞→n n n n n nS S ．（3）根据该数项级数的特点，先考虑指数函数xe 的幂级数12012!(1)!(2)!n n n xn n n xxxe n n n --∞∞∞======--∑∑∑，取1=x 得，012111!(1)!(2)!n n n e n n n ∞∞∞======--∑∑∑，因此级数的和∑∞=12!n n n1111(1)!(1)!n n n n n n ∞∞==-+===--∑∑21112(2)!(1)!n n e n n ∞∞==+=--∑∑．（4）因为)!12(1)1(0++-∑∞=n n n n)!12(22)1(210++-=∑∞=n n n n⎥⎦⎤⎢⎣⎡++++-=∑∞=)!12(1)!12(12)1(210n n n n n 01111(1)(1)2(2)!2(21)!nnn n n n ∞∞===-+-+∑∑又由于正弦函数)!12()1(sin 120+-=+∞=∑n xx n n n，余弦函数)!2()1(cos 20n xx nn n∑∞=-=，取1=x ，得)!12(1)1(1sin 0+-=∑∞=n n n，)!2(1)1(1cos 0n n n∑∞=-=，于是)!12(1)1(0++-∑∞=n n n n1(c o s 1s i n 1)2=+．练习题求下列数项级数的和（1）1121211()n n n aa∞+-=-∑；(1a -)（2）1312nn n ∞=-∑．（提示：考虑1(31)n n n x ∞=-∑，结果为5）例10．求极限])2....(842[lim 312719131nnn ∞→．解：因为该级数的一般项为23111231113339273333[248 (2)]22ninni n i n=++++∑== ，所以若求出级数∑∞=13n nn 的和，则∑=∞=∞→133127191312])2....(842[lim n nnn nn ．先求出幂级数∑∞=1n nnx 的和，再取31=x 即得数项级数∑∞=13n nn 的和．因为 1111()()nn nn n n S x n x x n x x x∞∞∞-==='===∑∑∑21()()1(1)nn x x x x x xx ∞=''===--∑，所以 43)311(313)31(20=-==∑∞=n nnS ，从而 211121113l i m ()3339273334l i m [248 (2)]222nnnn n nn nn ∞→∞=+++→∞∑=== ． 5．函数展为幂级数（用间接法展开）例11．将下列函数展为x 的幂级数（1） )1ln()(2++=x x x f ；（2）将)1()(xe dxd x f x-=展开为x 的幂级数，并求数项级数∑∞=+1)!1(n n n 的和；（3）已知61212π=∑∞=n n，求定积分dx xx ⎰-101ln ．解：（1）因为=)(x f )1ln(2++x x 的导数为122()(1)f x x -'=+，),21(2x u m =-=，又导函数122()(1)f x x -'=+的展开式为122()(1)f x x -'=+++-----++---+-+=nxn n x x 242)121()121)(21(!1)121)(21(!21)21(1+--+++-=nnxn n x x 242!)!2(!)!12()1(!!4!!3211∑∞=--+=12!)!2(!)!12()1(1n nnxn n ，上式两边从0到x 积分，得)11(,12!)!2(!)!12()1()(112≤≤-+--+=∑∞=+x n x n n x x f n n n．（2）因为 ),(,!!1!31!211032+∞-∞∈=++++++=∑∞=x n xx n x x x e n nnx，所以xe x1-+∞<<=++++++=∑∞=--||0,!!1413121111132x n xxn x x x n n n上式两边对x 求导，得 )1()(xe dx d xf x-=1122)!1(!1433221-∞=-∑+=+-++++=n n n xn nxn n x x ，当1=x ，即可得11)1()1()!1(1211=+-=-==+==∞=∑x xxx xn xe xexe dxd f n n．（3）因为)1,1(,110-∈=-∑∞=x x x n n，所以111ln ln ()(ln )1nnn n xdx x x dx x xdx x∞∞====-∑∑⎰⎰⎰11112000ln 1(1)n n n x x x n n +∞+=⎡⎤=-⎢⎥++⎢⎥⎣⎦∑ 1200ln 1lim 1(1)n x n x x n n ∞+→+=⎡⎤=-⎢⎥++⎣⎦∑。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A. 2 u n 1
B. ( u n 2 ) 1
C. 2 u n 1
D. u n nk
分析与解：注意到已知
un
收敛，由性质2知
1
2un
是收敛的；
1
由性质3 知，C、D 所示级数也是收敛的；
∵ lim n
un
0
，
∴ lni m (un2)20，
根据性质5，B 所示级数不收敛。
注意！性质5 的逆不真，即：
n1
解：记 un n a ，在第二章§2.6 我们就知道
ln i m u nln i m na10,
事实上，
⑴ 当 a 1 时， lni m unlni m n11 ;
⑵
当
a0,
时， a1
1
lnim un
liman
n
lim 1
a n n
a0 1
.
由上面的性质5，级数
un
发散。
n1
例2 若级数 u n 收敛，则下列级数不收敛的是（ B ） 1
当级数收敛(有和)时，部分和 s n 就是其和 S 的近似值，S 与 s n 之差：
R n s s n u n 1 u n 2
称为级数的余项。|Rn|称为用Sn估计S所产生的误差.
例1 讨论级数 aaa a
的敛散性.
n1
解因 Sn na , lni m Snlni m na, 故级数发散.
Snu1u2 un
称 S n 为前n项和或部分和。
n
uk
k1
显然， s1,s2, sn, 构成一个数列，称为级数
(7.1)的部分和数列。
定义2. 若级数(7.1)的部分和数列存在极限：
lim
n
sn
S
则称级数(7.1)收敛，其和为S,记为: u n S
n1
若
lim
n
sn
不存在，则称级数(7.1)发散，它没有和。
S n a a q a q 2 a q n 1
a (1 1
qn) q
(1)当∣q ∣< 1时,
lni m Snlni m a(11qqn)1aq
(2)当∣ q ∣>1时,
a(1qn)
lni m Sn
lim n
1q
(3)若 q = 1时, 则 lni m Snlni m na (4)若 q =–1时, 则级数为：a a a a
级数的敛散性不变。（当然，收敛时，和一般要变）
性质4. 收敛级数加括号后得到的级数仍收敛，且和不变。
此性质说明：加法的结合律对收敛的无穷级数仍成立。
注意：发散级数加括号后有可能成收敛级数，因此，加括号后级数收敛，原级数未必收敛。
例如： 1 1 1 1 ( 1 )n 1
∵
0 Sn 1
n为偶数 n为奇数
∴
lim
n
S
n
不存在，即原级数发散。
但 ( 1 1 ) ( 1 1 ) ( 1 1 ) 收敛。
性质5.(级数收敛的必要条件) 若
u n 收敛，则必有
n1
lim
n
un
0
由性质5 可知，若
lim
n
un
0
，则级数
u n 必发散。
n1
例1
a
0
为常数，试判断级数
na
的敛散性。
lni m un 0,
u n 不一定收敛。看下面的例：
n1
例3 证明调和级数
发散。
证这里我们用反证n 1 法n1 .
假设该调和级数收敛到S, 则有：而
（参见书P280例1）
与前者矛盾. 故调和级数发散. 但熟记此结论！
例4. 判断下列级数的敛散性，若是收敛的，则求其和。
⑴
1
,
1 (2n1)(2n1)
性质1. 若级数
un
与
v n 都收敛，它们的和分别
n1
n1
S及W，则 ( u n v n ) 也收敛。且其和为 S W 。
n1
性质2. 若级数 u n 收敛到S，常数 a 0 ,则级数
n1
a u n收敛到aS ;若级数 u n 发散，则 a u n
n1
n1
n1
也发散。
性质3. 将级数 u n 的前面加上(或去掉)有限项， n1
1 2
1
1 2n
1
1 2
(n时 ) .
1
即 ⑴ 所示级数收敛到 2
第七章无穷级数
（本章14学时）
学习目的及要求： 1. 掌握无穷级数的概念和性质; 2. 熟练掌握正项级数敛散性的判定; 3. 掌握一般项级数绝对收敛与条件收敛的概念及判定法,能熟练判定交错级数的敛散性; 4. 掌握幂级数的概念和性质,会求幂级数的收敛半径,收敛区间及收敛域; 5. 能利用幂级数的性质求幂级数的和函数; 6. 了解泰勒公式与泰勒级数,能用间接法将一些初等函数展成幂级数.
当 n 为偶数时, S n 0 当 n 为奇数时， S n a ,
从而
lim
n
S
n
不存在.
故原级数发散.
综上，几何级数： aqn1aaqaq2 aqn1 n1
当∣q ∣<1时，收敛.且有
aqn1
a
n1
1q
首项 (1－公比)
当∣ q ∣≥1时, 发散.
（请务必熟记上面的结论！）
§7.2 无穷级数的基本性质
⑵
1 6 1 (4n 5n ) .
解：⑴ 记
1 (2n1)(2n1)
1( 1 1 ) 2 2n1 2n1
可见，本小题可用连锁相销法。
S n 1 2 ( 1 1 3 ) (1 3 1 5 ) (1 5 1 7 ) (2 n 1 1 2 n 1 1 )
1 2 1 1 3 1 3 1 5 1 5 1 7 2 n 1 1 2 n 1 1
例2
判定级数
1 11 1
n 1n (n1 ) 1223 n (n1 )
的敛散性.若收敛, 则求出其和.
解因
1 11 u nn(n1)nn1(n1,2, )
且Sn11 2213
1 n(n1)
1 11 1 1 (1)( ) ( ) 1
1
2 2 3 nn1 n 1
所以ln i m Snln i m (1n1 1)1
§7.1 无穷级数的概念
定义1. 将一个数列 u1,u2, ,un, 的各项依次相加
的式子：
u 1 u 2 u n
( 7 .1 )
称为无穷级数(简称级数)，并将其简记为 u n . n1
其中相加的各加数称为级数的项，特别地，第n项 u n 称为级数的一般项或通项。
将级数(7.1)前n项的和记为：
故级数收敛,其和为1. (例2解法称为连锁相销法）
例3 讨论几何级数(等比级数)
aqn 1aaqaq2 aqn 1
n 1
的敛散性.若收敛,则求出其和.u(n 参aq见n1书P272例1）
(其中a≠0,为常数， q 称为级数的公比, un aqn1 为它的一般项)
解当 q ≠1时, 部分和

第七章 无穷级数38583

高等数学第七章无穷级数.ppt

第7章 无穷级数

高等数学无穷级数

第七章 无穷级数