单服务员的排队模型
排队模型——精选推荐
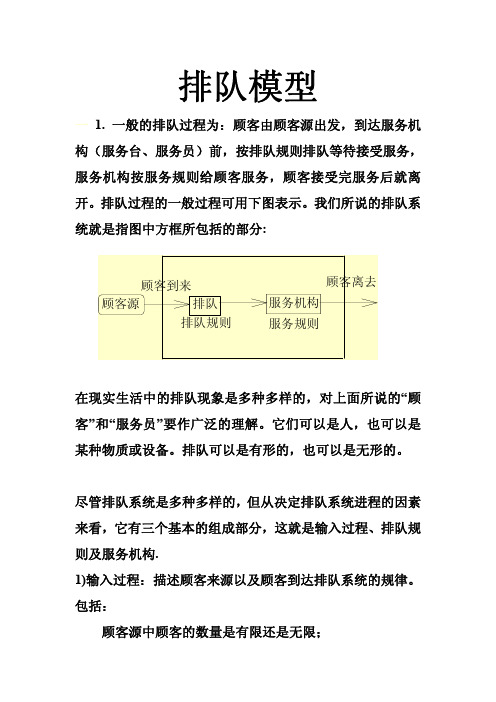
排队模型一 1. 一般的排队过程为:顾客由顾客源出发,到达服务机构(服务台、服务员)前,按排队规则排队等待接受服务,服务机构按服务规则给顾客服务,顾客接受完服务后就离开。
排队过程的一般过程可用下图表示。
我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的,对上面所说的“顾客”和“服务员”要作广泛的理解。
它们可以是人,也可以是某种物质或设备。
排队可以是有形的,也可以是无形的。
尽管排队系统是多种多样的,但从决定排队系统进程的因素来看,它有三个基本的组成部分,这就是输入过程、排队规则及服务机构.1)输入过程:描述顾客来源以及顾客到达排队系统的规律。
包括:顾客源中顾客的数量是有限还是无限;顾客到达的方式是单个到达还是成批到达;顾客相继到达的间隔时间分布是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2)排队规则:描述顾客排队等待的队列和接受服务的次序。
包括:即时制还是等待制;等待制下队列的情况(是单列还是多列,顾客能不能中途退出,多列时各列间的顾客能不能相互转移);等待制下顾客接受服务的次序(先到先服务,后到先服务,随机服务,有优先权的服务)。
3)服务机构:描述服务台(员)的机构形式和工作情况。
包括:服务台(员)的数目和排列情况;服务台(员)的服务方式;服务时间是确定型的还是随机型的,分布参数是什么,是否独立,是否平稳。
2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时,需要把有关的原始资料进行统计,确定顾客到达间隔和服务时间的经验分布,然后按照统计学的方法确定符合哪种理论分布。
mm1n排队论模型参数

mm1n排队论模型参数
M/M/1 排队论模型是一种简单的排队系统模型,用于分析单一服务台、顾客到达服从泊松分布、服务时间服从指数分布的系统。
在M/M/1 模型中,有三个主要参数:
1. 到达率(λ):表示单位时间内到达系统的顾客数的期望值,服从参数为λ的泊松分布。
到达率决定了系统中的顾客数量变化速率。
2. 服务率(μ):表示单位时间内一个顾客被服务完成的期望值,服从参数为μ的指数分布。
服务率决定了系统中顾客等待服务的速度。
3. 顾客到达和服务时间是独立的:这个条件表明顾客的到达和服务的完成之间没有影响,使得模型更具有现实意义。
通过平衡方程法,可以对M/M/1 模型进行稳态分析,计算出以下几个重要性质:
1. 队长(Ls):表示系统中的顾客数(n)的期望值。
2. 排队长(Lq):表示系统中排队等待服务的顾客数(n)的期望值。
3. 逗留时间(Ws):指一个顾客在系统中的全部停留时间,为期望值。
4. 等待时间(Wq):指顾客在系统中等待服务的時間,为期望值。
了解这些参数后,可以对M/M/1 模型进行评估和优化,以提高系统的效率和服务质量。
M/M/1 模型虽然简单,但在实际应用中具有广泛的价值,如电话交换系统、计算机网络、银行窗口等。
掌握M/M/1 模型的基本原理和分析方法对于学习排队论和实际应用具有重要意义。
排队论

f ( w n 1)
n!
e w
w0
f ( w ) Pn f ( w n 1) n0 ( w ) n w (1 ) n e ( )e ( ) w n0 n!
熊燕华
6.
忙期和闲期
系统忙的概率为ρ ,则闲的概率为1-ρ 。可以 认为在一段时间内,忙期和闲期的长度比为 ρ :(1-ρ ) 由于顾客到达间隔服从无记忆性的负指数分布, 且与服务时间无关。闲期I(系统从空闲开始到新 的顾客到达时刻)服从参数为λ 的负指数分布,则 E[I]=1/λ E[B]= ρ/(1-ρ) E[I]=1/(μ-λ )=Ws
熊燕华
L S n Pn
n0
1
Little公式
Ls=Lq+λ/μ Ws=Wq+1/μ
L q (n 1) Pn n 1
Ws=E(W)=1/(μ-λ) Wq=Ws-1/μ=ρ/(μ-λ)
Ws=Ls/λ
Wq=Lq/λ
熊燕华
定理: 对于存在平稳分布的任何排队系统,下列 关系成立:
熊燕华
七、随机过程知识准备
系统的状态
系统中的顾客数,即如果系统中有n个顾客即说系统 状态为n。在平稳过程中,在时刻t、系统状态为n的概率 Pn(t)是不变的,即Pn(t) =Pn是不随时间变化的统计平衡 状态解。
注:本章研究的均为平稳过程,即输入、输出过程 的概率分布、参数均不随时间变化,与所选取的时
第八章 排队论
基本概念 单服务台泊松到达负指数服务时间排队模型 多服务台泊松到达负指数服务时间排队模型 其他排队模型 经济分析
熊燕华
排队论之简单排队系统

1.//1/M M ∞排队系统//1/M M ∞排队系统是单服务台等待制排队模型,可描述为:假设顾客以Poisson 过程(具有速率λ)到达单服务员服务台,即相继到达时间间隔为独立的指数型随机变量,具有均值1λ,若服务员空闲,则直接接受服务,否则,顾客排队等待,服务完毕则该顾客离开系统,下一个排队中的顾客(若有)接受服务。
相继服务时间假定是独立的指数型随机变量,具有均值μ。
两个M 指的是相继到达的间隔时间和服务时间服从负指数分布,1指的是系统中只有一个服务台,∞指的是容量为无穷大,而且到达过程与服务过程是彼此独立的。
为分析之,我们首先确定极限概率0,1,2,n p n •••=,,为此,假定有无穷多房间,标号为 0,1,2,•••,并假设我们指导某人进入房间n (当有n 个顾客在系统中),则其状态转移框图如图所示。
图 //1/M M ∞排队系统状态转移速率框图由此,我们有状态 离开速率=进入速率0 01p p λμ=,1n n ≥ ()11n n n p p p λμλμ-++=+解方程组,容易得到00,1,2,ii p p i λμ•••⎛⎫== ⎪⎝⎭,再根据0011()1n n n n p p p λμλμ∞∞=====-∑∑得到:01p λμ=-, ()(1),1nn p n λλμμ=-≥ 令/ρλμ=,则ρ称为系统的交通强度(traffic intensity )。
值得注意的是这里要求1ρ<,因为若1ρ>,则0n p =,且系统中的人数随着时间的推移逐渐增多直至无穷,因此对大多数单服务排队系统,我们都假定1ρ<。
于是,在统计平衡的条件下(1ρ<),平均队长为,1,1j j L jp λρρμλρ∞====<--∑(5-52)由于a λλ=,根据式(5-2)、(5-3)以及上式,可得: 平均逗留时间为:1,1LW ρλμλ==<- (5-53) 平均等待时间为:1[],1()(1)Q W W E S W λρρμμμλμρ=-=-==<-- (5-54)平均等待队长为:22,1()1Q Q L W λρλρμμλρ===<-- (5-55)另外,根据队长分布易知,01ρρ=-也是系统空闲的概率,而ρ正是系统繁忙的概率。
排队模型的随机模拟

求导得分布函数
, 积分可得
λ
λ λ
。 由此对
分布函数求反函数,则随机变量的变化规律 ( , ),则 ( )。
,设
,因为
服务时间以1min为单位时间,而服务时间Y满足均匀分布,分布范围(0,2),由已知, 用rand()函数产生随机变量符合服务时间的要求。
蒙特卡诺随机模拟
Monte carlo 算法是以概率和统计理论方法为基础的一种计算方法。将所求解的问
对于以上问题,随机模拟100次的结果: 平均排队时间为0.6526分钟 服务员的空闲率49.63% 平均队伍长度0.60 日平均服务客人240人 随机模拟次数为200次的统计结果: 平均排队时间为0.6590分钟 服务员的空闲率49.78% 平均队伍长度0.60 日平均服务客人239人 同时,随机模拟次数为500次的统计结果: 平均排队时间为0.6600分钟 服务员的空闲率49.95% 平均队伍长度0.60 日平均服务客人239人
Y
i <480?
N
初始化到达时间与开始服务时间
到达时间 = 上个到达时间 + 到达时间间隔 ; 起始服务时间 =ma x( 到达时间,上一个结束服务时间)
累计等待时间,空闲时间营业范围内?YN输出结束
5
由于C语言包括服从均匀分布的随机变量函数rand() ,调用随机函数在VC6.0中运行程 序如下: #include<stdio.h> #include<time.h> #include<math.h> #include<stdlib.h> double AverageRandom(double min,double max) { while(1) { int p=rand(); if(p>=30000)continue; int q=rand(); if(q>=30000)continue; float s=fmod(p,max)+min+q%10000/10000.0; if(s>min && s<max) return s; } } double ExponentRandom(double landa) { double x; int q; while((q=rand())>30000); x=q%10000/10000.0; return -1.0/landa*log(1-x); } int main() { int i,j,k,Sumi=0; int count=0; srand(time(NULL)); double SumW=0,SumE=0; int LengthQ1,LengthQ2; double SumLQ=0,LastTime; while(count<200) { double TimeR[480]={0};//到达时间间隔 double TimeS[480]={0};//服务时间 double TimeB[480]={0};//开始服务时间 double TimeN[480]={0};//到达时间 double LQ[480]={0}; TimeR[0]=ExponentRandom(0.5); TimeS[0]=AverageRandom(0,2);
数学建模 排队模型2015-7-12讲解

ln
c
c
h
/
ln
2 排队模型——经典排队模型
例
一个码头,设待卸货船到达时间间隔服从负指数分 布,平均到达 2 艘/小时;服务台是1台吊车,卸货 时间服从负指数分布,平均每 20 分钟可卸一艘货 船,当被占用时,新到货船只能停在码头等待。求 在平稳状态下码头上货船的平均数;等待卸货船只 的平均数;每艘货船在码头的平均停留时间;货船 平均需等待多长时间可以开始卸货。
排1 排队队模模型型————简简介介 (基本概念)
一、排队模型的描述(组成) 基本排队过程 排队系统一般有三个基本组成部分: 1.输入过程;2.排队规则;3.服务机构
¹Ë ¿Í Ô´
˹ ¿Í µ½ ´ï Å ¶Ó ½á ¹ ·þ Îñ ¹æ Ôò ·þ Îñ »ú ¹
Àë È¥
Å ¶Ó ¹æ Ôò
ͼ 1 Å ¶Ó ϵ ͳ ʾ Òâ ͼ
排1 排队队模模型型————简简介介 (基本概念)
一、排队模型的描述(组成) 基本排队过程 1.输入过程
顾客是按怎样的规律到达排队系统的过程,有时也 把它称为顾客流 (1)顾客总数 有限 无限? (2)到达方式 单个 成批? (3)顾客流的概率分布族 相继到达的顾客间的概率分布
逗留时间 = 等待时间 + 服务时间
显然,Ws(或Wq)越大,顾客满意度越低。
排1 排队队模模型型————简简介介 (基本概念)
二、建模过程及主要指标 主要指标:
3. 忙期:从顾客到达空闲服务机构起到服务机构再次为 空闲这段时间长度。可以衡量服务机构效率的指标,及 工作强度
4. 绝对通行能力:单位时间内被服务完的平均顾客数
系 中
统 顾
单服务台排队系统仿真报告
单服务台排队系统仿真报告一、模型准备1、 顾客到达特性在该系统中,顾客的到达规模(成批到达还是单个到达)是单个到达,假设顾客到达率Ai 服从均值为 的指数分布,即2、 顾客服务时间顾客服务时间为Si ,服从指数分布,假设均值为,即二、 仿真模型设计1、 元素定义(Define )本系统的元素定义如表1所示。
2、 元素可视化设置(Display )本系统中各个元素的显示特征定义设置如图2所示:m in 5=A βAs Ae Af ββ/)(-=)0(≥A min 4=s βSA Se Sf ββ/)(-=)0(≥S图2 各元素的显示特征(1)Part元素可视化设置在元素选择窗口选择customer元素,鼠标右键点击Display,跳出Display 对话框(图3),设置它的Text(图4)、Icon(图5)。
图3 Display对话框图4 Display Text对话框图5 Display Icon对话框(2)Buffer元素可视化设置在元素选择窗口选择paidui元素,鼠标右键点击Display,跳出Display对话框(图3),设置它的Text、Icon、Rectangle(图6)。
图6 Display Rectangle对话框(3)Machine元素可视化设置在元素选择窗口选择Fuwuyuan元素,鼠标右键点击Display,跳出Display 对话框(图3),设置它的Text、Icon、Part Queue(图7)。
图7 Display Part Queue对话框(4)Variable元素可视化设置在元素选择窗口选择Jifen0元素,鼠标右键点击Display,跳出Display对话框(图3),设置它的Text 、Value(图8)。
图8 Display Value对话框(5)Timeseries元素可视化设置在元素选择窗口选择duichang元素,鼠标右键点击Display,跳出Display 对话框(图3),设置它的Text、Timeseries(图9)。
排队模型与模拟 ppt课件
pn
与初始状态无关而且满足 pn 1
n0
那么称这个排队模型是稳定的。
概率分布pn : n 0,1,2,称为队长的稳定解。
对于长时间连续不断运行的排队模型,稳定解 比瞬时解有更重要的意义。
PPT课件
20
令
,称为服务强度。
1 即 ,表明服务员有足够的能力完全 接待到来的全体顾客。可以证明排队模型是稳定的。 但这决不是说,每位顾客就不用等待了,因为在 系统运行中随机因素在起作用。
M——到达的过程为泊松过程或负指数分布
D——定长输入
EK——K阶爱尔朗分布 G——一般相互独立的随机分布
②——服务时间分布
③——服务台(员)个数
④——顾客源总数
⑤——系统内顾客的容量
PPT课件
29
四、排队系统的常见分布
1.泊松分布(Poisson distribution)
(1) 平稳性 在时间 t t 内,到达 n 个顾客的概率只与 t 和 n 的大小有关。
有确定的时间间隔,也有随机的时间间隔
PPT课件
12
2.排队规则:指服务台从队列中选取顾客 进行服务的顺序。
(1)损失制 ,这是指如果顾客到达排队系统时, 所有服务台都被先到的顾客占用, 那么他们就自动离开系统。
PPT课件
13
(2)等待制,指当顾客来到系统时,若服务 台没有空闲,则顾客排队等候服务。
, 顾客源无限,容量N,单列,混合制.
2.系统的状态概率和主要运行指标:
1
P0
1
1
N
1
1 N
1 1
n
P0
排队论大学课件7-MM排队模型
1 t L lim l ( x) dx t t 0
W是顾客平均的概念,是许许多多个不同顾客等待 时间的平均
1 n W lim wi n n i 1
一般来讲W比较容易从统计中获得,L比较容易从 理论分析中获得
补充:系统负载举例
例如: 某电话用户10~12点之间共拨打电话5次,总通话时间为30 分钟,求此用户线平均每小时的业务量 解: =5/(2×60) =5/30 承载的业务量为 a= / = 30/(2×60)=0.25erl 一个服务窗每小时最多提供 1erl 的业务承载量 传统电话网:
普通用户 0.1~0.2erl 集团交换机 0.1~0.6erl
单位时间内平均进入系统的顾客数
e p0
1
相对通过能力Q(即单位时间内被服务完的顾客数与请 求服务顾客数之比值) e 1 Q p0 1 绝对通过能力A(单位时间内被服务完顾客的均值)
A e p0
书44页
17:42:29
1
15
M/M/1/1例题
Q
状态0系统中顾客数为0 服务窗空闲 状态1 系统中有1个顾客,此顾客正在接受服务 系统顾客满服务窗忙
17:42:29
13
求解平稳分布
根据马氏链、生灭过程求平稳分布的公式: Q 0 列出平衡方程:
p1 p0 p0 p1 1 p0
17:42:29
26
Little公式应用
一个没有等待位置的餐厅,平均每小时服务完30人, 平均就餐时间为30分钟,请问平均就餐人数 = 30 W = 0.5 L = W = 0.5×30 = 15(人)
(完整word版)数学建模 港口问题_排队论
排队模型之港口系统本文通过排队论和蒙特卡洛方法解决了生产系统的效率问题,通过对工具到达时间和服务时间的计算机拟合,将基本模型确定在//1M M排队模型,通过对此基本模型的分析和改进,在概率论相关理论的基础之上使用计算机模拟仿真(蒙特卡洛法)对生产系统的整个运行过程进行模拟,得出最后的结论。
好。
关键词:问题提出:一个带有船只卸货设备的小港口,任何时间仅能为一艘船只卸货。
船只进港是为了卸货,响铃两艘船到达的时间间隔在15分钟到145分钟变化。
一艘船只卸货的时间有所卸货物的类型决定,在15分钟到90分钟之间变化。
那么,每艘船只在港口的平均时间和最长时间是多少?若一艘船只的等待时间是从到达到开始卸货的时间,每艘船只的平均等待时间和最长等待时间是多少?卸货设备空闲时间的百分比是多少?船只排队最长的长度是多少?问题分析:排队论:排队论(Queuing Theory) ,是研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法,又称随机服务系统理论,为运筹学的一个分支。
本题研究的是生产系统的效率问题,可以将磨损的工具认为顾客,将打磨机当做服务系统。
【1】M M:较为经典的一种排队论模式,按照前面的Kendall记号定义,//1前面的M代表顾客(工具)到达时间服从泊松分布,后面的M则表示服务时间服从负指数分布,1为仅有一个打磨机。
蒙特卡洛方法:蒙特卡洛法蒙特卡洛(Monte Carlo)方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。
这一方法源于美国在第一次世界大战进研制原子弹的“曼哈顿计划”。
该计划的主持人之一、数学家冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo—来命名这种方法,为它蒙上了一层神秘色彩。
(2)排队论研究的基本问题1.排队系统的统计推断:即判断一个给定的排队系统符合于哪种模型,以便根据排队理论进行研究。
2.系统性态问题:即研究各种排队系统的概率规律性,主要研究队长分布、等待时间分布和忙期分布等统计指标,包括了瞬态和稳态两种情形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单服务员的排队模型:在某商店有一个售货员,顾客陆续来到,售货员逐个地接待顾客.当到来的顾客较多时,一部分顾客便须排队等待,被接待后的顾客便离开商店.设:
1.顾客到来间隔时间服从参数为0.1的指数分布.
2.对顾客的服务时间服从[4,15]上的均匀分布.
3.排队按先到先服务规则,队长无限制.
(1)
模拟100个工作日,求出平均每日完成服务的个数及每日顾客的平均等待时间.
MATLAB程序:
clear
sm=0;%总工作时间,初始为0
m=0;%服务总个数
for j=1:100
j
w(j)=0;
i=2;
x(i)=exprnd(10);
c(i)=x(i);
b(i)=x(i);
while b(i)<=480
y(i)=unifrnd(4,15);
e(i)=b(i)+y(i);
w(j)=w(j)+b(i)-c(i);
i=i+1;
x(i)=exprnd(10);
c(i)=c(i-1)+x(i);
b(i)=max(c(i),e(i-1));
end
i=i-2;
t=w(j)/i %每j日顾客的平均等待时间
m=m+i;
sm=sm+w(j);%总的等待时间
end
m ; %100日服务总个数
am=m/100 %输出平均每日完成服务的个数
at= sm/m %输出平均每日顾客平均等待时间
运行结果:j =
1
t =
7.6488
j =
2
t =
21.5629
j =
3
t =
48.0306
j =
4
t =
15.3583
j =
5
t =
29.0681 j =
6
t =
43.9925 j =
7
t =
9.1838 j =
8
t =
29.3542 j =
9
t =
37.3775
j =
10
t =
36.6198 j =
11
t =
15.1372 j =
12
t =
11.9697 j =
13
t =
46.2765 j =
14
t =
5.0990 j =
15
t =
12.4896 j =
16
t =
19.3674 j =
17
t =
27.7045 j =
18
t =
13.7486 j =
19
t =
24.3442 j =
20
t =
10.8663 j =
21
t =
8.0429 j =
22
t =
10.3723
23
t =
11.8501 j =
24
t =
14.3409 j =
25
t =
46.0177 j =
26
t =
8.8139 j =
27
t =
5.3630 j =
28
t =
12.8179 j =
29
t =
7.2817 j =
30
t =
11.1612 j =
31
t =
9.3863
j =
32
t =
62.4873 j =
33
t =
13.0453 j =
34
t =
21.7910 j =
35
t =
16.5294 j =
36
t =
12.2347 j =
37
t =
24.9796 j =
38
t =
78.2435 j =
39
t =
24.3057 j =
40
t =
15.2035 j =
41
t =
46.8024 j =
42
t =
56.4635 j =
43
t =
37.1819 j =
44
t =
18.2931
45
t =
55.0295 j =
46
t =
35.6992 j =
47
t =
24.6073 j =
48
t =
12.9206 j =
49
t =
15.4886 j =
50
t =
17.0108 j =
51
t =
20.9452 j =
52
t =
21.8094 j =
53
t =
75.8497
j =
54
t =
25.1111 j =
55
t =
34.9260 j =
56
t =
32.5712 j =
57
t =
27.9767 j =
58
t =
29.5067 j =
59
t =
29.4701 j =
60
t =
19.2476 j =
61
t =
16.3576 j =
62
t =
8.8686 j =
63
t =
29.0910 j =
64
t =
14.7117 j =
65
t =
36.7096 j =
66
t =
46.9512
67
t =
7.7582 j =
68
t =
11.8390 j =
69
t =
43.2197 j =
70
t =
97.6024 j =
71
t =
70.4187 j =
72
t =
8.5048 j =
73
t =
4.1632 j =
74
t =
18.7508 j =
75
t =
41.1622
j =
76
t =
28.1712 j =
77
t =
56.6012 j =
78
t =
45.1566 j =
79
t =
12.9582 j =
80
t =
6.6022 j =
81
t =
19.3046 j =
82
t =
26.1914 j =
83
t =
8.4448 j =
84
t =
18.3721 j =
85
t =
18.1843 j =
86
t =
41.0727 j =
87
t =
7.7466 j =
88
t =
54.3138
89
t =
22.9150 j =
90
t =
68.9592 j =
91
t =
11.5373 j =
92
t =
14.4600 j =
93
t =
27.6556 j =
94
t =
41.1297 j =
95
t =
24.8645 j =
96
t =
36.2404 j =
97
t =
5.2884
j =
98
t =
7.2035 j =
99
t =
25.1523 j =
100
t =
24.6979 am =
44.1400 at =
27.1289。
