5.1相交线 第1课时 相交线——作业
5.1.1相交线
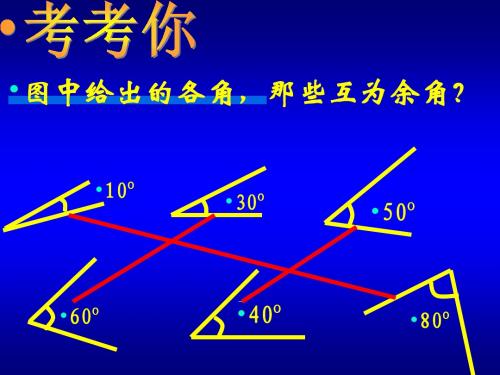
•10o
•30o
•50
o
•60
o•40o源自•80o•图中给出的各角,那些互为补角?
•10o
•30o
•60
o
•80o
•100o •120
o
•150
o
•170
o
第五章
相交线与平行线
5.1.1
教学重点:
相交线
邻补角的概念
对顶角的概念
对顶角的性质
2015/12/28 3
•阅读课本P2-P3并思考以下问题:
A
O 2 E D
B
作业:
1.(1) P3 练习 (2) P7 1、 2
2.如图,AB、CD、EF相交于点O,∠1=20°, ∠BOC=80°,求∠2 A O 2 E D C 1 F B
(邻补角的定义)
∴∠3=∠1=400(对顶角相等)
练习1:下列各图中∠1、∠2是对顶角 吗?为什么?
1 2
1 2
1
2
1
2
下列各图中∠1、∠2是邻补角吗?为 什么?
1
2
1
2
如图所示,三条直线AB、CD、EF相交于一 点O,∠AOC的对顶角是 ∠BOD ,∠COF的对 顶角是 ∠DOE ,∠COB的邻补角 是 ∠AOC、∠BOD 。
A C O E B
F D
判断:
由对顶角相等,可得相等的角是对顶角
×
1、两条直线相交形成的四个角中,共有 对 2 对顶角,共有 4 对邻补角。 2、如果三条直线相交于一点,则一共有 对 6 对顶角,共有 12 对邻补角。
•练习3 如图,AB、CD、EF相交于点O,∠1=15°, ∠AOD=85°,求∠2. C 1 F
人教版七年级数学下册第5章同步分层练习(含答案) :5.1.1相交线

人教版七年级数学下册第5章同步课时练习5.1.1 相交线★基础练习★【知识点1】对顶角、邻补角的认识1.下列各图中,∠1与∠2是对顶角的是()A.B.C.D.2.如图,图中对顶角共有()对.A.3B.6C.8D.12 3.如图,∠1与∠2互为邻补角的是()A.B.C.D.4.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有()第1页(共8页)A.4对B.6对C.7对D.8对【知识点2】对顶角、邻补角的性质5.如图,直线a,b相交于点O,若∠1等于30°,则∠2等于()A.60°B.70°C.150°D.170°6.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=()A.360°B.180°C.120°D.907.如图,直线AB与CD相交于点O,射线OE平分∠BOC,且∠BOC=70°,则∠AOE 的度数为()A.145°B.155°C.110°D.135°★提升练习★8.∠1与∠2互余且相等,∠1与∠3是邻补角,则∠3的大小是()A.30°B.105°C.120°D.135°9.如图,直线AB、CD相交于点O,OE平分∠BOC,∠FOD=90°,若∠BOD:∠BOE=1:2,则∠AOF的度数为()A.70°B.75°C.60°D.54°10.如图,直线AB,CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=40°,则∠AOF的度数是()A.65°B.60°C.50°D.40°11.如图,直线AB,CD相交于点O,∠AOE=90°,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB﹣2∠EOF.其中正确的结论为()A.①②④B.②③④C.①③④D.①②③④12.如图,直线AB、CD相交于点O,∠1=∠2,若∠AOD=68°,则∠1的度数为.第3页(共8页)13.如图,直线AB、CD交于点O,射线OM平分∠AOC,∠AOM=36°,则∠BOD =.14.如图,直线AB、CD相交于点O,下列描述:①∠1和∠2互为对顶角;②∠1和∠2互为邻补角;③∠1=∠2;④∠1=∠3;⑤∠1+∠4=180°,其中正确的是.15.已知,如图,直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE,∠COF =34°,求∠AOC和∠BOD的度数.16.如图,直线AB、CD相交于点O,OE平分∠BOC,∠COF=90°.(1)若∠BOE=64°,求∠AOF的度数;(2)若∠BOD:∠BOE=2:3,求∠AOF度数.17.如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.(1)求∠AOE的度数;(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.★拓展探究突破练习★18.已知直线AB和CD交于O,∠AOC的度数为x,∠BOE=90°,OF平分∠AOD.(1)当x=20°时,则∠EOC=度;∠FOD=度.(2)当x=60°时,射线OE′从OE开始以10°/秒的速度绕点O逆时针转动,同时射线OF′从OF开始以8°/秒的速度绕点O顺时针转动,当射线OE′转动一周时射线OF′也停止转动,求至少经过多少秒射线OE′与射线OF′重合?(3)在(2)的条件下,射线OE′在转动一周的过程中,当∠E′OF′=90°时,请直接写出射线OE′转动的时间.第5页(共8页)参考答案1.C.2.B.3.B.4.B.5.C.6.B.7.A.8.D.9.D.10.A.11.C.12.34°13.72°14.②④⑤.15.解:因为∠COE=90°,∠COF=34°,所以∠EOF=∠COE﹣∠COF=56°,因为OF是∠AOE的平分线,所以∠AOE=2∠EOF=112°,所以∠AOC=112°﹣90°=22°,∠EOB=180°﹣112°=68°,因为∠EOD是直角,所以∠BOD=22°.16.解:(1)∵OE平分∠BOC,∴∠BOC=2∠BOE=2×64°=128°,∴∠AOC=180°﹣128°=52°,∵∠COF=90°,∴∠AOF=38°;(2)∵OE平分∠BOC,∴∠BOC=2∠BOE,∵∠BOD:∠BOE=2:3,∴,∴∠AOC=∠BOD=45°,∵∠COF=90°,∴∠AOF=45°.17.解:(1)∵∠AOE:∠EOC=2:3.∴设∠AOE=2x,则∠EOC=3x,∴∠AOC=5x,∵∠AOC=∠BOD=75°,∴5x=75°,解得:x=15°,则2x=30°,∴∠AOE=30°;(2)OB是∠DOF的平分线;理由如下:∵∠AOE=30°,∴∠BOE=180°﹣∠AOE=150°,∵OF平分∠BOE,∴∠BOF=75°,∵∠BOD=75°,∴∠BOD=∠BOF,∴OB是∠COF的角平分线.18.解:(1)∵∠BOE=90°,∴∠AOE=90°,∵∠AOC=x=20°,∴∠EOC=90°﹣20°=70°,∠AOD=180°﹣20°=160°,∵OF平分∠AOD,∴∠FOD=∠AOD==80°;故答案为:70,80;(2)当x=60°,∠EOF=90°+60°=150°设当射线OE'与射线OF'重合时至少需要t秒,第7页(共8页)10t +8t =150,t =,答:当射线OE '与射线OF '重合时至少需要秒;(3)设射线OE '转动的时间为t 秒,由题意得:10908150t t ++=或10815090t t +=+或36010815090t t -=-+或36010360890360150t t -+-+=-,103t =或403或703或1003.答:射线OE '转动的时间为103秒或403秒或703秒或1003秒.。
5.1.1 相交线习题优秀课件习题优秀课件

知识点2:邻补角、对顶角的计算
6.(2017·河池)如图,点O在直线AB上,若∠BOC=60°,则∠AOC的
大小是(
)C
A.60° B.90° C.120° D.150°
7 . 如 图 , 直 线 l1 与 l2 相 交 于 点 O , 若 ∠ 1 和 ∠ 2 的 和 为 130° , 则 ∠ 3 为 ( D)
A.∠BOF B.∠DOF C.∠AOE D.∠DOE
4.邻补角是( D ) A.和为180°的两个角 B.有公共顶点且互补的两个角 C.有一条公共边且互补的两个角 D.有公共顶点且有一条公共边,另一边互为反向延长线的两个角
5.下列说法正确的是( D ) A.大小相等的两个角互为对顶角 B.有公共顶点且相等的两个角是对顶角 C.两直线相交所成的角互为对顶角 D.两边互为反向延长线且有公共顶点的两个角互为对顶角
A.50° B.130° C.125° D.115°
8.如图,直线AB,CD相交于点O.射线OM平分∠AOC,若∠BOD=
76°,则∠BOM等于(
C)
A.38°
B.104°
C.142°
D.144°
9.如图,点O是直线AB上一点,OE,OF分别平分∠AOC和∠BOC,
当OC的位置发生变化时(不与直线AB重合),那么∠EOF的度数(
解:因为∠BOC+∠1=180°,∠BOC=136°, 所以∠1=____4_4_°_____. 所以∠AOC=∠1=____4_4_°_____. 因为 OF 平分∠AOC,
所以∠FOC=12__∠__A__O_C___=____22_°_____. 因为∠1=∠2=____4_4_°____, 所以∠EOF=180°-___2_2_°___-___4_4_°___=____1_1_4_°____.
相交线5.1

例2 如图,直线a,b相交于点O,∠1= 4 0 , 求∠2 ,∠3 ,∠4 的度数. 解:由邻补角定义,可得 b 2 =1 8 0 1 O2 1 180 40 a 4 3 1 4 0 ;
由对顶角相等,可得
3 = 1 4 0 , 4 = 2 1 4 0 .
C E
O
D B
相交线所成角的数量关系 ∠1与∠2有怎样的数量关系?
C 2
A
互补
B
3
1 4O D
∠1与∠3有怎样的数量关系? 你是怎样得到的?
C 2 3 1 4O
相等
B
A
D
你能说出∠1=∠3的道理吗? 请你用数学的语言写出这个过程. 因为 ∠1与∠2 互补, A 1 4O ∠3与∠2 互补 D (邻补角的定义), 所以 ∠1=∠3(同角的补角相等), 同理 ∠2=∠4 .
C 2 A 3
图中还有哪些对顶角?
1 4O
B
D
例 1(2)下列各图中,∠1和∠2是对顶角吗? 为什么?
1 2
(1) 1 (4) 2
1
1 2
2 (3) 2 1 (5)
(2)
例 1(3)请分别画出图中∠1的对顶角 和∠2的邻补角.
1
2
例 1(4)如图,三条直线AB ,CD ,EF相交于 点O,∠AOE的对顶角 ∠FOB ∠FOD、 ∠COE 是 , ∠EOD的邻补角 A F 是 .
C 2 3 B
图中还有哪些邻补角? A
1 4O
D
例 1(1)下列各图中,∠1和∠2是邻补角吗? 为什么?
1 (1)
2
1
2
1
2
(2)
5.1相交线(邻补角、对顶角、垂线)

5.1.1 相交线一、选择题:1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个2.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120° 3.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个4.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30° 图3 二、填空题:(每小题2分,共16分)5.如图5所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.6.如图8所示,直线AB,CD 相交于点O,OE 平分∠AOC,若∠AOD-∠DOB=50°,•则∠BOE=_________.7.如图9所示,直线AB,CD 相交于点O,已知∠AOC=70°,OE 把∠BOD 分成两部分,• 且∠BOE:∠EOD=2:3,则 ∠EOD=________.图5 图8 图9三、 训练平台:(每小题10分,共20分)8.如图所示,AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE•的 度数.12121221OFE D CB A 60︒30︒34l 3l 2l 112O ED C BA OF EDC B A O ED C BAOE DCBA9.如图所示,直线a,b,c 两两相交,∠1=2∠3,∠2=65°,求∠4的度数.四、 探索发现:(每小题8分,共16分)10.若4条不同的直线相交于一点,则图中共有几对对顶角?几对邻补角?若n 条不同的直线相交于一点呢?垂线一、选择题:1.如图1所示,下列说法不正确的是( )A.点B 到AC 的垂线段是线段AB;B.点C 到AB 的垂线段是线段ACC.线段AD 是点D 到BC 的垂线段;D.线段BD 是点B 到AD 的垂线段 图1 2.如图1所示,能表示点到直线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条 3.下列说法正确的有( ) ①一条直线的垂线只有一条;②若两条直线相交所成的四个角相等,则这两条直线互相垂直 ③互相垂直的两条直线形成的四个角一定都是直角; ④在平面内,过一点有且只有一条直线垂直于已知直线. A.1个 B.2个 C.3个 D.4个4.如图2所示,AD ⊥BD,BC ⊥CD,AB=acm,BC=bcm,则BD 的范围是( )A.大于acmB.小于bcm 图2C.大于acm 或小于bcmD.大于bcm 且小于acm 5.到直线L 的距离等于2cm 的点有( )A.0个B.1个;C.无数个D.无法确定6.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到 直线m 的距离为( ) A.4cm B.2cm; C.小于2cm D.不大于2cmcb a 3412DCBADCBA三、训练平台:(共15分)7. 如图所示,直线AB,CD,EF 交于点O,OG 平分∠BOF,且CD ⊥EF,∠AOE=70°,•求∠DOG 的度数.五、探索发现:(共20分)8.如图6所示,O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线. (1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,并说明理由.六、中考题与竞赛题:(共20分)9.(2001.杭州)如图7所示,一辆汽车在直线形的公路AB 上由A 向B 行驶,M,N•分别是 位于公路AB 两侧的村庄,设汽车行驶到P 点位置时,离村庄M 最近,行驶到Q 点位置时,•离村庄N 最近,请你在AB 上分别画出P,Q 两点的位置.NM BA10. 如图,已知∠AOB 与∠BOC 互为邻补角,OD 是∠AOB 的平分线,OE 在∠BOC 内,∠BOE=0.5∠EOC , ∠DOE=72°,求∠EOC 的度数.11.(画图)画一个钝角三角形,将其三条边上的高作出来.G OF EDCBA ODC BA。
人教版七年级数学下册 教案5.1.1 第1课时《相交线》

人教版七年级数学下册教案5.1.1 第1课时《相交线》一. 教材分析《相交线》是人教版七年级数学下册第五章第一节的内容,主要介绍了相交线的定义、性质和应用。
本节课的内容是学生学习几何知识的基础,对于培养学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析七年级的学生已经具备了一定的观察和动手能力,对于基本的几何概念和性质有一定的了解。
但是,对于相交线的定义和性质可能还比较模糊,需要通过实例和操作来进一步理解和掌握。
三. 教学目标1.了解相交线的定义和性质。
2.能够识别和判断相交线。
3.能够运用相交线的性质解决简单的问题。
四. 教学重难点1.相交线的定义和性质。
2.运用相交线的性质解决实际问题。
五. 教学方法1.采用问题驱动的教学方法,引导学生通过观察和操作来发现相交线的性质。
2.使用多媒体辅助教学,通过动画和图片来形象地展示相交线的性质。
3.采用小组合作的学习方式,让学生在讨论和交流中加深对相交线性质的理解。
六. 教学准备1.多媒体教学设备。
2.相交线的图片和实例。
3.练习题和作业。
七. 教学过程导入(5分钟)教师通过展示一些生活中的实例,如铁路交叉、道路交汇等,引导学生观察和思考这些实例中的共同特点。
学生可能会发现这些实例都有两条线段或直线相交的情况。
教师进而提问:“什么是相交线?相交线有哪些性质?”从而引出本节课的主题。
呈现(10分钟)教师通过多媒体展示相交线的定义和性质,引导学生观察和理解相交线的概念。
同时,教师可以给出一些实例,让学生判断哪些是相交线,并解释原因。
操练(10分钟)教师给出一些练习题,让学生独立完成。
这些练习题可以包括判断相交线、找出相交线的性质等。
教师可以在学生完成后进行讲解和解析。
巩固(10分钟)教师可以通过一些实际问题来巩固学生对相交线的理解和掌握。
例如,给出一个几何图形,让学生找出其中的相交线,并解释其性质。
拓展(10分钟)教师可以引导学生进一步思考相交线的应用,例如在建筑设计、交通规划等领域中的应用。
人教版七年级下册数学5.1.1相交线与平行线练习题(含答案)
第五章相交线与平行线5.1.1相交线知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( )3.下面四个图形中,∠1与∠2是邻补角的是( )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是,∠1的对顶角是.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( )A.120° B.90° C.60°D.30°7.如图,测角器测得工件(圆台)的角度是度,其测量角的原理是.第4题图第5题图第6题图第7题图8.在括号内填写依据:如图,因为直线a,b相交于点O,所以∠1+∠3=180°( ),∠1=∠2( ).AB9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是___________,∠EOC 的对顶角是___________②∠AOC 的邻补角是_________________,∠BOE 的邻补角是__________________. ③若∠AOC=50°,求∠BOD ,∠COB 的度数. 解:∵∠AOC=50° ∴∠BOD=__________=________( ); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠________( )=180°-________°=________°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.【综合训练】11.下列说法正确的有( )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( )A .62°B .118°C .72°D .59°第12题图 第13题图14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x = . 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为 . 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD=__________=________( );∵OE 平分∠AOD ∴∠AOE=21___________( ) ∵∠AOD+∠AOC=180°∴∠AOD=180°-∠________( )=_________________________=___________ ∠AOE=____________.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数.20.探究题:(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有 个交点,最多有 个交点,对顶角有 对,邻补角有 对.OE DC BA第五章相交线与平行线5.1.1相交线答案知识点1认识邻补角和对顶角1.如图,下列各组角中,互为对顶角的是( A )A.∠1和∠2 B.∠1和∠3 C.∠2和∠4 D.∠2和∠5 2.如图所示,∠1和∠2是对顶角的图形是( C )3.下面四个图形中,∠1与∠2是邻补角的是( D )4.如图所示,AB与CD相交所成的四个角中,∠1的邻补角是∠2,∠4,∠1的对顶角是∠3.知识点2邻补角和对顶角的性质5.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )A.60° B.90° C.120° D.150°6.如图,已知∠1=120°,则∠2的度数是( A )A.120° B.90° C.60°D.30°AB 7.如图,测角器测得工件(圆台)的角度是40度,其测量角的原理是对顶角相等.8.在括号内填写依据:如图,因为直线a ,b 相交于点O , 所以∠1+∠3=180°(邻补角互补), ∠1=∠2(对顶角相等).9.如右图所示,直线AB,CD,EF 相交于点O ,则①∠AOD 的对顶角是_∠BOC__,∠EOC 的对顶角是__∠DOF___ ②∠AOC 的邻补角是_∠AOD____,∠BOE 的邻补角是___∠AOE__. ③若∠AOC=50°,求∠BOD ,∠COB 的度数.解:∵∠AOC=50°∴∠BOD=_∠AOC_=_50°(对顶角相等); ∵∠BOC+∠AOC=180°∴∠COB=180°-∠AOC (邻补角互补) =180°- 50° = 130°10.如图,直线AB ,CD 相交于点O ,∠EOC =70°,OA 平分∠EOC ,求∠BOD 的度数.解:因为OA 平分∠EOC ,∠EOC =70°, 所以∠AOC =12∠EOC =35°.所以∠BOD =∠AOC =35°. 【综合训练】11.下列说法正确的有( B )①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A .1个B .2个C .3个D .4个 12.如图,三条直线l 1,l 2,l 3相交于一点,则∠1+∠2+∠3=( C )A .90°B .120°C .180°D .360°13.如图所示,直线AB 和CD 相交于点O.若∠AOD 与∠BOC 的和为236°,则∠AOC 的度数为( A )A .62°B .118°C .72°D .59° 14.两条直线相交所成的四个角中,有两个角分别是(2x -10)°和(110-x )°,则x=40或80. 15.若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1的度数为135°. 16.如图,直线a ,b ,c 两两相交,∠1=80°,∠2=2∠3,则∠4=140°.17.如图所示, 直线AB,CD 相交于点O,OE 平分∠AOD,∠AOC=120°,求∠BOD,∠AOE 的度数.解:∵∠AOC=120°∴∠BOD= ∠AOC = 120° (对顶角相等); ∵OE 平分∠AOD∴∠AOE=21∠AOD∵∠AOD+∠AOC=180°∴∠AOD=180°-∠AOC (邻补角互补)=180°-120°= 60° ∠AOE= 30°.18.如图,直线AB ,CD 相交于点O ,∠AOE =∠BOE ,OB 平分∠DOF.若∠DOE =50°,求∠DOF 的度数.解:因为∠AOE =∠BOE ,且∠AOE +∠BOE =180°, 所以∠AOE =∠BOE =90°. 因为∠DOE =50°,所以∠DOB =∠BOE -∠DOE =40°.因为OB 平分∠DOF ,所以∠DOF =2∠DOB =80°.OE DCBA19.如图,l 1,l 2,l 3交于点O ,∠1=∠2,∠3∶∠1=8∶1,求∠4的度数. 解:设∠1=∠2=x °,则∠3=8x °. 由∠1+∠2+∠3=180°,得 10x =180.解得x =18. 所以∠1=∠2=18°. 所以∠4=∠1+∠2=36°. 20.探究题:(1)三条直线相交,最少有1个交点,最多有3个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(2)四条直线相交,最少有1个交点,最多有6个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;(3)依次类推,n 条直线相交,最少有1个交点,最多有n (n -1)2个交点,对顶角有n(n -1)对,邻补角有2n(n -1)对.解:(1)图略,对顶角有6对,邻补角有12对. (2)图略,对顶角有12对,邻补角有24对.。
《5.1相交线》练习题
(D)(C)(B)(A)22211121《5.1相交线》练习题一1、下列各图中,∠1和∠2是对顶角的是( )2、已知直线AB 、CD 相交于点O ,则与∠AOC 互补的角有 ( ) A 、1个 B 、2个 C 、3个 D 、4个3、如图,三条直线两两相交,其中对顶角共有 ( ) A 、3对 B 、4对 C 、5对 D 、6对4、如图,直线AB 、CD 交于点O ,OE 、OF 是过O 点的两条射线,其中构成对顶角的是 ( )A 、∠AOF 与 ∠DOEB 、∠EOF 与∠BOEC 、∠BOC 与∠AOD D 、∠COF 与∠BOD5、下列说法错误的是 ( )A 、对顶角的平分线成一个平角B 、对顶角相等C 、相等的角是对顶角D 、对顶角的余角相等 6、如图,直线AB 与CD 相交于点O ,∠AOD+∠BOC=236度,则∠AOC 的度数为 ( )A 、72度B 、62度C 、124度D 、144度 7、如图,点A 到直线CD 的距离是指哪条线段长 ( )A 、ACB 、CDC 、AD D 、BD 8、在“同一平面内,过一点有且只有一条直线与已知直线垂直”中这一点的位置 ( )A 、在直线的上方B 、在直线的下方C 、在直线上D 、可以任意位置9、下列说法中正确的个数有 ( ) (1)直线外一点与直线上各点连接的所有线中垂线段最短。
(2)画一条直线的垂线段可以画无数条。
(3)在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直。
(4)从直线外一点到这条直线的垂线段叫做点到直线的距离。
A 、1个 B 、2个 C 、3个 D 、4个10、如图2-27,∠BAC 和∠ACD 是( )A .同位角B .同旁内角C .内错角D .以上结论都不对O F E D CBA ODCBADABC11、如图2-28,∠1与∠2不能构成同位角的图形是 ( )12、如图2-29,图中共有同旁内角 对A .2B .3C .4D .513、如图2-30,与∠1构成同位角的共有 ( )A .1个B .2个C .3个D .4个 14、如图2-31,下列判断正确的是 [ ]A .4对同位角,4对内错角,2对同旁内角B .4对同位角、4对内错角,4对同旁内角C .6对同位角,4对内错角,4对同旁内角D .6对同位角,4对内错角,2对同旁内角15、如图,直线AB 、CD 相交于点O ,若∠AOC=50度,则∠BOC= ,∠AOD= ∠BOD= 。
人教版七年级数学下册《5.1相交线》同步练习(含答案)
人教版七年级数学下册第五章相交线与平行线 5.1 相交线同步练习一、单选题(共10题;共30分)1.如图所示,∠1和∠2是对顶角的图形有( )A. 1个B. 2个C. 3个D. 4个2.如图,下列说法不正确的是()A. ∠1和∠2是同旁内角B. ∠1和∠3是对顶角C. ∠3和∠4是同位角D. ∠1和∠4是内错角3.如图所示,∠1和∠2是对顶角的是()A. B. C. D.4.下列说法中正确的个数为()①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;③一条直线的垂线可以画无数条;④在同一平面内,经过一个已知点能画一条且只能画一条直线和已知直线垂直.A. 1B. 2C. 3D. 45.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为()A. 75°B. 15°C. 105°D. 165°6.如图所示,下列说法错误的是()A. ∠A和∠B是同旁内角B. ∠A和∠3是内错角C. ∠1和∠3是内错角D. ∠C和∠3是同位角7.如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于()A. 30°B. 34°C. 45°D. 56°8.在下列语句中,正确的是().A. 在平面上,一条直线只有一条垂线;B. 过直线上一点的直线只有一条;C. 过直线上一点且垂直于这条直线的直线有且只有一条;D. 垂线段就是点到直线的距离9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有( )A. 1个B. 2个C. 3个D. 4个10.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是()①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.A. ①②③B. ①②④C. ①③④D. ②③④二、填空题(共10题;共30分)11.如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=________12.如图,已知直线AB与CD相交于点O,OA平分∠COE,若∠DOE=70°,则∠BOD=________.13.如图,∠1和∠2是________角,∠2和∠3 是________角。
相交线教案与练习题
5.1.1 相交线教学目标1.通过动手观察、操作、推断、交流等数学活动,进一步发展空间观念,培养识图能力、推理能力和有条理表达能力.2.在具体情境中了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.重点、难点重点:邻补角、对顶角的概念,对顶角性质与应用.难点:理解对顶角相等的性质的探索.教学过程一、趣味导入1.同学们在上一学期的最后一章,咱们学了线段射线直线那么这一章我们要进行相交线,平行线的学习,那么老师给大家出一个脑筋急转弯儿,大家都知道,动物界的猴子是最聪明的猴子,跟咱们数学也有密切相关的东西,比如说猴子最喜欢的线是什么线呢?最不喜欢的线是什么线?为什么?二.教学内容(复习大一上学期学的锐角,直角,钝角,平角,周角,由平角导入本节课内容)1、认识邻补角和对顶角,探索对顶角性质画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角? 各对角的位置关系如何?根据不同的位置怎么将它们分类?学生思考并在小组内交流,全班交流. ∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线. ∠AOC和∠BOD有公共的顶点O,而是∠AOC的两边分别是∠BOD两边的反向延长线.2.学生用量角器分别量一量各个角的度数,以发现各类角的度数有什么关系,学生得出有“相邻”关系的两角互补,“对顶”关系的两角相等.3.学生根据观察和度量完成下表:5.教师再提问:如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗?得出结论,邻补角相加为180,组成平角。
补充两角互余相加为90.6.黑板上讲解例一。
再次强调总结结论。
7.然后挑同学上黑板上做P3练习。
4.概括形成邻补角、对顶角概念.(1)师生共同定义邻补角、对顶角.有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.5.1.2垂线教学目标:了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义, 并会度量点到直线的距离。
