(2021年整理)行列式练习题答案
高考数学压轴专题2020-2021备战高考《矩阵与变换》专项训练解析附答案

【最新】数学《矩阵与变换》专题解析一、151.关于x 的不等式201x a x+<的解集为()1,b -.()1求实数a ,b 的值;()2若1z a bi =+,2z cos isin αα=+,且12z z 为纯虚数,求tan α的值.【答案】(1)1a =-,2b =(2)12- 【解析】 【分析】(1)由题意可得:1-,b 是方程220x ax +-=的两个实数根,利用根与系数的关系即可得出答案;(2)利用(1)的结果得()()1222z z cos sin cos sin i αααα=--+-为纯虚数,利用纯虚数的定义即可得出. 【详解】 解:(1)不等式201x a x+<即()20x x a +-<的解集为()1,b -. 1∴-,b 是方程220x ax +-=的两个实数根,∴由1b a -+=-,2b -=-,解得1a =-,2b =. (2)由(1)知1,2a b =-=,()()()()121222z z i cos isin cos sin cos sin i αααααα∴=-++=--+-为纯虚数,20cos sin αα∴--=,20cos sin αα-≠,解得12tan α=-.【点睛】本题考查了行列式,复数的运算法则、纯虚数的定义、一元二次方程的根与系数的关系、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.2.a ,b 满足什么条件时,关于x ,y ,z 的方程组4424ax y z x by z x by z ++=⎧⎪++=⎨⎪++=⎩有唯一解.【答案】当0b ≠且1a ≠时 【解析】 【分析】计算对应行列式为()111110121aD bb a b ==-≠,计算得到答案.【详解】4424ax y z x by z x by z ++=⎧⎪++=⎨⎪++=⎩有唯一解,则()1111212110121a D b ab b b ab b a b ==++---=-≠ 所以当0b ≠且1a ≠时有唯一解 【点睛】本题考查了方程组的唯一解问题,意在考查学生的计算能力.3.解方程组()sin cos 2cos 0cos cos 2sin x y x y ααααπααα-=⎧≤≤⎨+=⎩.【答案】见解析. 【解析】 【分析】求出行列式D 、x D 、y D ,对D 分0D ≠和0D =两种情况分类讨论,利用方程组的解与行列式之间的关系求出方程组的解,或者将参数的值代入方程组进行求解,由此得出方程组的解. 【详解】由题意得()sin cos2cos cos2sin cos cos2D ααααααα=+=+,()cos cos2sin cos2sin cos cos2x D ααααααα=+=+,22sin cos cos2y D ααα=-=-.0απ≤≤Q ,022απ∴≤≤.①当0D ≠时,即当cos20α≠时,即当22πα≠且322πα≠时,即当4πα≠且34πα≠时,11sin cos x y D x DD y D αα⎧==⎪⎪⎨⎪==-⎪+⎩; ②当4πα=时,方程组为2222x x =⎪⎪⎪=⎪⎩,则该方程组的解为1x y R =⎧⎨∈⎩;③当34πα=时,方程组为2222x x =-⎪⎪⎨⎪-=⎪⎩,该方程组的解为1x y R =-⎧⎨∈⎩. 【点睛】本题考查二元一次方程组的求解,解题时要对系数行列式是否为零进行分类讨论,考查运算求解能力,属于中等题.4.不等式21101x xba xa->-的解是12x <<,试求a ,b 的值. 【答案】12a =-,1b =-或1a =-,2b =- . 【解析】 【分析】将行列式展开,由行列式大于0,即ax 2+(1+ab )x +b >0,由1和2是方程ax 2+(1+ab )x +b =0的两个根,由韦达定理可知,列方程组即可求得a 和b 的值. 【详解】2111x xb a x a -=-x 2×(﹣a )×(﹣1)+x +abx ﹣x 2×(﹣a )﹣ax 2﹣(﹣1)×b =ax 2+(1+ab )x +b >0,∵不等式的解为1<x <2,∴a <0,且1,2为一元二次方程:ax 2+(1+ab )x +b =0的两个根,由韦达定理可知:11212ab ab a +⎧+=-⎪⎪⎨⎪⨯=⎪⎩,整理得:2a 2+3a +1=0,解得:12a b =-⎧⎨=-⎩或121a b ⎧=-⎪⎨⎪=-⎩,故a =﹣1,b =﹣2或a 12=-,b =﹣1. 【点睛】本题考查行列式的展开,考查一元二次不等式与一元二次方程的关系及韦达定理,考查计算能力,属于中档题.5.已知直线1l :420mx y m +--=,2l :0x my m +-=,分别求实数m 满足什么条件时,直线1l 与2l 相交?平行?重合?【答案】当2m ≠且2m ≠-时,相交;当2m =-时,平行;当2m =时,重合 【解析】 【分析】计算出(2)(2)D m m =+-,(2)x D m m =-(1)(2)y D m m =+-,讨论是否为0得到答案. 【详解】42mx y m x my m +=+⎧⎨+=⎩244(2)(2)1m D m m m m==-=+-,24(2)4(2)x m D m m m m m mm+==+-=-22(2)(1)(2)1y m m D m m m m m+==-+=+-(1)当2m ≠且2m ≠-时,0D ≠,方程组有唯一解,1l 与2l 相交 (2)当2m =-时,0,80x D D ==≠,1l 与2l 平行 (3)当2m =时,0x y D D D ===,1l 与2l 重合 【点睛】本题考查了直线的位置关系,意在考查学生的计算能力.6.定义()111111n n n n x x n N y y +*+-⎛⎫⎛⎫⎛⎫=∈ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭为向量()111,n n n OP x y +++=u u u u u v 的一个矩阵变换, (1)若()12,3P ,求2OP u u u v ,3OP u u u v; (2)设向量()11,0OP =u u u v ,O 为坐标原点,请计算9OP u u u v 并探究2017OP u u u u u u v的坐标. 【答案】(1)()21,5OP =-u u u v ,()36,4OP =-u u u v ;(2)()25216,0. 【解析】 【分析】(1)根据递推关系可直接计算2OP uuu r ,3OP u u ur .(2)根据向量的递推关系可得816n n OP OP +=u u u u u ru u u r 对任意的*n N ∈恒成立,据此可求9OPu u u r、2017OP u u u u u u r的坐标.【详解】(1)因为()12,3P ,故123OP⎛⎫= ⎪⎝⎭u u u r ,设2x OP y ⎛⎫= ⎪⎝⎭u u u r , 则11211135x y --⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,所以215OP -⎛⎫= ⎪⎝⎭u u u r 即()21,5OP =-u u u r ,同理()36,4OP =-u u u r .(2)因为111111n n n n x x y y ++-⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以11n n n n nn x x y y x y ++-⎛⎫⎛⎫= ⎪ ⎪+⎝⎭⎝⎭, 故21121122n n n n n n n n x x y y y x y x ++++++--⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭,3223222222n n n n n n n n n n x x y y x y x y y x ++++++---⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪+-+⎝⎭⎝⎭⎝⎭,43343344n n n n n n n n x x y x y x y y ++++++--⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪+-⎝⎭⎝⎭⎝⎭,所以44n n OP OP +=-u u u u u r u u u r ,故816n n OP OP +=u u u u u r u u u r . 又9811=⨯+,20174504182521=⨯+=⨯+,()911616,0OP OP ==u u u r u u u r所以()252252201711616,0OP OP ==u u u u u u r u u u r . 【点睛】本题考查向量的坐标计算及向量的递推关系,解题过程中注意根据已知的递推关系构建新的递推关系,此问题为中档题.7.[选修4-2:矩阵与变换]已知矩阵11a A b ⎡⎤=⎢⎥-⎣⎦的一个特征值为2,其对应的一个特征向量为21α⎡⎤=⎢⎥⎣⎦. 若x a A y b ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,求x ,y 的值.【答案】x ,y 的值分别为0,1.【解析】试题分析:利用矩阵的乘法法则列出方程,解方程可得x ,y 的值分别为0,1. 试题解析:由条件知,2A αα=,即][1222111a b ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦,即][2422a b +⎡⎤=⎢⎥-+⎣⎦, 所以24,{22,a b +=-+= 解得2,{ 4.a b == 所以1214A ⎡⎤=⎢⎥-⎣⎦. 则][][][12221444xx x y A y y x y +⎡⎤⎡⎤===⎢⎥⎢⎥--+⎣⎦⎣⎦,所以22,{44,x y x y +=-+= 解得0,{ 1.x y == 所以x ,y 的值分别为0,1.8.解关于x 、y 、z 的三元一次方程组231231x y z x y az ay z +-=-⎧⎪-+=-⎨⎪-=⎩,并对解的情况进行讨论.【答案】答案不唯一,见解析 【解析】【分析】根据题意,分别求出D 、x D 、y D 、z D 关于a 的表达式,再由三元一次方程组解的公式对a 的取值进行讨论,即可得到原方程组解的各种情况. 【详解】(1)(25)D a a =--+,(11)(1)x D a a =+-,22y D a =-,55z D a =-;① 当1a =,0x y z D D D D ====,方程组有无穷多解; ② 当52a =-,0D =,且x D 、y D 、z D 不为零,方程组无解; ③ 当1a ≠且52a ≠-时,方程组的解为1125a x a +=-+,225y a =+,525z a =-+. 【点睛】本题考查三元一次方程组的行列式解法,解题关键是要分类讨论,属于常考题.9.已知1m >,1n >,且1000mn <,求证:lg 901lg 4m n <. 【答案】证明见解析 【解析】 【分析】由题意,求得11000mn <<,利用基本不等式,得到2lg lg 90lg lg 24m n m n +⎛⎫<<=⎪⎝⎭,再结合行列式的运算,即可求解. 【详解】由题意,实数1m >,1n >,且1000mn <,可得11000mn <<,则2lg lg 90lg lg 24m n m n +⎛⎫<<=⎪⎝⎭,又由lg 919lg ln 9lg ln 144lg 4m m n m n n=-⨯=-,所以lg 901lg 4m n <. 【点睛】本题主要考查了行列式的运算性质,以及对数的运算性质和基本不等式的应用,其中解答中熟记行列式的运算法则,以及合理应用对数的运算和基本不等式求解是解答的关键,着重考查了推理与运算能力,属于中档试题.10.已知等比数列{}n a 的首项11a =,公比为()0q q ≠.(1)求二价行列式1324a a a a 的值; (2)试就q 的不同取值情况,求解二元一次方程组132432a x a y a x a y +=⎧⎨+=⎩.【答案】(1)0;(2)当23q =时,方程组无数解,且439x ty t⎧=-⎪⎨⎪=⎩,t R ∈;当23q ≠且0q ≠时,方程组无解.【解析】 【分析】(1)由行列式定义计算,再根据等比数列的性质得结论; (2)由二元一次方程组解的情况分析求解. 【详解】(1)∵{}n a 是等比数列,∴1423a a a a =, ∴1324a a a a 14230a a a a =-=. (2)由(1)知方程组无解或有无数解.当241323a a q a a ===时,方程组有无数解,此时方程组中两个方程均为439x y +=, 解为439x t y t⎧=-⎪⎨⎪=⎩,当23q ≠且0q ≠时,方程组无解. 【点睛】本题考查行列式的概念,考查等比数列的性质,考查二元一次方程组的解的情况.掌握二元一次方程组的解的情况的判断是解题基础.11.已知a ,b R ∈,点()1,1P -在矩阵13a A b ⎡⎤=⎢⎥⎣⎦对应的变换下得到点()1,3Q . (1)求a ,b 的值;(2)求矩阵A 的特征值和特征向量;(3)若向量59β⎡⎤=⎢⎥⎣⎦u r,求4A βu r .【答案】(1)20a b =⎧⎨=⎩;(2)矩阵A 的特征值为1-,3,分别对应的一个特征值为13⎡⎤⎢⎥-⎣⎦,11⎡⎤⎢⎥⎣⎦;(3)485489⎡⎤⎢⎥⎣⎦【解析】 【分析】(1)直接利用矩阵的乘法运算即可; (2)利用特征多项式计算即可;(3)先计算出126βαα=-+u r u u ru u r ,再利用()4444121266A A A A βαααα=-+=-+u r u u r u u r u u r u u r 计算即可得到答案. 【详解】 (1)由题意知,11113133a a b b -⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦, 则1133a b -=⎧⎨-=⎩,解得2a b =⎧⎨=⎩. (2)由(1)知2130A ⎡⎤=⎢⎥⎣⎦,矩阵A 的特征多项式()()21233f λλλλλ--==---, 令()0f λ=,得到A 的特征值为11λ=-,13λ=. 将11λ=-代入方程组()2030x y x y λλ⎧--=⎨-+=⎩,解得3y x =-,所以矩阵A 的属于特征值1-的一个特征向量为113α⎡⎤=⎢⎥-⎣⎦u u r. 再将13λ=代入方程组()2030x y x y λλ⎧--=⎨-+=⎩,解得y x =,所以矩阵A 的属于特征值3的一个特征向量为211α⎡⎤=⎢⎥⎣⎦u u r.综上,矩阵A 的特征值为1-,3,分别对应的一个特征值为13⎡⎤⎢⎥-⎣⎦,11⎡⎤⎢⎥⎣⎦.(3)设12m n βαα=+u ru u r u u r ,即5119313m n m n m n +⎡⎤⎡⎤⎡⎤⎡⎤=+=⎢⎥⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦⎣⎦⎣⎦, 所以539m n m n +=⎧⎨-+=⎩,解得16m n =-⎧⎨=⎩,所以126βαα=-+u r u u r u u r ,所以()4444121266A A A A βαααα=-+=-+u r u u r u u r u u r u u r()441148516331489⎡⎤⎡⎤⎡⎤=--+⨯=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦. 【点睛】本题考查矩阵的乘法、特征值、特征向量,考查学生的基本计算能力,是一道中档题.12.设函数()271f x x ax =-++(a 为实数). (1)若1a =-,解不等式()0f x ≥; (2)若当01xx>-时,关于x 的不等式()1f x ≥成立,求a 的取值范围; (3)设21()1x g x ax +=--,若存在x 使不等式()()f x g x ≤成立,求a 的取值范围. 【答案】(1)8{|3x x ≤或6}x ≥;(2)[5,)-+∞;(3)[4,)-+∞ 【解析】 【分析】(1)代入1a =-直接解不等式即可; (2)由01xx>-解得01x <<,故可将()1f x ≥化为(2)70a x -+≥,从而求出a 的范围; (3)化简()g x ,故可将题设条件变为:存在x 使1|27||22|a x x -≥---成立,因此求出2722x x ---的最小值即可得出结论.【详解】(1)若1a =-,则()271f x x x =-+- 由()0f x ≥得|27|1x x -≥-, 即270271x x x ->⎧⎨-≥-⎩或270721x x x -≤⎧⎨-≥-⎩, 解得6x ≥或83x ≤, 故不等式的解集为8{|3x x ≤或6}x ≥; (2)由01xx>-解得01x <<, 由()1f x ≥得|27|0x ax -+≥,当01x <<时,该不等式即为(2)70a x -+≥, 设()(2)7F x a x =-+,则有(0)70(1)50F F a =>⎧⎨=+≥⎩解得5a ≥-,因此实数a 的取值范围为[5,)-+∞;(3)21()1x g x a x +=--2|1|(1)x a x =-++, 若存在x 使不等式()()f x g x ≤成立,即存在x 使271x ax -++2|1|(1)x a x ≤-++成立, 即存在x 使1|27||22|a x x -≥---成立, 又272227(22)5x x x x ---≤---=, 所以527225x x -≤---≤, 所以15a -≥-,即4a ≥-, 所以a 的取值范围为:[4,)-+∞ 【点睛】本题主要考查了绝对值不等式,结合了恒成立,能成立等问题,属于综合应用题.解决恒成立,能成立问题时,常将其转化为最值问题求解.13.用行列式讨论下列关于x 、y 、z 的方程组121ax y z x y az x y z --=⎧⎪+-=⎨⎪--=⎩的解的情况,并求出相应的解.【答案】(i )当1a ≠±时有唯一解.∴方程组的解为:02131x a y a z a ⎧⎪=⎪-⎪=⎨+⎪⎪=-⎪+⎩;(ii )当1a =-时,无解;(iii) 当1a =时,有无穷多解.∴通解为:3212x t y z t ⎧=+⎪⎪⎪=⎨⎪=⎪⎪⎩.【解析】 【分析】首先由二元一次方程组得到矩阵:,,,x y z D D D D ,然后根据条件判断a 的不同取值方程组解的情况,并分类讨论. 【详解】方程组可转化为: 1 111 1 21 1 11a x a y z --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦2 1 11 1 1(1)(1)1 1 1a D a a a a --=-=-=-+---,21 1 1 1 1 1 12 1 0, 1 2 32, 1 1 2331 1 11 1 11 1 1x y z a a D a D a a a D a ----=-==-=-+==-----Q(i )当1a ≠±时有唯一解.∴方程组的解为:02131x a y a z a ⎧⎪=⎪-⎪=⎨+⎪⎪=-⎪+⎩;(ii )当1a =-时,无解;(iii ) 当1a =时,有无穷多解.∴通解为:3212x t y z t ⎧=+⎪⎪⎪=⎨⎪=⎪⎪⎩.【点睛】本题考查了二元一次方程组和矩阵形式、以及行列式值的计算,考查了学生概念理解,数学运算的能力,属于中档题.14.已知曲线C :x 2+2xy +2y 2=1,矩阵A =1210⎡⎤⎢⎥⎣⎦所对应的变换T 把曲线C 变成曲线C 1,求曲线C 1的方程. 【答案】x 2+y 2=2 【解析】试题分析:由矩阵变换得相关点坐标关系x =y′,y =2x y '-',再代入已知曲线C 方程,得x 2+y 2=2.试题解析:解:设曲线C 上的任意一点P(x ,y),P 在矩阵A =1210⎡⎤⎢⎥⎣⎦对应的变换下得到点Q(x′,y′).则1210x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎣'⎦⎦', 即x +2y =x′,x =y′, 所以x =y′,y =2x y '-'.代入x 2+2xy +2y 2=1,得y′2+2y′2x y '-'+2(2x y '-')2=1,即x′2+y′2=2, 所以曲线C 1的方程为x 2+y 2=2.考点:矩阵变换,相关点法求轨迹方程15.[选修4-2:矩阵与变换]已知矩阵A=0110⎡⎤⎢⎥⎣⎦ ,B=1002⎡⎤⎢⎥⎣⎦. 求AB;若曲线C 1;22y =182x + 在矩阵AB 对应的变换作用下得到另一曲线C 2 ,求C 2的方程.【答案】(1)0210⎡⎤⎢⎥⎣⎦(2)228x y += 【解析】试题分析:(1)直接由矩阵乘法可得;(2)先根据矩阵乘法可得坐标之间关系,代入原曲线方程可得曲线2C 的方程.试题解析:解:(1)因为A =0110⎡⎤⎢⎥⎣⎦, B =1002⎡⎤⎢⎥⎣⎦, 所以AB =01101002⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦ 0110⎡⎤⎢⎥⎣⎦ 1002⎡⎤⎢⎥⎣⎦=0210⎡⎤⎢⎥⎣⎦ 0210⎡⎤⎢⎥⎣⎦. (2)设()00,Q x y 为曲线1C 上的任意一点, 它在矩阵AB 对应的变换作用下变为(),P x y ,则000210x x y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即002y x x y =⎧⎨=⎩,所以002x yx y =⎧⎪⎨=⎪⎩. 因为()00,Q x y 在曲线1C 上,所以2200188x y +=,从而22188x y +=,即228x y +=.因此曲线1C 在矩阵AB 对应的变换作用下得到曲线2C : 228x y +=. 点睛:(1)矩阵乘法注意对应相乘:a b m p am bn ap bq c d n q cm dn cp dq ++⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦;(2)矩阵变换:a b x x c d y y ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎣'⎦⎦'表示点(,)x y 在矩阵a b c d ⎡⎤⎢⎥⎣⎦变换下变成点(,)x y ''.16.矩阵与变换:变换1T 是逆时针旋转2π的旋转变换,对应的变换矩阵是1M 变换2T 对应用的变换矩阵是21101M ⎡⎤=⎢⎥⎣⎦求曲线221x y +=的图象依次在12,T T 变换的作用下所得曲线的方程.【答案】22221x xy y -+= 【解析】 【分析】旋转变换矩阵10110M -⎡⎤=⎢⎥⎣⎦,求出211110M M M -⎡⎤==⎢⎥⎣⎦,设x y ⎡⎤⎢⎥⎣⎦是变换后曲线上任一点,与之对应的变换前的点是00x y ⎡⎤⎢⎥⎣⎦,得到00x y y y x =⎧⎨=-⎩,即得解. 【详解】旋转变换矩阵10110M -⎡⎤=⎢⎥⎣⎦记21110111011010M M M --⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦设x y ⎡⎤⎢⎥⎣⎦是变换后曲线上任一点,与之对应的变换前的点是00x y ⎡⎤⎢⎥⎣⎦,面积00x x M y y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦,也就是000x x y y x =-⎧⎨=⎩,即00x y y y x =⎧⎨=-⎩,代入22001x y +=,得22()1y y x +-=,所以所求曲线的方程是22221x xy y -+= 【点睛】本题主要考查矩阵和变换,意在考查学生对这些知识的理解掌握水平和分析推理能力.17.已知矩阵1214A ⎡⎤=⎢⎥-⎣⎦,向量32α⎡⎤=⎢⎥⎣⎦,计算5A α. 【答案】5307275A α⎡⎤=⎢⎥⎣⎦【解析】 【分析】根据()0f λ=,得2λ=或3λ=,得到特征向量121α⎡⎤=⎢⎥⎣⎦,211α⎡⎤=⎢⎥⎣⎦,故()55551212A A A A ααααα=+=+,计算得到答案.【详解】 因为212()5614f λλλλλ--==-+-,由()0f λ=,得2λ=或3λ=.当2λ=时,对应的一个特征向量为121α⎡⎤=⎢⎥⎣⎦; 当3λ=时,对应的一个特征向量为211α⎡⎤=⎢⎥⎣⎦. 设321211m n ⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,解得11m n =⎧⎨=⎩,所以()55551212A A A A ααααα=+=+ 5521307121311275⎡⎤⎡⎤⎡⎤=⨯+⨯=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. 【点睛】本题考查了矩阵的计算,意在考查学生的计算能力.18.已知变换T 将平面上的点11,2⎛⎫⎪⎝⎭,(0,1)分别变换为点9,24⎛⎫- ⎪⎝⎭,3,42⎛⎫- ⎪⎝⎭.设变换T对应的矩阵为M . (1)求矩阵M ; (2)求矩阵M 的特征值.【答案】(1)33244M ⎡⎤-⎢⎥=⎢⎥-⎣⎦(2)1或6【解析】 【分析】(1)设a b M c d ⎡⎤=⎢⎥⎣⎦,根据变换可得关于a b c d ,,,的方程,解方程即可得到答案; (2)求出特征多项式,再解方程,即可得答案; 【详解】(1)设a b M c d ⎡⎤=⎢⎥⎣⎦,则194122a b cd ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦-⎣⎦⎣⎦,30214a b c d ⎡⎤-⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,即1924122324a b c d b d ⎧+=⎪⎪⎪+=-⎪⎨⎪=-⎪⎪⎪=⎩,解得33244a b c d =⎧⎪⎪=-⎪⎨⎪=-⎪=⎪⎩,则33244M ⎡⎤-⎢⎥=⎢⎥-⎣⎦.(2)设矩阵M 的特征多项式为()f λ,可得233()(3)(24)676244f λλλλλλ-==---=-+-, 令()0f λ=,可得1λ=或6λ=. 【点睛】本题考查矩阵的求解、矩阵M 的特征值,考查函数与方程思想、转化与化归思想,考查运算求解能力.19.已知矩阵1101A ⎡⎤=⎢⎥-⎣⎦,0614B ⎡⎤=⎢⎥-⎣⎦.若矩阵C 满足AC B =,求矩阵C 的特征值和相应的特征向量.【答案】特征值12λ=,相应的特征向量21⎡⎤⎢⎥⎣⎦;特征值23λ=,相应的特征向量11⎡⎤⎢⎥⎣⎦【解析】 【分析】设a b C c d ⎡⎤=⎢⎥⎣⎦,由矩阵乘法法则求得矩阵C ,再由特征多项式求得特征值,再得特征向量. 【详解】解:设a b C c d ⎡⎤=⎢⎥⎣⎦,由AC B =,即11060114a b c d ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦, 得0164a c c b d d +=⎧⎪-=⎪⎨+=⎪⎪-=-⎩,解得1214a b c d =⎧⎪=⎪⎨=-⎪⎪=⎩,所以1214C ⎡⎤=⎢⎥-⎣⎦. 设()()()2121425614fλλλλλλλ--==--+=-+-,令()0f λ=,得12λ=,23λ=,特征向量为x y ⎡⎤⎢⎥⎣⎦,当12λ=时,20x y -=,取121α⎡⎤=⎢⎥⎣⎦u u r;当23λ=时,220x y -=,取211α⎡⎤=⎢⎥⎣⎦u u r .【点睛】本题考查矩阵的乘法运算,考查特征值和特征向量,掌握矩阵乘法运算法则与特征多项式概念是解题基础.20.已知数列{}n a 满足条件1(1)(1)(1)n n n a n a +-=+-,且26a = (1)计算134,,a a a ,请猜测数列{}n a 的通项公式,并用数学归纳法证明;(2)请分别构造一个二阶和三阶行列式,使它们的值均为n a ,其中,要求所构造的三阶行列式主对角线下方的元素均为零,并用按某行或者某列展开的方法验证三阶行列式的值为n a【答案】(1)1341,15,28a a a ===,22n a n n =-;证明见解析 (2)2=1n n n a n,211101=001n n n a -,验证见解析 【解析】 【分析】(1)分别将1,2,3n =代回即可求得134,,a a a ,可猜测22n a n n =-,根据数学归纳法证明即可;(2)由(1)可构造二阶行列式为21n n n,根据要求可构造三阶行列式为211101001n n -,并展开求值进行验证即可 【详解】(1)当1n =时,()1021a =-,即11a =; 当2n =时,()()323136115a a =-=⨯-=; 当3n =时,()43241a a =-,则428a =;猜测22n a n n =-,证明:当1,2,3,4n =时,22n a n n =-成立; 假设当()5n k k =≥时,22k a k k =-成立,则()()()1111k k k a k a +-=+-,所以()()()()()2221112121123121111k k k a k k k k k k k k k k +++=--=+-=++=+-+--, 即当1n k =+时,等式也成立,综上,22n a n n =-成立(2)由(1),因为2221n a n n n n n =-=⋅-⋅,则可构造二阶行列式为21n n n;因为要求所构造的三阶行列式主对角线下方的元素均为零,可构造三阶行列式为211101001n n -,检验,()()()221110121110212001n n n n n n n n n a -=-⋅-⋅=-=-=,故该三阶行列式符合题意 【点睛】本题考查利用数学归纳法证明,考查行列式的应用,考查数列的通项公式,考查数列的项,考查运算能力,考查猜测推理的能力。
线性代数1_2章精选练习题

线性代数1_2章精选练习题第一章行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n (C) k n 2! (D)k n n 2)1(3. n 阶行列式的展开式中含1122a a 的项共有( )项.(A) 0 (B)2 n (C) )!2( n (D) )!1( n4.001001001001000( ).(A) 0 (B)1 (C) 1 (D) 25.001100000100100( ).(A) 0 (B)1 (C) 1 (D) 26.在函数10323211112)(x x x xx f 中3x 项的系数是( ).(A) 0 (B)1 (C) 1 (D) 27. 若21333231232221131211a a a a a a a a a D ,则 323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4 (C) 2 (D) 28.若a a a a a 22211211,则21112212ka a ka a ( ).(A)ka (B)ka (C)a k 2 (D)a k 29.已知4阶行列式中第1行元依次是3,1,0,4 , 第3行元的余子式依次为x ,1,5,2 , 则 x ( ).(A) 0 (B)3 (C) 3 (D) 210. 若5734111113263478D ,则D 中第一行元的代数余子式的和为( ).(A)1 (B)2 (C)3 (D)011. 若22351011110403D ,则D 中第四行元的余子式的和为( ).(A)1 (B)2 (C)3 (D)012. k 等于下列选项中哪个值时,齐次线性方程组00321321321x x kx x kx x kx x x 有非零解.( )(A)1 (B)2 (C)3 (D)0二、填空题1. n 2阶排列)12(13)2(24 n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是. 4.若一个n 阶行列式中至少有12 n n 个元素等于0, 则这个行列式的值等于.5. 行列式100111010100111.6.行列式100002000010nn .7.行列式01)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D 3332312322211312113233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式1111111111111111x x x x .11.n 阶行列式111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321D ,j A 4)4,3,2,1( j 为D 中第四行元的代数余子式,则44434241234A A A A .14.已知db c a cc a b b a b c a c, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321D ,j A 4为)4,3,2,1(4 j a j 的代数余子式,则4241A A ,4443A A .16.已知行列式nn D10301002112531,D 中第一行元的代数余子式的和为.17.齐次线性方程组020232121321x x x kx x x x kx 仅有零解的充要条件是. 18.若齐次线性方程组230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a db a dc a dc bd c b a dcbad c b a33332222; 2.yxyx x y x y y x y x ;3.解方程0011011101110 x x xx ; 4.111111321321221221221 n n n n a a a a x a a a a x a a a a x a a a a x ;5. na a a a111111111111210(n j a j ,,1,0,1 );6. bn b b )1(1111211111311 117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a xa a a a x a a a a x n nn321212121;9.2212221212121111nn n nn x x x x x x x x x x x x x x x ; 10.21 120000021000121 0001211.aa a aa a a a aD 110110001100001.四、证明题1.设1 abcd ,证明:011111111111122222222dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a x b a .3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b a d c b a . 4.nni in nn n n n n n nna aa aaaaa aa a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明01 11333 c b a c ba 的充要条件是0 cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题2.”“ ;3.43312214a a a a ;4.0;5.0;6.!)1(1n n ;7.1)1(212)1()1(n n n n n a a a ; 8.M 3 ; 9.160 ; 10.4x ; 11.1)( n n ;12.2 ; 13.0; 14.0; 15.9,12 ; 16.)11(!1 nk k n ; 17.3,2 k ;18.7 k 三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ; 2. )(233y x ; 3. 1,0,2 x ; 4.11)(n k kax5.)111()1(00nk knk k a a ; 6. ))2(()1)(2(b n b b ; 7. nk k kna b1)()1(; 8. nk k nk k a x a x 11)()(;9. nk k x 11; 10. 1 n ;11. )1)(1(42a a a . 四. 证明题 (略)第二章矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
高考数学线性代数练习题及答案

高考数学线性代数练习题及答案题目1:已知矩阵A = [2 1; 3 4],求矩阵A的逆矩阵。
解答:首先,我们计算矩阵A的行列式|A|,由行列式的定义可得:|A| = (2*4) - (1*3) = 8 - 3 = 5由于矩阵A的行列式不为0,所以矩阵A是可逆的。
接下来,我们需要求出矩阵A的伴随矩阵adj(A)。
矩阵A的伴随矩阵adj(A)的元素a_ij为A的代数余子式C_ij乘以(-1)^(i+j),即:adj(A) = [4 -1; -3 2]接下来,我们可以求解矩阵A的逆矩阵A_inv。
根据矩阵A的逆矩阵的计算公式,逆矩阵A_inv等于矩阵A的伴随矩阵adj(A)除以矩阵A的行列式|A|,即:A_inv = adj(A) / |A| = [4/5 -1/5; -3/5 2/5]综上所述,矩阵A的逆矩阵为:A_inv = [4/5 -1/5; -3/5 2/5]题目2:已知线性方程组:3x + 2y = 74x - 5y = 2求解该线性方程组的解。
解答:为了求解该线性方程组,我们可以使用矩阵的表示和运算方法。
首先,我们可以将该线性方程组的系数矩阵A和常数矩阵B表示如下:A = [3 2; 4 -5]B = [7; 2]为了求解线性方程组的解,我们需要求解方程组的增广矩阵[A | B]的行最简形。
对增广矩阵[A | B]进行初等行变换,将其化简为行最简形:[R2 - (4/3)R1][A | B] -> [1 -4/3; 0 -19/3 | -19/3 -4/3]化简后的行最简形为:1 -4/3 | -19/30 -19/3 | -19/3 -4/3从化简后的行最简形可以看出,方程组的解为:x = -19/3y = -19/3 -4/3 = -7综上所述,该线性方程组的解为:x = -19/3y = -7题目3:已知矩阵A = [1 2 3; 4 5 6; 7 8 9],求矩阵A的秩。
解答:要求矩阵A的秩,首先需要明确矩阵秩的定义。
2020-2021(1)《线性代数A》A卷参考答案
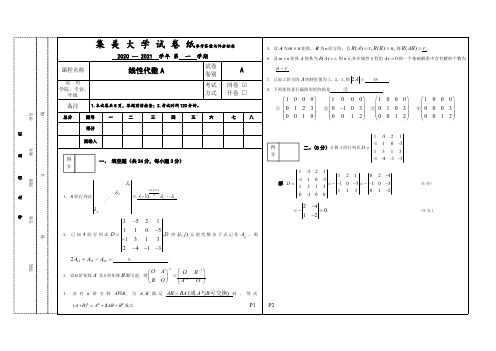
3 ,1)T . 2
(3) 当 k 1时 R( A) 1; 当 k 2 时 R( A) 2; 当 k 1且 k 2 时 R( A) 3.
(12 分) (15 分)
P5
x1 3x2 2x3 x4 3
得 分
六、(12
分)求非齐次线性方程组
x1 x1
x2 x2
x4 x3
1 2
五
六
七
八
得分
阅卷人
得
一、 填空题(共 24 分,每小题 3 分)
分
1. n 阶行列式
1
2
n ( n 1)
(1) 2 1n .
n
3 5 2 1
2. 已 知 4 阶 行 列 式 D 1 1 1 3
0 5 1 3 ,D 的 (i, j) 元 的 代 数 余 子 式 记 作 Aij , 则
2 4 1 3
学院
考 专业 装
生
信
息 姓名
班级
栏 学号 线
订
集 美 大 学 试 卷 纸参考答案与评分标准
2020 — 2021 学年 第 一 学期
课程名称
适用 学院、专业、
年级
线性代数 A
试卷 卷别
考试 方式
A
闭卷 □√ 开卷 □
备注
1.本试卷共 8 页,答题前请检查;2.考试时间 120 分钟。
总分
题号
一
二
三
四
生
信
息 姓名
班级
栏 学号 线
订
1 2 3k
得
五、(15
分)设矩阵
A
1 k
2k 2
3 3
,
分
(1)求行列式 A ;
线性代数第一章习题答案

习 题 1-11.计算下列二阶行列式: (1)xx 11; (2)ααααsin cos cos sin -.解 (1)()11112-=-=x x xx .(2)1)cos (sin sin cos cos sin 22=--=-αααααα.2.计算下列三阶行列式:(1)121223112--; (2)00000d c b a ; (3)222111c b a c ba; (4)cb a b a ac b a b a a cb a ++++++232. 解 (1)原式5)2(2213)1(12112)1()2(31122=-⨯⨯-⨯⨯--⨯⨯-⨯⨯-+-⨯⨯+⨯⨯=. (2)原式00000000000=⋅⋅-⋅⋅-⋅⋅-⋅⋅+⋅⋅+⋅⋅=dc b a c ad b . (3)原式))()((222222b c a c a b c b ac b a c a ab bc ---=---++=. (4)原式)()()2()23)((b a ac c b a ab b a ac c b a b a a +-++++++++=3)23())(2(a c b a ab c b a b a a =++-+++-.3.证明下列等式:=333231232221131211a a a a a a a a a 3332232211a a a aa 3331232112a a a a a -3231222113a a a a a +.证明 333231232221131211a a a a a a a a a 322311332112312213322113312312332211a a a a a a a a a a a a a a a a a a ---++=)()()(312232211331233321123223332211a a a a a a a a a a a a a a a -+---=3332232211a a a a a =3331232112a a a a a -3231222113a a a a a +.4.用行列式解下列方程组:(1)⎩⎨⎧=+=+643534y x y x ; (2)⎪⎩⎪⎨⎧-=-+=++-=+-1236132321321321x x x x x x x x x .解 (1)74334==D ,246351==D ,963542==D ,所以 721==D D x ,792==D D y . (2)23213111132-=--=D ,232111161311-=----=D , 462131611122-=---=D ,691136111323-=---=D ; 所以 111==D D x ,222==D Dx ,333==DD x .习 题 1-21.按自然数从小到大为标准次序,求下列各排列的逆序数: (1)4321; (2)2314; (3)1243; (4)3142;(5))2(42)12(31n n -; (6)2)22()2()12(31 --n n n .解 (1)是标准排列,其逆序数为0; (2)逆序有(4 1),(4 3),(4 2),(3 2),所以逆序数为4. (3)逆序有(3 2),(3 1),(4 2),(4 1),(2 1),所以逆序数为5. (4)逆序有(2 1),(4 1),(4 3),所以逆序数为3. (5)逆序有(3 2) 1个 (5 2),(5 4) 2个 (7 2),(7 4),(7 6) 3个 …………………()12(-n 2),()12(-n 4),()12(-n 6),…,()12(-n )22(-n ) )1(-n 个所以逆序数为 2)1(21-=+++n n n . (6)逆序有(3 2) 1个 (5 2),(5 4) 2个 …………………()12(-n 2),()12(-n 4),()12(-n 6),…,()12(-n )22(-n ) )1(-n 个 (4 2) 1个 (6 2),(6 4) 2个 …………………()2(n 2),()2(n 4),()2(n 6),…,()2(n )22(-n ) )1(-n 个所以逆序数为 )1(12)1()1(21-=+++-+-+++n n n n .2.写出四阶行列式中含有因子2311a a 的项.解 由定义知,四阶行列式的一般项为43214321)1(p p p p a a a a τ-,其中τ为4321p p p p 的逆序数.由于3,121==p p 已固定,4321p p p p 只能形如13□□,即1324或1342.对应的t 分别为10100=+++或22000=+++,所以44322311a a a a -和42342311a a a a 为所求.3.在5阶行列式)det(ij a =D 展开式中,下列各项应取什么符号?为什么? (1)5145342213a a a a a ; (2)2544133251a a a a a ; (3)2344153251a a a a a ; (4)4512345321a a a a a . 解 (1)因5)32451(=τ,所以前面带“-”号. (2)因7)53142(=τ,所以前面带“-”号.(3)因10)12543()53142(=+ττ,所以前面带“+”号. (4) 因7)13425()25314(=+ττ,所以前面带“-”号.4.若n 阶行列式)det(ij a =D 中元素ij a ),,2,1,(n j i =均为整数,则D 必为整数.这一结论对吗?为什么?解 这一结论正确,因整数经乘法运算后仍为整数,而D 为元素的乘法的代数和,因此结果仍为整数.5.证明:若n 阶行列式中有n n -2个以上的元素为零,则该行列式值为零.证明 因n 阶行列式中有2n 个元素,而有n n -2个以上元素为零,故不为零的元素的个数小于n .从而,在行列式展开式中的n 个元素的乘积项中至少有一个元素为零,所以乘积为零,代数和也为零,故该行列式的值为零.6.用行列式定义计算下列行列式:(1)0001100000100100; (2)0100111010100111; (3)nn 0000000010020001000-; (4)011,22111,111n n n n a a a a a a --. 解 (1)在展开式43214321)1(p p p p a a a a∑-τ中,不为0的项取自于113=a ,122=a ,134=a ,141=a ,而4)3241(=τ,所以行列式值为11111)1(4=⨯⨯⨯-. (2)在展开式43214321)1(p p p p a a a a∑-τ中,取14344==a a p ,则33p a 取为⎪⎩⎪⎨⎧====1134332333a a a a p p ,则⎪⎩⎪⎨⎧====1122224222a a a a p p ,11p a 取为111=a ,除此之外的项均为0.即行列式 4334221143322411)1()1(a a a a a a a a D ττ-+-=,而 2)1423(=τ,1)1243(=τ, 所以 0)1()1(2=-+-=D .(3)在展开式n np p p a a a2121)1(∑-τ中,不为0的项取为11,1=-n a ,22,2=-n a ,…,11,1-=-n a n ,n a nn =,而 2)1)(2()1)2)(1((--=--n n n n n τ,所以 !)1(2)1)(2(n D n n ---=.(4)在展开式n np p p a a a 2121)1(∑-τ中,不为0的项取n a 11,2-n a …1n a nn a .而2)1()1)2)(1((-=--n n n n n τ,所以 11,212)1()1(n n n n n a a a D ---=.习 题 1-31.设0333231232221131211≠==a a a a a a a a a a D ,据此计算下列行列式: (1)131211232221333231a a a a a a a a a ; (2)333231232221131211a ka a a ka a a ka a ; (3)333231131211232221444333222a a a a a a a a a ; (4)323233312222232112121311253225322532a a a a a a a a a a a a ------. 解 (1)a a a a a a a a a a r r a a a a a a a a a -=-↔33323123222113121131131211232221333231; (2)ka a a a a a a a a a k k k r a ka a a ka a a ka a =≠÷3332312322211312112333231232221131211)0(, 当0=k 时,结论仍成立.(3)33323123222113121121333231131211232221444222333444333222a a a a a a a a a r r a a a a a a a a a -↔ a a a a a a a a a a r r r 24)24(423333231232221131211321-=-÷÷÷.(4)3233312223211213113232323331222223211212131123223223225253225322532a a a a a a a a a c c a a a a a a a a a a a a ---------- a a a a a a a a a a c c a a a a a a a a a c c c 121212)2(3233323123222113121132323331222321121311321=↔-÷÷÷. 2.用行列式性质计算下列行列式:(1)111210321; (2)333222111321321321a a a a a a a a a +++++++++; (3)efcfbfde cd bdaeac ab ---;(4)yxyx x y x y yx y x+++;(5)28947104546333412------; (6)2605232112131412-. 解 (1)0111210000111210321321=--r r r . (2)02112112113213213213211213333222111=+++--+++++++++a a a cc c c a a a a a a a a a .(3)0202001321c e ec b adf rr r r e c be c b ec b adf ef cfbfde cd bdae ac ab-++---=---abcdef ec ecbadf r r 420002032=--↔. (4)yxyx x y x y x y x y y x c c c yxyx x y x y y x y x222222321++++++++++xy yy x y x y y x r r r r ---++--00)(21223 2)22()()22(y y x x y x y x +--+=)(2))((23322y x y x xy y x +-=--+=.(5)由于行列式中的第一列和第三列元素对应成比例,所以028947104546333412=------. (6)000002321121314122605232112131412214=----r r r .3.把下列行列式化为上三角形行列式,并计算其值:(1)3351110243152113------; (2)107825513315271391-------.解:(1)2113110243153351335111024315211341-------↔------r r 11101605510019182403351325141312---------+r r r r r r 111016019182401120335155323------↔÷r r r 2000320011203351533200760011203351581243432423-----↔+------+r r r r r r r r 402)2(215=⨯-⨯⨯⨯-=. (2)78130210017251307139121078255133152713*********------++---------r r r r r r r31224000210017251307139117324-=-----++r r r .4.用行列式性质证明下列等式:(1)yxzx zyz y x b a bz ay by ax bx az by ax bx az bzay bxaz bz ay by ax )(33+=+++++++++; (2)333222111333332222211111c b a c b a c b a c c b kb a c c b kb a c c b kb a =++++++; (3)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c cb b b b a a a a . 证明 (1)bz ay by ax z by ax bx az y bx az bz ay x a ++++++分开列按第左边1bzay by ax x by ax bx az z bxaz bz ay y b +++++++ bzay y zby ax x y bxaz z xab bz ay x zby ax z ybxaz y xa +++++++22分开列分别再按第bzay y xby ax x z bxaz z y b bz ay x xby ax z zbx az y y ab ++++++++2 z y z y x yx z xab y y z x x y zz xb a z x z y zy xy xb a y xzx z yzy xa 22233+++分开列分别再按第 zy xy x z x z yb y y x x x zzz yab z x xy z zxy yab y xxx z zzy y b a 3222++++ zy x y x zx z yb y x zx z yzy x a 330000+++++= =-+=y x z x zy zy xb y xzx z yzy x a 323)1(右边. (2)左边=-+++-3331221112133331222111132c b a c b a c b a kc c c b kb a c b kb a c b kb a c c 右边. (3)左边9644129644129644129644122222141312++++++++++++---d d d d c c c c b b b b a a a a c c c c c c 062126212621262123222221312=++++--d d c cb b a ac c c c .5.计算下列n 阶行列式:(1))1(3210321102113011321--------------n nn n n n n n;(2)1121122112111211111-----+++n n n n n b a a a a b a a a a b a a a a;(3)a b b b b a b b bb a b bb b a ;(4)11111000000000112211-----n n a a a a a a ; (5)xa a a a a a a x a a a a a a a x a a a a a a a xa a a a a a a a n n n nn n n n n n n n -+-+-+-+-------113211232113221132111321.解 (1))1(3210321102113011321--------------n nn n n n n n!0000210002)1(23002)1(262021321,,3,21n nn n nn n n nn n i r r i =----=+.(2)1121122112111211111-----+++n n n n n b a a a a b a a a a b a a a a∏-=--==-11121121100000001,,3,2n i i n n i b b b b a a a ni r r.(3)a b b b b a b b b b a b bb b a ab b bn a b b a b b n a ba b n a bb b b n ac c n i i)1()1(0)1()1(21-+--+-+-++∑= ni r r i ,,21 =-ba b a b a b b b b n a ----+00000)1()(])1([1b a b n a n --+=-.(4)11111000000000112211-----n n a a a a a a nn a a a n i c c n i i 13210000000000001,,2,11211-----=+-+∏-=--=111)1(n i i n a n .(5)x a a a a a a a x a a a a a a a x a a a a a a a xa a a a a a a a n n n nn n n n n n n n -+-+-+-+-------113211232113221132111321xa xa x a x a a a a a a n i r r n n n n i ----=----12211321100000000000,,3,2)())((1211x a x a x a a n ---=- .6.解下列方程:(1)0913251323221321122=--x x ; (2)0)1(11111)2(111112111111111111=------xn x n x x.解(1)因22341222400051320010*******2513232213211x x r r r r x x ------1221)4)(1(22x x --=0)4)(1(322=--=x x 所以解为 1±=x ,2±=x .(2)因左边n i r r i ,,3,21 =-xn x n x x ------)2(00000)3(000001000000111110])2[()1(=----=x n x x ,所以解为 2,,2,1,0-=n x .习 题 1-41.求行列式342102321-=D 中元素3和4的余子式和代数余子式.解 3的余子式8420213==M ,3的代数余子式8)1(133113=-=+M A . 4的余子式5123132-==M ,4的代数余子式5)1(322332=-=+M A . 2.已知210004321333231232221131211==a a a a a a a a a D ,求333231232221131211a a a a a a a a a .解:因为21)1(1000432133323123222113121111333231232221131211=-⋅==+a a a a a a a a a a a a a a a a a a D ,所以 21333231232221131211=a a a a a a a a a .3.已知四阶行列式D 的第3行元素依次为1,1,2,2-,它们的余子式依次为4,3,2,5,求行列式D . 解 将行列式D 按第三行元素降阶展开,有3434333332323131A a A a A a A a D +++=4)1()1(3)1(12)1(25)1(243332313⋅-⋅-+⋅-⋅+⋅-⋅+⋅-⋅=++++13=4.设四阶行列式的第二行元素依次为0,1,,2x ,其余子式分别为y ,2,6,2-,第三行的各元素的代数余子式分别为5,1,6,3,求此行列式.解 因03424332332223121=+++A a A a A a A a ,即05011632=⨯+⨯++⨯x ,所以 67-=x .从而 2424232322222121A a A a A a A a D +++=y x ⋅-⋅+-⋅-⋅+⋅-⋅+⋅-⋅=++++42322212)1(0)2()1(16)1(2)1(2 97262-=--=+-=x .5.按第三行展开并计算下列行列式:(1)5021011321014321---; (2)00000000052514241323125242322211514131211a a a a a a a a a a a a a a a a . 解:(1)原式501211431)1()1(502210432)1(33213--⋅-+--⋅=++ 021101321)1(0521201421)1()1(4333++-⋅+--⋅-+24181218-=-+-=. (2)原式=0000)1(000000)1(514125242321151413112323524225242322151413121331a a a a a a a a a a a a a a a a a a a a a a ++-⋅+-⋅ 353433000A A A ⋅+⋅+⋅+00025242315141341232524231514134231a a a a a a a a a a a a a a a a += 0=.6.证明下列各等式:(1)322)(11122b a b b a ab ab a -=+;(2)444422221111d c b a d c b a dc b a ))()()()()()((d c b a d c d b c b d a c a b a +++------=; (3)n n n n n n na x a x a x a x a a a a xx x ++++=+-------1111221100000100001.证明 (1)左边122222221312a b a b a a b a ab a c c c c ------ab a b a b a ab 22)1(22213-----=+21))((ab a a b a b +--==-=3)(b a 右边.(2)方法一左边44444442222222001ad a c a b a a d a c a b a a d a c a b a---------=)()()(4,3,22222222222222221a d d a c c a b b a d a c a b ad a c a b i c c i ---------=-)()()(111))()((222a d d a c c a b b a d a c a b a d a c a b ++++++---=))()((1312a d a c a b c c c c -----)()()()()(00122222a b b a d d a b b a c c a b b bd b c a b +-++-++--+ ))()()()((b d b c a d a c a b -----=)()()()(112222b d a b bd d b c a b bc c ++++++++=))()()()((d b c b d a c a b a -----))((d c b a d c +++-.方法二记D d c b a d c b a d c b a =444422221111,构造矩阵444443333322222111111x d c b a x d c b ax d c b a xd c b aD =,则1D 是范德蒙德行列式,其结果为))()()()()()()()()((1d x c x b x a x c d b d a d b c a c a b D ----------=,其中3x 的系数为))()()()()()((d c b a c d b d a d b c a c a b +++-------.由行列式的降阶展开法则知,55445335225151A x A x A x xA A D +-+-=,其中3x 的系数D A =-45,所以有))()()()()()((d c b a c d b d a d b c a c a b D +++------=,即444422221111d c b a d c b a dc b a ))()()()()()((d c b a d c d b c b d a c a b a +++------=. (3) 用数学归纳法证明 当2=n 时,2121221a x a x a x a x D ++=+-=,命题成立.假设对于)1(-n 阶行列式命题成立,即,122111-----++++=n n n n n a x a x a x D列展开按第则1n D1110010001)1(11----+=+-x x a xD D n n n n 右边=+=-n n a xD 1所以,对于n 阶行列式命题成立.7.计算下列各行列式:(1)3214214314321111; (2)ab c d e ed c b a 010000010000010;(3)328814412211111x x x--; (4)nn a a a a a 0100000000000010001321-. 解 (1)原式12312112112341213121200014,3,21------=------=-i c c i12304012112------r r 1613114=----=.(2)依次按第二行、第三行、第四行降阶展开,有abc d e edc ba 0100000100001022e a a e e a -==.(3)由范德蒙德行列式的结果知,328814412211111x x x--)4)(1(12)12)(22)(12)(2)(2)(1(2--=-----+--=x x x x x . (4)依次按第1,,3,2-n 行降阶展开,有nn a a a a a 000100000000000010001321 -)1(1111321132-==--n n n n a a a a a a a a a a .8.计算下列各行列式(k D 为k 阶行列式):(1)xyy x x y x y x n 0000000000000000=D ;(2)n n n n n a a a a a a a a a a a a a a a a ++++=1111321321321321D ;(3))det(ij n a =D ,其中||j i a ij -=;(4)nn a a a +++=11111111121D ,其中021≠n a a a ;(5)1111)()1()()1(1111n a a a n a a a n a a a n n n n n n n ------=---+D ;(提示:利用范德蒙德行列式的结果.)(6)nnnnn d c d c b a b a11112=D ,其中未写出的元素都是0.解 (1)按第1列降阶展开,有yxy y x yy xyx x y x x D n n0000000000)1(00000000001+-+=n n n y x 1)1(+-+=. (2)nn n n n a a a a a a a a a a a a a a a a ++++=1111D 3213213213211001010100111,23211---+=-ni a a a a ni r r∑=+ni ic c 211010*********n ni ia a a a ∑=+∑=+=ni i a 11.(3)ji a ij -=0432140123310122210113210)det(--------==n n n n n n n n a D ij n1,,2,11-=-+n i r r i i 0432111111111111111111111 --------------n n n nn i c c i ,3,21=+152423210222102210002100001---------------n n n n n212)1()1(----=n n n .(4)nn n nn ni na a a a a a a n i c c D +----=--11001001001,,2,1121Xa a a r a a r n n i i i n n 010010010012111--=∑+(其中∑-=++=111n i in n a aa X ))11()11(12111121∑∑=-=-+=++=ni in n i i n n n a a a a a a a a a a .(5)对第1+n 行,依次与上面相邻的行交换,直至交换到第1行,共需交换n 次.再把新的第1+n 行,依次与上面相邻的行交换,直至交换到第2行,共需交换1-n 次.依次类推,经2)1(1)1(+=++-+n n n n 次行交换,得 nn nn n n n n n n a a a n a a a n a a a D )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-⋅-⋅-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i .(6)nnnnn d c d c b a b a D11112=n n n n n nd d c d c b a b a a 0011111111----展开按第一行)1(1111111112nn n n n nn c d c d c b a b a b ----+-+2222---n n n n n n D c b D d a 展开都按最后一行,由此得递推公式222)--=n n n n n n D c b d a D ,所以 ∏=-=ni i i iin D c b da D 222)(,而 111111112c b d a d c b a D -==,所以 ∏=-=ni i i iin c b da D 12)(.习 题 1-51.用克拉默法则解下列方程组:(1)⎪⎪⎩⎪⎪⎨⎧=+-+-=+-=--=+-+067452296385243214324214321x x x x x x x x x x x x x x ;(2)⎪⎪⎩⎪⎪⎨⎧-=-++-=--+-=---=+++4326324231324321432143214321x x x x x x x x x x x x x x x x ;(3)⎪⎪⎩⎪⎪⎨⎧-=---=+++-=+-+=+++25320112324254321432143214321x x x x x x x x x x x x x x x x .解 (1)276741212060311512=-----=D , 8167402125603915181=------=D ,10867012150609115822-=-----=D , 2760412520693118123-=---=D 2707415120903185124=-----=D , 由克拉默法则知,方程组的解为311==D D x ,422-==D D x ,133-==D D x ,144==D Dx . (2)1531321113221133211-=------=D , 15313241136211432111=---------=D ,15313411162214332112=--------=D , 014211632241331113=-------=D ,15343216132411312114-=------=D ;由克拉默法则知,方程组的解为111-==D D x ,122-==D D x ,033==D D x ,144==D Dx . (3)14251321121341211111=----=D ,142513211210412211151=------=D 284512211203412111512=-----=D , 426523211013422115113=----=D , 14221320213212151114-=-----=D ,由克拉默法则知,方程组的解为111==D D x ,222==D D x ,333==D D x ,144-==DDx . 2.设曲线332210x a x a x a a y +++=通过四点),4,2(),3,1(),3,3()3,4(-,求系数3210,,,a a a a .解 由于曲线过四点,所以有⎪⎪⎩⎪⎪⎨⎧-=+++=+++=+++=+++36416432793484233210321032103210a a a a a a a a a a a a a a a a而126416412793184211111==D ,3664164327933842411131=-=D ,1864163127931844111312-=-=D , 246434127331842113113=-=D ,6316413931442131114-=-=D , 所以310==D D a ,2321-==D D a ,232==D D a ,2143-==D D a . 3.证明:对任意实数k ,线性方程组⎩⎨⎧=-+-=+-0)1(20)1(2121x k x kx x k 只有零解.证明 因系数行列式012)1(12122≠+=+-=---=k k k k k k D ,所以线性方程组只有零解.4.问λ取何值时,齐次线性方程组⎪⎩⎪⎨⎧=-+=-+=++-0)4(20)6(2022)5(3121321x x x x x x x λλλ有非零解? 解 系数行列式)210(4)4)(6)(5(402062225λλλλλλλ-----=---=D )8)(2)(5()82410)(5(2---=-+--=λλλλλλ,当0=D 时,即8,2,5===λλλ时,齐次线性方程组有非零解.5.问μλ,取何值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0200321321321x x x x x x x x x μμλ有非零解?解 系数行列式μλμμμλ-==12111113D , 当0=D 时,即10==λμ或时,齐次线性方程组有非零解.。
2021线性代数题库

2021线性代数题库线性代数b复习资料(2021)(一)单项选择题1.设a,b为n阶方阵,且(ab)=e,则以下各式中可能将不设立的就是()(a)a=b(b)aba=b(c)bab=a(d)(ba)2=e2.若由ab=ac必能推出b=c(a,b,c均为n阶矩阵)则a必须满足()(a)a≠o(b)a=o(c)a≠0(d)ab≠03.a为n阶方阵,若存在n阶方阵b,使ab=ba=a,则()(a)b为单位矩阵(b)b为零方阵(c)b=a(d)不一定4.设a为n×n阶矩阵,如果r(a)(a)a的任一一个行(列于)向量都就是其余行(列于)向量的线性组合(b)a的各行向量中至少存有一个为零向量(c)a的行(列)向量组中必有一个行(列)向量是其余各行(列)向量的线性组合(d)a的行(列)向量组中必有两个行(列)向量对应元素成比例5.已知向量组α1,α2,α3,α4线性无关,则向量组()(a)(b)(c)(d)α1+α2,α2+α3,α3+α4,α4+α1线性毫无关系α1-α2,α2-α3,α3-α4,α4-α1线性毫无关系α1+α2,α2+α3,α3+α4,α4-α1线性无关α1+α2,α2+α3,α3-α4,α4-α1线性无关6.以下观点不恰当的就是()(a)如果r个向量α1,仍然线性毫无关系(b)如果r个向量α1,组仍然线性毫无关系(c)如果r个向量α1,(d)如果r个向量α1,α2,,αr线性无关,则加入k个向量β1,β2,,βk后,α2,,αr线性毫无关系,则在每个向量中减少k个分量后税金向量α2,,αr线性相关,则重新加入k个向量后,仍然线性相关则在每个向量中去掉k个分量后所得向量组α2,,αr线性相关,7.设a就是m×n矩阵,齐次线性方程组ax=0仅有零解的充份必要条件就是()(a)a 的列向量线性毫无关系(b)a的列向量线性相关(c)a的行向量线性无关(d)a的行向量线性相关8.n元线性方程组ax=b,r(a,b)(a)无穷多组解(b)有唯一解(c)无解(d)不确定10.设a,b均为n阶非零矩阵,且ab =0,则a和b的秩()(a)必有一个等于零(b)一个等于n,一个小于n(c)都等于n(d)都小于n9.设立向量组α1,α2,,αs(s>1,α1≠0)线性相关,则()由α1,α2,,αi-1线性表出来。
线性代数机考练习题
1、设A ,B 为n 阶方阵,则AB A B =⋅. ( ) 参考答案:正确2、行列式如果互换任意两行,则行列式的值不变. ( )参考答案:错误3、行列式中如果有两列元素对应成比例,则此行列式等于零. ( )参考答案:正确4行列式1231112223331454=--. ( )参考答案:错误3202245,471011A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭,则7282491A B -⎛⎫+= ⎪-⎝⎭参考答案:正确6、若,,A B C 为矩阵,则有()()A B C B C A+=+参考答案:错误7、若,A B 为n 阶矩阵,则有222()2A B A AB B +=++参考答案:错误8、A 为任一n 阶方阵,且满足320A A E +-=,则122A A E -=+,参考答案:正确9、若25461321X -⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,则有22308X ⎛⎫= ⎪⎝⎭参考答案:错误10、对n 维向量组1,,m αα, 若有不全为零的常数1,,m k k , 使得011=++m m k k αα , 称向量组1,,m αα线性相关 ()参考答案:正确11、向量组12,,,,m ααα()2m ≥线性相关的充要条件是该向量组中任一个向量都可以用其余1m -个向量线性表示 ()参考答案:错误12、向量组123,,ααα线性无关, 则向量组112βαα=+, 223βαα=+, 331βαα=+也线性无关参考答案:正确13、⎪⎪⎪⎭⎫ ⎝⎛-=1011β列向量, ⎪⎪⎪⎭⎫ ⎝⎛=1112β, ⎪⎪⎪⎭⎫ ⎝⎛-=1133β, ⎪⎪⎪⎭⎫ ⎝⎛=1354β 则4β可由123,,βββ线性表示参考答案:正确14、齐次线性方程组 1231231230030kx x x x kx x x x x ++=⎧⎪++=⎨⎪-+=⎩有非零解,则0k =.( )参考答案 :错误15、如果两个矩阵等价,那么它们的秩相等.( )参考答案 :正确16、如果,AB C =则()()r C r A ≤.( )参考答案 :正确17、如果一个矩阵的秩是,r 那么所有r 阶子式都不为零.( )参考答案 :错误18、设λ是方阵A 的一个特征值,则1+λ是E A +的一个特征值参考答案:正确19、设A 是3阶方阵,1-A 的特征值有3,则A 一定有特征值31 参考答案:正确20、一个实二次型f的矩阵A的秩称为该二次型的秩参考答案:正确选择题1、三阶行列式0000ab cd的值为 ( ).选项A) abcd 选项B) ac bd-选项C) ad bc-选项D) 0参考答案:D2、若三阶行列式1231231232x x xy y yz z z=,则三阶行列式333222111x y zx y zx y z= ( ).选项A) 2-选项B) 2选项C) 0选项D) 1参考答案:A3、若三阶行列式1231231231x x xy y yz z z=,则三阶行列式123123123222x x xy y yz z z---= ( ).选项A) 0选项B) 2-选项C) 2选项D) 1-参考答案:B4、三阶行列式33424812246= ( ).选项A) 8选项B) 8-选项C) 1选项D) 0参考答案:D5、当x 取何值时,二阶行列式1019x x = ( ).选项A) 23x =选项B) 23x =- 选项C) 3x =选项D) 13x =-或13x =参考答案:D 6、已知三阶行列式123312231D =,则元素312a =的余子式 31M 为 ( ).选项A) 1选项B) 1-选项C) 2选项D) 2-参考答案: A7、已知三阶行列式3D 中第一行的元素自左向右依次为1,1,2-,它们的代数余子式分别为3,4,5-,则三阶行列式3D = ( ).选项A) 7-选项B) 8-选项C) 9-选项D) 10-参考答案: C8、已知210230004A ⎛⎫⎪= ⎪ ⎪⎝⎭,则1A -=( ).选项A )31012204001-⎛⎫⎪- ⎪ ⎪⎝⎭选项B )31012204001-⎛⎫⎪- ⎪ ⎪-⎝⎭选项C )310220001-⎛⎫⎪- ⎪⎪⎝⎭选项D )100122010345⎛⎫⎪⎪ ⎪⎝⎭参考答案:A9、设1234A ⎛⎫= ⎪⎝⎭,则A *=( ).选项A ) 1234⎛⎫⎪⎝⎭选项B ) 4231-⎛⎫⎪-⎝⎭选项C ) 4231⎛⎫⎪⎝⎭选项D ) 4231-⎛⎫⎪-⎝⎭参考答案:B10、设,A B 为n 阶矩阵,λ为数,下列错误的是( ).选项A )T A A =选项B )AB A B =选项C )BA A B =选项D )A A λλ=参考答案:D11、设A 为任一n 阶方阵,下列结论正确的是( ).选项A )T A A + 为反对称矩阵选项B )T A A -为对称矩阵选项C )A 可以表示为对称矩阵与反对称矩阵的和选项D )T A A +与T A A -都同为对称矩阵参考答案:C12、已知320224,471011A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭,则(2)T A B +=( ).选项A )728491-⎛⎫⎪⎝⎭选项B )342701⎛⎫⎪⎪ ⎪⎝⎭选项C) 202141⎛⎫⎪- ⎪ ⎪-⎝⎭选项D) 742981⎛⎫⎪- ⎪ ⎪-⎝⎭参考答案:D13、设13123,3132122A B ⎛⎫⎛⎫ ⎪== ⎪ ⎪⎝⎭ ⎪⎝⎭,则AB =( ).选项A )13111113⎛⎫ ⎪⎝⎭选项B )11131311⎛⎫ ⎪⎝⎭选项C )11111313⎛⎫ ⎪⎝⎭选项D )13131111⎛⎫⎪⎝⎭参考答案:A14、已知0112A ⎛⎫=⎪⎝⎭ ,则1A -=( ). 选项A )2110-⎛⎫ ⎪⎝⎭选项B )0112⎛⎫⎪⎝⎭选项C )2110--⎛⎫ ⎪-⎝⎭选项D )1101-⎛⎫⎪⎝⎭参考答案:A15、下列各行向量组线性相关的是( ).选项A )123(1,0,0),(0,1,0),(0,0,1)ααα===选项B )123(1,2,3),(4,5,6),(2,1,0)ααα===选项C )12(1,2,3),(2,4,5)αα==;选项D )123(1,2,2),(2,1,2),(2,2,1)ααα===参考答案:B16、下列各向量组中线性无关的是( ).选项A )12,,αα0选项B ))4,2(),2,1(选项C ))3,2(),2,1(),1,0(选项D ))3,1(),2,1(参考答案:D17、下列说法中错误的是( ).选项A )向量组线性相关,则向量组含有零向量选项B )向量组12,αα线性相关,则对应分量成比例选项C )向量组12,,,n ααα线性相关,则12,,,n ααα中至少有一个向量能表示为其余向量线性组合选项D )若向量组12,,,n ααα线性无关,则其部分向量组也线性无关参考答案:A18、向量组T T 12,-1,1,(4,4,4)k αα==-()(其中T 为转置符号)线性相关,则数=k ( ). 选项A )1-选项B ) 2选项C ) 3选项D ) 4参考答案:A19、向量组n ααα,,,21 线性无关的充要条件为( ).选项A) n ααα,,,21 均不为零选项B) n ααα,,,21 中任两个向量的分量不成比例选项C) n ααα,,,21 中任一个向量不能由其余向量线性表示选项D) n ααα,,,21 中有一部分向量线性无关参考答案:C20、设n 元齐次线性方程组Ax =0的系数矩阵A 的秩为r ,则Ax =0有非零解的充分必要条件是( ).选项A) r n =选项B) r n <选项C) r n ≥选项D) r n >参考答案:B21、线性方程组121200x x x x λλ+=⎧⎨+=⎩,当λ取何值时,方程组有非零解( ).选项A) 0选项B) 1±选项C) 2选项D) 任意实数参考答案:B22、已知A 是m n ⨯矩阵,()r A r =,下列结论正确的是( ).选项A) r n =时,Ax b =有唯一解选项B) m n =时,Ax b =有唯一解选项C )r n <时,Ax b =有无穷多解选项D) m n =时,Ax b =有解参考答案:A23、矩阵211311278⎛⎫⎪ ⎪ ⎪⎝⎭左乘初等矩阵100001010⎛⎫⎪⎪ ⎪⎝⎭相当于进行下列哪种初等变换( ).选项A) 第一行与第二行互换选项B) 第二行与第三行互换 选项C) 第一列与第二列互换 选项D) 第二列与第三列互换 参考答案:D24、设矩阵112331A -⎛⎫= ⎪-⎝⎭,则A 的秩是( ).选项A) 1选项B) 2选项C) 3选项D) 4参考答案:B25、用正交变换化二次型2221212x x x x ++为标准型是() 选项A) 212y选项B) 22212y y +选项C) 22212y y +选项D) 232221y y y ++参考答案:A26、矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛a a a 0000000 的特征值是 ( ). 选项A) a 选项B) 0选项C) 1选项D) 1,2,,n参考答案:A27、矩阵⎪⎪⎭⎫ ⎝⎛--3113的特征值2对应的一个特征向量是 ( ). 选项A) (1,2)选项B) (1,1)选项C) (1,3)选项D) (1,4)参考答案:B28、3阶矩阵A 的特征值为1,0,1-,矩阵E A A B 422++=的特征值为 选项A) 3,2,1选项B) 3,0,3选项C) 3,4,7选项D) 5,4,3参考答案:C29、已知向量T T )1,0,1(,)0,1,0(==βα下列计算不正确的是() 选项A) T)1,1,1(=+βα选项B) T)1,1,1(--=-βα选项C) 0),(=βα选项D) T)1,2,1(2=+βα参考答案:D30、矩阵A 有n 个特征值分别为1,4,3,2+n n ,B A ,相似,则)(=-E B选项A) 1选项B) 2选项C) n选项D) !n参考答案:D。
《线性代数》练习题库参考答案
《线性代数》练习测试题库一.选择题1、=-0000000000121nn a a a a ( B )A. n n a a a 21)1(-B. n n a a a 211)1(+-C. n a a a 212、n 阶行列式0000000000a a a a= ( B )A.na B. (1)2(1)n n n a -- C. (1)n n a -3、n21= ( B )A. (1)!nn - B. (1)2(1)!n n n -- C. 1(1)!n n +-4、 A 是n 阶方阵,m, l 是非负整数,以下说法不正确的是 ( C ). A. ()m l mlA A = B. mlm lA A A+⋅= C. m m mB A AB =)(5、A 、B 分别为m n ⨯、s t ⨯矩阵, ACB 有意义的条件是 ( C ) A. C 为m t ⨯矩阵; B. C 为n t ⨯矩阵; C. C 为n s ⨯矩阵6、下面不一定为方阵的是 (C )A.对称矩阵.B.可逆矩阵.C. 线性方程组的系数矩阵.7、 ⎥⎦⎤⎢⎣⎡-1021 的伴随矩阵是 (A ) A. ⎥⎦⎤⎢⎣⎡1021 B. ⎥⎦⎤⎢⎣⎡-1201 C. ⎥⎦⎤⎢⎣⎡-1021 8、 分块矩阵 00A B ⎡⎤⎢⎥⎣⎦(其中A 、B 为可逆矩阵)的逆矩阵是 ( A )A. 1100A B --⎡⎤⎢⎥⎣⎦ B. 00BA ⎡⎤⎢⎥⎣⎦ C. 1100B A --⎡⎤⎢⎥⎣⎦9、线性方程组Ax b = 有唯一解的条件是 ( A )A.()()r A r A b A ==的列数B.()()r A r A b = .C.()()r A r A b A ==的行数10、线性方程组 ⎪⎩⎪⎨⎧=++=++=++23213213211a ax x x a x ax x x x ax 有唯一解的条件是 (A )A. 2,1-≠aB. 21-==a a 或.C. 1≠a11、 的是则下面向量组线性无关),,,=(),,,=()6,2,4(054312--=--γβα(B )A. 0,,βα B. γβ, C. γα, 12、设A 为正交矩阵,下面结论中错误的是 ( C )A. A T 也为正交矩阵.B. A -1也为正交矩阵.C. 总有 1A =-13、二次型()233221214321342,,,,x x x x x x x x x x f --+=的矩阵为 ( C )A 、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---340402021B 、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---320201011 C 、⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---0000032002010011 14、设r 是实二次型),,,(21n x x x f 的秩,p 是二次型的正惯性指数,q 是二次型的负惯性指数,s 是二次型的符号差,那么 ( B )A. q p r -=;B. q p r +=;C. q p s +=; 15、下面二次型中正定的是 ( B )A. 21321),,(x x x x x f =B.2322213212),,(x x x x x x f ++= C.22213212),,(x x x x x f +=二、判断题1、若行列式主对角线上的元素全为0,则此行列式为0. ( ⨯ )2、A 与B 都是3×2矩阵,则A 与B 的乘积也是3×2矩阵。
线性代数练习题答案
线性代数练习题答案线性代数是一门研究向量空间及其线性映射的数学分支,以下是一些常见的线性代数练习题及其答案。
问题1:确定下列矩阵是否为可逆矩阵,并求其逆矩阵。
\[ A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \]答案1:矩阵A的行列式为 \( \det(A) = 1 \times 4 - 2 \times 3 = -2 \)。
因为行列式不为零,矩阵A是可逆的。
其逆矩阵为:\[ A^{-1} = \frac{1}{-2} \begin{pmatrix} 4 & -2 \\ -3 & 1\end{pmatrix} = \begin{pmatrix} -2 & 1 \\ 1.5 & -0.5\end{pmatrix} \]问题2:解线性方程组:\[ \begin{cases} x + 2y = 5 \\ 3x - y = 1 \end{cases} \]答案2:将方程组写成矩阵形式:\[ \begin{pmatrix} 1 & 2 \\ 3 & -1 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \]计算矩阵的逆:\[ A^{-1} = \begin{pmatrix} -1 & 2 \\ 3 & -1 \end{pmatrix} \] 然后求解:\[ \begin{pmatrix} x \\ y \end{pmatrix} = A^{-1}\begin{pmatrix} 5 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix} \]所以,\( x = 3 \),\( y = 1 \)。
线性代数练习题(附答案)
《线性代数与解析几何》练习题行列式部分一•填空题:1若排列1274i56k9是偶排列,则i 8 , k 32•已知a1i a25a3j a41a5k是五阶行列式中的一项,且带正号,其中(ii 2 , j 4 ,k 33•设A, B 是n 阶可逆阵,且A 5,贝U (A T A)356, 2A 2n5B 1A k B 5k(k为常数)4.已知3 1 2D 2 3 10 1 4用A j表示D的元素a j的代数余子式,贝U 2A21 3A22 A23 D 377.设j)则0 ,行列式D2372为4维列向量,且已知行列式 A 4, B 1,则行列式 A B6•设x 1 2 3f(x)3 x 1 22 3 x 11 2 3 x2, 3, 4均40A11 A12 A135.设有四阶矩阵A ( ,2,3,4),B ( 2 , 3, 4 ),其中8(|A| |B I)则f (4) 1602802 •计算行列式111111111111 112 32 125124 8 11 4151 14150 2512.23.23.231 x x x1 x x x1 x x x1, 2, 311 1 11 1 1 11 1 11 0 4 1 30 2 5 12 5 10 2 510 0910 0 9 1 140 044 120 0 14 14931 97解:D且AI 0 A I 。
求 AA T上述方程的解x8 .设A 是n 阶方阵,且的行列式 AA* 是A 的伴随矩阵,则X 1 x 2 X 3 09 •若齐次线性方程组x 1 x 2 X 3 0 只有零解,则 应满足X 1X 2X 3 0二.计算题:1.已知5阶行列式1 2 3 4 52 2 2 1 13 1 24 5271 1 12 24 3 15 0求 A 41A 42 A 43 和 A 44 A 45其中 A j 是元素3ij 的代数余子式。
1条件。
解:A 41 A 42 A 43 2(A 44 2(A 41A 42 A 43) A 44A 45) A 45A 41 A 44 A 42 A 45 A 43 183.设A 是n 阶方阵, A*n 1a27解:Al A AA A(l A T ) A] (A I)T A A IA 0 A I 04.设A 是n 阶实对称矩阵,A 2 2A 0,若r(A) k (0 k n),求A 3I2是k 重的特征值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
行列式练习题答案(推荐完整) ..... 行列式练习题答案(推荐完整)
编辑整理: 尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(行列式练习题答案(推荐完整))的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以下为行列式练习题答案(推荐完整)的全部内容。 行列式练习题答案(推荐完整)
..... 行列式练习题答案(推荐完整)
编辑整理:张嬗雒老师 尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望 行列式练习题答案(推荐完整) 这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力. 本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快 业绩进步,以下为 行列式练习题答案(推荐完整)
..... 第1章 行列式 (作业1)
一、填空题 1.设自然数从小到大为标准次序,则排列1 3 … )12(n2 4 … )2(n的逆序数为 ,排列1 3 … )12(n)2(n)22(n…2的逆序数为 . 2.在6阶行列式中,651456314223aaaaaa这项的符号为 。 3.所有n元排列中,奇排列的个数共 个. 二、选择题
1。由定义计算行列式nn0000000010020001000= ( ).
(A)!n (B)!)1(2)1(nnn (C)!)1(2)2)(1(nnn (D)!)1()1(nnn
2.在函数xxxxxxf21123232101)(中,3x的系数是( ). (A)1 (B)—1 (C)2 (D)3 3.四阶行列式的展开式中含有因子32a的项,共有( )个。 (A)4; (B)2; (C)6; (D)8.
三、请按下列不同要求准确写出n阶行列式)det(ijaD定义式: 1. 各项以行标为标准顺序排列;
2. 各项以列标为标准顺序排列; 3. 各项行列标均以任意顺序排列。 四、若n阶行列式中,等于零的元素个数大于nn2,则此行列式的值等于多少?说明理由. 行列式练习题答案(推荐完整)
..... 第1章 行列式 (作业2)
一、填空题
1.若D=._____324324324,13332313123222121131211111333231232221131211aaaaaaaaaaaaDaaaaaaaaa则
2.方程 229132513232213211xx=0的根为___________ . 二、计算题 1. 8171160451530169144312 2.dcba100110011001
3.abbbabbbaDn 行列式练习题答案(推荐完整)
..... 4。111113213211211211211nnnnnaaaaxaaa
axaa
aaxaaaaxD
5.计算n阶行列式)2(212121222111nnxxxnxxxnxxxDnnnn。 行列式练习题答案(推荐完整)
..... 第1章 行列式 (作业3)
一、填空题
1.当n为奇数时,行列式0000321323132231211312nnnnnnaaaaaaaaaaaa=_________。
2.行列式xyyxyxyx000000000000 . 二、选择题 1.设D是n阶行列式,则下列各式中正确的是( )。[ijA是D中ija的代数余子式].
(A);,,2,1,01njAaniijij (B) ;,,2,1,1njDAa
n
iijij (C) ;121DAanjjj (D) .,,2,1,01niAa
n
jijij 2.行列式结果等于))()()()()((cdbdbcadacab的行列式是( )。
(A)444422221111dcbadcbadcba;(B)3330001111dcbdcbadacab;(C)323232321111dddcccbbbaaa;(D)22
2
1110001ddadccacbbab
三、计算题 1.设4322321143113151A,计算,44434241AAAA 其中),,,(43214jAj是A中元素ja4的代数余子式. 行列式练习题答案(推荐完整)
..... 2.1221100000100001axaaaaxxxnnn
3.1111)()1()()1(1111naaanaaanaaaDnnnnnnn
4.nn
nn
ndcdcbabaD000011112
第1章 行列式 (作业4) 一、填空题
1.已知关于变量)3,1(ixi的线性方程组333221123322111332211dxcxcxcdxbxbxbdxaxaxa,由克莱姆法则,当满足
条件时,方程组有唯一解,且3x 。 行列式练习题答案(推荐完整) ..... 2.齐次线性方程组000221122221211212111nnnnnnnnnxaxaxaxaxaxaxaxaxa的系数行列式为D,那么0D是该行列式有非零解的 条件. 二、求解下列行列式
1.0432140123310122210113210nnnnnnnnDn 行列式练习题答案(推荐完整)
..... 2.nnaaaD11111111121 ,其中021naaa.
三、问取何值时,齐次线性方程组0)1(0)3(2042)1(321321321xxxxxxxxx 有非零解? 行列式练习题答案(推荐完整)
..... 第1章 行列式 (检测题)
一、填空题
1.若排列niii21的逆序数为k,则排列11iiinn的逆序数为 .
2. 0544101320000006543214321ccccccaaaaD 。
3. n阶行列式000000112212112211121aaaaaaaaaannnnnnnnnn= 。 4. 3232325551444111112221= . 二、选择题 1.121121121121121,,,,1121111P(x)nnnnnaaanxaaaaxaaaaxaaaa其中设是互不相同得实数,则方程P(x)=0( ). (A)无实根; (B)根为 1,2,。..,n—1 ; (C)根为 —1,-2,。。。,—(n—1); (D)根为0 . 2.设n阶行列式)det(ijaD,把D上下翻转、或逆时针旋转90、或依副对角线翻转,依次得
nnnnaaaaD11111, 11112nnnnaaaaD ,11113aaaaDnnnn
,则( )
(A)DDDD321; (B);DDDDDDnnn32)1(221,)(,)1(
(C)DDDDDnn2)1(321)1(,; (D)DDDDDnn32)1(21,)1( 。 行列式练习题答案(推荐完整)
..... 三、计算题
1. 2145320121252314123; 2. 0000abaaabbaaaba.
3.123181920212171819181716123191817212201918321D;
4.),1,(121nixaaxxxxaxxxxaxxxxaDinnn
行列式练习题答案(推荐完整)
..... 四、证明题
1. 行列式D中的每个数ija
分别用)0(bbji去乘,试证所得行列式1D与D相等。
2. 证明 sin)1sin(cos210001cos200000cos210001cos210001cos2nDn 答案 第1章 行列式(作业1) 答案 一. 填空题 1.2)1(nn,)1(nn 。 2.正号。 3.2
!n
二、选择题 1.(C); 2.(B); 3.(C) 三、1.)(21)(2212)1(ninnipppnpppppptaaa; 2.)(21)(2212)1(ninniqqqnqqqqqqtaaa
.
3. nnnniqpqpqpqqqtppptaaa2211212)()()1(。 四.值为0。 第1章 行列式(作业2) 答案 一、填空题1. —12。 2。 ±1,±2.
二、计算题 1.0; 2.1adcdababcd;3.)(])1([1babnan; 4。niiax1)(; 5. 当n=2时,212xxD; 当 n>2时,用拆项法可得0nD 。 第1章 行列式(作业3) 答案 一、填空题1。0. 2。nnnyx1)1(。 二、选择题 1 (B). 2(C),(D) 三、计算题
1。6; 2.nnnnaxaxax111; 3。11)(jinji;4。niiiiincbdaD12)(。
第1章 行列式(作业4) 答案
