中考数学复习知识点:三角形垂心-精选文档
三角形的内心、外心、垂心

一、三角形内心(一)定义在三角形中,三个角的角平分线的交点是这个三角形内切圆的圆心,而三角形内切圆的圆心就叫做三角形的内心,(二)三角形内心的性质:设△ABC的内切圆为☉I(r),角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.1、三角形的内心到三边的距离相等,都等于内切圆半径r.2、∠BIC=90°+A/2.3、如图在RT△ABC中,∠A=90°△内切圆切BC于D则S△ABC=BD*CD4、点O是平面ABC上任意一点,点I是△ABC内心的充要条件是:向量OI=[a(向量OA)+b(向量OB)+c(向量OC)]/(a+b+c).5、△ABC中,A(x1,y1),B(x2,y2),C(x3,y3),那么△ABC内心I的坐标是:(ax1/(a+b+c)+bx2/(a+b+c)+cx3/(a+b+c),ay1/(a+b+c)+by2/(a+b+c)+cy3/(a+b+c)).6、(欧拉定理)⊿ABC中,R和r分别为外接圆为和内切圆的半径,O和I分别为其外心和内心,则OI^2=R^2-2Rr.7、点O是平面ABC上任意一点,点I是△ABC内心的充要条件是:a(向量OA)+b(向量OB)+c(向量OC)=向量0.8、双曲线上任一支上一点与两焦点组成的三角形的内心在实轴的射影为对应支的顶点。
9、△ABC中,内切圆分别与AB,BC,CA相切于P,Q,R,则AP=AR=(b+c-a)/2,BP =BQ =(a+c-b)/2,CR =CQ =(b+a-c)/2,r=[(b+c-a)tan(A/2)]/2。
10、(内角平分线定理)△ABC中,0为内心,∠A 、∠B、∠C的内角平分线分别交BC、AC、AB于Q、P、R,则BQ/QC=c/b, CP/PA=a/c, BR/RA=a/b.(三)三角形内接圆半径1、在Rt△ABC中,∠C=90°,r=(a+b-c)/2.2、在RT△ABC中,∠C=90°,r=ab/a+b+c3任意△ABC中r=(2*S△ABC)/C△ABC (C为周长)二、三角形外心(一)定义三角形外接圆的圆心叫做三角形的外心.三角形外接圆的圆心也就是三角形三边中垂线的交点,三角形的三个顶点就在这个外接圆上(二)三角形外心的性质:设⊿ABC的外接圆为☉G(R),角A、B、C的对边分别为a、b、c,p=(a+b+c)/2.性质1:(1)锐角三角形的外心在三角形内;(2)直角三角形的外心在斜边上,与斜边中点重合;(3)钝角三角形的外心在三角形外.性质2:∠BGC=2∠A,(或∠BGC=2(180°-∠A).性质3:∠GAC+∠B=90°证明:如图所示延长AG与圆交与P∵A、C、B、P四点共圆∴∠P=∠B∵∠P+∠GAC=90°∴∠GAC+∠B=90°性质4:点G是平面ABC上一点,点P是平面ABC上任意一点,那么点G是⊿ABC 外心的充要条件是:(1)向量PG=((tanB+tanC)向量PA+(tanC+tanA)向量PB+(tanA+tanB)向量PC)/2(tanA+tanB+tanC).或(2)向量PG=(cosA/2sinBsinC)向量PA+(cosB/2sinCsinA)向量PB+(cosC/2sinAsinB)向量PC.性质5:三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.外心到三顶点的距离相等。
2022中考数学考点破解大全之三角形的垂心

2022中考数学考点破解大全之三角形的垂心
聪明出于勤奋,天才在于积累。
我们要振作精神,下苦功学习。
本店铺2022中考频道编辑2022中考数学考点的相关内容,以备借鉴。
三角形的垂心
锐角三角形垂心在三角形内部。
直角三角形垂心在三角形直角顶点。
钝角三角形垂心在三角形外部。
垂心是从三角形的各个顶点向其对边所作的三条垂线的交点。
三角形三个顶点,三个垂足,垂心这7个点可以得到6组四点共圆。
三角形上作三高,三高必于垂心交。
高线分割三角形,出现直角三对整,
直角三角有十二,构成九对相似形,
四点共圆图中有,细心分析可找清,
精品本店铺为大家提供的2022中考数学考点破解就到这里了,愿大家都能在学期努力,丰富自己,锻炼自己。
第 1 页共1 页。
第6课时 三角形的重心和垂心
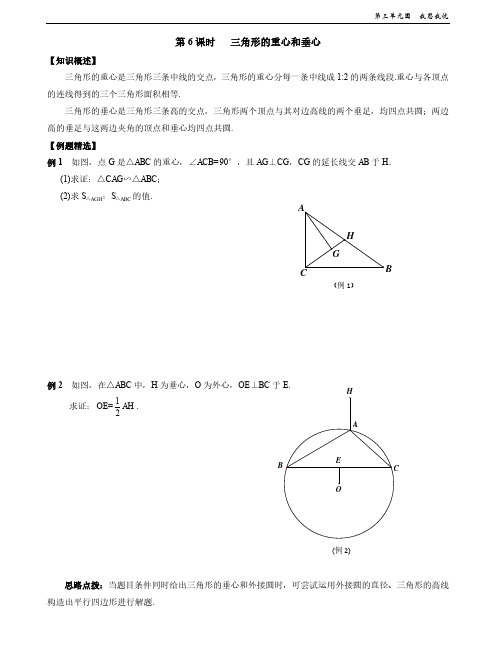
第6课时 三角形的重心和垂心【知识概述】三角形的重心是三角形三条中线的交点,三角形的重心分每一条中线成1:2的两条线段.重心与各顶点的连线得到的三个三角形面积相等.三角形的垂心是三角形三条高的交点,三角形两个顶点与其对边高线的两个垂足,均四点共圆;两边 高的垂足与这两边夹角的顶点和垂心均四点共圆. 【例题精选】例1 如图,点G 是△ABC 的重心,∠ACB=90°,且AG ⊥CG ,CG 的延长线交AB 于H .(1)求证:△CAG ∽△ABC ; (2)求S △AGH :S △ABC 的值.例2 如图,在△ABC 中,H 为垂心,O 为外心,OE ⊥BC 于E .求证:12OE=AH .思路点拨:当题目条件同时给出三角形的垂心和外接圆时,可尝试运用外接圆的直径、三角形的高线构造出平行四边形进行解题.(例2)(例1)【配套练习】1. 如图,G 是△ABC 的重心,AB >BC >CA ,记△GAB , △GBC , △GCA 的面积分别为S 1,S 2,S 3,则有( ) A. B . C . D .的大小关系不确定2.如图,H 是△ABC 的垂心,△ABC 的外接圆半径为R ,△BHC 的外接圆半径为r ,则R 与r 的大小关系是( ) A .R =rB .R >rC .R <rD .无法确定3.如图,锐角△ABC 的垂心为H ,三条高的垂足分为D 、E 、F ,则H 是△DEF 的( ) A .垂心B .重心C .内心D .外心4. 已知点G 是△ABC 的重心,AG 的延长线交BC 于点D ,过点G 作GE ∥BC 交AC 于点E ,如果BC=6,那么线段GE 的长为_____________.5. 已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A= ______度.6. 已知任意三角形的三条高交于一点,叫做三角形的垂心.如图AB 是半圆的直径,如图1,点C 在半圆外;如图2,点C 在半圆内,请仅用无刻度的直尺按要求画图并简要说明画法(不需证明). (1)在图1中,画出△ABC 的垂心,简要说明画法. (2)在图2中,画出△ABC 中AB 边上的高,简要说明画法.123S S S >>123S S S ==123S S S <<123S S S、、(第1题)(第3题)(第2题)(第7题)7. 如图,扇形OAB 的圆心角为90°,半径为6,点P 在AB ︵(不含端点)上运动,PH ⊥O A 于H ,△OPH 的重心为G .(1) 当点P 在AB ︵上运动时,线段GO 、GP 、GH 中有无长度保持不变的线段?如果有,请指出并求出其相应的长度;(2) 设PH = x ,GP =y ,求y 关于x 的函数解析式,并指出自变量x 的取值范围; (3) 如果△PGH 为等腰三角形,试求出线段PH 的长.8. 如图,锐角三角形ABC 内接于半径为R 的⊙O ,H 是三角形ABC 的垂心,AO 的延长线与BC 交于点M ,若OH ⊥AO ,BC=10,OA=6,求OM 的长.H (第7题) (第8题)第6课时 三角形的重心和垂心参考答案例1 (1)如图,设GH=a ,∵点G 是△ABC 的重心,∴CG=2HG=2a ,CH 为AB 边上的中线,∴CH=AH=BH=3a ,∠1=∠B ,∵AG ⊥CG ,∴∠2+∠3=90°,而∠1+∠2=90°,∴∠1=∠3,∴∠B=∠3,而∠ACB=∠AGC=90°,∴△CAG ∽△ABC ;(2)∵点G 是△ABC 的重心,∴CG=2HG ,∴HG=13CH ,∴S △AHG=13S △ACH ,∵AH =HB ,∴S △ACH = 12S △ABC ,∴S △AHG=16S △ABC ,∴S △AGH :S △ABC=1:6.例2 如图,作⊙O 的直径BF ,连结CF ,AF ,CH ,∴∠BCF=∠BAF=90°,∵OE ⊥BC ,∴BE =EC .∵OB=OF ,∴OE =12CF .∵H 是△ABC 的垂心,∴AH ⊥BC ,∵CF ⊥BC ,∴AH ∥CF ,同理可得:CH ∥AF ,∴四边形AHCF 是平行四边形,∴AH=CF ,∴OE =12 AH .【练习】1.B 2.A 3.C 4. 2 5. 60°6.(1) 如图1,连结AD ,BE 交于点P ,连结CP 并且延长交AB 于点F .(2) 如图2,延长AC 、BC 分别交半圆于点E 、D ,连结AD ,BE ,并延 长相交于点P ,连结PC 并延长交AB 于点T ,则CT 就是AB 上的高.7.(1)延长 HG 交OP 于点E ,延长PG 交AO 于D ,∵G 是△OPH 的重心,且∠PHO =90°,∴GH =23HE =23×12 OP =13×6=2,故在线段 GO 、GP 、GH 中.有长度保持不变的线段,就是GH .(2)OH12DH OH =DP ∴y =GP =23DP =1336+3x 2(06)x <<的中位线,. 练6 练8例21B例1。
【精品文档】201X中考数学知识点:三角形的重心-优秀word范文 (1页)

【精品文档】201X中考数学知识点:三角形的重心-优秀word范文
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为word格式,下载后可方便编辑和修改! ==
201X中考数学知识点:三角形的重心
为了能更好更全面的做好复习和迎考准备,确保将所涉及的201X中考考点全面复习到位,让孩子们充满信心的步入考场,现特准备了201X中考数学知识点。
三角形的重心
已知:△ABC中,D为BC中点,E为AC中点,AD与BE交于O,CO延长线交AB 于F。
求证:F为AB中点。
证明:根据燕尾定理,S(△AOB)=S(△AOC),又S(△AOB)=S(△BOC),
∴S(△AOC)=S(△BOC),再应用燕尾定理即得AF=BF,命题得证。
重心的几条性质:
1.重心和三角形3个顶点组成的3个三角形面积相等。
2.重心到三角形3个顶点距离的平方和最小。
3.在平面直角坐标系中,重心的坐标是顶点坐标的算术平均,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3);空间直角坐标系——横坐标:(X1+X2+X3)/3 纵坐标:(Y1+Y2+Y3)/3 竖坐标:(Z1+Z2+Z3)/3
4重心到顶点的距离与重心到对边中点的距离之比为2:1。
5.重心是三角形内到三边距离之积最大的点。
如果用塞瓦定理证,则极易证三条中线交于一点。
提供的201X中考数学知识点,是我们精心为大家准备的,希望大家能够合理的使用!。
初三数学重要知识点

初三数学重要知识点初三数学知识点梳理三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3.垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形。
5.H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
6.△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
7.在非直角三角形中,过O的直线交AB、AC所在直线分别于P、Q,则AB/AP?tanB+AC/AQtanC=tanA+tanB+tanC8.三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
9.设O,H分别为△ABC的外心和垂心,则∠BAO=∠HAC,∠ABH=∠OBC,∠BCO=∠HCA.10.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心;锐角三角形的内接三角形(顶点在原三角形的边上)中,以垂足三角形的周长最短。
12.西姆松(Simson)定理(西姆松线):从一点向三角形的三边所引垂线的垂足共线的重要条件是该点落在三角形的外接圆上。
13.设H为非直角三角形的垂心,且D、E、F分别为H在BC,CA,AB上的射影,H1,H2,H3分别为△AEF,△BDF,△CDE的垂心,则△DEF≌△H1H2H3.14.三角形垂心H的垂足三角形的三边,分别平行于原三角形外接圆在各顶点的切线。
九年级下册数学复习计划一、紧扣大纲,精心编制复习教案初中数学内容多而杂,其基础知识和基本技能又分散覆盖在三年的教科书中,学生往往学了新的,忘了旧的。
因此,必须依据大纲规定的内容和系统化的知识要点,精心编制复习计划。
计划的编写必须切合学生实际。
可采用基础知识习题化的方法,根据平时教学中掌握的学生应用知识的实际,编制一份渗透主要知识点的测试题,让学生在规定时间内独立完成。
三角形垂心及相关定理

三角形垂心及相关定理哎,说起三角形垂心,这事儿得从我那会儿上初中那会儿开始聊起。
那时候,数学课上,老师一讲到几何题,我的头就开始隐隐作痛。
尤其是涉及到三角形垂心那块儿,简直就是我的噩梦啊!不过呢,后来有一次,我在家里捣鼓三角板的时候,居然误打误撞地发现了三角形垂心的一个有趣现象,让我对这玩意儿有了新的认识。
那天下午,我闲得无聊,在家里翻腾出一些三角板、量角器和一堆草稿纸,打算自己动手画几个三角形玩玩。
我先是画了一个标准的等边三角形,然后就开始琢磨着怎么找到它的垂心。
垂心嘛,就是那个三条高线的交点,书上这么说,可我就是不明白为啥非得是三条高线的交点,就不能是别的啥线交点呢?我拿起铅笔,开始认真地画起三角形的高线来。
第一条高线,我画得挺顺利,就是从那个尖尖的顶点垂直于对边画过去,然后标出交点。
第二条高线也还好,就是换了个顶点,重复了一遍。
可到了第三条高线,我就有点头疼了,因为得用尺子量着角度,还得保证它是垂直于另一条边的,这可真不容易。
不过呢,经过一番折腾,我还是成功地把三条高线都给画出来了。
然后,我就用尺子去量这三个交点,想看看它们是不是在同一个点上。
结果,你猜怎么着?它们还真就在一块儿呢!那一刻,我简直不敢相信自己的眼睛,心里头那个激动啊,就像哥伦布发现了新大陆一样。
我琢磨着,这三角形垂心肯定不是偶然现象,肯定有啥定理或者规律在里头。
于是,我就开始翻箱倒柜地找我的数学课本,想看看书上是怎么说的。
结果,书上还真有那么几条定理,什么欧拉线定理啊,什么垂心定理啊,看得我眼花缭乱。
不过呢,虽然那些定理的名字都挺高大上的,但仔细一读,嘿,不就是说我刚才发现的那个现象嘛!从那以后,我就对三角形垂心有了新的认识,也不再觉得它是个难啃的骨头了。
每次做几何题,遇到跟垂心有关的题目,我就会想起自己那次在家里捣鼓三角板的经历,然后心里头就多了几分底气。
现在回想起来,那次经历还真挺有意思的。
它让我明白了一个道理,就是有些看似复杂的东西,其实只要你动手去试一试,去琢磨琢磨,就会发现它其实也挺简单的。
三角形垂心的3个结论
三角形垂心的3个结论三角形垂心是三角形中一个非常重要的概念。
在这篇文章中,我们将探讨关于三角形垂心的三个结论。
首先,让我们来明确一下什么是三角形的垂心。
三角形的垂心是指三角形三条高所在直线的交点。
结论一:锐角三角形的垂心在三角形内部。
对于锐角三角形来说,由于其三个内角都小于 90 度,所以三条高都在三角形内部,它们的交点,也就是垂心,自然也在三角形内部。
我们可以通过简单的作图来直观地理解这一点。
想象一个锐角三角形ABC,从顶点 A 向对边 BC 作垂线,垂足为 D;从顶点 B 向对边 AC作垂线,垂足为 E;从顶点 C 向对边 AB 作垂线,垂足为 F。
这三条垂线 AD、BE、CF 必然会相交于三角形内部的一点 H,这个点 H 就是锐角三角形 ABC 的垂心。
结论二:直角三角形的垂心在直角顶点上。
在直角三角形中,其中一个角是 90 度。
比如,在直角三角形 ABC 中,如果角 C 是直角,那么边 AB 就是直角所对的斜边。
从顶点 A 向BC 作垂线,垂足就是 B 点;从顶点 B 向 AC 作垂线,垂足就是 A 点。
这两条高的交点正好就是直角顶点 C,所以直角三角形的垂心就在直角顶点上。
这是因为直角三角形的两条直角边本身就是两条高,它们相交的点就是直角顶点。
结论三:钝角三角形的垂心在三角形外部。
对于钝角三角形,其有一个角大于 90 度。
假设在钝角三角形 ABC 中,角 A 是钝角。
从顶点 B 向 AC 作垂线,垂足为 D;从顶点 C 向AB 作垂线,垂足为 E。
这两条高会在三角形内部相交。
而从顶点 A 向BC 延长线作垂线,垂足为 F,此时三条高所在直线的交点 H 就在三角形的外部。
这是因为钝角的对边的高在三角形的外部,所以垂心也就位于三角形外部。
三角形垂心的这三个结论,对于我们深入理解三角形的性质和解决相关的几何问题都具有重要的意义。
我们还可以进一步探讨垂心的一些其他性质。
比如,三角形的垂心与顶点的连线垂直于对边。
内心、外心、重心、垂心定义及性质总结
内心、外心、重心、垂心定义及性质总结
内心、外心、重心、垂心定义及性质总结
1.内心:
(1)三条角平分线的交点,也是三角形内切圆的圆心。
(2)性质:到三边距离相等。
2外心:
(1)三条中垂线的交点,也是三角形外接圆的圆心。
(2)性质:到三个顶点距离相等。
3 重心:
(1)三条中线的交点。
(2)性质:三条中线的三等分点,到顶点距离为到对边中点距离的2倍。
4 垂心:三条高所在直线的交点。
5 重心: 三条中线定相交,交点位置真奇巧,
交点命名为“重心”,重心性质要明了,
重心分割中线段,数段之比听分晓;
长短之比二比一,灵活运用掌握好.
6 垂心: 三角形上作三高,三高必于垂心交.
高线分割三角形,出现直角三对整,直角三角形有十二,构成六对相似形,四点共圆图中有,细心分析可找清.
7内心: 三角对应三顶点,角角都有平分线,
三线相交定共点,叫做“内心”有根源;
点至三边均等距,可作三角形内切圆,
此圆圆心称“内心”如此定义理当然.
8外心: 三角形有六元素,三个内角有三边.
作三边的中垂线,三线相交共一点.
此点定义为“外心”,用它可作外接圆.
“内心”“外心”莫记混,“内切”“外接”是关键.如有侵权请联系告知删除,感谢你们的配合!
如有侵权请联系告知删除,感谢你们的配合!。
三角形垂心的性质及应用
在△和△中,由边比定理,得DEsin20。又乙=而丽丽矿AEsin20。刁E
丽
砍丽
。不可
(1)600+a=。00a=30:
答:匕D
君C
二30“
三、附练习题1已
知AB为半④O的直径,尸、M为半圆上两
511220
.云玩不0.亏而口口`和)
Sin2
0
.
Zeos20sin(20。+a)
:’由(1)、(2)得sin(20。+a)eosZ
o
。
=5insoosin(40。+a)
积化和,得sin(40。+a)一cos(xo。一a)二o
即s元n(40。+a)一5in(50。+a)=o由差化积,得
Z
eos(60。+a)sin(一20。)=
o
即。05(co。+a)二o,0。14
0
。
(2)
(3)
点,且PQ-IAB,MN上AB,MC上OP,Q、N、C
均为垂足求证:NC二尸Q2在△ABC中,D为BC的中点,过D作一直
线分别交卫C于万,交AB的延长线于F,求证:月E
:
EC=AF:B
F
参考资料:李家琪《边比定理和角比定理》嘎数宁通讯》
lga3年第6期
三角形垂心的性质
及应用
(上海)汪祖亨
垂心是三角形中的重要一点,鉴于知识的条理化、系列化,本文将归纳涉及三角形垂心的诸多性质及其应用。先不加证明地给出有关的性质。性质1三角形的三条高线相交于一点(这就是三角形的垂心定理)。性质ZH是锐角△ABC的垂心,过H交BC于D,交△ABC外接圆于L,有HD=刀L推论△ABC与△HBC的外接圆半径相同性质3在锐角或钝角△ABC中,H为垂心,D、E、F为三边上的垂足则有A、F、H、E,B、D、心,钝角三角形的垂心是其垂足兰角形的旁心H
DC式
D和B、F、E、C,C、D、
B等诸多的四点共
圆
_件奥扣男’t_赞今理BC些号甚誓导
沪
乍
形的内角平分线如图3,钝角△ABC的高是其重足三角形的内角或外角的平分线。推论锐角三角形的垂心是其垂足三角形的内怪}3图4性质5如图2,锐角△ABC的高AD、BE、CF相交于H,有△BCE认,△BHD△CAF氏△CH君,△ABD闪△AHF,△AEF田△DBF帕△DEC.△姓BC等(钝角三角形可仿图3类推相似的结论),性质6如图2,H为锐角△ABC的垂心,记△ABC的外接圆半径为R,则有AH=ZRcos月,BH=ZReosB,CH二ZReosC及HD=ZReosB·eosC,H君=ZReosC·eosA,HF=ZReosAeosB.性质7三角形的任一顶点到垂心的距离等于外心到对边的距离的二倍推论三角形的垂心、重心、外心三点共线,且,垂心到重心的距离为重心到外心距离的二倍:上述涉及三角形垂心的性质在解题中均有工具性李的作用。如飞例,M为正方形ABCD的对角线BD上的任意-一点,材E土AB,MF一AD求证:DE、刀尸、CM三线共点
三角形的五心-第3讲重心与垂心教师版
第三讲 三角形的重心与垂心 一、 基础知识 1. 重心的定义:三角形的三中线(或二中线)的交点叫做三角形的重心.
2. 重心的性质 1) 三角形的重心必在三角形的內部; 2) 三角形的重心到顶点的距离等于过这顶点的中线长的三分之二; 3) 三角形三中线分原三角形为六个等面积的三角形; 4) 三角形重心到三顶点的连线分原三角形为三个等面积的三角形; 5) 到三角形的三个顶点距离的平方和最小的点是这个三角形的重心;
3. 垂心的定义:三角形的三条高线的交点叫做三角形的垂心. 4. 垂心的性质 1) 锐角三角形垂心在三角形内部,直角三角形垂心在三角形直角顶点,钝角三角形垂心在三角形外部; 2) 垂心会在三角形内部产生很多相似直角三角形;同时会出现四点共圆问题;
二、 例题部分 第一部分 重心 例1. 如图34-2,已知△ABC与△CDA全等,点G、H分别是△ABC、△CDA的重心,则△AGH 的面积与△ABC的面积的比为 ( ) A.4:9 B.2:3 C.1:3 D.1:6
解答:C.设AC的中点为O,可证B、G、O、H、D在同一直线上,由重心性质得GO=13BO,OH=13OD, ∵BO=DO,∴GH=23BO. AGHS=23ABOS.又 ABOS=12ABCS. ∴AGHS=23×12ABCS=13ABCS.
例2. 在△ABC中,BC=3,AC=4,BC和AC的中线AE、BD互相垂直,则AB等于 ( ) A.36 B.5 C.22 D.7 解答:.B.设在AE与BD相交于G,且AE=3m,BD=3n,在Rt△AGD中.由勾股定理,得 22222mn (1) 同理在Rt△BGE中,可得
222322nm(2) 由(1)、(2),得2244mn=5 又在Rt△ABG中,2AB= 2244mn =5. ∴AB=5.
例3. 在直角三角形ABC中. A=90,G为重心,且GA=2,则22GBGC= . 解答:20.如图,过G 作GE⊥BC 则 2GB=142BC+BC·DE+2DE+2GE,2GC=142BC一BC·DE+2DE+2GE ∴2GB+2GC =122BC+22GD ∵BC=2AD=2·32AG=3AG,GD=12AG ∴2GB+2GC=12 (92AG+2AG)=52AG =20
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页
2018年中考数学复习知识点:三角形垂心
三角形的垂心的性质:
1.锐角三角形的垂心在三角形内;
直角三角形的垂心在直角顶点上;
钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形
的内心是它旁心三角形的垂心。
例如在△ABC中
3.垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的
直角三角形。
5.H、A、B、C四点中任一点是其余三点为顶点的三角形
的垂心(并称这样的四点为一—垂心组)。
6.△ABC,△ABO,△BCO,△ACO的外接圆是等圆。
7.在非直角三角形中,过O的直线交AB、AC所在直线分
别于P、Q,则AB/AP?tanB+AC/AQ tanC=tanA+tanB+tanC
8.三角形任一顶点到垂心的距离,等于外心到对边的距离
的2倍。
9.设O,H分别为△ABC的外心和垂心,则
∠BAO=∠HAC,∠ABH=∠OBC,
∠BCO=∠HCA.
10.锐角三角形的垂心到三顶点的距离之和等于其内切圆
第 2 页
与外接圆半径之和的2倍。
11.锐角三角形的垂心是垂足三角形的内心;锐角三角形
的内接三角形(顶点在原三角形的边上)中,以垂足三角形的
周长最短。
12.西姆松(Simson)定理(西姆松线):从一点向三角形的
三边所引垂线的垂足共线的重要条件是该点落在三角形的
外接圆上。
13.设H为非直角三角形的垂心,且D、E、F分别为H在
BC,CA,AB上的射影,H1,H2,H3分别为△AEF,△BDF,
△CDE的垂心,则△DEF≌△H1H2H3.
14.三角形垂心H的垂足三角形的三边,分别平行于原三
角形外接圆在各顶点的切线。
