高三暑假作业中的陌生方程
一元二次方程解法暑假作业

《一元二次方程解法》专练班级 姓名不求快,不求多,不间断。
解下例方程x 2=169; 45-x 2=0; x 2-12=04x 2=9 2x 2-3=0 12y 2-25=0;75-x 2=0; 4x 2-1=0 16x 2-25=0.x 2-214=0 3x 2-163=0 (2x+1)2=25;81(x-2)2=16 ; 3(2x+1)2=12 22)23()5(+=-x xx 2+2x+1=0; x 2+x+14=0 x 2+4x+4=0x 2-6x+9=4 x 2-4x+4=0 9x 2-6x+1=0例:用直接开平方法解方程:22)6(16)3(49+=-x x 解:开平方得,7(3)4(6)x x -=±+∴7(3)4(6)x x -=+由或7(3)4(6)x x -=-+由 ∴115.x =得,23.11x =-【点评】直接开平方法的要点是:通过等式变形变出2x n =或2()x m n -=的形式,再直接开平方; 另外注意方程解得书写格式1x 、2x . 用直接开平方法解下列一元二次方程2435x -= (2)(2)21x x -+= 2(2=9x );51)12(212=-y 4(x -3)2=25 24)23(2=+x()21-350x-=x2+2x+1=4 2269(52)x x x-+=-2216(1)9(1)x x-=+2249(3)16(6)x x-=+22((1x=x2+4x+4=0 x2-6x+9=16 x2-4x+4=10 x2+x+14=4用配方法解下列方程:x2-4x=5;x2-100x-101=0;x2+8x+9=0;y2+22y-4=0;x2+8x-2=0 x2-5x-6=0.2x 2-x=6 x²-2x-3=0 x²-4x+3=0 2x²+12x+10=0 4x²-4x-8=0 9x²-6x-8=0x 2+px +q =0 (p 2-4q ≥0).试用配方法证明:代数式x 2+3x-23的值不小于-415。
高中奥数方程问题

高中奥数方程问题引言高中奥数方程问题是高中奥数竞赛中的重要部分之一。
这些问题旨在考察学生对方程的理解和解题能力。
在解决这些问题时,学生需要运用代数知识和解方程的方法,找到未知数的值。
本文将介绍几种常见的高中奥数方程问题及其解决方法。
线性方程线性方程是最基本的方程类型之一。
线性方程的一般形式为ax + b = 0,其中a和b是已知数,x是未知数。
解线性方程的方法包括移项、合并同类项、系数倒数和取消系数等。
通过这些方法,可以计算出x的值。
二次方程二次方程是高中奥数中经常出现的方程类型之一。
二次方程的一般形式为ax^2 + bx + c = 0,其中a、b和c是已知数,x是未知数。
解二次方程的方法有因式分解法、配方法、求根公式等。
这些方法可以帮助我们求得二次方程的根。
倒数法倒数法是解决一些特殊方程的常用方法。
这种方法适用于方程中含有两个未知数之间的比例关系,通过求出两个未知数之间的倒数关系,可以得到方程的解。
无理方程无理方程是含有开方、立方根等无理数的方程。
解决无理方程可以使用分离变量、换元法、平方等方法。
这些方法允许我们得到方程的根。
综合运用在高中奥数方程问题中,常常会出现综合运用的情况。
这些问题可能结合了多种不同类型的方程,要求学生综合运用各种解题方法来解决。
在解决这类问题时,学生需要运用逻辑思维和灵活运算。
结论高中奥数方程问题是考察学生代数运算和解题能力的重要部分。
学生通过研究各种解方程的方法,可以更好地应对这类问题并提高自己的数学水平。
理解高中数学中的微分方程解法

理解高中数学中的微分方程解法微分方程是数学中的重要概念,广泛应用于物理、工程和经济等领域。
在高中数学中,微分方程的解法是一个重要的考点,也是学生们常常感到困惑的地方。
本文将从基本概念出发,深入探讨高中数学中微分方程解法的原理和方法。
1. 什么是微分方程微分方程是描述函数和其导数之间关系的方程。
一般形式为dy/dx = f(x),其中y是未知函数,f(x)是已知函数。
微分方程可以分为常微分方程和偏微分方程两类,高中数学主要涉及常微分方程。
2. 微分方程的解法高中数学中,常见的微分方程解法有分离变量法、齐次方程法和一阶线性微分方程法。
2.1 分离变量法分离变量法适用于形如dy/dx = f(x)g(y)的微分方程。
首先将方程两边分离变量,然后进行积分,得到关于y和x的方程。
最后解出y即可。
2.2 齐次方程法齐次方程法适用于形如dy/dx = f(y/x)的微分方程。
首先将方程进行变量替换,令y = vx,然后求出dy/dx和f(y/x)的关系式。
最后解出v,再代入y = vx求得y的表达式。
2.3 一阶线性微分方程法一阶线性微分方程法适用于形如dy/dx + p(x)y = q(x)的微分方程。
首先将方程写成dy/dx = -p(x)y + q(x)的形式,然后用积分因子法求出积分因子μ(x)。
最后将方程两边乘以μ(x),并进行积分,解出y的表达式。
3. 实例分析为了更好地理解微分方程的解法,我们来看一个实例。
例:求解微分方程dy/dx = x/y首先,我们可以将方程两边分离变量,得到ydy = xdx。
然后进行积分,得到∫ydy = ∫xdx,解得y^2/2 = x^2/2 + C。
最后解出y,得到y = ±√(x^2 + C)。
通过这个例子,我们可以看到分离变量法的应用。
同样的方法也可以用于其他类型的微分方程。
4. 注意事项在解微分方程时,需要注意以下几点:4.1 初始条件微分方程的解通常包含一个常数C,需要通过给定的初始条件来确定。
暑假作业第九课时 二次函数、二次方程与二次不等式

暑假作业第九课时二次函数、二次方程与二次不等式A 热身训练1.(2013•苏州)已知二次函数y=x2﹣3x+m(m为常数)的图象与x轴的一个交点为(1,23.(2012•资阳)如图是二次函数y=ax+bx+c的部分图象,由图象可知不等式ax+bx+c<04.(2011•黔东南州)如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图2从上表可知,下列说法中正确的是.(填写序号)①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是直线;④在对称轴左侧,y随x增大而增大.6.(2013•宿迁)若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是.7.抛物线:y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是.8.已知函数y=﹣x2+2x﹣.(1)用配方法求它的顶点坐标;(2)在平面直角坐标系中画出它的简图:(3)根据图象回答:x取什么值时,y>0.9.已知函数y=﹣x2﹣2x+5,当自变量x在下列取值范围内时,分别求函数的最大值和最小值,并求当函数取最大(小)值时所对应的自变量x的值:(1)x≤﹣2;(2)x≤2;(3)﹣2≤x≤1;(4)0≤x≤3.10.阅读材料,解答问题.利用图象法解一元二次不等式:x2﹣2x﹣3>0.解:设y=x2﹣2x﹣3,则y是x的二次函数.∵a=1>0,∴抛物线开口向上.又∵当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3.∴由此得抛物线y=x2﹣2x﹣3的大致图象如图所示.观察函数图象可知:当x<﹣1或x>3时,y>0.∴x2﹣2x﹣3>0的解集是:x<﹣1或x>3.(1)观察图象,直接写出一元二次不等式:x2﹣2x﹣3<0的解集是;(2)仿照上例,用图象法解一元二次不等式:x2﹣1>0.B 例题解析2例2、(2011•襄阳)已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是例3、(2013•荆门)若抛物线y=x2+bx+c与x轴只有一个交点,且过点A(m,n),B(m+6,n),求n的值。
总结简易方程知识点高中

总结简易方程知识点高中一、基本概念1.1、什么是方程方程是含有未知数的等式,通常用字母表示未知数。
一般的形式为“含有未知数的数学式等于另一数学式”。
1.2、方程中的元素方程中一般包括未知数、已知数、运算符(+、-、×、÷)和等号。
1.3、方程的解方程的解就是使方程成立的数。
1.4、方程的种类一元一次方程、一元二次方程、一元高次方程等。
二、一元一次方程2.1、方程的概念形如ax+b=0(a≠0)的方程叫一元一次方程。
2.2、方程的解法⑴、加减法解法用两边加上或减去相同的数,使一边的系数为1,从而得到解。
⑵、乘除法解法用两边乘除相同的数,使未知数系数消去,再进行计算求解。
2.3、一元一次方程的应用一元一次方程的应用十分广泛,可以解决很多实际问题,如求两个数的和为某一数值、某人的年龄等。
三、一元二次方程3.1、方程的概念形如ax²+bx+c=0(a≠0)的方程叫一元二次方程。
3.2、求解一元二次方程一元二次方程的求解可以分为以下几种情况:⑴、用配方法若方程左端可以写成两个完全平方的形式,便可以通过配方法进行求解。
⑵、用公式法利用一元二次方程的求根公式 x = (-b±√(b²-4ac))/2a 可以求解方程。
⑶、用因式分解法通过对一元二次方程进行因式分解,可以快速求解方程。
3.3、一元二次方程的应用一元二次方程在几何问题、物理问题等方面有着广泛的应用,如抛物线的求解、物体自由下落的问题等。
四、方程的常见误区4.1、方程解的唯一性在求解方程的过程中,有时候方程可能有多个解,也可能没有解。
因此,要注意方程解的唯一性。
4.2、方程的变形误区在求解方程的过程中,有时可能需要对方程进行变形,这时需要注意变形的正确性和严密性,避免出现错误。
五、解方程的一般步骤5.1、分析问题首先要对问题进行分析,确定方程的形式,并确定未知数的含义。
5.2、列方程通过分析问题,列出方程的表达式,常常包括许多已知数和未知数。
暑假作业10-实际问题与二元一次方程组(解析版)
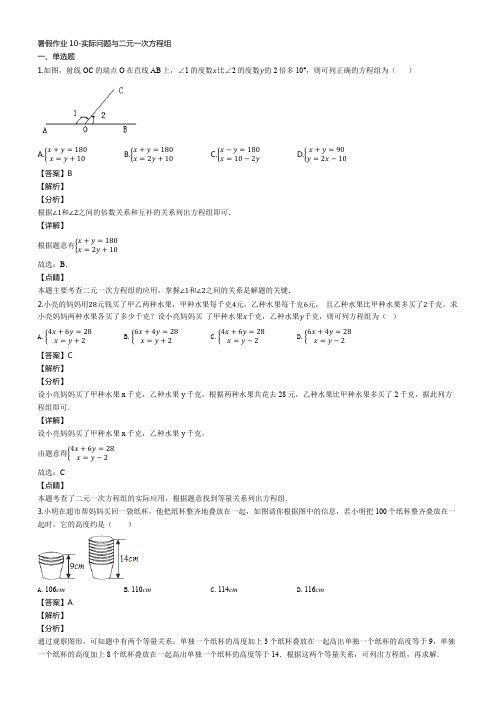
暑假作业10-实际问题与二元一次方程组一、单选题1.如图,射线OC 的端点O 在直线AB 上,∠1的度数x 比∠2的度数y 的2倍多10°,则可列正确的方程组为( )A.{x +y =180x =y +10B.{x +y =180x =2y +10C.{x −y =180x =10−2yD.{x +y =90y =2x −10【答案】B【解析】【分析】 根据∠1和∠2之间的倍数关系和互补的关系列出方程组即可.【详解】根据题意有{x +y =180x =2y +10故选:B .【点睛】本题主要考查二元一次方程组的应用,掌握∠1和∠2之间的关系是解题的关键.2.小亮的妈妈用28元钱买了甲乙两种水果,甲种水果每千克4元,乙种水果每千克6元, 且乙种水果比甲种水果多买了2千克,求小亮妈妈两种水果各买了多少千克?设小亮妈妈买 了甲种水果x 千克,乙种水果y 千克,则可列方程组为( )A.{4x +6y =28x =y +2B.{6x +4y =28x =y +2C.{4x +6y =28x =y −2D.{6x +4y =28x =y −2【答案】C【解析】【分析】设小亮妈妈买了甲种水果x 千克,乙种水果y 千克,根据两种水果共花去28元,乙种水果比甲种水果多买了2千克,据此列方程组即可.【详解】设小亮妈妈买了甲种水果x 千克,乙种水果y 千克,由题意得{4x +6y =28x =y −2故选:C【点睛】本题考查了二元一次方程组的实际应用,根据题意找到等量关系列出方程组.3.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )A.106cmB.110cmC.114cmD.116cm【答案】A【解析】【分析】 通过观察图形,可知题中有两个等量关系:单独一个纸杯的高度加上3个纸杯叠放在一起高出单独一个纸杯的高度等于9,单独一个纸杯的高度加上8个纸杯叠放在一起高出单独一个纸杯的高度等于14.根据这两个等量关系,可列出方程组,再求解.解:设每两个纸杯叠放在一起比单独的一个纸杯增高xcm ,单独一个纸杯的高度为ycm ,则{2x +y =97x +y =14,解得{x =1y =7 则99x +y =99×1+7=106即把100个纸杯整齐的叠放在一起时的高度约是106cm .故选:A .【点睛】本题以实物图形为题目主干,图形形象直观,直接反映了物体的数量关系,这是近年来比较流行的一种命题形式,主要考查信息的收集、处理能力.本题易错点是误把9cm 当作3个纸杯的高度,把14cm 当作8个纸杯的高度.4.有黑、白两种小球各若干个,且同色小球质量均相等,在如图所示的两次称量中,天平恰好平衡,如果每只砝码质量为5克,那么一只黑球和一只白球的质量和是( )A.1B.2C.3D.4【答案】D【解析】【分析】 设每只黑球和白球的质量分别是x 、y 克,根据图中信息和已知条件可以列出方程组{x +2y=53x +y=10,解方程组即可求出每只黑球和白球的质量.【详解】设每只黑球和白球的质量分别是x 、y 克,依题意得{x +2y=53x +y=10, 解得{x=3y=1, 3+1=4.故选D.【点睛】此题考查二元一次方程组,解题关键在于从图中找出隐含条件,然后列出方程组解决问题.5.五月底,全体九年级师生共422人参加社会实线活动,当时预备了49座和37座两种客车共10辆,刚好坐满.设49座客车x 辆,37座客车y 辆,根据题意可列出方程组( )A.{x +y =1049x +37y =422B.{x +y =1037x +49y =422C.{x +y =42249x +37y =10D.{x +y =42237x +49y =10【答案】A【解析】【分析】抓住本题中的两个等量关系:49座客车数量+37座客车数量=10,两种客车载客量之和=422即可列出二元一次方程组求解.【详解】解:设49座客车x 辆,37座客车y 辆,根据题意可列出方程组{x +y =1049x +37y =422 .【点睛】本题考查了由实际问题抽象出二元一次方程组,根据实际问题中的条件列方程组时,要注意抓住题目中的一些关键性词语,找出等量关系,列出方程组.6.某校七年级1班学生为了参加学校文化评比买了22张彩色的卡纸制作如下图形(每个图形由两个三角形和一个圆形组成),已知一张彩色卡纸可以剪5个三角形,或3个圆形,要使圆形和三角形正好配套,需要剪三角形的卡纸有x 张,剪圆形的卡纸有y 张,可列式为( )A.{x +y =225x =6yB.{x +y =226x =5yC.{x +y =223x =10yD.{x +y =2210x =3y【答案】A【解析】【分析】 设需要剪三角形的卡纸有x 张,剪圆形的卡纸有y 张,根据彩色卡纸的总张数为22张其剪出三角形的数量为圆的2倍,即可得出关于x 、y 的二元一次方程组,此题得解.【详解】设需要剪三角形的卡纸有x 张,剪圆形的卡纸有y 张,根据题意得:{x +y =225x =6y. 故选:A .【点睛】此题考查由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.二、填空题7.甲乙两人共有图书60本,若甲赠给乙12本书,两人的图书就一样多,如果甲乙两人原来分别有x 本、y 本,依题意可列二元一次方程组____.【答案】{x +y =60x −12=y +12【解析】【分析】设甲原来有x 本书,乙原来有y 本书,根据甲乙两人共有图书60本,若甲赠给乙12本书,两人的图书就一样多,列方程组即可.【详解】设甲原来有x 本书,乙原来有y 本书,根据题意可得:{x +y =60x −12=y +12故答案为:{x +y =60x −12=y +12本题考查由实际问题抽象出二元一次方程组,解题的关键根据题意找出等量关系. 53那么购买1支签字笔和1本笔记本应付________元.【答案】12【解析】【分析】设出签字笔与笔记本的单价,根据题意列出方程组,利用整体思想得到答案.【详解】解:设签字笔每支x 元,笔记本每本y 元,则{5x +3y =52①3x +5y =44②①+②得:8x +8y =96,∴x +y =12.所以购买1支签字笔和1本笔记本应付12元.故答案为:12.【点睛】本题考查二元一次方程组的应用,根据题意列方程组是解题关键.9.小东在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1所示.小林看见了说:“我也来试一试.”结果小林七拼八凑,拼成了如图2那样的正方形,中间还留下了一个恰好是边长为2cm 的小正方形,则这个小长方形的面积为______cm 2.【答案】60【解析】【分析】设每个小长方形的宽为xcm ,长为ycm ,根据两个拼图,列出关于x 、y 的二元一次方程组,并求解即可..【详解】解:设每个长方形的宽为xcm ,长为ycm ,那么可得出方程组为:{5x =3y 2x =y +2, 解得:{x =6y =10, 因此每个长方形的面积应该是xy =60cm 2.故答案为:60.【点睛】本题考查了二元一次方程组的应用,弄清题意、确定等量关系、列出二元一次方程组是解答本题的关键.10.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问每头牛、每只羊各值金多少两”,则每头牛值金_____两,每只羊值金________两.【答案】(1). 3421(2). 2021【解析】【分析】根据“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两”,得到等量关系,即可列出方程组然后求解即可.【详解】解:设每头牛值金x两,每只羊值金y两,根据题意得:{5x+2y=102x+5y=8,解之得:{x=3421y=2021故答案为:每头牛值金3421两,每只羊值金2021两.【点睛】本题考查了由实际问题抽象出二元一次方程组,解决本题的关键是找到题目中所存在的等量关系.三、解答题11.在抗击新型冠状肺炎期间,我市某企业向湖北武汉捐赠了价值26万元的甲、乙两种仪器共30套.已知甲种仪器每套8000元,乙种仪器每套10000元,问甲、乙两种仪器各捐赠了多少套?【答案】甲种仪器捐赠了20套,乙种仪器捐赠了10套【解析】【分析】根据题意,设甲、乙两种仪器各捐赠了x,y套,列出方程组,即可求解【详解】解:设甲、乙两种仪器各捐赠了x,y套,根据题意:{x+y=308000x+10000y=260000,解得{x=20y=10,故甲种仪器捐赠了20套,乙种仪器捐赠了10套.【点睛】本题目考查二元一次方程的实际应用,难度不大,正确理解题意,列出方程是顺利解题的关键.12.某工厂第一季度生产甲、乙两种机器共450台,改进生产技术后,计划第二季度生产这两种机器共520台,其中甲种机器增产10%,乙种机器增产20%,该厂第一季度生产甲、乙两种机器各多少台?【答案】该厂第一季度生产甲种机器200台,乙种机器250台.【解析】【分析】首先设该厂第一季度生产甲种机器x台,该厂第一季度生产乙种机器y台,根据题意可得等量关系:①第一季度甲种机器台数+乙种机器台数=450台;②第二季度甲种机器台数+乙种机器台数=520台,根据等量关系列出方程组即可.【详解】解:设该厂第一季度生产甲种机器x台,该厂第一季度生产乙种机器y台,由题意得:{x+y=450(1+10%)x+(1+20%)y=520解得:{x=200y=250所以该厂第一季度生产甲种机器200台,该厂第一季度生产乙种机器250台,答:该厂第一季度生产甲种机器200台,该厂第一季度生产乙种机器250台.【点睛】此题主要考查了二元一次方程组的应用,关键是正确理解题意,找出题目中的等量关系列出方程.13.为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒;甲,乙两种口罩的数量分别是20个/盒,25个/盒.(1)求新希望中学甲、乙两种口罩各购进了多少盒?(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教育局的要求?【答案】(1)甲口罩购进了400盒,乙口罩购进了600盒.(2)购买的口罩数量能满足教育局的要求.【解析】【分析】(1)设新希望中学甲口罩购进了x盒,乙口罩购进了y盒.根据“新希望中学33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒”列出二元一次方程组解答即可;(2)根据“甲,乙两种口罩的数量分别是20个/盒,25个/盒.”求出新希望中学共买口罩的个数,根据“新希望中学师生共计800人,每人每天2个口罩”求出两周师生需要的口罩总数进行比较即可.【详解】解:(1)设新希望中学甲口罩购进了x盒,乙口罩购进了y盒.由题意,得{x+y=100030x+35y=33000解得{x=400y=600答:新希望中学甲口罩购进了400盒,乙口罩购进了600盒.(2)甲,乙口罩共400×20+600×25=23000(个)全校师生两周共需800×2×14=22400(个)23000>22400答:购买的口罩数量能满足教育局的要求.故答案为(1)甲口罩购进了400盒,乙口罩购进了600盒.(2)购买的口罩数量能满足教育局的要求.【点睛】本题主要考查了二元一次方程组的实际应用. 解题的关键是找准等量关系,正确列出二元一次方程组.14.小李到农贸批发市场了解到苹果和西瓜的价格信息如下:他共用280元批发了苹果和西瓜共75公斤,(1)请问小李批发的苹果和西瓜各多少公斤?(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?【答案】(1)小李批发苹果25公斤,批发西瓜50公斤;(2)小李能赚70元钱.【解析】【分析】(1)设小李批发苹果x公斤,批发西瓜y公斤,根据小李用280元批发了苹果和西瓜共75公斤,即可得出关于x、y的二元一次方程组,解之即可得出结论;(2)根据总利润=每千克利润×购进数量,即可求出小李全部销售完的总利润.【详解】解:(1)设小李批发苹果x公斤,批发西瓜y公斤,根据题意得:{x+y=758x+1.6y=280,解得:{x=25y=50.答:小李批发苹果25公斤,批发西瓜50公斤.(2)(10−8)×25+(2−1.6)×50=70(元).答:小李能赚70元钱.【点睛】本题考查了二元一次方程组的应用,解题的关键是:(1)根据购物重量结合总价钱,列出关于x、y的二元一次方程组;(2)根据总利润=每千克利润×购进数量,列式计算.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
请按要求完成下列反应:
1、SO2通入酸性K2Cr2O7溶液中的离子方程式是
2、甲醇燃料电池在中性条件下负极的电极反应是
3、向盛有H2O2溶液的试管中,加入酸化的硫酸亚铁溶液的离子方程式是
4、FeCl2溶液与Cl2反应的离子方程式是
5、向Na2CO3溶液中通入少量Cl2,可制得某种生活中常用的漂白、消毒的物质。已知碳酸的酸性强于
次氯酸,则丙中发生反应的化学方程式是
6、O3和酸性碘化钾溶液反应生成O2和碘单质的离子方程式是_____________ _
7、亚铁离子和水、氧气反应得到Fe(OH)3沉淀的离子方程式是
8、以熔融碳酸盐为电解质,以CH4为燃料,空气为氧化剂,稀土金属材料为电极。
负极的电极反应是
9、稀硝酸处理阳极泥中的银的离子方程式:
10、用H2O2和稀硫酸浸泡废印刷电路板中的铜,试写出反应的离子方程式
11、若淡黄色固体过氧化钠与氯化亚铁溶液反应的物质的量之比为1 : 2,且无气体生成,
则该反应的离子方程式为
12、现以H2、O2、熔融盐Na2CO3组成的燃料电池,
写出负极上发生反应的电极反应式
13、探究氨气的还原性,氨气通入氧化铜中并加热。黑色CuO变为红色;白色无水CuSO4粉末变为蓝色;
同时生成一种无色气体,该气体无污染。请写出氨气与CuO反应的化学方程式
14、将两个石墨电极插人KOH溶液中,向两极分别通入CH4和O2,构成甲烷燃料电池。
通入CH4的一极,其电极反应式是:
15、向氯气的试管中滴入浓氨水发生反应的化学方程式是
2
16、将3.36 g Fe加到一定量稀硝酸溶液中,收集到1.12 L气体NO(已折算为标准状况),
则反应的离子方程式是
17、写出以氢氧化钾为电解质的甲醇燃料电池的负极反应式
18、硫酸亚铁在酸性条件下将MnO2还原为MnSO4的离子方程式为
19、As可与 次氯酸钠的水溶液反应,产物有As的最高价含氧酸的化学方程式为
20、将SO2通入由CuSO4和NaCl混合的浓溶液中,溶液颜色变浅,析出白色沉淀,取该沉淀进行元素
质量分数分析,知其中含Cl:35.7%,Cu:64.3%,
则该反应的离子方程式是
21、有人设想寻求合适的催化剂和电极材料,以N2、H2为电极反应物,以HCl-NH4Cl为电解质溶液
制取新型燃料电池。请写出该电池的正极反应式
22、在饱和氯水中加块状石灰石,能制得较浓HClO溶液,同时放出一种气体。其反应的
离子方程式是
23、废水中常用Cl2氧化CN-成CO2和N2,若参加反应的Cl2与CN-的物质的量之比为5︰2,
则该反应的离子方程式是
24、稀硫酸、稀硝酸与铜反应生成硫酸铜的化学方程式
25、现欲用电化学原理将CO2、SO2 转化为重要化工原料,A、B分别为两极通入的物质。
若A为SO2,B为O2,C为H2SO4,则负极的电极反应式为
26、反应NH3+O2→N2+H2O(未配平)可设计为燃料电池,在碱性条件下负极反应是
27、氧化铝与焦炭的混合物在氮气中高温加热反应,制得新型非金属材料AlN与一种中学常见气体X。
已知每转移3 mol e-,有1.5 mol化合物X生成,
此反应的化学方程式____________________________________ __
28、使用催化剂可以将汽车尾气的主要有害成分一氧化碳(CO)和氮氧化物(NOx)转化为无毒气体,
该反应的化学方程式为
29、碱液吸收法:用Na2CO3溶液吸收NO2生成CO2。若每9.2 g NO2和Na2CO3溶液反应时转移电子数为0.1 mol,
则反应的离子方程式是
30、氯的最高价氧化物水化物的浓溶液不稳定,受热可分解,产物之一是黄绿色气体,且当有28mol电子
转移时,共产生9mol气体,写出该反应的化学方程式
