中考数学《二次函数-动态几何问题》专项练习及答案
含参数的二次函数专题训练动态问题北京市中考数学题含答案解析

含参数的二次函数专题训练1.(2018·北京)在平面直角坐标系xOy 中,直线y=4x+4与x 轴、y 轴分别交于点A ,B ,抛物线y=ax 2 +bx −3a 经过点A ,将点B 向右平移5个单位长度,得到点C .(1)求点C 的坐标;(2)求抛物线的对称轴;(3)若抛物线与线段BC 恰有一个公共点,结合函数图象,求a 的取值范围.2.(2019·北京)在平面直角坐标系xOy 中,抛物线y =ax 2 +bx −a 1 与y 轴交于点A ,将点A 向右平移2个单位长度,得到点B ,点B 在抛物线上.(1)求点B 的坐标(用含a 的式子表示);(2)求抛物线的对称轴;(3)已知点P ⎪⎭⎫ ⎝⎛-a 1,21 ,Q (2,2),若抛物线与线段PQ 恰有一个公共点,结合函数图象,求a 的取值范围.含参数的二次函数专题训练答案解析1. 解: (1)∵直线y=4x+4与x 轴、y 轴交于点A ,B .∴A (−1,0),B (0,4),∴C (5,4).(2)抛物线y=ax 2+bx −3a 过A (−1,0),∴a −b −3a=0,b=−2a ,∴y=ax 2 −2ax −3a ,∴对称轴为直线x=1.(3)①当抛物线过点C 时,如答图①.25a −10a −3a=4,解得a=31 . ②当抛物线过点B 时,如答图②.−3a=4,解得a=34- . ③当抛物线顶点在BC 上时,如答图③.此时顶点为(1,4).∴a −2a −3a=4,解得a=−1.综上所述,a 的取值范围为a<34-或a ≥31 或a=−1.2.(2019·北京)在平面直角坐标系xOy 中,抛物线y =ax +bx − 与y 轴交于点A ,将点A 向右平移2个单位长度,得到点B ,点B 在抛物线上.(1)求点B 的坐标(用含a 的式子表示);(2)求抛物线的对称轴;(3)已知点P ,Q (2,2),若抛物线与线段PQ 恰有一个公共点,结合函数图象,求a 的取值范围.解: (1)将x =0代入y =ax 2 +bx −a 1,得y =−a1 , ∴点A 的坐标为(0,a1-) . ∴点B 的坐标为(2,a 1-) . (2)∵抛物线经过点A (0,a 1-) 和点B(2,a1-) , ∴抛物线的对称轴为直线x =1.(3)①当a >0时,a1- <0.根据抛物线的对称性,可知抛物线不能同时经过点A 和点P ,也不能同时经过点B 和点Q ,所以此时抛物线与线段PQ 没有交点;②当a <0时,a1- >0.根据抛物线的对称性,可知抛物线不能同时经过点A 和点P ;当点Q 在点B 上方或与点B 重合时,抛物线与线段PQ 恰有一个公共点,此时a 1-≤2,即a ≤21- . 综上可知,当a ≤21-时,抛物线与线段PQ 恰有一个公共点.。
初中数学二次函数的应用题型分类——动态几何图形问题15( 附答案)

初中数学二次函数的应用题型分类——动态几何图形问题15(附答案)1.如图一个五边形的空地ABCDE ,AB CD ∥,BC DE ∥,C 90︒∠=,已知4(m)AB =,10(m)BC =,14(m)CD =,5(m)DE =,准备在五边形中设计一个矩形的休闲亭MNPQ ,剩下部分设计绿植.设计要求NP CD ∥,PQ BC ∥,矩形MNPQ 到五边形ABCDE 三边AB ,BC ,CD 的距离相等,都等于(m)x ,延长QM 交AE 与H ,1(m)MH =.(1)五边形ABCDE 的面积为________()2m; (2)设矩形MNPQ 的面积为()2m y ,求y 关于x 的函数关系式;(3)若矩形MNPQ 休闲亭的造价为每平方米0.5万元,剩下部分绿植的造价为每平方米0.1万元,求总造价的最大值.2.如图所示,已知抛物线2(0)y ax a =≠与一次函数y kx b =+的图象相交于(1,1)A --,(2,4)-B 两点,点P 是抛物线上不与A ,B 重合的一个动点.(1)请求出a ,k ,b 的值;(2)当点P 在直线AB 上方时,过点P 作y 轴的平行线交直线AB 于点C ,设点P 的横坐标为m ,PC 的长度为L ,求出L 关于m 的解析式;(3)在(2)的基础上,设PAB ∆面积为S ,求出S 关于m 的解析式,并求出当m 取何值时,S 取最大值,最大值是多少?3.如图,在四边形ABCD 中,对角线AC 、BD 互相垂直20cm AC BD +=,设AC 的长度为cm x ,四边形的面积2cm S 随x 的变化而变化.(1)求S与x的函数关系式(不要求写出x的取值范围);(2)当x为何值时,这个四边形的面积有最大值,最大面积是多少?4.如图,在矩形ABCD中,AB=18,AD=12,点M是边AB的中点,连结DM,DM 与AC交于点G,点E,F分别是CD与DG上的点,连结EF,(1)求证:CG=2AG.(2)若DE=6,当以E,F,D为顶点的三角形与△CDG相似时,求EF的长.(3)若点E从点D出发,以每秒2个单位的速度向点C运动,点F从点G出发,以每秒1个单位的速度向点D运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG的面积的最小值.5.如图,在平面直角坐标系xOy中,抛物线y=ax2+8ax(a>0)与x轴交于O,A两点,顶点为M,对称轴与x轴交于H,与过O,A,M三点的⊙Q交于点B,⊙Q的半径为5,点C从点B出发,沿着圆周顺时针向点M运动,射线MC与x轴交于D,与抛物线交于E,过点E作ME的垂线交抛物线的对称轴于点F.(1)求抛物线的解析式;(2)当点C的运动路径长为10π3时,求证:3.(3)在点C运动过程中.是否存在这样的位置,使得以点M,E,F为顶点的三角形与△AHQ相似?若存在,求出此位置时点E的坐标;若不存在,请说明理由.6.如图,抛物线y=(x+2)2+m与x轴交于A,B两点,与y轴交于点C.点D在抛物线上,且与点C关于抛物线的对称轴对称,抛物线的顶点为M,点B的坐标为(﹣1,0).(1)求抛物线的解析式及A,C,D的坐标;(2)判断△ABM的形状,并证明你的结论;(3)若点P是直线BD上一个动点,是否存在以P,C,D为顶点的三角形与△ABD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由7.如图,已知抛物线与坐标轴交于A(﹣4,0)、B(2,0)、C(0,4),连接BC,AC.(1)求抛物线的解析式;(2)若点E是抛物线在第二象限上的一点,过点E作DE⊥AC于点D,求DE的最大值.(3)若点E是抛物线上第二象限上的一动点,过点E作DE⊥AC于点D,连接CE,若△CDE与△COB相似,直接写出点E的坐标.8.定义:有一组邻角相等的凸四边形叫做“梦想四边形”。
初中数学二次函数的应用题型分类——动态几何图形问题4( 附答案)
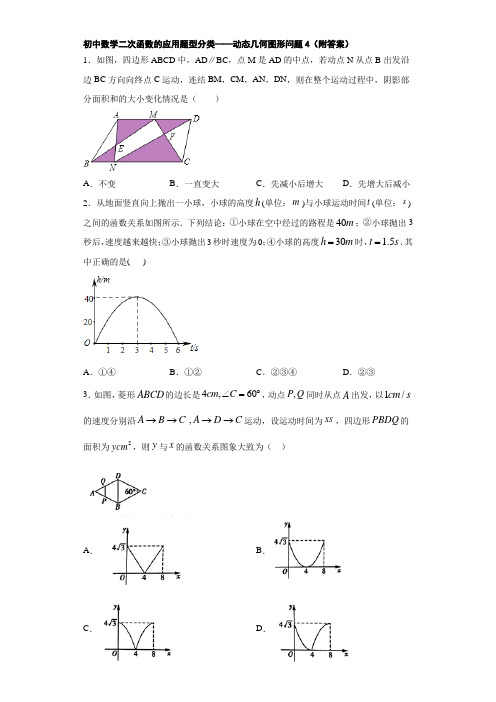
初中数学二次函数的应用题型分类——动态几何图形问题4(附答案)1.如图,四边形ABCD 中,AD ∥BC ,点M 是AD 的中点,若动点N 从点B 出发沿边BC 方向向终点C 运动,连结BM ,CM ,AN ,DN ,则在整个运动过程中,阴影部分面积和的大小变化情况是( )A .不变B .一直变大C .先减小后增大D .先增大后减小 2.从地面竖直向上抛出一小球,小球的高度h (单位:m )与小球运动时间t (单位:s )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是40m ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度30h m =时, 1.5t s =.其中正确的是( )A .①④B .①②C .②③④D .②③3.如图,菱形ABCD 的边长是4,60cm C ∠=︒,动点,P Q 同时从点A 出发,以1/cm s 的速度分别沿 ,A B C A D C →→→→运动,设运动时间为xs ,四边形PBDQ 的面积为2ycm ,则y 与x 的函数关系图象大致为( )A .B .C .D .4.设等边三角形的边长为x (x >0),面积为y ,则y 与x 的函数关系式是( ) A .y =12x 2 B .y =214x C .y =23x 2 D .y =234x 5.如图,Rt OAB △的顶点(2,4)A -在抛物线2y ax =上,将Rt OAB △绕点O 顺时针旋转90︒,得到OCD ,边CD 与该抛物线交于点P ,则点P 的坐标为( ).A .(2,2)B .(2,2)C .(2,2)D .(2,2) 6.如图所示,△ABC 为等腰直角三角形,∠ACB=90°,AC=BC=2,正方形DEFG 边长也为2,且AC 与DE 在同一直线上,△ABC 从C 点与D 点重合开始,沿直线DE 向右平移,直到点A 与点E 重合为止,设CD 的长为x ,△ABC 与正方形DEFG 重合部分(图中阴影部分)的面积为y ,则y 与x 之间的函数关系的图象大致是( )A .B .C .D .7.如图1,S 是矩形ABCD 的AD 边上一点,点E 以每秒k cm 的速度沿折线BS -SD -DC 匀速运动,同时点F 从点C 出发点,以每秒1cm 的速度沿边CB 匀速运动.已知点F 运动到点B 时,点E 也恰好运动到点C ,此时动点E ,F 同时停止运动.设点E ,F出发t 秒时,△EBF 的面积为2ycm .已知y 与t 的函数图像如图2所示.其中曲线OM ,NP 为两段抛物线,MN 为线段.则下列说法:①点E 运动到点S 时,用了2.5秒,运动到点D 时共用了4秒;②矩形ABCD 的两邻边长为BC =6cm ,CD =4cm ;③sin ∠ABS =32; ④点E 的运动速度为每秒2cm .其中正确的是( )A .①②③B .①③④C .①②④D .②③④ 8.如图(1)所示,E 为矩形ABCD 的边AD 上一点,动点P ,Q 同时从点B 出发,点P 沿折线BE ED DC --运动到点C 时停止,点Q 沿BC 运动到点C 时停止,它们运动的速度都是1/cm 秒,设P 、Q 同时出发t 秒时,BPQ ∆的面积为2ycm .已知y 与t 的函数关系图象如图(2)(曲线OM 为抛物线的一部分)则下列结论正确的是( )图(1) 图(2)A .:3:4AB AD =B .当BPQ ∆是等边三角形时,5t =秒C .当ABE QBP ∆∆时,7t =秒D .当BPQ ∆的面积为24cm 时,t 的值是10或秒4759.如图,AB 是半圆O 的直径,且AB =4cm ,动点P 从点O 出发,沿OA→AB →BO 的路径以每秒1cm 的速度运动一周.设运动时间为t ,s =OP 2,则下列图象能大致刻画s 与t 的关系的是( )A .B .C .D .10.如图等边ABC ∆的边长为4cm ,点P ,点Q 同时从点A 出发,点Q 沿AC 以1/cm s 的速度向点C 运动,点P 沿A B C --以2/cm s 的速度也向点C 运动,直到到达点C 时两点都停止运动,若APQ ∆的面积为2)(S cm ,点Q 的运动时间为()t s ,则下列最能反映S 与t 之间函数关系的图象是( )A .B .C .D .11.如图在平面直角坐标系中,点A 在抛物线y =x 2﹣4x+6上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,则对角线BD 的最小值为_____.12.如图,在ABC ∆中,90B ∠=︒,12AB =mm ,24BC =mm ,动点P 从点A 开始沿边AB 向B 以2mm/s 的速度移动(不与点B 重合),动点Q 从点B 开始沿边BC 向C 以4mm/s 的速度移动(不与点C 重合).如果P 、Q 分别从A 、B 同时出发,那么经过______秒,四边形APQC 的面积最小.13.如图,直线l 与半径为4的⊙O 相切于点A ,P 是⊙O 上的一个动点(不与点A 重合),过点P 作PB ⊥l ,垂足为B ,连接PA .设PA =x ,PB =y ,则(x -y )的最大值是 .14.如图,二次函数(2)(02)y x x x =-≤≤的图象记为1C ,它与x 轴交于点O ,1A ;将1C 绕点1A 旋转180得2C ,交x 轴于点2A ;将2C 绕点2A 旋转180得3C ,交x 轴于点3A ;……如此进行下去,得到一条“波浪线”.若(2019,)P m 在这条“波浪线”上,则m =________.15.如图,已知正方形OBCD 的三个顶点坐标分别为B(1,0),C(1,1), D(0,1). 若抛物线2()y x h =-与正方形OBCD 的边共有3个公共点,则h 的取值范围是___________.16.如图,⊙P 的半径为2,圆心P 在抛物线2132y x =-上运动,当⊙P 与x 轴相切时,圆心P 的坐标为___________.17.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =22,AD 为BC 边上的高,动点P 在AD 上,从点A 出发,沿A →D 方向运动,设AP =x ,△ABP 的面积为S 1,矩形PDFE 的面积为S 2,y =S 1+S 2,则y 与x 的关系式是_____.18.边长为2的正方形OABC 在平面直角坐标系中的位置如图所示,点D 是边OA 的中点,连接CD ,点E 在第一象限,且DE ⊥DC ,DE =DC .以直线AB 为对称轴的抛物线过C ,E 两点.点M 为直线AB 上一动点,点N 为抛物线上一动点,当以点M ,N ,D ,E 为顶点的四边形是平行四边形时点N 的坐标为___________.19.如图,已知AB =12,P 为线段AB 上的一个动点,分别以AP 、PB 为边在AB 的同侧作菱形APCD 和菱形PBFE ,点P 、C 、E 在一条直线上,∠DAP =60°.M 、N 分别是对角线AC 、BE 的中点.当点P 在线段AB 上移动时,点M 、N 之间的距离最短为______.(结果留根号)20.如图,抛物线212y x mx n =++与直线132y x =+交于A ,B 两点,交x 轴与D ,C 两点,连接AC ,已知A (0,3),C (3,0).(1)抛物线的解析式__;(2)设E 为线段AC 上一点(不含端点),连接DE ,一动点M 从点D 出发,沿线段DE 以每秒一个单位速度运动到E 点,再沿线段EA 以每秒2个单位的速度运动到A 后停止.若使点M 在整个运动中用时最少,则点E 的坐标__.21.如图,抛物线212y x bx c =++与轴交于点A 和点B ,与y 轴交于点C ,作直线BC ,点B 的坐标为()6,0,点C 的坐标为()0,6-.(1)求抛物线的解析式并写出其对称轴;(2)D 为抛物线对称轴上一点,当BCD 是以BC 为直角边的直角三角形,求D 点坐标;(3)若E 为y 轴上且位于点C 下方的一点,P 为直线BC 上的一点,在第四象限的抛物线上是否存在一点Q .使以,,,C E P Q 为顶点的四边形是菱形且CE 为菱形对角线?若存在,请求出Q 点的横坐标;若不存在,请说明理由.22.已知,如图,二次函数2y ax bx c =++图像交x 轴于(1,0)A -,交y 交轴于点(0,3)C ,D 是抛物线的顶点,对称轴DF 经过x 轴上的点(1,0)F .(1)求二次函数关系式;(2)对称轴DF 与BC 交于点M ,点P 为对称轴DF 上一动点.①求5AP +的最小值及取得最小值时点P 的坐标; ②在①的条件下,把APF 沿着x 轴向右平移t 个单位长度(04)t ≤≤时,设APF 与MBF 重叠部分面积记为S ,求S 与t 之间的函数表达式,并求出S 的最大值.23.如图,直线y =2x ﹣8分别交x 轴、y 轴于点A 、点B ,抛物线y =ax 2+bx (a≠0)经过点A ,且顶点Q 在直线AB 上.(1)求a ,b 的值.(2)点P 是第四象限内抛物线上的点,连结OP 、AP 、BP ,设点P 的横坐标为t ,△OAP 的面积为s 1,△OBP 的面积为s 2,记s =s 1+s 2,试求s 的最值.24.在平面直角坐标系中,矩形OABC 的顶点B 的坐标为(2,4),抛物线y=-2x 2+bx+c 经过A 、C 两点,与x 轴的另一个交点为点D .(1)如图1,求抛物线的函数表达式;(2)如图2,连接AC 、AD ,将△ABC 沿AC 折叠后与AD 、y 轴分别交于点交于E 、G ,求OG 的长度;(3)如图3,将抛物线在AC 上方的图象沿AC 折叠后与y 轴交与点F ,求点F 的坐标.25.如图,在矩形ABCD 中,边长18cm AB =,4cm AD =,两动点P 、Q 分别从A 、B 同时出发,点P 从A 沿AB 向B 匀速运动,每秒2cm ,点Q 从B 沿BC 向C 匀速运动,每秒1cm ,两点P 、Q 中有一点到达矩形的顶点则运动停止.设运动时间为x 秒,BPQ ∆的面积为2cm y(1)求y 与x 的函数关系式,并写出x 的取值范围;(2)当P 、Q 两点运动多少秒时,BPQ ∆的面积为214cm ;(3)当x 取何值时,BPQ ∆的面积最大?并求出其最大面积.26.如图,一次函数y=kx+b 与反比例函数y=a x的图象在第一象限内交于A ,B 两点,点A 的纵坐标为4,点B 的坐标为(3,2),连接0A ,OB .(1)求反比例函数的解析式;(2)点M 是线段AB 上的一动点(不与点A ,B 重合),过点M 作ME ⊥x 轴于点E ,作MN ⊥y 轴为于点N ,求四边形MEON 的最大面积;(3)将直线y=kx+b 向下平移n 个单位长度,若直线与反比例函数在第一象限内的图象只有一个交点,求n 的值.27.如图,在平面直角坐标系xoy 中,顶点为M 的抛物线1C :2y ax bx =-(0a <)经过点A 和x 轴上的点B ,2AO OB ==,120AOB ∠=︒.(1)求该抛物线的表达式;(2)联结AM ,求AOM S ;(3)将抛物线1C 向上平移得到抛物线2C ,抛物线2C 与x 轴分别交于点E F 、(点E 在点F 的左侧),如果MBF 与AOM 相似,求所有符合条件的抛物线2C 的表达式.28.如图1,在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠与x 轴交于()10A -,,0(4)B ,两点,与y 轴交于()023C ,.(1)求函数表达式;(2)点D 是线段BC 中点,点E 是BC 上方抛物线上一动点,连接CE ,DE .当CDE △的面积最大时,过点E 作y 轴垂线,垂足为F ,点p 为线段EF 上一动点,将CEF △绕点C 顺时针方向旋转90°,点F ,P ,E 的对应点分别是F ',P ',E ',点Q 从点P 出发,先沿适当的路径运动到点F '处,再沿F C '运动到点C 处,最后沿适当的路径运动到点P 处停止.求CDE △面积的最大值及点Q 经过的最短路径的长;29.如图,二次函数213y x bx 22=+-的图象与x 轴交于点A (﹣3,0)和点B ,以AB 为边在x 轴上方作正方形ABCD ,点P 是x 轴上一动点,连接DP ,过点P 作DP 的垂线与y 轴交于点E .(1)请直接写出点D 的坐标: ;(2)当点P 在线段AO (点P 不与A 、O 重合)上运动至何处时,线段OE 的长有最大值,求出这个最大值;(3)是否存在这样的点P ,使△PED 是等腰三角形?若存在,请求出点P 的坐标及此时△PED 与正方形ABCD 重叠部分的面积;若不存在,请说明理由.30.如图,在平面直角坐标系中,点 A 和点 C 分别在x 轴和 y 轴的正半轴上,OA=6,OC=4,以 OA ,OC 为邻边作矩形 OABC , 动点 M ,N 以每秒 1 个单位长度的速度分别从点 A 、C 同时出发,其中点 M 沿 AO 向终点 O 运动,点 N 沿 CB 向终点 B运动,当两个动点运动了 t 秒时,过点 N 作NP ⊥BC ,交 OB 于点 P ,连接 MP .(1)直接写出点 B 的坐标为 ,直线 OB 的函数表达式为 ;(2)记△OMP 的面积为 S ,求 S 与 t 的函数关系式()06t <<;并求 t 为何值时,S 有最大值,并求出最大值.参考答案1.C【解析】【分析】连接MN,根据平行线之间的距离处处相等可得: △AEB与△NME的面积相等,同理△NMF 与△CDF的面积相等,从而得出S阴影=S四边形ABCD﹣2S四边形MENF,设AM=MD=a,BC=b,BN=x,S△AMN=S△DMN=k,根据平行线分线段成比例得出各部分面积与x的函数关系式,再利用函数的增减性判断即可.【详解】解:连接MN,∵AD∥BC∴S△ABM=S△NMA,∴△AEB与△NME的面积相等,同理△NMF与△CDF的面积相等,∴S阴影=S四边形ABCD﹣2S四边形MENF,设AM=MD=a,BC=b,BN=x,S△AMN=S△DMN=k,k为常数∴AE AM EN BNax==所以S△AEM:S△AMN=a a x +∴S△AEM=ak a x +同理S△DFM=ak a b x +-令S=S△AEM+S△DFM=a a a ak k k a x a b x a x a b x⎛⎫+=+⎪++-++-⎝⎭=22()()a abak kx a b x+++-,其分子为常数令y =(a+x )(a+b ﹣x )=-x 2+bx+a 2+ab它的对称轴为x =2b ,开口向下 当0<x <2b 时,y 随x 的增大而增大,此时S 随着x 的增大而减小 所以S 四边形MENF =2k S -随x 的增大而增大所以S 空白=2S 四边形MENF 随x 的增大而增大所以S 阴影随x 的增大而减小 当2b <x <b 时,y 随x 的增大而减小,此时S 随着x 的增大而增大 所以S 阴影随x 的增大而增大综上所述:S 阴影先减小后增大故选:C .【点睛】此题考查的是动点问题与函数的增减性问题,掌握用函数思想解决问题和等高时,面积比与等于底之比是解决此题的关键.2.D【解析】【分析】根据函数的图象中的信息判断即可.【详解】①由图象知小球在空中达到的最大高度是40m ;故①错误;②小球抛出3秒后,速度越来越快;故②正确;③小球抛出3秒时达到最高点即速度为0;故③正确;④设函数解析式为:()2340h a t =-+,把()0,0O 代入得()200340a =-+,解得409a =-, ∴函数解析式为()2403409h t =--+, 把30h =代入解析式得,()240303409t =--+, 解得: 4.5t =或 1.5t =,∴小球的高度30h m =时, 1.5t s =或4.5s ,故④错误;故选D .【点睛】本题考查了二次函数的应用,解此题的关键是正确的理解题意3.C【解析】【分析】根据题意可以求出各段对应的函数解析式,再根据函数解析式即可判断哪个选项是符合题意的,本题得以解决.【详解】解:∵菱形ABCD 的边长为4cm ,∠A=60°,动点P ,Q 同时从点A 出发,都以1cms 的速度分别沿A→B→C 和A→D→C 的路径向点C 运动,∴△ABD 是等边三角形,∴当0<x≤4时,y=12×4×4×sin60°−124x 2=42 当4<x≤8时, y=12×4×4×sin60°−12×(8−x)×(8−x)×sin60°22 ∴选项C 中函数图像符合题意,故选:C.【点睛】本题考查动点问题的函数图象,解答本题的关键是明确题意,求出各段对应的函数解析式,利用数形结合的思想解答.4.D【解析】【分析】作出三角形的高,利用直角三角形的性质及勾股定理可得高,利用三角形的面积=12底×高,把相关数值代入即可求解.【详解】解:作出BC 边上的高AD .∵△ABC 是等边三角形,边长为x ,∴CD =12x , ∴高为h =3x , ∴y =12x ×h =23x 4. 故选:D .【点睛】此题主要考查了三角形的面积的求法,找到等边三角形一边上的高是难点,求出三角形的高是解决问题的关键.5.C【解析】【分析】先根据待定系数法求得抛物线的解析式,然后根据题意求得D (0,2),且DC ∥x 轴,从而求得P 的纵坐标为2,代入求得的解析式即可求得P 的坐标.【详解】∵Rt △OAB 的顶点A (−2,4)在抛物线2y ax =上,∴4=4a ,解得a =1,∴抛物线为2y x =,∵点A (−2,4),∴B (−2,0),∴OB =2,∵将Rt △OAB 绕点O 顺时针旋转90︒,得到△OCD ,∴D 点在y 轴上,且OD =OB =2,∴D (0,2),∵DC ⊥OD ,∴DC ∥x 轴,∴P 点的纵坐标为2,代入2y x =,得22x =,解得x = ∴P )2故答案为:)2. 【点睛】考查二次函数图象上点的坐标特征, 坐标与图形变化-旋转,掌握旋转的性质是解题的关键. 6.A【解析】【分析】此题可分为两段求解,即C 从D 点运动到E 点和A 从D 点运动到E 点,列出面积随动点变化的函数关系式即可.【详解】解:设CD 的长为x ABC ,与正方形DEFG 重合部分(图中阴影部分)的面积为y ∴当C 从D 点运动到E 点时,即02x ≤≤时,()()2111y 222x 2x x 2x 222=⨯⨯--⨯-=-+. 当A 从D 点运动到E 点时,即2x 4<≤时,()][()211y 2x 22x 2x 4x 822⎡⎤=⨯--⨯--=-+⎣⎦, y ∴与x 之间的函数关系()221y x 2x 0x 221y x 4x 8(2x 4)2⎧=-+≤≤⎪⎪⎨⎪=-+<≤⎪⎩由函数关系式可看出A 中的函数图象与所求的分段函数对应.故选A .【点睛】本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.7.C【解析】【分析】①根据函数图像的拐点是运动规律的变化点由图象即可判断.②设AB CD acm ==,BC AD bcm ==,由函数图像利用△EBF 面积列出方程组即可解决问题.③由 2.5BS k =,1.5SD k =,得53BS SD =,设3SD x =,5BS x =,在RT ABS ∆中,由222AB AS BS +=列出方程求出x ,即可判断.④求出BS 即可解决问题.【详解】解:函数图像的拐点时点运动的变化点根据由图象可知点E 运动到点S 时用了2.5秒,运动到点D 时共用了4秒.故①正确.设AB CD acm ==,BC AD bcm ==, 由题意,1··( 2.5)721·(4)42a b a b ⎧-=⎪⎪⎨⎪-=⎪⎩ 解得46a b =⎧⎨=⎩, 所以4AB CD cm ==,6BC AD cm ==,故②正确,2.5BS k =, 1.5SD k =, ∴53BS SD =,设3SD x =,5BS x =, 在Rt ABS ∆中,222AB AS BS +=,2224(63)(5)x x ∴+-=,解得1x =或134-(舍), 5BS ∴=,3SD =,3AS =,3sin 5AS ABS BS ∴∠==故③错误, 5BS =,5 2.5k ∴=, 2/k cm s ∴=,故④正确,故选:C .【点睛】本题考查二次函数综合题、锐角三角函数、勾股定理、三角形面积、函数图象问题等知识,读懂图象信息是解决问题的关键,学会设未知数列方程组解决问题,把问题转化为方程去思考,是数形结合的好题目,属于中考选择题中的压轴题.8.D【解析】【分析】先根据图象信息求出AB 、BE 、BE 、AE 、ED ,A 、直接求出比,B 、先判断出∠EBC≠60°,从而得出点P 可能在ED 上时,△PBQ 是等边三角形,但必须是AD 的中点,而AE >ED ,所以点P 不可能到AD 中点的位置,故△PBQ 不可能是等边三角形;C 、利用相似三角形性质列出方程解决,分两种情况讨论计算即可,D 、分点P 在BE 上和点P 在CD 上两种情况计算即可.【详解】由图象可知,AD =BC =BE =5,CD =AB =4,AE =3,DE =2,A 、∴AB :AD =5:4,故A 错误,B 、∵tan ∠ABE =AE 3AB 4, ∴∠ABE≠30°∴∠PBQ≠60°,∴点P 在ED 时,有可能△PBQ 是等边三角形,∵BE =BC ,∴点P 到点E 时,点Q 到点C ,∴点P在线段AD中点时,有可能△PBQ是等边三角形,∵AE>DE,∴点P不可能到AD的中点,∴△PBQ不可能是等边三角形,故B错误,C、∵△ABE∽△QBP,∴点E只有在CD上,且满足BC CP AB AE=,∴543CP =,∴CP=154.∴t=(BE+ED+DQ)÷1=5+2+(4−154)=494.故C错误,D、①如图(1)在Rt△ABE中,AB=4,BE=5sin∠AEB=45 ABBE=,∴sin∠CBE=4 5∵BP=t,∴PG=BPsin∠CBE=45t,∴S△BPQ=12BQ×PG=12×t×45t=25t2=4,∴t=10(舍)或t10,②当点P在CD上时,S△BPQ=12×BC×PC=12×5×(5+2+4−t)=52×(11−t)=4,∴t =475,∴当△BPQ 的面积为4cm 2时,t 或475秒,故D 正确, 故选:D .【点睛】此题是二次函数综合题,主要考查动点问题的函数图象、矩形的性质、三角形的面积公式等知识.解题的关键是读懂图象信息求出相应的线段,学会转化的思想,把问题转化为方程的思想解决,属于中考常考题型..9.C【解析】【分析】在半径AO 上运动时,s=OP 2=t 2;在弧BA 上运动时,s=OP 2=4;在BO 上运动时,s=OP 2=(4π+4-t )2,s 也是t 是二次函数;即可得出答案.【详解】解:利用图象可得出:当点P 在半径AO 上运动时,s=OP 2=t 2;在弧AB 上运动时,s=OP 2=4;在OB 上运动时,s=OP 2=(2π+4-t )2.结合图像可知C 选项正确故选:C .【点睛】此题考查了动点问题的函数图象,能够结合图形正确得出s 与时间t 之间的函数关系是解决问题的关键.10.C【解析】【分析】先计算点P 从点A 运动到点B 时APQ ∆的面积等式,再计算点P 从点B 运动到点C 时APQ ∆的面积等式,最后根据二次函数图象的性质即可得出答案.【详解】由等边三角形的性质得:4,60AB BC AC cm A C ===∠=∠=︒由题意,分点P 从点A 运动到点B 和点P 从点B 运动到点C 两段分析: (1)点P 从点A 运动到点B 点P 运动到点B 时,时间为4222AB t ===,此时点Q 运动到AC 的中点处 2,AP t AQ t ==1cos60cos 2AQ A AP ∴==︒= APQ ∴∆是直角三角形,223PQ AP AQ t =-=则APQ ∆的面积为21133(02)222S PQ AQ t t t t =⋅=⋅⋅=≤≤ (2)点P 从点B 运动到点C点P 运动到点C 时,时间为44422AB BC t ++===,此时点Q 运动到点C 处 如图,2,AB BP t AQ t +==()82,4CP AB BC AB BP t CQ AC AQ t ∴=+-+=-=-=-41cos60cos 822CQ t C CP t -∴===︒=- CPQ ∆∴是直角三角形,223(4)PQ CP CQ t =-=-则APQ ∆的面积为21133(4)23(24)22S PQ AQ t t t t t =⋅=⋅-⋅=-+<≤ 综上,223(02)323(24)2t t S t t t ⎧≤≤⎪=⎨⎪-+<≤⎪⎩ 根据二次函数图象的性质可得,只有C 项符合题意故选:C.本题考查了二次函数的几何应用,依据题意分两段讨论,分别求出面积S的表达式是解题关键.11.2【解析】【分析】先确定二次函数的最小值,依据矩形的对角线相等可得到BD=AC,然后确定出AC的最小值即可,【详解】解:∵y=x2﹣4x+6=(x﹣2)2+2,∴抛物线的顶点坐标为(2,2),∵四边形ABCD为矩形,∴BD=AC,∵AC⊥x轴,∴AC的长等于点A的纵坐标,当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为2,∴对角线BD的最小值为2.故答案为2.【点睛】本题主要考查的是矩形性质,配方法求二次函数的最值,解答关键是注意点A运动到抛物线顶点时,AC最小.12.3【解析】【分析】根据等量关系“四边形APQC的面积等于三角形ABC的面积减去三角形PBQ的面积”列出函数关系求最小值.【详解】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:S=S△ABC-S△PBQ=12×12×6-12(6-t)×2t=(t-3)2+27.∴当t=3s时,S取得最小值.故填:3.【点睛】本题考查了函数关系式的求法以及最值的求法,解题的关键是根据题意列出函数关系式,并根据二次函数的性质求出最值.13.2【解析】【详解】解:连AC,并延长AO交⊙O于点C,连CP∵AC是直径∴∠CPA=90°又∵AB是切线∴CA⊥AB,∵PB⊥l∴AC∥PB∴∠CAP=∠APB∴△APC∽△PBA∴=,∴=∴y=x2∴x﹣y=x﹣x2=﹣x2+x=﹣(x﹣4)2+2,因此当x=4时,x ﹣y 有最大值是2,考点:1.切线的性质;2.相似三角形的判定与性质;3.二次函数的最值.14.1.【解析】【分析】求出抛物线1C 与x 轴的交点坐标,观察图形可知第奇数号抛物线都在x 轴下方,然后判断点P 所在抛物线的位置,求出解析式然后把点P 的坐标代入计算即可.【详解】解:令0y =,则()20x x -=,解得120,2x x ==,∴图像与x 轴交点坐标为:()0,0O ,()12,0A∵将1C 绕点1A 旋转180得2C ,交x 轴于点2A ;将2C 绕点2A 旋转180得3C ,交x 轴于点3A ;……每隔4个单位长度图形便会进行重复,如此进行下去,由2019÷4=504……3可知抛物线505C 在x 轴下方,相当于抛物线1C 向右平移了4×505=2020个单位长度得到505C , ∴抛物线505C 的解析式为()()()2018202020182020y x x x =--≤≤∵(2019,)P m 在505C 上,∴()()20192018201920201m =--=故答案为1.【点睛】本题考查的是二次函数图像与几何变换和抛物线与坐标轴的交点,能够判断出点P 在505C 上是解题的关键.15.0<h<1【解析】【分析】分别画出h 不同取值时函数图象,由图直观得出与正方形有3个交点时h 的取值范围.【详解】图(1) 图(2) 图(3)图(1)当h=0时,抛物线与正方形有2个公共点,图(2)当 0<h<1时, 抛物线与正方形有3个公共点,图(3) 当h=1时,抛物线与正方形有2个公共点,所以当 0<h<1时符合要求.【点睛】本题考查函数图象的特点,数形结合是解答此题的关键.16.()()1022±±-,, 【解析】【分析】根据切线的性质得点P 到x 轴的距离为2,即P 点的纵坐标为2或−2,然后根据二次函数图象上点的坐标特征,分别计算出y =2或y =−2所对应的自变量的值,从而可确定P 点坐标.【详解】解:∵⊙P 与x 轴相切,∴点P 到x 轴的距离为2,即P 点的纵坐标为2或−2,当y =2时,即213=22y x =-,解得x 110,x 2=10 则P 102)或(102);当y =−2时,即213=-22y x =-,解得x 12,x 2=2-, 则P 2,−2)或(2-,−2),综上所述,圆心P ,2)或(2,−2)或(,−2).故答案为:,2)或(2,−2)或(,−2).【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了二次函数图象上点的坐标特征.注意分类讨论思想的运用.17.y ═﹣x 2+3x【解析】【分析】根据题意可以得到AP 、PD 、DE 的长,从而可以得到y 与x 的函数关系式,本题得以解决.【详解】∵在Rt △ABC 中,∠BAC =90°,AB =AC =,AD 为BC 边上的高,AP =x ,∴∠BAD =∠CAD =45°,BC =4,AD =2,∴AP =PE =x ,PD =AD ﹣AP =2﹣x ,∴y =S 1+S 2=22x +(2﹣x )•x =﹣x 2+3x 故答案为:y ═﹣x 2+3x .【点睛】本题考查矩形的性质、函数关系式,解题的关键是明确题意,利用数形结合的思想解答问题.18.(2,23)或(0,2)或(2,1) 【解析】【分析】分三种情况讨论:N 在抛物线顶点处;N 在抛物线对称轴左侧;N 在抛物线对称轴右侧.【详解】解:∵AB 为抛物线的对称轴,∴设抛物线的解析式为()2y a x h k =-+,∵正方形OABC 边长为2∴h=2,∵()2y a x 2k =-+经过C (0,2)和E 两点,过点E 作EF ⊥x 轴于点F ,如图1,∵DE ⊥DC ,∴∠CDO+∠EDF=90°,∵∠CDO+∠OCD=90°,∴∠OCD=∠EDF ,在△COD 和△DFE 中OCD FDE COD DFE CD DE ∠∠⎧⎪∠∠⎨⎪⎩===∴△COD ≌△DFE (AAS ),∴OD=EF ,DF=CO ,∵CO=OA=2,D 为OA 中点,∴EF=OD=DA=1,DF=OC=2,∴E (3,1);∴C (0,2)和E (3,1)两点代入()2y a x 2k =-+, 得:421a k a k +⎧⎨+⎩== ,解得:1323a k ⎧=⎪⎪⎨⎪=⎪⎩∴抛物线的解析式为()212233y x =-+, ∴点N 为抛物线上一动点,当以点M ,N ,D ,E 为顶点的四边形是平行四边形时点N 的坐标可以分三种情况讨论:(1) N 在抛物线顶点处时,如图2所示,此时,N点就是抛物线的顶点(2,23);(2)当N在抛物线对称轴左侧时,过点C作CM∥DE交抛物线对称轴于点M,连接ME,如图3,∵CM∥DE,DE⊥CD,∴CM⊥CD,∵OC⊥CB,∴∠OCD=∠BCM,在△OCD和△BCM中BCM OCDCBM CODCO CB∠∠⎧⎪∠∠⎨⎪⎩===∴△OCD≌△BCM(ASA),∴CM=CD=DE,BM=OD=1,∴CDEM是平行四边形,即N点与C占重合,∴N(0,2),(3)N在抛物线对称轴右侧时,N点在抛物线对称轴右侧,MN∥DE,如图4,作NG ⊥BA 于点G ,延长DM 交BN 于点H ,∵MNED 是平行四边形,∴∠MDE=MNE ,∠ENH=∠DHB ,∵BN ∥DF ,∴∠ADH=∠DHB=∠ENH ,∴∠MNB=∠EDF ,在△BMN 和△FED 中MBN EFD BNM FDE MN DE ∠∠⎧⎪∠∠⎨⎪⎩===∴△BMN ≌△FED (AAS ),∴BM=EF=1,BN=DF=2,∴M (2,1),综上所述,点N 的坐标为:(2,23)或(0,2)或(2,1) 【点睛】本题考查了全等三角形的判定与性质、待定系数法求二次函数解析式、待定系数法求一次函数解析式、平行四边形的判定与性质等知识点.19.32【解析】【分析】连接MP ,NP ,证明MP ⊥NP ,将M 、N 的距离转化为直角三角形的斜边最短,利用勾股定理结合二次函数即可求解;【详解】解:连接MP,NP,∵菱形APCD和菱形PBFE,∠DAP=60°,∴MP=12AP,NP=12BP,∵M、N分别是对角线AC、BE的中点,∴∠MPC=60°,∠EPN=30°,∴MP⊥NP,∴MN2=MP2+NP2,即MN2=(12AP)2+(12BP)2=14[AP2+(12-AP)2]=12(AP2-12AP+72)=12(AP-6)2+18,当AP=6时,MN有最小值2,∴点M、N之间的距离最短为2;故答案为2;【点睛】本题考查菱形的性质,二次函数的应用;将点的最短距离借助勾股定理转化为二次函数最小值是解题的关键.20.y=12x2﹣52x+3;(2,1).【解析】【分析】(1)根据待定系数法,可得函数解析式;(2)根据锐角三角函数,可得AE与NE的关系,根据路程与速度,可得点M在整个运动中所用的时间为DE+EN,根据两点之间线段最短,可得当D′、E、N三点共线时,DE+EN最小,根据矩形的判定与性质,可得ND′=OC=3,ON=D′C=DC,根据抛物线与x轴的交点可得OD的长,再求ON的长,可得答案.【详解】解:(1)把A (0,3),C (3,0)代入212y x mx n =++, 得193023m n n ⎧⨯++=⎪⎨⎪=⎩,解得523m n ⎧=-⎪⎨⎪=⎩.∴抛物线的解析式为y =12x 2﹣52x+3, 故答案为y =12x 2﹣52x+3; (2)∵A (0,3),C (3,0),∴OA =OC =3,∴△AOC 是等腰直角三角形,∴∠OAC =45°,过点E 作EN ⊥y 轴于N ,如图,在Rt △ANE 中,EN =AE•sin45°=2AE ,即AEEN , ∴点M在整个运动中所用的时间为DE 1+DE+EN , 作点D 关于AC 的对称点D′,连接D′E ,则有D′E =DE ,D′C =DC ,∠D′CA =∠DCA =45°,∴∠D′CD =90°,DE+EN =D′E+EN ,根据两点之间线段最短可得:当D′、E 、N 三点共线时,DE+EN =D′E+EN 最小, 此时,∵∠D′CD =∠D′NO =∠NOC =90°,∴四边形OCD′N 是矩形,∴ND′=OC =3,ON =D′C =DC .对于y =12x 2﹣52x+3,当y =0时,有12x 2﹣52x+3=0, 解得:x 1=2,x 2=3.∴D (2,0),OD =2,∴ON=DC=OC﹣OD=3﹣2=1,∴点E的坐标为(2,1),故答案为(2,1).【点睛】本题考查了二次函数的图象和性质,三角函数的应用,待定系数法求函数解析式以及矩形的判定与性质等.利用两点之间线段最短得出当D′、E、N三点共线时,DE+EN最小是解题关键.21.(1)21262y x x=--,对称轴2x=;(2)点()2,8D-或()2,4D;(3)点()2,8Q-.【解析】【分析】(1)将点B、C的坐标代入二次函数表达式,即可求解;(2)分∠BCD=90︒、∠DBC=90︒两种情况,分别求解即可;(3)根据CE为菱形的对角线时,PQ⊥CE,即PQ∥x轴,再根据CQ=CP得到方程组,联立即可求解.【详解】解:(1)将点B C、的坐标代入二次函数表达式得:1366026b cc⎧⨯++=⎪⎨⎪=-⎩,解得:26bc=-⎧⎨=-⎩,故抛物线的表达式为:21262y x x=--,令0y=,则2x=-或6,则点()2,0A-,则函数的对称轴2622x -+==; (2)①当90BCD ∠=︒时,设BC 的解析式为y=kx+b ,把B ()6,0、C ()0,6-代入得066k b b =+⎧⎨-=⎩解得16k b =⎧⎨=-⎩ ∴直线BC 的表达式为:6y x =-,∵BC ⊥CD ,∴可设直线CD 为y=-x+d把C ()0,6-代入y=-x+d 得-6=d ,∴直线CD 的表达式为:6y x =--,当2x =时,8y =-,故点()2,8D -;②当90DBC ∠=︒时,直线BC 的表达式为:6y x =-,∵BD ⊥CD ,∴可设直线BD 为y=-x+e把B ()6,0代入y=-x+e 得0=-6+e ,∴e=6∴直线BD 的表达式为:6y x =-+,当2x =时,4y =,故点()2,4D ,故点()2,8D -或()2,4D ;(3)由题意知CE 为菱形的对角线,则PQ CE ⊥,即PQ x 轴,设点(),6P m m -,则点(),6Q s m -,把Q 代入抛物线得216262m s s -=--…①, ∵直线BC 的表达式为:6y x =-,∴∠CPE=45°,∴△PCE 是等腰直角三角形,∵PE=-m ,∴2PC m =-,∵EQ=s ,CE= PE=-m∴222CQ s m =+,由题意得:CQ CP =,即:()2222m s m -=+…②联立①②并解得:6m =或-2(舍去6)故点()2,8-;∴点()2,8Q -.【点睛】本题考查的是二次函数综合运用,涉及到菱形的性质、图形的平移、面积的计算等,解题的关键是熟知二次函数的图像与性质、一次函数的性质及菱形、直角三角形的性质. 22.(1)2y x 2x 3=-++;(2)①855P 坐标为(1,1);②2221(2)1(01)4751(12)12331(4)(24)6t t S t t t t t ⎧--+≤≤⎪⎪⎪=-+-<<⎨⎪⎪-≤≤⎪⎩,当107t =时,S 最大值67=. 【解析】【分析】(1)函数对称轴为x=1,则点B (3,0),用交点式表达式得:y=a (x+1)(x-3)=a (x 2-2x-3),即可求解;(2)①连接BD ,过点A 作AH ⊥BD 于点H ,交DF 于点P ,PD=AP+PD ,此时PD=AH 最小,即可求解; ②根据题意,可分为0≤t≤1、1<t <2、2≤t≤4三种情况,分别求解,即可得到答案.【详解】解:(1)二次函数2y ax bx c =++对称轴为1x =,点A 坐标为(1,0)-,则点B 坐标为(3,0).又∵点C 坐标(0,3),则 93003a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得:123a b c =-⎧⎪=⎨⎪=⎩,∴函数表达式为2y x 2x 3=-++;(2)①连接BD∵(1,4),(1,0),(3,0)D F B∴2,4BF DF ==在Rt DBF △中,依勾股定理得:BD ===∴sin BF BDF BD ∠=== 过点A 作AH BD ⊥于点H ,交抛物线对称轴于点P则5sin PH PD FDB PD =⋅∠= 则5AP PD AP PH AH +=+= 依“垂线段最短”得此时AH 长度为最小值,即55AP PD +最小值为AH 的长度, ∵sin AH DF OBD AB DB∠== 则425AH =,855AH = 即5AP PD +最小值为855. 点P 坐标为(1,1).②A .当01t ≤≤时,如图依图知:APF AGH S S S =-△△。
中考数学总复习《二次函数的实际应用-几何问题》练习题附带答案

中考数学总复习《二次函数的实际应用-几何问题》练习题附带答案一、单选题(共12题;共24分)1.二次函数y=x2﹣8x+15的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使△PMN的面积等于12的点P共有()A.1个B.2个C.3个D.4个2.如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF△AE交△BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.3.如图,正方形ABCD的边长为1,E、F分别是边BC和CD上的动点(不与正方形的顶点重合),不管E、F怎样动,始终保持AE△EF.设BE=x,DF=y,则y是x的函数,函数关系式是()A.y=x+1 B.y=x﹣1C.y=x2﹣x+1D.y=x2﹣x﹣14.周长8m的铝合金制成如图所示形状的矩形窗柜,使窗户的透光面积最大,那么这个窗户的最大透光面积是()m²A.45B.83C.4D.565.抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②﹣1<m <2;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为√34+√2.其中正确的个数是()A.1B.2C.3D.46.如图,在△ABC中,△B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过()秒,四边形APQC的面积最小.A.1B.2C.3D.47.如图,抛物线y=x2−4x+3与x轴交于A,B两点,与y轴交于点C,顶点为M,连结AC,BC.在x轴上是否存在点N,使以B,M,N为顶点的三角形与△ABC相似,则满足条件的所有N点的坐标为()A.N1(73,0)B.N1(0,0)C.N1(73,0)D.N1(73,0)8.如图,矩形ABCD各边中点分别是E、F、G、H,AB=2 √3,BC=2,M为AB上一动点,过点M作直线l△AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l 扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是()A.B.C.D.9.如图所示,用长10m的铝合金条制成下部为矩形,上部为半圆的窗框(包括窗棂).若使此窗户的透光面积最大,则最大透光面积为()A.50B.50πC.508+πD.50 16+π10.如图,线段AB=10,点C、D在AB上AC=BD=1.已知点P从点C出发,以每秒1个单位长度的速度沿着AB向点D移动,到达点D后停止移动,在点P移动过程中作如下操作:先以点P为圆心,PA 、PB的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点P的移动时间为(秒).两个圆锥的底面面积之和为S.则S关于t的函数图象大致是()A.B.C.D.11.在Rt△ABC中,△C=90°,BC=a,AC=b,a+b=16,则Rt△ABC的面积S关于边长a的函数关系式为().A.S=12a 2−8a B.S=−12a2+8a C.S=a2−16a D.S=−a2+16a12.边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为()A.-23B.-12C.-2D.-√23二、填空题(共6题;共6分)13.如图,在正方形ABCD中,AB=4,E是BC上一点,F是CD上一点,且AE=AF.设S△AEF=y,EC=x.则y与x的函数关系式.14.如图,一块矩形土地ABCD由篱笆围着,并且由一条与CD边平行的篱笆EF分开.已知篱笆的总长为900m(篱笆的厚度忽略不计),当AB=m时,矩形土地ABCD的面积最大.15.如图,把一块长为40cm,宽为30cm的矩形硬纸板的四角剪去四个相同小正方形,然后把纸板的四边沿虚线折起,并用胶带粘好,即可做成一个无盖纸盒.若该无盖纸盒的底面积为600cm2,则无盖底盒的高为cm.16.如图,点A是抛物线y=x2﹣4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为.17.如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ΔACD和ΔBCE,那么DE长的最小值是.18.某菜农搭建一个横截面为抛物线的大棚,有关尺寸如图所示,若菜农身高为1.6米,则他在不弯腰的情况下在大棚里活动的范围是米.三、综合题(共6题;共55分)19.如图1,在△ABC中,AB=8,AC=6,BC=10,点D在边AB上(不与点B重合),以CD为一边作正方形CDEF,连接BE.(1)如图2,当BD=2时①求正方形CDEF的边长;②求证:BE=BC;(2)当点D在AB上运动时,求△BDE面积的最大值.20.已知抛物线L1:y=x2+bx+c经过点M(2,﹣3),与y轴交于点C(0,﹣3).(1)求抛物线L1的表达式;(2)平移抛物线L1,设平移后的抛物线为L2,抛物线L2的顶点记为P,它的对称轴与x轴交于点Q,已知点N(2,﹣8),怎样平移才能使得以M、N、P、Q为顶点的四边形为菱形?21.如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和100米长的木栏围成一个矩形菜园ABCD.(1)如图1,已知矩形菜园的一边靠墙,且AD≤MN,设AD=x米.①若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;②求矩形菜园ABCD面积的最大值;(2)如图2,若a=20,则旧墙和木栏能围成的矩形菜园ABCD面积的最大值是米2.22.如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x= −1 2.(1)求抛物线的解析式;(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.23.在直角坐标平面内,点O为坐标原点,二次函数y=x2+(k−5)x−(k+4)的图象交x轴于点A(x1, 0)、B(x2, 0)且(x1+1)(x2+1)=−8.(1)求二次函数解析式;(2)将上述二次函数图象沿x轴向右平移2个单位,设平移后的图象与y轴的交点为C,顶点为P,求△POC的面积.24.如图,抛物线y1=ax2+c的顶点为M,且抛物线与直线y2=kx+1相交于A,B两点,且点A在x轴上,点B的坐标为(2,3),连接AM,BM.(1)a=,c=,k=(直接写出结果);(2)当y1<y2时,则x的取值范围为(直接写出结果);(3)在直线AB下方的抛物线上是否存在一点P,使得ΔABP的面积最大?若存在,求出ΔABP的最大面积及点P坐标.参考答案1.【答案】D2.【答案】B3.【答案】C4.【答案】B5.【答案】D6.【答案】C7.【答案】D8.【答案】D9.【答案】C10.【答案】D11.【答案】B12.【答案】D13.【答案】y=−12x2+4x14.【答案】15015.【答案】516.【答案】(2,﹣1)或(2,2)17.【答案】118.【答案】√519.【答案】(1)解:①如图∵AB=8,AC=6∴AB2+AC2=BC2∴△BAC是直角三角形∴∠BAC=90°∵BD=2∴AD=6在Rt△ADC中CD=√AD2+AC2=√62+62=6√2;②由①可知∠ACD=45°∵四边形CDEF是正方形∴∠EDC=90°∴∠EDG=45°∴∠BDE=∠BDC=135°在△EBD 和△CBD 中{ED =CD ∠BDE =∠BDC BD =BD∴△EBD ≌△CBD(SAS)∴BE =BC .(2)解:过E 作EG ⊥BA 交BA 的延长线于G∵∠EDA +∠CDA =90° ∴∠CDA =∠DEG在△CDA 和△DEG 中{∠CAD =∠DGE ∠CDA =∠DEG ED =DC∴△CDA ≌△DEG(AAS)∴EG =AD设BD 长为x ,则EG =AD =8−xS △BDE =12BD •EG =12x(8−x) =−12(x −4)2+8(0≤x ≤8) ∵−12<0∴当x =4时,S 最大值=8.20.【答案】(1)解:抛物线 L 1 :y = x 2+bx +c 经过点(2,﹣3),点(0,﹣3).代入得 {c =−34+2b +c =−3 解得 {b =−2c =−3∴抛物线 L 1 的表达式为:y = x 2−2x −3 ; (2)解:由题意得,M (2,﹣3),N (2,﹣8) ∴MN△y 轴,MN =5∵PQ△MN△y 轴∴当PQ =MN =5时,四边形MNPQ 为平行四边形.设点Q (m ,0),则点P 的坐标为(m ,﹣5)要使得以M 、N 、P 、Q 为顶点的四边形为菱形只需PN =MN =5∴(m −2)2+(−5+8)2=52解得 m 1 =6, m 2 =﹣2∴点P 的坐标为(6,﹣5)或(﹣2,﹣5).∵抛物线 L 1 :y = x 2−2x −3 = (x −1)2−4∴抛物线 L 1 的顶点坐标为(1,﹣4)∴①当点P 的坐标为(6,﹣5)时,6﹣5=1,﹣5﹣(﹣4)=﹣1∴将原抛物线先向右平移5个单位,再向下平移1个单位,可得到符合条件的抛物线 L 2 ; ②当点P 的坐标为(﹣2,﹣5)时,﹣2﹣1=﹣3,﹣5﹣(﹣4)=﹣1∴将原抛物线先向左平移3个单位,再向下平移1个单位,可得到符合条件的抛物线 L 2 .21.【答案】(1)①∵AD =xm ,则 AB =12(100−x )m 根据题意得 x ·12(100−x )=450 ,解得x 1=90,(不合题意舍去) x 2=10答:AD 的长为10m ;②设AD=xm∴S =12x (100−x )=−12(x −50)2+1250 当a≥50时,则x=50时,S 的最大值为 1250 ;当0<a <50时,则当0<x≤a 时,S 随x 的增大而增大,当x=a 时,S 的最大值为 50a −12a 2 综上所述,当a≥50时,S 的最大值为1250m 2;当0<a <50时,S 的最大值为 (50a −12a 2)m 2 (2)90022.【答案】(1)解:设抛物线的解析式 y =a(x +12)2+k 把A (2,0)、C (0,3)代入得: {254a +k =014a +k =3 解得: {a =−12k =258∴y =−12(x +12)2+258即 y =−12x 2−12x +3 (2)解:由y=0得 −12(x +12)2+258=0 ∴x 1=2,x 2=﹣3∴B (﹣3,0)①CM=BM 时∵BO=CO=3 即△BOC 是等腰直角三角形∴当M 点在原点O 时,△MBC 是等腰三角形∴M 点坐标(0,0)②如图所示:当BC=BM 时在Rt△BOC 中,BO=CO=3由勾股定理得BC= √OC 2+OB 2∴BC= 3√2∴BM= 3√2∴M 点坐标( 3√2−3,0)综上所述:M 点坐标为:M 1( 3√2−3,0) ,M 2(0,0).23.【答案】(1)解:由已知 x 1 , x 2 是 x 2+(k −5)x −(k +4)=0 的两根,∴{x 1+x 2=−(k −5)x 1.x 2=−(K +4)又∵(x 1+1)(x 2+1)=−8 ∴x 1x 2+(x 1+x 2)+9=0∴−(k +4)−(k −5)+9=0∴k =5∴y =x 2−9 为所求;(2)解:由已知平移后的函数解析式为:y =(x −2)2−9 ,且 x =0 时 y =−5∴C(0, −5)∴S △POC =12×5×2=5 . 24.【答案】(1)1;-1;1(2)-1<x<2(3)解:过点P作y轴的平行线交直线y2=x+1于点Q设点P的坐标为(x,x2−1)(−1<x<2),则点Q的坐标为(x,x+1)∴PQ=x+1−(x2−1)=−x2+x+2S△ABP=12PQ·(x B−x A)=12×(−x2+x+2)×3=−32x2+32x+3∴S△ABP=−32(x+12)2+278当x=12时,△ABP的面积有最大值为278,此时P点坐标为(12,−34);。
九上数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年压轴题版

九上数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年压轴题版答案解析答案解析2020年九上数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题1.(2020.九上期末) 如图,抛物线y=ax ﹣ x+c (a≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,﹣2),已知B 点坐标为(4,0).(1) 求抛物线的解析式;(2) 若点M 是线段BC 下方的抛物线上一点,记点M 到线段BC 的距离为d ,当d 取最大值时,求出此时M 点的坐标;(3) 若点P 是抛物线上一点,点E 是直线y=﹣x 上的动点,是否存在点P 、E ,使以点A ,点B ,点P ,点E 为顶点的四边形是平行四边形?若存在,请直接写出点E 坐标;若不存在,请说明理由.考点: 二次函数的最值;二次函数的实际应用-动态几何问题;2.(2020建湖.九上期末) 如图,抛物线过 , 两点.备用图1 备用图2(1) 求该抛物线的解析式;(2) 点是抛物线上一点,且位于第一象限,当的面积为6时,求点 的坐标;(3)在线段 右侧的抛物线上是否存在一点,使得 分 的面积为 两部分?存在,求出点 的坐标;不存在,请说明理由.考点: 待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;3.(2020临颍.九上期末) 如图,抛物线C :y =x ﹣2x 与抛物线C :y =ax +bx 开口大小相同、方向相反,它们相交于O ,C 两点,且分别与x 轴的正半轴交于点B ,点A ,OA =2OB.(1) 求抛物线C 的解析式;212222答案解析答案解析答案解析(2) 在抛物线C 的对称轴上是否存在点P ,使PA+PC 的值最小?若存在,求出点P 的坐标,若不存在,说明理由;(3) M 是直线OC 上方抛物线C 上的一个动点,连接MO ,MC ,M 运动到什么位置时,△MOC 面积最大?并求出最大面积.考点: 二次函数图象与系数的关系;二次函数的实际应用-动态几何问题;轴对称的应用-最短距离问题;4.(2020宁波.九上期中) 在平面直角坐标系中,正方形ABCD 的四个顶点坐标分别为A(-2,4),B(-2,-2),C(4,-2),D(4,4).(1) 填空:正方形的面积为;当双曲线(k≠0)与正方形ABCD 有四个交点时,k 的取值范围是.(2) 已知抛物线L : (a>0)顶点P 在边BC 上,与边AB ,DC 分别相交于点E ,F ,过点B 的双曲线 (k≠0)与边DC 交于点N.①点Q(m ,-m -2m+3)是平面内一动点,在抛物线L 的运动过程中,点Q 随m 运动,分别求运动过程中点Q 在最高位置和最低位置时的坐标.②当点F 在点N下方,AE=NF ,点P 不与B ,C 两点重合时,求的值.③求证:抛物线L 与直线 的交点M 始终位于 轴下方.考点: 反比例函数图象上点的坐标特征;二次函数与一次函数的综合应用;二次函数的实际应用-动态几何问题;5.(2020昭平.九上期末)如图,已知抛物线y=ax +bx+c (a≠0)的对称轴为直线x=﹣1,且抛物线经过A (1,0),C (0,3)两点,抛物线与x 轴的另一交点为B .(1) 若直线y=mx+n 经过B 、C 两点,求直线BC 和抛物线的解析式;(2) 设点P 为抛物线的对称轴x=﹣1上的一个动点,求使△BPC 为直角三角形的点P 的坐标.考点: 二次函数的实际应用-动态几何问题;2020年九上数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题答案1.答案:22222.答案:3.答案:4.答案:5.答案:。
初中数学二次函数的应用题型分类——动态几何图形问题3( 附答案)

初中数学二次函数的应用题型分类——动态几何图形问题3(附答案)1.在平面直角坐标系中四边形OABC是边长为6的正方形,平行于对角线AC的直线l从O出发,沿x轴正方向以每秒一个单位长度的速度运动,运动到直线l与正方形没有交点为止,设直线l扫过正方形OABC的面积为S,直线l的运动时间为t(秒),下列能反映S与t之间的函数图象的是()A.B.C.D.2.如图等边△ABC的边长为4cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s 的速度向点C运动,点P沿A﹣B﹣C以2cm/s的速度也向点C运动,直到到达点C时停止运动,若△APQ的面积为S(cm2),点Q的运动时间为t(s),则下列最能反映S 与t之间大致图象是()A.B.C.D.3.如图所示,在平面直角坐标系中,抛物线y=-x2+23x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+12AP的最小值为().A.3 B.23C.3221+D.323+4.如图四边形ABCD中,AD∥BC,∠A=90°,已知AD=4,AB=43,∠C=30°,连接BD,P为BD边上的一个动点.现让P点从B点出发沿着B→D(P不与点B重合)以1cm/s的速度运动,Q为折线BCD上一动点,现让Q点从B出发沿着折线BCD以3cm/s的速度运动当其中一个点到达终点时另一点也停止运动.则△PBQ与△BCD重合部分的面积S随时间t的变化关系的图象大致为(3≈1.7)()A.B.C .D .5.如图,正方形ABCD 的边长为2,点P 和点Q 分别从点B 和点C 出发,沿射线BC 向右运动,且速度相同,过点Q 作QH ⊥BD ,垂足为H ,连接PH ,设点P 运动的距离为x (0<x ≤2),△BPH 的面积为S ,则能反映S 与x 之间的函数关系的图象大致为( )A .B .C .D .6.如图,在△ABC 中,∠B =90°,AB =3cm ,BC =6cm ,动点P 从点A 开始沿AB 向点B 以1cm /s 的速度移动,动点Q 从点B 开始沿BC 向点C 以2cm /s 的速度移动,若P ,Q 两点分别从A ,B 两点同时出发,P 点到达B 点运动停止,则△PBQ 的面积S 随出发时间t 的函数关系图象大致是( )A .B .C .D .7.如图,在ABC ∆中,90,30ACB B ∠=︒∠=︒,D 是AB 的中点,4AC =,动点M从点A 出发沿AB 向终点B 运动,动点N 从点D 出发沿折线DC CA -向终点A 运动,两点速度均为每秒1个单位,两点同时出发,当其中一点到达终点后,运动停止,设运动时间为()t s ,AMN ∆的面积为S (平方单位),则S 与t 之间的图象大致为( )A .B .C .D . 8.在△ABC 中,∠C =90°,AC =2BC ,AB =10,点P 在AB 边上,点Q 在直角边上(与A 、B 不重合)PQ ⊥AB ,△APQ 的面积y 与AP 的长x 间的函数图象大致为( )A .B .C .D .9.如图,正方形ABCD 的边长为4,点P 、Q 分别是CD 、AD 的中点,动点E 从点A 向点B 运动,到点B 时停止运动;同时,动点F 从点P 出发,沿P→D→Q 运动,点E 、F 的运动速度相同.设点E 的运动路程为x ,△AEF 的面积为y ,能大致刻画y 与x 的函数关系的图象是( )A .B .C .D .10.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,AC =6,BD =8,动点P 从点B 出发,沿着B ﹣A ﹣D 在菱形ABCD 的边上运动,运动到点D 停止,点P ′是点P 关于BD 的对称点,PP ′交BD 于点M ,若BM =x ,△OPP ′的面积为y ,则y 与x 之间的函数图象大致为( )A .B .C .D .11.如图1,△ABC 中,∠ACB =90°,∠A =30°,点P 是斜边AB 上一动点过点P 作PQ ⊥AB ,垂足为P ,交边AC (或边CB )于点Q ,设AP =x ,△APQ 的面积为y ,图2是y 关于x 的函数图象,则图象上最高点M 的坐标是_____.12.如图,直线l 1∥l 2∥l 3,A 、B 、C 分别为直线l 1,l 2,l 3上的动点,连接AB ,BC ,AC ,线段AC 交直线l 2于点D .设直线l 1,l 2之间的距离为m ,直线l 2,l 3之间的距离为n ,若∠ABC =90°,BD =3,且12m n =,则m +n 的最大值为___________.13.如图,抛物线211322y x x =+-与x 轴的负半轴交于点A ,与y 轴交于点B ,连接AB ,点,D E 分别是直线1x =-与抛物线上的点,若点,,,A B D E 围成的四边形是平行四边形,则点E 的坐标为__________.14.已知二次函数2()21y x a a =-++-(a 为常数),当a 取不同的值时,其图象构成一个“抛物线系”.如图分别是当a 取四个不同数值时此二次函数的图象.发现它们的顶点在同一条直线上,那么这条直线的表达式是_________.15.平面直角坐标系中,点P 是一动点,点A (6,0)绕点P 顺时针旋转90°到点B 处,点B 恰好落在直线y =﹣2x 上.当线段AP 最短时,点P 的坐标为_____.16.将函数y =x 2﹣x ﹣2的图象位于x 轴下方的部分沿x 轴翻折至其上方后,所得的图形是函数y =|x 2﹣x ﹣2|的图象,已知过点D (0,4)的直线y =kx +4恰好与y =|x 2﹣x ﹣2|的图象只有三个交点,则k 的值为_____.17.如图所示,一段抛物线:()()303y x x x =--≤≤,记为1C ,它与x 轴交于点O ,1A ;将1C 绕点1A 旋转180︒得2C ,交x 轴于点2A ;将2C 绕点2A 旋转180︒得3C ,交x 轴于点3A ;⋅⋅⋅如此进行下去,直到13C .若()37,P m 在第13段抛物线13C 上,则m =______.18.正方形ABCD ,边长为4,E 是边BC 上的一动点,连DE ,取DE 中点G ,将GE 绕E 顺时针旋转90°到EF ,连接CF ,当CE 为_____时,CF 取得最小值.19.如图,四边形OABC 是边长为1的正方形,OC 与x 轴正半轴的夹角为15°,点B 在抛物线2(0)y ax a =<的图像上,则a 的值为________________.20.抛物线y=2x 2-4x+3绕坐标原点旋转180º所得的抛物线的解析式是___________. 21.如图,直线l :y =﹣3x+3与x 轴、y 轴分别相交于A 、B 两点,抛物线y =ax 2﹣2ax+a+4(a <0)经过点B .(1)求该抛物线的函数表达式;(2)已知点M 是抛物线上的一个动点,并且点M 在第一象限内,连接AM 、BM ,设点M 的横坐标为m ,△ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值;(3)在(2)的条件下,当S 取得最大值时,动点M 相应的位置记为点M′.写出点M′的坐标.22.如图,二次函数2y ax 2x c =++的图象与x 轴交于点()1,0A -和点B ,与y 轴交于点()0,3C .()1求该二次函数的表达式;()2过点A 的直线//AD BC 且交抛物线于另一点D ,求直线AD 的函数表达式; ()3在()2的条件下,在x 轴上是否存在一点P ,使得以B 、C 、P 为顶点的三角形与ABD △相似?若存在,求出点P 的坐标;若不存在,请说明理由.23.如图,在平面直角坐标系中,点O 是原点,矩形OABC 的顶点A 在y 轴的正半轴上,顶点C 在x 轴的正半轴上,顶点B 的坐标为()2,4,抛物线22yx bx c 经过A ,C 两点,与x 轴的另一个交点为点D .(1)如图1,求抛物线的函数表达式;(2)如图2,连接AC ,AD ,将ABC ∆沿AC 折叠后与AD 、y 轴分别交于点E ,G ,求OG 的长度;(3)如图3,将抛物线在AC 上方的部分沿AC 折叠后与y 轴交于点F ,求点F 的坐标.24.如图,在△ABC 中,AB=5,AC=9,S △ABC =272,动点P 从A 点出发,沿射线AB 方向以每秒5个单位的速度运动,动点Q 从C 点出发,以相同的速度在线段AC 上由C向A 运动,当Q 点运动到A 点时,P 、Q 两点同时停止运动,以PQ 为边作正方形PQEF(P 、Q 、E 、F 按逆时针排序),以CQ 为边在AC 上方作正方形QCGH .(1)求tanA 的值;(2)设点P 运动时间为t ,正方形PQEF 的面积为S ,请探究S 是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;(3)当t 为何值时,正方形PQEF 的某个顶点(Q 点除外)落在正方形QCGH 的边上,请直接写出t 的值.25.在平面直角坐标系中,抛物线265y x mx =-+与y 轴的交点为A ,与x 轴的正半轴分别交于点B (b ,0),C (c ,0).(1)当b=1时,求抛物线相应的函数表达式;(2)当b=1时,如图,E (t ,0)是线段BC 上的一动点,过点E 作平行于y 轴的直线l 与抛物线的交点为P .求△APC 面积的最大值;(3)当c =b + n .时,且n 为正整数.线段BC (包括端点)上有且只有五个点的横坐标是整数,求b 的值.26.在ACB ∆中,90,6,?3B AB cm BC cm ︒∠===,点P 从A 点开始沿着AB 边向点B 以1/cm s 的速度移动,点Q 从B 点开始沿BC 边向点C 以2/cm s 的速度移动,如果,P Q 分别从,A B 同时出发,如果运动时间为t 秒.(1)t 为何值时, ,P Q 间的距离等于42cm ? (2)t 为何值时,PQB S ∆有最大值?最大值是多少?27.在△ABC 中,AB =17,BC =21,AC =10,动点P 从点C 出发,沿着CB 运动,速度为每秒3个单位,到达点B 时运动停止,设运动时间为t 秒,请解答下列问题:(1)求BC 上的高;(2)当t 为何值时,△ACP 为等腰三角形?28.如图,在平面直角坐标系中,直线+2y x =与x 轴交于点A ,与y 轴交于点B ,抛物线2y ax x c =-+经过点A ,B .(1)求出抛物线的解析式;(2)在抛物线上是否存在点P ,使PAB ∆的面积为1?若存在,请求出符合条件的所有点P 的坐标;若不存在,请说明理由.29.如图,抛物线y=-x 2+bx+c 与直线AB 交于A(-4,-4),B(0,4)两点,直线AC :y=-12x-6交y 轴与点C .点E 是直线AB 上的动点,过点E 作EF ⊥x 轴交AC 于点F ,交抛物线于点G .(1)求抛物线y=-x 2+bx+c 的表达式;(2)连接GB 、EO ,当四边形GEOB 是平行四边形时,求点G 的坐标;(3)①在y 轴上存在一点H ,连接EH 、HF ,当点E 运动到什么位置时,以A 、E 、F 、H 为顶点的四边形是矩形?求出此时点E 、H 的坐标;②在①的前提下,以点E 为圆心,EH 长为半径作圆,点M 为⊙E 上一动点,求12AM+CM 的最小值.30.如图,在平面直角坐标系中,抛物线y=-34x2+94x+3与x轴交于A,B两点(点A在点B左侧),与y轴交于点C:连接BC,点P为线段BC上方抛物线上的一动点,连接OP交BC于点Q.(1)如图1,当PQOQ值最大时,点E为线段AB上一点,在线段BC上有两动点M,N(M在N上方),且MN=1,求PM+MN+NE-35BE的最小值;(2)如图2,连接AC,将△AOC沿射线CB方向平移,点A,C,O平移后的对应点分别记作A1,C1,O1,当C1B=O1B时,连接A1B、O1B,将△A1O1B绕点O1沿顺时针方向旋转90°后得△A2O1B1在直线x=12上是否存在点K,使得△A2B1K为等腰三角形?若存在,直接写出点K的坐标;不存在,请说明理由.参考答案 1.A 【解析】 【分析】根据三角形的面积即可求出S 与t 的函数关系式,根据函数关系式选择图象即可.【详解】由题意得,如图,直线l 与AC 重合是一个临界位置,此时61OA t ==;直线l 运动到点B 是另一个临界位置,此时2121OD t OA ===,因此,分以下两部分: ①当06t ≤≤时,21122S t t t =⋅⋅=,即212S t = 该函数图象是开口向上的抛物线的一部分则B 、D 选项错误②当612t <≤时,2112(6)(6)22S t t t =-⨯-- 即2112362S t t =-+-该函数图象是开口向下的抛物线的一部分则C 选项错误故选:A .【点睛】本题考查了正方形的性质、一次函数与二次函数的几何应用等知识点,依据题意,确认两个临界位置是解题关键.2.C【解析】【分析】根据等边三角形的性质可得,然后根据点P的位置分类讨论,分别求出S与t的函数关系式即可得出结论.【详解】解:∵△ABC为等边三角形∴∠A=∠C=60°,AB=BC=AC=4当点P在AB边运动时,根据题意可得AP=2t,AQ=t∴△APQ为直角三角形S=12AQ×PQ=12AQ×(AP·sinA)=12×t×2t×3=3t2,图象为开口向上的抛物线,当点P在BC边运动时,如下图,根据题意可得PC=2×4-2t=8-2t,AQ=tS=12×AQ×PH=12×AQ×(PC·sinC)=12×t×(8﹣2t)×32=32t(4﹣t)=-32t2+23t,图象为开口向下的抛物线;故选:C.【点睛】此题考查的是根据动点判定函数的图象,掌握三角形面积的求法、二次函数的图象及性质和锐角三角函数是解决此题的关键.3.A【解析】【分析】连接AO,AB,PB,作PH⊥OA于H,BC⊥AO于C,解方程得到-x2+3得到点B,再利用配方法得到点A,得到OA的长度,判断△AOB为等边三角形,然后利用∠OAP=30°得到PH= 12AP,利用抛物线的性质得到PO=PB,再根据两点之间线段最短求解.【详解】连接AO,AB,PB,作PH ⊥OA 于H,BC ⊥AO 于C,如图当y=0时-x 2+3,得x 1=0,x 23所以B (3,0),由于y =-x 2+332+3,所以A 3),所以3,AO=AB=OB ,所以三角形AOB 为等边三角形,∠OAP=30°得到PH= 12AP,因为AP 垂直平分OB,所以PO=PB ,所以OP +12AP=PB+PH ,所以当H,P,B 共线时,PB+PH 最短,而3,所以最小值为3. 故选A.【点睛】 本题考查的是二次函数的综合运用,熟练掌握二次函数的性质和最短途径的解决方法是解题的关键.4.B【解析】【分析】当点Q 在BC 上运动时,211333sin 322S BQ BP DBC t t =⨯⨯∠=⨯⨯;当点Q 在CD 上运动时,BCD BCQ BDQ S S S S ∆∆∆=--,即可求解. 【详解】解:4=AD ,3AB =83BD =30ABD ∠=︒,故60DBC ∠=︒,则90BCD ∠=︒,当点Q 在BC 上运动时,211333sin 322S BQ BP DBC t t =⨯⨯∠=⨯⨯;当点Q 在CD 上运动时,如下图:则16CQ t =-,8PQ t =-,1683QD t =+-,BCD BCQ BDQ S S S S ∆∆∆=--1111883(8)(1683)16(16)2222t t t =⨯⨯--+--⨯⨯-⨯ 21(1243)2t t =-++ 故选:B .【点睛】本题考查的是动点图象问题,涉及到二次函数、解直角三角形等知识,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.5.A【解析】【分析】过点H 作HE ⊥BC ,垂足为E,易得△BHQ 为等腰直角三角形,进而得到HE=12BQ=22x +,再利用三角形面积公式表示出△BPH 的面积,建立S 与x 之间的函数关系式,即可判断图像.【详解】解:过点H 作HE ⊥BC ,垂足为E,如图,∵BD 是正方形的对角线∴∠DBC =45°∵QH ⊥BD∴△BHQ 是等腰直角三角形又∵HE ⊥BQ∴E 为BQ 边上的中点,即HE 为斜边BQ 上的中线∴HE=12BQ=22x + ∴△BPH 的面积S =12BP•HE =1222+⋅x x =21142x x + ∴S 与x 之间的函数关系是二次函数,且二次函数图象开口方向向上;因此,选项中只有A 选项符合条件.故选:A .【点睛】本题考查动点问题的函数图像,作出△BPH 的高HE ,利用面积公式建立S 与x 的函数关系式是解题的关键.6.C【解析】【分析】根据题意表示出△PBQ 的面积S 与t 的关系式,进而得出答案.【详解】由题意可得:PB =3﹣t ,BQ =2t ,则△PBQ 的面积S =12PB •BQ =12(3﹣t )×2t =﹣t 2+3t , 故△PBQ 的面积S 随出发时间t 的函数关系图象大致是二次函数图象,开口向下. 故选C .【点睛】此题主要考查了动点问题的函数图象,正确得出函数关系式是解题关键.7.A【解析】【分析】由∠ACB=90°,∠B=30°,D 是AB 的中点,得∆ACD 是等边三角形,分两类情况讨论:①当04t <≤时,AM=DN=t ,②当48t <≤时,AM=t ,AN=8-t ,分别得到S 与t 之间的函数关系式,进而即可得到答案.∵∠ACB=90°,∠B=30°, ∴∠CAB=60°, ∵D 是AB 的中点,∴CD=AD ,∴∆ACD 是等边三角形,∴AD=AC=4,∠ADC=60°,当04t <≤时,AM=DN=t ,如图1,过点N 作NH ⊥AD 于点H ,则NH=3sin 60t t ⋅︒=, ∴2113322S AN NH t t t =⋅⋅=⋅⋅=; 当48t <≤时,AM=t ,AN=8-t ,如图2,过点M 作ME ⊥AC 于点E ,则ME=3sin 602t t ⋅︒=, ∴21133(8)232224S AN ME t t t t =⋅⋅=⋅-⋅=-+; ∴S 与t 之间的函数图象大致为:选项A .故选A .如图1 如图2【点睛】本题主要考查二次函数的图象与三角形面积的综合,分类讨论,用含t 的代数式表示相关线段,根据三角形的面积公式得到二次函数关系式,是解题的关键.8.B【解析】当点Q 在线段AC 上运动时,2111224yAP PQ x xtanA x ,当点Q 在线段BC 上运动时,211122x y AP PQ x x x tan BQP ,即可求解.【详解】解:12BC tanA AC =, 当点Q 在线段AC 上运动时,2111224y AP PQ x xtanA x ,为开口向上的抛物线, 当点Q 在线段BC 上运动时,则∠BQP =∠A ,211122x y AP PQ x x x tan BQP ,为开口向下的抛物线,故选:B .【点睛】本题考查的是动点图象问题,涉及到二次函数、解直角三角形知识等,此类问题关键是,要弄清楚不同时间段,图象和图形的对应关系,进而求解.9.A【解析】【详解】当F 在PD 上运动时,△AEF 的面积为y=12AE•AD=2x (0≤x≤2), 当F 在DQ 上运动时,△AEF 的面积为y=12AE•AF=[]14-(2)2x x -=21-+32x x (2<x≤4), 图象为:故选A .10.D【解析】【详解】解:∵四边形ABCD 是菱形, ∴AB =BC =CD =DA ,OA =12AC =3,OB=12BD =4,AC ⊥BD , ①当BM ≤4时,∵点P′与点P 关于BD 对称,∴P′P ⊥BD ,∴P′P ∥AC ,∴△P′BP ∽△CBA , ∴=PP BM AC OB ',即=64PP x ', ∴PP′=32x , ∵OM =4-x ,∴△OPP′的面积y =12PP′•OM =12×233(4)324x x x x -=-+; ∴y 与x 之间的函数图象是抛物线,开口向下,过(0,0)和(4,0);②当BM ≥4时,y 与x 之间的函数图象的形状与①中的相同,过(4,0)和(8,0); 综上所述:y 与x 之间的函数图象大致为.故选D .【点睛】本题考查了动点问题的函数图象、菱形的性质、相似三角形的判定与性质、三角形面积的计算以及二次函数的运用;熟练掌握菱形的性质,根据题意得出二次函数解析式是解决问题的关键.11.(12,3【解析】【分析】当点Q 在线段AC 上时,y =12AP×PQ =12x×x×tanA =36x 2,当点Q 在点C 处时,即x =ACcosA =12,y 为最大值,即可求解.【详解】解:由图2知,AB =16,则BC =8,AC =则△ABC 的高=AC BC AB ⨯== 当点Q 在线段AC 上时,y =12AP×PQ =12x×x×tanA 2, 当点Q 在点C 处时,即x =ACcosA =12,y 212=即点M (,故答案为:(12,.【点睛】本题考查的知识点是动点问题的函数图象,解题的关键是由题目得出该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.12.274【解析】【分析】过B 作1BE l ⊥于E ,延长EB 交3l 于F ,过A 作2AN l ⊥于N ,过C 作2CM l ⊥于M ,设AE BN x ==,CF BM y ==,得到3DM y =-,4DN x =-,根据相似三角形的性质得到xy mn =,29y x =-+,由12m n =,得到2n m =,于是得到()3m n m +=最大,然后根据二次函数的性质即可得到结论.【详解】解:过B 作1BE l ⊥于E ,延长EB 交3l 于F ,过A 作2AN l ⊥于N ,过C 作2CM l ⊥于M ,设AE BN x ==,CF BM y ==,3BD =,3DM y ∴=-,3DN x =-,90ABC AEB BFC CMD AND ∠=∠=∠=∠=∠=︒,90EAB ABE ABE CBF ∴∠+∠=∠+∠=︒,EAB CBF ∴∠=∠,ABE BFC ∴∆∆∽, ∴AE BE BF CF =,即x m n y =, xy mn ∴=,ADN CDM ∠=∠,CMD AND ∴∆∆∽, ∴AN DN CM DM =,即3132m x n y -==-, 29y x ∴=-+,12m n =, 2n m ∴=,()3m n m ∴+=最大,∴当m 最大时,()3m n m +=最大,22(29)292mn xy x x x x m ==-+=-+=, ∴当92(29)4x =-=⨯-时,28128mn m ==最大, 94m ∴=最大, m n ∴+的最大值为927344⨯=.故答案为:274. 【点睛】 本题考查了平行线的性质,相似三角形的判定和性质,二次函数的性质,正确的作出辅助线,利用相似三角形转化线段关系,得出关于m 的函数解析式是解题的关键.13.()4,3-或()2,0或()2,2--【解析】【分析】根据二次函数211y=x x 322+-与x 轴的负半轴交于点A ,与y 轴交于点B .直接令x=0和y=0求出A ,B 的坐标.再根据平行四边形的性质分情况求出点E 的坐标.【详解】由抛物线的表达式求得点,A B 的坐标分别为()()3,0,0,3--.由题意知当AB 为平行四边形的边时,//AB DE ,且AB DE =,∴线段DE 可由线段AB 平移得到.∵点D 在直线1x =-上,①当点B 的对应点为1D 时,如图,需先将AB 向左平移1个单位长度,此时点A 的对应点1E 的横坐标为4-,将4x =-代入211322y x x =+-, 得3y =,∴1(4,3)E -.②当点A 的对应点为2D 时,同理,先将AB 向右平移2个单位长度,可得点B 的对应点2E的横坐标为2,将2x =代入211322y x x =+-得0y =,∴2(2,0)E 当AB 为平行四边形的对角线时,可知AB 的中点坐标为13,22⎛⎫-- ⎪⎝⎭, ∵3D 在直线1x =-上,∴根据对称性可知3E 的横坐标为2-,将2x =-代入211322y x x =+- 得2y =-,∴3(2,2)E --.综上所述,点E 的坐标为()4,3-或()2,0或()2,2--.【点睛】 本题是二次函数的综合题,主要考查了特殊点的坐标的确定,平行四边形的性质,解本题的关键是分情况解决问题的思想.14.21y x =--【解析】【分析】已知抛物线的顶点式,写出顶点坐标,用x 、y 代表顶点的横坐标、纵坐标,消去a 得出x 、y 的关系式.【详解】解:二次函数2()21y x a a =-++-中,顶点坐标为:(,21)a a --,设顶点坐标为(x ,y ),∴x a =-①,21y a =-②,由①⨯2+②,得22211x y a a +=-+-=-,∴21y x =--;故答案为:21y x =--.【点睛】本题考查了二次函数的性质,根据顶点式求顶点坐标的方法是解题的关键,注意运用消元的思想解题.15.(125,65) 【解析】【分析】在平面直角坐标系中,构造△PGB ≌△AHP ,设B (m ,﹣2m ),P (a ,b ),依据全等三角形的性质,即可得到663,22m m a b --==,再根据两点间距离公式以及配方法,即可得到m 的值,进而得出点P 的坐标.【详解】解:如图,构造△PGB ≌△AHP ,设B (m ,﹣2m ),P (a ,b ),由题可得PG =AH ,BG =PH ,即a ﹣m =b ,b +2m =6﹣a ,联立解得:a =62m -,632m b -=, 即P 663,22m m --⎛⎫ ⎪⎝⎭, ∴P A 2=()2222266315672651236222255m m PA m m m --⎛⎫⎛⎫⎛⎫=-+=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, ∴当m =65时,P A 最小, 此时126,55P ⎛⎫ ⎪⎝⎭. 故答案为:(125,65). 【点睛】 本题考查了动点和线段最值问题,解决本题的关键是正确理解题意,通过构造全等三角形,找到题目中蕴含的线段之间的内在关系.16.1﹣2或﹣2.【解析】【分析】根据题意和二次函数的解析式,求出将图像进行翻折后抛物线的解析式和自变量的取值范围,将一次函数和二次函数的解析式进行联立,根据直线与抛物线的交点的个数,通过△求取k的值,然后求取交点横坐标看是否符合题意即可解决.【详解】当y=0时,x2﹣x﹣2=0,解得x1=﹣1,x2=2,则抛物线y=x2﹣x﹣2与x轴的交点为(﹣1,0),(2,0),把抛物线y=x2+2x图象x轴下方的部分沿x轴翻折到x轴上方,则翻折部分的抛物线解析式为y=﹣x2+x+2(﹣1≤x≤2),当直线y=kx+4与抛物线y=﹣x2+x+2(﹣1≤x≤2)相切时,直线y=kx+4与函数y=|x2﹣x﹣2|的图象恰好有三个公共点,即﹣x2+x+2=kx+4有相等的实数解,整理得x2+(k﹣1)x+2=0,△=(k﹣1)2﹣8=0,解得k=1±,所以k的值为或1﹣.当k=1+2√2时,经检验,切点横坐标为x<﹣1不符合题意,舍去.当y=kx+4过(2,0)时,k=﹣2,也满足条件,故答案为1﹣或﹣2.【点睛】本题考查了二次函数图像的翻折,一次函数和二次函数交点问题,解决本题的关键是正确理解题意,熟练掌握函数与方程的关系,能够理解一次函数和二次函数的交点个数与方程根的个数的关系.17.2【解析】【分析】求出抛物线C1与x轴的交点坐标,观察图形可知第奇数号抛物线都在x轴上方,然后求出到抛物线C13平移的距离,再根据向右平移横坐标加表示出抛物线C13的解析式,然后把点P的坐标代入计算即可得解.【详解】解:令y=0,则-x(x-3)=0,解得x1=0,x2=3,∴A1(3,0),由图可知,抛物线C13在x轴上方,相当于抛物线C1向右平移6×6=36个单位得到,∴抛物线C13的解析式为y=-(x-36)(x-36-3)=-(x-36)(x-39),∵P(37,m)在第13段抛物线C13上,∴m=-(37-36)(37-39)=2.故答案为:2【点睛】本题考查了二次函数图象与几何变换,利用点的变化确定函数图象的变化更简便,平移的规律:左加右减,上加下减.18.8 5【解析】【分析】作GM⊥BC于M,FN⊥BC于N,证出GM是△CDE是中位线,得出CM=EM,GM=1 2CD=2,由旋转的性质得出EF=EG,∠GEF=90°,证明△GEM≌△EFN(AAS),得出GM=EN=2,EM=FN,设CE=x,则CM=EM=FN=12x,在Rt△CFN中,由勾股定理得出CF2=CN2+FN2=222215584(2)4424455x x x x x⎛⎫⎛⎫-+=-+=-+⎪ ⎪⎝⎭⎝⎭,由二次函数的性质即可得出答案.【详解】作GM⊥BC于M,FN⊥BC于N,如图所示:则GM∥CD,∵四边形ABCD是正方形,∴BC=CD=4,∵G是DE的中点,∴GM是△CDE是中位线,∴CM=EM,GM=12CD=2,由旋转的性质得:EF=EG,∠GEF=90°,即∠GEM+∠FEN=90°,∵∠GEM+∠EGM=90°,∴∠EGM=∠FEN,在△GEM和△EFN中,EGM FENGME ENF90 EG F ︒∠=∠⎧⎪∠=∠=⎨⎪=⎩,∴△GEM≌△EFN(AAS),∴GM=EN=2,EM=FN,设CE=x,则CM=EM=FN=12x,在Rt△CFN中,由勾股定理得:CF2=CN2+FN2=(x﹣2)2+(12x)2=54x2﹣4x+4=54(x﹣85)2+45,∴当x=85时,CF的最小值=45=25;故答案为:85.【点睛】本题考查了旋转的性质、正方形的性质、全等三角形的判定由性质、勾股定理以及二次函数的应用;熟练掌握旋转的性质,证明三角形全等是解题的关键.19.【解析】试题分析:如图,连接OB,∵四边形OABC是边长为1的正方形,∴∠BOC=45°,OB=1×2=2,过点B作BD⊥x轴于D,∵OC与x轴正半轴的夹角为15°,∴∠BOD=45°-15°=30°,∴BD=12OB=22,OD=2226(2)()22-=,∴点B的坐标为(62,-22),∵点B在抛物线的图象上,262()a=-,2a=-,故答案为-2 3.考点:二次函数综合题.20.y = -2243x x--【解析】【分析】根据旋转的性质,可得a的绝对值不变,根据中心对称,可得答案.【详解】将y=2x2﹣4x+3化为顶点式,得y=2(x﹣1)2+1,抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=﹣2(x+1)2﹣1,化为一般式,得y=﹣2x2﹣4x﹣3,故答案为y=﹣2x2﹣4x﹣3.21.(1)y=﹣x2+2x+3;(2)S=﹣12m2+52m,S的最大值为:258;(3)M′的坐标为:(52,74).【解析】【分析】(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值;(2)连接OM,设M的坐标为(m,-m2+2m+3),然后根据面积关系将△ABM的面积进行转化;(3)当S取得最大值时,此时,m=52,则y=-m2+2m+3=74,即可求解.【详解】(1)令x=0代入y=-3x+3,∴y=3,∴B(0,3),把B(0,3)代入y=ax2-2ax+a+4,∴3=a+4,∴a=-1,∴二次函数解析式为:y=-x2+2x+3;(2)连接OM,令y=0代入y=-x2+2x+3,∴0=-x2+2x+3,∴x=-1或3,∴抛物线与x轴的交点横坐标为-1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=-3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M 的坐标为(m ,-m 2+2m+3),S=S 四边形OAMB -S △AOB=S △OBM +S △OAM -S △AOB =12×m×3+12×1×(-m 2+2m+3)-12×1×3 21522m m =-+ 21525228m ⎛⎫=--+ ⎪⎝⎭ ∴当m=52时,S 取得最大值258 . (3)当S 取得最大值时,此时,m =52, 则y =﹣m 2+2m+3=74, 故点M′的坐标为:(52,74). 【点睛】 主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.22.(1)y=-x 2+2x+3;;(2)y=-x-1;(3)存在,P (35,0)或P (92-,0). 【解析】【分析】(1)把A (-1,0),C (0,3)代入y=ax 2+2x+c 即可得到结果;(2)在y=-x 2+2x+3中,令y=0,则-x 2+2x+3=0,得到B (3,0),由已知条件得直线BC 的解析式为y=-x+3,由于AD ∥BC ,设直线AD 的解析式为y=-x+b ,即可得到结论; (3)①由BC ∥AD ,得到∠DAB=∠CBA ,只要当BC PB AD AB =或BC PB AB AD=时,△PBC ∽△ABD,求出,AB=4,,代入比例式解得BP 的长度,即可得到P (35,0)或P (92-,0).【详解】解:(1)∵次函数y=ax 2+2x+c 的图象经过点A (-1,0)和点C (0,3),∴023a c c=-+⎧⎨=⎩ , 解得 13a c =-⎧⎨=⎩, ∴二次函数的表达式为y=-x 2+2x+3;(2)在y=-x 2+2x+3中,令y=0,则-x 2+2x+3=0,解得:x 1=-1,x 2=3,∴B (3,0),由已知条件得直线BC 的解析式为y=-x+3,∵AD ∥BC ,∴设直线AD 的解析式为y=-x+b ,∴0=1+b ,∴b=-1,∴直线AD 的解析式为y=-x-1.(3)①∵BC ∥AD ,∴∠DAB=∠CBA ,又∵D (4,-5),∴∠ABD≠45°,点P 在点B 得到左侧,∴只可能△ABD ∽△BPC 或△ABD ∽△BCP , ∴BC PB AD AB =或BC PB AB AD=时, ∵A (-1,0),B (3,0),C (0,3),D (4,-5),∵,AB=4,,即4PB =或4=, 解得BP=125或BP=152, ∵3-125=35,3-152=92-,∴P (35,0)或P (92-,0).【点睛】本题主要考查了二次函数解析式得确定、函数图象交点的求法,锐角三角形,最值得求法,相似三角形的判定和性质,解答(3)时,要分类讨论,以防漏解或错解.23.(1)2224y x x =-++;(2)32OG =;(3)730,32F ⎛⎫ ⎪⎝⎭. 【解析】【分析】(1)根据矩形性质分析出(0,4)A ,(2,0)C ,然后用待定系数法求函数解析式;(2)由折叠的性质可得ABC AB C '∆≅∆,然后结合全等三角形的性质,平行线的性质及等腰三角形的判定得到AG CG =.设OG x =,则4AG CG x ==-,利用勾股定理列方程求解;(3)在AC 上方的抛物线图象取点F 的对称点F′,过点F′作y 轴的平行线交直线AC 于点G .先证F′A=F′G .继而得直线AC 的解析式为y=-2x+4.设点F (n ,-2n 2+2n+4),则G (n ,-2n+4).根据F′A 2=F′G 2求出n 的值,从而得出FG =5532,F′A=F′G=FA=5532,从而得出点F 的坐标. 【详解】解:(1)四边形OABC 是矩形,()2,4B , )4(0,A ∴,(2,0)C ,抛物线22y x bx c 经过A ,C 两点,4820c b c =⎧∴⎨-++=⎩24b c =⎧∴⎨=⎩∴抛物线的函数表达式为2224y x x =-++.(2)由题意得:ABC AB C '∆≅∆,BCA B CA '∴∠=∠.//AO BC ,BCA OAC ∴∠=∠,B CA OAC '∴∠=∠,AG CG ∴=.设OG x =,则4AG CG x ==-.在Rt OGC ∆中,2222(4)x x +=- 解得32x =, 32OG ∴=. (3)如图,在AC 上方的抛物线上取点F 的对称点F ',过点F '作y 轴的平行线交直线AC 于点G .由题意得:FAC F AC '∠=∠,F A FA '=.//AO F G ',FAC AGF '∴∠=∠,F AC AGF ''∴∠=∠,F A FG ''∴=.易得直线AC 的解析式为:24y x =-+.设点()2,224F n n n '-++,则(,24)G n n -+224F G n n '∴=-+,()222222F A n n n '=+-+. F A F G ''=,22F A F G ''∴=,即:()()222222224n n n n n +-+=-+,化简得:328110n n -=,即2(811)0n n -=,解得0n =(不合题意,舍去)或118n =, 2552432F G n n '∴=-+=, 5532F A FG FA ''∴=== 557343232OF ∴=-=, 730,32F ⎛⎫∴ ⎪⎝⎭【点睛】本题是二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、矩形的性质、折叠变换的性质及勾股定理等知识点.24.(1)34;(2)存在.S 最小值=8110;(3)t 1=914;t 2=911;t 3=1,t 4=97. 【解析】【分析】(1)如图1,过点B 作BM ⊥AC 于点M ,利用面积法求得BM 的长度,利用勾股定理得到AM 的长度,最后由锐角三角函数的定义进行解答;(2)如图2,过点P 作PN ⊥AC 于点N .利用(1)中的结论和勾股定理得到PN 2+NQ 2=PQ 2,所以由正方形的面积公式得到S 关于t 的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;(3)需要分类讨论:当点E 在边HG 上、点F 在边HG 上、点P 边QH (或点E 在QC 上)、点F 边C 上时相对应的t 的值.【详解】解:(1)如图1,过点B作BM⊥AC于点M,∵AC=9,S△ABC=272,∴12AC•BM=272,即12×9•BM=272,解得BM=3.由勾股定理,得AM=2222534 AB BM-=-=则tanA=BM3 AM4=;(2)存在.如图2,过点P作PN⊥AC于点N.依题意得AP=CQ=5t.∵tanA=34,∴AN=4t,PN=3t.∴QN=AC﹣AN﹣CQ=9﹣9t.根据勾股定理得到:PN2+NQ2=PQ2,S正方形PQEF=PQ2=(3t)2+(9﹣9t)2=90t2﹣162t+81(0<t<95).∵1622290ba--=⨯=910在t的取值范围之内,∴S最小值=22 449081162=4490ac ba-⨯⨯-⨯=8110;(3)①如图3,当点E在边HG上时,t1=9 14;②如图4,当点F在边HG上时,t2=9 11;③如图5,当点P边QH(或点E在QC上)时,t3=1④如图6,当点F边C上时,t4=97.【点睛】本题考查四边形综合题.25.(1)y=2x﹣6x+5;(2)当t=52时,面积S有最大值1258;(3)1或5352-+.【解析】试题分析:(1)当b=1时,将点B(1,0)代入抛物线y=2x﹣6mx+5中求出m,即可解决问题.(2)如图1中,直线AC与PE交于点F.切线直线AC的解析式,构建二次函数,利用二次函数的性质即可解决问题.(3)分两种情形①当b整数时,n为整数,可知n=4,c=b+4.则b,b+4是方程x2﹣mx+5=0的两个根,分别代入方程中求解即可,②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程2x﹣6x+5=0的两个根.试题解析:(1)当b=1时,将点B(1,0)代入抛物线y=2x﹣6mx+5中,得m=1,∴y=2x﹣6x+5;(2)如图1中,直线AC 与PE 交于点F .当b=1时,求得A (0,5),B (1,0),C (5,0),可得AC 所在的一次函数表达式为y=﹣x+5,∵E (t ,0),∴P (t ,2t ﹣6t+5),直线l 与AC 的交点为F (t ,﹣t+5),∴PF=(﹣t+5)﹣(2t ﹣6t+5)=2t -+5t ,∴APC S =()21552t t ⨯-+⨯=255125228t ⎛⎫--+ ⎪⎝⎭, ∵52-<0, ∴当t=52时,面积S 有最大值1258; (3)①当b 整数时,n 为整数,∴n=4,c=b+4.则b ,b+4是方程2x ﹣mx+5=0的两个根,分别代入方程中,得2b ﹣mb+5=0①,()()24450b m b +-++=②,由①②可得2b +4b ﹣5=0,解得b=1或﹣5(舍);或由一元二次方程根与系数的关系得 b (b+4)=5解得b=1或﹣5(舍).②当b 小数时,n 为整数,∴n=5,c=b+5为小数,则b ,b+5是方程2x ﹣mx+5=0的两个根,同样可得535-+535--(舍弃);。
中考数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年压轴题版
中考数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年压轴题版答案答案2020年中考数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题~~第1题~~(2020杭州.中考模拟) 如图1,经过原点O 的抛物线y=ax +bx (a≠0)与x 轴交于另一点A ( ,0),在第一象限内与直线y=x 交于点B (2,t ).(1) 求这条抛物线的表达式;(2) 在第四象限内的抛物线上有一点C ,满足以B ,O ,C 为顶点的三角形的面积为2,求点C 的坐标;(3) 如图2,若点M 在这条抛物线上,且∠MBO=∠ABO ,在(2)的条件下,是否存在点P ,使得△POC ∽△MOB ?若存在,求出点P 的坐标;若不存在,请说明理由.考点: 一次函数的性质;待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;相似三角形的判定与性质;~~第2题~~(2020郑州.中考模拟) 如图,抛物线与x 轴交于点,点 ,与y 轴交于点C,且过点.点P 、Q 是抛物线 上的动点.(1)求抛物线的解析式;(2) 当点P 在直线OD 下方时,求 面积的最大值.(3) 直线OQ 与线段BC 相交于点E ,当 与 相似时,求点Q 的坐标.考点: 二次函数的实际应用-动态几何问题;~~第3题~~(2020百色.中考模拟) 如图,在平面直角坐标系中,二次函数y =﹣x +bx+c 的图象与x 轴交于A 、B 两点,A 点的坐标为(﹣3,0),B 点在原点的左侧,与y 轴交于点C (0,3),点P 是直线BC 上方的抛物线上一动点22答案答案答案(1) 求这个二次函数的表达式;(2) 连接PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP′C (如图1所示),那么是否存在点P ,使四边形POP′C 为菱形?若存在,请此时点P 的坐标:若不存在,请说明理由;(3) 当点P 运动到什么位置时,四边形ABCP 的面积最大,并求出其最大值.考点: 二次函数y=ax^2+bx+c 的性质;待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;~~第4题~~(2020湖州.中考模拟) 如图,已知抛物线的对称轴是直线x=3,且与x 轴相交于A ,B 两点(B 点在A 点右侧)与y 轴交于C 点 .(1) 求抛物线的解析式和A 、B 两点的坐标;(2) 若点P 是抛物线上B 、C 两点之间的一个动点(不与B 、C 重合),则是否存在一点P ,使△PBC 的面积最大.若存在,请求出△PBC 的最大面积;若不存在,试说明理由;(3) 若M 是抛物线上任意一点,过点M 作y 轴的平行线,交直线BC 于点N ,当MN=3时,求M 点的坐标.考点: 待定系数法求一次函数解析式;二次函数y=ax^2+bx+c 的性质;二次函数与一次函数的综合应用;二次函数的实际应用-动态几何问题;~~第5题~~(2020石家庄.中考期末) 如图,抛物线y =ax +(4a ﹣1)x ﹣4与x 轴交于点A 、B , 与y 轴交于点C , 且OC =2OB , 点D 为线段OB 上一动点(不与点B 重合),过点D 作矩形DEFH , 点H 、F 在抛物线上,点E 在x 轴上.(1) 求抛物线的解析式;(2) 当矩形DEFH 的周长最大时,求矩形DEFH 的面积;(3) 在(2)的条件下,矩形DEFH 不动,将抛物线沿着x 轴向左平移m 个单位,抛物线与矩形DEFH 的边交于点M 、N ,连接M 、N .若MN 恰好平分矩形DEFH 的面积,求m 的值.考点: 待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;2020年中考数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题答案1.答案:22.答案:3.答案:4.答案:5.答案:。
初中数学二次函数的应用题型分类——动态几何图形问题5( 附答案)
初中数学二次函数的应用题型分类——动态几何图形问题5(附答案)1.如图,已知直线334y x=-与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是()A.8 B.12 C.212D.1722.如图,在菱形ABCD中,AB=1,∠B=60°,点E在边BC上(与B、C不重合)EF∥AC,交AB于点F,记BE=x,△DEF的面积为S,则S关于x的函数图象是()A.B.C.D.3.如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是()A.B.C.D.4.如图,在矩形ABCD中,AD=6,AB=10,一个三角形的直角顶点E是边AB上的一动点,一直角边过点D,另一直角边与BC交于F,若AE=x,BF=y,则y关于x的函数关系的图象大致为()A.B.C.D.5.如图,等边ABC的边AB与正方形DEFG的边长均为2,且AB与DE在同一条直线上,开始时点B与点D重合,让ABC沿这条直线向右平移,直到点B与点E 重合为止,设BD的长为x,ABC与正方形DEFG重叠部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是()A.B.C.D.6.在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△OEF的面积为y,则能反映y与x之间关系的图象为()A.B.C.D.7.如图,在菱形ABCD中,AB=3,∠BAD=120°,点E从点B出发,沿BC和CD边移动,作EF⊥直线AB于点F,设点E移动的路程为x,△DEF的面积为y,则y关于x的函数图象为()A .B .C .D .8.如图,直线1:4l y x =-+与x 轴和y 轴分别相交于A 、B 两点,平行于直线1l 的直线2l 从原点O 出发,沿x 轴的正方向以每秒1个单位长度的速度运动,它与x 轴和y 轴分别相交于C 、D 两点,运动时间为t 秒(04)t ≤≤.以CD 为斜边作等腰直角CDE ∆(E 、O 两点分别在CD 两侧),若CDE ∆和OAB ∆的重合部分的面积为S ,则S 与t 之间的函数关系的图象大致是( )A .B .C .D .9.如图,等边ABC ∆的边长为3cm ,动点P 从点A 出发,以每秒1cm 的速度,沿A B C →→的方向运动,到达点C 时停止,设运动时间为x (s ),则y 关于x 的函数的图象大致是( )A .B .C .D .10.如图,四边形ABCD 是矩形,16AB =,8BC =,动点P 以每秒4个单位的速度从点A 沿线段AB 向B 点运动,同时动点Q 以每秒6个单位的速度从点B 出发沿B C D --的方向运动,当点Q 到达点D 时,P 、Q 同时停止运动,若记PQA ∆的面积为y ,运动时间为x ,则下列图象中能大致表示,y 与x 之间函数关系图象的是( )A .B .C .D .11.如图,将顶点为P(1,-2),且过原点的抛物线y 的一部分沿x 轴翻折并向右平移2个单位长度,得到抛物线y 1,其顶点为P 1,然后将抛物线y 1沿x 轴翻折并向右平移2个单位长度,得到抛物线y 2,其顶点为P 2;,如此进行下去,直至得到抛物线y 2019,则点P 2019坐标为 _______.12.如图,在边长为6cm 的正方形ABCD 中,点E 、F 、G 、H 分别从点A 、B 、C 、D 同时出发,均以1cm /s 的速度向点B 、C 、D 、A 匀速运动,当点E 到达点B 时,四个点同时停止运动,在运动过程中,运动时间t =_____秒时四边形EFGH 的面积最小.13.如图,抛物线y ₁=﹣x 2+2向右平移1个单位得到抛物线y 2,回答下列问题: (1)阴影部分的面积S =_____;(2)若再将抛物线y 2绕原点O 旋转180°得到抛物线y 3,则顶点坐标为_____.14.二次函数223y x =的图象如图所示,点A 0位于坐标原点,A 1,A 2,A 3,…,A 2009在y 轴的正半轴上,B 1,B 2,B 3,…,B 2009在二次函数223y x =第一象限的图象上,若△A 0B 1A 1,△A 1B 2A 2,△A 2B 3A 3,…,△A 2008B 2009A 2009都为等边三角形,计算出△A 2008B 2009A 2009的边长为_____.15.二次函数2y x 的函数图象如图,点0A 位于坐标原点,点12310,,A A A A ⋅⋅⋅在y 轴的正半轴上,点12310,,B B B B ⋅⋅⋅在二次函数2y x 位于第一象限的图象上,011A B A ∆,122A B A ∆, 23391010A B A A B A ∆⋅⋅⋅∆都是直角顶点在抛物线上的等腰直角三角形,则91010A B A ∆的斜边长为____________.16.飞机着陆后滑行的距离y (单位:m )关于滑行时间t (单位:s )的函数解析式是23602y t t =-.在飞机着陆滑行中,最后3s 滑行的距离是______m . 17.如图,点123⋯、、、、n A A A A 在抛物线2y x 图像上,点0123⋯、、、、、n B B B B B 在 y 轴上,若∆A 1B 0B 1 、∆A 2B 1B 2、…、∆An B n-1Bn 都为等腰直角三角形(点B 0是坐标原点处),则201920182019∆A B B 的腰长等于_____.18.在平面直角坐标系中,将函数y =2x 2+2的图象绕坐标原点0顺时针旋转45°后,得到新曲线l.(1)如图①,已知点A(-1,a),B(b,10)在函数y=2x2+2的图象上,若A’、B’是A、B 旋转后的对应点,连结OA’,OB’,则S△OA’B’=____.(2)如图②,曲线与直线322y 相交于点M、N,则S△OMN为_________.19.如图(1),菱形ABCD中,∠B=60°,动点P以1厘米秒的速度自A点出发沿AB 方向运动至B点停止,动点Q以2厘米/秒的速度自B点出发沿折线BCD运动至D点停止,若点P、Q同时出发运动了t秒,记△BPQ的面积为S厘米2,且S与t之间的函数关系的图象如图(2)所示,则图象中a的值为_____.20.如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣1交y轴于点A,过点A作AB∥x 轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是_____.21.综合与探究:如图,已知在△ABC 中,AB=AC ,∠BAC=90°,点 A 在 x 轴上,点 B 在 y 轴上,点()3,1C -在二次函数21332y x bx =-++的图像上. (1)求二次函数的表达式;(2)求点 A ,B 的坐标;(3)把△ABC 沿 x 轴正方向平移, 当点 B 落在抛物线上时, 求△ABC 扫过区域的面积.22.已知,如图,抛物线y =ax 2+bx +c (a ≠0)的顶点为M (1,9),经过抛物线上的两点A (﹣3,﹣7)和B (3,m )的直线交抛物线的对称轴于点C .(1)求抛物线的解析式及点B 的坐标.(2)在抛物线上A ,M 两点之间的部分(不包含A ,M 两点),是否存在点D ,使得S △DAC=2S △DCM ?若存在,求出点D 的坐标;若不存在,请说明理由.(3)上下平移直线AB ,设平移后的直线与抛物线交与A ′,B ′两点(A ′在左边,B '在右边),且与y 轴交与点P (0,n ),若∠A ′MB ′=90°,求n 的值.23.如图,y =﹣x 2+mx +3(m >0)与y 轴交于点C ,与x 指的正半轴交于点k ,过点C 作CB ∥x 轴交抛物线于另一点B ,点D 在x 轴的负半轴上,连结BD 交y 轴于点A ,若AB =2AD .(1)用含m 的代数式表示BC 的长;(2)当m=2时,判断点D是否落在抛物线上,并说明理由;(3)过点B作BE∥y轴交x轴于点F,延长BF那至E,使得EF=12BC,连结DE交y轴于点G,连结AE交x轴于点M,若△DOG的面积与△MFE的面积之比为1:2,则求出抛物线的解析式.24.抛物线C1:y=ax2﹣32x+2(a>0)与x轴交于A、B(点A在点B左侧),与y轴交于点C.(1)如图1,若A(2,0),连AC、BC.①直接写出C1的解析式及△ABC的面积;②将△AOC绕某一点逆时针旋转90°至△A′O′C′(其中A、O、C的对应点分别为A′、O′、C′).若旋转后的△A′O′C′恰有一边的两个端点落在抛物线C1的图象上,求点A′的坐标;(2)如图2,平移抛物线C1使平移后的新抛物线C2顶点在原点,P(12a,0)是x轴正半轴上一点,过P作直线交C2的图象于A、B,过A的直线y=x+b交C2于点C,过P作x轴的垂线交BC于点M,设点M的纵坐标为n,试判断an是否为定值?若是,求这个定值,若不是,说明理由.25.如图,抛物线与x轴相交于A、B两点,与y轴的交于点C,其中A点的坐标为(﹣3,0),点C的坐标为(0,﹣3),对称轴为直线x=﹣1.(1)求抛物线的解析式;(2)若点P在抛物线上,且S△POC=4S△BOC,求点P的坐标;(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.26.已知Rt△OAB,∠OAB=90︒,∠ABO=30︒,斜边OB=4,将Rt△OAB绕点O顺时针旋转60︒,得到△COD,如图1,连接BC.(1)求BC的长度;(2)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5个单位/秒,点N的运动速度为1个单位/秒,设运动时间为x秒,△OMN的面积为y,求y关于x的函数解析式,并直接写出自变量x的取值范围.27.在平面直角坐标系xOy中,直线y=4x+4与x轴,y轴分别交于点A,B,点A在抛物线y=ax2+bx-3a(a<0)上,将点B向右平移3个单位长度,得到点C.(1)抛物线的顶点坐标为(用含a的代数式表示)(2)若a=-1,当t-1≤x≤t时,函数y=a x2+bx-3a(a<0)的最大值为y1,最小值为y2,且y1-y2=2,求t的值;(3)若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.28.如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM 被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.29.如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.(1)求点E的坐标;(2)求抛物线的函数解析式;(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N 的坐标并求出四边形ABNO面积的最大值.30.如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E 逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.(1)求抛物线的解析式.(2)过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.(3)如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.①若S=PQ2(厘米),试写出S与t之间的函数关系式,并写出t的取值范围?②当S取最小时,在抛物线上是否存在点R,使得以P,A,Q,R为顶点的四边形是平行四边形?如果存在,求出R的坐标;如果不存在,请说明理由.参考答案1.C【解析】【分析】求出A、B的坐标,根据勾股定理求出AB,求出点C到AB的距离,即可求出圆C上点到AB的最大距离,根据面积公式求出即可.【详解】解:∵直线334y x=-与x轴、y轴分别交于A、B两点,∴A点的坐标为(4,0),B点的坐标为(0,﹣3),34120x y--=,即OA=4,OB=3,由勾股定理得:AB=5,过C作CM⊥AB于M,连接AC,则由三角形面积公式得:12×AB×CM=12×OA×OC+12×OA×OB,∴5×CM=4×1+3×4,∴CM=165,∴圆C上点到直线334y x=-的最大距离是1615+=215,∴△PAB面积的最大值是121525⨯⨯=212,故选C.【点睛】本题考查了三角形的面积,点到直线的距离公式的应用,解此题的关键是求出圆上的点到直线AB的最大距离,属于中档题目.2.A【解析】根据△DEF 的面积=菱形的面积-△ADF 的面积-△CDE 的面积-△BEF 的面积,据此表示出DEF 的面积即可.【详解】 ∵菱形ABCD 中,∠B=60°,∴△ABC 是等边三角形,∵EF ∥AC ,∴△BFE 是等边三角形BE BF x ∴==BE x =21332BEF x S x x ∴=⋅= 1AB =1EC AF x ∴==-1333(1)2244AFD CED S S x x ∴==-⋅=- 13312ABCD S =⨯⨯=菱形 ()223333321DEF S x x x ⎛⎫∴=---=-- ⎪ ⎪⎝⎭(其中01x <<)故选A【点睛】本题考查了等边三角形的性质、平行线的性质,二次函数和几何图形综合,解决本题的关键是用x 将每个图形的面积表示出来.3.C【解析】【分析】过作轴于,根据勾股定理和含30度角的直角三角形的性质求出,根据三角形的面积即可求出答案.解:过作轴于,,,,由勾股定理得:,①当时,如图所示,,,;②时,,,.故选.【点睛】本题主要考查对动点问题的函数图象,勾股定理,三角形的面积,二次函数的图象,正比例函数的图象,含30度角的直角三角形的性质,菱形的性质等知识点的理解和掌握,能根据这些性质进行计算是解此题的关键,用的数学思想是分类讨论思想..4.A【解析】【分析】设AE=x,BF=y,根据勾股定理有DE2=62+x2,EF2=(10-x)2+y2,DF2=(6-y)2+102;再由△DEF为直角三角形可得DE2+EF2=DF2,然后化简成二次函数的顶点式,然后根据顶点式的图像特点进行解答即可.【详解】解:设AE=x ,BF=y ,则DE 2=62+x2,EF 2=(10-x )2+y 2,DF 2=(6-y )2+102;∵△DEF 为直角三角形,∴DE 2+EF 2=DF 2,即62+x 2+(10-x )2+y 2=(6-y )2+102, 解得2215125(5)6366y x x x =-+=-+ 根据函数关系式可看出A 中的函数图象与之对应.故答案为A.【点睛】本题考查了二次函数图像的特点以及勾股定理的相关知识,其中根据勾股定理化简得到二次函数顶点式是解答本题的关键.5.D【解析】【分析】此题可分为两段求解,即B 从D 点运动到DE 的中点和A 从DE 的中点运动到E 点,列出面积随动点变化的函数关系式即可.【详解】解:设BD 的长为x ,△ABC 与正方形DEFG 重合部分(图中阴影部分)的面积为y ,当B 从D 点运动到DE 的中点时,即0≤x≤1时,y=12×x=x 2.当B 从DE 中点运动到E 点时,即1<x≤2时,12(2-x )2-x )2 由函数关系式可看出D 中的函数图象与所求的分段函数对应.故选D .6.B【解析】【分析】分析,EF 与x 的关系,他们的关系分两种情况,依情况来判断抛物线的开口方向.【详解】解:∵四边形ABCD 是正方形,∴AC =BD =,OB =OD =12BD =,①当P 在OB 上时,即,∵EF ∥AC ,∴△BEF ∽△BAC ,∴EF :AC =BP :OB ,∴EF =2BP =2x ,∴y =12EF•OP =12×2x (2x -)=2-x ;②当P 在OD <x≤,∵EF ∥AC ,∴△DEF ∽△DAC ,∴EF :AC =DP :OD ,即EF :x (),∴EF =2(x ),∴y =12EF•OP =1222x x ⨯-()()=2-4x +-, 这是一个二次函数,根据二次函数的性质可知:二次函数的图象是一条抛物线,开口方向取决于二次项的系数.当系数>0时,抛物线开口向上;系数<0时,开口向下.根据题意可知符合题意的图象只有选项B .故选B .【点睛】本题主要考查了动点问题的函数图象、二次函数的性质等知识点,利用三角形的面积公式列出二次函数解析式是解题的关键.7.C【解析】【分析】就点E在BC和CD上,分两种情况求出y与x的关系即可解答. 【详解】解:①当E在BC边上时,y=S菱形ABCD﹣S△BEF﹣S△ADF﹣S△DEC=2×3×32﹣12•2x•3x﹣12•(3﹣12x)•33﹣12•(3﹣x)•33=﹣3x2+93x.②当点E在CD上时,y=12•(6﹣x)3333x93,故答案为C.【点睛】本题考查动点问题函数图像、分段函数、菱形的性质、等边三角形的性质等知识,解题的关键是学会构建分段函数解决实际问题.8.C【解析】【分析】分别求出0<t≤2和2<t≤4时,S与t的函数关系式即可判断.【详解】当0<t≤2时,S=12t2,当2<t≤4时,S=12t2−12(2t−4)2=−32t2+8t−8,观察图象可知,S与t之间的函数关系的图象大致是C.故选:C.【点睛】本题考查动点问题的函数图象,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.9.C【解析】【分析】过C作CD⊥AB,则分开两段函数进行讨论:①当点P从A到B时;②当点P从B到C时,分别求出解析式,即可得到答案.【详解】解:过C作CD⊥AB,则AD=1.5cm,332,点P在AB上时,AP=xcm,PD=|1.5-x|cm,∴y=PC2=3322+(1.5-x)2=x2-3x+9(0≤x≤3),该函数图象是开口向上的抛物线;②当3<x≤6时,即点P在线段BC上时,PC=(6-x)cm(3<x≤6);则y=(6-x)2=(x-6)2(3<x≤6),∴该函数的图象是在3<x≤6上的抛物线;故选择:C.【点睛】本题考查了动点问题的函数图象.解答该题时,需要对点P的位置进行分类讨论,以防错选.10.B【解析】【分析】根据题意,分两种情况:(1)当动点Q在BC边上运动时;(2)当动点Q在CD边上运动时;然后根据三角形的面积的求法,分类讨论,求出y与x之间函数关系式,进而判断出y 与x之间函数关系图象的是哪个即可.【详解】(1)如图1,当动点Q在BC边上运动时,∵8÷6=43(秒),∴动点Q从点B运动到点C向右的时间是43秒,∵AP=4x,BQ=6x,∴y=4x×6x÷2=12x2(0<x≤43),∴抛物线开口向上;(2)如图,当动点Q在CD边上运动时,,∵(16+8)÷6=4(秒),4−43=83(秒),∴动点Q从点C运动到点D需要的时间是83秒,∵AP=4x,BC=8,∴y=4x×8÷2=16x(43<x≤4),单调递增,综上,可得24120341643x xyx x⎧⎛⎫≤⎪⎪⎪⎝⎭=⎨⎪≤⎪⎩<(<),∴能大致表示y与x之间函数关系图象的是:.故选:B.【点睛】(1)此题主要考查了动点问题的函数图象,考查了函数解析式的求法,以及分类讨论思想的应用,要熟练掌握.(2)此题还考查了三角形的面积的求法,要熟练掌握,解答此题的关键是熟练掌握三角形的面积公式.11.(4039,2)【解析】【分析】根据图形的变换,可得规律:第n次平移变换点的横坐标是2n+1,偶数次变换平移点的纵坐标是−2,奇数次变换平移点的坐标是2,可得答案.【详解】第一次变换平移点的坐标是(3,2),,第二次变换平移点的坐标是(5,2)第三次变换平移点的坐标是(7,2,)n,偶数次变换平移点的纵坐标是-2,奇数次变换平移点的第n次平移变换点的横坐标是21坐标是2, 点P2019坐标为(4039,2)【点睛】本题考查了二次函数图象与几何变换,观察发现规律是解题关键,规律:第n次平移变换点的横坐标是2n+1,偶数次变换平移点的纵坐标是−2,奇数次变换平移点的坐标是2.12.3.【解析】【分析】设点E运动的时间为t秒,EFGH的面积为Scm2,则AE=t,EB=6﹣t,由四边形EFGH的面积=正方形ABCD的面积-4个△AEH的面积,即可得出S四边形EFGH关于t的函数关系式,配方后即可得出结论.【详解】设点E运动的时间为t秒,EFGH的面积为Scm2,则AE=t,EB=6﹣t,S=62﹣(6)2t t×4=36+2(t﹣3)2﹣18=2(t﹣3)2+18∴当t=3时,S取得最小值,此时S=18,故答案为:3.【点睛】本题考查了二次函数的最值、三角形以及正方形的面积,通过分割图形求面积法找出S四边形EFGH关于t的函数关系式是解题的关键.13.2 (﹣1,﹣2)【解析】【分析】(1)利用平移规律得出阴影部分等于底边为1高为2的平行四边形,进而得出答案;(2)由题意得抛物线y2的顶点坐标为(1,2),由对称性得抛物线y3的顶点坐标.【详解】(1)把阴影部分进行平移,可得到阴影部分的面积=平行四边形ABCD的面积=1×2=2;(2)由题意可得:抛物线y3的顶点与抛物线y2的顶点关于原O成中心对称,∴抛物线y3的顶点坐标为(﹣1,﹣2).故答案为:2,(﹣1,﹣2).【点睛】本题考查了二次函数的相关知识以及平移的性质,得出平移图形形状是解题的关键.14.2009【解析】【分析】此题需要从简单的例子入手寻找各三角形边长的规律;可设出△A 0A 1B 1的边长为m 1,由于此三角形是正三角形,则∠B 1A 0A 1=60°,∠B 1A 0x =30°,可用边长m 1表示出B 1的坐标,代入抛物线的解析式中,即可得到m 1的值,同理可求出△A 1B 2A 2、△A 2B 3A 3的边长,通过观察得到这些三角形边长值的变化规律来求得到△A 2008B 2009A 2009的边长.【详解】解:设△A 0A 1B 1的边长为m 1;∵△A 0A 1B 1是等边三角形,∴∠A 1A 0B 1=60°,∠B 1A 0x =30°;故B 1,1m 2); 由于点B 1在抛物线的图象上,则有:23×(2m 1)2=1m 2,解得m 1=1; 同理设△A 1A 2B 2的边长为m 2;同上可得B 2,1+2m 2); 由于点B 2也在抛物线的图象上,则有:23×2)2=2m 2+1,解得m 2=2; 依此类推,△A 2B 3A 3的边长为:m 3=3,…△A n B n+1A n+1的边长为m n+1=n+1;∴△A 2008B 2009A 2009的边长为2009.【点睛】此题是典型的规律型试题,需要从简单的例子入手来找出题目的一般化规律,然后根据得到的规律求出特定的值.15.20【解析】【分析】先计算出△A 0B 1A 1 ;△A 1B 2A 2 ;△A 2B 3A 3的边长,推理出斜边长组成的数列各项之间的排列规律,依据规律得到△A 9B 10A 10的边长.【详解】∵等腰三角形A 0B 1A 1,A 0为原点;∴y =x ;∵y =x ,y =x 2, ∴B 1的坐标为(1,1),则A 1的坐标为(0,2);∴A 0A 1=2;∵A 1的坐标为(0,2),斜率k =1, ∴直线A 0B :y =x +2∴B 2(2,4), ∴A 1A 2=4;∵A 2坐标为(6,0), 等腰三角形A 2B 3A 3 ;∴直线A 2B 3:y =x +6;∴B 3坐标为(3,9),则A 2A 3=6;综上,由此可以推断出△A 9B 10A 10的斜边为20.【点睛】本题考查的是二次函数的定义和图像,熟练掌握这两点是解题的关键.16.13.5【解析】【分析】当y 取得最大值时,飞机停下来,y=60t-32t 2=-32(t-20)2+600,即当t=20时,飞机滑行600才停下来,当t=17时,y=586.5,即可求解.【详解】解:当y 取得最大值时,飞机停下来,则2260 1.5 1.5(20)600y t t t =-=--+,此时20t =,飞机着陆后滑行600米才能停下来.因此t 的取值范围是020t ;即当17t =时,586.5y =,所以600586.513.5-=(米). 故答案是:13.5.【点睛】考查了二次函数的性质在实际生活中的应用,本题要首先确定飞机最大滑行时间,然后确定最后3秒滑行的距离.17.【解析】【分析】根据图像与等腰直角三角形的性质求出1A,得到腰长A1B0,再求出B1的坐标,同理求出A2的坐标,再得到腰长A2B1,再发现腰长的变化规律即可求解.【详解】过点A1⊥x轴与点D,A1C⊥y轴于点C,过点A2⊥x轴与点F,A2C⊥y轴于点E,∵∆A1B0B1、∆A2B1B2都为等腰直角三角形∴B1C=B0C=B0D=A1D,B2E=B1E,y x求出x1=1,(x1=0舍去)设点A1(x1,y1),把x1=y1,代入2由勾股定理求出A1B0=2y x求出x2=2(-1舍去)∴B0B1=2,设A2的坐标为(x2,x2+2),代入2∴A2B1=22同理得A3B2=32∴A n B n-1=2n∴A2019B2018=20192∆A B B的腰长等于20192则201920182019故填:20192.【点睛】此题主要考查坐标的规律探索,解题的关键是熟知二次函数、等腰直角三角形及勾股定理的运用.18.9 9 4【解析】【分析】(1)如图③,连结OA、OB、AB,则由旋转的性质可知S△OA’B’=S△OAB.根据题意求出A,B 坐标,构造三角形即可求出S△OAB.(2)先画出图形,根据旋转的性质,可知S△OMN=S△OM’N’.由题意可知直线M’ N’的解析式为y=x+3,从而求出M’ ,N’的横坐标分别为12-、1,得出直线M’ N’与y轴的交点记为C,其坐标为(0,3),即可得出S△OAB.【详解】(1)如图③,连结OA、OB、AB,则由旋转的性质可知S△OA’B’=S△OAB.由A、B在函数y=2x2+2的图象上,可求得A(-1,4)、B(2,10).分别过点A、B作x轴的垂线,垂足分别记为P、Q,则有:S△OAB=S梯形APQB-S△PAO-S△QBO=12×(4+10)×3-12×1×4-12×2×10=9.(2)将曲线l、直线322y=和△OMN绕着原点O逆时针旋转45°,旋转之后的图象如图④所示: △OMN旋转到△OM’ N’的位置,直线322y=旋转到直线M’ N’的位置.图④根据旋转的性质,可知S △OMN = S △OM’N’.直线MN 与y 轴的交点 (0,322)经过旋转之后,其坐标变为(-32,32),显然该点在直线M’ N’. 而直线M’ N’的斜率为1,易求得直线M’ N’的解析式为y=x+3.令2x 2+2=x+3,整理得2x 2-x-1=0,解得x=1或12-,即M’ 、N’的横坐标分别为12-、1. 直线M’ N’与y 轴的交点记为C ,其坐标为(0,3).故S △OMN = S △OM’N’=12OC ’’-M N x x =12×3×1--12=94. 【点睛】本题考查了二次函数性质及旋转的性质,熟练掌握性质定理是解题的关键.193【解析】【分析】应根据0≤t <2和2≤t <4两种情况进行讨论.把t 当作已知数值,就可以求出S ,从而得到函数的解析式,进一步即可求解.【详解】解:当0≤t <2时,21332(4)232S t t t =⨯-=+; 当2≤t <4时,134(4)34322S t t =⨯⨯-=+ 当t =3时,33433S a ==-=,【点睛】本题主要考查了动点问题的函数图象,利用图形的关系求函数的解析式,注意数形结合是解决本题的关键.20.2【解析】【分析】求得C 的坐标,进而求得B 的坐标,根据点P 关于x 轴的对称点恰好落在直线AB 上得出三角形的高,然后根据三角形面积公式即可求得.【详解】解:令x=0,则y=x 2-2x-1=-1,∴A(0,-1),把y=-1代入y=x 2-2x-1得-1=x 2-2x-1,解得x 1=0,x 2=2,∴B(2,-1),∴AB=2,∵点P 关于x 轴的对称点恰好落在直线AB 上,∴△PAB 边AB 上的高为2,∴S=12×2×2=2. 故答案为2.【点睛】本题考查了二次函数图象上点的坐标特征,求得A 、B 的坐标以及三角形的高是解题的关键. 21.(1)2113362y x x =-++;(2)(1,0),(0,2)A B -;(3)192. 【解析】【分析】(1)将点(3,1)C -代入二次函数解析式即可;(2)过点C 作CD x ⊥轴,证明BAO ACD ≅即可得到1,2OA CD OB AD ====即可得出点 A ,B 的坐标;(3)设点E 的坐标为()2(0)E m m ->,,解方程21132362m m -++=-得出四边形ABEF 为平行四边形,求出AC ,AB 的值,通过ABC 扫过区域的面积=EFC ABEF S S ∆+四边形代入计算即可. 【详解】解:(1)∵点(3,1)C -在二次函数的图象上,21333132b ∴-⨯++=-.解方程,得16b =∴二次函数的表达式为2113362y x x =-++. (2)如图1,过点C 作CD x ⊥轴,垂足为D .90CDA ∴∠=︒90CAD ACD ∴∠+∠=︒.90BAC ∠=︒, 90BAO CAD ∴∠+∠=︒BAO ACD ∴∠=∠.在Rt BAO 和Rt ACD △中,∵90BOA ADC BAO ACD AB CA ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, BAO ACD ∴≅.∵点C 的坐标为(3)1-,, 1,312OA CD OB AD ∴====-=.(1,0),(0,2)A B ∴-.(3)如图2,把ABC ∆沿x 轴正方向平移,当点B 落在抛物线上点E 处时,设点E 的坐标为()2(0)E m m ->,. 解方程21132362m m -++=-得:3m =-(舍去)或72m = 由平移的性质知,AB EF =且//AB EF , ∴四边形ABEF 为平行四边形,72AF BE ∴==2222215AC AB OB AO ==+=+ ABC ∴扫过区域的面积=EFC ABEF S S ∆+四边形=171255222OB AF AB AC ⋅+⋅=⨯+192=. 【点睛】本题考查了二次函数与几何综合问题,涉及全等三角形的判定与性质,平行四边形的性质与判定,勾股定理解直角三角形,解题的关键是灵活运用二次函数的性质与几何的性质. 22.(1)y =﹣x 2+2x +8,B (3,5);(2)存在,点D (﹣1,5);(3)n =3 【解析】 【分析】(1)抛物线的表达式为:y =a (x ﹣1)2+9,将点A 的坐标代入上式并解得:a =﹣1,即可求解;(2)S △DAC =2S △DCM ,则HN =2GH ,即1﹣k ﹣(3k ﹣7)=2(9﹣k ﹣1+k ),即可求解; (3)∠GA′M =∠HMB′,故tan ∠GA′M =tan ∠HMB′,即:122119(29(2))1x x n x n x -+=-+--,而x1+x2=0,x1x2=n﹣8,y1+y2=2n,y1y2=4n﹣32+n2,即可求解.【详解】解:(1)抛物线的表达式为:y=a(x﹣1)2+9,将点A的坐标代入上式并解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+8,将点B坐标代入上式并解得:m=5,故点B(3,5);(2)过点M、C、A分别作三条相互平移的平行线,分别交y轴于点G、H、N,直线l与抛物线交于点D,设直线m的表达式为:y=kx+t,将点M的坐标代入上式并解得:t=9﹣k,故直线m的表达式为:y=kx+9﹣t,即点G(0,9﹣t),同理直线l的表达式为:y=kx+1﹣k,故点H(0,1﹣k),同理直线n的表达式为:y=kx+3k﹣7,故点N(0,3k﹣7),S△DAC=2S△DCM,则HN=2GH,即1﹣k﹣(3k﹣7)=2(9﹣k﹣1+k),解得:k=﹣2,故直线l的表达式为:y=﹣2x+3…②,联立①②并解得:x=5(舍去)或﹣1,故点D(﹣1,5);(3)直线A′B′的表达式为:y=2x+n,设点A′、B′的坐标分别为:(x 1,y 1)、(x 2,y 2), 将抛物线与直线A′B′的表达式联立并整理得: x 2+n ﹣8=0,故x 1+x 2=0,x 1x 2=n ﹣8,y 1+y 2=2(x 1+x 2)+2n =2n ,同理可得:y 1y 2=4n ﹣32+n 2,过点M 作x 轴的平行线交过点A′与y 轴的平行线于点G ,交过点B′与y 轴的平行线于点H ,∵∠A′MB′=90°,∴∠GMA′+∠GA′M =90°,∠GMA′+∠MHB′=90°, ∴∠GA′M =∠HMB′,故tan ∠GA′M =tan ∠HMB′,即:122119(29(2))1x x n x n x -+=-+--,而x 1+x 2=0,x 1x 2=n ﹣8,y 1+y 2=2n ,y 1y 2=4n ﹣32+n 2, 整理得:n 2﹣13n+30=0, 解得:n =3或10(舍去10), 故n =3. 【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.23.(1)BC =m ;(2)当m =2时,点D 落在抛物线上;(3)y =﹣x 2+x +3. 【解析】【分析】(1)因为抛物线的对称轴为x=m2,由对称性即可得出BC的长;(2)当m=2时,BC=2,由题意,可得△AOD∽△ACB,利用相似三角形对应边成比例求得点D(﹣1,0),即可判断点D是否落在抛物线上;(3)由△AOD∽△ACB,求得A(0,1),D(﹣m2,0),因为点E(m,﹣m2),用待定系数法分别求得直线AE,DE的表达式,即可得出点M,点G的坐标,根据△DOG的面积与△MFE的面积之比为1:2,列出方程,解方程即可求得m的值.【详解】(1)∵y=﹣x2+mx+3(m>0).∵抛物线的对称轴为x=m2,∴BC=m.(2)当m=2时,BC=2,y=﹣x2+2x+3∵CB∥x轴,∴△AOD∽△ACB,∴DO:BC=AD:AB=1:2,∴DO=1,即点D(﹣1,0),当x=﹣1时,y=﹣(﹣1)2+2×(﹣1)+3=0,∴当m=2时,点D落在抛物线上;(3)∵过点B作BE∥y轴交x轴于点F,延长BF至E,使得EF=12 BC,∴点E(m,﹣m2).∵C(0,3),OD:BC=OA:AC=AD:AB=1:2,∴OA=1,OD=m2,∴A(0,1),D(﹣m2,0),设直线AE表达式为y=kx+b,把E(m,﹣m2),A(0,1)代入得∴12bmk b=⎧⎪⎨=-+⎪⎩,解得:m2k2mb1+⎧=-⎪⎨⎪=⎩,∴直线AE表达式为y=﹣22mm+x+1,∴点M坐标为(22mm+,0),设直线DE表达式为y=ax+t,将D(﹣m2,0),E(m,﹣m2)代入得22ma tmam t⎧=-+⎪⎪⎨⎪-=+⎪⎩,解得:136amt⎧=-⎪⎪⎨⎪=-⎪⎩,∴直线DE表达式为y=﹣13x﹣m6,∴点G坐标为(0,﹣m6).∵△DOG的面积与△MFE的面积之比为1:2,∴2×12×m2×m6=12×m2×(m﹣22mm+).∵m>0,∴m=1.故该抛物线解析式是:y=﹣x2+x+3.【点睛】本题考查二次函数的性质,用待定系数法求一次函数表达式,相似三角形知识.利用相似三角形对应边成比例得出点的坐标是解题的关键.24.(1)①y=14x2﹣32x+2,2;②A′(6,2);(2)an为定值,an=12.【解析】【分析】(1)①将A(2,0)代入y=ax2﹣32x+2(a>0),可得抛物线C1的解析式为:y=14x2﹣32x+2(a>0),求出C(0,2),OC=2B(4,0),AB=4﹣2=2,所以S△ABC=12AB•OC=12×2×2=2;②若C '、Q '在抛物线C 1上,当x =3时,y =﹣14,可得O '(3,﹣14),A '(3,74);若C '、A '在抛物线C 1上,设C '(t ,24t ﹣32t +2),则A '(t +2,24t ﹣32t +4),将A '代入C 1解得t=4,A ′(6,2);(2)平移后的新抛物线C 2的解析式为:y =ax 2,设AP 的直线解析式为y =k (x ﹣12a),联立2k y kx 2a y ax⎧=-⎪⎨⎪=⎩,ax 2﹣kx +k 2a =0,x A +x B =k a ,x A x B =2k 2a ,x A x B =12a (x A +x B ),联立2y x b y ax =+⎧⎨=⎩,ax 2﹣x ﹣b =0,x A +x C =1a ,x C =1a ﹣x A ,直线BC 的解析式为y =px +q ,联立2y px q y ax =+⎧⎨=⎩,ax 2﹣px ﹣q =0,x B +x C =p a ,x B x C =﹣q a ,可得x B ﹣x A =1p a -①,x B (1a ﹣x A )=﹣q a ,x B ﹣x A =﹣2q ②,由①②可得q =12p a-,将M 代入y =px +q ,求得an =12.【详解】解:(1)①将A (2,0)代入y =ax 2﹣32x +2(a >0), 得:0=4a ﹣3+2,解得:a =14, ∴抛物线C 1的解析式为:y =14x 2﹣32x +2(a >0)令x =0,得y =2, ∴C (0,2),OC =2 令y =0,得14x 2﹣32x +2=0,解得:x 1=2,x 2=4,∴B (4,0), ∴AB =4﹣2=2 ∴S △ABC =12AB •OC =12×2×2=2; ②若C '、Q '在抛物线C 1上, ∵C 'O '=CO =2, ∴当x =3时,y =﹣14, ∴O '(3,﹣14),∴A '(3,74); 若C '、A '在抛物线C 1上,设C '(t ,24t ﹣32t +2),则A '(t +2,24t ﹣32t +4),将A '代入C 1得:14(t +2)2﹣32(t +2)+2=24t ﹣32t +4,解得t =4, ∴A ′(6,2);(2)∵平移后的新抛物线C 2顶点在原点,∴平移后的新抛物线C 2的解析式为:y =ax 2, 设AP 的直线解析式为y =k (x ﹣12a), 联立2k y kx 2a y ax ⎧=-⎪⎨⎪=⎩,ax 2﹣kx +k 2a =0,∴x A +x B =ka ,x A x B =2k 2a , ∴x A x B =12a(x A +x B ),联立2y x by ax=+⎧⎨=⎩,ax 2﹣x ﹣b =0, ∴x A +x C =1a ,x C =1a﹣x A , 设直线BC 的解析式为y =px +q ,联立2y px qy ax =+⎧⎨=⎩,ax 2﹣px ﹣q =0, ∴x B +x C =pa,x B x C =﹣q a ,∴x B +(1a ﹣x A )=p a,∴x B ﹣x A =1p a-①,x B (1a ﹣x A )=﹣q a ,x B ﹣x A =﹣2q ②,由①②可得q =12pa-,将M 代入y =px +q ,∴n =q •12a +12p a -=12a ,∴an =12.【点睛】本题考查二次函数的综合;熟练掌握二次函数、一次函数的图象及性质,熟练应用韦达定理,并能数形结合解题是关键.。
初中数学二次函数的应用题型分类——动态几何图形问题8( 附答案)
高,正方形 DEFG 的边 DE 在高 CH 上,F ,G 两点分别在 AC , AH 上.将正方形
DEFG 以每秒1cm 的速度沿射线 DB 方向匀速运动,当点 G 与点 B 重合时停止运
动.设运动时间为 ts ,正方形 DEFG 与 BHC 重叠部分的面积为 Scm2 ,则能反映 S 与
t 的函数关系的图象( )
2.二次函数 y= 2 3x2 的图象如图所示,点 O 为坐标原点,点 A 在 y 轴的正半轴上,
点 B. C 在函数图象上,四边形 OBAC 为菱形,且∠AOB=30 0 ,则点 C 的坐标为( )
A.
1 2
,
3
B.
1 2
,
3 2
C.
1,
3 2
D. 1, 3
3.如图,在等腰直角三角形 ABC 中,ACB 90 , AB 8cm ,CH 是 AB 边上的
初中数学二次函数的应用题型分类——动态几何图形问题 8(附答案)
1.汽车刹车后行驶的距离 s(单位:米)关于行驶的时间 t(单位:秒)的函数解析式
为 s=-6t2+bt(b 为常数).已知 t= 1 时,s=6,则汽车刹车后行驶的最大距离为( ) 2
A. 15 米 2
B.8 米
C. 75 米 8
D.10 米
的大小变化情况是( ).
A.一直减小
B.一直不变
C.先减小后增大
D.先增大后减小
9.在▭ABCD 中,对角线 AC=4,BD=6,P 是线段 BD 上一动点,过 P 作 EF∥AC,与
▱ ABCD 的两边分别交于 E、F.设 BP=x,EF=y,则反映 y 与 x 之间关系的图象是( )
A.
B.
中考数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年解答题版
中考数学每日一练:二次函数的实际应用-动态几何问题练习题及答案_2020年解答题版答案答案2020年中考数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题~~第1题~~(2019滨州.中考模拟) 如图,在平面直角坐标系中,抛物线y =x +mx +n 经过点A (3,0)、B (0,-3),点P 是直线AB 上的动点,过点P 作x 轴的垂线交抛物线于点M , 设点P 的横坐标为t .(1) 分别求出直线AB 和这条抛物线的解析式.(2) 若点P 在第四象限,连接AM 、BM ,当线段PM 最长时,求△ABM 的面积.(3) 是否存在这样的点P ,使得以点P 、M 、B 、O 为顶点的四边形为平行四边形?若存在,请直接写出点P 的横坐标;若不存在,请说明理由.考点: 二次函数y=ax^2+bx+c 的性质;待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;~~第2题~~(2018嘉兴.中考模拟) 如图,平面直角坐标系xOy 中,抛物线y=a (x+1)(x-9)经过A ,B 两点,四边形OABC 矩形,已知点A 坐标为(0,6)。
(1) 求抛物线解析式;(2) 点E 在线段AC 上移动(不与C 重合),过点E 作EF ⊥BE ,交x 轴于点F .请判断的值是否变化;若不变,求出它的值;若变化,请说明理由。
(3) 在(2)的条件下,若E 在直线AC 上移动,当点E 关于直线BF 的对称点E 在抛物线对称轴上时,请求出BE 的长度。
考点: 待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;相似三角形的判定与性质;锐角三角函数的定义;~~第3题~~(2018湖州.中考模拟) 已知,如图,过点E(0,-1)作平行于轴的直线 , 抛物线上的两点A 、B 的横坐标分别为1和4,直线AB 交y 轴于点F,过点A 、B 分别作直线l 的垂线,垂足分别为点C 、D ,连接CF ,DF .(1)求点A,B,F 的坐标;2答案答案答案(2)求证:;(3)点是抛物线对称轴右侧图象上的一动点,过点P 作交X 轴于点Q ,是否存在点P 使得与相似?若存在,请求出所有符合条件的点P 的坐标;若不存在,请说明理由.考点: 待定系数法求二次函数解析式;二次函数的实际应用-动态几何问题;勾股定理;矩形的性质;相似三角形的性质;~~第4题~~(2017河北.中考模拟) 如图,已知二次函数y=ax +bx+c (a ,b ,c 为常数)的对称轴为x=1,与y 轴的交点为c (0,4),y 的最大值为5,顶点为M ,过点D (0,1)且平行于x 轴的直线与抛物线交于点A ,B .(Ⅰ)求该二次函数的解析式和点A 、B 的坐标;(Ⅱ)点P 是直线AC 上的动点,若点P ,点C ,点M 所构成的三角形与△BCD 相似,求出所有点P 的坐标.考点: 两一次函数图象相交或平行问题;二次函数的三种形式;二次函数的实际应用-动态几何问题;勾股定理;相似三角形的判定与性质;~~第5题~~(2017槐荫.中考模拟) 如图,抛物线y=x ﹣ x+c 与y轴交于点A (0,﹣ ),与x 轴交于B 、C 两点,其对称轴与x 轴交于点D ,直线l ∥AB 且过点D .(1)求AB 所在直线的函数表达式;(2)请你判断△ABD 的形状并证明你的结论;(3)点E 在线段AD 上运动且与点A 、D 不重合,点F 在直线l 上运动,且∠BEF=60°,连接BF ,求出△BEF 面积的最小值.解:考点: 二次函数与一次函数的综合应用;二次函数的实际应用-动态几何问题;全等三角形的判定与性质;等边三角形的判定;特殊角的三角函数值;2020年中考数学:函数_二次函数_二次函数的实际应用-动态几何问题练习题答案1.答案:222.答案:3.答案:4.答案:5.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学《二次函数-动态几何问题》专项练习及答案一、单选题1.如图1,在△ABC中,△B=90°,△C=30°,动点P从点B开始沿边BA、AC向点C以恒定的速度移动,动点Q从点B开始沿边BC向点C以恒定的速度移动,两点同时到达点C,设△BPQ的面积为y(cm2).运动时间为x(s),y与x之间关系如图2所示,当点P恰好为AC的中点时,PQ的长为()A.2B.4C.2 √3D.4 √32.如图,在四边形DEFG中,△E=△F=90°,△DGF=45°,DE=1,FG=3,Rt△ABC的直角顶点C与点G重合,另一个顶点B(在点C左侧)在射线FG上,且BC=1,AC=2,将△ABC沿GF方向平移,点C与点F重合时停止.设CG的长为x,△ABC在平移过程中与四边形DEFG重叠部分的面积为y,则下列图象能正确反映y与x函数关系的是()A.B.C.D.3.点C是线段AB上的一点,AB=1,分别以AC和CB为一边作正方形,用S表示这两个正方形的面积之和,下列判断正确的是()A.当C是AB的中点时,S最小B.当C是AB的中点时,S最大C.当C为AB的三等分点时,S最小D.当C是AB的三等分点时,S最大4.下列函数属于二次函数的是()A.y=5x+3B.y=1x2C.y=2x2+x+1D.y=√x2+15.在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是()A.y=3(x+1)2+2B.y=3(x+1)2﹣2C.y=3(x﹣1)2+2D.y=3(x﹣1)2﹣26.如图,直线l1:y=−x+4与x轴和y轴分别相交于A、B两点,平行于直线l1的直线l2从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,它与x轴和y轴分别相交于C、D两点,运动时间为t秒(0≤t≤4).以CD为斜边作等腰直角ΔCDE(E、O两点分别在CD两侧),若ΔCDE和ΔOAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是()A.B.C.D.7.如图,菱形ABCD的边长为2,△A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH△BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为()A.B.C.D.8.把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为()A.y=﹣2(x+1)2+2B.y=﹣2(x+1)2﹣2C.y=﹣2(x﹣1)2+2D.y=﹣2(x﹣1)2﹣29.如图,AC=BC,点D是以线段AB为弦的圆弧的中点,AB=4,点E是线段CD上任意一点,点F 是线段AB上的动点,设AF=x,AE2﹣FE2=y,则能表示y与x的函数关系的图象是()A.B.C.D.10.如图,在△ABC中,△ACB=90°,AC=4,BC=2.P是AB边上一动点,PD△AC于点D,点E 在P的右侧,且PE=1,连结CE.P从点A出发,沿AB方向运动,当E到达点B时,P停止运动.在整个运动过程中,图中阴影部分面积S1+S2的大小变化情况是()A.一直减小B.一直不变C.先减小后增大D.先增大后减小11.将抛物线y=-2x2先向左平移1个单位,再向上平移3个单位,两次平移后得到的抛物线的解析式为()A.y=-2(x+1)2+3 B.y=-2(x+1)2-3C.y=-2(x-1)2+3 D.y=-2(x-1)2-312.如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且△APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是()A.B.C.D.二、填空题13.如图,在Rt△ABC中,△C=90°,BC=4,BA=5,点D在边AC上的一动点,过点D作DE△AB 交边BC于点E,过点B作BF△BC交DE的延长线于点F,分别以DE,EF为对角线画矩形CDGE 和矩形HEBF,则在D从A到C的运动过程中,当矩形CDGE和矩形HEBF的面积和最小时,则EF 的长度为.14.已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点。
小明经探究发现:当b a的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定。
若抛物线y=ax2+bx+2(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则ba的值是15.如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为s时,四边形EFGH的面积最小,其最小值是cm2.16.已知抛德物线y=14x2+1有下性质:该抛物线上任意一点到定点F(0,2)的距离与到轴的距离始终相等,如图,点M的坐标为(√2,3),P是抛物线y=14x2+1上一个动点,则△PMF周长的最小值是.17.如图,在Rt△ABC中,△B=90°,AB=6cm,BC=8cm,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,则P、Q分别从A、B同时出发,经过秒钟,使△PBQ的面积最大.18.如图,已知二次函数y=−12x2+32x+2的图象交x轴于A(-1,0),B(4,0),交y轴于点C,点P是直线BC上方抛物线上一动点(不与B,C重合),过点P作PE△BC,PF△y轴交BC与F,则△PEF面积的最大值是.三、综合题19.如图,抛物线y=(x+1)2+k与x轴交于A、B两点,与y轴交于点C(0,﹣3).(1)求抛物线的解析式;(2)若点M是抛物线上一动点,且在第三象限,当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.20.如图,抛物线y=x2+x﹣2与x轴交于A,B两点,与y轴交于点C.(1)求点A,点B和点C的坐标;(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.21.如图,直线y=﹣23x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+ 103x+c经过B、C两点.(1)求抛物线的解析式;(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.22.如图,在直角坐标系中,直线y=13x+1与x轴、y轴的交点分别为A、B,以x=﹣1为对称轴的抛物线y=﹣x2+bx+c与x轴分别交于点A、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,设抛物线的对称轴l与x轴交于一点D,连接PD,交AB于E,求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标;(3)若点Q在第二象限内,且tan△AQD=2,线段CQ是否存在最小值?如果存在直接写出最小值,如果不存在,请说明理由.23.如图,已知抛物线y= - x2+mx+3与x轴交于A、B两点,与y轴交于点C,点B的坐标为(3,0).(1)求m的值及抛物线的顶点坐标;(2)求抛物线与坐标轴的交点所围成的三角形面积;(3)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标24.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣1a(a<0)与y轴交于点A,将点A向右平移3个单位长度,得到点B,点B在抛物线上.(1)求点B的坐标(用含a的式子表示)和抛物线的对称轴;(2)当B的纵坐标为3时,求a 的值;(3)已知点P(12,﹣1a),Q(3,3).若抛物线与线段PQ恰有一个公共点,请结合函数图象直接写出a的取值范围.参考答案1.【答案】C 2.【答案】B 3.【答案】A 4.【答案】C 5.【答案】C 6.【答案】C 7.【答案】A 8.【答案】C 9.【答案】C 10.【答案】C 11.【答案】A 12.【答案】C 13.【答案】5214.【答案】2或-8 15.【答案】3;18 16.【答案】√3 +3 17.【答案】3 18.【答案】4519.【答案】(1)解:∵y =(x+1)2+k 与y 轴交于点C (0,﹣3)﹣3=1+k ,得,k =﹣4∴抛物线解析式为y =(x+1)2﹣4 即y =x 2+2x ﹣3. (2)解:如图1所示:连接AC ,过点M 作MD△AC ,交AD 于点D .令y =0得:x 2+2x ﹣3=0 解得x 1=﹣3,x 2=1 ∴A (﹣3,0)、B (1,0). 设直线AC 的解析式为y =kx+b .∵将A (﹣3,0)、C (0,﹣3)代入得:{−3k +b =0b =−3解得k =﹣1,b =﹣3.∴直线AC 解析式为y =﹣x ﹣3.设M (x ,x 2+2x ﹣3),则D (x ,﹣x ﹣3),则MD =﹣x 2﹣3x . ∵四边形AMCB 的面积=△ABC 面积+△AMC 面积∴四边形AMCB 的面积=12MD ⋅AO +12AB ⋅OC=12×(−x 2−3x)×3+12×4×3 =−32x 2−92x +6=−32(x +32)2+758∴当x =−32时,S 最大值为758,点M 的坐标为(﹣32,﹣154).20.【答案】(1)解:由 y=0,得 x 2+x ﹣2=0 解得 x 1=﹣2, x 2=1∴A (﹣2,0),B (1,0) 由 x=0,得 y=﹣2 ∴C (0,﹣2)(2)解:连接AC 与对称轴的交点即为点P .设直线 AC 为 y=kx+b ,则﹣2k+b=0 b=﹣2:得 k=﹣1,y=﹣x ﹣2.对称轴为 x=﹣ 12 ,当 x=﹣ 12 时,y=_(﹣ 12 )﹣2=﹣ 32∴P (﹣ 12 ,﹣ 32 )(3)解:过点M 作MN 丄x 轴与点N设点M (x ,x 2+x ﹣2),则AN=x+2,0N=﹣x ,0B=1,0C=2,MN=﹣(x 2+x ﹣2)=﹣x 2﹣x+2 S 四边形ABCM =S △AOM +S △OCM +S △BOC = 12 (x+2)(﹣x 2﹣x+2)+ 12 (2﹣x 2﹣x+2)(﹣x )+ 12×1×2 =﹣x 2﹣2x+3=﹣(x+1)2+4.∵﹣1<0∴当x=_l 时,S 四边形ABCM 的最大值为421.【答案】(1)解:当 x =0 时∴B(0,4)当 y =0 时x =6,∴C(6,0)把 B(0,4) 和 C(6,0) 代入抛物线 y =ax 2+103x +c 中得: {c =436a +103×6+c =0 解得: {a =−23c =4∴抛物线的解析式为: y =−23x 2+103x +4; (2)解:如图1,过E 作EG△y 轴,交直线BC 于G∵点M在直线y=−23x+4上∴点M的坐标是(3,2),又∵点A的坐标是(﹣1,0),点Q的横坐标为2根据M到Q的平移规律:可知:P的横坐标为﹣2∴P(−2,−16 3).②如图3,以AM为边时,四边形AMPQ是平行四边形由(2),可得点M的横坐标是2∵A(﹣1,0),且Q的横坐标为2∴P的横坐标为6∴P(6,0)(此时P与C重合);③以AM为对角线时,如图4∵M到Q的平移规律可得P到A的平移规律∴点P的坐标是(0,4)综上所述,在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形点P的坐标是(−2,−163)或(6,0)或(0,4).22.【答案】(1)解:∵直线y=13x+1与x轴交点为A ∴点A的坐标为(﹣3,0)∵抛物线的对称轴为x=﹣1∴点C的坐标为(1,0)∵抛物线y=﹣x2+bx+c与x轴分别交于点A、C∴抛物线为y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3;(2)解:∵抛物线y =﹣x 2﹣2x+3的对称轴为x =﹣1∴点D 的坐标为(﹣1,0)①当△ADE =90°时,△ADE△△AOB .此时点P 在对称轴上,即点P 为抛物线的顶点,坐标为(﹣1,4);②当△AED =90°时,△AED△△AOB .过点P 作PG△AC 于点G ,则△AED△△PGD .于是GD PG =DE AE =OB OA =13∴PG =3GD .即:﹣t 2﹣2t+3=3(﹣1﹣t )解得 t 1=﹣2,t 2=3(不合题意,舍去).当t =﹣2时,﹣22+2×2+3=3所以此时点P 的坐标为(﹣2,3).综上所述,点P 的坐标是(﹣1,4)或(﹣2,3);(3)存在,CQ 的最小值为√372-√5223.【答案】(1)解:将点B 的坐标(3,0)代入抛物线表达式得:0=﹣9+3m+3,解得:m =2 则函数对称轴为:x =﹣b 2a=1,代入y= - x 2+2x+3,y= 4,则顶点的坐标为(1,4); (2)解:函数的表达式为:y =﹣x 2+2x+3,令y =0,则x =3或﹣1,令x =0,则y =3,故点A 、C 的坐标分别为(﹣1,0)、(0,3)AB=4,OC=3△ABC 的面积为12AB ·OC =12×4×3=6.(3)解:点A 关于函数对称轴的对称点为B ,连接BC 交函数对称轴于点P ,此时点P 即为所求点将点B 、C 的坐标代入一次函数表达式:y =kx+b 得:{0=3k +b b =3,解得:{k =−1b =3故直线BC 的表达式为:y =﹣x+3当x =1时,y =2,故点P (1,2).24.【答案】(1)解:当x=0时,y=−1a∴点A 的坐标为:(0,−1a) ∵将点A 向右平移3个单位长度,得到点B∴点B (3,−1a) ∴点A ,B 是对称点∴对称轴为直线x =3+02=1.5 ∴对称轴为直线x=1.5;(2)解:当 −1a =3时,a= −13(3)解:当 a ≤−13时满足题意。
