附录2重要平面曲线
工程力学附录II1-讲义

dA d d
zC
Sy A
4R
3
y
5
组合图形的静矩与形心
(1) 当平面图形是由若干个简单图形(如圆形、矩形等)组成 的,由静矩的定义可知,各组合部分对于某一轴的静矩的 代数和,等于该平面图形对于同一轴的静矩。
(2) 由于简单图形的面积和形心位置均为已知,因此可得到方 便地计算由 n 个简单图形组成的组合图形的静矩。
若以 表示 dA 到坐标原点 O 的距离,定义平面图形对坐标
原点的极惯性矩为
Ip
2dA
A
(II.9)
z dA
极惯性矩也称为二次极矩 (second polar moment of an area)。
z
A
惯性矩的单位:m4,mm4
Oy
y
注意:极惯性矩恒为“+”。
Ip I y Iz (II.10)
yC
A
A
(6.30) zdA
zC
A
A
yC
Sz A
zC
Sy A
(II.2)
Sz AyC Sy AzC (II.3)
z zC O
若已知横截面面积 A 和形心坐标 yC , zC 时,就可按上式方便地求得此截面 对 y 轴和 z 轴的静矩。
dA C A
yC y
y
静矩与形心的关系
(1) 平面图形对某一轴的静矩若为零,该轴通过此图形的形心。
Iy
z2dA
A
2 0
R ( sin )2 dd
0
d
y
R4 D4
4 64
Iz
( II.6 )
Iy
R4
4
D4
64
8. 重要平面曲线表
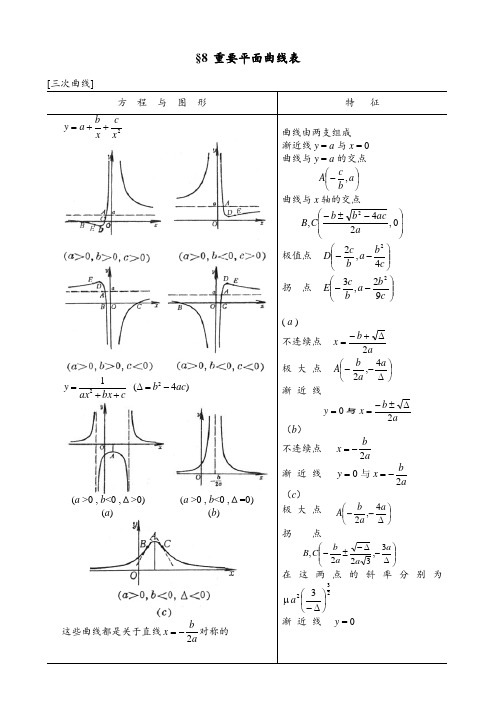
§8 重要平面曲线表+ax+bxc2cbx ax ++=α, β为方程02=++c bx ax 的两个根,并设上述三次曲线的图形,只列出a >0的情况,对于a <0时,除曲线2xcx b a y ++=(当a >0时渐近线在x 轴上方,当a <0时,渐近线在x 轴下方)外,一般作适当变化后,与a >0时的曲线都是关于x 轴对称的.例如a <0时,两条曲线:c bx ax y ++=21与cbx ax y ---=21是关于x 轴对称的,而后者x 2系数0>-a .立方抛物线)()3,0(323ac b a d cx bx ax y -=∆>+++=nax y =(m , n 为两个互素的整数) nm 的各种情况(曲线关于y 轴对称关于原点对称箕舌线]⎩⎨⎧==+=a y a x a x a 223cos tan 或[笛卡儿叶形线] axy y x 333=+环索线]尼哥米德蚌线]cos ±=ϕ)()(222222y x b ax y x +=-+或 ⎩⎨⎧+=+=t b t t a y t b t a x s i n s i nc o s c o sc o s 2或 )为圆的直径a b a (c o s +=ϕρ曲线是使OM = OP ± b 的点M 的轨迹(P 点在直径为a 的圆周上) 顶 点 A k , B k (a ± b , 0)(k =1, 2, 3, 4, 5),B 2与原点重合结 点(b <a 时)O (0, 0),在该点的切线的斜率为bb a 22-±,该点的曲率半径为2221b a - 尖 点(b =a 时)O (0, 0) 孤立点(b >a 时)O (0, 0)极值点 当b <a 时有4个,当b ≥a 时有2个:)5,4,3,2,1(48cos ,,2211=⎪⎪⎭⎫⎝⎛+±-=''k a ab b D C D C k k ϕ和当b 从0变到∞时,所有极值点构成蔓叶线ϕϕρcos sin 2a =拐点(a <b <2a 时)⎪⎪⎭⎫⎝⎛+-=ϕab b a F E 32cos ,22二重切线的切点(b <2a 时):)3,2(44,4,222=⎪⎪⎭⎫⎝⎛-±-k a b a b a b H G k k 这些切点在圆ρ = - a cos ϕ上蜗线所围成的面积222b a S ππ+= (当b <a 时,内圆的面积计算了两次) [注] 当b =a 时,即为心脏线. [卡西尼卵形线]44222222)(2)(c a y x c y x -=--+ 或)0(2sin 2cos 24422>-±=c c a c ϕϕρ曲线是使MF 1⋅MF 2 = a 2的点M 的轨迹(F 1, F 2为固定焦点,F 1F 2 = 2c ,a 为常数).顶 点 )0,(,2211a c B A -±'')5,4,3,2,1()0,(,22=-±''k c a B A k k极值点 )5,4,3(),0(,22=-±'k c a C C kk )3,2,1(2,24,,,244=⎪⎪⎭⎫ ⎝⎛±-±''k c a c a c H G H G k k k k或⎪⎪⎭⎫ ⎝⎛==222sin ,c a c ϕρ 当a 从0变到2c 时,所有极值点构成一个圆(半径为c ) 拐 点 )2(时c a c <<)4,3,2,1(2,2=⎪⎪⎭⎫ ⎝⎛+±-±k n m n m E k 其中 244443,3c c a n c a m -=-=或⎪⎭⎫ ⎝⎛-==22cos ,c m m ϕρ当a 从c 变到2c 时,所有拐点构成双纽线a长轴(λ>1)短轴(λ<1)[圆内旋轮线(内摆线)]⎪⎪⎩⎪⎪⎨⎧---=-+-=tb b a b t b a y t bb a b t b a x sin sin )(cos cos )( (a 为定圆半径,b 为动圆半径,t = ∠COx )曲线是一圆周沿另一圆周的内部滚动而无滑动时,圆周上一点M所描成的轨迹.圆内旋轮线的尖点、顶点的坐标,弧长,曲率半径及面积公式都与圆外旋轮线一样,只须把“+b”换成“-b”.bam=总是大于1,特别,当m = 4时,曲线有4只,称为星形线,其方程为⎪⎩⎪⎨⎧==taytax33sincos或323232ayx=+全曲线长L = 6a曲线所围成的面积383aSπ=[长(或短)辐圆外旋轮线(外次摆线)]⎪⎪⎩⎪⎪⎨⎧+-+=+-+=tbbatbaytbbatbaxs i ns i n)(c o sc o s)(λλ(a为定圆半径,b为动圆半径)曲线是一圆周沿另一圆周的外部滚动而无滑动时,圆周外部(或内部)一点M 所描成的轨迹. [长(或短)辐圆内旋轮线(内次摆线)]⎪⎩⎪⎨⎧---=-+-=tb b a t b a y t b b a t b a x sin sin )(cos cos )(λλ(a 为定圆半径,b 为动圆半径)长辐)(b >λ 短辐)(b <λ 曲线是一圆周沿另一圆周的内部滚动而无滑动时,圆周外部(或内部)一点M 所描成的轨ϕρa=渐近点 极点O (当±∞→ϕ时) 渐近线 y =a 曲率半径321⎪⎪⎭⎫⎝⎛+=ϕϕϕa R 扇形M 1OM 2的面积 ⎪⎪⎭⎫ ⎝⎛-=212112ϕϕa S 曲线由两支组成,它们关于y 轴对称 [连锁螺线]ϕρa=曲线是当N 在x 轴上移动时,使圆扇形OMN 的面积保持一定⎪⎭⎫⎝⎛22a 的点M 的轨迹渐近点 极点O (当∞→+ϕ时)渐近线 x 轴(当0→ϕ时)∠⎩。
第二章平面曲线

2.纸上定线
以直线为主定交点:主要用于平原、微丘区,是根据地形、地物条件,选设定作为路 线基本轴线的直线,再根据两两直线相交得交点,继而设置圆曲线和缓和曲线,该方法称以 直线为主定交点法,也是传统的方法。
以曲线为主定交点:常用于互通立交匝道布线、定线或山岭、重丘区高速公路、一级 公路选线、定线,是根据地形及环境条件和路线技术要求设置圆曲线(或圆曲线与缓和曲线
一定建筑物等措施。 长直线或长下坡尽头的平曲线,应对路面超高、停
车视距等进行检验,必要时须采用设置标志、增加 路面抗滑能力等安全措施。
2.直线的最小长度
相邻两曲线之间应有一定长度的直线,这个直线是指前一曲线的终点(HZ或YZ)到 后一曲线的起点(ZH或ZY)之间的长度。
(1)同向曲线间的直线最小长度 同向曲线:是指两个转向相同的相邻曲线之间连以直线而形成的平面线形。 断背曲线:同向曲线间连以短的直线。
断背曲线的错觉 ①当直线较短时,在视觉上容易形成直线与两端曲线构成反弯的错觉; ②当直线过短甚至把两个曲线看成是一个曲线。
危害: 破坏了线形的连续性,造成驾驶操作失误,应尽量避免。
解决办法: 因为是视觉上的判断错觉,最好的办法是在两同向曲线间插入长的直线段,让驾驶
员在前一个曲线上看不到下一个曲线。
在直线纵坡路段,易错误估计车间距离、行车 速度及上坡坡度。
易对长直线估计得过短或产生急躁情绪,超速 行驶。
二、直线的运用
采用直线线形时必须注意线形与地形的关系,在运用直 线线形并决定其长度时,必须慎重考虑,一般不宜采用长直线。 路线完全不受地形、地物限制的平坦地区或山间的宽阔河谷
地带; 城镇及其近郊道路,或以直线为主体进行规划的地区; 长大桥梁、隧道等构造物路段; 路线交叉点及其附近; 双车道公路提供超车的路段。
《数学课程标准》” 图形与几何“领域的解读

第七章图形与几何第一节:总体主线和关键点分析“图形与几何”的课程内容,以发展学生的空间观念、几何直观、推理能力为核心展开,主要有:空间和平面基本图形的认识,图形的性质、分类和度量;图形的平移、旋转、轴对称、相似和投影;平面图形基本性质的证明;物体和图形的位置及运动的描述,以及利用坐标对其的刻画。
1.图形的认识正确理解与把握《标准》对图形认识的要求,分析学生学习这部分内容时的特点,对于课程的实施和目标的达成是十分重要的。
(1)明确认识的对象在第一学段,《标准》要求“能根据具体事物、照片或直观图辨认从不同角度观察到的简单物体”;“能通过实物和模型辨认长方体、正方体、圆柱和球等几何体”;“能辨认长方形、正方形、三角形、平行四边形、圆等简单图形”等,其中既涉及到了对简单几何体的认识,也涉及到了经过抽象后的三维图形和二维图形。
在第二学段中,认识的图形增加了线段、射线和直线等一维图形;对角的认识扩大到了平角、周角,增加了梯形、扇形,对三角形的认识从一般三角形到等腰三角形、等边三角形、直角三角形、锐角三角形、钝角三角形等;三维图形的认识对象增加了圆锥。
在第三学段,除增加了点、平面、菱形外,而更多的是对已有图形从整体到局部的认识,如“理解三角形及其内角、外角、中线、高线、角平分线等概念”,“理解圆、弧、弦、圆心角、圆周角的概念”等。
与其他二维、三维图形相比,点、直线、平面这些基本图形抽象的程度更高,因此必须结合对现实生活中的物体的抽象才能更好地理解它们。
《标准》关于“图形的认识”内容的安排,体现了从生活到数学、从直观到抽象,从整体到局部的特点,且三维、二维、一维图形交替出现,目标要求逐渐提高。
(2)明确图形认识的要求图形认识的要求主要包括两个方面,一是对图形自身特征的认识,二是对图形各元素之间、图形与图形之间关系的认识。
对图形自身的特征认识,是进一步研究图形的基础。
在三个学段中,认识同一个或同一类图形的要求有明显的层次性:从“辨认”到“初步认识”,再从“认识”到“探索并证明”。
极限侧摩阻力标准贯入试验报告

*****二期强夯地基各土层桩的极限侧摩阻力标准值试验报告********测绘有限公司2013 年8 月 16 日*******二期工程强夯地基各土层桩的极限侧摩阻力标准值试验报告报告编写:核定:审查:批准:*******测绘有限公司2013年8月16日试验声明1、试验报告涂改无效。
2、试验报告无“检测专用章”或单位公章无效。
3、试验报告无主检、审核、批准人签字或等同标识无效。
4、未经本单位书面批准,不得全部或部分复制本检测报告。
5、试验数量达不到抽检比例时,仅对被试验点负责;一般情况下,仅对来样负责。
6、对试验报告若有异议,应于收到报告之日起15日内向本单位书面提请复议。
地址:邮编:255086 电话:传真:目录首页 (1)1 前言 ·····················································································22 工程地质状况 ·········································································23 试验目的、试验方法、试验依据及主要仪器设备 ····························53.1试验目的 ·········································································53.2试验方法 ·········································································53.3 试验依据 ········································································73.4 主要仪器设备 ··································································84 试验结果的整理与分析 ·····························································84.1资料整理 ·········································································84.2 桩身极限侧摩阻力标准值计算 ·············································85 试验结论 ...............................................................................9附录1试验点位平面图 . (10)附录2标贯试验曲线图 (11)共11页第1页工程质量试验报告批准:审核:主检:报告编写:共15页第2页1 前言济南金艺林房地产开发有限公司拟建的济南市鲁商·凤凰城二期工程位于济南市济南市幼安路北侧,唐冶中路西侧。
平面曲线的切线与法线掌握平面曲线的切线与法线的计算方法

平面曲线的切线与法线掌握平面曲线的切线与法线的计算方法在数学中,平面曲线的切线与法线是研究曲线性质的重要概念。
切线是曲线上一点的切线,通过该点切线能够与曲线拥有公共的切点,而法线则垂直于切线,并与曲线相交于该点。
一、平面曲线的切线计算方法对于平面曲线的切线计算方法,一般分为两种情况:在某一点求切线方程和求解全部切线方程。
1. 在某一点求切线方程设曲线方程为 y=f(x),点P(x0, y0)为曲线上的一点,我们需要求解通过点P的切线方程。
这可以通过以下步骤实现:步骤1:计算点P的切线斜率k。
对于给定的点P,可通过求函数f(x)在x=x0处的导数f'(x0)得到切线斜率k。
步骤2:利用点斜式(y-y0=k(x-x0))或两点式(y-y0=k(x-x0)和P(x0, y0))得到切线方程的具体形式。
2. 求解全部切线方程对于某些曲线,我们希望找到所有切线方程而不仅仅是某一个特定点的切线方程。
这可以通过以下步骤实现:步骤1:计算曲线方程 y=f(x) 的导数 f'(x)。
步骤2:列出切线方程的一般形式为 y=f'(x0)(x-x0)+y0,其中(x0, y0)是曲线上的任意一点。
步骤3:将已知的曲线方程 y=f(x) 代入切线方程中,得到切线方程的具体形式。
二、平面曲线的法线计算方法与切线计算类似,平面曲线的法线也可以分为两种情况:在某一点求法线方程和求解全部法线方程。
1. 在某一点求法线方程设曲线方程为 y=f(x),点P(x0, y0)为曲线上的一点,我们需要求解通过点P的法线方程。
这可以通过以下步骤实现:步骤1:计算点P的斜率k。
斜率k为曲线在点P处的切线的斜率,因此我们可以通过计算f'(x0)来得到k。
步骤2:法线的斜率是切线斜率的相反数的倒数,即-1/k。
步骤3:利用点斜式(y-y0=k(x-x0))或两点式(y-y0=k(x-x0)和P(x0, y0))得到法线方程的具体形式。
二次曲线的一般式-概述说明以及解释
二次曲线的一般式-概述说明以及解释1.引言1.1 概述二次曲线是数学中重要的曲线类型之一。
它由二次方程所表示,是平面上的曲线。
在二次曲线上,点到定点的距离与点到定直线的距离的比值恒定,这是二次曲线独特的性质之一。
二次曲线广泛应用于几何学、物理学、工程学和计算机图形学等领域。
在几何学中,二次曲线的性质和特点被用于解决许多关于曲线的问题,如焦点、直径、切线和法线等。
在物理学中,二次曲线的运动方程被用于描述抛物线运动或者椭圆轨道等运动问题。
在工程学中,二次曲线常用于设计道路、桥梁和建筑物的曲线部分,以达到美观和结构稳定的目的。
在计算机图形学中,二次曲线被广泛应用于绘制曲线和曲面,用于创建平滑的图形效果。
本文将深入探讨二次曲线的一般式,包括其定义、性质和特点。
我们将介绍二次曲线的一般形式,并重点讨论其中的关键概念和公式。
通过学习二次曲线的一般式,读者能够更好地理解二次曲线的特性,并能够应用这些知识解决相关问题。
接下来的章节将按照以下结构展开:首先,我们将介绍二次曲线的定义和一般形式,包括其方程和基本图形。
然后,我们将深入研究二次曲线的性质和特点,例如焦点、直径和切线等。
最后,我们将总结二次曲线的一般式,并探讨其应用和意义。
在本文的剩余部分,读者将逐步了解二次曲线的复杂性和多样性,以及它们在数学和实际应用中的作用。
无论读者是初学者还是对二次曲线较为熟悉的人,本文都将为他们提供全面而深入的知识,帮助他们更好地理解和运用二次曲线的一般式。
文章1.2文章结构部分的内容可以如下编写:文章结构是指文章的整体组织和布局方式,在本文中分为引言、正文和结论三个部分。
引言部分是文章的开端,概述了二次曲线的一般式的主题和背景,引起读者的兴趣。
其中,1.1小节对二次曲线的概念和定义进行解释,确保读者了解文章所涉及的数学概念。
1.2小节则介绍了本文的文章结构,提供了整篇文章的脉络,为读者理解文章内容奠定基础。
最后,1.3小节明确了本文的目的,即探究二次曲线的一般式,并说明了相关探究的意义。
高等数学中重要平面曲线
无滑动地滚动时 ,
其上
x
定点 M 的轨迹即为摆线 .
点击图中任意点动画开始或暂停
结束
摆线(续)
• 周 期:
x a( sin ) y
y a(1 cos )
M ta
T 2 a
o
x1
• 极大点: xk (2k 1) a (k 1, 2,)
• 曲率半径: • 一拱长:
• 尖点: (0, 0)
• 面积: • 弧长:
3 2
a2
8a
结束
心形线的另一种形式
x2 y2 ax a x2 y2
即 r a(1 cos )
y
oa
点击图中任意点 动画开始或暂停
• 尖点: (0, 0)
x
• 面积:
3 2
a
2
• 弧长: 8a
结束
外摆线 (圆外旋轮线) 族
结束
蔓叶线
或
y
Q
P M
(t tan ) oa x
播点 放击 开图 始片 或任 暂意 停处
• 轨迹: M 是半径为 a 的母圆上的动点 , 满足 OM = PQ 之点 P 的轨迹即为 蔓叶线
• 渐近线: • 曲线与渐近线之间的面积:
结束
笛卡儿叶形线
x
3at 1 t3
y
3at 2 1 t3
x
(a
b)
cos
t
b
cos
ab b
t
y
(a
b)
sin
t
b
sin
ab b
t
附录Ⅱ 重要平面曲线
或
尖点: (0, 0)
面积:
弧长:
轨迹: 外摆线的一种
点击图中任意点 动画开始或暂停
动圆直径 = 定圆直径 = a
魔励馒社垫特妆贸济氦队赊序茹跨芭氦梭梅羽乎恤梦惦鞋诚卡雏灵促鉴九重要平面曲线重要平面曲线
心形线的另一种形式
即
尖点: (0, 0)
面积:
弧长:
点击图中任意点 动画开始或暂停
忙尾巧言撑宫斧裸醒丝崎乾渤玫宏溺僻飞押计汰执绸温罪绕班变螺的折壕重要平面曲线重要平面曲线
双曲螺线
渐近点 :
极点 O
渐近线 :
曲率半径 :
扇形
曲线由两支组成 ,
它们关于 y 轴对称
动画走向为
点击图中任意点 动画开始或暂停
蚁骗眨矣讣壬吓背连古东汪八执跌篓肄劫卉龙癌峰糙鸳腮疹矿剁梧赐厕炕重要平面曲线重要平面曲线
涂践内台萌瞎玩犊皖庸市妆珍零椿趴派侗恫淮愧胞硷光褥椅豹投江诅丁植重要平面曲线重要平面曲线
外摆线 (圆外旋轮线) 族
定圆圆心为 (0,0), 半径为 a, 动圆半径为 b,
m = 1为心形线
点击图中任意点 动画开始或暂停
甘傻劲钥伙蛤联叼屑磐猾瘫饥棵哎供嗅已港姨俐依依芍茨砾氖姜掏粤仍欢重要平面曲线重要平面曲线
极值点:
曲率半径:
双纽面积:
极 值 :
即
对应点:
储莎诸香微犬苔伙芋夜郊痊弧霹忍功戒挎婆眶匡歉背弥洪剿伙侯姥饮火淳重要平面曲线重要平面曲线
三叶玫瑰线
点击图中任意点 动画开始或暂停
织党读川刚缕笑榔媚塘棒耳变蛹内厌寝骂庞搓优离扑阁喜埂民定妆凳另曝重要平面曲线重要平面曲线
四叶玫瑰线
点击图中任意点 动画开始或暂停
6.1.1立体图形与平面图形+教案2024-2025学年人教版(2024)七年级数学+上册+ (1)
立体图形与平面图形教学目标:1.通过观察生活中的大量物体,认识基本几何体,从立体图形发展到平面图形.2.从图形的旋转、翻折、平移等运动,初步探索图形之间的变换关系,发展空间观念,培养创新能力.3.通过主视图、左视图、俯视图教学,引导学生感悟“从不同方向看同一个物体,看到的图形往往是不同的.4.经历从现实世界中抽象出图形的过程,感受图形世界的多姿多彩,发展空间观念,增强用数学的意识.教学重点:研究立体图形与平面图形相互联系.教学难点:将平面图形折叠成立体图形并说出名称.教学过程:我们生活在丰富的图形世界里,多姿多彩的图形美化了我们的生活,也给我们带来了很多思考:怎样从具体实物中抽象出几何体和平面图形?怎样用平面图形来表现一个物体?怎样设计一个产品的包装盒?等等,所有这些,都需要我们去了解更多的图形知识.在本章,我们将通过对图形的观察、展开、折叠等活动,探索丰富的图形世界.1.认识几何体从右面的图片中,你能看出哪些常见的几何体.如图,如果只考虑物体的大小和形状,而不考虑其他属性(例如材料、颜色、质量等),我们就可以将物体抽象成几何体.活动一 请从下列实物中抽象出几何体.教师出示实物对于这么多的几何体,我们可以将它们分一下类,如果按柱、锥、球分:正方体、长方体、圆柱称为柱体,圆锥属于锥体,球是一类为球体.2.几何体的构成几何体由点、线、面组成.面与面相交得到线,线与线相交得到点. 魔方 足球 礼品盒 易拉罐 斗笠球 正方体 长方体 圆柱 圆锥小结:通过实物、图片认识长方体、圆柱中的相关元素,通过分析比较,感悟“几何图形由点、线、面组成” .3.图形的形成既然几何体由点、线、面组成,这些图形又是怎么由点、线、面变化来的呢?(1)点动成线:笔头看作一个点,这个点在黑板上运动时就形成线(直线或曲线)(2)线动成面:粉笔横画成面、钟表秒针转动等(3)面动成体:长方形面、三角形面、圆面——球体(电脑动画)三种运动:旋转、翻折、平移(电脑动画)小结:通过实例,从图形运动变化的角度感悟“点动成线,线动成面,面动成体”的形象 .感悟到让图形“动”起来,是研究图形性质的重要方法.4.展开与折叠既然几何图形是由点、线、面组成的,那么,我们是否可以将它们展开成平面图形呢? 活动二 拿出圆柱和圆锥实物,想一想,你会将圆柱和圆锥展开成平面图形吗?(学生上台操作)结论:圆柱的表面展开图是:两个圆(作底面)和一个长方形(作侧面).圆锥的表面展开图是:一个圆(作底面)和一个扇形(作侧面).活动三 分组合作学习1.请大家使用实验手册附录10的七巧板模型,拼出新的平面图形.2.请大家使用实验手册附录2-7,自选几个平面图形,将它们折叠成立体图形.并思考:(1)你能否说出折叠成的立体图形的名称?(2)平面图形是不是都能折叠成立体图形?结论:通过展开、折叠,感受立体图形与平面图形之间的关系:有些立体图形可以按不同的方式展开成平面图形,有些平面图形也可以折叠成立体图形.经历、体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯.5.主视图、左视图、俯视图请同学们观看正方体的形状,六个面都是相同的正方形.长方体的六个面呢?它的前后、上下、左右两个面相同,所以,一般情况下,可以从三个方向看数学图形.一般我们选择从正面看、从左面看、从上面看.棱 侧面 底面顶点 底面 侧面 棱(1)从正面、左面、上面看一个长方体,看到的图形分别是什么?(电脑演示)(2)从正面、左面、上面看一个圆柱,看到的图形分别是什么?从正面看到的图形,称为主视图;从左面看到的图形,称为左视图;从上面看到的图形,称为俯视图.从这三个方向上看到的图形,叫作这个几何体的三个视图.(3)反过来,根据下图所示物体的主视图、左视图、俯视图,想象物体的形状,说出相应几何体的名称.由三视图到物体(观看动画)小结:物体的主视图、左视图、俯视图可以确定物体的形状和大小,由三视图(平面图形)与简单物体(几何图形)之间可以相互转化.将立体图形通过设计画出三视图(平面图形)——设计师工作,根据一个物体的三视图做出实物(立体图形)——工程师工作.课堂小结:1.数学思想:抽象、转化、分类、运动.2.古诗欣赏《题西林壁》,感悟其中的道理.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M
P
o
a
x
播点 放击 开图 始片 或任 暂意 停处
• 轨迹:
M 是半径为 a 的母圆上的动点 , 满足 OM = PQ 之点 P 的轨迹即为 蔓叶线 • 渐近线:
• 曲线与渐近线之间的面积:
结束
笛卡儿叶形线 3at x 1 t3 2 3at y 1 t3
动点 画击 开图 始中 或任 暂意 停点
t 1
参数的几何意义: t tan
t (,1) ( , ) 2 4
t (1, 0] ( 34 , ]
图形在第四象限 图形在第二象限
动画走向: -∞→-1 -1→+∞
t [0 , ) [0 , ) 2
结束
对数螺线 (等角螺线) r e a
• 等角性 : 曲线与所有过极点的射线
A 1
o
A1 A0 A2
的交角 都相等:
• 等比性: 过极点的射线与曲线交于 成等比级数, 公比为
M
M 2x
M1
动点 画击 开图 始中 或任 暂意 停点
, A1 , A0 , A1 , 则 , OA 1 , OA0 , OA1 , 各线段
m = 1为心形线
m2
m3
m4
m3 2
m5
结束
阿基米德螺线
r a
a0
a0
• 物理意义: 动点 M 以常速 v 沿一射线运动, 该射线又 以定速 绕极点转动时, 点M 的轨迹即为 阿基米德螺线 v r
结束
阿基米德螺线(续)
• 等距性: 过极点的射线与曲线
交于 A1 , A2 , A3 ,,
• 轨迹: 半径为 a 的圆周沿直线 无滑动地滚动时 , 其上
y M
o
a
x
定点 M 的轨迹即为摆线 .
点击图中任意点动画开始或暂停
结束
摆线(续)
•周
x a( sin ) y a(1 cos )
y M
期: T 2 a
o
t a
x1
2 a x
• 极大点: xk (2k 1) a (k 1, 2 ,)
B D
C
A
a
• 极值点:
极 值:
对应点:
• 曲率半径:
• 双纽面积:
点击图中任意点 动画开始或暂停
结束
三叶玫瑰线
a
a
点击图中任意点 动画开始或暂停
结束
四叶玫瑰线
a
a
点击图中任意点 动画开始或暂停
结束
• 弧长 :
• 曲率半径 :
动画走向为
结束
双曲螺线 r a
• 曲线由两支组成 , 它们关于 y 轴对称 • 渐近点 : 极点 O
y a M 2
M1
o
1 2
x
( ) • 渐近线 : y a a • 曲率半径 : R
动点 画击 开图 始中 或任 暂意 停点
3
11 12
它们之间的间隔都是
M2 M 1 A2A3 A1 M o
x
2 a • 弧 长 : LOM a ( 2 1 arsh ) 2
其中arsh ln( 1 2 )
• 曲率半径 : R a
3 ( 2 1) 2
2 2
2 • 扇形 M 1O M 2 的面积 : S 1 a 2 ( 1 2 ) 2 6
t • 曲率半径: R 4 a sin 2
• 一拱长:
8a • 一拱面积: S 3 a 2
• 渐屈线: 仍为摆线
y
M
在 o 坐标系下
与原摆线一致
o
a
o
2 a
x
结束
心形线
y
x y ax a x y 或 r a(1 cos )
2
2
2
2
o
x
限
结束
笛卡儿叶形线(续)
y A
x
3at3 1 t
3at 1 t 3
2
t 1
y
• 结点:
a o a
x
在该点与 x 轴 y 轴相切, 曲率半径为 • 顶点:
• 渐近线: • 圈套所围面积:
• 曲线与渐近线之间的面积:
结束
摆线
x a( sin ) y a(1 cos )
附录Ⅱ 重要平面曲线
(1) 三次抛物线 (3) 概率曲线 (2) 半立方抛物线 (4) 箕舌线 (7) 星形线 (10) 双曲螺线
(5) 蔓叶线 (8) 摆线
(11) 对数螺线
(6) 笛卡儿叶形线
(9) 心形线
(12) 阿基米德螺线 (13) 伯努利双纽线 (14) 三叶玫瑰线 (15) 四叶玫瑰线
• 与 x 轴之间的面积: 1
结束
箕舌线
• 轨迹 : M是直径为a 的圆上的动点,
或
y a
t
Q是射线OM与 y = a 的交点,
QP⊥x 轴 , MP∥x 轴 P点轨迹即为箕舌线 .
x
o
• 渐近线: y = 0 • 曲线与渐近线之间的面积:
点击图中任意点 动画开始或暂停
结束
蔓叶线
y
Q
或
(t tan )
结束
三次抛物线
y
半立方抛物线
y
x
x
• 拐点: (0, 0) • 关于原点对称
• 尖点: (0, 0) • 在尖点处与 x 轴相切 • 关于 x 轴对称
结束
概率曲线
A
y
B
x
• 拐点: • 拐点处切线斜率:
• 渐近线: • 与 x 轴之间的面积:
• 关于 y 轴对称
设 服从标准正态分布 , 则其概率密度函数为 1 x22 f ( x) e 2 • 拐点:
F2
P o F1
a 2
x
OF1 OF2
• 双纽线上的点 M 满足 : MF1 MF2
2
1 a2 2
• 以 F1 为圆心 , 1 a 为半径作圆, 自O 作射线交圆于P, Q 则双纽线右支上的点满足 : OM PQ 由对称性 , 左支也有类似结果
结束
伯努利双纽线 即 • 结点(同拐点) : 在该点的切线为 x , y 轴 • 顶点:
a
x
• 面积:
3 a2 2
• 弧长: 8a
结束
x (a b) cos t b cos ab t b 外摆线 (圆外旋轮线) 族 y (a b) sin t b sin ab t b 定圆圆心为 (0,0), 半径为 a, 动圆半径为 b, m b a
动点 画击 开图 始中 或任 暂意 停点
动圆直径 = 定圆直径 = a • 尖点: (0, 0)
点击图中任意点 动画开始或暂停
3 a2 • 面积: 2
• 弧长: 8a
结束
心形线的另一种形式
x2 y2 a x a x2 y2
即 r a(1 cos )
y
点击图中任意点 动画开始或暂停
o
• 尖点: (0, 0)
结束
• 扇形 M1O M 2 的面积 :
S
动画走向为
a2 2
伯努利双纽线
或 • 结点(同拐点) : 在该点的切线斜率为±1 •顶 点:
B D D y
C
o
C
A x
• 极值点:
极 值: 对应点: • 曲率半径: • 双纽面积:
点击图中任意点 动画开始或暂停
结束
伯努利双纽线的轨迹特点 y
M Q
