套代数上的非线性三元Lie导子
导子 约当导子 全可导点 约当全可导点 可导线性映射 内导子 矩阵代数 上三角代数

导子论文:导子和约当导子的局部特征【中文摘要】最近几年来,算子代数中导子的特征的刻画逐步成为算子代数领域中的活跃分支,取得了不少的研究成果。
1990年,rson和R.V.Kadison各自独立地提出了局部导子的概念,Larson证明了Banach空间X的算子空间上的局部导子是导子,Kadison得到了Von Neumann代数上的每个范数拓扑连续的局部导子为导子。
张建华证明了在上三角代数中所有的约当导子都是内导子。
后来,荆武、鲁世杰和李鹏同得到了Nest代数中每一个在O点处可导的线性映射(?)((?)(I)=0)是个内导子;朱军和熊昌萍证明了有限CSL代数上每一个在0点处关于范数拓扑连续广义可导的线性映射是个广义导子以及套代数中每一个在单位算子I点处关于强算子拓扑连续可导的线性映射是个内导子(即单位算子I是套代数中的关于强算子拓扑连续的全可导点)。
陆芳言得到了在Banach空间中每一个幂等元都是全可导点。
最近,朱军等人又证明了:(1)任意一个元素G 是上三角矩阵代数的一个全可导点当且仅当G≠0;(2)任意一个矩阵G是n×n矩阵代数中的一个全可导点当且仅当G≠O。
2007年安润玲和侯晋川证明了在上三角代数中一些幂等元是约当全可导点,然后次...【英文摘要】In recent years there has been considerable interest in studying which linear mapping on operator algebras are derivations, and we have obtained a lot of results. In 1990,the notion of local derivations was introduced independently by D. R. Larson and R. V. Kadison. Larson proved that every local derivation on B(H) is a derivation, where X is a Banach space, Kadison proved that every norm-continuous local derivation on a von Neumann algebra is a derivation. Zhang Jianhua showed that every Jordan derivable ...【关键词】导子约当导子全可导点约当全可导点可导线性映射内导子矩阵代数上三角代数【英文关键词】derivation Jordan derivation all-derivable point Jordan all-derivable point derivative linear mapping inner derivation the matrices algebra the triangular algebra 【索购全文】联系Q1:138113721 Q2:139938848【目录】导子和约当导子的局部特征摘要5-7ABSTRACT7-8第1章绪论10-14 1.1 一些记号与定义10 1.2 导子的国内外研究现状10-13 1.3 本文的内容及研究的目的和意义13-14第2章三角矩阵的全可导点和约当全可导点一些结论14-31 2.1 定理及其证明14-30 2.2 本章小结30-31第3章三角矩阵中的所有约当可导点31-58 3.1 引理及其证明31-55 3.2 上三角矩阵上的所有约当全可导点55-57 3.3 本章小结57-58致谢58-59参考文献59-62附录62在读期间发表的学术论文62参加的科研项目62。
套代数上的零点σ-可导映射

P+:i { n Q∈Ⅳ Q>P}P一:s Q∈Ⅳ:Q< 。 f : , u p{ P} 如果 一个 套 中至少 包 含一 个非 平凡 投影 , 称 这个 套 为非平 凡套 。若 P是一 个投 影 , 则 我们 令 P , :
一
P。相 应于套 Ⅳ 的套 代数 记 为 ( , 定 义 为 Ⅳ)并 ( N):{ T∈B( :P P: VP∈N} H) T 0, 。 如果 Ⅳ是一 个套 , 么 N 那 :{ P :P∈N} 为一 个 套 , 也 并且 ( Ⅳ ): Ⅳ) 。vnN u an代 数 ( o em n ( n Ⅳ) 称为 ( 的对角 , 为 D( 。R( 表 示 由 { T :P∈N, Ⅳ) ( ’ Ⅳ) 记 Ⅳ) Ⅳ) PP T∈B( } 成 的范 数 闭 H) 生
的代 数 。
定义 1 1 设 A是一个 代 数 , 是从 A到其 自身 的线 性 映射 , 是 A上 的一 个 自同构 。 . r o
() 1 如果对 任 意 的 A, B∈A, 4( B ( +o( ) B) 则称 咖是 A上 的一个 o一导 子 。 有 " A ): ) r a 咖( , r
性 映射 , 则存 在一 个可逆 元 丁 Ⅳ) A∈C 使得 对 任 意 的 A∈丁 Ⅳ) 有 6 A)= ( ( 和 ( 都 ( A)+A , 中 为 其
一
个 一导子 。
磁四极透镜的Lie代数分析――三级近似

收稿日期:1998209206;修回日期:1998212216作者简介:吕建钦(1946—),男,山东巨野人,教授,加速器物理及应用专业 第34卷第3期原子能科学技术Vol.34,No.3 2000年5月Atomic Energy Science and TechnologyMay 2000磁四极透镜的Lie 代数分析———三级近似吕建钦(北京大学重离子物理研究所,北京 100871)摘要:用Lie 代数方法分析了带电粒子在四极透镜中的运动,得到六维相空间中粒子轨迹的三级近似解,并包含了运动的相对论效应。
当需要时,还可以扩展到更高级像差。
关键词:Lie 映射;四极透镜;三级近似中图分类号:O15215 文献标识码:A 文章编号:100026931(2000)0320228210A 1J 1Dragt [1]曾用Lie 代数方法分析了四极透镜中的像差,但没有给出详细结果;K 1L 1Brown [2]直接求解非相对论粒子运动的微分方程,导出其二级近似解,但不包含纵向运动的二级近似项,而且其一级纵向运动分量是指路径差,而不是脉冲长度。
用Lie 代数方法可导出六维相空间中相对论粒子在四极透镜中的三级轨迹,在其中的纵向相空间中,得到的是脉冲束长度。
当带电粒子在束流传输系统中运动时,它在六维相空间中的初始坐标与最终坐标可由辛映射M 相联系。
此映射又可以用一系列Lie 变换的乘积表示。
将映射M 作用于粒子的初始坐标,并取一定的近似,就可得到粒子轨迹的一级、二级和三级…近似。
这一过程就是Lie 代数分析方法。
1 Lie 算符与Lie 变换设ζ=(q ,p )为六维相空间中的一组坐标变量。
当带电粒子在电磁场中从初始位置0运动到最终位置f 时,粒子的初始坐标ζ与最终坐标ζf之间的关系可用下式表示:ζfj =∑kR j ,k ζk+∑klS j ,k ,l ζk ζl+∑klmTj ,k ,l ,m ζk ζl ζm+…(1)其中:R 表示一级传输矩阵,S 和T 分别表示二级和三级像差系数…。
【国家自然科学基金】_jordan代数_基金支持热词逐年推荐_【万方软件创新助手】_20140729
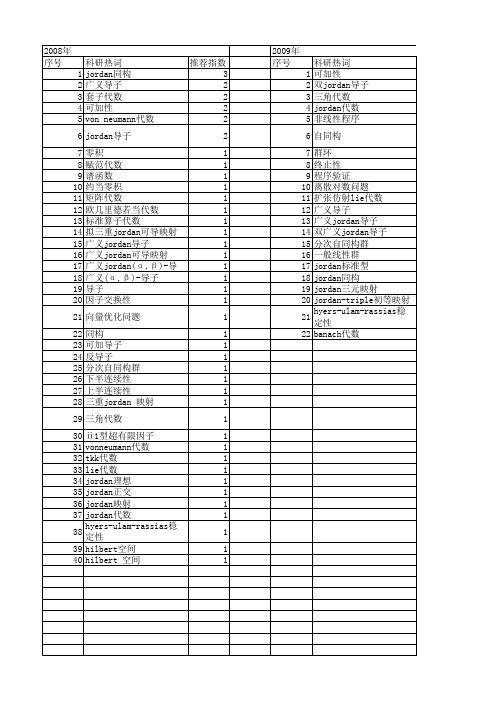
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 推荐指数 同构 3 标准算子代数 2 半*-jordan积 2 邻域跟踪算法 1 线性映射 1 广义jordan triple可导映射 1 对称锥规划 1 宽邻域 1 多项式复杂性 1 内点法 1 vorl 1 von neumann代数 1 neumann代数 1 jordan同构 1 euclid jordan代数 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2011年 科研热词 推荐指数 三角代数 5 零点jordan可导 2 自伴算子空间 2 广义高阶导子 2 von neumann代数 2 自jordan积 1 线性映射 1 矩阵的秩 1 广义高阶jordan导子 1 广义约当高阶导子 1 幂零矩阵 1 导子系 1 导子 1 实对称矩阵代数 1 完全分配csl代数 1 保持映射 1 中心化子 1 ⅰ点jordan可导 1 φ )-导子 1 lie中心化子 1 jordan积 1 jordan标准形 1 jordan映射 1 jordan导子系 1 jordan可导映射 1 jordan中心化子 1 jordan(θ 1 i点jordan可导 1 hyers-ulam-rassias稳定性 1 euclidean jordan代数 1 (θ 1
2014年 序号 1 2 3 4 5 6 7 8 9 10
2014年 科研热词 推荐指数 双线性映射 2 零积决定的代数 1 零积 1 完备jordan李超代数 1 单位积决定的代数 1 分解唯一性 1 不可分解jordan李超代数 1 l的l-自同态 1 jordan零积 1 jordan李超代数 1
三元数及其在实数域上三维代数

三元数及其在实数域上三维代数
夏新念
【期刊名称】《武汉工程大学学报》
【年(卷),期】2004(026)002
【摘要】三元数系是建立在实数域上的三维代数,与普通的多维代数不同,它的乘法运算不满足群的规则.针对此问题,需要重新制定其运算规则.在建立三元数与向量之间的联系之后,提出三元数的乘法在几何上对应于空间向量的旋转.通过正交分解,将两个三元数的乘法先分解成两个同构关系,然后引进两类不同的群,再按各自群的规则分别进行计算.亦即将不满足群规则的两个三元数的乘法计算转化成在群的规则下的运算,初步证实三元数系的存在.
【总页数】3页(P80-82)
【作者】夏新念
【作者单位】武汉化工学院机械工程学院,湖北,武汉,430073
【正文语种】中文
【中图分类】O153
【相关文献】
1.n元数与实数域上的可除代数 [J], 高煦;顾沛;周迈
2.实数域R上n+1维n-Lie代数的内导子代数 [J], 白瑞蒲;安宏伟
3.用实数卷积计算代数数域上整数卷积 [J], 张起帆
4.实数域上三维李双代数的Atiyah class [J], 申丹丹; 乔雨
5.实数域R上的无穷级数的基本代数系统 [J], 冯蕴珍;陈荣庭
因版权原因,仅展示原文概要,查看原文内容请购买。
可换环上矩阵代数的三重导子

数 。对 M R)上 的一个 线性 变换 , 任意 的 , ( 对 y Z ∈ M R),都 有 ( Z) = ( Y + , ( XY X) Z () Y Z+
子。
2 …, , n—t.其 中 为 X 单 位矩 阵 。如 果 r=
0, D 令 = da ( 2 … , ). ig E ,E ,
( z), 则称 为 ( 上 的三 重导 )
下 面给 出 M, R)的标 准三重 导子 。 , (
() 1 内导 子
本 文决 定 了含 幺可 换环 矩 阵代 数 的所 有 三
文章编号
10 5 6 (0 1 0 一 04— 3 0 0— 29 2 1 ) l 0 1 0
可 换 环 上 矩 阵代 数 的 三 重 导 子
孔 祥 源 ,李娜 娜 ,周 丽 丽
( 国矿 业 大 学 理学 院 ,江 苏 徐 州 2 10 ) 中 2 0 8
摘
要 : 文研 究 了可换 环 上矩 阵代 数 的三 重 导 子 , 本 通过 构 造 特 殊 矩 阵并 利 用这 些矩 阵进 行运
第2 8卷 第 t期
21 0 1年 2月
贵 州 大学 学 t N tr c ne) ora o G i uU i sy( aua S i cs h ei l e
Vo . 2 . 1 1 8 No Fe b. 2 01l
近年来 , 于 导 子 的研 究 备 受 关 注 , 献 关 文 分 别给 出 了可换环 上 一 些 矩 阵李 代 数 和一 般 线 性 李 代数 的抛 物 子 代 数 以 及 上 三 角 矩 阵环 的导 子 。 C R b  ̄Mi s 首 先将 导 子 的 概 念加 以推 广 , . oe e r 决 定 了 V nN u n o eman代 数 的 李 三 导 子 , 后 , 培 之 纪 胜 和张建 华 分 别 给 出 了套 代 数 和 T H U F代 数 上 的李 三导子 , 近 , 最 王恒 太 又 刻 画 了可 换 环 上 严 格上三 角矩 阵 李代 数 的李 三 导子 。本 文 将 研 究
套子代数上的零点可导映射
线性映射. 主要证 明了: 如果 在零点可导 , 么存 在导子 6 ag 一 M和 A ∈C, 那 :l 使得对任意 的 A∈ a lJ gB
有 ( A)=8 A)+A . ( A 关键词 : 零点可导 ; o e m n vnN u an代数 ; 子代数 套
中图 分 类 号 : 17 1 07. 文献标识码 : A 文 章 编 号 :0 1 3 5 2 0 )50 3 -3 10 — 9 (0 8 0 -5 80 8
S t 2 08 ep., 0 V0 . 1 31. . No 5
套 子 代数 上 的零 点 可导 映 射
李红 霞
( 西南科技大学 理学 院,四川 绵 阳 6 1 1 n 设B O eman代数 M中的任意一个套 ,l I ag卢是相应 的套 子代数 , a 一 M是一个 :l g
的和 , 多 5个幂 等算子 的和 以及 有 限 多个 投 影 的 最 线 性组合 . 引理 13l 套 代数 的换 位是 平凡 的 , . O ] 即套代
子代 数上 的零点 广义 可 导 映射 , 外 文 [ ] 明 了 另 6 证 有 限套代 数 上 的按 范数 连 续 的 在 零 点广 义 可 导 的 线性 映 射是 广义 导 子. 由于 套代 数 和 vnN u n o eman 代数 中的套子 代数 有着根本 的区别 , 如套 代数 包含 丰 富的结 构 清晰 的 一秩算 子 , 一 般 vnN u n 但 o eman
1 定 义 及 引理
定 义 1 1 设 是 一代数 , . 是 一 彩 双边 模 , : 6
一
套子 代数 ag 的对 角代 数 ( 为 vnN u a n l 卢) o em n
代数 ag卢 n a 由 { P) T ∈ M, ∈ } lM l / . P ( g3 : P
《(2+1)-维非线性薛定谔方程组的Lie对称、一维优化系统及约化》范文
《(2+1)-维非线性薛定谔方程组的Lie对称、一维优化系统及约化》篇一摘要本文将讨论(2+1)-维非线性薛定谔方程组的Lie对称性、一维优化系统及其约化方法。
我们将详细探讨如何通过Lie对称性分析非线性系统,并通过一维优化系统寻找最佳的解决方案。
同时,我们也将探讨约化方法如何帮助简化复杂的高阶偏微分方程,以得到更易于处理的低阶或一维系统。
一、引言(2+1)-维非线性薛定谔方程组在物理学中具有广泛的应用,如流体动力学、光学和量子力学等领域。
然而,由于高阶非线性项的存在,这些方程往往非常复杂且难以解决。
因此,我们需要找到有效的分析方法,以理解其动力学行为并寻求其解决方案。
本文将主要关注以下三个方面:(2+1)-维非线性薛定谔方程组的Lie对称性、一维优化系统以及约化方法。
二、(2+1)-维非线性薛定谔方程组的Lie对称性Lie对称性是一种有效的工具,用于研究非线性系统的动力学行为。
我们可以通过构建Lie代数,研究(2+1)-维非线性薛定谔方程组的对称性。
具体来说,我们将利用Lie群理论中的变换和代数结构,寻找能够使方程组保持不变的变换。
这将有助于我们更好地理解方程组的性质和动力学行为。
三、一维优化系统一维优化系统是一种用于寻找最优解的数学模型。
我们将利用一维优化系统来寻找(2+1)-维非线性薛定谔方程组的最佳解决方案。
我们将建立相应的数学模型,并根据具体问题的需求设计适当的算法。
这将帮助我们快速找到问题的最优解,并确保其准确性和有效性。
四、约化方法为了简化高阶偏微分方程的求解过程,我们可以采用约化方法。
通过适当的变换和简化过程,将高阶或多维问题转化为低阶或一维问题。
这可以大大降低求解的复杂度,使问题更易于处理。
我们将探讨不同类型的约化方法,如变换法、摄动法等,并给出具体的应用示例。
五、案例分析本部分将通过具体案例来展示(2+1)-维非线性薛定谔方程组的Lie对称性、一维优化系统及约化的应用。
我们将选取典型的非线性薛定谔方程,分析其Lie对称性;利用一维优化系统来寻找最佳的初始条件或参数设置;通过应用不同的约化方法来简化问题的求解过程,并给出求解结果的验证和评估。
δ-李超三系线性变换构成的六类代数
δ-李超三系线性变换构成的六类代数邢晋;牛艳君;陈良云【摘要】We considered six types of algebras generated by linear transformations of a δ-Lie supertriple system T:the derivation algebraDer(T),the quasiderivation algebra QDer(T),the generalized derivation algebra GDer(T),the central derivation algebra ZDer(T),the centroid algebra C(T),and the quasicentroid algebra QC(T).We first proved that ZDer(T) was an ideal of Der(T) and ZDer(T)(≤)Der(T)(≤)QDer(T)(≤)GDer(T)(≤)End(T),then obtained that[Der(T),C(T)](≤)C(T),[QDer(T),QC(T)](≤)QC(T),[QC(T),QC(T)](≤)QDer(T),QDer( T)+QC(T)=GDer(T) and [C(T),QC(T)](≤)End(T,Z(T)).Moreover,we proved that if a δ-Lie supertriple system was decomposable,then its generalized derivation algebra,quasiderivation algebra,centroid algebra,and quasicentroid algebra also had corresponding decomposition,respectively.%考虑δ-李超三系T线性变换构成的六类代数:导子代数Der(T)、拟导子代数QDer(T)、广义导子代数GDer(T)、中心导子代数ZDer(T)、型心代数C(T)、拟型心代数QC(T).证明ZDer(T)是Der(T)的理想,且ZDer(T)(≤)Der(T)(≤)QDer(T)(≤)GDer(T)(≤)End(T),得到了[Der(T),C(T)](≤)C(T),[QDer(T),QC(T)](≤)QC(T),[QC(T),QC(T)](≤)QDer(T),QDer( T)+QC(T)=GDer(T),[C(T),QC(T)](≤)End(T,Z(T)).同时,证明一个δ-李超三系若是可分解的,则它的广义导子代数、拟导子代数、型心代数和拟型心代数也有相应的分解.【期刊名称】《吉林大学学报(理学版)》【年(卷),期】2017(055)004【总页数】7页(P784-790)【关键词】李超三系;δ-李超三系;广义导子;拟型心【作者】邢晋;牛艳君;陈良云【作者单位】长春广播电视大学财经系,长春 130051;长春工程学院理学院,长春130012;东北师范大学数学与统计学院,长春 130024【正文语种】中文【中图分类】O152.5李三系[1]可视为关于三元括积封闭的李代数的子空间, 其在几何、物理和量子力学中应用广泛[2], 例如: 对称空间的切代数是一个李三系;李三系是李代数和Jordan代数之间的桥梁[1,3]; 李三系的研究方法和结论已被用于Jordan代数的研究中[1,4]. 目前,在Yang-Baxter方程的研究中已引进了李超三系的概念[5-6],李超三系作为李三系的推广, 已成为研究物理系统的有效工具. 关于李超三系的研究已有许多结果[7-14]. 特别地, 文献[5]利用李超三系得出了Yang-Baxter方程的一些新解和一个简单解, 即Yang-Baxter方程可以简化为一个三元乘法关系. 文献[15]给出了δ-李超三系的概念, 当δ=1时, δ-李超三系即为李超三系. 又由于李超代数都可以视为一个特殊的李超三系, 因此δ-李超三系比李超代数和李超三系更广泛, 它与Jordan李三系、李三系、 Freudenthal-Kantor三系、 Jordan李超三系、 Freudenthal-Kantor李超三系、 Jordan李超三系和李超三系等代数关系密切[16].积[,,]:1) d([x,y,z])≡(d(x)+d(y)+d(z))(mod 2);2) [x,y,z]=-(-1)xy[y,x,z];3) (-1)d(x)d(z)[x,y,z]+(-1)d(y)d(x)[y,z,x]+(-1)d(z)d(y)[z,x,y]=0;4) [u,v,[x,y,z]]=[[u,v,x],y,z]+(-1)d(u+v)d(x)[x,[u,v,y],z]+(-1)d(u+v)d(x+y)[x,y,[u,v,z]], ∀x,y,z,u,v∈T.本文定义d(x)为d(x).定义2[17] 设⊕为一个超代数, 其乘法记为[,], 即∀α,β∈Z2, [Lα,Lβ]⊆Lα+β. 如果其乘法满足下列等式:1) [a,b]=-(-1)d(a)d(b)[b,a];2) [a,[b,c]]=[[a,b],c]+(-1)d(a)d(b)[b,[a,c]], ∀a,b,c∈L.则称L为李超代数.注1 设L是李超代数(李代数), 由[x,y,z]=[[x,y],z](∀x,y,z∈T)引入一个三元乘法[x,y,z], 则L成为一个李超三系(李三系). 所以在这种意义下每个李超代数(李代数)都是一个李超三系(李三系). 一般地, 李代数的许多重要性质对李超代数不成立, 例如: 李代数的李定理和\%Levi\%定理对李超代数一般都不成立. 同理, 李三系的许多重要性质对李超三系也不一定成立.定义3[15] 设L是Z2-阶化向量空间, 即⊕若二元线性运算[·,·]: L⊗L→L满足:1) d([x,y])≡(d(x)+d(y))(mod 2);2) [y,x]=-δ(-1)d(x)d(y)[x,y];3) (-1)d(x)d(z)[[x,y],z]+(-1)d(y)d(x)[[y,z],x]+(-1)d(z)d(y)[[z,x],y]=0,∀x,y,z,u,v∈L.则称L是δ-李超代数. 显然, 当δ=1时, δ-李超代数是李超代数.三元括积[,,]:1) d([x,y,z])≡(d(x)+d(y)+d(z))(mod 2);2) [x,y,z]=-δ(-1)xy[y,x,z];3) (-1)d(x)d(z)[x,y,z]+(-1)d(y)d(x)[y,z,x]+(-1)d(z)d(y)[z,x,y]=0;4) [u,v,[x,y,z]]=[[u,v,x],y,z]+(-1)d(u+v)d(x)[x,[u,v,y],z]+δ(-1)d(u+v)d(x+y)[x,y[u,v,z]], ∀x,y,z,u,v∈T, δ=±1.注2 1) 由定义1和定义4可知, 当δ=1时, δ-李超三系即为李超三系. 设L是δ-李超代数(李代数), 由[x,y,z]=[[x,y],z](∀x,y,z∈L)引入一个三元乘法[x,y,z], 则L成为一个δ-李超三系(李三系). 所以在这种意义下每个δ-李超代数(李代数)都是一个δ-李超三系(李三系), 所以δ-李超三系是比δ-李超代数和李超三系更广泛的代数. 2) 对任意一个δ-李超三系T, 均可视为一个δ-李超代数的子空间. 事实上, 令Ls(T)=InnDer(T)⊕T, 其中T. 按照运算其中:x1,x2∈T; D1,D2∈InnDer(T). 直接验证可知Ls(T)构成δ-李超代数.定义5 设T是一个δ-李超三系, 若[S,S,S]⊆S, 则T的子空间S称为L的子系; 若[I,T,T]⊆I, 则T的子系I称为T的理想; 若[I,T,T]=0, 则称I为T的交换理想. 设I是T的非空子集. 令(a,x)=0, ∀a∈I}, 其中R(a,x)z=(-1)d(z)(d(a)+d(x))[z,a,x], 则ZT(I) 称为I在T中的中心化子. 特别地,称为T的中心, 记作Z(T).定义6 设T是域F上δ-李超三系. 如果T的齐次线性映射D: T→T满足则称D为T的k-导子. 记d(D)为齐次线性映射D的Z2-阶化次数, T的所有k-导子的集合为Derk(T).引理1 设任意D∈Derk(T), D′∈Ders(T), 满足[D,D′]=DD′-(-1)d(D)d(D′)D′D, 则[D,D′]∈Derk+s(T).证明: ∀x,y,z∈T, 有即[D,D′]∈Derk+s(T)成立. 证毕.令(T), 由引理1知Der(T)是李超代数, 因此Der(T)是End(T)子代数, 称为T的导子代数.定义7 设T是δ-李超三系, 若存在D,D′,D″,D‴∈E nd(T), 它们的次数相同, 且满足则D∈End(T)称为T的k-阶广义导子. 记T的广义导子集合构成的代数为GDer(T)(T).定义8 设T是δ-李超三系, 若存在D,D′∈End(T), 它们的次数相同, 且满足则D∈End(T)称为k-阶拟导子. 记T的拟导子集合构成的代数为QDer(T)(T).定义9 设T是δ-李超三系, 若∀x,y,z∈T, 有则Ck(T)称为T的k-阶型心. 记T的型心集合构成的代数为C(T)(T).定义10 设T是δ-李超三系, 若∀x,y,z∈T, 有则QC(T)称为T的拟型心代数.定义11 设T是δ-李超三系, 若则ZDer(T)称为T的中心导子代数.定理1 设T是δ-李超三系, 则下列结论成立:1) GDer(T), QGer(T)和C(T)是End(T)的子代数;2) ZDer(T)是Der(T)的理想;3) ZDer(T)⊆Der(T)⊆QDer(T)⊆GDer(T)⊆End(T).证明: 1) 设D1∈GDerk(T), D2∈GDers(T). 用类似引理1的证明可得[D1,D2]∈Ck+s(T), 因此C(T)是End(T)的子代数.2) 设D1∈ZDer(T), D2∈Derk(T), 则∀x,y,z∈T, 有由广义导子和中心导子的定义得故[D1,D2]∈ZDer(T), 因此ZDer(T)是Der(T)的理想.3) 根据定义直接验证即可.定理2 设T是δ-李超三系, 则下列结论成立:1) [Der(T),C(T)]⊆C(T); 2) [QDer(T),QC(T)]⊆QC(T); 3) D(Der(T))⊆Der(T), ∀D∈C(T); 4) QC(T)⊆QDer(T); 5) [QC(T),QC(T)]⊆QDer(T); 6)QDer(T)+QC(T)=GDer(T).证明: 1) 设D1∈Derk(T), D2∈Cs(T), 则∀x,y,z∈T, 有从而且故同理因此[D1,D2]∈Ck+s(T), 即[Der(T),C(T)]⊆C(T).2) 类似1)的证明.3) 设D1∈Ck(T), D2∈Ders(T), 则∀x,y,z∈T, 有因此D1D2∈Derk+s(T).4) 设D∈QC(T). 则∀x,y,z∈T, 有存在k使得令D′=3δkD∈End(T), 则D∈QDer(T).5) 设D1,D2∈QC(T), 则∀x,y,z∈T, 有且因此故[D1,D2]∈QDer(T).6) 易见QDer(T)+QC(T)⊆GDer(T). 另一方面, 若D∈GDerk(T), 则存在D′,D″,D‴∈End(T)且∀x,y,z∈T, d(D)=d(D′)=d(D″)=d(D‴), 使得则进而故D′∈GDerk(T). 由[式(1)+式(2)]/2得且故从而进而可得即(T).推论1 设T是δ-李超三系, 若T有平凡中心, 则C(T)是GDer(L)的交换子代数. 证明: 由定理2知C(T)是GDer(T)的子代数, 且D1∈Ck(T), D2∈Cs(T), x,y,z∈T, 则故[(D1D2(-1)d(D1)d(D2)D2D1)(x),y,z]=0. 又T中心为0, 则[D1,D2](x)=0. 由x 的任意性可得[D1,D2]=0. 故结论成立.推论2 设T是δ-李超三系, 则QC(T)+[QC(T),QC(T)]是GDer(T)的子代数.证明: 由定理2中5),6), 得QC(T)+[QC(T),QC(T)]⊆GDer(T), 且由李超代数的阶化Jacobi恒等式, 易证[QDer(L),[QC(L),QC(L)]]⊆[QC(L),QC(L)]. 因而故结论成立.引理2 1) 设T是δ-李超三系, I是T的理想, 则ZT(I)是T的理想; 特别地,Z(T)=ZT(T)与Z(I)=ZI(I)是T的理想;2) 设T是δ-李超三系, 且T可分解为两个理想的直和, 即T=A⊕B, 则Z(T)=Z(A)⊕Z(B);3) 若Z(T)=0, 则Der(T)=Der(A)⊕Der(B).证明: 证明类似文献[10]中李超三系的证明, 故略.定理3 设δ-李超三系T可分解为两个理想的直和, 且T有平凡中心, 即T=A⊕B且Z(T)=0, 则下列结论成立:1) GDer(T)=GDer(A)⊕GDer(B);2) QDer(T)=QDer(A)⊕QDer(B);3) C(T)=C(A)⊕C(B);4) QC(T)=QC(A)⊕QC(B).证明: 1) 设D′∈GDerk(A), 将其扩张为T上的线性变换, 并令D′(a+b)=D′(a),∀a∈A, b∈B. 显然, D′∈GDerk(T), GDer(A)⊆GDer(T). 同理GDer(B)⊆GDer(T). 设a∈A, b1,b2∈B, D∈Derk(T), 则设D(a)=a′+b′, 其中a′∈A, b′∈B, 则0=[D(a),b1,b2]=[a′,b1,b2]+[b′,b1,b2]. 故[b′,b1,b2]=0, b′∈Z(B). 由引理2知Z(T)=Z(A)⊕Z(B)且b′=0. 因此D(a)=a′∈A, 即D(A)⊆A. 同理D(B)⊆B.设D∈GDer(T), x=a+b∈A+B, 其中a∈A, b∈B. 定义E,F∈End(T)为E(a+b)=D(a), F(a+b)=D(b), 则E∈GDer(A), F∈GDer(B). 故D=E+F∈GDer(A)+GDer(B). 又GDer(A)∩Ger(B)={0}, 因而作为子空间,GDer(T)=GDer(A)GDer(B).设E∈GDer(A), F∈GDer(B), b∈B. 则[E,D]=(ED-(-1)d(D)d(E)DE)(b)=0. 因此[E,D]∈GDer(A), GDer(A)◁GDer(T). 同理GDer(B)◁GDer(T).2)~4)的证明方法类似1), 故略.定理4 设T是δ-李超三系, 则[C(T),QC(T)]⊆End(T,Z(T)). 特别地, 若Z(T)={0}, 则[C(T),QC(T)]={0}.证明: 设D1∈Ck(T), D2∈QC(T), 则∀x,y,z∈T, 有因此[D1,D2](x)∈Z(T), 进而[D1,D2]∈End(T,Z(T)). 若Z(T)={0}, 则[C(T),QC(T)]={0}.【相关文献】[1] Jacobson N. Lie and Jordan Triple Systems [J]. Amer J Math, 1949, 71(1): 149-170.[2] Okubo S. Triple Products and Yang-Baxter Equation.Ⅱ.Orthogonal and Symplectic Ternary Systems [J]. J Math Phys, 1993, 34: 3292-3315.[3] Bars I, Gündaydin M. Construction of Lie Algebras and Lie Superalgebras from Ternary Algeras [J]. J Math Phys, 1997, 20(9): 1977-1993.[4] Lister W G. A Structure Theory of Lie Triple Systems [J]. Trans Amer Math Soc, 1952, 72(2): 217-242.[5] Okubo S. Parastatistics as Lie-Supertriple Systems [J]. J Math Phys, 1994, 35(6): 2785-2803.[6] Okubo S, Kamiya N. Quasi-classical Lie Superalgebras and Lie Supertriple Systems [J]. Comm Alg, 2002, 30(8): 3825-3850.[7] 林洁, 陈良云, 杨吉. 一类李超三系的构造 [J]. 东北师大学报(自然科学版), 2009, 41(1): 6-9. (LIN Jie, CHEN Liangyun, YANG Ji. A Constitution of Lie Supertriple Systems [J]. Journal of Northeast Normal University (Natural Science Edition), 2009, 41(1): 6-9.)[8] 林洁, 陈良云, 汪金燕. 关于可解李超三系 [J]. 数学年刊A辑(中文版), 2009, 30(4): 505-516. (LIN Jie, CHEN Liangyun, WANG Jinyan. Solvable Lie Triple Supersystems [J]. Chinese Ann Math (Ser A), 2009, 30(4): 505-516.)[9] 马瑶, 陈良云, 刘东. 李超三系的广义导子 [J]. 数学学报(中文版), 2013, 56(6): 961-970. (MA Yao, CHEN Liangyun, LIU Dong. On Generalized Derivations of Lie Supertriple Systems [J]. Acta Math Sin (Chin Ser), 2013, 56(6): 961-970.)[10] 潘玉霞, 张庆成. 李超三系的分解唯一性 [J]. 数学物理学报, 2008, 28A(6): 1058-1066. (PAN Yuxia, ZHANG Qingcheng. The Uniqueness of the Decomposition of Lie Supertriple Systems [J]. Acta Math Sci, 2008, 28A(6): 1058-1066.)[11] PENG Jianrong, CHEN Liangyun, SUN Bing. Centroids of Lie Supertriple Systems [J]. Adv Math Phys, 2015, 2015: 949046.[12] 宋华, 周佳, 陈良云. c-可补李超三系和E-李超三系 [J]. 吉林大学学报(理学版), 2012, 50(4): 681-685. (SONG Hua, ZHOU Jia, CHEN Liangyun. c-Supplemented Lie Supertriple Systems and E-Lie Supertriple Systems [J]. Journal of Jilin University (Science Edition), 2012, 50(4): 681-685.)[13] 吴险峰. 低维李超三系的分类 [J]. 吉林大学学报(理学版), 2009, 47(4): 671-676. (WU Xianfeng. Classification of Low Dimensional Lie Supertriple Systems [J]. Journal of Jilin University (Science Edition), 2009, 47(4): 671-676.)[14] WU Xianfeng, CHEN Liangyun. The Frattini Subsystem of a Lie Supertriple System [J]. J Math Res Exposition, 2010, 30(3): 399-406.[15] Okubo S, Kamiya N. Jordan-Lie Super Algebra and Jordan-Lie Triple System [J]. J Algebra, 1997, 198(2): 388-411.[16] Kamiya N, Okubo S. On δ-Lie Supe rtriple Systems Associated with (,δ)-Freudenthal-Kantor Supertriple Systems [J]. Proc Edinburgh Math Soc, 2000, 43(2): 243-260. [17] Scheunert M. The Theory of Lie Superalgebras [M]. Berlin: Springer, 1979: 270.。
《(2+1)-维非线性薛定谔方程组的Lie对称、一维优化系统及约化》范文
《(2+1)-维非线性薛定谔方程组的Lie对称、一维优化系统及约化》篇一(2+1)-维非线性薛定谔方程组的Lie对称、一维优化系统及约化研究摘要本文主要研究了(2+1)-维非线性薛定谔方程组的Lie对称性质、一维优化系统以及方程的约化问题。
首先,我们通过Lie对称分析方法,探讨了该方程组的对称性;其次,我们建立了一维优化系统模型,并对其进行了优化处理;最后,我们通过约化方法,将高维非线性问题转化为低维可解问题。
本文的研究对于理解(2+1)-维非线性薛定谔方程组的性质及其在物理领域的应用具有重要意义。
一、引言(2+1)-维非线性薛定谔方程是物理学中重要的偏微分方程之一,它在描述物理现象如非线性光学、流体力学、量子力学等领域具有广泛的应用。
本文旨在研究该方程组的Lie对称性质、一维优化系统以及约化问题。
二、(2+1)-维非线性薛定谔方程组的Lie对称性质我们利用Lie对称分析方法,研究了(2+1)-维非线性薛定谔方程组的对称性。
通过构建Lie代数,我们找到了该方程组的对称变换和守恒量。
这些对称性和守恒量有助于我们更好地理解方程的解的性质和演化规律。
三、一维优化系统模型及其优化处理为了更好地解决(2+1)-维非线性薛定谔方程,我们建立了一维优化系统模型。
该模型将原高维问题转化为低维可解问题,从而降低了问题的复杂度。
我们采用优化算法对模型进行了优化处理,得到了优化后的参数和结果。
四、(2+1)-维非线性薛定谔方程的约化问题为了解决(2+1)-维非线性薛定谔方程的高维非线性问题,我们采用了约化方法。
通过适当的变换和近似,我们将原高维问题转化为低维可解问题。
我们详细讨论了约化的过程和结果,并给出了具体的数值例子。
五、结论本文研究了(2+1)-维非线性薛定谔方程组的Lie对称性质、一维优化系统及约化问题。
通过Lie对称分析,我们找到了该方程组的对称性和守恒量;通过建立一维优化系统模型并进行优化处理,我们得到了优化后的参数和结果;通过约化方法,我们将高维非线性问题转化为低维可解问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( )设 口 2 EA i , , 果 任 给 b ∈A , 有 口 1= 0 则 a ,一1 2 如 。 2都 ¨b。= , 一0 如果 b = ; ∈A 2 有 b2 一0 则 都 l a ;
n2 = 0。 2
* 收 稿 日期 :2 1 7 1 0 卜O — 3
基 金 项 目 :国 家 自然科 学 基金 (0 7 1 7 1911) 作 者 简 介 :陈 剑 慧 ( 9 6) 男 , 江 台州 人 , 士 研 究 生 , 究 方 向 : 子 代 数 。 1 8一 , 浙 硕 研 算
Ea E ] b =- b , ] E , ] - [ a + a ] 6 ] B( 中的 中心 拟幂 零 算 子 , 1 , 为 p H) 由[ 1 定
即 b z a 一 [ , ] 对任 给 的 b [ 。,。] 6。 EA 。 成 立 。由 引理 1 1得 , 在 a 都 . 存 EF, 得 [ , ] [ , 使 十 z
性 ( ) 性映射 称 为线性 ( ) 性 三 元 L e导 子 , 任 给 a b C 非 线 非 线 i 指 , , EA, 声 E a,] c ) [ a , ] c + 有 ( E 6 ,] 一[ ( ) 6 ,3 [n, 6 ] c +[ n 5 , () 。关 于三元 L e系统 的结构 研究 可见 文 献 [ — ] 其 中在文 献 [ 3 , 芳 言研 [ ( ) ,] [ ,1 乒 c ] i 59 , 7中 陆 究 套代 数上 线性 三元 Le导子 的结 构 。本 文 目标是 研 究套代 数 上 的非线 性三 元 L e i i 导子 的结 构 。 设 H 为复 或实 数域 F上 的 Hi et 间 , H) l r空 b B( 表示 H 上 有 界线 性 算 子构 成 的代 数 , 上 的 一个 套 N H 指 H 的一 个 闭子空 间链 , 它包 含 H 和 { } 并且 在 交 和 闭 线性 扩 张 运 算下 封 闭 。令 T( 表 示 相 应 于套 N 0, N) 的套代 数 , T( 一{ EB( 即 N) n H): M M , a VM EN} T( 的 中心 z—F , 于套 代数 系 统知识 可 参见 文 , N) I关
矩阵, A 记 一P T( p , 一P T( P , N) 则 丁( 一A 。 N) A N) 。A。一P T( P , N) 0 A 0 A。。设 a , 然 EA 显
当 ≠愚时 ,i 一0 an j 。 在定 理 的证 明过程 中 , 我们 常用 到下 面 引理 : 引理 1 11 ( )设 a EA¨i , 。如果 任 给 b2 . [] 1 o 一1 2 lEA1, 有 a11—62 2, a1 E Z。 2都 1 2 1 2 则 l+a2 b a 2
陈剑 慧 ,纪 培 胜 ,姜 华
( 岛大学数 学科 学学 院 ,山 东 青 岛 2 6 7 ) 青 6 0 1 摘 要 : 明 了套代 数上 的每个 非 线 性 的 三元 L e 子 , 一个 可 加 导 子 与 一个 到其 中心 证 i导 是
上 的映 射 的和 , 而该 映射将 三元 积 映成 0 。 关 键词 : 代 数 ;三元 L e导子 ; 加导 子 套 i 可 中图分 类号 : 1 7 1 0 7 . 文献 标 志码 : A
上 式 中左乘 P 以右 乘 以 P 可得
0一 a1P2 ( ) 2 P1 P2一 P1 ( ) n1 1 P1 2 ( .2) 2
即 n 。 P ) z ( ) P ( P —P P a
由(. ) (. ) 2 1 和 2 2 得
由于 口 的任 意性 , 由引理 1 1得 .
线性 ( ) 非 线性 L e 子 , 任 给 a b i导 指 ,EA, 乒 [ ,] 一[ n ,] [ , 6 ] 有 ( n 6 ) ( )6 + 。 () 。关于 代数 和环 上 的线性 ( P t 线 性 ) i 导 子 的结构 的研 究有 很 多 , 文献 [ — ] 其参 考文 献 。 Le 见 14 及 A 中的一个 三 元 Le系统 A。 A 的一个 子 空 间且 关 于 三元 Le积 [ n 6 ,] 闭 的 。A。 的一个 线 i 指 i [ ,] c 封 上
弓 理 2 2 P ( ) +P ( ) l 且 声 az EA1。 I . 1 2 1P Z, E ( ) 2
证 明 任 给 a EA 由于 n: [ , , , 而 有 。 , 。一[ a P ] P ] 从 ( ) ( [ , , ) [ n , , + [nz ( ) , +[ az P ] ( ] ( ) a 一 [ a P ] P ] 一[ ( ) P ] P ] [ , ] P ] [ , , P ) 一[ “z P 一P ( 1 , 1 +[ 1 1 一 ( ) 1, 1 +[ 1, ( 1] 以2 P ] &2 ) ( ) 1口2 P ] 一n2 乒 p ) 一 ( ) 一P 声 a2 P 一P ( ) l 以2 + 口2 1 1 ( 】) 1 1 nz P +P ( )
P】 ( ) + P2 1P 1 P1 ( ) 1 Z。 E
 ̄( l) P ( l) x 。 a2 一 l n 2 P2 EA z
令 s ( p , ( )= n 一[ 5 。显 然 ,为 T( 上 的非 线性 三元 Le导子 ; f p )=5户 ) —P 户 ) 厂 n = ( ) 口, = ] N) i 且 ( = j 一 =(
n =a , 而 [ ] l从 n ] 和 [ , ] 。由于 [ 一a a 一a n
理 1 3 1 得 口 一0 故 口 。所 以[ ..] , 一0 n
1 O
青 岛 大 学 学 报 (自然 科 学 版 )
第 2 4卷
2 定 理 的 证 明
定理 的证 明分 成 几个 引理 。
引理 2 1 . ( ) 0 0: 。
证 明
( ) ( E ,] O ) [ 0 ,] 0 +E o ( ) ,] E o O , 0 ] 。 0 一 E o O , ] 一[ ( ) 0 ,] F , O ] O 一 E ,] ( ) 一0
P 声 ) 2 P 乒 p ) l ( P 一 l ( P + 2 P ) 2 f a ̄ 一 a E A 2 x ( 1P Z; ( l) ( 1) 。 E 2 引理 2 一 . P) 厂 EZ。 (
证 明 同引 理 2 2的证 明可得 P ( + . p)
0 一, [ 日 P ] P ] 一E f a ) P ] P ] [n , ( ] P ] E P ] f p ) 一P f a ) z ( [ , , ) E ( , , + [ f p ) , +E a , , ( ] ( P ,
所 以 f a ) 1 ( 1 2 ( 2 ( 一P f a ) 0 f a ) EA1 A2。 1 0 2 记 / n1 一 1 2 f a2 一 l+ 2, 给 b2 ’ 1) l ( + 2, ( 2) 1 2任 1EAl, 2 有 0 厂 [ n a , ] 一 E f a ,。 , ] [ n f a ] b +[ n b , ) 一[ a ] 6。 + 一- [ , ] b ) E ( )a b。 + [ , ( ) , ] [ ] /( 。 ] [ :,。 , ] ( ] 6
( , r [ n 5 ,1 一0 使得 ( )= n +r a J Va N) 有 ( [ ,3 e ) , n= = ) ( ) , ∈T( 。 ( N)
设 Mo , Mo { ) H。记 H 到 M 。 N 且 E ≠ o, 上投 影为 P , P 一1 记 一P 。T( 对 应 的矩 阵表 示 是上 三 角 N)
Au g. 2 0 1 1
文 章 编 号 :0 6 0 7 2 1 ) 3—00 一O 10 —13 (0 1 0 09 5
d i 1 . 9 9 jis . 0 6—1 3 . 0 1 0 . 0 o : 0 3 6 /. sn 1 0 0721.803
套代数上的非线性三元 L e i 导子
( ) 由 ( [ , , ) p EZ。 [ P ] P ] 一0及 f p ) ( E z可得
0 ( [ P ] P ] 一 E f( , , +[ p , P ) , + [ 户 , , ( ] 一厂 [ p , , ) E P ) P ] P ] [ 厂( ] P ] [ z P ] - P ) :f( P —P / 厂 P ) -
献 E o 。本 文 的结果 是 l]
定 理 设 H 为 数域 F上 的 Hi et 间 , 为 H 上 的一个 非平 凡 套 ( N≠ {0 , ) 设 : N) T( l r空 b N 即 { ) H} , T( 一 N) 为 T N) 的非 线性 三 元 L e 子 , ( 上 i导 则存 在 T( 上 的可加 导 子 d和 函数 r T( 一 F满 足 任给 a b C N) : N) , ,ET
a P ) 一 ( 1 e 2 +Pl 1 P ) Pl ( ) 1一 a 2 ( ) 1 2 ( 1 Pl P ) lPl a2 ( 1 一 声 1 a 2 1 P1 + ( ) ]一 P ( 1) 2 - 2 P1 P2 P1 a2 l a2 户 +O ( ) 1P 2 一 P ( 1 P1 l一a 2 2 p ) + P { P1 P1 1, 1 P ) a2 1P ( 1 P2 l6 ) a2 ( ( .1 2 )
MR(0 0 主题分 类 号 :4 L 0 4 HI 20 ) 72; 6 O
1 问题
设 A 是 一个 结合 代数 , 上 的一个 可加 映射 称为 可加 导 子 , 任 给 a b A 指 , EA, ( 6 一d( ) +a ( ) 在 d 口) n6 d6 ; A 上定 义 括积 [ ,] 6 n 6 一日 一 , , EA, A是 一个 L e ab 则 i 代数 。A 上 的一个 线 性 ( ) 性 映射 : A 成为 非 线 A—
