高中数学教师必备的知识定积分的概念和性质公式

第五章_第一节_不定积分的概念、性质.
经济数学——微积分 4 不定积分的概念与性质 原函数与不定积分的概念 不定积分的几何意义 基本积分表 不定积分的性质 小结思考题 经济数学——积分 二—原函数与不定积分的概念 定义如果在区I 刖内,可导函数尸(X)的 导函数为/(X ),即 We/,都有F\x) = f(x) 或 dF(x) = /(x)dx,那么函数F(x)就称为/(x) 或f(x)dx 在区间 /内原函数?(primitive furwtion ) 例(sinx) =cosx sinx 是 cos 兀的原函数. (inx) =— (X >0) X In X 是1在区间((),+oo)内的原函数. X 第一节 五、
定理原函数存在定理: 如果函数八X)在区间内连续, 那么在区 间^内存在可导函数F(x), 使Hxef,都有F\x) = f(x). 简言之:连续函数一定有原函数. 问题:(1)原函数是否唯一? (2)若不唯一它们之间有什么联系? 1 f 例(sinx) =cosx (sinx + C) =cosx (C为任意常数) 经济数学一微积分 关于原函数的说明: (1) (2) 证 说明F(x)+c是f (兀舶全部原粛或 经济数学一微积分
经济数学——微积分 不定积分(indefinite integral )的定义: 在区间/内,函数/(兀)的带有任意 常数项的原函数称为/(兀)在区I 可内的 不定积分,记为f/(xMr ? 经济数学——微积分 6 =X% /. fx^dx =—— 十 C. J 」 6 例2求f --------- dr. J 1 + X- / J 解?/ (arctanx)= ,, I ‘ 1 + 疋 心& =皿2 被积函数 『积分号 积分变量 寒积表达式 F(x)
定积分的概念和性质公式
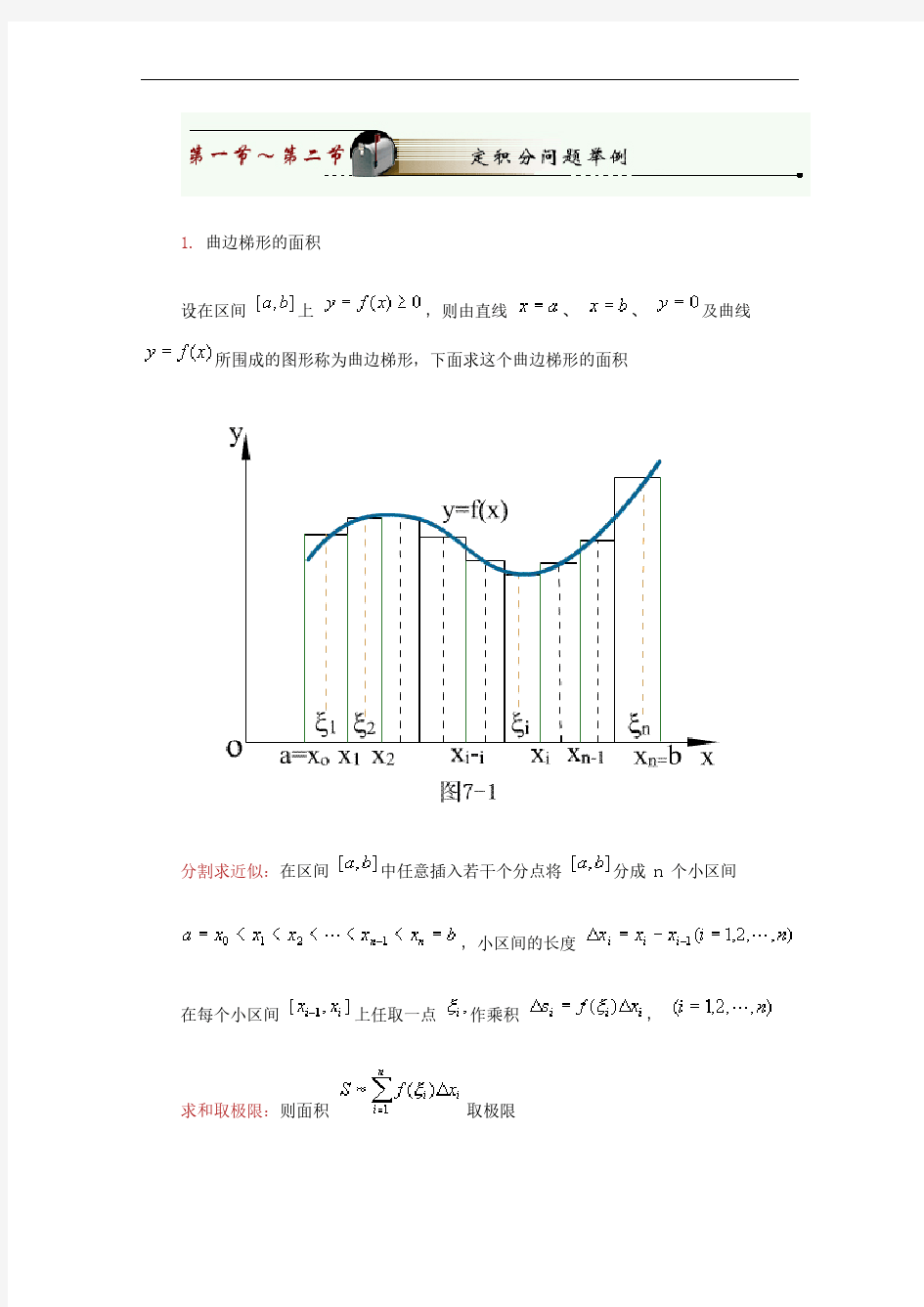
1. 曲边梯形的面积 设在区间上,则由直线、、及曲线 所围成的图形称为曲边梯形,下面求这个曲边梯形的面积 分割求近似:在区间中任意插入若干个分点将分成 n 个小区间 ,小区间的长度 在每个小区间上任取一点作乘积, 求和取极限:则面积取极限
其中,即小区间长度最大者趋于零。 2.变速直线运动的路程 设某物体作变速直线运动,速度是上的连续函数,且,求在这段时间内物体所经过的路程。 分割求近似:在内插入若干分点将其分成 n 个小区间,小区间长度,。任取, 做 求和取极限:则路程取极限 定义设函数在上有界,在中任意插入若干个分点 将分成 n 个小区间,其长度为,在每个小区间 上任取一点,作乘积,并求和, 记,如果不论对怎样分法,也不论小区间上的点
怎样取法,只要当时,和总趋于确定的极限,则称这个极限 为函数在区间上的定积分,记作,即 ,(*) 其中叫被积函数,叫被积表达式,叫积分变量,叫积分下限, 叫积分上限,叫积分区间。叫积分和式。 说明: 1.如果(*)式右边极限存在,称在区间可积,下面两类函数在区间 可积,(1)在区间上连续,则在可积。(2)在区间 上有界且只有有限个间断点,则在上可积。 2.由定义可知,定积分的值只与被积函数和积分区间有关,而与积分变量无关,所以 3.规定 时 , 在上时, 表示曲线、两条直线、 与轴所围成的曲边梯形的面积;
在上时, 表示曲线、两条直线、 与轴所围成的曲边梯形的面积(此时,曲边梯形在轴的下方); 例1 利用定积分的几何意义写出下列积分值 (1)(三角形面积)(2)(半圆面积)
设可积 性质1 性质2 性质3 (定积分对区间的可加性)对任何三个不同的数,有 性质4 性质5 如果在区间上,,则 推论 性质6 (定积分的估值)设 M 及 m 分别是函数在区间上的最大值及最小值,则 性质7 (定积分中值定理) 如果函数在区间上连续,则在上至少有一点, 使成立
定积分的概念和性质公式
1.曲边梯形的面积 设在区间*I上:;--L ,则由直线工’=■<、応匚、V 1及曲线■V °/W所围成的图形称为曲边梯形,下面求这个曲边梯形的面积 分割求近似:在区间-八「中任意插入若干个分点将宀…-分成n个小区间 兀5 5 <…,小区间的长度&广呜一為」(T三12… 在每个小区间- :-一I〕上任取一点-■■作乘积 求和取极限:则面积取极限
J=1 其中;'1 ; J L厂V '…,即小区间长度最大者趋于零。 2.变速直线运动的路程 设某物体作变速直线运动,速度| I「是上*的连续函数,且1■求在这段时间内物体所经过的路程。 分割求近似:在「〔[内插入若干分点■- _ "将其分成 n 个小区间「—,小区间长度■- _■'.-1, ■1丄。任取? _ _ 做 求和取极限:则路程一取极限 将分成n个小区间-,其长度为2 - —,在每个小区间 上任取一点「:,作乘积■- ' ■',并求和 r , 记1■r 1,如果不论对怎样分法,也不论小区间[:■ 上的 点「怎样取法,只要当「「I;时,和总趋于确定的极限,则称这个极限 为函数-—I在区间上的定积分,记作J ',即 定义设函数」?、在L?二上有界,在-亠二中任意插入若干个分点
其中叫被积函数,一’,八叫被积表达式,'‘叫积分变量,二叫积分下限, 「叫积分上限,-’」叫积分区间。■叫积分和式。 说明: 1.如果(*)式右边极限存在,称-’’」在区间-仁丄可积,下面两类函数在区间 上…-可积,(1)」在区间-LL■- - 上连续,则■' J'-在可积。(2)-’八在区间-‘丄-上有界且只有有限个间断点,则在--"-■ 上可积。 2.由定义可知,定积分的值只与被积函数和积分区间有关,而与积分变量无关,所 3.
高中数学定积分知识点
数学选修2-2知识点总结 一、导数 1.函数的平均变化率为 =??=??x f x y x x f x x f x x x f x f ?-?+=--)()()()(111212 注1:其中x ?是自变量的改变量,可正,可负,可零。 注2:函数的平均变化率可以看作是物体运动的平均速度。 2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000,则称函数)(x f y =在点0x 处可导,并把这个极限叫做)(x f y =在0x 处的导数,记作)(0'x f 或 0|'x x y =,即)(0'x f =x x f x x f x y x x ?-?+=??→?→?)()(lim lim 0000. 3.函数的平均变化率的几何意义是割线的斜率; 函数的导数的几何意义是切线的斜率。 4导数的背景(1)切线的斜率;(2)瞬时速度;
6、常见的导数和定积分运算公式:若() g x均可导(可积),则有: f x,() 用导数求函数单调区间的步骤: ①求函数f(x)的导数'() f x ②令'() f x>0,解不等式,得x的范围就是递增区间. ③令'() f x<0,解不等式,得x的范围,就是递减区间; [注]:求单调区间之前一定要先看原函数的定义域。 7.求可导函数f(x)的极值的步骤: (1)确定函数的定义域。 (2) 求函数f(x)的导数'() f x (3)求方程'() f x=0的根 (4) 用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查/() f x在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如
定积分的性质和基本定理
第二节 定积分的性质 和基本定理 用求积分和式的极限的方法来计算定积分不是很方便,在很情况下难以求出定积分的值。因此,我们在定积分定义的基础上,讨论它的各种性质,揭 示定积分与微分的内在联系,寻找定积分的有效 §2.1 一、定积分的基本性质 性质 1 b a 1dx=∫b a dx=b-a 证 0 lim →λ∑=n 1 i f(ξi )Δx i = lim →λ∑=n 1 i 1·Δx i =0 lim →λ (b-a)=b-a b a 1dx=∫b a dx=b-a 性质2(线性运算法则),设f(x),g(x)在[a,b ]上可积,对任何常数α、β,则αf(x)+βg(x)在[a,b ]
b a [αf(x)+βg(x)]dx=α∫b a f(x)dx+β ∫b a g(x)dx 证:设F(x)=αf(x)+β g(x), lim →λ∑=n 1 i F(ξi )Δx i =0 lim →λ[αf(ξi )+βg(ξi )] Δx i =0 lim →λ[α∑ =n 1 i f(ξi )Δx i +β ∑ =n 1 i g(ξi )Δ x i ] =αb a f(x)dx+β∫b a g(x)dx αf(x)+βg(x)在[a,b b a [αf(x)+βg(x)]dx=α∫ b a f(x)dx+β ∫b a g(x)dx 特别当α=1,β=± 1 b a [f(x)±g(x)]dx=∫ b a f(x)dx ±∫ b a g(x)dx 当β =0 b a αf(x)dx=α∫ b a f(x)dx 性质 2 性质3 对于任意三个实数a,b,c ,若f(x)在任意 两点构成的区间上可
高中数学-定积分的概念测试
高中数学-定积分的概念测试 1.定积分??0 1 1d x 的值等于 ( ) A .0 B .1 C.1 2 D .2 答案 B 2.已知??1 3 f (x )d x =56,则 ( ) A.??1 2 f (x )d x =28 B.??2 3f (x )d x =28 C.??1 22f (x )d x =56 D.??12f (x )d x +??2 3 f (x )d x =56 答案 D 3.如图所示,??a b f 1(x )d x =M ,??a b f 2(x )d x =N ,则阴影部分的面积为 ( ) A .M +N B .M C .N D .M -N 答案 D
4.不用计算,根据图形,用不等号连接下列各式 ( ) (1)??01 x d x ________??0 1x 2d x (图1); (2)??01x d x ________??1 2 x d x (图2); (3)??024-x 2d x ________??0 2 2d x (图3). 答案 (1)> (2)< (3)<
1.定积分可以表示图形的面积 从几何上看,如果在区间[a ,b ]上,函数f (x )连续且恒有f (x )≥0,那么定积分??a b f (x )d x 就表示由直线x =a ,x =b (a ≠b ),y =0和曲线y =f (x )所围成的曲边梯形的面积,这就是定积分??a b f (x )d x 的几何意义. 2.定积分表示图形面积的代数和 被积函数是正的,定积分的值也为正,如果被积函数是负的,函数曲线在x 轴之下,定积分的值就是带负号的曲边梯形的面积.当被积函数在积分区间上有正有负时,定积分就是x 轴之上的正的面积与x 轴之下的负的面积的代数和. 3.此外,定积分还有更多的实际意义,比如在物理学中,可以用定积分表示功、路程、压力、体积等. 4.定积分是一个数值(极限值),它的值仅仅取决于被积函数与积分的上、下限,而与积分变量用什么字母表示无关,即??a b f (x )d x =??a b f (u )d u =??a b f (t )d t =…(称为积分形式的不变性),另外定积分??a b f (x )d x 与积分区间[a ,b ]息息相关,不同的积分区间,所得的值也不同,例如??01(x 2+1)d x 与??0 3(x 2 +1)d x 的值就不同.
定积分基本公式
定积分基本公式 定积分是高等数学中一个重要的基本概念,在几何、物理、经济学等各个领域中都有广泛的应用.本章将由典型实例引入定积分概念,讨论定积分性质和计算方法,举例说明定积分在实际问题中的具体运用等. 第二节 微积分基本公式 一、变上限的定积分 设函数()f x 在[[,]a b ] 上连续,x ∈[,]a b ,于是积分()d x a f x x ?是一个定数, 这种写法有一个不方便之处,就是 x 既表示积分上限,又表示积分变量.为避免 t ,于是这个积分就写成了 ()d x a f t t ? . x 值,积分()d x a f t t ?就有一个确定的的一个函数,记作 ()Φx =()d x a f t t ? ( a ≤x ≤ b )通常称函数 ()Φx 为变上限积分函数或变上限积分,其几何意义如图所示. 定理1 如果函数()f x 在区间[,]a b 上连续,则变上限积分 ()Φx =()d x a f t t ?在[,]a b 上可导,且其导数是 d ()()d ()d x a Φx f t t f x x '= =?( a ≤x ≤ b ). 推论 连续函数的原函数一定存在. 且函数()Φx =()d x a f t t ?即为其原函数.
例1 计算()Φx =2 0sin d x t t ?在x =0 ,处的导数. 解 因为2 d sin d d x t t x ?=2sin x ,故 2 (0)sin 00Φ'==; πsin 242Φ'==. 例2 求下列函数的导数: (1) e ln ()d (0)x a t Φx t a t =>? ; 解 这里()Φx 是x 的复合函数,其中中间变量e x u =,所以按复合函数求导 法则,有 d d ln d(e )ln e (d )e d d d e x x u x x a Φt t x x u t x ===?. (2) 2 1()(0) x Φx x θ=>? . 解 21d d d d x Φx x θ=-?2 2()x x ='=2sin 2sin 2x x x x x =- ?=-. 二、牛顿-莱布尼茨(Newton-Leibniz )公式 定理2 设函数()f x 在闭区间[,]a b 上连续,又 ()F x 是()f x 的任一个原函数,则有()d ()() b a f x x F b F a =-? . 证 由定理1知,变上限积分 ()()d x a Φx f t t =?也是()f x 的一个原函数,于 是知0()()Φx F x C -=, 0C 为一常数, 即 0 ()d ()x a f t t F x C =+?.
定积分计算公式和性质
第二节 定积分计算公式和性质 一、变上限函数 设函数在区间上连续,并且设x 为上的任一点, 于是, 在区间 上的定积分为 这里x 既是积分上限,又是积分变量,由于定积分与积分变量无关,故可将此改为 如果上限x 在区 间上任意变动,则对 于每一个取定的x 值,定积分有一个确定值与之对应,所以定积分在 上定义了一个以x 为自变量的函数,我们把 称为函数 在区间 上 变上限函数 记为 从几何上看,也很显然。因为X 是上一个动点, 从而以线段 为底的曲边梯形的面积,必然随着底数 端点的变化而变化,所以阴影部分的面积是端点x 的函数(见图5-10) 图 5-10
定积分计算公式 利用定义计算定积分的值是十分麻烦的,有时甚至无法计算。因此,必须寻求计算定积分的简便方法。 我们知道:如果物体以速度作直线运动,那么在时间区间上所经过的路程s 为 另一方面,如果物体经过的路程s 是时间t 的函数,那么物体 从t=a 到t=b 所经过的路程应该是(见图5-11) 即 由导数的物理意义可知:即 是 一个原函数,因此,为了求出定积分,应先求出被积函数 的原函数 , 再求 在区间 上的增量 即可。 如果抛开上面物理意义,便可得出计算定积分的一般 方法: 设函数在闭区间上连续, 是 的一个原函数, 即 ,则 图 5-11
这个公式叫做牛顿-莱布尼兹公式。 为了使用方便,将公式写成 牛顿-莱布尼兹公式通常也叫做微积分基本公式。它表示一个函数定积分等于这个函数的原函数在积分上、下限处函数值之差。它揭示了定积分和不定积分的内在联系,提供了计算定积分有效而简便的方法,从而使定积分得到了广泛的应用。 例1 计算 因为是的一个原函数所以 例 2 求曲线 和直线x=0、x= 及y=0所围成图形面积A(5-12) 解 这个图形的面积为 二、定积分的性质 设 、 在相应区间上连续,利用前面学过的知识,可以 得到定积分以下几个简单性质: 图 5-12
高等数学第五章定积分总结
第五章 定积分 内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。 要求:理解定积分的概念和性质。掌握牛顿-莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。 重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。 难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。 §1.定积分的概念 一、实例分析 1.曲边梯形的面积 设函数)(x f y =∈C[a , b ], 且)(x f y =>0. 由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形. 如何定义曲边梯形的面积?(1) 矩形面积=底高. (2) 预备一张细长条的纸, 其面积底高. (3) 预备一张呈曲边梯形状的纸, 将其撕成许多细长条. (4) 启示: 将曲边梯形分割为许多细长条, 分割得越细, 误差越小. y =f (x ) x =a x =b y =f (x ) a=x 0 x 1 x i-1 x i x n =b
第i 个细长条面积)],,[()(11---=?∈??≈?i i i i i i i i i x x x x x x f S ξξ 曲边梯形面积: ∑=?≈ n i i i x f S 1 )(ξ 定积分概念示意图.ppt 定义: ),,2,1,max {()(lim 1 n i x x f S i n i i i Λ=?=?=∑=→λξλ 抛开上述过程的几何意义,将其数学过程定义为定积分. 二、定积分的定义 1. 定义 设)(x f y =在[a , b ]有定义, 且有界. (1) 分割: 用分点b x x x a n =<<<=Λ10把[a , b ]分割成n 个小区间: } ,,2,1,max{,,,2,1],,[11n i x x x x n i x x i i i i i i ΛΛ=?=-=?=--λ记 (2) 取点: 在每个小区间],[1i i x x -上任取一点i , 做乘积: i i x f ?)(ξ. (3) 求和: ∑=?n i i i x f 1 )(ξ (4) 取极限: ∑=→?n i i i x f 1 )(lim ξλ 若极限存在, 则其为)(x f 在[a , b ]上的定积分, 记作: ? b a dx x f )(. 即: ∑? =→?=n i i i b a x f dx x f 1 )(lim )(ξλ [a , b ]: 积分区间;a :积分下限;b :积分上限; ∑=?n i i i x f 1 )(ξ积分和式. 问题: 定积分是极限值, 在求极限的过程中, 谁是常量, 谁是变量?
高中数学-定积分的概念练习
高中数学-定积分的概念练习 一、基础达标 1.下列命题不正确的是 ( ) A .若f (x )是连续的奇函数,则 B .若f (x )是连续的偶函数,则 C .若f (x )在[a ,b ]上连续且恒正,则??a b f (x )d x >0 D .若f (x )在[a ,b ]上连续且??a b f (x )d x >0,则f (x )在[a ,b ]上恒正 答案 D 2.直线x =1,x =-1,y =0及曲线y =x 3 +sin x 围成的平面图形的面积可表示为 ( ) A. B .2??0 1(x 3 +sin x )d x C . D.??0 1(x 3 +sin x )d x 答案 B 3.已知??a b [f (x )+g (x )]d x =18,??a b g (x )d x =10,则??a b f (x )d x 等于 ( ) A .8 B .10 C .18 D .不确定 答案 A 4.已知定积分??06f (x )d x =8,则f (x )为奇函数,则??-6 6f (x )d x = ( ) A .0 B .16 C .12 D .8 答案 A 5.根据定积分的几何意义,用积分表示如图所示各图的阴影部分的面积, S =________.
答案 ??a b [f 1(x )-f 2(x )]d x (两图积分式相同) 6.由定积分的几何意义,定积分sin x d x 表示________. 答案 由直线x =0,x =π 2,y =0和曲线y =sin x 围成的曲边梯形的面积 7.根据定积分的几何意义推出下列积分的值. (1) x d x ;(2) cos x d x . 解 若x ∈[a ,b ]时,f (x )≥0,则??a b f (x )d x 的几何意义是表示由直线x =a ,x=b y =0和曲线y =f (x )围成的平面图形的面积;若x ∈[a ,b ]时,f (x )≤0,则??a b f (x )d x 表示所围成的图形面积的负值. (1)如图①,x d x =-A 1+A 1=0. (2)如图②,cos x d x =A 1-A 2+A 3=0. 二、能力提升 8.和式 1n +1+1n +2+ (12) ,当n →∞时的极限值用定积分式子可表示为 ( ) A.??011x d x B.? ?0 1 1 x +1d x
5.1 定积分的概念与性质-习题
1.利用定积分的定义计算下列积分: ⑴ b a xdx ? (a b <); 【解】第一步:分割 在区间[,]a b 中插入1n -个等分点:k b a x k n -=,(1,2,,1k n =-),将区间[,]a b 分为n 个等长的小区间[(1),]b a b a a k a k n n --+-+, (1,2,,k n =),每个小区间的长度均为k b a n -?=, 取每个小区间的右端点k b a x a k n -=+, (1,2,,k n =), 第二步:求和 对于函数()f x x =,构造和式 1 ()n n k k k S f x ==??∑1 n k k k x ==??∑1 ()n k b a b a a k n n =--=+ ?∑ 1()n k b a b a a k n n =--=+∑1 ()n k b a b a na k n n =--=+∑ 1()n k b a b a na k n n =--=+∑(1) []2 b a b a n n na n n ---=+? ^ 1()[(1)]2b a b a a n -=-+ ?-1 ()()22b a b a b a a n --=-+-? 1 ()()22b a b a b a n +-=--? 第三步:取极限 令n →∞求极限 1 lim lim ()n n k k n n k S f x →∞ →∞ ==??∑1 lim()( )22n b a b a b a n →∞ +-=--? ()(0)22 b a b a b a +-=--?()2b a b a +=-222b a -=, 即得 b a xdx ? 22 2 b a -=。
定积分的概念与性质练习
第一节 定积分的概念与性质 一、选择题 1. A ; 2. C . 二、填空题 1. (1)1; (2)0; (3)4 π. 2. (1)1 2 x dx ? > 1 30 x dx ? , (2)2 1ln xdx ? > () 2 2 1ln x dx ?, (3) 20 xdx π ? < 20 sin xdx π ? , (4)4 3 ln xdx ? < () 4 2 3ln x dx ?. 三、 解 由于()3f x x =在[]0,1上连续,故积分2 21 x dx -? 是存在的,且它与分法无关,同 时也与点的取法无关. 将区间[]0,1n 等分,得1 i x n = ,取() 1,2,, i i i n n ξ== 作和 ()2 3 2 1 1 13 344 0001114 n n n n i i i i i n n i S x i n n n n ξ---===+??==== ???∑∑∑ 于是 1 lim 4n n S →∞= 即 13 014 x dx =?. 四、 细棒的质量()0 l x dx ρ?. 五、 1 13 x e dx -+? 311 x e dx +-=-?. 设()()1 1,0x x f x e f x e ++'==>,所以()f x 在[]1,3-内单调增加, 从而 ()()()13f f x f -≤≤,即1 41x e e +≤≤. 于是 3 141 44x e dx e +-≤≤? 从而 1 4 13 44x e e dx -+-≤ ≤-? . 六、 设()()2 21,41f x x x f x x '=-+=-,令()0,f x '=得驻点1 4 x = . ()17101,,1482f f f ???? === ? ????? .所以 min ()f x =1, max ()f x =78. 1≤≤ 由定积分性质,得 1 2012≤≤ ?.
高中数学定积分的概念教案新人教版选修2-2
§1.5.3定积分的概念 教学目标: 1.通过求曲边梯形的面积和汽车行驶的路程,了解定积分的背景; 2.借助于几何直观定积分的基本思想,了解定积分的概念,能用定积分定义求简单的定积分; 3.理解掌握定积分的几何意义. 教学重点:定积分的概念、用定义求简单的定积分、定积分的几何意义. 教学难点:定积分的概念、定积分的几何意义. 教学过程: 一.创设情景 复习: 1. 2二.新课讲授 1.定积分的概念 一般地,设函数()f x 在区间[ ,]a b 上连续,用分点 0121i i n a x x x x x x b -=<<<<<<<=L L 将区间[,]a b 等分成n 个小区间,每个小区间长度为x D (b a x n -D =),在每个小区间 []1,i i x x -上任取一点()1,2, ,i i n x =L ,作和式: 11 ()()n n n i i i i b a S f x f n x x ==-=D =邋 如果x D 无限接近于0(亦即n ? )时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。记为:()b a S f x dx =ò, 其中 - ò积分号,b -积分上限,a -积分下限,()f x -被积函数,x -积分变量, [,]a b -积分区间,( )f x dx -被积式。 说明:(1)定积分() b a f x dx ò是一个常数,即n S 无限趋近的常数S (n ? 时)记 为 ()b a f x dx ò,而不是n S . (2)用定义求定积分的一般方法是:①分割:n 等分区间[],a b ;②近似代替:取 点[]1,i i i x x x -?;③求和:1 ()n i i b a f n x =-?;④取极限:() 1 ()l i m n b i n a i b a f x dx f n x =-=?ò (3)曲边图形面积:()b a S f x dx = ò;变速运动路程2 1 ()t t S v t dt =ò ;变力做功 ()b a W F r dr = ò 2.定积分的几何意义
人教版高中数学定积分概念及其运算
第 1 页 定 积 分 一、定积分的概念 1、曲边梯形的面积 分割→近似取代→求和→求极限 说明:(1)常用的求和公式 )12)(1(61...3212222++=++++n n n n 223333)1(4 1...321+=++++n n n (2)在定积分理论中,这种分割是任意的,只要保证每个区间的长度都向于0.在这里“等分”与“任意分割”等价的。 2、定积分的概念 一般地,设函数()f x 在区间[,]a b 上连续,用分点 0121i i n a x x x x x x b -=<<<<<<<= 将区间[,]a b 等分成n 个小区间,每个小区间长度为x ?(b a x n -?= ),在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ,作和式:11()()n n n i i i i b a S f x f n ξξ==-=?=∑∑ 如果x ?无限接近于0(亦即n →+∞)时,上述和式n S 无限趋近于常数S ,那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。记为:()b a S f x dx =? 其中()f x 成为被积函数,x 叫做积分变量,[,]a b 为积分区间,b 积分上限,a 积分下限。 3、定积分的几何意义 从几何上看,如果在区间[]b a ,上函数 )(x f 连续且恒有0)(≥x f 。那么定积分?b a dx x f )(表示由直线a x = b x =,)(b a <,0=y 和曲线)(x f y =所围成的曲边梯形 的面积。 4.性质1 、 ??=b a b a dx x f k dx x kf )()( (其中k 是不为0的常数) (定积分的线性性质) 性质2、 1212[()()]()()b b b a a a f x f x dx f x dx f x dx ±=±??? (定积分的线性性质) 性质3 、 ()()()() b c b a a c f x dx f x dx f x dx a c b =+<
(新课程)高中数学《1.5定积分的概念》导学案 新人教A版选修22
学习目标 1.理解曲边梯形面积的求解思想, 掌握其方法步骤; 2.了解定积分的定义、性质及函数在上可积的充分条件; 3.明确定积分的几何意义和物理意义; 4.无限细分和无穷累积的思维方法. 学习过程 一、课前准备 (预习教材,找出疑惑之处) 复习1:函数23 (sin) y x =的导数是 复习2:若函数2 log(23) a y x x =--的增区间是(,1) -∞-,则a的取值范围是 二、新课导学 学习探究 探究任务一:曲边梯形的面积 问题:下图的阴影部分类似于一个梯形,但有一边是曲线() y f x =的一段,我们把直线x a =,x b =() a b ≠,0 y=和曲线() y f x =所围成的图形称为曲边梯形. 如何计算这个曲边梯形的面积呢? 研究特例:对于1 x=,0 y=,2 y x =围成的图形(曲边三角形)的面积如何来求呢? 新知:1.用流程图表示求曲边三角形面积的过程 分割?近似代替?求和?取极限 2.定积分的定义: 1 ()lim() n b i a n i b a f x dx f n ξ →∞ = - =∑ ? 3.定积分的几何意义:
4.定积分的性质: (1)()()b b a a kf x dx k f x dx =?? (k 为常数) (2)1212[()()]()() b b b a a a f x f x dx f x dx f x dx ±=±??? (3)()()() b c b a a c f x dx f x dx f x dx =+???(其中a c b <<) 试试:求直线0,2,0x x y ===与曲线2y x =所围成的曲边梯形的面积. 反思:在求曲边梯形面积过程中,你认为最让你感到困难的是什么?(如何分割,求和逼近是两大难点) 典型例题 例1 利用定积分的定义,计算1 30x dx ?的值 变式:计算2 30x dx ?的值,并从几何上解释这个值表示什么?
数学分析定积分的基本性质
牡丹江师范学院教案 学院系别:理学院 课程名称数学分析(2)授课专业和班级 授课内容定积分的基本性质 授课学时 2学时 教学目的使学生理解定积分的五个基本性质,并能够运用这些性质进行定积分的计算和估值等问题的处理 教学重点定积分的五个基本性质 教学难点区间可加性及其应用 教具和媒体使用 教学方法 启发式几何直观 反例 教学过程 包括复习旧课、引入新课、重点难点讲授、作业和习题布置、问题讨论、归纳总结及课后辅导等内容 时间分配 (90分钟)一、复习所需要的知识1.定积分的概念2.可积准则 二、逐次给出定积分的五个基本性质,并加以证明和应用 1、线性运算法则 2、乘积的可积性 3、绝对可积性 4、保不等式性 5、积分区间上的可加性 6、说明一个重要结论定积分与函数再有限点处的值无关三、处理两个综合性问题: 1、证明Schwartz 不等式 2、处理一个与保不等式性相关的重要结论四、总结作业 5 60205板书设计 定积分的基本性质 性质1性质4性质6性质2性质5证明Schwarz 不等式性质3问题2 讲授新拓展内容 关于 ],[2b a L 的介绍 课后总结 定积分的性质再定积分的计算与估值中的作用 系主任 年 月 日
教学过程全设计与教学内容 教学内容 备注 一、复习定积分的概念与可积准则(教师板书) 给出本次课程在概念和可积准则的基础上来研究定积分的基本性质 定积分的基本性质(板书) 二.定积分的基本性质及其证明1.定积分的线性运算法则 定理1若函数,[,]f g R a b ∈,则对任意的常数,R αβ∈有+[,]f g R a b αβ∈,且 []()()d ()d ()d b b b a a a f x g x x f x x g x x αβαβ+=+?? ?证明:应用定积分的定义,此处略。2.定积分的乘积可积性 ,[,]f g R a b ∈,则有[,]f g R a b ?∈. 证明:因,[,]f g R a b ∈,记|()|, |()|f g f x M g x M ≤≤则对任意的0ε>,存在分割1T ,使得1 ()2i T g f x M ε ω?< ∑,同理存在分割2T ,使得2 ()2i T f g x M ε ω?< ∑取分割分割12T T T =+,在此分割下,我们记每个小区间为i ?因使得,则 |()()()()||()()()()||()()()()|,,[,]f x g x f y g y f x g x f x g y f x g y f x g y x y a b -≤-+-?∈进而有 ,,,sup |()()()()|sup |()()|sup |()()()()|, i i i f g x y x y x y f x g x f y g y M g x g y M f x g y f x g y ∈?∈?∈?-≤-+-12 12 12 2 1 ()()()()()i f i g i f i g i T T T T T T T T fg x M g x M f x M g x M f x ωωωωωε +++?≤?+?≤?+?<∑∑∑∑∑(根据分割加细大和不增,小和不减的性质),所以有结论成立。关于乘积可积性的一个注 一般地,()()d ()d ()d b b b a a a f x g x x f x x g x x ≠???3.绝对可积性 [,]f R a b ∈,则有||[,]f R a b ∈.且有不等式()|()|b b a a f x dx f x dx ≤??. 证明应用可积准则,略!绝对可积性的一个注
最新定积分的概念与性质
定积分的概念与性质
第五章定积分 第一节定积分的概念与性质 教学目的:理解定积分的定义,掌握定积分的性质,特别是中值定理. 教学重点:连续变量的累积,熟练运用性质. 教学难点:连续变量的累积,中值定理. 教学内容: 一、定积分的定义 1.曲边梯形的面积 设?Skip Record If...?在?Skip Record If...?上非负,连续,由直线?Skip Record If...?,?Skip Record If...?,?Skip Record If...?及曲线?Skip Record If...? 所围成的图形,称为曲边梯形. 求面积: 在区间?Skip Record If...?中任意插入若干个分点 ?Skip Record If...?, 把?Skip Record If...?分成?Skip Record If...?个小区间[?Skip Record If...?],[?Skip Record If...?], … [?Skip Record If...?],它们的长度依次为: ?Skip Record If...? 经过每一个分点作平行于?Skip Record If...?轴的直线段,把曲边梯形分成?Skip Record If...?个窄曲边梯形,在每个小区间[?Skip Record If...?]上任取一点?Skip Record If...?,以[?Skip Record If...?]为底,?Skip Record If...?为高的窄边矩形近似替代第?Skip Record If...?个窄边梯形?Skip Record If...?,把这样得到的
定积分的基本性质
定积分的基本性质 一、定积分的基本性质 性质1: ∫b a1dx=∫b a dx=b-a 证: f(ξi)Δx i= 1·Δx i= (b-a)=b-a 所以 ∫b a1dx=∫b a dx=b-a 性质2:(线性运算法则):设f(x),g(x)在[a,b]上可积,对任何常数α、β,则αf(x)+βg(x)在[a,b]上可积,且 ∫b a[αf(x)+βg(x)]dx=α∫b a f(x)dx+β∫b a g(x)dx 证:设F(x)=αf(x)+βg(x),由 F(ξi)Δx i=[αf(ξi)+βg(ξi)]Δx i =[αf(ξi)Δx i+βg(ξi)Δx i]
=α ∫b a f(x)dx+β∫b a g(x)dx, 因此 αf(x)+βg(x)在[a,b]上可积,且 ∫b a[αf(x)+βg(x)]dx=α∫b a f(x)dx+β∫b a g(x)dx 特别当α=1,β=±1时,有 ∫b a[f(x)±g(x)]dx=∫b a f(x)dx±∫b a g(x)dx 当β=0时 ∫b aαf(x)dx=α∫b a f(x)dx 性质2主要用于定积分的计算 性质3:对于任意三个实数a,b,c,若f(x)在任意两点构成的区间上可积,则 ∫b a f(x)dx=∫c a f(x)dx+∫b c f(x)dx 证:a,b,c的位置,由排列知有六种顺序 (i)当a f(ξi)Δx i =[f(ξi)Δx i+f(ξi)Δx i] =f(ξi)Δx i+f(ξi)Δx i = ∫c a f(x)dx+∫b c f(x)dx (ii)当c §1.5.3定积分的概念 【学情分析】: 前面两节(曲边梯形的面积和汽车行驶的路程)课程的学习为定积分的概念的引入做好了铺垫。学生对定积分的思想方法已有了一定的了解。 【教学目标】: (1)知识与技能:定积分的概念、几何意义及性质 (2)过程与方法:在定积分概念形成的过程中,培养学生的抽象概括能力和探索提升能力。 (3)情感态度与价值观:让学生了解定积分概念形成的背景,培养学生探究数学的兴趣. 【教学重点】: 理解定积分的概念及其几何意义,定积分的性质 【教学难点】: 对定积分概念形成过程的理解 练习与测试: (基础题) 1.函数()f x 在[] ,a b 上的定积分是积分和的极限,即 ()b a f x dx =? _________________ . 答案:0 1 lim ()n i i i f x λξ→=?∑ 2.定积分的值只与______及_______有关,而与_________的记法无关 . 答案:被积函数,积分区间,积分变量; 3.定积分的几何意义是_______________________ . 答案:介于曲线()y f x =,x 轴 ,直线,x a x b ==之间各部分面积的代数和; 4.据定积分的几何意义()a b <,则________;b a dx =?________.b a xdx =? 答案:b a - , 22 2 b a - (提高题) 5.将和式极限表示成定积分 (1). 2 1 lim (12)n n n →∞+++L 解:122 011 11 1 lim (12)lim lim n n n n n i i i n i xdx n n n n →∞→∞→∞==+++===∑∑?L (2). 2 1lim ()n i i i f x λξ→=?∑,其中{}0121,[,],n i i i i x a x x x b x x Max x ξλ-=<<<<=∈=L 解:2 20 1 lim ()()()n b b i i a a i f x g x dx f x dx λξ→=?==∑?? 6. 利用定义计算定积分 2 1 1 .dx x ? 解:在[1,2]中插入分点2 1 ,,,n q q q -L ,典型小区间为1[,]i i q q -,(1,2,,i n =L ) 小区间的长度11(1)i i i i x q q q q --?=-=-,取1 i i q ξ-=,(1,2,,i n =L ) 1 11 111 1()(1)n n n i i i i i i i i i f x x q q q ξξ--===?=?=-∑ ∑∑1 (1)(1)n i q n q ==-=-∑ 取2n q =即12n q =, 11 ()(21),n n i i i f x n ξ=?=-∑ 1 121 lim (21)lim ln 2,1 x x x x x x →+∞ →+∞--==Q 1lim (21)ln 2,n n n →∞ ∴-= 12 1 0111 lim lim (21)ln 2.n n i n i i dx x n x λξ→→∞==?=-=∑? () i g ξi x ?i ξ 高中数学-定积分的概念课后练习 课时演练·促提升 A组 1. 如图所示,f(x)d x等于() A.S1+S2+S3 B.S1-S2+S3 C.-S1+S2-S3 D.-S1-S2+S3 解析:由定积分的几何意义,当f(x)≥0时,f(x)d x表示面积S,当f(x)≤0时,f(x)d x=-S.故选C.答案:C 2. 图中阴影部分的面积用定积分表示为() A.2x d x B.(2x-1)d x C.(2x+1)d x D.(1-2x)d x 答案:B 3.已知x d x=2,则x d x等于() A.0 B.2 C.-1 D.-2 解析:∵f(x)为奇函数,∴x d x=-x d x=-2. 答案:D 4.已知f(x)=x3-x+sin x,则f(x)d x的值为() A.等于0 B.大于0 C.小于0 D.不确定 解析:易知f (x)为奇函数,由奇函数的性质f(x)d x=-f(x)d x,而f(x)d x=f(x)d x+f(x)d x=0. 答案:A 5.设a=d x,b=x2d x,c=x3d x,则a, b,c的大小关系是() A.c>a>b B.a>b>c C.a=b>c D.a>c>b 解析:根据定积分的几何意义,易知x3d x人教版高中数学定积分的概念第3课时
高中数学-定积分的概念课后练习
