圆柱圆锥练习题及答案
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷加精品答案
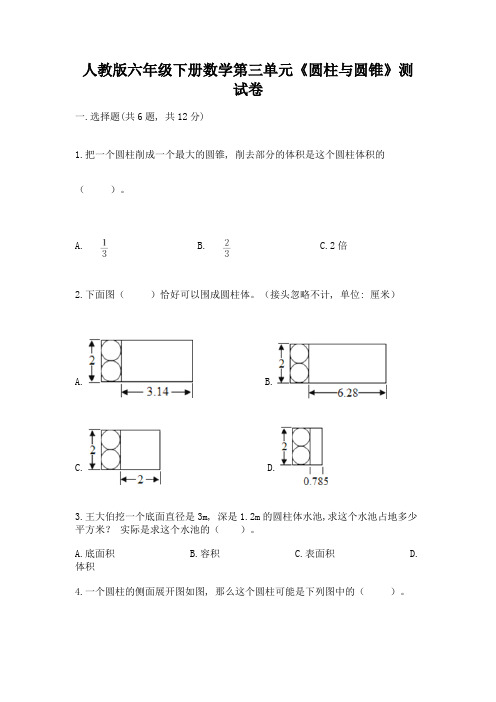
人教版六年级下册数学第三单元《圆柱与圆锥》测试卷一.选择题(共6题, 共12分)1.把一个圆柱削成一个最大的圆锥, 削去部分的体积是这个圆柱体积的()。
A. B. C.2倍2.下面图()恰好可以围成圆柱体。
(接头忽略不计, 单位: 厘米)A. B.C. D.3.王大伯挖一个底面直径是3m, 深是1.2m的圆柱体水池,求这个水池占地多少平方米?实际是求这个水池的()。
A.底面积B.容积C.表面积D.体积4.一个圆柱的侧面展开图如图, 那么这个圆柱可能是下列图中的()。
A. B. C.5.用一个高36厘米的圆锥形容器盛满水, 倒入和它等底等高的圆柱形容器中, 水的高度是()厘米。
A.36B.18C.16D.126.下面第()个图形是圆柱的展开图。
A. B.C. D.二.判断题(共6题, 共12分)1.一个正方体木料, 加工成一个最大的圆锥, 圆锥的体积是正方体体积的/。
()2.圆柱的表面积等于底面积乘高。
()3.把一个土豆放在一个盛水的圆柱形容器里, 完全浸没, 土豆的体积等于上升的水的体积, 可以通过求圆柱的体积来计算。
()4.粉笔是最常见的圆柱。
()5.一个圆柱的直径和高相等, 则圆柱体的侧面展开图是正方形。
()6.一个圆锥和一个圆柱的高相等, 它们底面积的比是3:2, 圆锥的体积与圆柱的体积的比是1:2。
()三.填空题(共6题, 共11分)1.一根2米长的圆柱形木材, 锯成3段小圆柱后, 它们的表面积总和比原来增加了12.56dm2, 原来这根木材的体积是()dm3。
2.一个圆柱的体积是15立方厘米, 与它等底等高的圆锥的体积是()立方厘米。
3.圆锥的体积=()用字母表示()。
4.把圆柱的侧面沿高剪开, 得到一个(), 这个()的长等于圆柱底面的(), 宽等于圆柱的(), 所以圆柱的侧面积等于()。
5.一个圆柱的侧面积9.42平方厘米, 高4厘米, 这个圆柱的表面积是()平方厘米。
6.一个圆柱的底面直径是15 cm, 高是8 cm, 这个圆柱的侧面积是()cm2。
圆柱圆锥练习题及答案

圆柱圆锥练习题及答案### 圆柱圆锥练习题及答案#### 一、选择题1. 圆柱的底面半径为3厘米,高为5厘米,其体积是()立方厘米。
A. 141.3B. 94.2C. 235.5D. 47.12. 圆锥的底面半径为4厘米,高为9厘米,其体积是()立方厘米。
A. 50.24B. 100.48C. 150.72D. 200.963. 一个圆柱与一个圆锥等底等高,圆柱的体积是圆锥体积的()倍。
A. 1B. 2C. 3D. 4#### 二、填空题4. 圆柱的体积公式是V = πr²h,其中 r 代表________,h 代表________。
5. 圆锥的体积公式是V = ________πr²h,其中 1/3 是因为圆锥的体积是与它等底等高的圆柱体积的________。
#### 三、计算题6. 一个圆柱形水桶,底面直径为20厘米,高为30厘米,求水桶的体积。
7. 一个圆锥形沙堆,底面半径为6米,高为10米,求沙堆的体积。
8. 一个圆柱形容器内装满了水,容器的底面半径为8厘米,高为12厘米。
如果将容器内的水倒入一个底面半径为4厘米,高为18厘米的圆锥形容器中,问水能否完全倒入?#### 四、解答题9. 一个圆柱形的油桶,底面半径为0.5米,高为3米。
如果油桶里的油占油桶体积的75%,求油桶里油的体积。
10. 一个圆锥形的奖杯,底面半径为0.2米,高为0.5米。
如果奖杯的材质是铜,铜的密度为8.96克/立方厘米,求这个奖杯的质量。
#### 答案1. A. 141.3 立方厘米(V = π × 3² × 5 = 141.3)2. B. 100.48 立方厘米(V = 1/3 × π × 4² × 9 = 100.48)3. C. 3 倍(等底等高的圆柱体积是圆锥体积的3倍)4. 底面半径,高5. 1/3,三分之一6. 体积为3.14 × (20/2)² × 30 = 3.14 × 100 × 30 = 9420 立方厘米7. 体积为1/3 × 3.14 × 6² × 10 = 3.14 × 12 × 10 = 376.8 立方米8. 圆柱体积为3.14 × 8² × 12 = 2411.52 立方厘米,圆锥体积为1/3 × 3.14 × 4² × 18 = 301.44 立方厘米。
圆柱圆锥练习题和答案

圆柱圆锥练习题和答案一、选择题1. 圆柱的体积公式是()A. V = πr²hB. V = πr² + hC. V = πr² - hD. V = πrh2. 圆锥的体积公式是()A. V = 1/3πr²hB. V = 3πr²hC. V = πr²h/3D. V = πr²h3. 圆柱的表面积公式是()A. S = 2πrh + 2πr²B. S = πrh + πr²C. S = 2πrhD. S = πr²4. 圆锥的侧面展开图是()A. 圆形B. 长方形C. 扇形D. 三角形5. 圆柱和圆锥的底面都是()A. 圆形B. 长方形C. 扇形D. 三角形二、填空题6. 一个圆柱的底面半径为3厘米,高为5厘米,其体积是_________立方厘米。
7. 一个圆锥的底面半径为4厘米,高为9厘米,其体积是_________立方厘米。
8. 一个圆柱的底面周长为12.56厘米,高为4厘米,其表面积是_________平方厘米。
9. 一个圆锥的底面半径为2厘米,高为6厘米,其表面积是_________平方厘米。
三、计算题10. 一个圆柱形容器的底面直径为20厘米,高为30厘米,求其容积。
11. 一个圆锥形沙堆,底面半径为5米,高为3米,如果将沙堆铺在长10米,宽6米的长方形地面上,求铺成的沙堆高度。
四、解答题12. 一个圆柱形油桶,底面半径为0.8米,高为1.5米,求油桶的表面积和体积。
13. 一个圆锥形漏斗,底面半径为0.6米,高为0.9米,求漏斗的体积。
答案:1. A2. A3. A4. C5. A6. 141.37. 75.368. 150.729. 37.6810. 圆柱形容器的容积为3.14 × (20/2)² × 30 = 3000π 立方厘米。
11. 圆锥形沙堆的体积为1/3 × 3.14 × 5² × 3 = 78.5π 立方米。
人教版数学6年级下册 第3单元(圆柱和圆锥)课后作业练习题(含答案)

人教版六年级下册第三单元圆柱和圆锥课后作业练习题一.选择题1.把一个棱长是4分米的立方体钢坯切削成一个最大的圆柱,它的体积是()立方分米。
A.50.24B.56.52C.16.75D.200.962.36个铁圆柱,可以熔铸成等底等高的圆锥体的个数是()A.12个B.18个C.36个D.108个3.两个圆柱的底面积相等,高之比是3:2,它们的体积之比是()A.3:2B.2:3C.9:44.一个圆柱与一个圆锥等底等高,已知圆柱的体积比圆锥的体积多9立方米,圆锥的体积是()立方米.A.4.5B.3C.95.用两张同样的长方形硬纸板围成两个不同的圆柱形纸筒,再分别装上两个底面,那么这两个圆柱形纸筒的()一定相等。
A.底面积B.侧面积C.表面积D.体积6.一个圆柱与一个圆锥体积相等,底面直径也相等,则圆锥的高是圆柱的高的()A.13B.23C.3倍D.6倍7.一个圆柱和一个圆锥的底面直径相等,圆柱的高是圆锥的3倍,圆锥的体积是5立方分米,圆柱的体积是()立方分米.A.5B.15C.458.一个圆柱的体积比与它等底等高的圆锥的体积大()A.3倍B.2倍C.1 3二.填空题9.底面积是212cm、高是9cm的圆锥的体积是3cm,和它等底等高的圆柱的体积是3cm.10.把6个形状完全相同的圆柱体铁块熔化后,可浇铸成与这种圆柱体等底等高的圆锥体铁块件。
11.一个圆柱的体积是3188.4cm,高是15cm,它的底面积是2cm.12.一个圆柱的底面周长是9.42分米,高3分米,它个圆柱的侧面积是平方分米,体积是立方分米。
13.把一根3米长的圆柱体木材截成三段圆柱体,表面积增加了12平方分米,这根木料的体积是立方分米。
14.一个圆柱和一个圆锥等底等高,它们的体积差是94.2立方厘米,这个圆柱的体积是立方厘米.又知圆锥的底面半径是3厘米,这个圆柱的侧面面积是平方厘米.15.做一节底面直径是10厘米,长为1米的圆柱形烟囱,至少需要一张平方厘米的铁皮。
六年级下册数学《圆柱与圆锥》专项练习题50道及答案【名师系列】
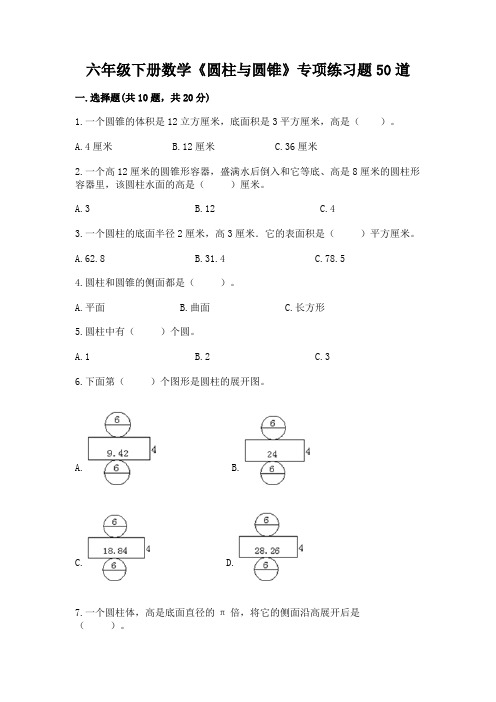
六年级下册数学《圆柱与圆锥》专项练习题50道一.选择题(共10题,共20分)1.一个圆锥的体积是12立方厘米,底面积是3平方厘米,高是()。
A.4厘米B.12厘米C.36厘米2.一个高12厘米的圆锥形容器,盛满水后倒入和它等底、高是8厘米的圆柱形容器里,该圆柱水面的高是()厘米。
A.3B.12C.43.一个圆柱的底面半径2厘米,高3厘米.它的表面积是()平方厘米。
A.62.8B.31.4C.78.54.圆柱和圆锥的侧面都是()。
A.平面B.曲面C.长方形5.圆柱中有()个圆。
A.1B.2C.36.下面第()个图形是圆柱的展开图。
A. B.C. D.7.一个圆柱体,高是底面直径的π倍,将它的侧面沿高展开后是()。
A.长方形B.正方形C.平行四边形8.一个圆锥的体积是48立方厘米,底面积是16平方厘米,高是()。
A.9B.3C.69.圆柱体的底面直径20厘米,高是底面直径的。
它的表面积是()。
A.528cm2B.628cm2C.1570cm2D.1256cm210.一个圆柱的高有()条。
A.1B.2C.无数D.10二.判断题(共10题,共20分)1.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米。
()2.一个圆锥的底面半径扩大3倍,高缩小9倍,圆锥的体积不变。
()3.圆柱的底面半径扩大到原来的2倍,高缩小到原来的二分之一,它的体积不变。
()4.等底等高的圆柱和长方体的体积相等。
()5.一个圆锥底面积不变,高扩大5倍,它的体积就扩大15倍。
()6.两个圆柱的体积相等,那么它们的表面积也相等。
()7.一个圆锥的底面直径和高都是4分米,如果沿着底面直径切成两半,表面积增加16平方分米。
()8.圆柱体的底面直径是3厘米,高是9.42厘米,它的侧面展开后是一个正方形。
()9.测量圆锥的高只要测出顶点到底面圆周上的一点就是圆锥的高。
()10.圆柱的体积是圆锥体积的3倍。
()三.填空题(共10题,共21分)1.圆锥的体积=()用字母表示()。
(完整版)六年级数学圆柱圆锥练习题及答案

(四)例例2、求下面立体图形的底面周长和底面积。
半径3厘米直径10米例3、判断:圆柱和圆锥都有无数条高。
例4、(圆柱的侧面积)体育一个圆柱,底面直径是5厘米,高是12厘米。
求它的侧面积。
例6、(辨析)一个无盖的圆柱铁皮水桶,底面直径是30厘米,高是50厘米。
做这样一个水桶,至少需用铁皮6123平方厘米。
例7、(考点透视)一个圆柱的侧面积展开是一个边长15.7厘米的正方形。
这个圆柱的表面积是多少平方厘米?例8、(考点透视)一个圆柱形的游泳池,底面直径是10米,高是4米。
在它的四周和底部涂水泥,每千克水泥可涂5平方米,共需多少千克水泥?例9、(考点透视)把一个底面半径是2分米,长是9分米的圆柱形木头锯成长短不同的三小段圆柱形木头,表面积增加了多少平方分米?4、求下列圆柱体的侧面积(1)底面半径是3厘米,高是4厘米。
(3)底面周长是12.56厘米,高是4厘米。
5、求下列圆柱体的表面积(1)底面半径是4厘米,高是6厘米。
(3)底面周长是25.12厘米,高是8厘米。
6、用铁皮制作一个圆柱形烟囱,要求底面直径是3分米,高是15分米,制作这个烟囱至少需要铁皮多少平方分米?(接头处不计,得数保留整平方分米)7、请你制作一个无盖圆柱形水桶,有以下几种型号的铁皮可供搭配选择。
8、一个圆柱形蓄水池,底面周长是25.12米,高是4米,将这个蓄水池四周及底部抹上水泥。
如果每平方米要用水泥20千克,一共要用多少千克水泥?一、圆柱体积1、求下面各圆柱的体积。
(3)底面直径是8米,高是10米。
(4)底面周长是25.12分米,高是2分米。
2、有两个底面积相等的圆柱,第一个圆柱的高是第二个圆柱的4/7。
第一个圆柱的体积是24立方厘米,第二个圆柱的的体积比第一个圆柱多多少立方厘米?3、在直径0.8米的水管中,水流速度是每秒2米,那么1分钟流过的水有多少立方米?4、牙膏出口处直径为5毫米,小红每次刷牙都挤出1厘米长的牙膏。
这支牙膏可用36次。
六年级圆柱圆锥练习题及答案
六年级圆柱圆锥练习题及答案题一:圆柱问题某个圆柱的底面半径为5cm,高度为8cm。
请计算:1. 圆柱的侧面积;2. 圆柱的表面积;3. 圆柱的体积。
解答:1. 圆柱的侧面积计算公式为:侧面积= 2 × π × 底面半径 ×高度。
代入已知数据,侧面积= 2 × 3.14 × 5 × 8 ≈ 251.2 平方厘米。
2. 圆柱的表面积计算公式为:表面积= 2 × π × 底面半径 × (底面半径 + 高度) + 底面积。
代入已知数据,表面积= 2 × 3.14 × 5 × (5 + 8) + (3.14 × 5^2) ≈ 329 平方厘米。
3. 圆柱的体积计算公式为:体积 = 底面积 ×高度。
代入已知数据,体积= (3.14 × 5^2) × 8 ≈ 628 平方厘米。
题二:圆锥问题一个圆锥的底面半径为3cm,高度为6cm。
请计算:1. 圆锥的侧面积;2. 圆锥的表面积;3. 圆锥的体积。
解答:1. 圆锥的侧面积计算公式为:侧面积= π × 底面半径 ×斜高。
斜高可以通过勾股定理求出:斜高= √(底面半径^2 + 高度^2)。
代入已知数据,侧面积= 3.14 × 3 × √(3^2 + 6^2) ≈ 55.63 平方厘米。
2. 圆锥的表面积计算公式为:表面积= π × 底面半径 ×斜高 + 底面积。
代入已知数据,表面积= 3.14 × 3 × √(3^2 + 6^2) + (3.14 × 3^2) ≈ 84.78 平方厘米。
3. 圆锥的体积计算公式为:体积 = (底面积 ×高度) / 3。
代入已知数据,体积 = (3.14 × 3^2 ×6) / 3 ≈ 56.52 平方厘米。
小学圆锥与圆柱试卷及答案
小学圆锥与圆柱试卷及答案一、选择题(每题2分,共20分)1. 一个圆柱的底面半径为3厘米,高为4厘米,其体积是()立方厘米。
A. 36B. 37.68C. 113.04D. 150.722. 圆锥的底面半径为2厘米,高为3厘米,其体积是()立方厘米。
A. 6B. 12C. 18D. 243. 一个圆柱的体积是314立方厘米,底面半径为10厘米,其高是()厘米。
A. 1B. 2C. 3D. 44. 圆柱的底面积是3.14平方厘米,高是2厘米,其体积是()立方厘米。
A. 6.28B. 3.14C. 1.57D. 2.595. 圆锥的体积是圆柱体积的1/3,如果圆锥的底面积和圆柱的底面积相等,圆锥的高是圆柱高的()倍。
A. 1B. 3C. 6D. 96. 一个圆柱和一个圆锥等底等高,圆柱的体积是圆锥体积的()倍。
A. 1B. 2C. 3D. 47. 一个圆锥的底面半径为4厘米,高为12厘米,圆锥的体积是()立方厘米。
A. 100.48B. 200.96C. 301.44D. 401.928. 一个圆柱的底面直径为6厘米,高为5厘米,其体积是()立方厘米。
A. 47.1B. 94.2C. 141.3D. 188.49. 圆柱的体积是圆锥体积的3倍,如果圆柱的底面积是圆锥底面积的2倍,圆柱的高是圆锥高的()倍。
A. 1B. 1/2C. 1/3D. 1/610. 一个圆锥的底面半径为3厘米,高为6厘米,圆锥的体积是()立方厘米。
A. 56.52B. 113.04C. 226.08D. 452.16二、填空题(每题2分,共20分)11. 圆柱的体积公式是:________。
12. 圆锥的体积公式是:________。
13. 如果圆柱和圆锥等底等高,圆柱的体积是圆锥体积的________倍。
14. 圆柱的底面积是S,高是h,那么圆柱的体积是________。
15. 圆锥的底面积是S,高是h,那么圆锥的体积是________。
六年级下册数学圆柱圆锥练习题(含答案)
六年级下册数学圆柱圆锥练习题(含答案)一、1. 一个圆柱的底面直径为8厘米,高为10厘米,求其体积和表面积。
解:圆柱的体积公式为V = πr^2h,表面积公式为S = 2πr(r+h)。
其中r为底面半径,h为高度。
先求出底面半径r = 8/2 = 4厘米。
体积V = π(4^2)×10 = 160π≈ 502.65 cm^3表面积S = 2π×4(4+10) = 2π×4×14 ≈ 351.86 cm^22. 一个圆锥的底面半径为6厘米,高为8厘米,求其体积和表面积。
解:圆锥的体积公式为V = 1/3πr^2h,表面积公式为S = πr(r+√(r^2+h^2))。
先求出底面半径r = 6厘米。
体积V = 1/3π(6^2)×8 = 96π≈ 301.59 cm^3表面积S = π×6(6+√(6^2+8^2)) ≈ 150.80 cm^2二、3. 一个圆柱的底面直径是12.6厘米,高是16厘米,求其体积和表面积。
解:首先计算底面半径r = 12.6/2 = 6.3厘米。
体积V = π(6.3^2)×16 = 633.6π≈ 1991.05 cm^3表面积S = 2π×6.3(6.3+16) ≈ 570.97 cm^24. 一个圆锥的底面直径是9.8厘米,高是12厘米,求其体积和表面积。
解:先计算底面半径r = 9.8/2 = 4.9厘米。
体积V = 1/3π(4.9^2)×12 ≈ 237.67 cm^3表面积S = π×4.9(4.9+√(4.9^2+12^2)) ≈ 145.55 cm^2三、5. 一个圆柱的底面半径是5厘米,高是18厘米,求其体积和表面积。
解:底面半径r = 5厘米。
体积V = π(5^2)×18 = 450π≈ 1413.72 cm^3表面积S = 2π×5(5+18) ≈ 376.99 cm^26. 一个圆锥的底面半径是7厘米,高是10厘米,求其体积和表面积。
圆柱圆锥练习题以及答案
圆柱圆锥练习题以及答案圆柱圆锥练习题以及答案圆柱和圆锥是几何学中常见的几何体,它们具有广泛的应用。
在学习几何学时,我们经常会遇到与圆柱和圆锥相关的练习题。
下面,我将给大家提供一些圆柱和圆锥的练习题以及相应的答案,希望能帮助大家更好地理解和掌握这些概念。
练习题一:计算圆柱的体积已知一个圆柱的底面半径为5cm,高度为10cm,求其体积。
解答:圆柱的体积公式为V = πr²h,其中r为底面半径,h为高度。
将已知数据代入公式,可得V = 3.14 × 5² × 10 = 785 cm³。
因此,该圆柱的体积为785立方厘米。
练习题二:计算圆锥的体积已知一个圆锥的底面半径为8cm,高度为12cm,求其体积。
解答:圆锥的体积公式为V = (1/3)πr²h,其中r为底面半径,h为高度。
将已知数据代入公式,可得V = (1/3) × 3.14 × 8² × 12 = 803.84 cm³。
因此,该圆锥的体积为803.84立方厘米。
练习题三:计算圆柱的表面积已知一个圆柱的底面半径为6cm,高度为15cm,求其表面积。
解答:圆柱的表面积由底面积和侧面积组成。
底面积为πr²,侧面积为2πrh。
将已知数据代入公式,底面积为3.14 × 6² = 113.04平方厘米,侧面积为2 ×3.14 × 6 × 15 = 565.2平方厘米。
因此,该圆柱的表面积为113.04 + 565.2 = 678.24平方厘米。
练习题四:计算圆锥的表面积已知一个圆锥的底面半径为10cm,高度为16cm,求其表面积。
解答:圆锥的表面积由底面积、侧面积和底面到顶点的距离构成。
底面积为πr²,侧面积为πrl,其中l为底面到顶点的距离。
根据勾股定理,l = √(r² + h²)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆柱圆锥练习题及答案
一、选择题
1. 下列图形中,可以看作是圆柱的是:
A. 棱台
B. 球体
C. 圆锥
D. 圆筒
答案:D. 圆筒
2. 已知圆锥的底面半径为3cm,高度为4cm,求圆锥的体积(取π=
3.14)。
A. 18.84cm³
B. 37.68cm³
C. 25.12cm³
D. 75.36cm³
答案:B. 37.68cm³(计算公式:体积V = (1/3)πr²h = (1/3) × 3.14 × 3² × 4 = 37.68cm³)
3. 在一个圆锥中,底面圆的周长为12cm,高度为5cm,求圆锥的侧面积(取π=3.14)。
A. 52.2cm²
B. 57.68cm²
C. 62.8cm²
D. 63.4cm²
答案:C. 62.8cm²(计算公式:侧面积S = πrl = 3.14 × 3 × 5 =
47.1cm²)
二、填空题
1. 已知圆柱的底面半径为4cm,高度为12cm,求圆柱的体积(取π=3.14)。
答案:V = πr²h = 3.14 × 4² × 12 = 602.88cm³
2. 在一个圆锥中,底面圆的半径为6cm,高度为8cm,求圆锥的侧面积(取π=
3.14)。
答案:S = πrl = 3.14 × 6 × 10 = 188.4cm²
3. 在一个圆柱中,底面圆的半径为5cm,高度为7cm,求圆柱的表面积(取π=3.14)。
答案:S = 2πrh + 2πr² = 2 × 3.14 × 5 × 7 + 2 × 3.14 × 5² = 219.8cm²
三、解答题
1. 一个圆柱的底面圆的周长为20cm,高度为8cm,求圆柱的体积和表面积(取π=3.14)。
解:
首先求出圆柱的底面半径:周长C = 2πr = 20cm,r = 10cm
计算体积V:V = πr²h = 3.14 × 10² × 8 = 2512cm³
计算表面积S:S = 2πrh + 2πr² = 2 × 3.14 × 10 × 8 + 2 × 3.14 × 10² = 1004.8cm²
所以,圆柱的体积为2512cm³,表面积为1004.8cm²。
2. 一个圆锥的底面半径为4cm,高度为6cm,求圆锥的体积和侧面积(取π=
3.14)。
解:
计算体积V:V = (1/3)πr²h = (1/3) × 3.14 × 4² × 6 = 100.48cm³
计算侧面积S:S = πrl = 3.14 × 4 × 7.21 = 90.19cm² (根据勾股定理,r² + h² = l²,计算得到l≈7.21cm)
所以,圆锥的体积为100.48cm³,侧面积为90.19cm²。
总结:
通过上述练习题的解答,我们可以熟悉圆柱和圆锥的计算方法,包括体积和表面积的计算公式。
掌握这些知识,有助于我们在实际问题中应用,解决相关的计算和分析。
希望同学们通过练习和理解,对圆柱和圆锥的性质有更深入的认识和应用能力提升。
